实验1 超精密车床振动控制系统设计
数控机床振动的抑制与系统精度的优化调整

动 的状 态 。机 床 刚性 好 , 静动摩 擦力 小 , 电动机轴 与滚 珠 丝杠 轴连接 的 同轴度 高 , 动机 就 能很 轻 松地 驱 动 电 工作 台移 动 , 样测 出来 的 频率 响应 图 就很 好 ; 之 , 这 反
数 控 机床 振 动 的抑 制 与 系统 精 度 的优 化调 整
朱 仕 学
( 深圳 职业技 术 学院 , 东 深圳 5 8 5 ) 广 10 5
摘
要 : 控机床 的振 动和 加工精 度都 可 以通 过 系统 调试 软 件 加 以 改善 。本 文 以 F N 数 A UC 系统 为例 对 系统
共振 宽 度 大 约 分 别 为 10 H 0 z和 10 H , S V O 2 z 在 E R G I E参数 菜单 里找 到 “ 波 器 ” 然 后 打 开 “ 除共 UD 滤 , 消
女 深圳市科技计划项 目( J20 190 0 15 K 0 S2 0 00 0 5 )
; u 幂朋 ‘訾 ’ b 年
1 抑 制 振 动 的调 整
F N C S V O G I E有 个 重 要 的 功 能 , A U E R U D 即测 量
机床频率 响应 。它 的原理 是通 过 S V O G IE 生成 E R UD
以下程序 :
G91 4 G9
Nl 0. 0 0F1 0. 0 0 G01 X1 O 0 2 00 G04 X0. 1 N9 9GO1 9 X一1 0 0 0. 0 0F1 0 0 00 2 0. 0 M9 9
超精密数控机床控制系统技术方案

超精密数控机床控制系统技术方案1、系统组成超精密数控机床系统主要有三个部分:主轴、横向进给机构、纵向进给机构。
其平面布局如图1所示。
图1 超精密数控机床平面布局示意图主轴由空气磁力轴承支承,用带有变频器的电动机驱动,功率为1500W;横向进给机构与纵向进给机构均采用花岗石滑台与方导轨结构,各由一台伺服电动机直接驱动滚珠丝杠带动滑台在导轨上移动,电动机功率为850W。
2、技术要求(1) 横、纵向进给的操作采用手柄式控制开关操作(十字选择开关,中间有快速选择按钮)。
(2) 进给的速度可调(最小为2mm/min),可实现自动/手动进给,移动精度为0.1μm。
(3) 横、纵向的移动应有锁定开关。
(4) 主轴旋转可调速50-1800r/min(60Hz达到1800r)采用无级变速,且有相对的转速指示。
(5) 主轴旋转的起、停均需有缓冲过程(慢爬、慢停),主轴旋转应有保护电路,断电时应缓慢停止旋转。
(6) 气压保护,控制机床的正常运转(0.4MPa),低于设定值时机床不能工作(或停止工作)。
(7) 电源、气源有正常工作灯指示。
(8) 其余要求按常规机床实施。
有电控箱、人机对话控制台、手柄式控制进给操作手柄组成。
3、系统功能需求3.1 主轴(1)无级变速,要求50~1800转;(2)启停应有一个过渡过程(即从慢到快启动,从快到慢停止);(3)转速设定;3.2横向进给机构(4)任意位置停止锁定;(5)移动距离设定;(6)设置快速移动操作手柄;3.3纵向进给机构(1)任意位置停止锁定;(2)移动距离设定;(3)设置快速移动操作手柄;3.4控制面板(1)主轴转速设定、显示;(2)横向进给量设定、显示;(3)纵向进给量设定、显示;(4)纵横向进给手动控制;(5)电源总快关3.5系统整体(1)主轴中心线位置定位(原点、二次定位点)(2)刀具轨迹程序编制4、控制系统解决方案4.1 硬件解决方案根据数控机床的功能需求与技术要求,拟定其控制系统硬件解决方案如图2所示。
基于降维观测器的超周密车床振动操纵

现代操纵理论基础上机实验报告之一基于降维观测器的超周密车床振动操纵院系自动操纵原理课程设计专业航天学院自动化专业姓名班级学号指导教师强盛哈尔滨工业大学2021年6月16日一:降维观测器设计的工程背景简介在实验一中针对亚微米超周密车床的振动操纵系统,咱们采纳全状态反馈法设计了操纵规律。
可是在工程实践中,传感器一样只能测量基座和床身的位移信号,不能测量它们的速度及加速度信号,因尔后两个状态变量不能取得,换句话说全状态反馈很难真正实现。
为了解决那个问题,本实验设计一个降维(2维)状态观测器,用来解决状态变量 2x 、3x 的估量问题,从而真正实现全状态反馈操纵。
二:实验目的通过本次上机实验,使同窗们熟练把握:降维状态观测器的概念及设计原理;线性系统分离原理的内涵;进一步熟悉极点配置及状态反馈操纵律的设计进程;MATLAB 语言的应用三:闭环系统的性能指标要求闭环系统渐近稳固;降维观测器渐近稳固。
四:实际给定参数假设某一亚微米超周密车床隔振系统的各个参数为:01200N /m k =980N /A e k = kg 120=m 2.0=c Ω300=R H 95.0=L五:操纵系统的开环状态空间模型u x x x x x x⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡1008.3155.109.3157100010321.3.2.1[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=321006.8x x x y 六:降维观测器方程的推导进程设⎥⎦⎤⎢⎣⎡=21l l L ,那么带入1222LA A -可得: ⎥⎦⎤⎢⎣⎡----=-8.3155.101211222l l LA A211212225.108.315)8.315(l l l LA A I +++++=+-λλλ (1) 将降维观测器极点配置在-180,-180,那么:32400360)'(2++=λλλf(2)(1)式与(2)式对应项系数相等,即: ⎩⎨⎧=++=+324005.108.3153608.315211l l l (3) 解(3)求得:⎩⎨⎧==14.184312.4421l l易知:u B y L x LA A x 21222)('++-=(4)将L 带入(4)式得:u y x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡---=1014.184312.44'8.31564.1844112.44'令:⎩⎨⎧-=-=Ly x z y L x z ''(5) 将(5)带入(4)式,可得:u x z ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡---=108.31564.1844112.44u y z ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡---=105.66356745.164778.31564.1844112.44七:基于降维观测器的状态反馈操纵律设计依如实验1已得出状态反馈操纵律为3218.1975.19341.11342x x x u +--=(6) 此刻应当改成'8.197'5.19341.11342321x x x u +--=)14.18431(8.197)2.44(5.19341.1134212111x z x z x +++--=121492.35488328.1975.1934x z z ++-=至此,整个闭环系统的方程能够写为:)492.35488328.1975.1934(1008.3155.109.3157100010121321.3.2.1x z z x x x x x x ++-⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡)492.35488328.1975.1934(105.66356745.164778.31564.1844112.44121x z z y z z ++-⨯⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡---=八:闭环系统数字仿真给定初始条件:51(0)610m x -=⨯,52(0)210m/s x -=⨯,523(0)0.810m/s x -=-⨯,21(0) 1.810z -=⨯,2(0)6z =。
现代控制理论大作业-基于MATLAB的机床主动减振系统仿真
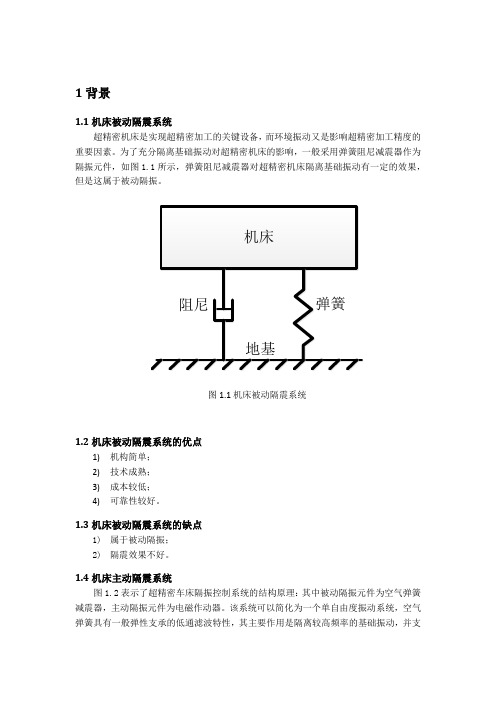
1背景1.1机床被动隔震系统超精密机床是实现超精密加工的关键设备,而环境振动又是影响超精密加工精度的重要因素。
为了充分隔离基础振动对超精密机床的影响,一般采用弹簧阻尼减震器作为隔振元件,如图1.1所示,弹簧阻尼减震器对超精密机床隔离基础振动有一定的效果,但是这属于被动隔振。
图1.1机床被动隔震系统1.2机床被动隔震系统的优点1)机构简单;2)技术成熟;3)成本较低;4)可靠性较好。
1.3机床被动隔震系统的缺点1)属于被动隔振;2)隔震效果不好。
1.4机床主动隔震系统图1.2表示了超精密车床隔振控制系统的结构原理:其中被动隔振元件为空气弹簧减震器,主动隔振元件为电磁作动器。
该系统可以简化为一个单自由度振动系统,空气弹簧具有一般弹性支承的低通滤波特性,其主要作用是隔离较高频率的基础振动,并支承机床系统;主动隔振系统具有高通滤波特性,其主要作用是有效地隔离较低频率的基础振动。
主、被动隔振系统相结合可有效地隔离整个频率范围内的振动。
地基ss0图1.2 机床主动隔震系统其中:m——机床质量c——空气弹簧粘性阻尼系数k0——空气弹簧刚度系数s——机床位移s0——地基位移1.5系统性能指标闭环系统单位阶跃响应的:超调量不大于5%;过渡过程时间不大于0.5秒。
2系统建模床身质量的运动方程为:其中:pF——空气弹簧所产生的被动控制力F——作动器所产生的主动控制力a假设空气弹簧温度恒定,则被动控制力可以表示为:其中:主动控制力可近似线性化地表示为:其中:其中,电枢电流Ia满足微分方程:其中:1.性能指标:闭环系统单位阶跃响应的:超调量不大于5%;过渡过程时间不大于0.5秒( =0.02)2.实际给定参数:某一车床的已知参数3.开环系统状态空间数学模型的推导过程: 对式0y s s =-两边求二次导,.....011()({1[/()]})n p a r r r e e e a y s F F c y k y p V V A y A k I m m==-+=-++-++对上式再求一次导,()01e a y cy k y k I m η=-+++其中1/()r r r e ep V V A y A η⎧⎫''⎡⎤=-+⎨⎬⎣⎦⎩⎭则I a=−my +cy +k 0y+ηK a,又由I a=−my +cy +k 0y+ηK a,代入Li̇a +RI a +E (I a ,ẏ)=u(t)00(,)()a e emy cy k y my cy k y LR E I y u t k k ηη++++++--+=,即Lmy ⃛+(Lc +Rm )ÿ+(Lk 0+Rc )ẏ+Rk 0y +Lω+Rω−k 0E (I a ,ẏ)=−k e u(t)令状态变量为x 1=y,x 2=ẏ,x 3=ÿ,得系统开环的状态方程为:1223003123e x x x x Rk Lk Rc k Lc Rm x x x x uLm Lm Lm Lm ⎧⎪=⎪=⎨⎪++⎪=----⎩ 于是状态空间表达式为:[]1122003312301000010100e x x x x uRkLk Rc x k Lc Rm x Lm Lm Lm Lm x y x x ⎧⎡⎤⎡⎤⎪⎢⎥⎢⎥⎡⎤⎡⎤⎪⎢⎥⎢⎥⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎢⎥⎢⎥⎪⎢⎥⎢⎥⎢⎥⎢⎥++⎪⎣⎦⎣⎦----⎢⎥⎢⎥⎨⎣⎦⎣⎦⎪⎪⎡⎤⎪⎢⎥=⎪⎢⎥⎪⎢⎥⎣⎦⎩代入系统参数,用MATLAB 求解得: 系统矩阵A 为:.[]112233123010000103157.8910.53315.798.60100x x x x u x x x y x x ⎧⎡⎤⎡⎤⎡⎤⎡⎤⎪⎢⎥⎢⎥⎢⎥⎢⎥=+⎪⎢⎥⎢⎥⎢⎥⎢⎥⎪⎢⎥⎢⎥⎢⎥⎢⎥----⎪⎣⎦⎣⎦⎣⎦⎣⎦⎨⎡⎤⎪⎢⎥⎪=⎢⎥⎪⎢⎥⎪⎣⎦⎩3稳定性分析3.1李雅普诺夫第一法:用eig()函数,求得系统特征值为3个特征值均有负实部,故系统是稳定的。
数控车床的振动切削试验系统设计

太阳能电池行业英语词汇A,Ampere的缩写, 安培a-Si:H, amorphous silicon的缩写, 含氢的, 非结晶性硅.Absorption, 吸收.Absorption of the photons:光吸收;当能量大于禁带宽度的光子入射时,太阳电池内的电子能量从价带迁到导带,产生电子——空穴对的作用,称为光吸收。
Absorptions coefficient, 吸收系数, 吸收强度.AC, 交流电.Ah, 安培小时.Acceptor, 接收者, 在半导体中可以接收一个电子. Alternating current, 交流电,简称“交流. 一般指大小和方向随时间作周期性变化的电压或电流. 它的最基本的形式是正弦电流. 我国交流电供电的标准频率规定为50赫兹。
交流电随时间变化的形式可以是多种多样的。
不同变化形式的交流电其应用范围和产生的效果也是不同的。
以正弦交流电应用最为广泛,且其他非正弦交流电一般都可以经过数学处理后,化成为正弦交流电的迭加。
AM, air mass的缩写, 空气质量.直射阳光光束透过大气层所通过的路程,以直射太阳光束从天顶到达海平面所通过的路程的倍数来表示。
当大气压力P=1.013巴,天空无云时,海平面处的大气质量为1。
amorphous silicon solar cell:非晶硅太阳电池(a—si 太阳电池)用非晶硅材料及其合金制造的太阳电池称为非晶硅太阳电池,亦称无定形硅太阳电池,简称a—si太阳电池。
Angle of inclination, 倾斜角,即电池板和水平方向的夹角,0-90度之间。
Anode, 阳极, 正极.BBack Surface Field, 缩写BSF, 在晶体太阳能电池板背部附加的电子层, 来提高电流值.Bandbreak, 在半导体中, 价带和导带之间的空隙,对于半导体的吸收特性有重要意义.Becquerel, Alexandre-Edmond, 法国物理学家, 在1839年发现了电池板效应.BSF, back surface field的缩写.Bypass-Diode, 与太阳能电池并联的二极管, 当一个太阳能电池被挡住, 其他太阳能电池产生的电流可以从它处通过.CCadmium-Tellurium, 缩写CdTe; 位于II/VI位的半导体, 带空隙值为1,45eV, 有很好的吸收性, 应用于超薄太阳能电池板, 或者是连接半导体.Cathode, 阴极,或负极,是在电池板电解液里的带负电的电极,是电池板电解液里带电粒子和导线里导电电子的过渡点。
超精密装置PID振动控制系统的设计与动(论文)

摘要在仿生啄木鸟头部独特生物构造和隔振机理的基础上,采用主动隔振技术建立了超精密装置隔振系统结构及动力学模型。
结合超精密装置隔振系统的结构特点和性能要求,采用闭环PID主动控制系统,用MATLAB软件进行了仿真分析研究。
仿真分析结果表明,该振动控制系统宽频率范围内具有良好的减振效果,该系统可应用于超精密测量、超精密制造设备的隔振领域。
关键词:超精密装置;仿生学;主动振动控制;PID控制ABSTRACTTo keep the ultra-precision device from the micro-disturbance of environment, a structure and kinetic model of a vibration control system were established with a passive air-spring which reduces vibrations of high-frequency area and a giant magneto strictive actuator which reduces those of low-frequency area, which is imitative of the isolation mechanics and special organic texture of woodpecker’s brain. In consideration of complex vibration environment and nonlinear ultra-precision device, a closed loop PID active control system was adopted. The system was simulated by Matlab. Results of simulations show that the control system can effectively restrain the disturbance whose frequency range form 0-100 Hz. It can be applied to the vibration isolation field of the ultra-precision measuring and manufacturing device.Key words:ultra-precision device; bionics; active vibration control; PID control目录1 概述 (1)2 超精密装置隔振系统模型 (2)2.1超精密装置隔振系统结构模型 (2)2.2 超精密装置隔振系统的动力学模型........... 错误!未定义书签。
实验1_超精密车床振动控制系统设计

THE END
17
ke = 980N/A
m = 120kg
c = 0.2
R = 300Ω
L = 0.95H
12
闭环系统的性能指标
闭环系统单位阶跃响应的: 超调量不大于5%; 过渡过程时间不大于0.5秒( ∆ = 0.02 )。
13
实验内容
建立车床振动系统的开环状态空间模型; 根据时域设计指标求出闭环极点的希望位置; 求出状态反馈控制律的数学表达式; 编写MATLAB程序,对闭环系统进行单位阶跃 响应的数字仿真,并检验设计指标; 撰写实验报告。
14
实验报告要求
(1)封面格式如下 )
(A4纸单面打 纸单面打 左侧装订) 印、左侧装订)
15
(2)报告正文内容 ) 1. 系统的工程背景及物理描述; 2. 实验目的; 3. 性能指标; 4. 实际给定参数; 5. 开环系统状态空间数学模型的推导过程;
16
6. 状态反馈控制律的设计过程,包括指标转换 和极点配置等内容; 7. 闭环系统数字仿真的MATLAB编程,包括源 程序和单位阶跃响应的仿真曲线(也可以用 simulink仿真工具); 8. 实验结论及心得(包括性能指标的检验)。
4
工程背景的物理描述
工件
床身 作动器 空气弹簧 作动器 地基
5
s
传感器
床身 m
s0
k0
c
地 基
G
控制器
传感器
m c k0 G
机床质量 空气弹簧粘性阻尼系数 空气弹簧刚度系数
s s0
机床位移 地基位移
6
主动隔振系统作动器(不表示参数)
上图表示了亚微米超精密车床隔振控制 系统的结构原理,其中被动隔振元件为空气 弹簧,主动隔振元件为采用状态反馈控制策 略的电磁作动器。 上图表示一个单自由度振动系统, 空气弹簧具有 一般弹性支承的低通滤波特性,其主要作用是隔离较 高频率的基础振动,并支承机床系统;主动隔振系统 具有高通滤波特性,其主要作用是有效地隔离较低频 率的基础振动。主、被动隔振系统相结合可有效地隔 离整个频率范围内的振动。
超精密机床的主动隔振系统研究_王加春

位移小 、力较大
金属相变
响应慢 ,
柔性智能结构
位移 、力较大
磁致效应
响应快 ,
柔性智能珩架
位移 、力大
流体相变
响应快 , 力较大
主动阻尼
液压传动 响应中等 , 大型土木结构 位移 、力很大
气压传动 响应中等 ,
车辆减振
位移大 、力较大
电气传动
响应快 ,
位移 、力较大
通用型
图 3 磁致伸缩作动器结构简图 1 —压紧螺母 ;2 —压紧弹簧 ;3 —外套 ;4 —线圈 ; 5 —永久磁铁 ;6 —Terfenol-D 棒 ;7 —高渗透性铁 ;8 —基座
本文以哈尔滨工业大学自行研制的 HCM- I 型超 精密车床为背景 ,研究了超精密机床的主动隔振 。
1 力学模型的建立
响合起来看成是外扰力 p 对机床的影响 。建立机床 的隔振系统力学模型如图 2 所示 。m 为机床质量 , k 为 空气弹簧刚度 , c 为空气弹簧阻尼 , f 为作动器作动 力。
图 2 机床隔振系统力学模型
质量 m 的运动方程为 :
m¨x1 + k ( x1 - x0) + c ( x1 - x0) = p + f
(1)
的影响也可忽略掉 。
2 作动器的选择
为了简化分析 ,可以把电机与主轴质量偏心的影
Ξ 收稿日期 :1999 - 11 - 01 修改稿收到日期 :1999 - 11 - 30 第一作者 王加春 男 ,博士研究生 ,讲师 ,1968 年 1 月生 。
APPROXIMATE ANALYTICAL SOL UTION OF WAVEFORM DISTORTION OF UL TRA-LOW FREQUENCY STANDARD VIBRATOR
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图5 全状态响应Simulink仿真框图
仿真前设定初值 , 的响应曲线如下图6所示:
图6 状态变量响应曲线
从仿真曲线可以看出,参考输入为零时,状态变量最后趋于零,满足稳定要求。
8.实验结论及心得
本次实验以实际系统为物理背景,主要包括建立系统模型,根据指标选定闭环极点进而设计状态反馈控制律,最后通过MATLAB仿真进行指标检测这几个主要步骤。本次实验选择的参数达到了系统指标的要求,调整时间小于0.5秒,超调量约为2.2%。
●控制系统机理建模
●时域性能指标与极点配置的关系
●状态反馈控制律设计
●MATLAB语言的应用
●4个知识点
3.性能指标
闭环系统单位阶跃响应的:
●超调量不大于5%
●过渡过程时间不大于0.5s(Δ=0.02)
4.实际给定参数
5.开环系统状体空间数学模型的推导过程
床身质量的运动方程为:
(1)
其中:
为空气弹簧所产生的Βιβλιοθήκη 动控制力 为作动器所产生的主动控制力
假设空气弹簧内为绝热过程,则被动控制力可以表示为:
(2)
其中:
为标准压力下的空气弹簧体积 为空气弹簧的参考压力 为相对位移(被控制量) 为参考压力下单一弹簧的面积 为参考压力下空气弹簧的总面积 为绝热系数
电磁作动器的主动控制力与电枢电流、磁场的磁通量密度及永久磁铁和电磁铁之间的间隙面积有关,这一关系具有强非线性。由于系统工作在微振动状况,且在低于作动器截止频率的低频范围内,因此主动控制力可近似线性化地表示为:
通过本次实验,我在一定程度上了解了《现代控制理论基础》课程介绍的状态空间法在实际工程中的应用,并掌握了部分控制系统建模、控制规律设计与系统仿真的应用技巧,加深了对状态反馈内容的理解,进一步熟练了Simulink在状态反馈中的应用。
最后感谢老师对实验内容的精心设计。
图2单自由度振动系统
图2表示一个单自由度振动系统,空气弹簧具有一般弹性支承的低通滤波特性,其主要作用是隔离较高频率的基础振动,并支承机床系统;主动隔振系统具有高通滤波特性,其主要作用是有效地隔离较低频率的基础振动。主、被动隔振系统相结合可有效地隔离整个频率范围内的振动。
2.实验目的
通过本次上机实验,使同学们熟练掌握:
这种被动隔振方法难以满足超精密加工对隔振系统的要求。为了解决这个问题,有必要研究被动隔振和主动隔振控制相结合的混合控制技术。其中,主动隔振控制系统采用状态空间法设计,这就是本次上机实验的工程背景。
图1隔振控制系统的结构原理
图1表示了亚微米超精密车床隔振控制系统的结构原理,其中被动隔振元件为空气弹簧,主动隔振元件为采用状态反馈控制策略的电磁作动器。
(3)
其中:
为力-电流转换系数 为电枢电流
满足微分方程:
(4)
其中:
为控制回路电枢电感系数 为控制回路电枢电阻
为控制回路反电动势 为控制电压
将式(2)、(3)带入式(1),得:
设 为常值干扰,则易得: 。
上式可记为:
(5)
对式(5)两边求导得:
(6)
其中:
将式(5)、(6)代入式(4),消去 得
将非线性部分 、 视为系统噪声,在建模时忽略,则上式可化为:
设系统的状态控制律为:
则其状态方程:
可知:
将参数代入解方程组,得:
综上,控制律为
系统的闭环传递函数为:
7.闭环系统Simulink仿真
(1)通过状态反馈后的阶跃响应Simulink仿真框图如下图3所示:
图3 阶跃响应Simulink仿真框图
示波器仿真输出结果如下图4所示:
图4 阶跃响应
从阶跃响应曲线可以看出,调整时间小于0.5秒,超调量约为2.2%,满足了所要求的性能指标。
现代控制理论基础
上机实验报告之一
亚微米超精密车床振动控制系统
的状态空间法设计
院系
专业
姓名
班号
指导教师
哈尔滨工业大学
2013年5月8日
1.系统的工程背景及物理描述
超精密机床是实现超精密加工的关键设备,而环境振动又是影响超精密加工精度的重要因素。为了充分隔离基础振动对超精密机床的影响,目前国内外均采用空气弹簧作为隔振元件,并取得了一定的效果,但是这属于被动隔振,这类隔振系统的固有频率一般在2Hz左右。
(7)
设状态变量:
根据式(7)可列出系统状态方程如下:
6.状态反馈控制律的设计过程
系统 的能空性判别矩阵为:
,所以系统完全能观,可以用状态反馈实现极点任意配置。
根据系统指标,由公式:
求得 , ,所以 。为留有余量,取 , 。
此时系统的闭环极点 。为使其为主导极点,设第三个极点 。此系统的特征多项式为:
