工程断裂力学第三章new
第三章 断裂力学与断裂韧度

定义
也就是G表示弹性应变能的释放率或者为裂纹扩展力。 也就是 表示弹性应变能的释放率或者为裂纹扩展力。 表示弹性应变能的释放率或者为裂纹扩展力 因为G是裂纹扩展的动力,当G达到怎样的数值时, 达到怎样的数值时, 因为 是裂纹扩展的动力, 是裂纹扩展的动力 达到怎样的数值时 裂纹就开始失稳扩展呢? 裂纹就开始失稳扩展呢 按照Griffith断裂条件 断裂条件G≥R R=γs 按照 断裂条件 γ 按照Orowan修正公式 修正公式G≥R R=2(γ s+γ p) 按照 修正公式 γ γ
如对无限大平板内中心含有穿透K 如对无限大平板内中心含有穿透 1为
因此, 线弹性断裂力学并不象传统力学那样 , 单 因此 , 线弹性断裂力学并不象传统力学那样, 纯用应力大小来描述裂纹尖端的应力场, 纯用应力大小来描述裂纹尖端的应力场 , 而是同 时考虑应力与裂纹形状及尺寸的综合影响。 时考虑应力与裂纹形状及尺寸的综合影响。 教材p67 教材
其研究结果在当时并未引起重视
对于大多数金属材料, 对于大多数金属材料 , 虽然裂纹尖端由于应力集中 作用, 局部应力很高, 作用 , 局部应力很高 , 但是一旦超过材料的屈服强 就会发生塑性变形。 在裂纹尖端有一塑性区, 度 , 就会发生塑性变形 。 在裂纹尖端有一塑性区 , 材料的塑性越好强度越低, 材料的塑性越好强度越低 , 产生的塑性区尺寸就越 裂纹扩展必须首先通过塑性区, 大 。 裂纹扩展必须首先通过塑性区 , 裂纹扩展功主 要耗费在塑性变形上, 要耗费在塑性变形上 , 金属材料和陶瓷的断裂过程 不同,主要区别也在这里。 不同,主要区别也在这里。
工作应力σ<许用应力 工作应力 许用应力[σ] 许用应力
即认为是安全的
塑性材料 脆性材料
断裂力学第三章

KI − iKII = 2 2π lim z − aφ′(z)
z→a
KI − iKII = 2 2πξ[φ′(z) + ic]
σ x +σ y = 4 Re[φ′(z)]
KI − iKII 2 Re σ x +σ y = ξ 2π
y z
1
ξ
=
1 reiθ KI
= = =
Re Re
ξ
iKII
ξ
−θ 2 2 cos θ − KI siniKII σ x σσ y+ σ = (KI Re KII + = ) x yπr 2 ξ2 2π 2
ξ
r
θ
P
x
−a
o
a
§3.2 复变函数法计算K 复变函数法计算K
§3.2 复变函数法计算K 复变函数法计算K
弹性力学平面问题的复变函数解法回顾
复应力函数 Φ(x, y) = Re[ zφ(z) + ∫ψ (z)dz] 应力组合的复势表示 σ y +σ x = 4 Re[φ′(z)]
σ y −σ x + 2iτ xy = 2[zφ′′(z) +ψ ′(z)] 位移组合的复势表示
§3.3 加权残差法
子域法
选取权函数为
1 Wi = 0 在子域Vi内 在子域Vi外 i =1, 2, L, N
残差方程变为
∫
Vi
R(x)dV = 0
子域法把域V分割成 个子域 子域法把域 分割成N个子域,在每个子域内近 分割成 个子域, 似解残差的算术平均值为零
§3.3 加权残差法
工程断裂力学课件3弹塑性断裂力学(EPFM)简要

第三章弹塑性断裂力学(EPFM)简要§3-1 Dugdale方法(D-M模型)§3-2 裂纹尖端张开位移CTOD(COD)定义及准则§3-3 COD 与K1的一致性§3-4 COD准则的应用34COD§3-5 J 积分的定义及守恒性§3-5-1 J 积分的定义§3-5-2 J 积分的守恒性§3-6 线弹性条件下J 与K的关系§3-7 在弹塑性条件下J 与CTOD的关系常见的定义有以下几种:(1)弹塑性交界线与裂纹表面的交界点处的张开位移看作CTOD。
对D-M模型描述的裂纹,经Paris等人的工作,Well 在1965年用大量试验得出,可以用裂纹尖端的CTOD ()作为表征裂纹δ弹塑性应力应变场的单一参数,当此参数值达到材料的临界值,材料就会发生开裂。
即为开裂准则。
使用这一准则必须解决两个问题:(1)使用小试样能方便准确地测量出材料稳定(与外载荷裂纹尺寸及裂纹几何的关系(即cδδ=的开裂参数;(2)建立裂纹尖端的与外载荷、裂纹尺寸及裂纹几何的关系(即的表达式)。
c δδ(,,)f p a Y δ=试验表明用TPB 、CT 等小试样可以实现,试验证明开裂点的是材料常数,但失稳扩展点的不是常数!换句话说,CTOD 只是开裂判据,不是破坏判据!c δc δδGB/T 2358-1994对的测试方法做了详尽的说明,本课不讲实验测试(大家要c c δ用时,严格按标准的要求技术细节做即可,不用讲了就忘了)。
CTOD 方法在中低强度钢压力容器和管道,即焊接结构等方面在工程上有广泛应用它的优点是方法简单直观易测缺点是定义不明确理论依据不足用。
它的优点是方法简单、直观,易测,缺点是定义不明确,理论依据不足。
§3-5 J 积分的定义及守恒性3-5JJ 积分是J.R .Rice在1968年提出的,并由此建立了弹塑性断裂力学的另一个方法。
断裂力学精品文档

一、引例
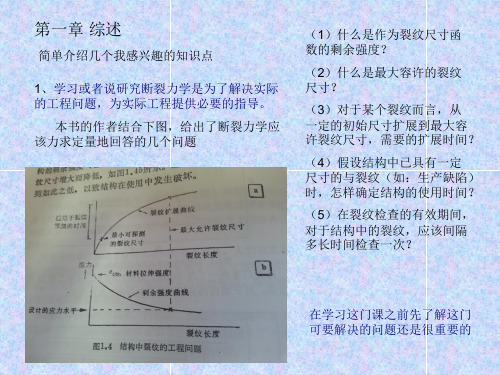
第一章 绪 论
s
s s [s ]
s
2a
2b
s
2a
s
s max
s
1
2
a b
Inglis(1913)
s
?
第一章 绪论
用分子论观点计算出绝大部分固体材 料的强度103MPa,而实际断裂强度 100MPa?
裂力学,断裂动力学和界面断裂力学。
五、断裂力学的任务
第一章 绪论
1.研究裂纹体的应力场、应变场与位移场,寻 找控制材料开裂的物理参量;
2.研究材料抵抗裂纹扩展的能力——韧性指标 的变化规律,确定其数值及测定方法;
3.建立裂纹扩展的临界条件——断裂准则;
4.含裂纹的各种几何构形在不同载荷作用下, 控制材料开裂物理参量的计算。
一、Griffith理论
3.Griffith理论
s
1) b厚度板开裂前后应变能增量
V
s 2 πa2b A2ab πs 2 A2
E
4Eb
A:裂纹单侧自由表面面积
2a
2)表面自由能
ES 4ab 2A
s
V ES πs 2 A 2
A A 2Eb
2.2 断裂力学的能量方法
一、Griffith理论
4.1954年1月10日英国大型喷气民航客机彗星号坠 落,同时期共三架坠落;
第一章 绪论
二、工程中的断裂事故
5.1958美国北极星号导弹固体燃料发动机壳体爆 炸;
6.1969年11月美国F3左翼脱落; 7.1972年我国歼5坠毁; 8.近年来桥梁、房屋、锅炉和压力容器、汽车等
断裂力学总结
平面应变状态下的裂纹扩展阻力(R)曲线的
GⅠ GⅠC
GⅠ 裂纹扩展的动力
GⅠC 平面应变情况下裂纹扩展的阻力率
R GⅠ
1
2
GⅠC
A
C
GⅠ
1 2
E
KⅠ2
KⅠ a
GⅠ
1 2 E
2a
若 一定,则G与a的关系
1、若给定外载荷,则可求得相应情况下的临界裂纹尺寸 2、若给定裂纹尺寸,则可判断在一定载荷作用下,结构
G Ua 1 Ua A A B a
Ua
1 2
P
cP
C为弹性体的柔度 c ca
d 0 d pdc cdP 0
dU a
1 2
Pd
1 dP 2
1 cPdP 2
1 2
p 2 dc
G Ua 1 p2 c A A 2B a
2a
P
2、恒载荷情况
dU a
A cos C cos 0
A
(
1)sin B sin
C D
( 1)sin sin 0
0
B ( 1) cos D ( 1) cos 0
线性齐次方程组有非零解,系数行列式为零,解之,得:
sin 2 0
这种方法的得到的结果为级数形式,敛散性没法确定,且远端的边 界条件不好代入。课本上的方法克服以上缺点但应力函数在未知的 条件下比较难找。
2a
裂纹平板的总能量为
U
U0
Ua
Ur
U0
2a2 E
4a e
dU 0 且
da
dU0 0 da
d da
2a2 E
4a e
0
2 E
2a
4
断裂力学(优质课件)

材料不是完美无瑕的
绪论
工程材料都有缺陷(先天— 夹杂、夹渣、瑕疵、空洞、裂缝
后天— 冶炼、加工、制造、安装、使用)
材料中的宏观尺寸缺陷—这里通称为裂纹(尖裂纹或钝裂纹)。
由于材料有缺陷,材料的自身强度是理论强度的1/10-1/100;
由于材料有缺陷,材料在受力后会在缺陷处产生严重的应力集中;
由于材料有缺陷,材料会在某种应力作用下产生亚临界裂纹扩展,材料对
研究20的21/重6/1要6 方向)。因此断裂研究有重大的经济和社会意义 。
5
绪论
尽管社会不断发展,断裂问题仍层出不穷
多少世纪来,人们积累了大量有关断裂的现象和经验,但一般的解决方法就 是替换,换新的或找更强的材料代替,对断裂的认识停留在现象上。18世纪以来随 着工业的发展,对构件需求和要求更高,开始探索断裂理论,以材料力学为代表的
理论、 模型等随后提出几十个。但随着新材料(如高强度钢)新工艺(如焊接)的 发展,断裂问题仍层出不穷。Why ? 这一方面说明断裂问题的复杂性,另一方面说 明,已有的断裂理论还解决不了全部问题。 上世纪中,在现代工业发展和战争的的 推动下,人们对断裂现象认识的进一步深化,对材料强度、缺陷、位错、应力集中 等理论研究不断深入,断裂力学终于在1957年应运而生,成为学科,且已经在生产 和设计中发挥重大作用,并继续承受检验。
什么是断裂力学?
断裂力学是一门研究含裂纹物体,裂纹的启裂、扩展到断裂的宏观过程及断裂
条2件021的/6/科16学。
6
绪论
● 代表人物
谈到断裂力学发展,它归功很多人,有三个人值得我们特别提出,他们是:
Inglis, Griffith, Irwin.
Inglis 把缺陷看成材料内部的小孔, 1913年理论计算了无限大板中心椭圆孔
第三章 断裂力学与断裂韧度11

b. 另一方面,K1c和G1c虽然都是材料固有的性能,但从实验测 定来说,K1c更容易些,因此多数材料在各种热处理状态下所 给出的是K1c的实验数据。 但是,G判据的物理意义更加明确,便于接受,所以两者既是 统一的,由各有利弊。
引言
二、从选材方面考虑,对材料与裂纹的关系提出的问题
➢什么材料比较不容易萌生裂纹? ➢什么材料可以允许比较长的裂纹存在而不发生断裂? ➢什么材料抵抗裂纹扩展的性能比较好? ➢怎样冶炼、加工和热处理可以达到最佳的效果?
第一节 材料的断裂理论
一、理论断裂强度
假设:理想的、完整的晶体 理论断裂强度σc :在外加正应力作用下,将晶体的两
➢平面应力:指所有的应力都在一个平面内,平面应力问题 主要讨论的弹性体是薄板,薄壁厚度远远小于结构另外两个 方向的尺度。薄板的中面为平面,所受外力均平行于中面面 内,并沿厚度方向不变,而且薄板的两个表面不受外力作用。 ➢平面应变:指所有的应变都在一个平面内。平面应变问题 比如压力管道、水坝等,这些弹性体是具有很长的纵向轴的 柱状物体,横截面大小和形状沿轴线长度不变,作用外力与 纵向轴垂直,且沿长度不变,柱体的两段受固定约束。
几种常见裂纹的应力强度因子
(1)对无限大平板中心有穿透裂纹
几种常见裂纹的应力强度因子
(2)对无限大平板,板的一侧有单边裂纹
(3)对有限宽平板,中心有穿透裂纹 Y是2a/w的函数,可由图中实线所示查出
几种常见裂纹的应力强度因子
(4)对有限宽平板,板的两侧有双边裂纹
Y也是2a/w的函数,但由图中虚线所查出
清华大学断裂力学讲义第三章-线弹性断裂力学PPT课件

III型裂纹的复变函数表示方法 为了统一
应力场 位移场
32 i 31 ZIII
u3 Im ZIII
III型中心裂纹承受远场均匀剪切
lim
r0
2
r
22 12
r,0
r,
0
32
r
,
0
KI,II,III与G之间的关系?
George Rankine Irwin
G.R. Irwin. Analysis of stresses and strains near the end of a crack traversing a plate. Journal3of Applied Mechanics 24, 361-364 (1957).
a
0 i2
x1,
0
ui
a
x1,
dx1
wtip a
5
如果不是固定位移载荷加载(如固定力),是何结论?
可由能量平衡来理解
F
裂纹扩展
Gda dU Fd
逐渐放松保持力过程
wtip da dU Fd
F
这种假设裂纹闭合张开的虚拟过程的分析仍然适用。
x2
x2
σ
x1
首先假设固定位移加载
针对III型裂纹
x2
A
B
σ
x1
a
x2
u
u
x1
a
KIII
lim
x1 0
2 x1 32 x1, 0
32 x1, 0
KIII
2 x1
u3 u3+ a x1, u3- a x1, =2u3+ a x1, =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a 当 =0 c
形状因子
从上述例子可见,强度因子总是与载荷成正比 (这里指单向加载的拉伸应力或集中力),而且在均 匀拉伸下,恒有 K = Yσ πa 的形式。这里Y是与载荷 无关,而与几何变数(裂纹长度或位置、物体形状等) 有关的量,故称为几何因子或形状因子(geometric factor)。
3-5 叠加原理及其应用
线弹性力学的本构关系是线性的,因此, 裂纹问题的应力强度因子可以利用叠加原理来 求得。下面举例介绍叠加原理在求应力强度因 子方面的几种应用。
半椭圆形表面裂纹
Fσ πa KA = Φ
a a 1.8+ c a 1.10 + 5.2× (0.5)5a / c × ( ) 当 >0 B c F = 1.12 − 0.23( a ) +10.6( a )2 − 21.71( a )3 + 30.38( a )4 B B B B
K=
2
π
σ πa
椭圆裂纹的应力强度因子
K=
σ πa
Φ
a 2 sin θ + 2 cos θ c
2 2
1/ 4
Φ为第二类椭圆积分:
Φ=∫
π /2
0
c −a 2 sin Φ dΦ 1 − 2 c
2 2
1/ 2
在短轴的端点,K有最大值。在长轴的端点,K有最小值。
2 3 4
圆孔萌生的单边裂纹—工程近似解的应力强度因 子
无限大平板的圆孔萌生了一条穿 透板厚的裂纹,裂长为L。若平板受 到无穷远处的均匀拉伸,当L<<R时, 应力强度因子的上限为:
K = 1.12(3σ ) πL
若裂纹较长,则下限用 :
K = σ π ( R + L / 2)
圆孔萌生的双边裂纹—工程近似解的应力强度因 子
有限宽的长条板有中心裂纹,受到无穷远处的均 匀拉伸的应力强度因子
πa K = σ πa sec h
有限宽的长条板有单边裂纹,受到无穷远处的均 匀拉伸的应力强度因子
a K = σ πa f h a a a a a f = 1.12 − 0.23 + 10.6 − 21.71 + 30.38 h h h h h a << h K = 1.12σ πa
Kt =1+ 2
a
ρ
a为椭圆的长半轴,ρ为椭圆长轴端点的曲率半径。
应力奇异性
由于a大于ρ,所以Kt恒大于3,即椭圆应力集中的 程度比圆孔问题严重。若是短轴长趋于零,则ρ也将 趋于零,此时应力集中系数Kt 将趋于无限大。在没有 特别说明的情况下,断裂力学所指的裂纹,其裂端的 曲率半径是为零的;在不受力的情况下,上下两个裂 纹面是互相接触的。因此,裂纹即裂端曲率半径趋于 零时的椭圆孔,其裂端有无限大应力。
我们的兴趣不在于得到精确的应变场形式,而在于知道应变 分量也只由应力强度因子来确定。
I型裂纹的位移场
通过应变一位移关系,经过复杂的计算,可以得到裂端区的 位移场为:
θ θ r 2µu = KI (κ −1) + 2sin 2 cos 2 2 2π
1/ 2
θ θ r 2µv = KI (κ +1) − 2cos2 sin 2 2 2π
σx =
+高次项
在裂端区,即r足够小的情形下,式中r的高次项比首项小得 多,因而可以忽略 。
I型裂纹的应变场
从上式可见,裂端区应力场的形式恒定,其强度完全由KI值的 大小来决定,因此就称KI为I型裂纹的应力强度因子 应力强度因子。裂端区的应 变场可以由弹性力学公式求得为:
εij =
KI fij (θ ), i, j = x, y 2πr
Griffith裂纹的应力强度因子
K = σ πa
无限大平板有中心裂纹,裂纹表面受到均匀拉伸 应力作用的应力强度因子
K = σ πa
无限大平板有中心裂纹,裂纹表面某处受到一对 集中拉力P(单位厚度集中力)作用 的应力强度 因子
P KA = πa P KB = πa a+b a −b a −b a+b
裂纹的应力强度因子
应力强度因子的值由载荷、裂纹数目、长度和位置 以及物体的几何形状等共同决定。它的单位是 [ 力 ]•[ 长 度 ]-3/2 。 常 用 单 位 为 制 的 百 万 牛 顿 • 米 3/2(MN/m3/2)或用公制的公斤力•毫米-3/2。
由于I型裂纹是最主要的裂纹型,下面介绍一些标 准裂纹问题,给出实验室常用试件和工程零构件最常 见I型裂纹的应力强度因子(用K表示)。
1/ 2
这里 u和 v分别为x和y方向的位移分量,μ是剪切模量,κ与 泊松比ν的关系为:
ν 3− 4 κ = 3−ν 1+ν
平面应力 平面应变
II型和III型裂纹
对于II型和III型裂纹,裂端 区的应力场和位移场的形式也是恒 定的,而且其表达式与I型裂纹相 似。II型和III型裂纹的应力强度 因子分别用KII和KIII表示。由于II 型裂纹也是平面问题,可采用上面 的坐标系来描述,而且只有应力分 量σx 、σy 和τxy 存在。III型裂 纹问题是反平面剪切问题,位移分 量仅有z方向的w,应力分量仅有 τxz 和τyz 。
2 3 4
有限宽的长条板有单边裂纹,受到无穷远处的纯 弯曲的应力强度因子
设 则
σ = 6M / h2
a K = σ πa f h
a a a a a f = 1.12 − 1.40 + 7.33 − 13.08 + 14.0 h h h h h a << h K = 1.12σ πa
1/ 2
θ θ r 2µu = KII (κ +1) + 2cos2 sin 2 2 2π θ θ r 2µv = KII − (κ −1) + 2sin 2 cos 2 2 2π
1/ 2
III型裂纹的应力场和位移场
习题
当应力奇异性是由r-n来决定时,n就称为应力奇异 性的指数。当线弹性体的裂纹端点具有指数n为1/2的 应力奇异性时,试由量纲分析着手,证明裂端区的应 变能将是有界的。若要裂端区的应变能有界,能否反 过来从数学上证明应力奇异性指数不得大于或等于1?
3-4 常见裂纹的应力强度因子
应力强度因子可以用来表征裂纹端点区应力应变场强 度的参量,因此,在工程应用前,首先要计算应力强度因 子。计算应力强度因子有解析法和数值法两种,前者包括 应力函数法、积分变换法、契合问题解法等等;后者包括 有限单元法、边界元法、边界配置法等。 从五十年代中期以来,已建立了许多的计算应力强度 因子的方法,对很多常见裂纹问题的应力强度因子已汇集 成手册。因此,可以根据手册的结果,作一定的简化和近 似后,来解决工程问题。
3-1 裂纹的基本型
一般将裂纹问题分为三种基本型,如图所示
张开型
滑移型
撕裂型
裂纹基本型
第一种称为张开型(opening mode)或拉伸型(tension mode),简称I型。其裂纹面的位移方向是在使裂纹张开的裂纹面 法线方向(y方向)。它通常发生在载荷和几何形状对称于裂纹平面 的情形,例如Griffith裂纹是I型裂纹,其裂纹的扩展方向是正前 方(x方向)。若物体是均匀厚度的平板,裂纹贯穿板厚,则问题 是二维的(平面问题);若物体不是平板或者裂纹没有贯穿板厚, 则是三维问题。许多工程上常见的断裂都是I型裂纹的断裂,这也 是最危险的裂纹类型。
应力是看不见的,它是个抽象的概念,然 而位移过程是可以看到的。物体上个别点(无 限远处除外)具有无限大的应力并不会使该点 的位移趋于无限。因此,裂端具有无限大应力 是允许的。同时可以证明,这并不影响裂端区 应变能的有界。
三种基本裂纹型裂端区某点的应力值、应变值、 位移值和应变能密度值都由应力强度因子及其位置来 决定。因此,只要知道应力强度因子,裂端区的应力、 应变、位移和应变能密度就都能求得。由于有这一特 点,应力强度因子可以作为表征裂端应力应变场强度 的参量。近代断裂力学,就是Irwin在五十年代中期提 出了应力强度因子的概念,认识到它的意义后才开始 发展起来的。
II型裂纹的应力场和位移场
θ θ θ KII 3 sin 2 + cos cos 2 2 2 2πr KII θ θ 3 θ σy = sin cos cos 2 2 2 2πr σx = τ xy =
KII θ θ 3 θ cos 1−sin sin 2 2 2 2πr
KIII θ τ xz = − sin 2 2πr KIII θ τ zy = cos 2 2πr
θ 2KIII r w= sin µ 2π 2
1/ 2
思考题
如图所示的坐标系, I型和II型裂纹的裂端 区应力场在裂纹表面有 何特点?在裂纹正前方 又分别有何特点?裂端 区位移分量在裂纹表面 和正前方又有何特点?
第三章
应力强度因子
断裂发生时在裂纹端点要释放出多余的能量,因此, 裂端区的应力场和应变场必然与此裂端的能量释放率有关。 若裂端应力应变场的强度(intensity)足够大,断裂即可 发生,反之则不发生。因此,得到裂端区应力应变场的解 析解是个关键。 近代断裂力学是用弹性力学的解析方法来完成这一工 作的,而这些解析法需要用高深的数学工具,这对于初次 接触断裂力学的读者来说,是比较困难的。因此,本章只 给出一些主要的概念和结果,并介绍一些工程近似方法。
K = σ π ( R + ( L1 + L2 ) / 2)
圆裂纹的应力强度因子
又称为钱币裂纹(pennyshaped crack),是三维的I 型裂纹问题,裂纹表面呈圆形。 假设受到垂直裂纹表面的拉伸 应力,当弹性体的体积远大于 圆裂纹尺寸,且拉伸应力为均 布时,圆周上每一点的应力强 度因子(精确解)为 :
