2017-2018年四川省雅安中学高二上学期期中数学试卷及解析(理科)

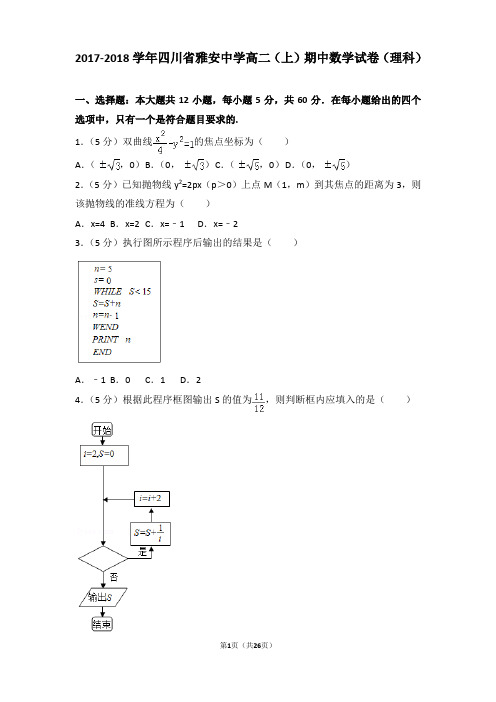
2017-2018学年四川省雅安中学高二（上）期中数学试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个是符合题目要求的.1．（5分）双曲线的焦点坐标为（）A．（，0）B．（0，）C．（，0）D．（0，）2．（5分）已知抛物线y2=2px（p＞0）上点M（1，m）到其焦点的距离为3，则该抛物线的准线方程为（）A．x=4 B．x=2 C．x=﹣1 D．x=﹣23．（5分）执行图所示程序后输出的结果是（）A．﹣1 B．0 C．1 D．24．（5分）根据此程序框图输出S的值为，则判断框内应填入的是（）A．i≤8？B．i≤6？C．i≥8？D．i≥6？5．（5分）椭圆3x2+ky2=1的一个焦点的坐标为（0，1），则其离心率为（）A．2 B．C．D．6．（5分）已知抛物线y2=2px（p＞0）的准线与圆x2+y2﹣6x﹣7=0相切，则p的值为（）A．B．1 C．2 D．47．（5分）不论k为何值，直线y=kx+1与焦点在x轴上的椭圆+=1恒有公共点，则实数m的取值范围是（）A．（0，1） B．（0，7） C．[1，7） D．（1，7]8．（5分）直线l1：kx﹣y﹣3=0和l2：x+（2k+3）y﹣2=0互相垂直，则k=（）A．﹣3 B．﹣2 C．﹣或﹣1 D．或19．（5分）若关于x的方程=x+m有两个不同实根，则实数m的取值范围是（）A．（2，2）B．[）C．（）D．（]10．（5分）椭圆=1上存在n个不同的点P1，P2，…，P n，椭圆的右焦点为F．数列{|P n F|}是公差大于的等差数列，则n的最大值是（）A．16 B．15 C．14 D．1311．（5分）直线l经过点P（2，3），且与两坐标轴的正半轴交于A，B两点，则△OAB（O为坐标原点）面积的最小值为（）A．B．25 C．12 D．2412．（5分）如图，已知A（﹣2，0），B（2，0），等腰梯形ABCD满足|AB|=2|CD|，E为AC上一点，且．又以A、B为焦点的双曲线过C、D、E三点．若，则双曲线离心率e的取值范围为（）A．B．C．D．二.填空题：本大题共4小题，每小题5分，共20分.13．（5分）斜率为1的直线l被圆x2+y2=4x截得的弦长为4，则l的方程为．14．（5分）执行如图所示的框图，输出值x=．15．（5分）已知{（x，y）|（m+3）x+y=3m﹣4}∩{（x，y）|7x+（5﹣m）y﹣8=0}=∅，则直线（m+3）x+y=3m+4与坐标轴围成的三角形面积是．16．（5分）已知椭圆C：=1，设直线l：y=x+m（m∈R）与椭圆C交于不同两点A、B，且|AB|=3．若点P（x0，2）满足||=||，则x0=．三、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）（1）直线l经过点A（﹣2，3）且与直线l0：x+2y﹣3=0平行，求直线l的方程；（2）已知直线m的方程为（a+1）x+ay﹣3a=0（a∈R），求坐标原点O到m的距离的最大值．18．（12分）F1、F2分别为等轴双曲线C的左、右焦点，且f2到双曲线C的一条渐近线的距离为1，（1）求双曲线C的标准方程；（2）P是双曲线C上一点，若•=0，求△PF1F2的面积．19．（12分）已知圆C圆心在直线3x﹣y=0上，且经过点A（2，﹣3），B（﹣1，0）（1）求圆C的标准方程；（2）若点P（x，y）在圆C上，求的取值范围．20．（12分）已知动点P（x，y）到点F（1，0）的距离比到直线x=﹣3的距离小2，（1）求动点P（x，y）的轨迹方程；（2）若直线l过点M（m，0）（m＞0）且与P的轨迹交于A，B两点，则是否存在常数m使得=5恒成立？若存在，求出常数m，不存在，说明理由．21．（12分）已知椭圆C与曲线x2﹣=1有相同的焦点，且过直线x+y﹣6=0上一点M（1）当椭圆C长轴最短时，求其标准方程；（2）过点P（1，2）的直线与（1）中椭圆C交于A、B两点，若P恰好是AB 的中点，求直线AB的方程．22．（12分）已知椭圆C：=1（a＞b＞0）上的任一点到焦点的距离最大值为3，离心率为，（1）求椭圆C的标准方程；（2）若P，Q为曲线C上两点，O为坐标原点，直线OP，OQ的斜率分别为k1，k2且k1k2=﹣，求直线PQ被圆O：x2+y2=3截得弦长的最大值及此时直线PQ的方程．2017-2018学年四川省雅安中学高二（上）期中数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个是符合题目要求的.1．（5分）双曲线的焦点坐标为（）A．（，0）B．（0，）C．（，0）D．（0，）【解答】解：∵双曲线的方程为，∴a2=4，b2=1，可得c==由此可得双曲线的焦点坐标为（±，0）故选：C．2．（5分）已知抛物线y2=2px（p＞0）上点M（1，m）到其焦点的距离为3，则该抛物线的准线方程为（）A．x=4 B．x=2 C．x=﹣1 D．x=﹣2【解答】解：∵抛物线方程为y2=2px，过M（1，m），则p＞0，∴抛物线焦点为F（，0），准线方程为x=﹣，又∵点M（1，m）到其焦点的距离为3，∴p＞0，根据抛物线的定义，得1+=3，∴p=4，∴准线方程为x=﹣2．故选：D．3．（5分）执行图所示程序后输出的结果是（）A．﹣1 B．0 C．1 D．2【解答】解：模拟程序的运行，可得n=5，s=0满足条件s＜15，执行循环体，s=5，n=4满足条件s＜15，执行循环体，s=9，n=3满足条件s＜15，执行循环体，s=12，n=2满足条件s＜15，执行循环体，s=14，n=1满足条件s＜15，执行循环体，s=15，n=0此时，不满足条件s＜15，退出循环，输出s的值为0．故选：B．4．（5分）根据此程序框图输出S的值为，则判断框内应填入的是（）A．i≤8？B．i≤6？C．i≥8？D．i≥6？【解答】解：模拟程序的运行，可得i=2，S=0满足条件，执行循环体，S=，i=4满足条件，执行循环体，S=+，i=6满足条件，执行循环体，S=++=，i=8由题意，此时，应该不满足条件，退出循环，输出S的值为．结合选项，可得判断框内应填入的是：i≤6．故选：B．5．（5分）椭圆3x2+ky2=1的一个焦点的坐标为（0，1），则其离心率为（）A．2 B．C．D．【解答】解：由题意，b2=，a2=∴c2=﹣=1，∴k=∴e2=k=∴e=故选：D．6．（5分）已知抛物线y2=2px（p＞0）的准线与圆x2+y2﹣6x﹣7=0相切，则p的值为（）A．B．1 C．2 D．4【解答】解：抛物线y2=2px（p＞0）的准线方程为，因为抛物线y2=2px（p＞0）的准线与圆（x﹣3）2+y2=16相切，所以故选：C．7．（5分）不论k为何值，直线y=kx+1与焦点在x轴上的椭圆+=1恒有公共点，则实数m的取值范围是（）A．（0，1） B．（0，7） C．[1，7） D．（1，7]【解答】解：把直线y=kx+1代入椭圆+=1化为（m+7k2）x2+14kx+7﹣7m=0（m≠7，m＞0）．∵直线y=kx+1与椭圆+=1有公共点，∴m+7k2≠0，△=（14k）2﹣4（m+7k2）（7﹣7m）≥0恒成立．化为1﹣m≤7k2．上式对于任意实数k都成立，∴1﹣m≤0，解得m≥1．焦点在x轴上的椭圆+=1，m＜7．∴实数m的范围是[1，7）．故选：C．8．（5分）直线l1：kx﹣y﹣3=0和l2：x+（2k+3）y﹣2=0互相垂直，则k=（）A．﹣3 B．﹣2 C．﹣或﹣1 D．或1【解答】解：∵直线l1：kx﹣y﹣3=0和l2：x+（2k+3）y﹣2=0互相垂直∴k﹣（2k+3）=0∴k=﹣3故选：A．9．（5分）若关于x的方程=x+m有两个不同实根，则实数m的取值范围是（）A．（2，2）B．[）C．（）D．（]【解答】解：分别作出函数y=，y=x+m的图象．可知：直线y=x+m经过点A（﹣2，0），B（0，2）时，与半圆y=相交于两点，m=2．当直线与半圆相切时，可得=2，m＞0，解得m=2．因此当时，直线与半圆有且只有两个交点．即关于x的方程=x+m有两个不同实根．故选：B．10．（5分）椭圆=1上存在n个不同的点P1，P2，…，P n，椭圆的右焦点为F．数列{|P n F|}是公差大于的等差数列，则n的最大值是（）A．16 B．15 C．14 D．13【解答】解：∵（|P n F|）min≥|a﹣c|=，（|P n F|）max≤a+c=3，||P n F|=|P1F|+（n﹣1）d∵数列{|P n F|}是公差d大于的等差数列，∴d=＞，解得n＜10+1，则n的最大值为15故选：B．11．（5分）直线l经过点P（2，3），且与两坐标轴的正半轴交于A，B两点，则△OAB（O为坐标原点）面积的最小值为（）A．B．25 C．12 D．24【解答】解：∵过A、B两点的直线方程l为+=1（a＞0，b＞0）；且点P在直线AB上，∴+=1；△AOB的面积为S=ab，∵+=1，∴2≤+=1，∴ab≥24，当且仅当=，即a=4、b=6时取“=”；∴a=4，b=6时，△AOB的面积取得最小值S=12，故选：C．12．（5分）如图，已知A（﹣2，0），B（2，0），等腰梯形ABCD满足|AB|=2|CD|，E为AC上一点，且．又以A、B为焦点的双曲线过C、D、E三点．若，则双曲线离心率e的取值范围为（）A．B．C．D．【解答】解：如图，以AB的垂直平分线为γ轴，直线AB为x轴，建立直角坐标系xOγ，则CD⊥γ轴．因为双曲线经过点C、D，且以A、B为焦点，由双曲线的对称性知C、D关于γ轴对称，设c为双曲线的半焦距（c=2），依题意，记，h是梯形的高，由定比分点坐标公式得，．设双曲线的方程为，则离心率，由点C、E在双曲线上，将点C、E坐标和代入双曲线的方程，得，①．②由①式得，③将③式代入②式，整理得，故由题设得，，解得，所以，双曲线的离心率的取值范围为[]．故选：A．二.填空题：本大题共4小题，每小题5分，共20分.13．（5分）斜率为1的直线l被圆x2+y2=4x截得的弦长为4，则l的方程为y=x ﹣2．【解答】解：由题意设直线方程是y=x+b，则由，得：2x2+（2b﹣4）x+b2=0，故x1+x2=2﹣b，x1x2=，故弦长为•=4，即•=4，故（b+2）2=0，解得：b=﹣2，故直线方程是：y=x﹣2，故答案为：y=x﹣2．14．（5分）执行如图所示的框图，输出值x=12．【解答】解：模拟程序框图的运行过程，如下；x=1是奇数，则x+1=2是偶数，x+2=4，4+1=5是奇数，则5+1=6，6+2=8，8+1=9是奇数，9+1=10，10+2=12＞8；输出x=12．故答案为：12．15．（5分）已知{（x，y）|（m+3）x+y=3m﹣4}∩{（x，y）|7x+（5﹣m）y﹣8=0}=∅，则直线（m+3）x+y=3m+4与坐标轴围成的三角形面积是50．【解答】解：由题意得：直线（m+3）x+y=3m﹣4与直线7x+（5﹣m）y﹣8=0平行，∴斜率相等，∴﹣（m+3）=﹣，∴m=4，或m=﹣2，由于m=4时两直线重合，故m=﹣2，∴直线（m+3）x+y=3m﹣4即x+y=﹣10，它们与坐标轴围成的三角形面积是：50．故答案为50．16．（5分）已知椭圆C：=1，设直线l：y=x+m（m∈R）与椭圆C交于不同两点A、B，且|AB|=3．若点P（x0，2）满足||=||，则x0=﹣1或﹣3；．【解答】解：设A（（x1，y1），B（x2，y2）由得4x2+6mx+3m2﹣12=0．，|AB|=，解得m=±2，当m=2时，AB的中点M（﹣）则有，得x0=﹣3，同理可得当m=﹣2时，得x0=﹣1故答案为：﹣1或﹣3；三、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）（1）直线l经过点A（﹣2，3）且与直线l0：x+2y﹣3=0平行，求直线l的方程；（2）已知直线m的方程为（a+1）x+ay﹣3a=0（a∈R），求坐标原点O到m的距离的最大值．【解答】解：（1）设与直线l0：x+2y﹣3=0平行的直线l的方程为：x+2y+m=0，把点A（﹣2，3）代入可得：﹣2+6+m=0，解得m=﹣4．可得直线l的方程为：x+2y﹣4=0．（2）直线m的方程为（a+1）x+ay﹣3a=0（a∈R），化为：a（x+y﹣3）+x=0，令，可得．可得直线m恒过定点B（0，3），故原点O到直线m的距离d≤|OB|=3，∴O到直线m的距离的最大值为3．18．（12分）F1、F2分别为等轴双曲线C的左、右焦点，且f2到双曲线C的一条渐近线的距离为1，（1）求双曲线C的标准方程；（2）P是双曲线C上一点，若•=0，求△PF1F2的面积．【解答】解：（1）由题意可设双曲线的方程为x2﹣y2=a2，F2（a，0）到一条渐近线：y=x的距离为=1，即a=1，则双曲线C的标准方程为x2﹣y2=1；（2）P是双曲线C上一点，若•=0，可得PF1⊥PF2，设|PF1|=m，|PF2|=n，由双曲线的定义可得|m﹣n|=2a=2，①又m2+n2=8a2=8，②①2﹣②可得mn=2，则△PF1F2的面积为mn=1．19．（12分）已知圆C圆心在直线3x﹣y=0上，且经过点A（2，﹣3），B（﹣1，0）（1）求圆C的标准方程；（2）若点P（x，y）在圆C上，求的取值范围．【解答】解：（1）∵圆C圆心在直线3x﹣y=0上，且经过点A（2，﹣3），B（﹣1，0），设圆心C（a，b），∴，解得a=﹣1，b=﹣3．∴r==3，∴圆C的标准方程为：（x+1）2+（y+3）2=9．…（6分）．（2）∵点P（x，y）在圆C上，A（2，2），∴k AP=，当AP与切线AD重合时，取最小值，当AP与切线AB重合时，k AP=取最大值，设过A（2，2）的圆C的切线为y﹣2=k（x﹣2），即kx﹣y﹣2k+2=0，圆心C（﹣1，﹣3）到切线的距离d==3，解得k=，∴k AD=，切线AB⊥x轴，∴的取值范围：[，+∞）．…（12分）．20．（12分）已知动点P（x，y）到点F（1，0）的距离比到直线x=﹣3的距离小2，（1）求动点P（x，y）的轨迹方程；（2）若直线l过点M（m，0）（m＞0）且与P的轨迹交于A，B两点，则是否存在常数m使得=5恒成立？若存在，求出常数m，不存在，说明理由．【解答】解：（1）根据题意，点M到点F（1，0）的距离比它到直线x=﹣3的距离小1，即点M到点F（1，0）的距离与其到直线x=﹣1的距离相等，则点M的轨迹为抛物线，且其焦点为F（1，0），准线为x=﹣1，则其轨迹方程为y2=4x；（2）设直线l方程为：x=ky+m，代入P（x，y）的轨迹方程可得：y2﹣4my﹣4=0，其中△＞0，设A（x1，y1），B（x2，y2），∴y1•y2=﹣4m，x1•x2=m2，由=5知x1x2+y1y2=m2﹣4m=5，∴m=5（舍去负值），故存在常数m=5使得=5恒成立．21．（12分）已知椭圆C与曲线x2﹣=1有相同的焦点，且过直线x+y﹣6=0上一点M（1）当椭圆C长轴最短时，求其标准方程；（2）过点P（1，2）的直线与（1）中椭圆C交于A、B两点，若P恰好是AB 的中点，求直线AB的方程．【解答】解：（1）曲线x2﹣=1的焦点为（﹣2，0），（2，0），设椭圆方程为：+=1（a＞b＞0），求得其焦点为：F1（﹣2，0），F2（2，0），设F2（2，0）关于x+y﹣6=0的对称点F2'（m，n），由，解得m=6，n=4，即有F2'（6，4），则2a=|MF1|+|MF2|=|MF1|+|MF2'|≥|F1F2'|==4，可得椭圆C长轴最短时a=2，b===4，则椭圆C的标准方程为+=1；（2）由P（1，2），+＜1，可得P在椭圆内，设A（x1，y1），B（x2，y2），可得+=1，+=1，相减可得+=0，由题意可得x1+x2=2，y1+y2=4，即有k AB==﹣=﹣=﹣，则直线AB的方程为y﹣2=﹣（x﹣1），即为2x+5y﹣12=0．22．（12分）已知椭圆C：=1（a＞b＞0）上的任一点到焦点的距离最大值为3，离心率为，（1）求椭圆C的标准方程；（2）若P，Q为曲线C上两点，O为坐标原点，直线OP，OQ的斜率分别为k1，k2且k1k2=﹣，求直线PQ被圆O：x2+y2=3截得弦长的最大值及此时直线PQ的方程．【解答】解：（1）∵椭圆C：=1（a＞b＞0）上的任一点到焦点的距离最大值为3，离心率为，∴，解得a=2，c=1，b=，∴椭圆C的方程为：．…（2分）（2）设P（x1，y1），Q（x2，y2），直线PQ与圆O：x2+y2=3的交点为M，N．①当直线PQ⊥x轴时，Q（x1，﹣y1），由，得或，此时|MN|=2=2．…（4分）②当直线PQ与x轴不垂直时，设直线PQ的方程为y=kx+m，联立，消y得：（4k2+3）x2+8kmx+4m2﹣12=0，△=64k2m2﹣4（4k2+3）（4m2﹣12）=48（4k2﹣m2+3），，，…（6分）∴y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2=k2•+km•+m2=，由k1k2=，得==﹣，整理，得：，此时．圆O：x2+y2=3的圆心到直线PQ的距离为d=，…（8分）∴|MN|=2，∴|MN|2=4（3﹣）=4（3﹣）=4[3﹣]=4+，所以当k=0，m=时，|MN|最大，最大值为，综合①②知，直线PQ被圆O：x2+y2=3截得弦长的最大值为，此时，直线PQ的方程为y=．…（12分）。