巴蜀中学高2012级11-12学年(下)第一次月考——数学理
巴蜀中学高2012级10-11学年(下)第一次月考——物理

重庆巴蜀中学高2012级高二(下)第一次月考试物理试题卷命题人:高亚浩一、选择题(本题包括10小题,每小题5分。
每小题只有一个....选项符合题意)1.以下说法正确的是:( )A.某品牌电视机铭牌“220V,100W”是指电视机上加的最大电压是220VB.当穿过闭合电路中的磁通量为零时,闭合电路中感应电动势一定为零C.日光灯镇流器的作用是工作时维持灯管两端有高于电源的电压,使灯管正常工作D.变压器低压线圈匝数少,电流大,导线粗2.如图所示,把矩形闭合线圈放在匀强磁场中,线圈平面与磁感线平行,下面能使线圈产生感应电流的是:()A.线圈以ab边为轴做匀速转动B.线圈以bc边为轴做匀速转动C.线圈沿磁感线方向做匀加速运动D.线圈沿垂直磁感线方向做匀速运动3.如图所示,把电阻、电感线圈、电容器并联接到某一交流电源上,三个电流表的示数相同。
若保持电源电压不变,而将频率加大,则三个电流表的示数I1、I2、I3的大小关系是()A.I1=I2=I3B.I1>I2>I3C.I2>I1>I3D.I3>I1>I24.如图所示,金属杆ab以恒定的速率v在光滑的平行导轨上向右滑行,设整个电路中总电阻为R(恒定不变),整个装置置于垂直于纸面向里的匀强磁场中,下列说法不正确的是()A.ab杆中的电流与速率v成正比B.磁场作用于ab杆的安培力与速率v成正比C.电阻R上产生的电热功率与速率v平方成正比D.外力对ab杆做功的功率与速率v的成正比5.如图14所示,A、B、C是相同的白炽灯,L是自感系数很大、电阻很小的自感线圈,今将S闭合,下面说法正确的是()A.B、C灯同时亮,A灯后亮B .A 、B 、C 同时亮,然后A 灯逐渐暗,最后灭 C .A 灯一直不亮,只有B 和C 灯亮D .A 、B 、C 灯同时亮,并且亮暗没有变化6.如图12所示,两根和水平方向成α角的光滑平行的金属轨道,上端接有可变电阻R ,下端足够长,空间有垂直轨道平面的匀强磁场,磁感强度为B ,一根质量为m 的金属杆从轨道上由静止滑下,经过足够长的时间后,金属杆的速度会趋近于一个最大速度m v ,不计轨道电阻,则:( ) A .如果B 增大,m v 将变大 B .如果α变小,m v 将变大 C .如果R 变大,m v 将变大 D .如果m 变小,m v 将变大7.如图所示,竖直面内的虚线上方是一匀强磁场B ,从虚线下方竖直上抛一正方形线圈,线圈越过虚线进入磁场,最后又落回原处,运动过程中线圈平面保持在竖直平面内,不计空气阻力,则( )A .上升过程克服磁场力做的功大于下降过程克服磁场力做的功B .上升过程克服磁场力做的功等于下降过程克服磁场力做的功C .上升过程克服重力做功的平均功率于下降过程中重力的平均功率D .上升过程克服重力做功的平均功率小于下降过程中重力的平均功率8.如图甲所示,线圈A 、B 紧靠在一起,当给线圈A 通以如图乙所示的电流(规定由a 进入b 流出为电流正方向)时,则电压表的示数变化情况(规定电流由c 进入电压表为正方向)应为下列图中的( )9.多数同学家里都有调光台灯、调速电风扇,过去是用变压器来实现上述调节的,缺点是成本高、体积大、效率低,且不能任意调节灯的亮度或风扇的转速,现在的调光台灯、调速电风扇是用可控硅电子元件来实现调节的,如图所示为一个经过双向I -IA B C D-U U -U UU -U可控硅电子元件调节后加在电灯上的电压,即在正弦交流电的每一个21周期中,前面的41被截去,从而改变了电灯上的电压.则现在的电灯上的电压为:( ) A .m U B.2m UC. 2m UD. 4m U10.如图所示,两平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab 、cd 与导轨构成闭合回路且都可沿导轨无摩擦滑动.两棒ab 、cd 的质量之比为2:1.用一沿导轨方向的恒力F 水平向右拉棒cd ,经过足够长时间以后( ) A .棒ab 、棒cd 都做匀速运动 B .棒ab 上的电流方向是由a 向b C .棒cd 所受安培力的大小等于32FD .两棒间距离保持不变二、实验题(本题包括两个小题,共计18分)11、(9分)用如图所示的电路来验证楞次定律,在试验步骤中有重要的疏漏,主要实验步骤如下:①把电池、开关、滑动变阻器和线圈A 串联成一个电路;②把电流表和线圈B 串联成另一个电路;③接通电源,给线圈A 通电,并记下线圈A 中电流的方向,把线圈A 插入线圈B 中,停一会再取出来,当线圈A 在插入和取出的过程中,以及停止运动时,观察电流表的指针有无偏转 ,并记下指针偏转的方向;④改变线圈A 中电流的方向,按照步骤(3)重复做实验,观察电流表的指针有无偏转,并记下指针偏转的方向。
2012秋巴蜀中学初二9月月考数学试题

重庆市巴蜀中学2012-2013学年度第一学期定时作业初2014级(二上)数学试题卷命题人:胡雯雯—、选择题(每题4分.共40分)1、下列说法中①分数都是有理数②有理数和数轴上的点一一对应③16的平方根是4.④49是无理数.正确的有( )个。
A.1 B.2 C .3 D .42、下列各式中正确的是( )。
A.16=±4B.283-=- C.4)4(2-=- D. 525=±3、下列是直角三角形的有( )个 ①△ABC 中222b c a -= ②△ABC 的三内角之比为3∶4∶7 ③△ABC 的三边平方之比为1∶2∶3 ④三角形三边之比为3∶4∶5A.1B.2C.3D.44、若a =5,b =3,则15.0 的值b a .表示为( )A.10b a + B.10a b - C.10ab D.ab5、如图,图中所有四边形都是正方形,所有三角形都是直角三角形,其中最大正方形的面积为7,图中所有正方形的面积之和为( )A.7B.14C.21D.286、一根旗杆长12米,大风吹过,旗杆在B 处折断,旗杆顶端落在离底部6米的A 处,旗杆折断处离旗杆底部C 处( )米 A.4.5B.7.5C. 8D.10.57、若等腰三角形的两边长分别为32和25,那么这个三角形的周长为( ) A.21034+B.2534+C.21032+D.210322534++或8、如图,一牧童在A 处放马,牧童家在B 处,A 、B 处相距河岸的距离AC 、BD 长分别为500m 和700m 且C 、D 两地距离为500m ,天黑前牧童从A 处将马牵到河边饮水,再赶回家,那么,牧童最少要走( )A.m 29100B.1300mC.1200mD.17009、△ABC 中,AB=15,AC=13,高AD=12,则三角形的周长是( )A.42B.32C.42或32D.37或3310、x 、y 、a 满足2)1042(22020--++-+=--⋅-+a y x a y x y x y x ,则a 的值是( )A.50 B.10 C.20 D.40二、填空题(每题3分,共30分) 11、16的算术平方根是 12、下列实数中4,2,010010001.1,)12(,010101.3,216,5,5103π---,其中无理数有 个。
重庆市巴蜀中学月考(一)2024届高三数学答案

数学参考答案·第1页(共8页) 巴蜀中学2024届高考适应性月考卷(一)数学参考答案一、单项选择题(本大题共8小题,每小题5分,共40分)题号 12345678答案 C A D A B C B D【解析】1.{|13}A x x =-≤≤, {|2}B x x =≥,所以[23]A B = ,,故选C .数学参考答案·第2页(共8页)图1ln ()x f x ,则1()()ln ()0g x f x x f x x''=+< ,0,所以当01x <<时,()0g x >,当1x >时,g 时,ln 0x >,所以当)1(0x ∈,时,()0f x <. 0时,()0f x <;又()f x 为奇函数,所以当x 0>可化为09850x x <⎧⎨->⎩,或09850x x >⎧⎨-<⎩,,解得0,故选D .(本大题共4小题,每小题5分,共20分. 在每小题给出的选项中,有多项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分)题号 9 10 11 12 答案 BC AC ACD ABC【解析】A 选项错误;11()()()24P A P B P AB P ====,图2(本大题共4小题,每小题5分,共20分)13 14 15128 30数学参考答案·第3页(共8页)数学参考答案·第4页(共8页) 【解析】17.(本小题满分10分)(1)证明:1211(1)140b a a =+=++=≠,……………………………………………(1分)1222121221(1)12222(1)2n n n n n n n b a a a a a b ++++=+=++=+=+=+=,…………………(3分) ∴12n nb b +=,∴{}n b 为以4为首项,2为公比的等比数列.……………………………(5分) (2)解:由(1)知:11122142221n n n n n n b a a -++=+===- ,,∴……………………(6分) 又112212112122n n n n n a a a ++--=+=-=-,,∴……………………………………………(7分) 所以2135212462()()n n n S a a a a a a a a -=+++++++++34(12)4(12)2238.1212n n n n n n +⎡⎤⎡⎤--=-+-=--⎢⎥⎢⎥--⎣⎦⎣⎦……………………………………(10分)数学参考答案·第5页(共8页) 18.(本小题满分12分)……………………………………………………………………………………(12分)19.(本小题满分12分) (1)证明:222111AC A C AA A C AC +=⊥,,∵∴又1111111ACC A ABC ACC A ABC AC A C ACC A ⊥=⊂ 平面平面,平面平面,平面,1.A C ABC ⊥平面∴又AB ABC ⊂平面,1.A C AB ⊥∴ ………………………………………………………(4分)(2)解:由111111121222332B ACC A B ACA A ABC ABC V V V S A C AC BC A C ---====⨯⨯⨯ △133BC == BC =∴………………………………………………………………………………(5分)以C 为坐标原点,1CA CB CA,,分别为x y z ,,的正向建立空间直角坐标系,则各点坐标如下:数学参考答案·第6页(共8页)1(000)00)(00)(00C A B A ,,,,,,,, ………………………………(7分)取平面1CA B 的法向量为(100)m = ,,,设平面11A BB 的法向量为000()n x y z =,,,取111(0(0BB AA A B ===,,则01100x n BB n A B ⎧=⎪=⎨=⎪⎩,………………………………………………(10分) 设二面角11C A B B --的大小为θ,则|cos ||cos |m n θ=〈〉==,所以二面角11C A B B --的正弦值为sin θ== …………………………(12分)20.(本小题满分12分)解:(1)患病者被误诊即被判定为阴性的概率为: 197.5950.002(10095)0.5%.10095P -=⨯⨯-=- ………………………………………………(3分)(2)当[95100)c ∈,时, 95()5%0.002(10095)(15%)10095c f c -=⨯⨯⨯-+-⨯-41000.010(10095)0.002(105100)(949500)1010095c c --⎡⎤⨯⨯-+⨯-=-+⨯⎢⎥-⎣⎦,…………(6分)当[100105]c ∈,时,100105()5%0.002(10095)0.012(105100)(15%)105100105100c c f c --⎡⎤=⨯⨯-+⨯⨯-+-⨯⎢⎥--⎣⎦40.002(105100)(131400)10c -⨯⨯-=-+⨯,……………………………………………(9分)∴44(949500)10[95100)()(131400)10[100105]c c f c c c --⎧-+⨯∈⎪=⎨-+⨯∈⎪⎩,,,,,,………………………………………(10分) ()f c ∵在[95105]c ∈,单调递减,所以105c =时()f c ,最小.……………………(12分)21.(本小题满分12分)数学参考答案·第7页(共8页)数学参考答案·第8页(共8页)。
重庆巴蜀中学2020-2021学年下期高一第一次月考数学试题和参考答案

得到 cos C 3 即 C=30 ,进而 A 60 , B 90 ,由 a 3 ,得到 c 2
由 SABC
1 (a 2
b
c)r
即
33 2
= 1(3+3 2
得到 3 ( AB BC)2 75 , 4
即 ( AB BC)max 10 km (当且仅当 AB BC 时取得最值)……12 分
22、解析:(1) OA 0, 2 2e2 , OB 2, 1 2e1 e2 ,其中 e1 、 e2 是成 60 夹角的两单位向量
第4页共5页
则
选项 B : 向量 a 、 b 、 c 都为非零向量时,平行具有传递性,选项 B 正确;
选项 C : 向量 a 与 b 模长相等,但是方向不一定相同或相反,可以为任意夹角,选项 C 错误;
选项 D :
由
|
a
b
||
a
b
|
得到
a
2
2a
b
2 b
a
2
2a
b
b
2
,即 a b 0 ,选项 D 正确。
故选 BD .
10、解析:由正弦定理
a sin
A
b sin
B
知
sin
2 45
b sin
B
,得
sin
B
b 2
第1页共5页
选项 A : sin B 5 无解,选项 A 正确; 2
选项 B : sin B 1 ,恰有一解 B ,选项 B 正确; 2
选项 C : sin B 3 ,解得 B 或 B 2 ,有两解,选项 C 正确;
重庆市巴蜀中学高三数学下第一次月考试题 文
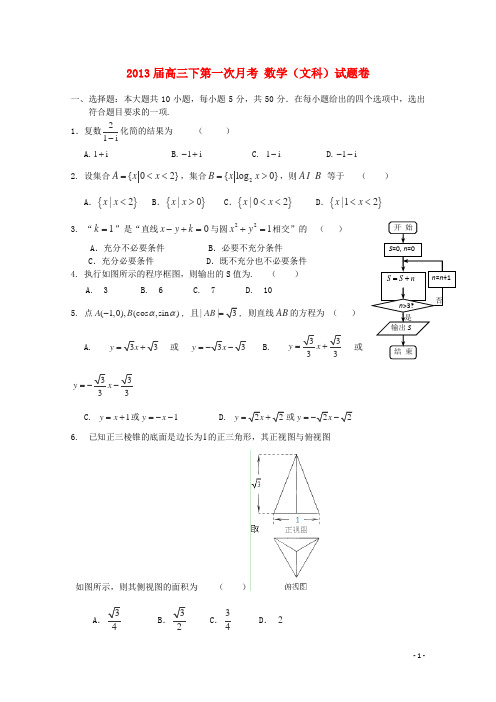
2013届高三下第一次月考 数学(文科)试题卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.复数21i-化简的结果为 ( ) A.1i + B.1i -+ C. 1i - D.1i -- 2. 设集合{02}A x x =<<,集合2{log 0}B x x =>,则A B I 等于 ( ) A .{}|2x x < B .{}|x x >0 C .{}|02x x << D .{}|12x x << 3. “1k =”是“直线0x y k -+=与圆221x y +=相交”的 ( ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 4. 执行如图所示的程序框图,则输出的S 值为. ( )A. 3B. 6C. 7D. 105. 点(1,0),(cos ,sin )A B αα-, 且||3AB =, 则直线AB 的方程为 ( )A. 33y x =+或33y x =--B. 3333y x =+或3333y x =-- C. 1y x =+或1y x =-- D. 22y x =+或22y x =-- 6. 已知正三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为 ( )A 3B 3C .34D . 2 S S n =+开 始结 束S =0, n =0输出S n =n +1n >3? 否是7. 平行四边形ABCD 中,E 为CD 的中点.若在平行四边形ABCD 内部随机取 一点M ,则点M 取自△ABE 内部的概率为 ( )ABC .12D .18. 某汽车租赁公司为了调查A ,B 两种车型的出租情况,现随机抽取这两种车型各50辆,分别统计了每辆车在某个星期内的出租天数,统计数据如下表:A 型车B 型车根据上面的统计数据,判断这两种车型在本星期内出租天数的方差的大小关系为 ( ) A .B A S S > B .B A S S <C .B A S S =D .无法判断9. 在直角三角形ABC 中,90ACB ∠=︒,2AC BC ==,点P 是斜边AB 上的一个三等分点,则CP CB CP CA ⋅+⋅=u u u r u u u r u u u r u u u r( )AB .2CD .410. 任给实数,,a b 定义, 0,, 0.a b a b a b a a b b⨯⨯≥⎧⎪⊕=⎨⨯<⎪⎩ 设函数()l n f x x x =⊕,若{}n a 是公比大于0的等比数列,且51a =,123781()()()()(=,f a f a f a f a f a a +++++L )则1___.a = ( ) A. 2e B. e C. 2 D. 1第二部分(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡上. 11. 把函数()s i n 2f x x=的图象向左平移4π个单位,所得图像的解析式是__________.12. 已知数列1,,9a 是等比数列,数列121,,,9b b 是等差数列,则12a b b +的值为 .13.已知双曲线中心在原点,一个焦点为)0,5(1-F ,点P 在双曲线上,且线段1PF 的中点坐标为(0,2),则此双曲线的方程是14. 若函数2l o g ,0,()(),0x x f x g x x >⎧=⎨<⎩是奇函数,则(8)g -=______.15. 已知c b a ,,都是正数,则2222c b a bcab +++的最大值为_________三、解答题:本大题共6小题,共75分.解答应写出文字说明,演算步骤或证明过程. 16. (本小题满分13分)已知}{n a 是公差大于零的等差数列,且212428a a a ==+,. (1)求数列}{n a 的通项公式;(2)若2na n nb a =+,求数列{}n b 的前n 项和n S .17. (本小题满分13分)某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:(1)写出,,,a b x y 的值;(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率; (ⅱ)求所抽取的2名同学来自同一组的概率.18. (本小题满分13分)已知函数2()sincos cos 1222x x xf x =+-. (1)求函数()f x 的最小正周期及单调递减区间; (2)求函数()f x 在[,]π3π42上的最小值.19. (本小题满分12分)在长方体1111ABCD-A B C D 中,12AA =AD=,E 是棱CD 上的一点. (1)求证:1AD ⊥平面11A B D ; (2)求证:11B E AD ⊥;(3)若E 是棱CD 的中点,在棱1AA 上是否存在点P , 使得DP ∥平面1B AE ?若存在,求出线段AP 的长; 若不存在,请说明理由.20. (本小题满分12分)如图,椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1(0)F c -,,2(0)F c ,.已知点2(3,)2M 在椭圆上,且点M 到两焦点距离之和为4. (1)求椭圆的方程;(2)设与MO (O 为坐标原点)垂直的直线交椭圆于,A B (,A B 不重合),求OB OA ⋅的取值范围.21. (本小题满分12分)设函数x ax x x f +-=221ln )( (1)当2=a 时,求)(x f 的最大值;(2)令)30(21)()(2≤<+-+=x xax ax x f x F ,以其图象上任意一点),(00y x P 为切点的切线的斜率21≤k 恒成立,求实数a 的取值范围: (3)当0=a 时,方程2)(x x mf =有唯一实数解,求正数m 的值.答案(2)66=MO k ,∴6-=AB k . 设直线AB 的方程:m x y +-=6,A 1B 1CBD 1C 1ADEPM。
巴蜀中学高2012级10-11学年(上)第一次月考——数学理

重庆巴蜀中学高2012级高二(上)第一次月考数 学 试 题 卷(理科)命题人:付洪健一、选择题(本题10个小题,每个5分,共50分):1.直线l 的方程是2=x ,则直线l 的倾斜角为( )A 0B 2arctanC 2π D 不存在 2.设R b a ∈,,则“b a >2”是“b a >”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件3.关于x 的不等式312<-x 的解集是( )A. {}21|<<x xB. {}21|<<-x xC. {}12|-<>x x x 或D. {}12|<>x x x 或4.直线过点(2,-3),且方向向量为(-1,2),则该直线的方程是( )A 012=-+y xB 072=--y xC 072=-+y xD 0135=-+y x5.函数)1(1622>-++=x x x x y 的最小值是( ) A 4 B 6 C 9 D 106.设a 、b 是正数,R y x ∈、且1=+b a ,22by ax A +=,2)(by ax B +=,则A 、B 的大小关系是( )A. B A ≥B.B A >C. B A ≤D. B A <7.已知两直线的方程分别为1l :0=++b ay x ,2l :0=++d cy x ,它们在坐标系中的位置如图所示,则( )A c a d b <<>,0,0B c a d b ><>,0,0C c a d b >><,0,0D c a d b <><,0,08.对一切实数x ,若不等式|2||3|+-->x x a 有解,则实数a 的取值范围是( )A 5≥aB 5-≥aC 5-<aD 5->a9.设0,()a b f x<<=,则下列不等式成立的是( )A ()()2a b f a f f +<<B ()()2a b f b f f +<<C ()()2a b f f b f +<<D ()()2a b f f f b +<< 10.若实数y x ,满足22222=++y xy x ,则22y x +的取值范围是( ) A ]12,12[+- B ]25,25[+- C ]53,53[+- D ]5,1[二、填空题(本题5个小题,每个5分,共25分):11.经过点)1,1(-和点)3,3(的直线的方程是 。
巴蜀中学高2012级11-12学年(下)第一次月考——数学文

重庆市巴蜀中学高2012级高三(下)第六次月考数学试题(文科)命题人:李水艳 杨先佑第I 卷(选择题,共50分)一.选择题(本大题共10小题,每小题5分,共50分)1.设{}11,<-==x x A R U ,{}1>=x x B ,则=B C A U ( )A .{|01}x x ≤<B .{|01}x x <≤C .{|0}x x <D .{|1}x x > 2. 函数()1)1lg(1>-+=x x y 的反函数是 ( ) A.()01101>-=+x y x B.()01101>+=-x y x C.()R x y x ∈-=+1101 D.()R x y x ∈+=-11013.已知抛物线()012>=a x a y 的焦点恰好为椭圆182422=+x y 的焦点,则=a ( ) A .161 B .81 C .8 D .164.圆()()161222=-+-y x 上到直线0543=++y x 的距离等于1的点有 ( ) A. 1个 B. 2个 C. 3个 D. 4个5.等比数列{}n a 中,已知3579a a a a 11243a =,则2911a a = ( )A .9B .3C .6D .186.将函数234sin -⎪⎭⎫⎝⎛+=πx y 的图像上各点的横坐标伸长为原来的2倍,再按向量⎪⎭⎫⎝⎛-=2,6πa 平移,所得函数图像的一个对称中心是( )A .,06π⎛⎫⎪⎝⎭B .,03π⎛⎫⎪⎝⎭C .,02π⎛⎫⎪⎝⎭D .,04π⎛⎫⎪⎝⎭7.已知y x ,满足约束条件⎪⎩⎪⎨⎧≥-≤-≤0021y x y x y , 且)0,0(>>+=b a by ax z 的最大值为4,则ba 12+最小值为 ( )A.49 B.25C. 2D. 4223+8.如图,正方体1111D C B A ABCD -中,则下列四个命题: ①P 在直线1BC 上运动时,三棱锥C AD P 1-的体积不变;②P 在直线1BC 上运动时,直线AP 与平面1ACD 所成角的大小不变; ③P 在直线1BC 上运动时,二面角C AD P --1的大小不变;④M 是平面1111D C B A 上到点D 和1C 距离相等的点,则M 点的轨迹是过1D 点的直线. 其中真命题的个数 ( )1.A 个 .B 2个 C.3个 .D 4个9.过双曲线22221(0,0)x y a b a b-=>>的左焦点(,0)(0)F c c ->,作圆2224a x y +=的切线,切点为E ,延长FE 交双曲线右支于点P ,若()12OE OF OP =+,则双曲线的离心率( ) A .102B .105C .10D .210.设()f x 是定义在R 上的偶函数,且满足(2)()0,01f x f x x +-=≤≤当时,()2x x f =, 函数()⎪⎭⎫⎝⎛-=41x k x g ,若方程()()f x g x =恰有两解,则满足条件的k 的个数为( ) 1.A 个 .B 2个 C.3个 .D 4个第II 卷(非选择题 共100分) 二.填空题(本大题共5个小题,每小题5分,共25分)11.已知向量,a b 满足:||1,||6,()2,|2|a b a b a a b ==⋅-=-则= .12.棱长为2的正方体1111D C B A ABCD -中,直线11C B 到平面11BCD A 的距离为____ 13.直线l 为曲线321213y x x x =-++的切线,则l 的斜率的取值范围是___14.如图:正四面体BCD A -中,O 为BCD ∆的重心,M 是AC 的中点,E 是 AO 的中点,则异面直线OM 与BE 所成的角的余弦值为_________ 15.数列{}n a 中,111,111++⎪⎭⎫⎝⎛+==+n a n a a n n ,数列ABDCOEM⎭⎬⎫⎩⎨⎧n a 1的前n 项和为n S ,对任意的正整数n ,k S n <恒成立,则实数k 的取值范围为___________三.解答题(本大题共6个小题,共75分。
重庆市巴蜀中学高三数学12月月考试题 理(含解析)新人教A版

重庆市巴蜀中学2015届高三12月月考【试卷综述】本试卷注重对数学基础知识、基本技能、基本思想和方法的考查,突出了对数学的计算能力、逻辑思维能力等方面的考察。
突出考查数学主干知识 ,侧重于中学数学学科的基础知识和基本技能的考查;侧重于知识交汇点的考查。
注重双基和数学思想数学方法的复习,注重运算能力思维能力的培养。
较多试题是以综合题的形式出现,在考查学生基础知识的同时,能考查学生的能力。
【题文】一、选择题:(本大题共10小题,每小题5分,共50分)【题文】1.已知集合A={1,3,4,6,7,8},B={1,2,4,5,6}则集合A ∩B 有( )个子集 A.3 B.4 C.7 D.8【知识点】集合运算;子集的概念. A1【答案】【解析】D 解析:∵ A ∩B={1,4,6},∴A ∩B 有328=个子集,故选D. 【思路点拨】求得A ∩B ,再用公式求其子集个数.【题文】2.设向量,a b 满足||15,11a b a b +=-=,则a b ⋅=( ) A.1 B.2 C.3 D.5【知识点】向量的模与与向量数量积的关系. F1 F3【答案】【解析】A 解析:因为||15,11a b a b +=-=,所以222215,a b a a b b +=+⋅+=222211,a b a a b b -=-⋅+=两式相减得:4a b ⋅=4,所以a b ⋅=1,故选A.【思路点拨】将向量的模平方,转化为向量数量积运算,再相减得结论. 【题文】3.已知a,b 为实数,命题甲:2ab b >,命题乙:110b a<<,则甲是乙的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 【知识点】充分条件;必要条件的判定. A2 【答案】【解析】B 解析:当a=2,b=1时,2ab b >,但110b a <<不成立;当110b a<<时, 20ab <,则22211ab ab ab b b a⨯>⨯⇒>成立,所以选B.【思路点拨】只需判断命题:“若甲则乙”与“若乙则甲”的真假.【题文】4.已知变量y x ,满足约束条件⎪⎩⎪⎨⎧≤-≥+≤142y x y x y ,则y x z +=3的最大值为( )A.8B.11C.9D.12 【知识点】简单的线性规划. E5【答案】【解析】B 解析:画出可行域,平移目标函数得最优解为直线y=2与x-y=1的交点(3,2)所以y x z +=3的最大值为11,故选B.【思路点拨】画出可行域,平移目标函数确定最优解即可. 【题文】5.已知()(){}3,3,,202y M x y N x y ax y a x ⎧-⎫===++=⎨⎬-⎩⎭且∅=⋂N M ,则a =( )A.-6或-2B.-6C.2或-6D.2【知识点】两个集合交集是空集的条件. A1【答案】【解析】A 解析:若∅=⋂N M ,则3232aa ⎧-=⎪⎪⎨⎪-≠-⎪⎩或32260a a a ⎧-≠⎪⎨⎪++=⎩,解得a= -6或a= -2,故选A.【思路点拨】要使∅=⋂N M ,需使:缺少点(2,3)的直线y-3=3(x-2)与直线ax+2y+a=0平行,或者直线ax+2y+a=0过点(2,3),但不与直线y-3=3(x-2)重合即可.【题文】6已知正项等比数列{}n a 满足:5672a a a +=,若存在两项n m a a ,使得14a a a n m =,则nm 41+的最小值为( ) A.23 B. 35 C. 625 D. 不存在 【知识点】等比数列的性质;基本不等式 D3 E6【答案】【解析】A 解析:设等比数列{}n a 的首项为1a ,公比为q, 7652a a a =+,则()654211122021a q a q a q q q q q ⋅=⋅+⋅∴--=∴==-或舍若()114144,66a m n m n m n m n ⎛⎫⎛⎫=+=∴+=++ ⎪ ⎪⎝⎭⎝⎭则41493554962n m m n m n ⎛⎫=++≥+=∴+≥= ⎪⎝⎭,故选A 14a =,求出m,n 的和,再结合基本不等式,即可得到答案.【题文】7设斜率为22的直线l 与椭圆()012222>>=+b a b ya x 交于不同的两点,且这两个交点在x 轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )A.33 B.12 C.22D.13【知识点】直线与圆锥曲线 H8【答案】【解析】C 解析:两个交点的横坐标为-c,c ,所以两个交点分别为,,22c c c ⎛⎫⎛⎫-- ⎪⎪ ⎪⎪⎝⎭⎝⎭,代入椭圆222212c c a b +=,两边乘以222a b 则()()()22222222222222220c b a a b b a c a c a c +==-∴--=22120122c e e a =<<∴=或,故选C. 【思路点拨】先根据题意表示出两个焦点的交点坐标,代入椭圆方程,再解有关于a 与c 的关系式即可. 【题文】8若8cos82cos8cos πππn S n +++= (*∈N n ),则在201521,,,S S S 中,正数的个数是( )A. 882B. 756C.750D. 378 【知识点】三角函数的性质 C3 【答案】【解析】B 解析:由题意可知1234223234cos,coscos,cos cos cos ,cos cos cos cos ,8888888888S S S S ππππππππππ==+=++=+++52345coscoscos cos cos88888S πππππ=++++623456cos cos cos cos cos cos ,888888S ππππππ=+++++,由三角函数值与三角函数的周期性可知前16个值中有6个正数,分别为123456,,,,,S S S S S S ,16个值为一组呈现周期性,2015为1251615⨯+,所以正数的个数为12566756⨯+=,故选B【思路点拨】由三角函数值与三角函数的周期性可知前16个值为一个周期,其16个值中有6个正数,分别为123456,,,,,S S S S S S ,类推可得结果.【题文】9已知A ,B ,C ,D 是函数()ϕω+=x y sin 一个周期内的图象上的四个点,如图所示,⎪⎭⎫⎝⎛-0,6πA ,B 为y 轴上的点,C 为图像上的最低点,E 为该函数图像的一个对称中心,B 与D 关于点E 对称,在x 轴上的投影为12π,则ϕω,的值为( )A. 3,21πϕω==B .6,21πϕω== C. 6,2πϕω== D.3,2πϕω== 【知识点】三角函数的图象与性质 C4【答案】【解析】D 解析:因为A ,B ,C ,D ,E 是函数y=sin (ωx+ ϕ)(ω>0,0<ϕ<一个周期内的图象上的五个点,如图所示,,B 为y 轴上的点,C 为图象上的最低点,E 为该函数图象的一个对称中心,B 与D 关于点E 对称,在x 轴上的投影为,所以T=4×()=π,所以ω=2,因为,所以0=sin (﹣+ ϕ),0<ϕ<,ϕ=.故选D .【思路点拨】通过函数的图象,结合已知条件求出函数的周期,推出ω,利用A 的坐标求出ϕ的值即可.【题文】10.如图,已知B 、C 是以原点O 为圆心,半径为1的圆与a 轴的交点,点A 在劣弧PQ (包括端点)上运动,其中︒=∠60POx ,OP ⊥OQ ,作AH ⊥BC 于H 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆市巴蜀中学高2012级高三(下)第六次月考
数学试题(理科)
命题人:吴树才
第I 卷(选择题,共50分)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,选出正确选项填在答题卡相应位置)
1.已知集合2{|30}A x R x x a =∈-+>,且2A ∉,则实数a 的取值范围是( )
A .(,2]-∞
B .[2,)+∞
C .(,2]-∞-
D .[2,)-+∞
2. 已知向量a 与b 的夹角为
23
π
,且||1,||2a b ==,若(3)a b a λ+⊥,则实数λ=( ) A .3
B .-3
C .32
D .3
2
-
3.已知变量x ,y 满足约束条件10,
310,10,x y x y x y +-≤⎧⎪
-+≥⎨⎪--≤⎩
则2z x y =+的最大值为( )
A .1
B .2
C .3
D .4 4. 设m,n 是空间两条不同直线,是空间两个不同平面,当时,下列命题正确的是( )
A. 若n m //,则βα//
B.若n m ⊥,则βα⊥
C. 若β⊥m ,则n m ⊥
D.若α⊥n ,则β⊥m
5. 设a 为实数,函数32
()(3)f x x ax a x =++-的导函数为()f x ',且()f x '是偶函数,则曲线()y f x =
在原点处的切线方程为( )
A .31y x =+
B .33y x =-
C .3y x =-
D .31y x =-+
6.已知数列{}n a 是无穷等比数列,其前n 项和是n S ,若232a a +=,341a a +=,则lim n n S →∞
的值
为( ) A .
23 B .43 C .83
D .16
3 7.在等差数列{}n a 中前n 项和为n S ,且201110072011,1S a =-=,则2012a 的值为 ( )
A .1007
B .2012
C .1006
D .2011
8. 已知4
x π
=是()sin cos f x a x b x =+一条对称轴,且最大值为22,则函数()sin g x a x b
=+
( )
A .最大值是4,最小值为0
B .最大值是2,最小值为2-
C .最大值可能是0
D .最小值不可能是4-
9.已知椭圆22
221(0)x y a b a b
+=>>的右焦点为F ,下顶点为A ,直线AF 与椭圆的另一交点为B ,点B 关于
x 轴的对称点为C ,若四边形OACB 为平行四边形(O 为坐标原点),则椭圆的离心率等于( )
A .
1
3
B .
1
2
C .33
D .22
10.如题(10)图,在直角梯形ABCD 中,
,1,3,AB AD AD DC AB ⊥===动点P 在以点C 为圆心且与直
线BD 相切的圆内运动....,设(,)A P A D A B R αβαβ=+∈,
则αβ+的取值范围是( ) A .4
(0,)3
B .5(0,)3
C .4(1,)3
D .5(1,)3
二、填空题:(本大题5个小题,每小题5分,共计25分。
各题答案必须填写在答题卷相应位置上,只填结果,不要过程)
11.若函数)(x f 的反函数为)0()(21
>=-x x x f
,则)4(f =
12.抛物线2
8y x =的准线为l ,点Q 在圆22:68210C x y x y ++++=上,设抛物线上任意一点P 到直 线l 的距离为m ,则||m PQ +的最小值为 .
13.若关于x 的不等于2|2||3|1x x a a ---≥++的解集为空集,则实数a 的取值范围是 . 14. 如图,已知平面β⊥α平面, A 、B 是平面α与平面β的交线上的两个定点,β⊂β⊂CB ,DA , 且α⊥α⊥CB ,DA ,,6AB ,8CB ,4DA ===,在平面α内 有一个动点P ,使得BPC APD ∠=∠,则PAB ∆的面积的最大 值是
15. ∆ABC 的三边b c a 、、和面积S 满足: S ()2
2a b c =--,且∆ABC 的外接圆的周长为17π,则面
积S 的最大值等于 . 三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.) 16. (本题满分13分)
已知向量
函数
且最小正周期
为. (I )求函数
的最大值,并写出相应的x 的取值集合;
(II)在ABC ∆中,角A ,B, C 所对的边分别为a, b,c,且,c =3, 36S
A BC =∆,求b 的值.
A
B C
D
P
α
β
A 1
C 1
B 1
B
D
C
A
如图,SD 垂直于正方形ABCD 所在的平面,1, 3.AB SB == (1)求证:;BC SC ⊥ (2)设棱SA 的中点为,M 求异面直线DM 与SC 所成角的大小. (3)求直线AC 和平面SBC 所成角的大小.
18. (本小题满分13分) 已知函数2
1()21ln(1)2
f x mx x x =
-+++()R m ∈,(Ⅰ)当0m =时,求函数()f x 的最大值; (Ⅱ)当01m <≤时,曲线:()C y f x =在点(0,1)P 处的切线l 与C 有且只有一个公共 点,求m 的值.
19.(本小题满分12分)
如图,正三棱柱111ABC A B C -中,D 是BC 的中点,21==AB AA .(I )求证:1A C //平面1AB D ; (II )求二面角1B AB D --的大小; (III )求点C 到平面1AB D 的距离.
S
D
C
A
B
M
已知圆22:(2)24C x y ++=,定点A (2,0),M 为圆C 上一动点,点P 在AM 上,点N 在C 、M 上(C 为圆心),且满足2,0AM AP NP AM =⋅=,设点N 的轨迹为曲线E . (1)求曲线E 的方程; (2)过点B (m ,0)作倾斜角为
5
6
π的直线l 交曲线E 于C 、D 两点.若点Q (1,0)恰在 以线段CD 为直径的圆的内部,求实数m 的取值范围.
21.(本小题满分12分)
已知数列}{n a 满足:0>n a ,且对一切*N n ∈,有2
33231n
n S a a a =+++ ,其中n S 为数列}{n a 的前n 项和.(Ⅰ)求数列}{n a 的通项公式;
(Ⅱ)证明:
*),2()1(22
3ln 1ln 1ln 1232N n n n n n n a a a n ∈≥+-->+++。
