切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比
(完整word版)切比雪夫低通滤波器

(完整word版)切比雪夫低通滤波器课程设计题目:院(系):专业:学生姓名:学号:指导教师:2014 年01 月03 日切比雪夫低通滤波器摘要:利用ADS2008软件设计切比雪夫型低通滤波器,通过最终的图像,分析该滤波器的功能特性,并与其他滤波器对比分析,阐明此种滤波器的优点所在。
关键字:ADS2008软件切比雪夫低通滤波器功能特性目录摘要 (1)1滤波器概述 (3)1。
1滤波器分类 (3)1。
2根据滤波器的选频作用分类 (4)1.3根据“最佳逼近特性”标准分类 (4)1。
4理想滤波器 (5)2切比雪夫低通滤波器设计 (7)2.1新建滤波器工程 (7)2.2建立一个低通滤波器设计 (7)3 设计心得 (12)4 参考文献 (13)1、滤波器概述滤波器是一种选频装置,可以使信号中特定的频率成分通过,而极大地衰减其它频率成分。
在测试装置中,利用滤波器的这种选频作用,可以滤除干扰噪声或进行频谱分析。
广义地讲,任何一种信息传输的通道(媒质)都可视为是一种滤波器。
因为,任何装置的响应特性都是激励频率的函数,都可用频域函数描述其传输特性.因此,构成测试系统的任何一个环节,诸如机械系统、电气网络、仪器仪表甚至连接导线等等,都将在一定频率范围内,按其频域特性,对所通过的信号进行变换与处理.1.1 滤波器分类:滤波器特性可以用其频率响应来描述,按其特性的不同,可以分为低通滤波器,高通滤波器,带通滤波器和带阻滤波器等.低通滤波器有很多种,其中,最通用的就是巴特沃斯滤波器和切比雪夫滤波器。
巴特沃斯滤波器是滤波器的一种设计分类,其采用的是巴特沃斯传递函数,有高通、低通、带通、带阻等多种滤波器类型.巴特沃斯滤波器在通频带内外都有平稳的幅频特性,但有较长的过渡带,在过渡带上很容易造成失真。
切比雪夫滤波器同巴特沃斯滤波器相添加图片比,切比雪夫滤波器的过渡带很窄,但内部的幅频特性却很不稳定。
巴特沃斯响应能够最大化滤波器的通带平坦度.该响应非常平坦,非常接近DC信号,然后慢慢衰减至截止频率.巴特沃斯滤波器特别适用于低频应用,其对于维护增益的平坦性来说非常重要。
一阶滤波二阶滤波

一阶滤波二阶滤波一阶滤波和二阶滤波是信号处理领域中常用的滤波器类型。
它们在滤波过程中起到了不同的作用和效果。
本文将对一阶滤波和二阶滤波进行详细介绍,并对它们的特点和应用进行分析。
一阶滤波器是指滤波器的阶数为1的情况。
在一阶滤波器中,信号的输出值仅与当前输入值和前一个输出值有关,即具有一阶差分方程的特点。
一阶滤波器常用于对信号进行平滑处理,去除高频噪声或快速变化的成分。
一阶滤波器的特点是简单、易于实现,并且具有较快的响应速度。
在电子电路中,一阶低通滤波器常用于去除高频噪声,一阶高通滤波器常用于去除低频噪声。
二阶滤波器是指滤波器的阶数为2的情况。
在二阶滤波器中,信号的输出值与当前输入值、前一个输出值和前两个输出值有关,即具有二阶差分方程的特点。
二阶滤波器常用于对信号进行更精细的处理,可以实现更复杂的滤波效果。
与一阶滤波器相比,二阶滤波器具有更好的滤波特性,可以实现更陡峭的滚降曲线和更低的截止频率。
在音频处理和图像处理中,二阶滤波器常用于对信号进行均衡调节和频率分析。
一阶滤波器和二阶滤波器在滤波效果上存在一定的差异。
由于二阶滤波器具有更复杂的差分方程,因此可以实现更精确的频率响应和更陡峭的滚降曲线。
在一些对信号响应速度要求不高但需要更精细滤波效果的应用场合,可以选择使用二阶滤波器。
而在一些对信号响应速度要求较高但滤波效果相对简单的应用场合,可以选择使用一阶滤波器。
除了滤波效果的差异,一阶滤波器和二阶滤波器在实现和设计上也存在一些不同。
由于一阶滤波器的差分方程较简单,因此实现起来相对容易。
而二阶滤波器由于差分方程的复杂性,需要更多的计算和参数调整,实现起来相对困难一些。
在实际应用中,需要根据具体需求和系统要求来选择合适的滤波器类型。
总结一下,一阶滤波器和二阶滤波器是信号处理中常用的滤波器类型。
一阶滤波器适用于对信号进行平滑处理和去除高频噪声,具有简单、易实现的特点;二阶滤波器适用于对信号进行更精细的处理和实现更复杂的滤波效果,具有更好的滤波特性。
切比雪夫滤波电路

切比雪夫滤波电路
切比雪夫滤波电路是一种常见的滤波电路,其设计理念基于切比雪夫多项式。
其主要应用于数字信号处理领域,用于滤除信号中某个特定频率范围内的噪声。
该电路的设计灵活性极高,适用范围十分广泛。
它能够对数字信号进行高效的滤波处理,减小信号中的噪声干扰,并能够有效地提高信号的质量。
它的抑制效果好、抗干扰性能优秀,是数字信号处理中常见的滤波器之一。
切比雪夫滤波电路具有以下优点:
1. 抗干扰性能好
切比雪夫滤波器是一种递归滤波器,可以用于抵抗信号中的高斯白噪声和其他干扰。
当干扰在滤波器的截止频率之外时,对于滤波器的启波抑制能力越强,抗干扰性能也越好。
2. 抑制效果好
切比雪夫滤波器的抑制效果是一种可持续性的衰减方式。
相比于频率
截止多项式,切比雪夫滤波器的抑制效果更好,这是因为其采用的是最优出血方式,比较高级的优化算法使得在整个过渡区(从通带到阻带)的频率响应中,都比较平滑的过度。
3. 传递带波纹小
在通带内,切比雪夫滤波器的透过系数是倒数对数幅度函数,随着滤波器的级数增加而呈现出更平缓的曲线。
这种曲线的外观让模拟频率响应具有波纹的因素,但这种波纹是在频率通带之内的。
因此,与其他类型的滤波器相比,切比雪夫滤波器的传递带波纹要小得多。
总之,切比雪夫滤波电路是一种高效、灵活的滤波电路,在数字信号处理领域具有广泛的应用。
它的抗干扰性能好、抑制效果优秀、传递带波纹小,无论是在音频处理、图像处理还是其他领域中,都有着不可替代的作用。
基于切比雪夫1的IIR低通滤波器

课程设计课程设计名称:DSP课程设计专业班级:电信1005班学生姓名:学号:指导教师:李相国课程设计时间:2013年6月数字信号处理专业课程设计任务书说明:本表由指导教师填写,由教研室主任审核后下达给选题学生,装订在设计(论文)首页填表说明1.“课题性质”一栏:A.工程设计;B.工程技术研究;C.软件工程(如CAI课题等);D.文献型综述;E.其它。
2.“课题来源”一栏:A.自然科学基金与部、省、市级以上科研课题;B.企、事业单位委托课题;C.校、院(系、部)级基金课题;D.自拟课题。
1 需求分析数字滤波器是指完成信号滤波处理功能的,用有限精度算法实现的离散时间线性非时变系统,其输入是一组数字量,其输出是经过变换的另一组数字量。
因此,它本身即可以是用数字硬件装配成的一台完成给定运算的专用数字计算机,也可以是将所需运算编成程序,让通用计算机来执行。
在本次课程设计中,我做的是基于双线性变换法设计 Chebyshev-I 型 IIR 数字低通滤波器,看到这个题目,我们很快就能联系到数字信号处理中的 IIR 数字滤波器的设计,根据以前学习的东西我们知道,要想设计一个数字低通滤波器,我们可以把所给的数字指标转换为模拟参数,通过设计一个模拟低通的滤波器,对设计好的模拟低通滤波器进行数字化就可以得到一个数字低通滤波器。
在本次实验中,我们首先将所给的滤波器数字指标转换为模拟指标,利用Chebyshev-I型函数设计一个 Chebyshev-I 型低通模拟滤波器,然后对所设计好的 Chebyshev-I型低通模拟滤波器进行参数分析,接下来利用双线性变化法将此模拟低通滤波器转变为数字低通滤波器。
2 概要设计3 运行环境PC 机,windows2000及其以上,matlab 软件。
4 开发工具和编程语言MATLAB 软件,编程语言为DSP 设计语言。
5 详细设计第一步:将数字低通滤波器的性能指标转化成模拟低通滤波器指标Chebyshev-I 型IIR 数字低通滤波器的性能指标:p ω=0.25π,s ω=0.4π,p δ=0.01,s δ=0.001程序模块: %转化成模拟量 rp=-20*log10(1-lp); rs=-20*log10(ls); Omgp=tan(wp/2) Omgs=tan(ws/2) Fs=0.5;第二步:利用切比学夫逼近法设计模拟滤波器切比雪夫1低通滤波器的原理:幅度平方函数为: 其中ε为小于1的正数,表示通带内幅度波动的程度,p Ω称为通带截止频率。
切比雪夫I型数字带通滤波器要点(1)

课程设计课程名称:数字信号处理题目编号: 0801题目名称:切比雪夫I型带通IIR数字滤波器专业名称:电子信息工程班级: 1203班学号:学生姓名:段超任课教师:陈忠泽2015年08月30日目 录1. 数字滤波器的设计任务及要求(编号0801) ................... 2 2. 数字滤波器的设计及仿真 .. (2)2.1数字滤波器(编号0801)的设计 ................................... 2 2.2数字滤波器(编号0801)的性能分析 . (4)3. 数字滤波器的实现结构对其性能影响的分析 (6)3.1数字滤波器的实现结构一(0801)及其幅频响应 ...................... 7 3.2数字滤波器的实现结构二(0801)及其幅频响应 ...................... 9 3.3 数字滤波器的实现结构对其性能影响的小结 (12)4. 数字滤波器的参数字长对其性能影响的分析 (12)4.1数字滤波器的实现结构一(0801)参数字长及幅频响应特性变化 ...... 14 4.2数字滤波器的实现结构二(0801)参数字长及幅频响应特性变化 ....... 17 4.3 数字滤波器的参数字长对其性能影响的小结 (20)5. 结论及体会 (20)5.1 滤波器设计、分析结论 .......................................... 21 5.2 我的体会 ...................................................... 21 5.3 展望 . (21)1. 数字滤波器的设计任务及要求(1)切比雪夫I 型带通IIR 数字滤波器各项指标如下: 阻带下截止频率1s ω=radi d π32)ln(;通带下截止频率1p ω=rad i i d d π⎪⎪⎭⎫ ⎝⎛+20)(32)ln(log 10;通带上截止频率2p ω=rad i i d d π⎪⎪⎭⎫ ⎝⎛-20)(32)ln(-1log 10;阻带上截止频率2s ω=radi d π⎪⎪⎭⎫ ⎝⎛32)ln(-1; 通带最大衰减p α=1dB; 阻带最小衰减s α=60dB.其中的i d 为抽到的题目的四位数编号,我的题目编号是0801,所以取 i d 为801. (2)滤波器的初始设计通过手工计算完成;(3)在计算机辅助计算基础上分析滤波器结构对其性能指标的影响(至少两种 合适的滤波器结构进行分析);(4)在计算机辅助计算基础上分析滤波器参数的字长对其性能指标的影响; (5)以上各项要有理论分析和推导、原程序以及表示计算结果的图表; (6)课程设计结束时提交说明书。
切比雪夫Ⅱ型低通滤波器
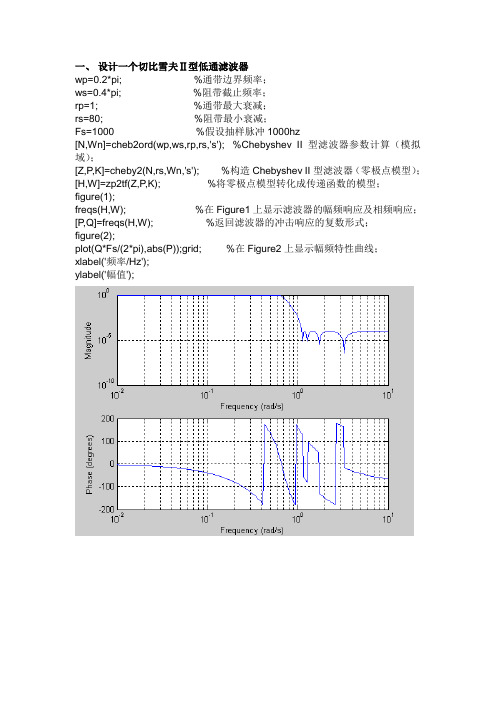
一、设计一个切比雪夫Ⅱ型低通滤波器wp=0.2*pi; %通带边界频率;ws=0.4*pi; %阻带截止频率;rp=1; %通带最大衰减;rs=80; %阻带最小衰减;Fs=1000 %假设抽样脉冲1000hz[N,Wn]=cheb2ord(wp,ws,rp,rs,'s'); %Chebyshev II型滤波器参数计算(模拟域);[Z,P,K]=cheby2(N,rs,Wn,'s'); %构造Chebyshev II型滤波器(零极点模型);[H,W]=zp2tf(Z,P,K); %将零极点模型转化成传递函数的模型;figure(1);freqs(H,W); %在Figure1上显示滤波器的幅频响应及相频响应;[P,Q]=freqs(H,W); %返回滤波器的冲击响应的复数形式;figure(2);plot(Q*Fs/(2*pi),abs(P));grid; %在Figure2上显示幅频特性曲线;xlabel('频率/Hz');ylabel('幅值');二、设计一个高通Chebyshow型数字滤波器wp=100;ws=80;Fs=300;rp=1;rs=45; %数字滤波器的各项指标;WP=100*2*pi; %把数字滤波器的频率特征转换成模拟滤波器的频率特征;WS=300*2*pi;[N,Wn]=cheb2ord(WP,WS,rp,rs,'s'); %Chebyshev II型滤波器参数计算(模拟域);[Z,P,K]=cheb2ap(N,rs); %创建Chebyshev滤波器原型;[A,B,C,D]=zp2ss(Z,P,K); %表达式从零极点增益形式转换成状态方程形式;[AA,BB,CC,DD]=lp2hp(A,B,C,D,Wn); %实现低通到高通滤波器类型的转换;[a,b,c,d]=bilinear(AA,BB,CC,DD,Fs); %采用双线性变换法,从模拟高通到数字高通;[P,Q]=ss2tf(a,b,c,d); %表达式从状态方程形形式转换成传输函数形式;figure(1);freqz(P,Q); %绘出频率响应;[H,W]=freqz(P,Q);figure(2);plot(W*Fs/(2*pi),abs(H));grid;xlabel('频率/Hz');ylabel('幅值');三、设计一个带通切比雪夫数字滤波器W1=100;W2=200;rp=1;rs=30;Fs=1000; %数字滤波器的各项指标;WP=[100,200];WS=[50,250];[N,Wn]=cheb1ord(WP/(Fs/2),WS/(Fs/2),rp,rs);%Chebyshev I型滤波器参数计算(数字域);[P,Q]=cheby1(N,rp,Wn,'bandpass');%创建Chebyshev带通滤波器;figure(1);freqz(P,Q); %显示产生滤波器的幅频及相频曲线;[H,W]=freqz(P,Q);figure(2);plot(W*Fs/(2*pi),abs(H));grid;xlabel('频率/Hz');ylabel('幅度');。
信号处理课件第6章无限冲激响应(IIR)滤波器设计

3. 滤波器的技术要求
低通:
:通带允许的最大衰减; :阻带内应达到的最小衰减
单位 (dB)
若幅度下降到 0.707, 则幅平方下降 0.5 (半 功率点):
若幅度下降到 0.01:
高通:
:通带允许的最大衰减; :阻带内应达到的最小衰减
带通:
:通带允许的最大衰减; : 阻带内应达到的最小衰减
带阻:
最直接到方法,将:
p ,s , p ,s
利用:
利用上一节的方法,可设计出模拟滤波器
G( p), G(s)
H(z)
H (z) G(s) s 1 ln z Ts
但这样做,H (z) 将不再是 z 的有理多项式,给
极-零分析带来困难。
数字滤波器的 单位抽样响应
模拟滤波器 的冲激响应
令:
冲激响应 不变法
(2)
b, a 是AF LP 的分子、分母的系数向量,B, A是转换后 的的分子、分母的系数向量;在(1)中,Wo是低通或 高通滤波器的截止频率;在(2)中,Wo是带通或带阻 滤波器的中心频率,Bw是其带宽。
4.bilinear.m :双线性变换,由模拟滤波器 得到数字滤波器。
[Bz, Az]=bilinear(B, A, Fs) 式中B, A分别是G(s)的分子、分母多项式 的系数向量,Bz, Az分别是H(z)的分子、分 母多项式的系数向量,Fs是抽样频率。
2. 切比雪夫I型(Chebyshev-I)滤波器
3. 切比雪夫II型滤波器
4. 椭圆滤波器
Un2() :Jacobian 函数 本课程只讨论 Butterworth 和 Chebyshev-I
滤波器的设计
二、Butterworth滤波器的设计
切比雪夫滤波器结构

切比雪夫滤波器结构1.引言1.1 概述切比雪夫滤波器是一种常用的数字滤波器,它以俄罗斯数学家彼得·勃列兹尼卡诺夫(Peter Chebyshev)的名字命名。
切比雪夫滤波器的设计基于切比雪夫多项式,具有一些独特的特点和优势。
切比雪夫滤波器本质上是一种频率选择性滤波器,用于在数字信号处理中滤除指定频率范围的噪声或干扰。
与其他滤波器相比,切比雪夫滤波器在频率响应方面具有更强的灵活性和自由度。
它可以实现对特定频率信号的很好衰减,同时保持较为平坦的通带响应。
该滤波器的设计主要基于两个关键因素:过渡带宽和阻带衰减。
过渡带宽是指从通带到阻带的过渡区域,而阻带衰减则是指在阻带内信号的衰减量。
切比雪夫滤波器的结构特点在于其衰减特性可调节,可以根据特定需求选择不同的阻带衰减量。
这使得切比雪夫滤波器在一些应用场景中具有较大的优势,例如在语音和音频处理中,可以有效滤除噪声,提高信号质量。
此外,切比雪夫滤波器还具有一些其他优点,如具有较为紧凑的滤波器结构、较低的实现成本和较高的运算速度等。
这使得它在实际工程中得到了广泛应用。
总之,切比雪夫滤波器是一种功能强大且灵活的数字滤波器。
通过调节其阻带衰减量,可以根据具体需求实现不同的滤波效果。
在各种应用领域中,切比雪夫滤波器都具有重要的作用,并具有广阔的应用前景。
1.2文章结构1.2 文章结构本文将按照以下结构进行论述切比雪夫滤波器的结构和特点:1.2.1 引言在引言部分,将对切比雪夫滤波器进行概述,介绍其在信号处理领域的应用背景,以及本文对切比雪夫滤波器结构的研究目的。
1.2.2 切比雪夫滤波器的定义和原理在本节中,将详细介绍切比雪夫滤波器的定义和原理。
首先解释什么是切比雪夫滤波器,其基本工作原理,并讨论切比雪夫滤波器相对于其他类型滤波器的优势和适用场景。
1.2.3 切比雪夫滤波器的结构和特点该部分将重点介绍切比雪夫滤波器的结构和特点。
首先详细描述切比雪夫滤波器的不同组成部分,例如传输函数、零极点分布等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设计流程图如下:
设计思想:
首先设计一个源信号和一个混合信号,通过其频谱对比得出最大和最小通
带,最大和最小阻带;然后再根据得到的参数来设计切比雪夫滤波器,最后通过
切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比来得出那种效果好。
切比雪夫滤波器设计原理:
设计一个源信号
设计一个混合信号
将两个信号转换成频谱图
将两个频谱图进行对比
分析设计带阻滤波器
对得出的波形进行分析
设计切比雪I型带阻滤波器 设计切比雪Ⅱ型带阻滤波器
得出结论
切比雪夫滤波器的振幅具有等波纹特性,它有两种形式:1)振幅特性在通
带内是等波纹的、在阻带内是单调的切比雪夫I 型滤波器;2)振幅特性在通带
内是单调的、在阻带内是等波纹的切比雪夫II型滤波器,采用何种形式的切比
雪夫滤波器取决于实际用途.
切比雪夫滤波器的设计方法就是将逼近精确度均匀分布在整个通带内,或
者均匀分布在整个阻带内,或者均匀分布在两者之内,这样就可以使滤波器阶
数大大降低。
切比雪夫I型滤波器平方幅度响应函数表示为:
2
)(jG
=[1+2C2N()]2/1
其中 <1(正数),它与通带波纹有关,越大,波纹也越大;CN() 是切比
雪夫多项式,它被定义为:
CN()=cos(Narccos()),≤1, CN()=cosh(Narcosh()),>1.
而切比雪夫II型滤波器平方幅度响应函数表示为:
)(jG
2={1+2{ C2N()/[2N(/c)]2}}1
其中 <1(正数),表示波纹变化情况;c为截止频率;N为滤波器的阶次,也
是 CN(N/) 的阶次。
源信号编码及其图形:
t=-1:0.01:1
y=(cos(2*pi*10*t)+cos(2*pi*40*t));
N=length(y);
fx=fft(y);
df=100/N;
n=0:N/2;
f=n*df;
subplot(2,1,1);
plot(f,abs(fx(n+1))*2/N); grid;
title('源波形频谱')
图(一)
混合信号编码及其图形:
t=-1:0.01:1;
X=(cos(2*pi*10*t)+cos(2*pi*25*t)+cos(2*pi*40*t));
N=length(X);
fx=fft(X);
df=100/N;
n=0:N/2;
f=n*df;
subplot(2,1,2);
plot(f,abs(fx(n+1))*2/N); grid;
title('混合波形频谱')
图(二)
从图(一)和图(二)对比可以得出:为了能达到和满足我们的要求,我们取以
下的参数,最大通带wp2:0.5,最小通带wp1:0.05,最大阻带ws2:0.3,最小阻带
ws1:0.1。
切比雪夫Ⅰ型滤波器设计如下:
ws1=0.1*pi;ws2=0.3*pi; %滤波器的阻带截止频率
wp1=0.05*pi;wp2=0.5*pi; %滤波器的通带截止频率
Rp=1;As=20; %滤波器的通阻带衰减指标
%转换为模拟滤波器的技术指标
T=0.01;Fs=1/T;
Omgp1=(2/T)*tan(wp1/2);Omgp2=(2/T)*tan(wp2/2);
Omgp=[Omgp1,Omgp2];
Omgs1=(2/T)*tan(ws1/2);Omgs2=(2/T)*tan(ws2/2);
Omgs=[Omgs1,Omgs2];
bw=Omgp2-Omgp1;w0=sqrt(Omgp1*Omgp2); %模拟通带带宽和中心频率
ripple=10^(-Rp/20); %滤波器的通带衰减对应的幅度值
Attn=10^(-As/20); %滤波器的阻带衰减对应的幅度值
%模拟原型滤波器计算
[n,Omgn]=cheb1ord(Omgp,Omgs,Rp,As,'s') %计算阶数n和截止频率
[z0,p0,k0]=cheb1ap(n,Rp); %设计归一化的模拟滤波器原型
ba1=k0*real(poly(z0)); %求原型滤波器的系数b
aa1=real(poly(p0)); %求原型滤波器的系数a
[ba,aa]=lp2bs(ba1,aa1,w0,bw);
%用双线性变换法计算数字滤波器系数
[bd,ad]=bilinear(ba,aa,Fs)
%求数字系统的频率特性
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H)));
subplot(2,2,1);plot(w/pi,abs(H));
ylabel('|H|');xlabel('频率(\pi)');title('幅度响应');axis([0,1,0,1.1]);
set(gca,'XTickMode','manual','XTick',[0,0.2,0.3,0.7,0.8]);
set(gca,'YTickMode','manual','YTick',[0,Attn,ripple,1]);grid
图(三)
n =3
Omgn =16.1402 200.0000
bd =0.1698 -0.8703 1.9961 -2.5870 1.9961 -0.8703 0.1698
ad =1.0000 -2.5450 2.5332 -1.7356 0.9605 -0.0469 -0.1619
分析:由图(三)运行结果可知,最大通带0.5,最小通带0.05,最大阻带0.3,
最小阻带0.1;切比雪夫Ⅰ型滤波器的设计的个性技术指标精确度是均匀分布的。
而其幅度特性在通带内是等波纹的,在阻带内是单调下降的。虽然达到了所设计
滤波器的要求,滤除了我们不需要的波形,但是存在一些问题,如误差等。
切比雪夫Ⅱ型滤波器设计如下:
ws1=0.1*pi;ws2=0.3*pi; %滤波器的阻带截止频率
wp1=0.05*pi;wp2=0.5*pi; %滤波器的通带截止频率
Rp=1;As=20; %滤波器的通阻带衰减指标
%转换为模拟滤波器的技术指标
T=0.01;Fs=1/T;
Omgp1=(2/T)*tan(wp1/2);Omgp2=(2/T)*tan(wp2/2);
Omgp=[Omgp1,Omgp2];
Omgs1=(2/T)*tan(ws1/2);Omgs2=(2/T)*tan(ws2/2);
Omgs=[Omgs1,Omgs2];
bw=Omgp2-Omgp1;w0=sqrt(Omgp1*Omgp2); %模拟通带带宽和中心频率
ripple=10^(-Rp/20); %滤波器的通带衰减对应的幅度值
Attn=10^(-As/20); %滤波器的阻带衰减对应的幅度值
%模拟原型滤波器计算
[n,Omgn]=cheb2ord(Omgp,Omgs,Rp,As,'s')
[z0,p0,k0]=cheb2ap(n,As); %设计归一化的cheb2型模拟滤波器原型
ba1=k0*real(poly(z0)); %求原型滤波器的系数b
aa1=real(poly(p0)); %求原型滤波器的系数a
[ba,aa]=lp2bs(ba1,aa1,w0,bw); %变换为模拟带通滤波器
%用双线性变换法计算数字滤波器系数
[bd,ad]=bilinear(ba,aa,Fs)
%求数字系统的频率特性
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H)));
subplot(2,2,1);plot(w/pi,abs(H));
ylabel('|H|');xlabel('频率(\pi)');title('幅度响应');axis([0,1,0,1.1]);
set(gca,'XTickMode','manual','XTick',[0,0.2,0.3,0.7,0.8]);
set(gca,'YTickMode','manual','YTick',[0,Attn,ripple,1]);grid
图(四)
n =3
Omgn =25.7347 125.4348
bd =0.2179 -0.8532 1.5781 -1.8819 1.5781 -0.8532 0.2179
ad =1.0000 -2.2979 1.7456 -0.9183 0.8465 -0.3721 -0.0002
分析:由图(四)的运行结果可知,最大通带0.5,最小通带0.05,最大阻带0.3,
最小阻带0.1;所设计的切比雪夫Ⅱ型滤波器的各项技术指标精确度是均匀分布
的。而其幅度特性在通带内是单调的,在阻带内是等波纹的。虽然也达到了所设
计滤波器的要求,滤除了我们不需要的并行,但是也还是存在误差,这是可以理
解的。
由图(三)和图(四)的运行结果对比来看,切比雪夫Ⅰ型滤波器在阻带跟通带
过渡时要比切比雪夫Ⅱ型滤波器过渡时平稳许多,所以切比雪夫Ⅰ型滤波器要比
切比雪夫Ⅱ型滤波器所做出来的效果要好。
在实际的生活用途中,我们要根据我们的不同需求和要工作的不同场合,来选择
切比雪夫Ⅰ型滤波器或者切比雪夫Ⅱ型滤波器,这样才能达到我们的要求,来满
足我们的各项需要。
