基于量子粒子群优化算法的压缩感知数据重构方法
压缩感知介绍PPT-最终版

3
采样速率需达到信号带宽的两倍以上才能精确重构信号。这样的采样硬件成本昂贵,获取效率低下,对宽带信号处理的困难日益加剧。
1.1 传统采样理论介绍及问题提出
1 背景介绍
而现实生活中,随着信息技术的高速发展,信息量的需求增加,携带信息的信号所占带宽也越来越大
01
01
02
这就大大考验了数字化社会对信息处理的能力,包括:数据存储、传输和处理速度,基于Nyquist采样的理论遭到严峻的考验。
这是压缩感知理论的基础和前提,也是信号精确重构的保证。对稀疏表示研究的热点主要有两个方面: 1、基函数字典下的稀疏表示: 寻找一个正交基使得信号表示的稀疏系数尽可能的少。比较常用的稀疏基有:高斯矩阵、小波基、正(余)弦基、Curvelet基等。Candes和Tao经研究发现光滑信号的Fourier 系数、小波系数、有界变差函数的全变差范数、振荡信号的Gabor 系数及具有不连续边缘的图像信号的Curvelet 系数等都具有足够的稀疏性,可以通过压缩感知理论恢复信号。 2、超完备库下的稀疏表示: 用超完备的冗余函数库来取代基函数,称之为冗余字典,字典中的元素被称之为原子,目的是从冗余字典中找到具有最佳线性组合的K项原子来逼近表示一个信号,称作信号的稀疏逼近或高度非线性逼近。
背景介绍
01
传统采样理论介绍及问题提出
02
压缩感知理论的基本思想
03
传统的基于Nyquist采样定理指导下的信息的处理主要表现在两个方面:
1
2
在实际应用中,为了降低成本,人们常将采样的数据经压缩后以较少的比特数表示信号,而很多非重要的数据被抛弃,这种高速采样再压缩的方式浪费了大量的采样资源,另外一旦压缩数据中的某个或某几个丢失,可能将造成信号恢复的错误。
基于量子粒子群优化极限学习机的频谱感知算法

收稿日期:2019-10-08基金项目:吉林省科技厅重点科技成果转化项目(20150307032GX )作者简介:郭熠(1995-),男,硕士研究生,E-mail :*******************通讯作者:郭滨(1965-),男,博士,教授,博士生导师,E-mail :***************.cn基于量子粒子群优化极限学习机的频谱感知算法郭熠,张晨洁,郭滨,汤云琪(长春理工大学电子信息工程学院,长春130022)摘要:针对无线信道环境中低信噪比情况下主用户信号检测率较低的问题,提出了一种基于量子粒子群优化极限学习机(ELM )算法的认知无线电网络频谱感知方法。
针对极限学习机算法的特点通过量子粒子群算法(QPSO )优化极限学习机参数,并构建引入结构风险思想的QPSO-ELM 模型,降低算法的经验风险提高模型的泛化能力,提高算法的频谱感知性能。
仿真实验表明,与人工神经网络(ANN )、支持向量机(SVM )和极限学习机(ELM )三种机器学习算法,在信噪比为-15dB 时的频谱感知性能进行比较,分别提高了16%、28%、9%,仿真证明所提算法在低信噪比情况下具有较高的性能,可有效地实现对主用户信号的频谱感知。
关键词:认知无线电;频谱感知;量子粒子群;极限学习机中图分类号:TN925文献标志码:A文章编号:1672-9870(2021)01-0109-08A Spectrum Sensing Algorithm Based on Q uantum Particle Swarm Optimization and ExtremeLearning MachineGUO Yi ,ZHANG Chen-jie ,GUO Bin ,TANG Yun-qi(School of Electronics and Information Engineering ,Changchun University of Science and Technology ,Changchun 130022)Abstract :A spectrum sensing method for cognitive radio networks based on quantum particle swarm optimization (QPSO )and extreme learning machine (ELM )algorithm is proposed to solve the problem of low detection rate of primary user sig-nals in low SNR wireless channel environment.According to the characteristics of extreme learning machine algorithm ,the parameters of extreme learning machine are optimized by quantum particle swarm optimization ;and a QPSO-ELM model with structural risk is constructedto reduce the empirical risk of the algorithm and improve the generalization ability of the model ,thereby improving the spectrum sensing performance of the algorithm.The simulation results show that comparing the three machine learning algorithms of ANN ,SVM and ELM ,the performance of spectrum sensing is improved by 16%,28%and 9%respectivelyas SNR is -15dB.The simulation results show that the proposed algorithm has high performance in low SNR and can effectively realize spectrum sensing of primary user signals.Key words :cognitive radio ;spectrum sensing ;quantum particle swarm ;extreme learning machine随着通信行业的发展和人们对网络速度和质量的要求越来越高,无线电频谱资源愈加稀缺[1],各国根据无线电业务的技术特点、业务能力、宽带需求等因素分配固定频段给固定业务。
基于压缩感知理论的WSNs时序信号分段压缩算法

基于压缩感知理论的WSNs时序信号分段压缩算法刘洲洲;徐继良;韩莹;王晓柱【摘要】针对压缩感知理论(CS)应用在无线传感器网络中时序信号在传输过程存在压缩比率低、通信能耗高等问题,提出了一种时序信号分段压缩算法来解决在信号稀疏度未知及高稀疏度条件下,压缩感知数据重构算法中存在的重构效率低,重构精度差,影响网络生命周期的问题.该算法将采集数据中非零元素个数作为分段依据,通过减少段内非零元素组合数量来提高信号重构精度,同时利用了压缩感知理论特性实现了对信号的高压缩率.实验结果表明,在以混沌量子免疫克隆重构(Q-CSDR)算法为重构算法、在信号盲稀疏度及稀疏度高于40的条件下,能够以大于0.4的压缩比率对信号进行压缩,其重构信号的均方误差小于0.01,能够延长网络寿命2倍左右.%For compressive sensing(CS)application timing signal during transmission in the wireless sensor net-works has low compression ratio,high energy consumption of communication,the timing signal segment compres-sion algorithms is proposed to solve the unknown signal sparsity and high sparsity under conditions of low compres-sive sensing reconstruction efficiency data reconstruction algorithm when the reconstruction accuracy is poor. As the basis of segmentation,the number of non zero elements is collected in the data,by reducing the number of com-binations of nonzero elements within the segment to improve the accuracy of signal reconstruction ,while taking ad-vantage of the characteristics of compressive sensing theory to achieve a high compression ratio of the signal. Experi-mental results show that,under the chaotic quantum clonal Reconstruction(Q-CSDR)algorithm as thereconstruc-tion algorithm,the blind signal sparsity and sparse conditions is higher than 40,the compression ratio can be great-er than 0.4,the signal has been compressed,and square error of less than 0.01 of its reconstructed signal,and the network lifetime is prolonged by about 2 times.【期刊名称】《传感技术学报》【年(卷),期】2016(029)001【总页数】7页(P122-128)【关键词】无线传感器网络;压缩感知理论;时序信号;稀疏度;压缩比率【作者】刘洲洲;徐继良;韩莹;王晓柱【作者单位】西安航空学院,西安710077;空军西安飞行学院第五训练旅,四川南充637100;中国电子进出口总公司,北京100036;西安航空学院,西安710077【正文语种】中文【中图分类】TP393时序信号即为普通时域内的信号,其幅值按照时间先后顺序依次排列。
面向压缩感知的稀疏信号重构算法研究

面向压缩感知的稀疏信号重构算法研究一、内容概括本文旨在深入研究面向压缩感知的稀疏信号重构算法。
压缩感知作为一种新兴的信号处理技术,其核心思想在于通过引入信号的稀疏性先验信息,实现在远低于传统Nyquist采样定理所要求的采样率下对原始信号的准确重构。
这一技术的出现,极大地拓宽了信号采样与处理的研究与应用领域,为众多实际问题提供了全新的解决思路。
我们重点关注稀疏信号重构算法的研究,这不仅是压缩感知理论的重要组成部分,也是实现压缩感知技术实际应用的关键环节。
我们介绍了压缩感知的基本理论框架,包括信号的稀疏表示、压缩采样以及重构算法等核心概念。
我们详细探讨了现有的稀疏信号重构算法,包括基于贪婪策略的重构算法、基于凸优化的重构算法以及混合重构算法等,并对这些算法的性能特点进行了对比分析。
为了克服现有算法的不足,我们提出了一种新型的基于最优化导向的稀疏信号重构算法。
该算法充分利用了信号的稀疏性先验信息,通过优化目标函数来寻找最优的信号重构解。
我们设计了一种高效的支撑集估计策略,能够准确地识别出信号的非零元素位置,并在此基础上实现信号的高效重构。
我们还针对多信源联合稀疏信号重构问题进行了深入研究,提出了一种基于混合支撑集模型的联合重构算法,能够有效地处理多个相关信源之间的信息交互与融合。
为了验证所提出算法的有效性,我们进行了大量的仿真实验。
实验结果表明,本文提出的稀疏信号重构算法在重构精度、计算复杂度以及鲁棒性等方面均表现出优越的性能。
我们还讨论了算法在实际应用中的潜在价值与挑战,为未来的研究提供了有益的参考与启示。
本文面向压缩感知的稀疏信号重构算法进行了深入研究,提出了一系列创新的算法与策略,为压缩感知技术的发展与应用奠定了坚实的基础。
1. 压缩感知理论概述压缩感知(Compressed Sensing,CS)理论,作为信号处理领域的一种革命性技术,其核心思想在于突破了传统信号采样与重构的范式,实现了采样与压缩过程的融合。
基于改进平滑L0范数的压缩感知重构算法
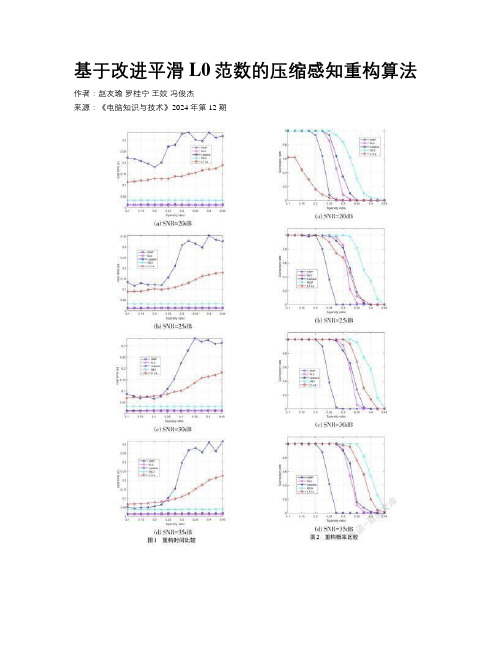
基于改进平滑L0范数的压缩感知重构算法作者:赵友瑜罗桂宁王姣冯俊杰来源:《电脑知识与技术》2024年第12期关键词:压缩感知;稀疏信号重构;平滑L0范数;负指数函数0 引言随着信息时代的到来,如图像、语音、视频等信号的传输与处理技术已经被广泛应用,同时对信号传输、采集、处理等提出了更高的要求。
因此,如何对信号进行有效的采样压缩,实现信号的精确重构,成为信号处理领域的重要问题。
奈奎斯特采样定理指出,如果要从采样信号中无失真地恢复出原始信号,则采样率至少是信号频带的两倍以上。
随着信息技术的发展和对信息需求的增加,信号带宽不断扩大,采样率和处理速度也随之提高,相应地增加了信号采样的成本以及数据存储、传输的代价,这导致实际应用中的硬件要求和传输压力增加。
传统的信息获取与处理流程通常是先对信号进行采样,再对获得的采样数据进行压缩处理,但采集与压缩过程中去除大量冗余数据会造成采样资源的浪费。
近年来,充分利用信号的稀疏性或可压缩性特征,压缩感知(Compressive Sensing, CS)理论作为一种基于信号稀疏性的采样理论被提出。
相比传统的数据采样理论,该理论在采样中完成了数据压缩的过程,从而显著降低了系统采样的硬件需求和时间损耗 [1]。
压缩感知理论是基于数学优化问题,针对海量数据进行采样、编码和优化重构的新理论。
该理论指出,如果被测信号在某个变换域是稀疏的或者信号是可压缩的,则可采用低于奈奎斯特采样频率的方式对信号进行测量,并能通过测量值重构原始信号。
CS理论表明,对于稀疏信号或可压缩信号,可以同时进行数据采样和压缩,通过设计与稀疏基不相关的观测矩阵将高维稀疏信号降为低维信号,然后通过最小范数优化求解原始信号,极大地降低存储空间和计算的复杂度,且质量损失较小,实现精确重构。
该理论利用信号的稀疏性,实现了低采样率采样,从而降低了高速采样、A/D 变换、变换编码的成本。
对于以低采样率采样得到的数据,压缩感知理论通过在约束条件下对L1(或L0)范数优化重构该稀疏信号。
基于压缩感知的图像重构算法

基于压缩感知的图像重构算法作者:李春晓李静辉石翠萍周仕坤那与晶刘欢欢关硕来源:《科技视界》2019年第01期【摘要】奈奎斯特定理具有一定的局限性,在奈奎斯特采样定理中指出采样过程需要满足一个条件,其采样频率不得低于模拟信号最高频率两倍。
然而在过去十几年时间里,随着信息需求量的高速增长导致信号带宽也必须随之增长。
这就导致了对技术以及设备要求越来越高,无法有效处理海量的数据。
为了提高处理效率,我们利用图像信号的稀疏性对图片处理,通过压缩感知重建算法将图片精准的恢复出来。
因为图像有一定的相似性,所以在处理图像的过程中,导致了图像数据的计算复杂度高,恢复图像的精度低。
对于这个问题,可以通过压缩感知算法分析图像数据处理。
【关键字】压缩感知;稀疏;图像重建;采样中图分类号: TN911.7 文献标识码: A 文章编号: 2095-2457(2019)01-0065-0020 引言随着信息的高速发展,在生活中需要与图像相关的应用越来越多。
面对海量的图像数据,奈奎斯特采样定律显得力不从心。
近年来,基于压缩感知框架下的图像重构得到广大学者研究[1-3]。
图像处理便是社会和生活不可或缺的一部分。
在最近的十多年,人们对于信息的需求量剧增,图像信号中包含很多数据,尤其是超分辨图像[4-6],因此这也导致了处理信息的精度问题和效率问题。
基于压缩感知的图像处理是通过信号的稀疏来表示的,对信号进行采样压缩,信号重构。
信号稀疏其主要的任务就是字典的生成和对信号进行信号稀疏分解。
Mallat提出的匹配追踪算法,目前,基于重构可以实现图像去噪、压缩和音频恢复等。
基于分类可以构造稀疏向量,通过稀疏表示可以获得稀疏信号进一步根据数学模型进行数据分析,通过测量矩阵:随机高斯矩阵、随机贝努力矩阵和正交矩阵来实现低维信号恢复出高维原始信号的过程,这样可以保证恢复信号的质量。
如盲源分离、音乐表示和人脸识别、文本检测信号[1]。
对于目前我们所接触的信号来说,大多数都是非稀疏信号,因此需要将其转换为稀疏信号。
基于压缩感知的电能质量信号重构算法

基于压缩感知的电能质量信号重构算法
压缩感知技术是一种有效的信号压缩和重构方法,可以在保持信息完整性的前提下实现信号的高效压缩和重构。
本文提出了一种基于压缩感知的电能质量信号重构算法,旨在实现对电能质量信号的高效压缩和重构。
该算法主要包括以下几个步骤:首先,将电能质量信号转换为频域信号,并对其进行压缩感知采样,以减小信号的维度;然后,使用稀疏表示和迭代重构算法对采样信号进行重构,还原原始信号;最后,进行重构信号的修正和精细调整,使其更加接近原始信号。
实验结果表明,与传统的信号压缩算法相比,基于压缩感知的电能质量信号重构算法具有更高的重构准确度和更小的重构误差,可以有效提高电能质量监测系统的性能和效率。
因此,该算法具有广泛的应用前景,在电力系统等领域具有很大的发展潜力。
基于改进量子粒子群算法的配电网络优化重构

基于改进量子粒子群算法的配电网络优化重构潘欢;杨丽;胡钢墩【摘要】为了更好地利用分布式电源(DG),需要调整配电网开关状态优化网络结构.基于此,旨在利用一种智能算法对含DG的配电网进行优化重构.以网损最小为目标函数,建立配电网重构模型,并给出重构需要满足的约束条件;按照DG接入配电网的接口类型将其分为PQ型、PV型、PI型和PQ(Ⅴ)型四种类型,选择前推回代法对含DG的配电网进行潮流计算;通过分析二进制粒子群算法(BPSO)与量子粒子群算法(QPSO),提出了一种改进的量子粒子群算法一加权的二进制量子粒子群算法(WBQPSO).以IEEE33节点配电系统为例,采用二进制编码方式,通过仿真结果可以发现WBQPSO通过对粒子的平均最好位置加权处理,改善种群多样性,提高收敛速度,可以得到更好的网络重构的优化结果.【期刊名称】《电测与仪表》【年(卷),期】2018(055)018【总页数】7页(P31-36,49)【关键词】配电网重构;分布式电源;粒子群算法;量子粒子群算法;二进制【作者】潘欢;杨丽;胡钢墩【作者单位】宁夏大学物理与电子电气工程学院宁夏沙漠信息智能感知重点实验室,银川750021;宁夏大学物理与电子电气工程学院宁夏沙漠信息智能感知重点实验室,银川750021;宁夏大学物理与电子电气工程学院宁夏沙漠信息智能感知重点实验室,银川750021【正文语种】中文【中图分类】TM7260 引言配电网通常具有以下特点,即闭环设计、开环运行,节点间存在分段开关,整个网络有少量联络开关。
在保证电力供需平衡和满足潮流约束的条件下,配电网需要调整开关的开合状态完成网络重构,实现降低网损、提高供电质量和均衡负荷等目的。
优化重构一直是配电网领域的热点研究问题,近年来国内外学者均对此展开了分析与讨论[1-16]。
早期的配电网重构主要集中在传统配电网上,在满足约束条件下,应用智能算法确定线路中两种开关的闭合状态,以使电网实现某种运行指标最佳[1-6]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第28卷第6期 2015年6月 传感技术学报
CHINESE JOURNAL OF SENSORS AND ACTUATORS Vo1.28 No.6
June 2015
Perceptual Data Reconstruction for Compressed Sensing Based on Quantum Behaved Particle Swarm Optimization
L/U Zhouzhou ,LI Yanping (1.Xi’an Aeronautical University,Xi ̄an 710077,China; 2.Department ofComputer and Information Engineering,Heze University,Heze Shandong 274015,China)
Abstract:According to wireless sensor network monitoring object features,the compressed sensing theory is applied to data compression to reduce the communication energy.Considering that reconstruction accuracy of existing data reconstruction in compressed sensing can be easily influenced by sparsity,after analysis of compressed sensing data reconstruction principle,with sub-flame processing the original signal in fixed length to reduce the solution space, and applying quantum theory encoding in Particle Swarm Optimization,Compressed Sensing Data Reconstruction that based on Quantum—behaved Particle Swarm Optimization appears.According to wireless sensor network monito- ring object features,this algorithm improves the accuracy of the data reconstruction by improving particle initial po— sition and update mode in Particle Swarm Optimization from Statistics.Simulation results show that under conditions of sparsity less than 50,QP—CSDR gets 20%~40%performance improvement on Reconstruction accuracy comparing to existing algorithms.Now the algorithm has been applied to micro—earthquakes and audio monitoring system,and in actual inspection,the actual system life is extended about 2-4 times with assurance data accuracy. Key words:wireless sensor network;quantum theory;particle swarm optimization algorithm;compressed sensor; data reconstrueti0n EEACC:7230 doi:10.3 .issn.1004—1699.2015.06.011
基于量子粒子群优化算法的压缩感知数据重构方法 刘洲洲 ,李艳平 (1.西安航空学院,西安710077;2.菏泽学院计算机与信息工程系,山东菏泽274015)
术
摘 要:针对传感器监测对象特点,将压缩感知理论应用于数据压缩过程以降低通信能耗,并根据现有压缩感知数据重构算 法存在的重构精度受稀疏度影响较大的缺点,在分析了压缩感知数据重构原理后,提出了将原始信号按固定长度进行分帧处 理以减少算法解空间的数量,并将量子理论中的编码方式应用于粒子群优化算法,提出了基于量子粒子群优化算法的压缩感 知数据重构方法QP—CSDR。算法根据传感器监测对象特点,从统计学角度出发对粒子群优化算法中的粒子初始位置及粒子 群更新方式加以改进,以提高数据重构精度。仿真实验结果表明,在稀疏度小于5O的条件下,QP—CSDR算法相对已有算法在 重构精度方面性能提升20%~40%,该算法已应用于微地震及音频监测系统中,经实际检验算法在保证数据精度的前提下延 长系统寿命2倍~4倍左右。 关键词:量子理论;粒子群优化算法;压缩感知;数据重构 中图分类号:TP393 文献标识码:A 文章编号:1004-1699(2015)06-0836-06
压缩感知是目前数据压缩的重点研究方向,能够 以高压缩比对数据进行压缩,并通过数据重构算法对 数据实现重构。国外对如何将压缩感知应用于无线 传感器网络及相关数据重构方法进行了大量研 究¨1 。数据重构算法的关键问题在于如何快速的、 准确的从已知的低维数据中恢复出高维数据。目前
项目来源:国家自然科学基金项目(No.61103242) 收稿日期:2014—07-29 修改日期:2015—02-05
压缩感知数据重构算法主要分为两类l3 J:第1类算法 则是基于最小化l 范数的算法,包括基追踪算法BP (Basis Pursuit) ,线性规划算法LP(Linear Program— ming)E5 3等。这类算法具有重建精度高的优点,但其 算法的复杂度较高,且执行效率低,使用性较差;第2 类是基于最小化l 范数的方法,即贪婪算法,包括正 第6期 刘洲洲,李艳平:基于量子粒子群优化算法的压缩感知数据重构方法837 交匹配追踪算法OMP(Orthogonal Matching Pursuit) J、正则化正交匹配算法ROMP(Regularized Orthogonal Matching Pursuit) 、压缩采样匹配追踪算 法 CoSaMP (Compressive Sampling Matching Pursuit) J、迭代硬阈值算法IHT(herative Hard Thresholding) J、基于感知字典的迭代硬阈值算法 SDIHT(Sending Dictionary-based Iterative Hard Thresh- olding) 101、基于混沌量子免疫克隆算法的正交匹配 算法OMP—QICA(Orthogonal Matching Pursuit based on Quantum.inspired Immune Clona1)… 、基于遗传算法 的压缩感知重构算法 、稀疏度K自适应的稀疏自 适应匹配追踪算法SAMP(Sparsity Adaptive Matching Pursuit) 131等,这类算法主要通过迭代更新当前估计 来优化信号恢复情况,在原始信号稀疏度较小的情况 下具有很好的重构精度及重构速度,但对于稀疏度较 高的信号重构问题却无能为力。 粒子群优化算法PSO(Particle Swarm Optimiza— tion)是目前国内外的研究热点¨ ,在问题寻优的 过程中要比其他经典算法具有更好的优势及可行 性,应用于N—P完全问题,PSO算法也取得了比以 往算法更好的效果。尽管PSO算法具有自身的优 势,但在实际应用中还是常出现陷入局部极值等现 象。应用于压缩感知数据重构过程中常出现适应度 较低但重构误差极大的情况。 针对这些不足,将量子免疫克隆理论带入粒子 群优化算法,提出基于量子理论的粒子群优化算法 QP—CSDR(Quantum-inspired immune clonal based Particle Swarm Optimization in Compressed Sensor Data Reconstruction)并将其应用于压缩感知数据重 构过程中。旨在利用量子免疫克隆算法中的种群生 成方法以及种群更新方法来实现种群扩张,为粒子 群优化算法提供更广泛、更丰富的粒子位置,扩大了 搜索空间,提高了局部搜索能力,避免算法陷入局部 最优出现早熟现象。 1数据重构算法 1.1 固定长度分帧 固定长度分帧方式就是将原始长信号按照固定 的数据长度分为若干帧。假设信号采集端采集的原 始信号长度为Ⅳ,则按算法设定的帧长度n将原始 信号分为frame=ceil(N/n)个帧,每个帧内包含的非 零元素个数不等。举例说明: 假设原始信号 为: 0 0 0 1 l l 0 1 0 l 0 1 0 0 1 0 0 0 1 0 1 1 0 1 0 0 1 0 0 0 其原始信号长度为30,按每帧长度为5个数据 分帧,则可分为以下6个帧: 0 0 0 1 1 I 1 0 1 0 1 l O 1 0 O 1 l 0 0 0 1 0 l 1 1 0 1 0 1 0 1 0 0 0 这种方法的特点是每帧的长度相同,而稀疏度 不同。 设信号采集端采集的原始信号长度为,v,信号 稀疏度为K,则原始信号的非零元素的可能位置有 c 种可能,设其幅值 分布在[min,max]上,且服 从正态分布。概率密度函数为:
exp _O/i2)㈩ 、/27r \ /
则根据概率论相关知识可知:其重建概率为: 斋 ) 采用固定长度分帧方法后,第 帧的非零元素 的位置有c 种可能,n为固定分帧长度,k 为第i 帧中的非零元素个数。其重建概率如公式所示: ceil( N/n) 1 H 斋 )
以上述数据为例,表1显示未分帧及分帧后的 原始信号 中非零元素位置组合数量(为计算简便, 这里假设数据为均匀分布): 表1 固定长度分帧前后非零元素位置组合数量
可以看出,较短的分帧长度会降低组合数量,但 在实际过程中会因为分帧长度过短导致帧数量增 加,导致通信包数量急剧增加,提高了通信开销,造 成网络拥塞,使分帧方法的实用性降低。而当n取 值过大时,虽然能够减少通信包数量,降低通信开 销,但也会造成非零元素位置组合数量急剧增加,降 低了数据的重构概率。 1.2改进的量子粒子群优化算法 假设初始状态下,PSO系统中的每个粒子的位 置不能确定,每个粒子位置的量子位状态是随机的, 可以为0或1,也可为0到1间的任意随机数,其状 态表示为公式: I )=O/l 0) l 1) (4) 式中:OL, 表示相应状态出现概率的两个复数,其关 系为 =1。 具有m个量子比特位的粒子群可以描述为
