5.6立方根
2021年八年级数学上册 5.6立方根教学案(无答案) 青岛版

2019-2020年八年级数学上册 5.6立方根教学案(无答案)青岛版一、学习目标:1.了解立方根的概念,会用符合表示一个数的立方根,知道任何一个数都有立方根;2.会用立方运算求某些数立方根。
3.经历从立方运算到开立方运算的演变过程,发展逆向思维能力。
二、教学重点:会用立方运算求某些数的立方根三、知识回顾(1)64的算数平方根是。
(2)(-6)的平方根。
(3)若a的平方根只有一个,那么a= .(4)若数b的一个平方根是1.2,则它的另一个平方根是。
(5)的算数平方根是。
四、自主预习1 立方根(1)定义:一般的,如果,那么x叫做a的立方根,或三次方根(2)a的立方根用符合表示,读作___________,其中a叫做_____________,左上角的3叫做________________.(3)立方根的特征:正数的立方根为_____________,负数的立方根为______________,0的立方根是______________2开立方求一个数的__________运算,叫做开立方。
开立方与__________互为逆运算。
五、复习引入:()3=8 ()3=27()3=1000 ()3=-六探索新知一个立方体形状的水箱,是它的容积为125立方米,你能计算正方体的棱长吗?想一想,与同学交流。
一般的,如果x=a,那么x叫做a的____________,或___________。
数a的立方根记作_______读作__________,其中a叫做__________,左上角的3叫做____________求一个数立方根的运算叫做__________。
开立方与___________互为逆运算。
例1 求下列个数的立方根(1)64 (2)(3)-0.125 (4)7议一议:(1)2的立方等于8,是否还有其它的数立方等于8.(2)-3的立方等于-27,是否还有其它的数立方等于-27.(3)-的立方等于-,是否还有其它的数立方等于-。
八年级数学上册《5.6立方根》(第2课时)教案青岛版

《5.6 立方根》教案一、教与学目标:1、了解立方根的意义,会用符号表示一个数的立方根,知道任何一个数都有立方根;2、会用立方运算求某些数的立方根。
3、经历从立方运算到开立方运算的演变过程,发展逆向思维能力。
二、教与学重点难点:1. 立方根的概念与性质。
2. 会求某些数的立方根。
三、教与学方法:启发式,讲练结合。
四、教与学过程:请同学们回忆一下,平方根我们是如何定义的?平方根有哪些性质?在同学们回答后,启发学生是否可试着给数的立方根下个定义.(一)、创设情境,导入新课:要做一个立方体形状的水箱,使它的容积为125立方米,你能计算出水箱的棱长吗?1.()的立方为125。
2.容积为125立方米的水箱的棱长是()。
(二)、探究新知::自主学习:读146页框中所有内容,完成下列要求。
1).立方根的定义,符号表示,组成;2).开立方定义。
小组交流:小组内交流以上问题,互相提问。
1.立方根的概念:一般地,如果x3=a,那么x叫做a的立方根,或三次方根。
2.立方根的表示方法:数a的立方根记作3a,读作“三次根号a”,其中a叫做被开方数,左上角的3叫做根指数。
注意,在前面我们学习平方根的表示方法说过当根指数为2时可以省略不写,现在是立方根了,这个根指数3是绝对不可省的,否则就会与平方根混淆了,例如表示125的立方根,而则表示125的算术平方根.3.开立方概念:求一个数的立方根的运算叫做开立方。
4.开立方运算与立方运算互为逆运算.个性化设计:1、理解立方根的意义2、掌握立方根的表示方法及求法。
(难点)3、掌握立方根的性质和开立方运算(重点)因此,我们可以根据立方运算来求一些数的立方根.合作探究: 【探究问题】 说出1 ,0 ,8 ,-27这几个数的立方根。
【探究结论】1的立方根是1;0的立方根是0;8的立方根是2,;-27的立方根是-3练习:用根号表示下列各数的立方根: 216 , -3 ,0 , 1000 , 例1. 求下列各数的立方根: (1)64 ; (2)127 ;(3)-0.125 ;(4) 7解:(1) ∵ 3464= ∴364=4(2) ∵311()327= ∴311273= (3)∵ 3(0.5)0.125-=- ∴30.1250.5-=-(4) 7的立方根是37下面我们思考这样一个问题:一个正数有几个平方根?负数有没有平方根?一个正数有几个立方根?负数有没有立方根?请学生来回答这个问题.由前面刚刚做过的题我们不难看出像8、125、127、 这样的正数,有一个正的立方根;像-8、-0.125 、 这样的负数有一个负的立方根;0的立方根是0.由此我们得了立方根的性质. 5.立方根的性质:(1)正数有一个正的立方根. (2)负数有一个负的立方根. (3)0的立方根是0.个性化设计:(三)合作交流:1、同桌之间交流一下: 一个数的立方根的符号怎样确定;正数有一个_的立方根,负数有一个_的立方根,0的立方根是_。
立方根及乘方开方表

?cm1-3 立方根及乘方開方表一、重點整理你知道2的三次方等於8,但你知道什麼數的三次方等於2嗎?有沒有這樣的數?這個數怎 麼表示?它到底是多少?用心學過這個單元之後,這些疑惑就可以迎刃而解了。
(1) 正數的立方根體積是125立方公分的正方體,它的邊長是多少公分? 這個問題就是找一個正數,使這個正數的立方(三次方) 等於125。
12555553=⨯⨯=,即12553=5的立方是125,我們就稱5是125的立方根。
例題:(1)1的立方是1,即113=,1是1的立方根。
(2)2的立方是8,即823=,2是8的立方根。
(3)3的立方是27,即2733=,3是27的立方根。
(2) 負數的立方根 125)5()5()5()5(3-=-⨯-⨯-=-,即125)5(3-=-5-的立方是125-,我們就稱5-是125-的立方根。
例題:1. (1)1)1()1()1()1(3-=-⨯-⨯-=-,所以1-是1-的立方根。
(2)8)2()2()2()2(3-=-⨯-⨯-=-,所以2-是8-的立方根。
(3)27)3()3()3()3(3-=-⨯-⨯-=-,所以3-是27-的立方根。
(4)64)4()4()4()4(3-=-⨯-⨯-=-,所以4-是64-的立方根。
例題:2. (1)問3是不是27的立方根?(2)問3-是不是27的立方根?解:(1)因為2733333=⨯⨯=,所以3是27的立方根。
(2)因為2727)3()3()3()3(3≠-=-⨯-⨯-=-,所以3-不是27的立方根。
答:(1)是;(2)不是(3) 立方根的表示法 1. 正數的立方根是正的,零的立方根是零,負數的立方根是負的。
2. 表示法: 以3a (讀作三次跟號a )表示a 的立方根說明:平方跟號就是2讀作“二次根號”。
例1: (1) 823=∴2是8的立方根,記作283=(2) 8)2(3-=-∴2-是8-的立方根,記作283-=-例2: (1)3273= (2) 3273-=-(3) 0=(4) 乘方開方表我們也可以用乘方開方表來查平方根與立方根。
5.6立方根

学科数学年级八时间总序号课题5.6立方根主备人授课人教学目标和学习目标1.了解立方根的意义,会用符号表示一个数的立方根,知道任何一个数都有立方根2.会用立方运算求某些数的立方根教学重点教学难点立方根的意义求某些数的立方根师生互动过程教学内容和学生活动教师活动一、复习提问,引入新课:1. 64的算术平方根是()2. (-6)2的平方根是()3. 若a的平方根只有一个,那么a=( )4. 若数b 的一个平方根是1.2,那么b的另一个平方根是()5. 8的算术平方根()6. ( )3=8( )3=27( )3=1000( )3= 0( ) 3=—278引导学生平方根意义,以此引入立方根的学习。
师生互动过程教学内容和学生活动教师活动二、交流实践,探索新知:①2的立方等于多少?是否有其它的数,它的立方是8?-3的立方等于多少?是否有其它的数,它的立方也是-27?②—65的立方等于多少?是否有其它的数。
③0.7的立方是多少?是否有其它的数,它的立方是0.343 ?0的立方是多少?立方根的性质:任何数都只有一个立方根;正数的立方根是正数;0 的立方根是0;负数的立方根是负数。
三、拓展与延伸:例 1 求下列个数的立方根(1)64 (2)271(3)—0.125 (4)7例2 求下列各式的值:(1)327(2)3008.0引导学生注意平方根与立方根的区别师生互动过程教学内容和学生活动教师活动(3)—312527(4)(35)3思考:一个数的立方根的符号怎样确定?与同学交流正数的立方根为正数,负数的立方根为负数,0的立方根是0四、课堂小结;本节课你有什么收获?五、布置作业:课本p147l练习1、2板书设计一、立方根与开立开立方二、立方根的性质三、拓展与延伸四、小结。
5.6立方根(1)青岛版

立 方
开立方
8 -27 -1 -8 1 27 1 -1 8 -8 27 -27 -3 +1 -2 +3 -1 +2
+1
-1
+2
-2 +3
-3
求一个数的立方根(三次方根)的运算,叫做开立方
立方与开立方的运算互为逆运算
(4)正数、0、负数的 立方根各有什么特点?
正数有立方根 吗?如果有, 看看下面的填空有几个。 3 27 ,27的立方根是( ) 负数呢? 1 1 3 零呢? , 的立方根是( )
正数a的算术平方根是:
a
3.正数有几个平方根?它们之间的关系是什么?负数有没有 平方根?0平方根是什么?
正数有两个平方根,它们互为相反数; 0的平方根是0;负数没有平方根。
创设情境 导入新课
要做一个体积为 8cm3的立方体魔方(如 图),它的棱要取多少 长?你是怎么知道的?
设立方体的棱长为xcm
则
3 2
±2
.
(7) 3 512 的立方根为 -2
.
因为
3
343
3
=
, -7
343 = -7 .
3
= 3 343 343 所以 3 512 -8 3 512 -8 因为 = = , 3 3 512 所以 512 =
你能从上述问题中总结出互为相反数的两个数a与 -a的立方根的关系吗? 3 3
∴-27的立方根是-3 即 3
1 3 1 (3)∵ ( ) 3 27
∴
1 1 的立方根是 27 3
27 3
3
1 1 即 27 3
1 ~ 10 的立方表
立方根表1到100

立方根表1到100在数学中,立方根是指一个数的立方的倒数。
计算立方根常常在科学、工程和数学领域中使用,因此,我将为您提供1到100的立方根表。
计算方法要计算一个数的立方根,可以使用以下的数学公式:cbrt(x) = x^(1/3) = x^(0.333...)其中,cbrt(x)表示x的立方根。
立方根表下面是1到100的立方根表:数字立方根112 1.263 1.444 1.595 1.716 1.827 1.91 829 2.0810 2.1511 2.2212 2.2913 2.3514 2.4115 2.4616 2.5217 2.5718 2.6219 2.6720 2.7121 2.7622 2.8023 2.8424 2.8825 2.9226 2.96 27328 3.0429 3.0730 3.1131 3.1432 3.1733 3.2134 3.2435 3.2736 3.3037 3.3338 3.3639 3.3940 3.4241 3.4542 3.4843 3.5144 3.5345 3.5646 3.5947 3.6148 3.6449 3.6650 3.6951 3.7152 3.7453 3.7654 3.7955 3.8156 3.8357 3.8658 3.8859 3.9060 3.9261 3.9562 3.9763 3.99 64465 4.0266 4.0567 4.0768 4.0969 4.1170 4.1371 4.1672 4.1873 4.2074 4.2275 4.2476 4.2677 4.2978 4.3179 4.3380 4.3581 4.3782 4.3983 4.4184 4.4385 4.4586 4.4787 4.4988 4.5189 4.5390 4.5591 4.5792 4.5993 4.6194 4.6395 4.6596 4.6797 4.6998 4.7199 4.72100 4.74请注意,立方根的计算结果保留两位小数。
实用的平方根表立方根表
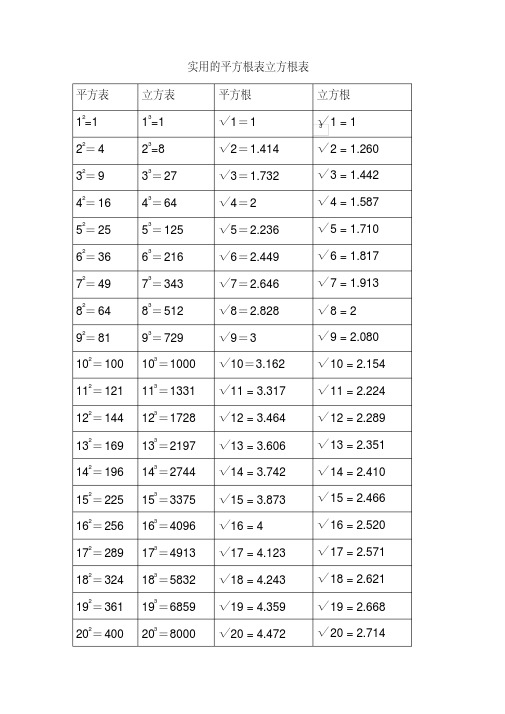
3 实用的平方根表立方根表平方表立方表平方根立方根12=1 13=1 √1=1 √1 = 1 22=4 23=8 √2=1.414 √2 = 1.260 32=9 33=27 √3=1.732 √3 = 1.442 42=16 43=64 √4=2 √4 = 1.587 52=25 53=125 √5=2.236 √5 = 1.710 62=36 63=216 √6=2.449 √6 = 1.817 72=49 73=343 √7=2.646 √7 = 1.913 82=64 83=512 √8=2.828 √8 = 2 92=81 93=729 √9=3 √9 = 2.080 102=100 103=1000 √10=3.162 √10 = 2.154 112=121 113=1331 √11 = 3.317 √11 = 2.224 122=144 123=1728 √12 = 3.464 √12 = 2.289 132=169 133=2197 √13 = 3.606 √13 = 2.351 142=196 143=2744 √14 = 3.742 √14 = 2.410 152=225 153=3375 √15 = 3.873 √15 = 2.466 162=256 163=4096 √16 = 4 √16 = 2.520 172=289 173=4913 √17 = 4.123 √17 = 2.571 182=324 183=5832 √18 = 4.243 √18 = 2.621 192=361 193=6859 √19 = 4.359 √19 = 2.668 202=400203=8000√20 = 4.472√20 = 2.7143√0 = 0(表示根号0等于0,下平方根表立方根表√1 = 1√2 = 1.414√3 = 1.732√4 = 2√5 = 2.236√6 = 2.449√7 = 2.646√8 = 2.828√9 = 3√10 = 3.162√11 = 3.317√12 = 3.464√13 = 3.606√14 = 3.742√15 = 3.873√16 = 4√17 = 4.123√18 = 4.243√19 = 4.359√20 = 4.472其中专业理论知识内容包括:保安理论知识、消防业务知识、职业道德、法律常识、保安礼仪、救护知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立方根(宋爱玲)
教师寄语:路漫漫其修远兮,吾将上下而求索
学习目标:1、了解立方根的概念,会用符号表示一个数的立方根
2、能够利用立方运算求某些数的立方根,了解开立方与立方的互逆运算关系,类比思想。
3、数学知识源于现实生活并应用于现实生活
学习过程:
(一)课前准备
1、小明的爸爸打算制作一个封闭的铁皮正方体,其体积为1.728m3,你能帮其求一下要准备多大面积的铁皮吗?
2、请同学们回忆一下,平方根我们是如何定义的?平方根有哪些性质?
(二)自主学习
1、看课本P146了解立方根的产生
2、立方根的概念:
立方根的表示方法:
开立方:
3、回顾引例,设正方体边长为x,则可以得到什么式子?
在你所得到的式子中,谁是谁的立方根?
练习:用根号表示下列各数的立方根:
(三)合作交流
1、尝试对比平方根的性质,讨论一下立方根的性质?
2、立方根的性质
3、同桌共同解决以下几个问题:
①立方等于-8的数有几个?-8的立方根是多少?
②立方等于-8/27的数有几个?-8/27的立方根是多少?
③27/8的立方根是多少?-27/8的立方根是多少?0的立方根是多少?
(四)归纳总结
你能总结出平方根和立方根的异同点吗?
相同点: (1)0的平方根、立方根都有一个是0
(2)平方根、立方根都是开方的结果。
不同点:(1)定义不同。
(2)个数不同。
(3)表示方法不同。
(4)被开方数的取值范围不同。
1、分析以下判断题,并指明其错误
①327的立方根是3。
②327的立方根是±33。
2、求下列各数的立方根:
3、理解立方与开立方的区别与联系。
本节课的收获:通过本节课的学习,你的收获是什么?
(六)有效训练:
1、已知x 3=b ,则b 是x 的 ,x 是b 的 。
2、8/125的立方根是 。
3、-327=_______=________。
4、若x 3=64,则
5、若y 3=64,则
6、38开立方所得的数是 。
7、(2005黄冈)立方等于-64的数是 。
补充练习
1.求下列各数的立方根: 0,1,-8127,6,-1000
125,0.001 2.求下列各式的值:
3233333333)27
8(;)2(;)2(;16463;1251;1;027.0------ 3.下列说法对不对?
-4没有立方根;
1的立方根是±1;
36
1的立方根是61; -5的立方根是-35;
64的算术平方根是
4.某化工厂使用一种球形储气罐储藏气体.现在要造一个新的球形储气罐,如果它的体积是原来的8倍,那么它的半径是原储气罐半径的多少倍?
(七)课后作业:A 层:完成课本P147 练习 P148 A 组
B 层:完成课本P148 B 组。
