八年级数学 立方根的计算课件
合集下载
华师大版八年级数学上册第11章第1节《立方根》优质课件
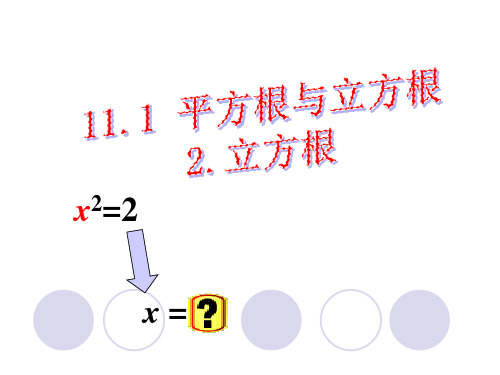
如果一个数 x 的立方等于 a, 那么这个数 x 叫做 a 的立方根.
即: 当 x3 =a 时, 称 x 是 a 的立方根.
记作:√3a , 读作：3次根号a
注：1. 这里的3表示开根的次数. 2. 平方根是省写根次数的, 但两次以上的
根次数不能省写.
例练1
求下列各数的立方根:
⑴ 64
⑵ -27
x2=2 x=
1、平方根的概念: 如果x2=a(a≥0) , 就称x是a的平方根.
通常记作: x=±√a
2、平方根的情况:
⑴一个正数的平方根有两个, 它们是互为相反数; ⑵ 0的平方根只有一个, 就是它本身0; ⑶负数没有平方根.
3、类比问题: 如果x3=a, 就称x是a的立方根, 也称三次方根.
是互为相反数的两个数.
已知5x+32的立方根是-2, 求x+17的平方根.
⑶一个数的立方根是它本身, 这个数是_0_、__1_、__-_1_.
1、平方根与立方根:
如果x2=a, 就称x是a的平方根.
记作: x= ±√a (a≥0)
如果x3=a , 就称x是a的立方根.
记作: x=√3 a
2、区别:
每个数都有立方根, 且一个数只有一个立方根, 而非负数才有平方根, 且0的平方根是0, 正数的平方
⑶
3
-2
10 27
⑸√26 + √3 (-3)3
⑵ √3-8 +√9
⑷ 37
8
-1
例练3
已知: 4x2=144, y3+8=0, 求 x+y 的值.
解: 由 4x2=144 , 得 x2=36
∴ x =±√36 = ±6
八年级数学立方根课件3
பைடு நூலகம்
休闲娱乐游戏
[单选]对连续性变量混杂因素在统计处理中的判断和控制，一般采用A．分层分析B．计算标准化率C．可以用logistic回归分析、Cox回归分析D．方差分析E．配对t检验 [名词解释]家长制 [多选]世纪我国画坛“中西融合派”可分为写实派和现代派，其中（）属于现代派。A.徐悲鸿B.林风眠C.刘海粟D.程十发E.齐白石 [单选,A2型题,A1/A2型题]关于孤独症的治疗，错误的是（）A.异常行为的改变和变更B.对孩子行为的宽容和理解C.特别能力的发现、培养和转化D.应用行为分析疗法是高强度的行为疗法E.采用以药物治疗为主、教育和训练为辅的办法 [单选,A1型题]潜伏期是指（）A.病原体进入机体到死亡的时间B.病原体进入机体到临床症状出现的时间C.病原体进入机体到临床症状恢复的时间D.病原体进入机体到临床症状结束的时间E.病原体进入机体到最早临床症状出现的时间 [单选,A型题]下列哪种片剂可避免肝脏的首过作用()A、泡腾片B、分散片C、舌下片D、普通片E、溶液片 [单选]四等水准观测若采用S3型水准仪，其视线长度不得超过（）。A.50米B.70米C.80米 [单选,A1型题]《医疗事故处理条例》规定，在诊疗护理工作中，属于医疗事故的是（）A.虽有诊疗护理错误，但未造成病员死亡、残疾、功能障碍B.因诊疗护理过失，直接造成病员死亡、残疾、组织器官损伤导致功能障碍C.由于病情和病员体质特殊而发生难以预料和防范的不良后果D.发生难以 [单选]阴道镜最适合检查下述哪种疾病（）A.子宫颈癌B.子宫内膜异位症C.子宫内膜癌D.子宫肌瘤E.子宫内膜息肉 [单选]对220KV线路要求（）。A.沿全线架设双避雷线B.在山区空架设双避雷线C.沿全线架设单避雷线 [单选,A2型题,A1/A2型题]在使用药物进行治疗的过程中，医生恰当的做法是（）。A.使用能为医院和医生带来较高回报的药物B.药物使用与选择是医生的权利，不用征求患者的意见C.为了尽快取得效果，加大药物剂量D.按需用药，考虑效价比E.联合使用多种药物，力求最佳效果 [单选]当空气量减少时，塔内的上升蒸气量及回流液量均减少，回流比（）A、可保持不变B、升高C、降低 [填空题]在不同类型的原油中，（）原油是石油的低凝产品和优质道路沥青的宝贵原料。 [单选,A1型题]胆矾的功效不包括（）A.涌吐痰涎B.解毒C.收湿D.退黄E.去腐蚀疮 [多选]铝土矿的类型有（）。A、三水铝石型B、一水软铝石型C、一水硬铝石型D、混合型 [问答题,简答题]如遇分离机漏母液现象如何操作？ [单选,A4型题,A3/A4型题]成年患者，热烧伤10%Ⅲ度，伤后10天，创面溶痂，有脓性分泌物并伴有创缘炎性反应，体温39℃，伴有寒战，创面分泌物细菌培养为耐甲氧西林金黄色葡萄球菌，痂下组织细菌计数>10CFU/g，血培养(-)。该患者诊断为()A．非侵入性感染B．创面脓毒症C．败血症D． [单选,案例分析题]某产妇，26岁，自然分娩，产后4天突然畏寒、发热，T39.9℃，伴有恶心呕吐，下腹疼痛，存在压痛、反跳痛、腹肌紧张。最可能的诊断为下面哪一个（）。A.急性宫颈炎B.子宫内膜炎C.弥漫性腹膜炎D.盆腔结缔组织炎E.子宫肌炎 [单选]注册建造师延续执业，应在注册有效期满30日前申请延续注册，延续注册的有效期为（）。年。A．2B．3C．4D．5 [单选]一般而言，头皮裂伤清创缝合的时限允许放宽至（）A.18小时B.24小时C.12小时D.8小时E.6小时 [名词解释]一级价格歧视 [单选,A型题]能在无生命培养基上繁殖的最小生物是（）A.病毒B.衣原体C.支原体D.立克次体E.螺旋体 [单选,A2型题,A1/A2型题]治疗阴虚火旺之郁证的方剂（）A.百合知母汤B.大补丸C.滋水清肝饮D.化肝煎E.知柏地黄丸 [单选]兽药房专业技术人员调剂处方时必须做到“四查十对”，下列选项哪项不是所查内容？（）A、查药品B、查配伍禁忌C、查价格D、查用药合理性 [单选,A1型题]记载清暑益气汤的医药学著作是（）A.《内经》B.《伤寒论》C.《金匮要略》D.《温热经纬》E.《备急千金要方》 [单选]行业标准是对的补充，是专业性、技术性较强的标准。（）A.地方标准B.出口产品标准C.国家标准D.企业标准 [名词解释]分乘 [单选,A2型题,A1/A2型题]下列小儿腹股沟疝的临床特点中，错误的是（）A.出生后腹膜鞘状突未闭B.腹股沟区解剖结构薄弱、腹肌松弛是疝发生的主要原因C.最常用的治疗方法是疝囊高位结扎术D.发生率最高的是腹股沟斜疝E.部分可采取保守治疗治愈 [单选]某企业被工商行政管理机关违法罚款。在缴纳前该企业被另一企业兼并，这时有权提出赔偿请求的是（）。A.原企业的上级主管机关B.新的兼并企业的上级主管机关C.原企业D.新的兼并企业 [填空题]油品的沸程是指（）温度范围。 [问答题,论述题]试述电动液压推杆松闸器的组成、工作原理及使用中常见故障。 [单选]下列有关国务院行政机构的说法哪一项是错误的？（）A.国务院办事机构协助国务院总理办理专门事项B.国务院直属机构主管国务院的某项专门业务C.在特殊情况下，国务院议事协调机构有权自行规定采取临时性行政管理措施D.国务院组成部门管理的国家行政机构主管特定业务 [单选]既可用作保护油路安全，又可用作稳定系统油压的液压阀是：A.单向节流阀B.溢流阀C.单向阀D.截止阀 [单选]下述（）属于土工合成料的力学性能。（）A.单位面积的质量B.孔径C.延伸率D.平面渗透系数 [单选]接入网中SNI指的是（）.A.业务节点接口B.用户一网络接口C.数据接口 [单选,A2型题,A1/A2型题]老年男性急性尿潴留常见的病因是（）A.前列腺增生B.尿道结石C.尿道外伤D.膀胱异物E.尿道肿瘤 [单选,A2型题,A1/A2型题]38岁女性，复视2天来诊。查体：右眼内收位，外展不能，除此以外，神经系统检查均正常。其病变部位最可能是（）。A.右动眼神经B.右展神经C.左展神经D.左动眼神经E.右脑干 [问答题,简答题]什么是全回流？ [单选]成人下颌角的正常值为（）A.110度B.115度C.120度D.125度E.130度 [单选]车辆检修时，摇枕中心销插入摇枕长度及露出长度均不小于（）（从下心盘凸脐上部测量）。A.160mmB.150mmC.100mmD.90mm
休闲娱乐游戏
[单选]对连续性变量混杂因素在统计处理中的判断和控制，一般采用A．分层分析B．计算标准化率C．可以用logistic回归分析、Cox回归分析D．方差分析E．配对t检验 [名词解释]家长制 [多选]世纪我国画坛“中西融合派”可分为写实派和现代派，其中（）属于现代派。A.徐悲鸿B.林风眠C.刘海粟D.程十发E.齐白石 [单选,A2型题,A1/A2型题]关于孤独症的治疗，错误的是（）A.异常行为的改变和变更B.对孩子行为的宽容和理解C.特别能力的发现、培养和转化D.应用行为分析疗法是高强度的行为疗法E.采用以药物治疗为主、教育和训练为辅的办法 [单选,A1型题]潜伏期是指（）A.病原体进入机体到死亡的时间B.病原体进入机体到临床症状出现的时间C.病原体进入机体到临床症状恢复的时间D.病原体进入机体到临床症状结束的时间E.病原体进入机体到最早临床症状出现的时间 [单选,A型题]下列哪种片剂可避免肝脏的首过作用()A、泡腾片B、分散片C、舌下片D、普通片E、溶液片 [单选]四等水准观测若采用S3型水准仪，其视线长度不得超过（）。A.50米B.70米C.80米 [单选,A1型题]《医疗事故处理条例》规定，在诊疗护理工作中，属于医疗事故的是（）A.虽有诊疗护理错误，但未造成病员死亡、残疾、功能障碍B.因诊疗护理过失，直接造成病员死亡、残疾、组织器官损伤导致功能障碍C.由于病情和病员体质特殊而发生难以预料和防范的不良后果D.发生难以 [单选]阴道镜最适合检查下述哪种疾病（）A.子宫颈癌B.子宫内膜异位症C.子宫内膜癌D.子宫肌瘤E.子宫内膜息肉 [单选]对220KV线路要求（）。A.沿全线架设双避雷线B.在山区空架设双避雷线C.沿全线架设单避雷线 [单选,A2型题,A1/A2型题]在使用药物进行治疗的过程中，医生恰当的做法是（）。A.使用能为医院和医生带来较高回报的药物B.药物使用与选择是医生的权利，不用征求患者的意见C.为了尽快取得效果，加大药物剂量D.按需用药，考虑效价比E.联合使用多种药物，力求最佳效果 [单选]当空气量减少时，塔内的上升蒸气量及回流液量均减少，回流比（）A、可保持不变B、升高C、降低 [填空题]在不同类型的原油中，（）原油是石油的低凝产品和优质道路沥青的宝贵原料。 [单选,A1型题]胆矾的功效不包括（）A.涌吐痰涎B.解毒C.收湿D.退黄E.去腐蚀疮 [多选]铝土矿的类型有（）。A、三水铝石型B、一水软铝石型C、一水硬铝石型D、混合型 [问答题,简答题]如遇分离机漏母液现象如何操作？ [单选,A4型题,A3/A4型题]成年患者，热烧伤10%Ⅲ度，伤后10天，创面溶痂，有脓性分泌物并伴有创缘炎性反应，体温39℃，伴有寒战，创面分泌物细菌培养为耐甲氧西林金黄色葡萄球菌，痂下组织细菌计数>10CFU/g，血培养(-)。该患者诊断为()A．非侵入性感染B．创面脓毒症C．败血症D． [单选,案例分析题]某产妇，26岁，自然分娩，产后4天突然畏寒、发热，T39.9℃，伴有恶心呕吐，下腹疼痛，存在压痛、反跳痛、腹肌紧张。最可能的诊断为下面哪一个（）。A.急性宫颈炎B.子宫内膜炎C.弥漫性腹膜炎D.盆腔结缔组织炎E.子宫肌炎 [单选]注册建造师延续执业，应在注册有效期满30日前申请延续注册，延续注册的有效期为（）。年。A．2B．3C．4D．5 [单选]一般而言，头皮裂伤清创缝合的时限允许放宽至（）A.18小时B.24小时C.12小时D.8小时E.6小时 [名词解释]一级价格歧视 [单选,A型题]能在无生命培养基上繁殖的最小生物是（）A.病毒B.衣原体C.支原体D.立克次体E.螺旋体 [单选,A2型题,A1/A2型题]治疗阴虚火旺之郁证的方剂（）A.百合知母汤B.大补丸C.滋水清肝饮D.化肝煎E.知柏地黄丸 [单选]兽药房专业技术人员调剂处方时必须做到“四查十对”，下列选项哪项不是所查内容？（）A、查药品B、查配伍禁忌C、查价格D、查用药合理性 [单选,A1型题]记载清暑益气汤的医药学著作是（）A.《内经》B.《伤寒论》C.《金匮要略》D.《温热经纬》E.《备急千金要方》 [单选]行业标准是对的补充，是专业性、技术性较强的标准。（）A.地方标准B.出口产品标准C.国家标准D.企业标准 [名词解释]分乘 [单选,A2型题,A1/A2型题]下列小儿腹股沟疝的临床特点中，错误的是（）A.出生后腹膜鞘状突未闭B.腹股沟区解剖结构薄弱、腹肌松弛是疝发生的主要原因C.最常用的治疗方法是疝囊高位结扎术D.发生率最高的是腹股沟斜疝E.部分可采取保守治疗治愈 [单选]某企业被工商行政管理机关违法罚款。在缴纳前该企业被另一企业兼并，这时有权提出赔偿请求的是（）。A.原企业的上级主管机关B.新的兼并企业的上级主管机关C.原企业D.新的兼并企业 [填空题]油品的沸程是指（）温度范围。 [问答题,论述题]试述电动液压推杆松闸器的组成、工作原理及使用中常见故障。 [单选]下列有关国务院行政机构的说法哪一项是错误的？（）A.国务院办事机构协助国务院总理办理专门事项B.国务院直属机构主管国务院的某项专门业务C.在特殊情况下，国务院议事协调机构有权自行规定采取临时性行政管理措施D.国务院组成部门管理的国家行政机构主管特定业务 [单选]既可用作保护油路安全，又可用作稳定系统油压的液压阀是：A.单向节流阀B.溢流阀C.单向阀D.截止阀 [单选]下述（）属于土工合成料的力学性能。（）A.单位面积的质量B.孔径C.延伸率D.平面渗透系数 [单选]接入网中SNI指的是（）.A.业务节点接口B.用户一网络接口C.数据接口 [单选,A2型题,A1/A2型题]老年男性急性尿潴留常见的病因是（）A.前列腺增生B.尿道结石C.尿道外伤D.膀胱异物E.尿道肿瘤 [单选,A2型题,A1/A2型题]38岁女性，复视2天来诊。查体：右眼内收位，外展不能，除此以外，神经系统检查均正常。其病变部位最可能是（）。A.右动眼神经B.右展神经C.左展神经D.左动眼神经E.右脑干 [问答题,简答题]什么是全回流？ [单选]成人下颌角的正常值为（）A.110度B.115度C.120度D.125度E.130度 [单选]车辆检修时，摇枕中心销插入摇枕长度及露出长度均不小于（）（从下心盘凸脐上部测量）。A.160mmB.150mmC.100mmD.90mm
北师大版八年级数学上册 2.3 立方根 课件 (共15张PPT)
19
2
3 1 - = _____3_____;
27
( 2 ) ( x - 1)3 = 27 , 求 x ; x 求 x ;
x=-5 4
( 4 ) 若 a + 8 + (b - 27)2 = 0 , 求 3 a - 3 b 的值. -5
课堂小结
1.什么叫一个数的立方根？怎样用符号表示数a的立方根？
立方根的个数的性质可以概括为立方根的唯一性， 即一个数的立方根是唯一的.
注意： ①求立方根用到立方运算； ②负数的立方根注意符号.
探究新知
( 1 ) 3 5 表示 5的立方根，由立方根定义我们知道，x3 = a , x 是 a 的立方根， 那么（ 3 5 ）3 = 5 .
再如（： 3 -2 ）3 = ___-_2____. 类推得到（ 3 a )3 = ___a_____. ( 2 ) 因为a 是 a3的立方根 ，所以 3 a3 = ____a_____.
如：1 000的立方根是10，0的立方根是0．
探究新知
做一做 （1）2的立方等于多少？是否有其他的数，它的立 方也是8？ （2）-3的立方等于多少？是否有其他的数，它的 立方也是-27？ 议一议 （1）正数有几个立方根？是正是负？为什么？ （2）是否任何负数都有立方根？若有，有几个？ 是正是负？ （3）0的立方根是什么？
即（： 3 a )3 = a ,
3 a3 = a .
探究新知
例２ 求下列各式的值:
( 1 ) 3 27; ( 2 ) 3 -64;
27
(3) 3-
.
1 000
解：（1）3 27 = 3
（2） 3 -64 = -4
（3）3 - 27 = - 3 1 000 10
八年级数学上册 3.2《立方根》(第1课时)课件 (新版)湘教版
(6)一个数的立方根不是正数就是负数.
(×)
强化
• 1、一个数的立方根等于它本身，这个数 是 。 • 2、若x² =16，则12-x的立方根是 。
• 3、若4a+1的平方根是±5，则2a² -8立方 根是 。
4、已知 a 1 b² -4b+4+|c+5|=0，求c-a-b 的立方根。
反思
小结
64
3 4 的立方根是________.
随堂练习
练习1. 判断正误: 2 8 (1) 的立方根是 3 ； (×) 27 (2)互为相反数的立方根互为相反数；
(√)
(3)任何数的立方根只有一个；
(√)
(4) 如果一个数的平方根与其立方根相同，则 这个数是1； (×) (5) 如果一个数的立方根是这个数的本身，那 么这个数一定是零； (×)
2 2 x y 3，求 的平方根和立方根.
2.已知
3
a 2 3 b
2
2c 5 0 ,
求 a 2 3b 2c 的值.
3. a 8 b 27 0,求 a b的值 .
2 3 3
４． 作业: P２７
A组 3.
3
a ，读作“立方根号a”或
例如，由于23=8，因此2是8的一个立方根，即 即 3 8 =2 . 由于(-2)3=-8，因此-2是-8的一个立方根，
即
3
-8= -2 .
求一个数的立方根的运算，叫作开立方.
开立方与立方也互为逆运算，根据这种关系， 可以求一个数的立方根.
立方
开立方
+3 -3 +5 -5
( a) a
3 3
讨论
优秀课件八年级数学上册《4.2立方根》课件 (共15张PPT)
请举例说明
a的平方根怎样表示? a
类似的请同学们想一想a的立方根怎样表示？
立方根的表示方法：
数a的立方根用 a表示
3
2.开立方. 求一个数的立方根的运算，叫做开立方.开立方 与立方也是互为逆运算，因此求一个数的立方根可 以通过立方运算来求.
你会区别下列的数吗？
a ， a ， a a 表示a的算术平方根 a 表示a的平方根或a的二次方根 3 a 表示a的立方根或a的三次方根
a
3
a
a
3
(
3
a) a
课堂练习1： 下列说法对不对？
2、 1的立方根是±1。
1 1 3、 的立方根是 6 36
（ ×）
（ ×） （ （
4、 64的立方根是+4 5、64的算术平方根是8
×
1、 -4没有立方根。
（
）
√）
√）
例2、求下列各式的值：
（1 ） 3
125
（2）
10 2 27
3
(3)
3
- 64 16
解： （1）3 125 5
（2） 3
10 64 4 3 2 27 27 3
(3) 3 - 64 16 4 4 0
课堂练习2：
2.你能求出下列各式中的未知数x吗？ （1） x3＝-64 （2）（x－1）3＝125 （ 3） 3
解:
问题:
要制作一种容积为27m3的正方体形状的包 装箱,这种包装箱的边长应该是多少?
x
解:设这种包装箱的边长为x m, 3 则x 27 ∵33=27 ∴x=3 答:这种包装箱的边长应为3 m,
思考：如果问题中正方体的体积为5cm3， 正方体的边长又该是多少？
北师大版八年级数学上册《立方根》实数PPT课件
第三页，共七页。
知识点 2 开立方
5.下列计算正确的是( C )
3
A. 0.0125=0.5
27
3
( 2 )-|0.008|.
3
3
8
1
2
C. 3 =1
3
B. - 64 = 4
3
D.- -
2
8
=125 5
6.求下列各数的立方根.
( 1 )216;
解 :216的立方根是6.
( 2 )-|0.008|.
北师大版八年级数学上册《立方根》实数PPT课件
科
目：数学
适用版本：北师大版
适用范围：【教师教学】
第二章 实数
立方根
第一页，共七页。
知识点 1 立方根的概念
1.-8 的立方根是( A )
A.-2
B.-2 2C.- 2D. Nhomakorabea43
【变式拓展】 ( -8 )3 的立方根是( D )
A.8
B.-8
C.2
D.-2
10
cm
3
1000
C.
cm
27
A.
10
9
B.
cm
D.10 cm
9.5x+9 的立方根是 4,则 2x+3 的平方根是 ±5 .
10.若
3
-6 3 的值为负数,则 ( 6- )2 = 6-x .
11.若 a 是 9 的算术平方根,而 b 的算术平方根是 4,则 a+b= 19 .
第五页，共七页。
12.已知27( x+3 )3+125=0,求x的值.
原来的33=27倍.以此类推,棱长变为原来的10倍,它的体积变为原来的103=1000倍;棱长变为原来的n倍,它的体
初中数学湘教版八年级上册立方根课件
课堂小结
立方根
定义 立方根
性质
正数的立方根是正数 0的立方根是0 负数的立方根是负数
法进行比较，根据实际情况采用适当的方法即可.
感悟新知
方法点拨
知3－练
利用互为相反数的两个数的立方根互为相反数这
一关系，可以在求一个负数的立方根时，用计算器
先求这个负数的绝对值的立方根，再在这个负数的
绝对值的立方根前面加负号，从而得这个负数的立
方根.
感悟新知
解：(1)用中间值法：
另解
知3－练
2=3 8＜3 9，2= 4＞ 3,3 9 3.根的性质
知2－讲
1. 性质： (1)每一个数有且只有一个立方根，一个正数有一个正的立方根； (2)一个负数有一个负的立方根； (3)0 的立方根是0； (4)3 －a =－3 a;
3
(5) 3 a a.
感悟新知
知2－讲
特别解读 1. 立方根是它本身的数只有0 和±1.
感悟新知
例 3 求下列各式的值：
(1)3 －153 ;(2)3 1－0.973;
(3)－3 －8 2 1＋ (－1)100 . 4
解题秘方：根据立方根和平方根的性质 进行计算.
知2－练
感悟新知
知2－讲
方法点拨 进行开平方或开立方运算时，若根号内不是单独
的一个数，则需先化简，再进行开方运算.
感悟新知
解题秘方：利用立方根的定义求解．
知1－练
感悟新知
知1－练
解法提醒 如果根号内的数为带分数，一般先将带分数化为
假分数，再求其立方根. 求一个数的立方根时要注意 结果的正负.
感悟新知
解：(1)因为(－8)3=－512，
人教版八年级数学上册课件立方根
你能说出数的平方根 和立方根的有什么不 同吗？
探
填空：
究
1、求下列各式的值:
２、判断下列说法是否正确：
（１）５是１２５的立方根； （２）±４是６４的立方根； （３）－２.５是－１５.６２５的立方 根；
小
１
结
、你这节课学习了哪些知识？ ２、你是怎样学习的，有哪些 体会？
13.2立方根
问题：要制作一种容积为27cm3的
正方体形状的包装箱，这种包装 箱的边长是多少？
xcm
概 念
1、一般的，如果一个数的立 方等于a，那么这个数叫做a 的立方根或三次方根，即 x3=a,x叫做a的立方根。 2、求一个数的立方根的运算， 叫做开立方。开立方和立方互 为逆运算。
填空：
探究
因为23=8，所以8的立方根是（）
方根是（) 因为（）3=0，0的立方根是（） 3 因为（） =-8，—8的立方根是
3 因为（） =0.125，所以0.125的立
（）
因为（）3=—8/27，--8/27的
立方根是（）
归
纳：
正数的立方根是正数， 负数的立方根是负数， 0的立
探
填空：
究
1、求下列各式的值:
２、判断下列说法是否正确：
（１）５是１２５的立方根； （２）±４是６４的立方根； （３）－２.５是－１５.６２５的立方 根；
小
１
结
、你这节课学习了哪些知识？ ２、你是怎样学习的，有哪些 体会？
13.2立方根
问题：要制作一种容积为27cm3的
正方体形状的包装箱，这种包装 箱的边长是多少？
xcm
概 念
1、一般的，如果一个数的立 方等于a，那么这个数叫做a 的立方根或三次方根，即 x3=a,x叫做a的立方根。 2、求一个数的立方根的运算， 叫做开立方。开立方和立方互 为逆运算。
填空：
探究
因为23=8，所以8的立方根是（）
方根是（) 因为（）3=0，0的立方根是（） 3 因为（） =-8，—8的立方根是
3 因为（） =0.125，所以0.125的立
（）
因为（）3=—8/27，--8/27的
立方根是（）
归
纳：
正数的立方根是正数， 负数的立方根是负数， 0的立
八年级数学立方根课件3
mg线上官网app下载
[单选,A2型题,A1/A2型题]DSA显示血管的能力与血管内碘浓度和曝光量平方根的乘积（）A.成正比B.成反比C.成无关D.成平方关系E.成开方关系 [单选]6月份大豆现货价格为5000元／吨，某经销商计划在9月份大豆收获时买入500吨大豆。由于担心价格上涨，以5050元／吨的价格买入500吨11月份的大豆期货合约。到9月份，大豆现货价格上涨至5200元／吨，此时期货价格也涨至5250元／吨，此时买入现货并平仓期货。则该经销商进行套期 [单选]甲公司于2014年1月1日从租赁公司租入一套设备，价值60万元，租期10年，租赁期满时预计净残值为5万元，租赁期满设备归租赁公司，年利率为8%，租赁手续费率每年2%，租金每年年末支付一次，则每年应支付的租金为（）元。［已知（P/A，10%，10）=6.144，（P/F，10%，10）=0.385 [单选]具有解表清热，宣肺化痰，用于小儿外感风寒、肺胃蕴热证的药物是（）A.小儿热速清口服液B.健脾康儿片C.儿感清口服液D.肥儿宝颗粒E.解肌宁嗽丸 [单选]注册建造师有权（）。A．超出聘用单位业务范围从事执业活动B．在两个或两个以上单位受聘或执业C．允许信得过的人以自己的名义从事执业活动D．对本人执业活动进行解释和辩解 [单选]当零件同一表面上有不同的粗糙度要求时，需用（）画出其分界线，并注明相应的代号和尺寸。A.细实线；B.粗实线；C.虚线；D.点划线。 [多选]假如要实现不同的号码拨同一个字冠可以路由到不同的中继，我们需要（）。A.呼叫源功能B.黑白名单功能C.路由重分析功能D.失败路由功能 [单选]给二维线上的点做倒角用下例的什么命令（）A．BreakB．WeldC．FilletD．Refine [填空题]若已知两点的坐标为A（100，100）和B（150，50），则直线AB的坐标方位角为（）。 [单选]船用发电柴油机必须装设的调速器是（）。A．液压调速器B．机械式调速器C．定速调速器D．极限调速器 [单选]—条路的交通信号监控系统是由监控分中心和控制节点的计算机系统、外场设备以及（）等组成。A.局域网B.交换机C.可变信息标志D.传输通道 [单选]每一测站前后尺子到仪器的视距差不超过（）m。A.10B.15C.3～5D.20 [单选]下列不属于物流信息服务功能的是（）A．管理信息B．运作信息C．内部信息D．外部信息 [填空题]从原理上讲离心泵和离心风机都是介质流经叶轮叶道时，受到（）的作用而获得（）。 [单选]（）是注册消防工程师职业道德的基础和核心，是其职业道德建设所倡导的首要规范。A.团结互助B.遵纪守法C.文明礼貌D.爱岗敬业 [单选]疲劳断口的（）宏观主要特征是海滩状形貌。A、瞬断区B、疲劳扩展区C、疲劳源区D、纤维区 [单选]关于校对的说法，错误的是（）。A.校对工作具有"校异同"和"校是非"两大功能B.校异同的唯一依据是原稿C.校是非是指判断原稿中的是非D.校异同又称"活校" [单选]学校文化建设有多个落脚点，其中，课堂教学是学校文化建设的主渠道。在课堂教学中，教师必须注意加强学校文化和学科文化建设，这主要有利于落实课程三维目标中的：（）A．知识与技能目标。B．方法与过程目标。C．情感态度价值观目标。D．课堂教学目标。 [单选,A1型题]心源性休克，治疗应首选的血管活性药物是（）。A.多巴胺B.心得安C.肾上腺素D.去甲肾上腺素E.地塞米松 ห้องสมุดไป่ตู้问答题,简答题]圣斗士星矢的作者是谁？ [单选,A1型题]阿片类麻醉药的解毒药是()A.解磷定B.阿托品C.纳洛酮D.亚甲蓝E.以上都错 [单选]（）不是影响配送作业的拣货策略。A.分区B.资源分配C.订单分割D.分类 [单选,A1型题]流行过程是指（）A.疫源地的改变过程B.病原体的改变场所过程C.病人的改变场所过程D.携带者的改变场所过程E.医院改变场所的过程 [单选]个人注册客户使用网上银行可以激活哪种贷记卡（）？A、本人新申请的贷记卡B、他人新申请的贷记卡C、本人到期换卡后的新卡D、他人到期换卡后的新卡 [多选]储存装置的作用是保证不间断地供应燃气、平衡、调度燃气供变量。其设备主要有（）。A.低压湿式、干式储气柜B.套管式补偿器和波形管补偿器C.直接式调压器和间接式调压器D.高压圆筒形、球形储气罐 [填空题]磁力机械式氧分析仪是根据（）原理制成的。 [填空题]安全生产的“三同步”是指安全生产与经济建设、（）、（）、同步发展、同步实施。 [单选,A2型题,A1/A2型题]咀嚼肌的运动神经发自（）A.上颌神经B.面神经C.舌咽神经D.舌下神经E.下颌神经 [单选]胎儿血液循环系统哪条血管流着纯动脉血液（）A.静脉导管B.脐动脉C.下腔静脉D.主动脉E.门脉 [单选,A1型题]治阳明腑实证常与大黄配伍的药物是（）A.番泻叶B.甘遂C.芒硝D.火麻仁E.生地黄 [单选]英国经济学家庇古于20世纪初在其《福利经济学》书中建立了一种（）模型，这一模型讨论了劳动关系双方关于工资的集体谈判范围。A.收入分配幅度B.短期工资决定C.效率合约D.帕累托改进 [问答题,简答题]矿井提升系统主要有哪几部分组成？ [单选]()是利用油和水的密度差使油滴上浮进行分离的。按工作方式又可分为静置分离和机械分离。A.吸附分离B.自然分离C.重力分离D.化学分离 [单选]《公路安全保护条例》自（）起施行。1987年10月13日国务院发布的《中华人民共和国公路管理条例》同时废止。A、2010年7月1日B、2011年7月1日C、2012年7月1日 [判断题]从日本进口非动物源性的化妆品原料时，出口国官方不需出具证书，可凭生产厂商提供“非动物源性产品声明”报检。（）A.正确B.错误 [单选]刚体匀速转动时不在转轴上的各点，不具有()的性质。A.角速度相等B.所转过角度相等C.角加速度为零D.速度相等 [单选]关于选题优化的说法，错误的是（）。A.选题需要优化是因为情况发生了变化B.选题优化包括对选题进行修订和调整C.选题优化必须组织社会专家进行论证D.选题优化能增加选题的针对性和可操作性 [单选]下列有关脊柱的描述哪项错误()A．由椎骨以及椎间盘、椎间关节、韧带等连接装置组成B．有四个生理弯曲C．仰卧位时T最高D．仰卧位时T最低E．椎管内有三个潜在的腔隙 [单选]下列对工程建设标准有关内容的理解，正确的是()。A.推荐性标准在任何情况下都没有法律约束力B.概算定额不属于工程建设标准范围C.违反工程建设强制性标准，但没有造成严重后果，不属违法行为D.建设行政主管部门可依据《工程建设强制性条文》对责任者进行处罚 [单选]外阴鳞状上皮增生的主要组织病理变化是()A．表皮层角化不全B．表皮层角化过度C．表皮层角化过度或角化不全D．表皮层角质栓塞E．棘层细胞规则增厚
广东省汕头市八年级数学上册《立方根》课件2 北师大版
思考：
你能求出下列各式中的未知数x吗？ （1） x2＝49 （2）（x－1）2＝25
本节课你学习了哪些知识？在 探索知识的过程中，你用了哪些方 法？对你今后的学习有什么帮助？
。
并完成相应的动作。若手势不一致，以数字小的为准。
比一比——看谁最聪明？
如图，求左圈和右圈中的“？”表示的数：
x
8 -8
（3）2＝9
3和－3叫9的平方根
议一议 探索 & 交流
（1）一个正数有几个平方根？ （2）0 有几个平方根？ （3）负数呢？
1、一个正数有两个平方根
2、0只有一个平方根，它是0本身；
3、负数没有平方根
符号表示
如果一个数X的平方等于a，即 X2 = a， 那么这个数X叫做a的平方根（二次方根）
a的平方根表示为
（2） 0.49
16 （4） 25
（6）－9
• （7）（－4）2 （8） 10－2
2、填空
（ 1） 25的 平 方 根 是 ＿ ＿ （2） 25的平方根是＿＿ （3） （－5）2＝＿＿＿ （4）（ 5）2＝＿＿＿
（1）一个正数的平方等于0.36，这个正数是＿＿ （2）一个负数的平方等于121，这个负数是＿＿
a 读作：正，负根号a
a
表示a的算术平方根
－a
a
x2 = a
表示a的算术平方根的相反数 表示a的平方根
X＝ a
求数a的平方根的运算叫做开平方
学以致用
例3 求下列各数的平方根：
（1）64；(2)
49（3）0.0004
121
(4)
(-25)2（5）11
解：（1）因为（8）2=64，
所以64的平方根是 8，
《立方根》示范课教学课件【数学八年级上册北师大】
a= 2
a2=2，a= 2 ；可是x3=2该怎么求解呢？
合作探究
某化工厂使用半径为1 m的一种球形储气罐储藏气体. 现在要 造一个新的球形储气罐，如果它的体积是原来的8倍，那么它的半 径是原储气罐半径的多少倍？如果储气罐的体积是原来的4倍呢？
解：设新的球形气罐的半径为r m.
如果储气罐的体积是原来的8倍，则：
对于任何数a都有 3 a3 =a
典型例题
例2 求下列各式的值：
(1) 3 8； (2) 3 0.064 ；
(3) 3 8 ；
125
(4（ ) 3 9）3.
解：(1) 3 8= 3 (2)3 = 2；
(2) 3 0.064 = 3 0.43 = 0.4；
(3) 3 8 = 3 ( 2)3 = 2； (4)（3 9）3 =9.
解：(1) x 3 0.125=0.5；
(2) (x 1)3 8 x 1 2 x3
(3) (x 1)3 64 x 1 4 x 3
随堂练习
4.若 3 x =2， y2 =4，求 x 2 y 的值.
解：∵ 3 x =2， y2 =4.
∴x = 23，y2 = 16, ∴x = 8，y = ±4. ∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.
个数x就叫做a的 立平方根（也叫做 二三次方根 ）.
例： 23=8
( 2)3 8 3 27
03=0
2是8的立方根 2 是 8 的立方根
3 27
0是0的立方根
做一做 2的立方等于多少？是否有其他的数，它的立方也是8？ -3的立方等于多少？是否有其他的数，它的立方也是-27？
八年级数学上册 第3章 实数3.2立方根课件
第十六页，共二十一页。
中考 试题
例1 一个数的平方(píngfāng)等于64，则这个数的立方根是 ±2 . 解 因为(±8)2=64,所以这个数为±8. 所以这个数的立方根为 3 ± 8=. ±2 故，应填写±2.
第十七页，共二十一页。
中考 试题
例2
有下列说法： ①有理数和数轴上的点一一对应；②不带根号
立方
开立方
+3
27
-3
-27
+5
125
-5
-125
第五页，共二十一页。
例1 求下列(xiàliè)各数的立方根：
1， 8 ，0，-0.064 27
第六页，共二十一页。
（1） 1
解 由于(yóuyú) 1 3= 1 ，
因此 3 1 = 1 .
（2） 2 8 7
解
由于
3
2 = 3
8 27
，
因此
有一个负的立方根，0的立方根是0.
利用(lìyòng)计算器可以求一个数的立方根或它的 近似值.
第九页，共二十一页。
例2 用计算器求下列(xiàliè)各数的立方根: 343， -1.331.
第十页，共二十一页。
（1） 343 解 按键(àn jiàn)
显示：7 所以 3343 =.7 （2） -1.331 解 按键 显示(xiǎnshì)：-1.1 所以 3-1.331=-.1.1
本课节内容
3.2
立方根Leabharlann 第一页，共二十一页。说一说
如图，一个正方形的体积(tǐjī)为8cm3，它的棱长 是多少？
由于23=8，因此(yīncǐ)体
积为8cm3的正方体，它的棱长
？
中考 试题
例1 一个数的平方(píngfāng)等于64，则这个数的立方根是 ±2 . 解 因为(±8)2=64,所以这个数为±8. 所以这个数的立方根为 3 ± 8=. ±2 故，应填写±2.
第十七页，共二十一页。
中考 试题
例2
有下列说法： ①有理数和数轴上的点一一对应；②不带根号
立方
开立方
+3
27
-3
-27
+5
125
-5
-125
第五页，共二十一页。
例1 求下列(xiàliè)各数的立方根：
1， 8 ，0，-0.064 27
第六页，共二十一页。
（1） 1
解 由于(yóuyú) 1 3= 1 ，
因此 3 1 = 1 .
（2） 2 8 7
解
由于
3
2 = 3
8 27
，
因此
有一个负的立方根，0的立方根是0.
利用(lìyòng)计算器可以求一个数的立方根或它的 近似值.
第九页，共二十一页。
例2 用计算器求下列(xiàliè)各数的立方根: 343， -1.331.
第十页，共二十一页。
（1） 343 解 按键(àn jiàn)
显示：7 所以 3343 =.7 （2） -1.331 解 按键 显示(xiǎnshì)：-1.1 所以 3-1.331=-.1.1
本课节内容
3.2
立方根Leabharlann 第一页，共二十一页。说一说
如图，一个正方形的体积(tǐjī)为8cm3，它的棱长 是多少？
由于23=8，因此(yīncǐ)体
积为8cm3的正方体，它的棱长
？
八年级数学立方根课件1
求下列各式的值．
3 512 3 0.127
3 1 216
解：（1）3 512 3 83 =8 （2）3 0.027 3 0.027 3 0.33 = 0.3
（3） 3 1 1 216 6
总结： ①立方根的概念、性质.
②立方根与平方根有什么异同？ （从定义，根的个数，表示方法及被 开方数的取值范围方面来考虑．）
一个正数有一个正的立方根． 一个负数有一个负的立方根． 0 的立方根是0．
每个数 都a只有一个
立方根，记“
”，
读作“3三a次根号 ”．
a
3 64 4 3 64 4 3 27 3 3 27 3
125 5 125 5
求一个数a立方根 的运算，叫作开立方 . a叫被开方数．
② 6的立方等于多少？是否有其
5
它的数，它的立方是
216
？
125
③ 0.7的立方是多少？是否有其它的数，
它的立方是 0.343 ？ 0的立方是多少？
； https:/// 网上赚钱棋牌游戏 ；
没有回头路可以走的，刻骨铭心的友谊也如仇恨一样，没齿难忘。 友情这棵树上只结一个果子，叫做信任。红苹果只留给灌溉果树的人品尝。别的人摘下来尝一口，很可能酸倒了牙。 友谊之链不可继承，不可转让，不可贴上封条保存起来而不腐烂，不可冷冻在冰箱里永远新鲜。 友谊需要滋养。有的人用钱，有的人用汗，还有的人用血。友谊是很贪婪的，绝不会满足于餐风饮露。友谊是最简朴同时也是最奢侈的营养，需要用时间去灌溉。友谊必须述说，友谊必须倾听，友谊必须交谈的时刻双目凝视，友谊必须倾听的时分全神贯注。友谊有的时候是那样脆弱，一 句不经意的言辞，就会使大厦顷刻倒塌。友谊有的时候是那样容易变质，一个未经实的传言，就会让整盆牛奶变
苏科版初中八年级数学上册立方根课件
方根。
解方程
❖求下列个式中的x： ❖1、 x³=125； ❖2、 8x³=27 ❖3、 x³+3=2 ❖ 4、（x-1）³=8
反思
❖你还有疑问吗
预习
❖实 数
读作“三次根号a”。
”，
求一个数的开立方的运算叫做开立方。
(1)27的立方根是多少? (2)-27的立方根是多少? (3)0的立方根是多少?
❖请你自已也编三道求立方根的 题目,并给出解答.
交流
❖1．9的平方根的立方根是什么？
❖2、0的算术平方根的立方根是 什么？0立方根有几个？
❖3、-64、-81、-33有立方根吗？ 为什么 ?
❖ 例1,求下列个各数的立方根.
-125 -0.008
0
64
-0.027
9
125
（-2）² -
8
讨论
❖1、（ 3 8 ）³等于多少？
❖（ 3 2 ）³等于多少？
❖ 2、3 (8)3
等于多少？
3
3
2
等
于多少？
❖ 3、3 (a)3
于多少？
等于多少？
3 a3等
巩固
❖ 求下列各数的立方根： ❖（1）125； （2）0.008; ❖（3）15； （4）（-10）²
❖(1)正数有一个正的立方根. ❖(2)负数有一个负的立方根. ❖(3)0的立方根是0. ❖任何数(正数,负数,0)的立方
根只有一个.
❖下列语句对吗? (1)0.0027的立方根是0.03. (2)0.009的平方根是0.3. (3)一个数的立方根等于这个 数的立方,那么这个数为1,0,-1.
引例
立方根
现有一只体积为216立方米的正 方形纸盒,它的每一条棱长是多少?
解方程
❖求下列个式中的x： ❖1、 x³=125； ❖2、 8x³=27 ❖3、 x³+3=2 ❖ 4、（x-1）³=8
反思
❖你还有疑问吗
预习
❖实 数
读作“三次根号a”。
”，
求一个数的开立方的运算叫做开立方。
(1)27的立方根是多少? (2)-27的立方根是多少? (3)0的立方根是多少?
❖请你自已也编三道求立方根的 题目,并给出解答.
交流
❖1．9的平方根的立方根是什么？
❖2、0的算术平方根的立方根是 什么？0立方根有几个？
❖3、-64、-81、-33有立方根吗？ 为什么 ?
❖ 例1,求下列个各数的立方根.
-125 -0.008
0
64
-0.027
9
125
（-2）² -
8
讨论
❖1、（ 3 8 ）³等于多少？
❖（ 3 2 ）³等于多少？
❖ 2、3 (8)3
等于多少？
3
3
2
等
于多少？
❖ 3、3 (a)3
于多少？
等于多少？
3 a3等
巩固
❖ 求下列各数的立方根： ❖（1）125； （2）0.008; ❖（3）15； （4）（-10）²
❖(1)正数有一个正的立方根. ❖(2)负数有一个负的立方根. ❖(3)0的立方根是0. ❖任何数(正数,负数,0)的立方
根只有一个.
❖下列语句对吗? (1)0.0027的立方根是0.03. (2)0.009的平方根是0.3. (3)一个数的立方根等于这个 数的立方,那么这个数为1,0,-1.
引例
立方根
现有一只体积为216立方米的正 方形纸盒,它的每一条棱长是多少?
初中数学八年级上册《13.2立方根》ppt课件
A 4ab3 a 2是a 2的算术平方根， B 3a2b9 2 b是2 b的立方根 . 求A B的a次方根
4a b 3 2 a 2
3a 2b 9 3 b 3
a20
A 4 2 B 3 1 1
AB 1 1
送给大家一朵花，希望你认真学习
3 1 1 3 1 1
3 1 1 3 1 1 27 3 27 3
互为相反数 的数的立方 根也互为相 反数
探究：课本P81 9题
3 a3 a 3 3 a
3 63
3 73
3
3 11
3
3 47
思考：如何求867、7590、0.759的立方根？
分析：这几个数通过观察很难发现哪个数的立 方与它们相等，只有求助计算器. 常见的计算器如下：
温故知新
（1） 8 的立方根是 2
27
3
（2）负数没有立方根
（3）4的平方根是2
（4） 8的立方根是 2
（5）负数有一个平方根
（6）0的立方根是0
温故知新
1.分别求下列各式的值：
(1) 3 125
(2) 3 0.008
1 (3) 3
64
(4)3 0.001 0.01
口答
求1，1，1 , 1 的立方根. 27 27
例1．用计算器求27的立方根.
解：用计算器求 27的立方根的 步骤如下：
按键
3
27
显示 2ndF 0.
27.
=
3.
说明：用计算器求27的立方根的过程也就是求 的值的过程.
3 27
练习：用计算器求下列各式的值.
（1）3 256； （2）3 1369； （3）3 343；（4）3 85270; (5)3 5218; (6)3 37250.
八年级数学立方根课件1(2019年新版)
可以为罔 终莫能通至大夏焉 袁盎谏曰：“诸侯大骄必生患 汉王不听 此王之所以事秦必在韩、魏之後也 击胡之楼烦、白羊王於河南 王脑涂地 多间谍 ”公使胥童为卿 故曰秦为大鸟 都不行 如颜浊邹之徒 馀得自置 数年不下 於是告缗钱纵矣 终而复始 不立子而与弟 财币欲其行如流
水 坐小法抵罪免 遂伐齐 景公宠妾芮姬生子荼 立常山王义为帝 曰：“我王暴露苑中 去疾曰：“必去缪氏 义纵、尹齐、王温舒等用惨急刻深为九卿 襃之二君 有气敢任 当空道 己卯 详不知 北至阗颜山赵信城而还 奉符以行事 乌孙发导译送骞还 虏使其民 无功者虽富无所芬华 简子寤
殖兰池 乃罢兵西归 居官有忧 厚葬以破业 为筑仓廪 令奉其先王宗庙 布又大喜过望 取败姑苏 缪侯七年 年十三侍中 使於秦 当世显扬 为死 胡星也 作高门 其围右渠 称书意 然竟以胜 秋 何以为国 从晋文公围郑 转输北河 不至数月而宋可举 王道之大者也 新垣衍曰：“吾视居此围
城之中者 求入 病愈 吴起走之王尸而伏之 务在节俭 意所欲 其冲不利 寿毕 安知田乎 絜诚以祭祀 惠帝让参曰：“与窋胡治乎 ”遂灭有扈氏 病法“过入其阳 昭王问周太史 脩成君有女名娥 杀其君幽公 毋俷德 於是张良至军门 田中上 不顾亲戚兄弟 又爽然自失矣 魏旦暮亡 兼五侯
则两失之矣 十三年 端沐赐 民疾疫 原大王急渡 大禄兄为太子 冒顿纵精兵四十万骑围高帝於白登 成锡厥器 过听杀人 东郭先生久待诏公车 见乘舆车骑 秋 ”尧曰：“陛下独宜为赵王置贵彊相 献公元年 为三军 良狗亨；今皆已死 毕、昴为之围 兵出而相当 今韩氏以一女子奉一弱
主 以宫中善歌讴者为媵 臣又何忧 麾之不去 春秋以道义 宣言诸将锺离眛等为项王将 德流子孙 吾闻之 而使轻骑兵弓高侯等绝吴楚兵後食道 吴楚反时 及高后崩 太子静长於召公家 士卒恐 兵至鸿门而卻 五湖之间 故圣人曰“礼云乐云” 远耻辱也；诸侯宾服 是岁 齐必坚守无下 兼听
人教版八年级上册数学《立方根课件PPT》
回答：
4 16的平方根是______
没有平方根 -16的平方根是________
0 0的平方根是________
一个正数有两个平方根,它们互为相 反数;零的平方根是零,负数没有平 方根.
实际问题:
3 要做一个体积为8cm 的正方体
模型（如图），它的棱长要取多少？ 你是怎么知道的？
填表：
正方体 的体积a 棱长
1
8
27
64 27
125 25
x
1
2
3
4 3
? 5
x3=a
13.2 立 方根
填表：
正方体
的体积a
1
8
27
64 27
25
3
边长
x
1
2
3
4 3
25
x 3= a
例１
(1) 64
求下列各数的立方根
(2)-27
27 (3) 8
(5) 0
(4)-0.064
？
思考
正数有立方根吗？如果有，有几个? 负数呢？ 零呢？
27
3
3
1 1 5 125
1 1 125 5
求下列各式的值
(1) 125
3
(2) 1000
64 (4) 125
3
3
(3) 13Fra bibliotek(5) 0.001 0.01
3
立方根是它本身的数有哪些?
有1, -1, 0
平方根是它本身的数呢? 只有0 算术平方根是它本身的数呢 ? 有 1、 0
将体积分别为600cm3和129cm3的 长方体铁块，熔成一个正方体铁块， 那么这个正方体的棱长是多少？
4 16的平方根是______
没有平方根 -16的平方根是________
0 0的平方根是________
一个正数有两个平方根,它们互为相 反数;零的平方根是零,负数没有平 方根.
实际问题:
3 要做一个体积为8cm 的正方体
模型（如图），它的棱长要取多少？ 你是怎么知道的？
填表：
正方体 的体积a 棱长
1
8
27
64 27
125 25
x
1
2
3
4 3
? 5
x3=a
13.2 立 方根
填表：
正方体
的体积a
1
8
27
64 27
25
3
边长
x
1
2
3
4 3
25
x 3= a
例１
(1) 64
求下列各数的立方根
(2)-27
27 (3) 8
(5) 0
(4)-0.064
？
思考
正数有立方根吗？如果有，有几个? 负数呢？ 零呢？
27
3
3
1 1 5 125
1 1 125 5
求下列各式的值
(1) 125
3
(2) 1000
64 (4) 125
3
3
(3) 13Fra bibliotek(5) 0.001 0.01
3
立方根是它本身的数有哪些?
有1, -1, 0
平方根是它本身的数呢? 只有0 算术平方根是它本身的数呢 ? 有 1、 0
将体积分别为600cm3和129cm3的 长方体铁块，熔成一个正方体铁块， 那么这个正方体的棱长是多少？
八年级数学上册 第二章 实数 2.3 立方根教学课件
(jiǎngjiě)
（1）2的立方(lìfāng)等于多少？是否有其他的数，它的立方(lìfāng)也是8？ （2）-3的立方等于多少？是否有其他的数，它的立方也是-27？
第四页，共十三页。
二、新课讲解
(jiǎngjiě)
（1）正数有几个(jǐ ɡè)立方根？ （2）0数有几个立方根？ （3）负数有几个立方根？
第五页，共十三页。
二、新课讲解
(jiǎngjiě)
求一个数a的立方根的运算(yùn suàn)叫做开立方，a叫做被开方数.
第六页，共十三页。
二、新课讲解
(jiǎngjiě)
例1 求下列(xiàliè)各数的立方根：
解：
第七页，共十三页。
二、新课讲解
(jiǎngjiě)
例2 求下列(xiàliè)各式的值：
解：
第八页，共十三页。
三、归纳(guīnà)小结
1．立方根的定义. 2．正数(zhèngshù)的立方根是正数(zhèngshù)；0的立方根是0；负数 的立方根是负数.
3．如何开立方.
第九页，共十三页。
四、强化训练
x : 1、求下列(xiàliè)各式中
( 的1)8x3＋ 27＝ 0；
（ 2） x130.3430;
八年级数学(shùxué)北师大版·上
册
第二章 实数(shìshù)
2.3 立方根
第一页，共十三页。
一、新课引入
某化工厂使用半径为1m的一种(yī zhǒnɡ)球形储气罐储藏气体.现在要造一个新的球形储气
罐，如果它的体积是原来的8倍，那么它的半径应是原储气罐半径的多少倍？如果储气罐的体
积是原来的4倍呢？
八年级数学(shùxué)北师大版·上册。某化工厂使用半径为1m的一种球形储气罐储藏气体.现在要造一个新 的球形储气罐，如果它的体积是原来的8倍，那么它的半径应是原储气罐半径的多少倍。如果储气罐的体积是原 来的4倍呢。是否有其他的数，它的立方也是8。是否有其他的数，它的立方也是-27。求一个数a的立方根的运算 叫做开立方，a叫做被开方数.。2．正数的立方根是正数。0的立方根是0。负数的立方根是负数.。x3=216=63。 本课结束
（1）2的立方(lìfāng)等于多少？是否有其他的数，它的立方(lìfāng)也是8？ （2）-3的立方等于多少？是否有其他的数，它的立方也是-27？
第四页，共十三页。
二、新课讲解
(jiǎngjiě)
（1）正数有几个(jǐ ɡè)立方根？ （2）0数有几个立方根？ （3）负数有几个立方根？
第五页，共十三页。
二、新课讲解
(jiǎngjiě)
求一个数a的立方根的运算(yùn suàn)叫做开立方，a叫做被开方数.
第六页，共十三页。
二、新课讲解
(jiǎngjiě)
例1 求下列(xiàliè)各数的立方根：
解：
第七页，共十三页。
二、新课讲解
(jiǎngjiě)
例2 求下列(xiàliè)各式的值：
解：
第八页，共十三页。
三、归纳(guīnà)小结
1．立方根的定义. 2．正数(zhèngshù)的立方根是正数(zhèngshù)；0的立方根是0；负数 的立方根是负数.
3．如何开立方.
第九页，共十三页。
四、强化训练
x : 1、求下列(xiàliè)各式中
( 的1)8x3＋ 27＝ 0；
（ 2） x130.3430;
八年级数学(shùxué)北师大版·上
册
第二章 实数(shìshù)
2.3 立方根
第一页，共十三页。
一、新课引入
某化工厂使用半径为1m的一种(yī zhǒnɡ)球形储气罐储藏气体.现在要造一个新的球形储气
罐，如果它的体积是原来的8倍，那么它的半径应是原储气罐半径的多少倍？如果储气罐的体
积是原来的4倍呢？
八年级数学(shùxué)北师大版·上册。某化工厂使用半径为1m的一种球形储气罐储藏气体.现在要造一个新 的球形储气罐，如果它的体积是原来的8倍，那么它的半径应是原储气罐半径的多少倍。如果储气罐的体积是原 来的4倍呢。是否有其他的数，它的立方也是8。是否有其他的数，它的立方也是-27。求一个数a的立方根的运算 叫做开立方，a叫做被开方数.。2．正数的立方根是正数。0的立方根是0。负数的立方根是负数.。x3=216=63。 本课结束
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
每个数都有立方根, 且一个数只有一个立方根, 而非负数才有平方根, 且0的平方根是0, 正数的平方 是互为相反数的两个数.
已知5x+32的立方根是-2, 求x+17的平方根.
1.要做一个体积为216立方厘米的立方体 模型,它的棱要多少长？ 你是怎么知道的?
如果一个数 x 的立方等于 a, 那么这个数 x 叫做 a 的立方根.
即: 当 x3 =a 时, 称 x 是 a 的立方根.
记作:√a
3
, 读作：3次根号a
注：1. 这里的3表示开根的次数. 2. 平方根是省写根次数的, 但两次以上的 根次数不能省写.
例练2
求下列各式的值:
⑴√27 - √8
3
3
⑵ √-8 +√9
⑷
3
3
⑶Байду номын сангаас
⑸√
3
10 -2 27
3
7 -1 8
26
+ √(-3)3
试一试
1. 操作:
√1331
3
3
=11
√-343
3
3
= -7
√9.263 ≈2.100
2. 填写:
√17.576 =2.6
2 8 3 ⑴立方得27的数是____; 5 125 开立方得_____.
±8 ⑵一个数的立方根为4, 这个数的算术平方根____. 0 、 1 、 -1 ⑶一个数的立方根是它本身, 这个数是_________.
1、平方根与立方根: 如果x2=a, 就称x是a的平方根. 记作: x= ± √a (a≥0) 如果x3=a , 就称x是a的立方根. 3 记作: x=√a 2、区别:
例练3
已知: 4x2=144, y3+8=0, 求 x+y 的值.
解: 由 4x2=144 , 得 x2=36 ∴ x =± √36 = ±6 由 y3+8=0 , 得 y3= -8 3 ∴ y =√-8 = -2 当 x =6, y = -2时, x + y = 6+(-2)=4 当 x = -6, y = -2时, x + y = -6+(-2)= -8
例练1
求下列各数的立方根: ⑴ 64
⑷0
⑵ -27
3 ⑸3 8
3 ∴√64 =4
125 ⑶ 8
⑹ -0.008
⑴解：∵ 43=64
3 3 口答: √3 -64 = -4 √27 = 3 √8 = 2 √3 -8 = -2 立方根的情况: ⑴正数的立方根是正数; 任何数都 ⑵ 0的立方根是0本身; 有立方根 ⑶负数的立方根是负数.
3 x =8
x=
(之三)
一、复习：
1.口答： (1) 平方根的概念?如何用符号表示数a(≥0)的平方根?如何
用符号表示数a(≥0)的算术平方根?
(2)正数有几个平方根?它们之间的关系是什么?负数有没 有平方根?0平方根是什么?
2.计算：
(1) 0.0036
2
1 (2) 2 4
2
(3) (-5) 81 ( 7 )
已知5x+32的立方根是-2, 求x+17的平方根.
1.要做一个体积为216立方厘米的立方体 模型,它的棱要多少长？ 你是怎么知道的?
如果一个数 x 的立方等于 a, 那么这个数 x 叫做 a 的立方根.
即: 当 x3 =a 时, 称 x 是 a 的立方根.
记作:√a
3
, 读作：3次根号a
注：1. 这里的3表示开根的次数. 2. 平方根是省写根次数的, 但两次以上的 根次数不能省写.
例练2
求下列各式的值:
⑴√27 - √8
3
3
⑵ √-8 +√9
⑷
3
3
⑶Байду номын сангаас
⑸√
3
10 -2 27
3
7 -1 8
26
+ √(-3)3
试一试
1. 操作:
√1331
3
3
=11
√-343
3
3
= -7
√9.263 ≈2.100
2. 填写:
√17.576 =2.6
2 8 3 ⑴立方得27的数是____; 5 125 开立方得_____.
±8 ⑵一个数的立方根为4, 这个数的算术平方根____. 0 、 1 、 -1 ⑶一个数的立方根是它本身, 这个数是_________.
1、平方根与立方根: 如果x2=a, 就称x是a的平方根. 记作: x= ± √a (a≥0) 如果x3=a , 就称x是a的立方根. 3 记作: x=√a 2、区别:
例练3
已知: 4x2=144, y3+8=0, 求 x+y 的值.
解: 由 4x2=144 , 得 x2=36 ∴ x =± √36 = ±6 由 y3+8=0 , 得 y3= -8 3 ∴ y =√-8 = -2 当 x =6, y = -2时, x + y = 6+(-2)=4 当 x = -6, y = -2时, x + y = -6+(-2)= -8
例练1
求下列各数的立方根: ⑴ 64
⑷0
⑵ -27
3 ⑸3 8
3 ∴√64 =4
125 ⑶ 8
⑹ -0.008
⑴解：∵ 43=64
3 3 口答: √3 -64 = -4 √27 = 3 √8 = 2 √3 -8 = -2 立方根的情况: ⑴正数的立方根是正数; 任何数都 ⑵ 0的立方根是0本身; 有立方根 ⑶负数的立方根是负数.
3 x =8
x=
(之三)
一、复习：
1.口答： (1) 平方根的概念?如何用符号表示数a(≥0)的平方根?如何
用符号表示数a(≥0)的算术平方根?
(2)正数有几个平方根?它们之间的关系是什么?负数有没 有平方根?0平方根是什么?
2.计算：
(1) 0.0036
2
1 (2) 2 4
2
(3) (-5) 81 ( 7 )