《圆的基本性质》测试题
圆的基本性质 单元能力测试(含答案)

第7题第8题第三章 圆的基本性质能力提升测试卷一、选择题(共10小题,每小题3分,共30分)1. 如图,在⊙O 中,弦AB ∥CD ,若︒=∠40ABC ,则=∠BOD ( ) A. ︒20 B. ︒40 C. ︒50 D. ︒802.如图,点A 、B 、C 在⊙O 上,∠ACB =30°,则sin ∠AOB 的值是( ) A . B .C .D .3.用圆心角为120°,半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( ) A .cm B .3cm C .4cm D .4cm4.如图,AD 为⊙O 的直径,作⊙O 的内接正三角形ABC ,甲、乙两人的作法分别是:甲:1、作OD 的中垂线,交⊙O 于B ,C 两点,2、连接AB ,AC ,△ABC 即为所求的三角形 乙:1、以D 为圆心,OD 长为半径作圆弧,交⊙O 于B ,C 两点。
2、连接AB ,BC ,CA .△ABC 即为所求的三角形。
对于甲、乙两人的作法,可判断( )A .甲、乙均正确B .甲、乙均错误C .甲正确、乙错误D .甲错误,乙正确第4题 第5题 5.如图,已知BD 是⊙O 直径,点A 、C 在⊙O 上,⌒AB =⌒BC,∠AOB =60°,则∠BDC 的 度数是( )A.20°B.25°C.30°D. 40°6.如图,AB 为⊙O 的直径,弦CD ⊥AB 于E ,已知CD =12,则⊙O 的直径为( ) A. 8 B. 10 C.16 D.20第1题 第2题 第3题DCB AO第9题7.如图所示,扇形AOB的圆心角为120︒,半径为2,则图中阴影部分的面积为( )334.-πA2334.-πB3234.-πC34.πD8.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是()A.CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是()A.CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD10.如图所示,圆O的弦AB垂直平分半径OC,则四边形OACB()A、是正方形B、是长方形C、是菱形D、以上答案都不对二、填空题(共6小题,每小题4分,共24分)如图所示的圆面图案是用相同半径的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在黑色区域的概率为.12.如图,AB是⊙O的弦,OC⊥AB于C.若AB=23,0C=1,则半径OB的长为________.13.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为.14.如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成. 已知正三角形的边长为1,则凸轮的周长等于_________.15.如图所示,AB为⊙O的直径,AC为弦,OD∥BC交AC于点D,若AB=20cm,∠A=30°,则AD=cm.16.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交AB于E,交⊙O于D.则AD=_____________.三、解答题(共7题,共66分)17、(本题8分)如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的A BCO第10题第11题第12题第13题第14题第15题第16题中点,AD ⊥BC 于点D .求证:AD =12BF .18(本题8分).如图,⊙O 的直径AB 和弦CD 相交于点E ,∠CEA =30°, 求CD 的长.19.(本题8分)如图所示,OA 、OB 、OC都是圆O 的半径,∠AOB =2∠BOC . 求证:∠ACB =2∠BAC .20、(本题10分)如图,弧AC 是劣弧,M 是弧AC 中点,B 为弧AC 上任意一点,自M 向BC 弦引垂线,垂足为D ,求证:AB +BD =DC 。
圆的基本性质练习(含答案)

圆的基本性质练习(含答案)圆的基本性质考点1 对称性圆既是__________ ①______ 对称图形,又是 _________ ②____ 对称图形。
任何一条直径所在的直线都是它的 _____ ③。
它的对称中心是_ ④ _____________________ 。
同时圆又具有旋转不变性。
温馨提示:轴对称图形的对称轴是一条直线,因此在谈及圆的对称轴时不能说圆的对称轴是直径。
考点2 垂径定理定理:垂直于弦的直径平分_________ ⑤______ 并且平分弦所对的两条__⑥ __________ 。
常用推论:平分弦(不是直径)的直径垂直于__________ ⑦ _______ ,并且平分弦所对的两条 _______ ⑧ ___________ 。
温馨提示:垂径定理是中考中的重点考查内容,每年基本上都以选择或填空的形式出现,一般分值都在3分左右,这个题目难度不大,只要在平时的练习中,多注意总结它所用的数学方法或数学思想等,以及常用的辅助线的作法。
在这里总结一下:(1)垂径定理和勾股定理的有机结合是计算弦长、半径等问题的有效方法,其关键是构造直角三角形;(2)常用的辅助线:连接半径;过顶点作垂线;(3)另外要注意答案不唯一的情况,若点的位置不确定,则要考虑优弧、劣弧的区别;(4)为了更好理解垂径定理,一条直线只要满足:①过圆心;②垂直于弦;③平分弦;④ 平分弦所对的优弧;⑤平分弦所对的劣弧;考点3 圆心角、弧、弦之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧___________ ⑨ _____ ,所对的弦也______ ⑩_________ o常用的还有:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角—a ______________ ,所对的弦____ J2 __________ o(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 _______ 13 _____________ ,所对的弧 __________ 14方法点拨:为了便于理解和记忆,圆心角、弧、弦之间的关系定理,可以归纳为:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应地其余各组量也都相等。
(完整版)圆的基本性质检测试题

圆的基本性质测试题班级 姓名 得分一:选择题(每题3分,共30分)( )1.下列语句中不正确的有①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,对称轴是任意一条直径所在的直线, ④半圆是弧,⑸直径是圆内 最长的弦,⑥等弧所对的圆周角相等. A .3个 B.4个 C .5个 D.6个( )2. 如图,已知⊙O 的半径为5,弦AB=6,M 是AB 上任意一点,则线段OM 的长可能是:A .2.5B .3.5C .4.5D .5.5 ( )3.如图,,已知AB 是⊙O 的直径,∠BOC=400,那么∠AOE=A.400B. 600C.800D.1200( )4.如图,将圆沿AB 折叠后,圆弧 恰好经过圆心,则 ∠AOB 等于:A .60°B .90°C .120°D .150°(第3题) (第4题) (第5题) (第6题)( )5. 两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为A .(45)+ cmB .9 cmC .45cmD .62cm( )6. 如图,BD 是⊙O 的直径,圆周角∠A = 30︒,则∠CBD 的度数是 A .30︒ B .45︒ C .60︒ D .80︒( )7.AB 为⊙O 的直径,C 、D 是⊙O 上的两点,∠BAC =30º,AD =CD ,则∠DAC 的度数是:A .30ºB .60ºC .45ºD .75º(第7题) (第8题) (第9题) (第10题)( )8.如图,在⊙O 中,CD 是直径,弦AB ⊥CD ,垂足为E ,连接BC ,若AB =2cm ,∠BCD =22°30′,则⊙O 的半径为: A .4cm B.2cm C.1cm D.0.5cm ( )9. 已知⊙O 的直径AB=12,弦AC=6,AD=62,则∠CAD=A. 60°B. 450C.1050 或150D. 60°或 450( )10.如图,AB 是⊙O 的直径,AB=2,点C 在⊙O 上,∠CAB=30°,D 为的中点,P 是直径AB 上一动点,则PC+PD 的最小值为: A.22 B.2 C.1 D.2二:填空题(每题3分,共18分)11. 如图,⊙O 的半径OA=10cm ,弦AB=16cm ,P 为AB 上一动点,则点P 到圆心O 的最短距 离为 。
圆基本性质测试

圆的基本性质小测一、选择题(30)()1、如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16, 那么线段OE的长为A、10 B、8 C、6 D、4()2、一条排水管的截面如图所示.已知排水管的截面圆半径10O B=,截面圆圆心O到水面的距离O C是6,则水面宽A B是A.16B.10C.8D.6()3、如图,⊙O是△A BC的外接圆,∠OCB=40°,则∠A的度数等于A.60° B.50° C.40° D.30°()4、如图,⊙O过点B、C,圆心O∠BAC=90°,OA=1,BC=6。
则⊙O的半径为 A.6D.()5、如图,若AB是⊙0的直径,ABD=58°,则∠BCD =A 116°B 32°C 58°D 64°()6、如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为 A.1 B C.2 D.()7、矩形ABCD中,AB=8,BC=P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是A 点B、C均在圆P外;B 点B在圆P外、点C在圆P内;C 点B在圆P内、点C在圆P外D 点B、C均在圆P内.()8、如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD =105°,则∠DCE的大小是A. 115° B. 105°C. 100°D. 95°()9、如图,已知E F是⊙O的直径,把A∠为60 的直角三角板ABC的一条直角边B C放在直线E F上,斜边A B与⊙O交于点P,点B与点O重合.将三角板ABC沿O E方向平移,使得点B与点E重合为止.设POF x∠= ,则x的取值范围是 A.3060x≤≤ B.3090x≤≤C.30120x≤≤ D.60120x≤≤()10、下列说法正确的是A、三点确定一个圆B、直径所对的圆周角是直角C、度数相等的弧是等弧D、相等的圆心角所对的弧相等二、填空题11、若O为ABC∆的外心,且60=∠BOC,则__________=∠BAC12、点P是⊙O所在平面上一定点,点P到圆上的最大距离和最小距离分别为10和2,则该圆的直径为13、在⊙O中,AB为直径,CD为弦,AB⊥CD,P为圆周上与C,D不重合的任意一点,若∠COB=50°,则∠CPD是______________度14、在半径为1的⊙O中,弦AB、AC的长分别为3和2,则∠BAC的度数是___________15、圆的弦长等于它的半径,那么这条弦所对的圆周角的度数是____16、在半径为5cm的⊙O中,弦AB=6cm,弦CD=8cm,且AB∥CD,求AB与CD之间的距离是_________17、在同一平面内有三条公路两两相交,一供电站到这三条公路的距离都相等,则这样的供电站可以建___个18、点M是半径为5的⊙O内一点,且OM=4,在过M点的所有⊙O的弦中,你认为弦长为整数的弦的条数有_____条19、已知点A(2,0),B(-2,0),圆D的圆心为(0,3),半径为2.5。
圆的基本性质练习题

圆的基本性质练习题姓名______________学号__________一.选择题:(本题共10小题,每小题3分,共30分)1. 已知扇形的弧长为π8,扇形的圆心角为060,则这个扇形的半径为( )A. 12B. 24C. 62D. 482.如图,△ABC 的顶点A 、B 、C 均在⊙O 上,若∠ABC+∠AOC=90°,则∠AOC 的大小是( )A. 030B. 045C. 060D. 0703.下列说法正确的是( )A .半圆是弧,弧也是半圆B .三点确定一个圆C .平分弦的直径垂直于弦D .直径是同一圆中最长的弦4.如图,DC 是⊙O 直径,弦AB ⊥CD 于F ,连接BC ,DB ,则下列结论错误的是( )A .弧AD=弧BDB .AF=BFC .OF=CFD D .∠DBC=90°5.已知⊙O 的直径为10,若PO=5,则点P 与⊙O 的位置关系是( )A .点P 在⊙O 内B .点P 在⊙O 上C .点P 在⊙O 外D .无法判断6.如图,A 、B 、C 、D 四个点均在⊙O 上,∠AOD=70°,AO ∥DC ,则∠B 的度数为( )A.40°B.45°C.50°D.55°7.如图,⊙O 的半径为10,若OP=8,则经过点P 的弦长可能是( )A .10B .6C .19D .228. 如图,在半径为13cm 的圆形铁片上切下一块高为8cm 的弓形铁片,则弓形弦AB 的长为( )A 、10cmB 、16cmC 、24cmD 、26cm9.如图,点C 是以AB 为直径的半圆O 的三等分点,AC=2,则图中阴影部分的面积是( )A 、334-πB 、3234-πC 、332-πD 、332-π 10.如图,Rt △ABC 中,AB ⊥BC ,AB=6,BC=4,P 是△ABC 内部的一个动点,且满足∠PAB=∠PBC ,则线段CP 长的最小值为( )A .23 B .2 C .13138 D .131312 二.填空题(本题共6小题,每题4分,共24分)温馨提示:填空题必须是最简洁最正确的答案! 11.一正六边的边长为8,则它的外接圆的直径为_______________12.四边形ABCD 内接于⊙O ,弧AB :弧BC :弧CD=2:3:5,∠BAD=120°,则∠ABC=_____13.如图,将弧AC 沿弦AC 折叠交直径AB 于圆心O ,则弧AC= 度.14.在半径为2的圆中,弦AC 长为1,M 为AC 中点,过M 点最长的弦为BD ,则四边形ABCD 的面积为15.如图,⊙O 是△ABC 的外接圆,AO ⊥BC 于点F ,D 为弧AC 的中点,且弧CD 的度数为70°,则∠BAF=16.如图,⊙O 的半径OD ⊥弦AB 于点C ,连结AO 并延长交⊙O 于点E ,连结EC .若AB=8,CD=2,则EC 的长为________________17. 已知△ABC 的边BC=23cm ,且△ABC 内接于半径为2cm 的⊙O ,则∠A= 度.18.如图,C 、D 是以AB 为直径的圆O 上的两个动点(点C 、D 不与A 、B 重合),在运动过程中弦CD 始终保持不变,M 是弦CD 的中点,过点C 作CP ⊥AB 于点P .若CD=3,AB=5,PM=x ,则x 的最大值是_________.19.如图,△ABC 内接于⊙O ,∠B=90°,AB=BC ,D 是⊙O 上与点B关于圆心O 成中心对称的点,P 是BC 边上一点,连接AD 、DC 、AP .已知AB=8,CP=2,Q 是线段AP 上一动点,连接BQ 并延长交四边形ABCD 的一边于点R ,且满足AP=BR ,则=QRBQ ______ 三.解答题(共6题,共66分) 温馨提示:解答题应将必要的解答过程呈现出来!20(本题6分)如图,AB ,CD 是⊙O 的两条直径,过点A 作AE ∥CD 交⊙O 于点E ,连接BD ,DE ,求证:BD=DE .21(本题8分).如图所示,AB=AC ,AB 为⊙O 的直径,AC 、BC 分别交⊙O 于E 、D ,连结ED 、BE .(1)求证:BE ⊥AC ;(2)求证:BD=DE ;22(本题8分).如图,在直角坐标系中,⊙E 的半径为5,点E (1,﹣4).(1)求弦AB 与弦CD 的长;(2)求点A ,B 坐标.23(本题10分).如图,AB 是⊙O 的直径,弦CD⊥AB 于点E ,点P 在⊙O 上,PB 与CD 交于点F ,∠PBC=∠C.(1)求证:CB∥PD;(2)若∠PBC=22.5°,⊙O 的半径R=2,求劣弧AC 的长度.24.如图,在⊙O 中,两弦AB 与CD 的中点分别是P 、Q ,且⋂⋂=CD AB ,连结PQ ,求证:∠APQ =∠CQP 。
圆的基本性质-测试题
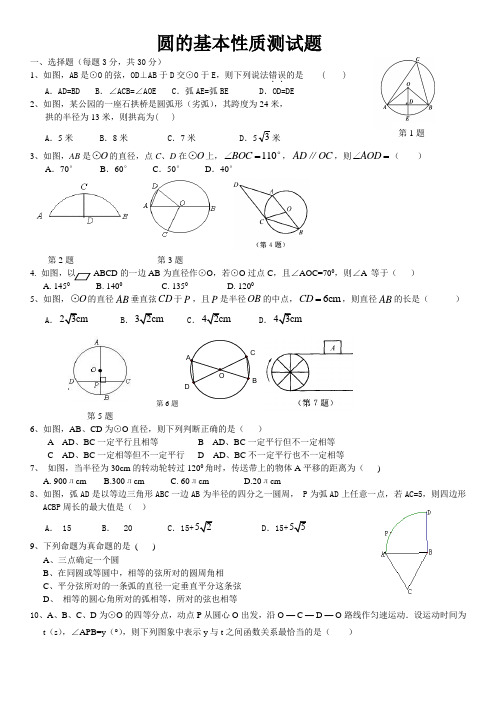
CBOAD圆的基本性质测试题一、选择题(每题3分,共30分)1、如图,AB 是⊙O 的弦,OD ⊥AB 于D 交⊙O 于E ,则下列说法错误..的是 ( ) A .AD=BD B .∠ACB=∠AOE C .弧AE=弧BE D .OD=DE2、如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )A .5米B .8米C .7米D .53米3、如图,AB 是O ⊙的直径,点C 、D 在O ⊙上,110BOC ∠=°,AD OC ∥,则AOD ∠=( )A .70°B .60°C .50°D .40°第2题 第3题4. 如图,以 ABCD 的一边AB 为直径作⊙O ,若⊙O 过点C ,且∠AOC=700,则∠A 等于( ) A. 1450 B. 1400 C. 1350 D. 12005、如图,O ⊙的直径AB 垂直弦CD 于P ,且P 是半径OB 的中点,6cm CD =,则直径AB 的长是( )A .23cmB .32cmC .42cmD .43cm第5题6、如图,AB 、CD 为⊙O 直径,则下列判断正确的是( )A AD 、BC 一定平行且相等B AD 、BC 一定平行但不一定相等 C AD 、BC 一定相等但不一定平行 D AD 、BC 不一定平行也不一定相等7、 如图,当半径为30cm 的转动轮转过1200角时,传送带上的物体A 平移的距离为( ) A. 900лcm B.300лcm C. 60лcm D.20лcm8、如图,弧AD 是以等边三角形ABC 一边AB 为半径的四分之一圆周, P 为弧AD 上任意一点,若AC=5,则四边形ACBP 周长的最大值是( )A . 15B . 20C .15+52D .15+55 9、下列命题为真命题的是 ()A 、三点确定一个圆B 、在同圆或等圆中,相等的弦所对的圆周角相C 、平分弦所对的一条弧的直径一定垂直平分这条弦D 、 相等的圆心角所对的弧相等,所对的弦也相等10、A 、B 、C 、D 为⊙O 的四等分点,动点P 从圆心O 出发,沿O — C — D — O 路线作匀速运动.设运动时间为t (s ),∠APB=y (°),则下列图象中表示y 与t 之间函数关系最恰当的是( )第6题第1题OAC B第16题 第14题图ECDAB二、填空题(每题4分,共32分)11、已知⊙O 的周长为6π,当PO 时,点P 在⊙O 上。
圆的基本测试

圆的基本性质测试一、选择题1.在下列命题中, 正确的是 ( )A.在同圆中, 大弧对大弦B.在同圆中, 大弦对大弧C.在同圆中, 等弧对等弦D.在同圆中, 等弦对等弧 2.如图, AB 是⊙O 的直径, CD 是AO 的垂直平分线, EF 是OB 的垂直 平分线, 则下列结论正确的是 ( )A . AD DF FB == B . AD DF >C . DF FB <D . AD BFDF =≠ 3.在⊙O 中,如果弦AB 所对的圆心角为70°,那么劣弧AB 所对的圆周角是( )A .140°B .70°C .35°D .145° 4.如图:AC 是⊙O 的直径,AB ,CD 是⊙O 的两条弦,且 AB ∥CD .如果∠BAC=32°,则∠AOD=( )A .16°B .32°C .48°D .64° 5.若圆内接四边形一组对边平行,另一组对边相等,则这个四边形是( ) A .平行四边形 B.矩形 C.等腰梯形 D.矩形或等腰梯形 6.若ABCD 内接于圆,则∠A ∶∠B ∶∠C ∶∠D 可能为( ) A .2∶3∶4∶5 B.3∶4∶5∶2 C.4∶5∶3∶2 D.5∶4∶3∶27.如图:圆内接四边形ABCD 的边BA 、DC 延长线交于P ,下列各式中成立的是( )A .P A ∶PC =PB ∶PD B.P A ∶PB =AC ∶BD C.P A ∶PC =PD ∶PB D.PB ∶PD =AD ∶BC8.下列命题中不正确的是( )A. 圆内接平行四边形是矩形B. 圆内接菱形是正方形C. 圆内接梯形是等腰梯形D. 圆内接矩形是正方形9.⊙O 的直径AB = 5,弦CD ⊥AB 于E ,CD = 2 6 ,则AE 为( )(A )2或3 (B )2 (C )3 (D ) 610.如图,△ABC 内接于⊙O ,CE 平分∠BCD 交⊙O 于点E ,连结AE ,BE ,则下列结论一定正确的是 ( )(A )AB = AE (B )AB = BE (C )AE = BE (D )AB = AC⌒⌒二.填空题:11.已知⊙O 的半径为2 cm,弦AB 所对的劣弧为圆的31,则弦AB 的长为________ cm ,12.弦MN 把⊙O 分成两条弧,它们的度数比为4∶5, 如果P 为MN 的中点,那么∠MOP =________.13.圆内接五边形ABCDE 中,AB =BC =CD ,∠BAD =50°, 则∠AED 的度数为________.14.如图,四边形ABCD 为圆内接四边形,E 为BC 延长线上的一点,若 ∠A ∶∠B ∶∠D =1∶2∶3,则∠DCE =________;15.如图,两圆相交于A 、B ,且⊙O 2经过小圆圆心O 1,若∠D=50°,则∠C= 。
圆的基本性质练习题
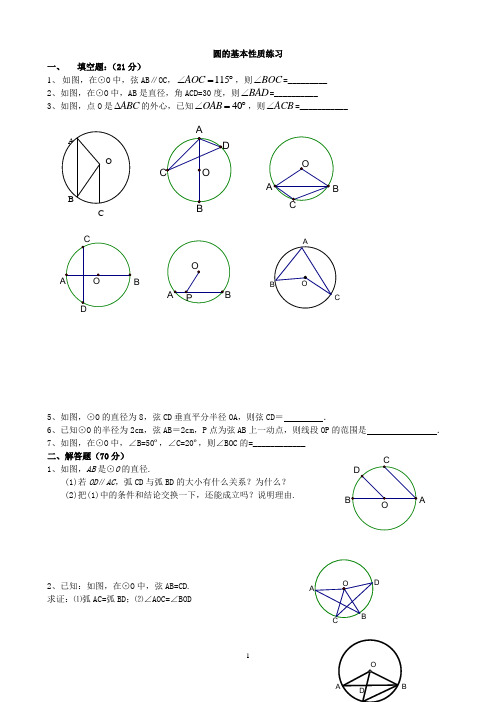
圆的基本性质练习一、 填空题:(21分)1、 如图,在⊙O 中,弦AB ∥OC ,115AOC ∠=︒,则BOC ∠=_________2、如图,在⊙O 中,AB 是直径,角ACD=30度,则BAD ∠=__________3、如图,点O 是ABC ∆的外心,已知40OAB ∠=︒,则ACB ∠=___________5、如图,⊙O 的直径为8,弦CD 垂直平分半径OA ,则弦CD = .6、已知⊙O 的半径为2cm ,弦AB =2cm ,P 点为弦AB 上一动点,则线段OP 的范围是 .7、如图,在⊙O 中,∠B=50º,∠C=20º,则∠BOC 的=____________ 二、解答题(70分)1、如图,AB 是⊙O 的直径. (1)若OD ∥AC ,弧CD 与弧BD 的大小有什么关系?为什么? (2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.2、已知:如图,在⊙O 中,弦AB=CD. 求证:⑴弧AC=弧BD ;⑵∠AOC=∠BODABC3、如图,已知:⊙O 中,AB 、BC 为弦,OC 交AB 于D , 求证:(1)∠ODB>∠OBD ,(2)∠ODB>∠OBC ;4、已知如图,AB 为⊙O 的弦,半径OE 、OF 分别交AB 于点C 、D , 且AC=BD 。
求证:CE=DF5、已知如图,,AB 、AC 为弦,OM ⊥AB 于M ,ON ⊥AC 于N ,MN 是△ABC 的中位线吗?6、已知⊙O 中,M 、N 分别是不平行的两条弦AB 和CD 的中点, 且AB = CD ,求证:∠AMN=∠CNM8、已知如图,AB 是⊙O 的直径,C 是⊙O 上的一点,CD ⊥AB 于D ,CE 平分∠DCO ,交⊙O 于E ,求证:弧AE=弧EB9、已知如图,以等腰△ABC 的一腰AB 为直径的⊙O 交另一腰于F ,交底边BC 于D ,则BC 与DF 的关系,证明你的观点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
第三章《圆的基本性质》测试题
班级 姓名 学号
一、选择题(每题3分,共30分) 1、下列命题为真命题的是 ( )
A 、点确定一个圆
B 、度数相等的弧相等
C 、圆周角是直角的所对弦是直径
D 、 相等的圆心角所对的弧相等,所对的弦也相等 E.圆有且只有一个内接三角形; F.三角形只有一个外接圆;
G 同弧或等弧所对的圆周角相等
2、若一个三角形的外心在这个三角形的边上,那么这个三角形是 ( ) A 、锐角三角形 B 、直角三角形 C 、钝角三角形 D 、不能确定
3、一个点到圆的最小距离为4cm ,最大距离为9cm ,则该圆的半径是( )
A 、2.5 cm 或6.5 cm
B 、2.5 cm
C 、6.5 cm
D 、5 cm 或13cm
4. 如图,
ABCD 的一边AB 为直径作⊙O ,若⊙O 过点C ,且∠AOC=700,则∠A 等于( )
A. 1450
B. 1400
C. 1350
D. 1200
目
5、如图,⊙O 的直径CD=10,AB 是⊙O 的弦,AB ⊥CD 于M ,且DM ∶MC=4∶1,则AB 的长是( )
A 2
B 8
C 16 D
91
6、如图,AB 、CD 为⊙O 直径,则下列判断正确的是( )
A AD 、BC 一定平行且相等
B AD 、B
C 一定平行但不一定相等 C A
D 、BC 一定相等但不一定平行 D AD 、BC 不一定平行也不一定相等
7、 如图,当半径为30cm 的转动轮转过1200角时,传送带上的物体A 平移的距离为( ) A. 900лcm B.300лcm C. 60лcm D.20лcm
8、点P 为⊙O 内一点,且OP =4,若⊙O 的半径为6,则过点P 的弦长不可能为 ( )
A 302
B 12
C 8
D 10.5
第5题 第6题
第16题图
9、A、B、C、D为⊙O的四等分点,动点P从圆心O出发,沿O — C — D — O路线作匀
速运动.设运动时间为t(s),∠APB=y(°),则下列图象中表示y与t之间函数关系最恰当的是()
10(2009黄石)如图5,AB是⊙O的直径,且AB=10,弦MN的长
为8,若弦MN的两端在圆上滑动时,始终与AB相交,记点A、B
到MN的距离分别为h1,h2,则|h1-h2| 等于()
A、5
B、6
C、7
D、8
二、填空题(每题4分,共24分)
11、在⊙O中,弦AB=AOB=120°,则⊙O的半径为。
12、圆的内接平行四边形是。
(填“矩形”或“菱形”或“正方形”)
13、已知圆锥的侧面积为10лcm2,底面半径为2cm,则圆锥的母线长为cm. 14,点A、B、C在⊙O上,∠C=150°,则∠AOB=。
15. 如图,AB为⊙O的直径,弦CD⊥AB,E为 BC上一点,若∠CEA=28 ,则∠ABD=
°.
16、(8分)如图是小明制作的一个圆锥形纸帽的示意图,则这个纸帽的纸的面积是________
圆锥的高___________
B
17.(2008自贡)如上右图所示,草地上一根长5米的绳子,一端拴在墙角的木桩上,加一端栓着一只小羊R。
那么,小羊在草地上的最大活动区域的面积是______________ m2.第9题
O
P
D C
B
A
A B C D
18(2007淄博)如图,已知:△ABC 是⊙O 的内接三角形,AD ⊥BC 于D 点,且AC =5,DC =3,AB =24,则⊙O 的直径等于 。
三、解答题(共46分)
19、(6分)已知 AB ,画点C ,使C 平分 AB . (画图工具不限,保留画图痕迹,不写画
法)
20、(8分)如图①,点A 、B 、C 在⊙O 上,连结OC 、OB :
⑴ 求证:∠A=∠B+∠C ;
⑵ 若点A 在圆上移动(不与点B 、C 重合),请分析∠A 、∠B 、∠C 三者之间的数量关系。
(写出结论即可,)
21、(8分)如图,AB 为⊙O 的直径,CD ⊥AB 于点E ,交⊙O 于点D ,OF ⊥AC 于点F . (1)请写出两条与BC 有关的正确结论;
(2)当∠D=30°,BC=1时,求圆中阴影部分的面积.
B A
C
22、如图,在⊙O中,直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D。
求BC和AD的长。
23、(8分)如图,BC是圆O的直径,AD垂直BC于D,弧BA等于弧AF,BF与AD交于E,求证:(1)AE=BE,(2)若A,F把半圆三等分,BC=12,求AE的长。
B A
C D
E
F。
