(完整版)高三数学立体几何历年高考题(2011年-2017年)

合集下载

2011-2017全国1卷分类汇编立体几何

2011-2017高考全国I 卷分类汇编——立体几何【2011年全国】（19）如图，四棱锥S ABCD -中，AB CD ,BC CD ⊥，侧面SAB 为等边三角形，2,1AB BC CD SD ====. （Ⅰ）证明：SD SAB ⊥;（Ⅱ)求AB 与平面SBC 所成角的大小.【2012年全国】（19）（本小题满分12分）如图，直三棱柱111ABC A B C -中，112AC BC AA ==，D 是棱1AA 的中点，1DC BD ⊥。

（Ⅰ）证明：1DC BC ⊥（Ⅱ）求二面角11A BD C --的大小。

【2013年全国】18、（本小题满分12分）如图，三棱柱ABC-A 1B 1C 1中，CA=CB ，AB=A A 1，∠BA A 1=60°. （Ⅰ）证明AB ⊥A【2014年全国】19. (本小题满分12分)如图三棱锥111ABC AB C -中，侧面11BB C C 为菱形，A 11AB B C ⊥.(Ⅰ) 证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o160CBB ∠=，AB=Bc ，求二面角111A A B C --的余弦值.【2015年全国】（18）如图，，四边形ABCD 为菱形，∠ABC=120°，E ，F 是平面ABCD同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE=2DF ，AE ⊥EC 。

（1）证明：平面AEC ⊥平面AFC（2）求直线AE 与直线CF 所成角的余弦值【2016年全国】（18）（本题满分为12分）如图，在已A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF =2FD ，90AFD ∠=，且二面角D -AF -E 与二面角C -BE -F 都是60．（I ）证明；平面ABEF ⊥平面EFDC ；（II ）求二面角E -BC -A 的余弦值．【2017年全国】18．（12分）如图，在四棱锥P−ABCD 中，AB//CD ，且90BAP CDP ∠=∠=.（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠=，求二面角A −PB −C 的余弦值.。

新课标全国卷历年高考立体几何真题(含答案)

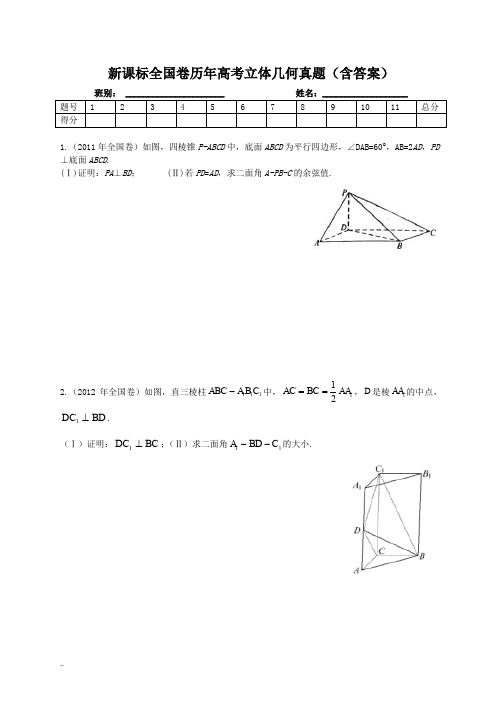
新课标全国卷历年高考立体几何真题（含答案）班别： ______________________ 姓名：___________________1.（2011年全国卷）如图，四棱锥P-ABCD 中，底面ABCD 为平行四边形，∠DAB=60°，AB=2AD ，PD ⊥底面ABCD .(Ⅰ)证明：PA ⊥BD ； (Ⅱ)若PD =AD ，求二面角A-PB-C 的余弦值.2.（2012年全国卷）如图，直三棱柱111ABC A B C -中，112AC BC AA ==，D 是棱1AA 的中点，BD DC ⊥1.（Ⅰ）证明：BC DC ⊥1；（Ⅱ）求二面角11C BD A --的大小.3.（2013年全国Ⅱ卷）如图，直棱柱ABC-A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点，AA 1=AC=CB=2AB. （Ⅰ）证明：BC 1//平面A 1CD ，（Ⅱ）求二面角D-A 1C-E 的正弦值4.（2013年全国Ⅰ卷）如图，三棱柱111C B A ABC -中，CB CA =，1AA AB =， 601=∠BAA .（Ⅰ）证明C A AB 1⊥；（Ⅱ）若平面ABC ⊥平面AA 1B 1B ，AB=CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值.5.（2014年全国Ⅱ卷）如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ；(Ⅱ)设二面角D-AE-C 为60°，AP=1，，求三棱锥E-ACD 的体积.6.（2014年全国Ⅰ卷）如图三棱柱111ABC A B C -中，侧面11BB C C 为菱形，1AB B C ⊥. （Ⅰ）证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o160CBB ∠=，AB=BC ，求二面角111A A B C --的余弦值.7.（2015年全国Ⅱ卷）如图，长方体ABCD-A 1B 1C 1D 1中，AB=16，BC=10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E=D 1F=4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说出画法和理由)；(Ⅱ)求直线AF 与平面α所成角的正弦值.8.（2015年全国Ⅰ卷）如图，四边形ABCD 为菱形，∠ABC=120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE=2DF ，AE ⊥EC.(Ⅰ)证明:平面AEC ⊥平面AFC ；(Ⅱ)求直线AE 与直线CF 所成角的余弦值.9.（2016年全国Ⅱ卷）如图，菱形ABCD 的对角线AC 与BD 交于点O ，5,6AB AC ==，点,E F分别在,AD CD 上，54AE CF ==，EF 交BD 于点H ．将DEF ∆沿EF 折到'D EF ∆位置，OD '=（Ⅰ）证明：D H'⊥平面ABCD ；（Ⅱ）求二面角B D A C '--的正弦值．10.（2016年全国Ⅰ卷）如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF =2FD ，90AFD ∠=，且二面角D -AF -E 与二面角C -BE -F 都是60．（I ）证明：平面ABEF ⊥平面EFDC ；（II ）求二面角E -BC -A 的余弦值．11.（2016年全国3卷）如图，四棱锥P ABC -中，PA ⊥底面面ABCD ，AD ∥BC ，3AB AD AC ===，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN平面PAB ；（II ）求直线AN 与平面PMN 所成角的正弦值.自我总结：新课标全国卷历年高考例题几何真题（广西多用2卷）1.解：（Ⅰ）因为60,2DAB AB AD ∠=︒=,由余弦定理得BD = 从而BD 2+AD 2= AB 2，故BD⊥AD;又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴射线DB 为y 轴的正半轴，射线DP 为z 轴的正半轴，建立空间直角坐标系D-xyz ，则()1,0,0A,()0B,()C -,()0,0,1P.(1),(1,0,0)ABPB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为n =（x,y,z ），则0⎧⋅=⎪⎨⋅=⎪⎩n AB n PB ,即00x z -+=-= 因此可取n =设平面PBC 的法向量为m ，则0⎧⋅=⎪⎨⋅=⎪⎩m PB m BC 可取m =（0，-1，，cos 7<>==-m,n 故二面角A-PB-C 的余弦值为 . 2.证明（Ⅰ）（1）在Rt DAC ∆中，AD AC =得：45ADC ︒∠=，同理：1114590A DC CDC ︒︒∠=⇒∠=，得：1,DC DC DC BD DC ⊥⊥⇒⊥又∵11,DC DC DC BD DC ⊥⊥⇒⊥平面1BCD DC BC ⇒⊥. （Ⅱ）（2）11,DC BC CC BC BC ⊥⊥⇒⊥平面11ACC A BC AC ⇒⊥取11A B 的中点O ，过点O 作OH BD ⊥于点H ，连接11,C O C H ，1111111AC B C C O A B =⇒⊥，C 1O ⊥A 1D 1C O ⇒⊥面1ABD 1OH BD C H BD ⊥⇒⊥ 得：点H 与点D 重合，即1C DO ∠是二面角11C BD A --的平面角设AC a =，则1C O =111230C D C O C DO ︒==⇒∠= 即二面角11C BD A --的大小为30︒.3.（1）连接1AC ，交1A C 于点F ，连结1,DF BC ，则F 为1AC 的中点，因为D 为AB 的中点，所以DF//1BC ，又因为111FD ACD BC AC D ⊂⊄平面，平面，所以11//BC ACD 平面. (2)由AA 1AC CB AB ===，可设：AB ＝2a,则1,AA AC CB ===所以AC BC ⊥，又因为ABC-A 1B 1C 1为直三棱柱，所以以点C 为坐标原点，建立空间直角坐标系如图.则C （0,0,0）、)1,0A D ⎫⎪⎪⎝⎭、、,E ⎛⎫⎪ ⎪⎝⎭()122,0,2,,0CA a a CD a ⎛⎫== ⎪⎪⎝⎭，.CE ⎛⎫= ⎪ ⎪⎝⎭设平面1A CD 的法向量为(),,,n x y z =则0n CD ⋅=且10,n CA ⋅=可解得,y x z =-=令1,x =得平面1A CD 的一个法向量为()1,1,1n =--，同理可得平面1A CE 的一个法向量为()2,1,2m =-，则3cos ,n m <>=，所以6sin ,n m <>=所以二面角1D A C E -- 4.【解析】（Ⅰ）取AB 的中点O ，连结OC ，1OA ，B A 1.因为CB CA =，所以AB OC ⊥.由于1AA AB =， 601=∠BAA ，故B AA 1∆为等边三角形，所以AB OA ⊥1.因为O OA OC =1 ，所以⊥AB 面C OA 1.又⊂C A 1平面C OA 1，故C A AB 1⊥. （Ⅱ）由（Ⅰ）知，AB OC ⊥，AB OA ⊥1，又平面⊥ABC 平面11BB AA ，交线为AB ，所以⊥OC 平面11BB AA ，故OA ，OC ，1OA 两两互相垂直.以O 为坐标原点，的方向为x 轴的正方向，||为单位长度，建立如图所示的空间直角坐标系xyz O -，则有)0,0,1(A ，)0,3,0(1A ,)3,0,0(C ,)0,0,1(-B .则)3,0,1(=， )0,3,1(1-==AA BB ， )3,3,0(-=.设平面C C BB 11的法向量为),,(z y x =，则有⎪⎩⎪⎨⎧=⋅=⋅01BB ，即⎪⎩⎪⎨⎧=+-=+0303y x z x ，可取)1,1,3(-=.故510||||,cos 111-=⋅>=<C A n C A n C A n ，所以直线C A 1与平面C C BB 11所成角的正弦值为510.5.【解析】(1) 连接BD 交AC 于点为G,连接EG.在三角形PBD 中,中位线EG ∥PB, 且EG 在平面AEC 上，所以PB ∥平面AEC.(2)设CD=m,分别以AD,AB,AP 为x,y,z 轴建立坐标系,则A(0,0,0),D(,0,0),E 12⎫⎪⎪⎝⎭,C(,m,0).所以AD=(,0,0), AE=12⎫⎪⎪⎝⎭,AC=),0m .设平面ADE 的法向量为1n =(x 1,y 1,z 1),则1n AD ⋅=0, 1n AE ⋅=0,解得一个1n =(0,1,0).同理设平面ACE 的法向量为2n =(x 2,y 2,z 2),则2n AC ⋅=0, 2n AE ⋅=0,解得一个2n因为cos 3π=|cos<12,n n >|=1212n n n n⋅==12,解得m=32. 设F 为AD 的中点,则PA ∥EF,且PA=2EF =12,EF ⊥面ACD,即为三棱锥E-ACD 的高. 所以V E-ACD =·S △ACD ·EF=13×12×32×12.所以,三棱锥E-ACD .为坐标原点，方向，||为单位长度，的方向为y 轴的正方向，的方向为z 轴的正方向建立空间直角坐标系，∵∠，，（0，，0） =，，=，=设向量=，可取，）的一个法向量，），＞=A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),=(0,-6,8).=+080z .由∠ABC=120°,可得AG=GC=.由BE ⊥平面ABCD,AB=BC可知AE=EC.又AE ⊥EC,所以EG=,且EG ⊥AC.在Rt △EBG 中,可得BE=,故DF=.在Rt △FDG 中,可得FG=.在直角梯形BDFE 中,由BD=2,BE=,DF=,可得EF=.从而EG 2+FG 2=EF 2,所以EG ⊥FG.,又AC ∩FG=G,可得EG ⊥平面AFC.又因为EG ⊂平面AEC,所以平面AEC ⊥平面AFC. (2)如图,以G 为坐标原点,分别以,的方向为x 轴,y 轴正方向,||为单位长度,建立空间直角坐标系G-xyz.由(1)可得(,)A 00,(,E 10,(,F -10,()C 00，所以(AE =1,(,CF =-1. 故cos ,||||AE CF AE CF AE CF ⋅<>==-3.所以直线AE 与直线CF所成角的余弦值为3 9.【解析】⑴∵ABEF 为正方形 ∴AF EF ⊥ ∵90AFD ∠=︒ ∴AF DF ⊥∵=DF EF F ∴AF ⊥面EFDC AF ⊥面ABEF ∴平面ABEF ⊥平面EFDC ⑵ 由⑴知60DFE CEF ∠=∠=︒∵AB EF ∥ AB ⊄平面EFDC EF ⊂平面EFDC ∴AB ∥平面ABCD AB ⊂平面ABCD ∵面ABCD 面EFDC CD = ∴AB CD ∥,∴CD EF ∥ ∴四边形EFDC 为等腰梯形以E 为原点，如图建标系，设FD a =()()000020E B a ，，，， ()02202a CA a a ⎛⎫ ⎪ ⎪⎝⎭，，， ()020EB a =，，，22a BC a ⎛⎫=- ⎪ ⎪⎝⎭，，()200AB a =-，，设面BEC 法向量为()m x y z =，，.00m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩，即111120202a y a x ay z ⋅=⎧⎪⎨⋅-+⋅=⎪⎩， ()301m =-，，设面ABC 法向量为()222n x y z =，， =00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩.即222220220a x ay ax ⎧-+=⎪⎨⎪=⎩，()034n=，设二面角E BC A --的大小为θ.cos 3m nm n θ⋅===+⋅ ∴二面角E BC A --的余弦值为 10.【解析】⑴证明：∵54AE CF ==，∴AE CF AD CD=，∴EF AC ∥．∵四边形ABCD 为菱形，∴AC BD ⊥，∴EF BD ⊥，∴EF DH ⊥，∴EF D H '⊥．∵6AC =，∴3AO =；又5AB =，AO OB ⊥，∴4OB =， ∴1AE OH OD AO=⋅=，∴3DH D H '==，∴222'OD OH D H '=+， ∴'D H OH ⊥．又∵OH EF H =I ，∴'D H ⊥面ABCD ．⑵建立如图坐标系H xyz -．()500B ，，，()130C ，，，()'003D ，，，()130A -，，，()430AB =uu u r ，，，()'133AD =-uuur ，，，()060AC =uuu r ，，，设面'ABD 法向量()1n x y z =，，u r ，由1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩得430330x y x y z +=⎧⎨-++=⎩，取345xy z=⎧⎪=-⎨⎪=⎩，∴()1345n =-u r ，，．同理可得面'AD C 的法向量()2301n =u u r ，，，∴1212cos n n n n θ⋅===u r u u r u r u u r∴sin θ=11.设),,(z y x =为平面PMN 的法向量，则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM ，即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ，可取)1,2,0(=，于是2558|||||,cos |==><AN n .。

2011高考数学立体几何大题汇总

2011高考数学立体几何大题汇总(1)(本小题满分12分)如图，四棱锥P —ABCD 中，底面ABCD 为平行四边形，∠DAB=60,AB=2AD,PD ⊥底面ABCD. (Ⅰ)证明：PA ⊥BD ；(Ⅱ)若PD=AD ，求二面角A-PB-C 的余弦值。

(1)解：（Ⅰ ）因为60,2DAB AB AD ∠=︒=, 由余弦定理得3BD AD = 从而BD 2+AD 2= AB 2，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故PA ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ，则()1,0,0A ,()03,0B ，,()1,3,0C -,()0,0,1P 。

(1,3,0),(0,3,1),(1,0,0)AB PB BC =-=-=-设平面PAB 的法向量为n=（x,y,z ），则即3030x y z -=-=（II ）由AB ⊥平面SDE 知，平面ABCD ⊥平面SED 。

作,SF DE ⊥垂足为F ，则SF ⊥平面ABCD ，3SD SE SF DE⨯== 作FG BC ⊥，垂足为G ，则FG=DC=1。

连结SG ，则SG BC ⊥，又,BC FG SG FG G ⊥=，故BC ⊥平面SFG ，平面SBC ⊥平面SFG 。

…………9分作FH SG ⊥，H 为垂足，则FH ⊥平面SBC 。

37SF FG FH SG ⨯==，即F 到平面SBC 的距离为217 由于ED//BC ，所以ED//平面SBC ，E 到平面SBC 的距离d 也有217 设AB 与平面SBC 所成的角为α，则2121sin arcsin 77d EBαα=== …………12分解法二：以C 为坐标原点，射线CD 为x 轴正半轴，建立如图所示的空间直角坐标系C —xyz 。

设D （1，0，0），则A （2，2，0）、B （0，2，0）。

【精品】立体几何十年高考题(带详细解析)

【精品】立体几何十年高考题(带详细解析) ●考点阐释高考试卷中，立体几何考查的立足点放在空间图形上，突出对空间观念和空间想象能力的考查.立体几何的基础是对点、线、面的各种位置关系的讨论和研究，进而讨论几何体，而且采用了公理化体系的方法，在中学数学教育中，通过这部分内容培养学生空间观念和公理化体系处理数学问题的思想方法，这又是考生进入高校所必须具备的一项重要的数学基础，因此高考命题时，突出空间图形的特点，侧重于直线与直线、直线与平面、平面与平面的各种位置关系的考查，以便审核考生立体几何的知识水平和能力.多面体和旋转体是在空间直线与平面的理论基础上，研究以柱、锥、台、球为代表的最基本的几何体的概念、性质、各主要元素间的关系、直观图画法、侧面展开图以及表面和体积的求法等问题.它是“直线和平面”问题的延续和深化.在高考中不仅有直接求多面体、旋转体的面积和体积问题，也有已知面积或体积求某些元素的量或元素间的位置关系问题.近些年来即使考查空间线面的位置关系问题，也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想，会把组合体求积问题转化为基本几何体的求积问题，会等体积转化求解问题，会把立体问题转化为平面问题求解，会运用“割补法”等求解.本章主要考查平面的性质、空间两直线、直线和平面、两个平面的位置关系以及空间角和距离面积及体积.●试题类编一、选择题1.（2003京春文11，理8）如图9—1，在正三角形ABC 中，D ，E ，F 分别为各边的中点，G ，H ，I ，J 分别为AF ，AD ，BE ，DE 的中点.将△ABC 沿DE ，EF ，DF 折成三棱锥以后，GH 与IJ 所成角的度数为（）A.90°B.60°C.45°D.0°2.（2003上海春，13）关于直线a 、b 、l 及平面M 、N ，下列命题中正确的是（）A.若a ∥M ，b ∥M ，则a ∥bB.若a ∥M ，b ⊥a ，则b ⊥MC.若a M ，b M ，且l ⊥a ，l ⊥b ，则l ⊥MD.若a ⊥M ，a ∥N ，则M ⊥N3.（2002北京春，2）已知三条直线m 、n 、l ，三个平面α、β、γ.下面四个命题中，正确的是（）A.⇒⎭⎬⎫⊥⊥γβγαα∥β B.⇒⎭⎬⎫⊥m l m β//l ⊥βC.⇒⎭⎬⎫γγ////n m m ∥n D.⇒⎭⎬⎫⊥⊥γγn m m ∥n4.（2002北京文，4）在下列四个正方体中，能得出AB ⊥CD 的是（）图9—15.（2002上海，14）已知直线l 、m ，平面α、β，且l ⊥α，m β，给出下列四个命题：（1）若α∥β，则l ⊥m （2）若l ⊥m ，则α∥β（3）若α⊥β，则l ∥m（4）若l ∥m ，则α⊥β其中正确命题的个数是（）A.1B.2C.3D.46.（2002京皖春，7）在△ABC 中，AB =2，BC =1.5，∠ABC =120°（如图9—2），若将△ABC 绕直线BC 旋转一周，则所形成的旋转体的体积是（） A.29π B.27π C.25π D.23π 7.（2002京、皖、春，12）用一张钢板制作一个容积为4 m 3的无盖长方体水箱.可用的长方形钢板有四种不同的规格（长×宽的尺寸如选项所示，单位均为m ）若既要够用，又要所剩最少，则应选择钢板的规格是（）A.2×5B.2×5.5C.2×6.1D.3×58.（2002全国文8，理7）一个圆锥和一个半球有公共底面，如果圆锥的体积恰好与半球的体积相等，那么，这个圆锥轴截面顶角的余弦值是（）A.43 B.54 C.53 D.－53 9.（2002北京文5，理4）64个直径都为4a 的球，记它们的体积之和为V 甲，表面积之和为S 甲；一个直径为a 的球，记其体积为V 乙，表面积为S 乙，则（）A.V 甲＞V 乙且S 甲＞S 乙B.V 甲＜V 乙且S 甲＜S 乙C.V 甲=V 乙且S 甲＞S 乙D.V 甲=V 乙且S 甲=S 乙10.（2002北京理，10）设命题甲：“直四棱柱ABCD －A 1B 1C 1D 1中，平面ACB 1与对角面BB 1D 1D 垂直”；命题乙：“直四棱柱ABCD －A 1B 1C 1D 1是正方体”.那么，甲是乙的（）A.充分必要条件B.充分非必要条件C.必要非充分条件D.既非充分又非必要条件11.（2002全国理，8）正六棱柱ABCDEF —A 1B 1C 1D 1E 1F 1的底面边长为1，侧棱长为2，则这个棱柱的侧面对角线E 1D 与BC 1所成的角是（）A.90°B.60°C.45°D.30° 图9—212.（2001上海，15）已知a、b为两条不同的直线,α、β为两个不同的平面，且a⊥α, b⊥β，则下列命题中的假命题．．．是（）A.若a∥b，则α∥βB.若α⊥β，则a⊥bC.若a、b相交，则α、β相交D.若α、β相交，则a、b相交13.（2001京皖春，11）图9—3是正方体的平面展开图．在这个正方体．．．中，①BM与ED平行②CN与BE是异面直线③CN与BM成60°角④DM与BN垂直以上四个命题中，正确命题的序号是（）A.①②③B.②④C.③④D.②③④14.（2001全国文，3）若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的全面积是（）A.3πB.33πC.6πD.9π15.（2001全国，11）一间民房的屋顶有如图9—4三种不同的盖法：①单向倾斜；②双向倾斜；③四向倾斜.记三种盖法屋顶面积分别为P1、P2、P3.图9—4若屋顶斜面与水平面所成的角都是α，则（）A.P3＞P2＞P1B.P3＞P2＝P1C.P3＝P2＞P1D.P3＝P2＝P116.（2001全国，9）在正三棱柱ABC—A1B1C1中，若AB＝2BB1，则AB1与C1B 所成的角的大小为（）A.60°B.90°C.105°D.75°17.（2001京皖春，9）如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角（圆锥轴截面中两条母线的夹角）是（）A.30°B.45°C.60°D.90°18.（2000上海，14）设有不同的直线a、b和不同的平面α、β、γ，给出下列三个命题：（1）若a∥α，b∥α，则a∥b．（2）若a∥α，a∥β，则α∥β．（3）若α⊥γ，β⊥γ，则α∥β．其中正确的个数是（）A.0 B．1 C．2 D．319.（2000京皖春，5）一个圆锥的底面直径和高都同一个球的直径相等，那么圆锥与球的体积之比是（）图9—3A.1∶3B.2∶3C.1∶2D.2∶920.（2000全国，3）一个长方体共一顶点的三个面的面积分别是6,3,2，这个长方体对角线的长是（） A.23 B.32 C.6 D.621.（2000全国文，12）如图9—5，OA 是圆锥底面中心O 到母线的垂线，OA 绕轴旋转一周所得曲面将圆锥分成相等的两部分，则母线与轴的夹角的余弦值为（）A.321B.21C.21D.421 22.（2000全国理，9）一个圆柱的侧面积展开图是一个正方形，这个圆柱的全面积与侧面积的比是（）A.ππ221+B.ππ441+C.ππ21+D.ππ241+ 23.（1999全国，7）若干毫升水倒入底面半径为2 cm 的圆柱形器皿中，量得水面的高度为6 cm.若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是（）A.63cm B ．6 cm C.2318cm D.3312cm24.（1999全国，12）如果圆台的上底面半径为5，下底面半径为R ，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1∶2，那么R 等于（）A.10B.15C.20D.2525.（1999全国理，10）如图9—6，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，EF ∥AB ，EF =23，EF 与面AC 的距离为2，则该多面体的体积是（）A.29B.5C.6D.215 26.（1998全国，7）已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为（）A.120°B.150°C.180°D.240°27.（1998全国，9）如果棱台的两底面积分别是S 、S ′，中截面的面积是S 0，那么（）A.S S S '+=02B.S S S '=0C.2S 0＝S ＋S ′D.S 02＝2S ′S图9—5图9—628.（1998全国，13）球面上有3个点，其中任意两点的球面距离都等于大圆周长的61，经过这3个点的小圆的周长为4π，那么这个球的半径为（） A.43 B.23 C.2 D. 329.（1998上海）在下列命题中，假命题是（）A.若平面α内的一条直线垂直于平面β内的任一直线，则α⊥βB.若平面α内任一直线平行于平面β，则α∥βC.若平面α⊥平面β，任取直线l α，则必有l ⊥βD.若平面α∥平面β，任取直线l α，则必有l ∥β30.（1997全国，8）长方体一个顶点上三条棱的长分别是3、4、5，且它的八个顶点都在同一个球面上，这个球的表面积是（）A.202πB.252πC.50πD.200π31.（1997全国，12）圆台上、下底面积分别为π、4π，侧面积为6π，这个圆台的体积是（）A.332πB.23πC.637πD.337π 32.（1996全国理，14）母线长为1的圆锥体积最大时，其侧面展开图圆心角ϕ等于（） A.322π B.332π C.2π D.362π 33.（1996全国文12，理9）将边长为a 的正方体ABCD 沿对角线AC 折起，使得BD ＝a ，则三棱锥D —ABC 的体积为（）A.63aB.123aC.3123aD.3122a 34.（1996全国文7，理5）如果直线l 、m 与平面α、β、γ满足：l ＝β∩γ，l ∥α，m ⊂α和m ⊥γ，那么必有（）A.α⊥γ且l ⊥mB.α⊥γ且m ∥βC.m ∥β且l ⊥mD.α∥β且α⊥γ35.（1996上海，4）在下列命题中，真命题是（）A.若直线m 、n 都平行于平面α，则m ∥nB.设α—l —β是直二面角，若直线m ⊥l ，则m ⊥βC.若直线m 、n 在平面α内的射影依次是一个点和一条直线，且m ⊥n ，则n 在α内或n 与α平行D.设m 、n 是异面直线，若m 与平面α平行，则n 与α相交36.（1996全国文，10）圆锥母线长为1，侧面展开图的圆心角为240°，该圆锥的体积等于（）A.8122πB.818πC.8154π D.8110π 37.（1995全国文，10）如图9—7，ABCD —A 1B 1C 1D 1是正方体，B 1E 1＝D 1F 1＝411B A ，则BE 1与DF 1所成角的余弦值是（） A.1715 B.21 C.178 D.23 38.（1995全国，4）正方体的全面积是a 2，它的顶点都在球面上，这个球的表面积是（）A.32a π B.22a π C.2πa 2 D.3πa 239.（1995上海，4）设棱锥的底面面积为8 cm 2，那么这个棱锥的中截面（过棱锥高的中点且平行于底面的截面）的面积是（）A.4 cm 2B.22 cm 2C.2 cm 2D. 2 cm 240.（1995全国理，10）已知直线l ⊥平面α，直线m 平面β，有下面四个命题： ①α∥β⇒l ⊥m ； ②α⊥β⇒l ∥m ； ③l ∥m ⇒α⊥β；④l ⊥m ⇒α∥β 其中正确的两个命题是（）A.①②B.③④C.②④D.①③41.（1995全国理，15）如图9—8，A 1B 1C 1—ABC 是直三棱柱，∠BCA =90°，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC =CA =CC 1，则BD 1与AF 1所成角的余弦值是（）A.1030B.21C.1530D.1015 42.（1994全国，11）对于直线m 、n 和平面α、β，α⊥β的一个充分条件是（）A.m ⊥n ，m ∥α，n ∥βB.m ⊥n ，α∩β＝m ，n ⊂αC.m ∥n ，n ⊥β，m ⊂αD.m ∥n ，m ⊥α，n ⊥β43.（1994上海，14）已知a 、b 是异面直线，直线c 平行于直线a ，那么c 与b （）A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线44.（1994全国，7）已知正六棱台的上、下底面边长分别为2和4，高为2，则其体积为（）A.323B.283C.243D.20345.（1994全国，13）已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半，且AB ＝BC ＝CA ＝2，则球面面积是（）A.916πB.38π C.4π D.964π 二、填空题46.（2003京春理13，文14）如图9—9，一个底面半径为R 的圆柱形量杯中装有适量图9—8的水.若放入一个半径为r 的实心铁球，水面高度恰好升高r，则r R =.图9—947.（2003上海春，10）若正三棱锥底面边长为4，体积为1，则侧面和底面所成二面角的大小等于（结果用反三角函数值表示）.48.（2002上海春，12）如图9—10，若从点O 所作的两条射线OM 、ON 上分别有点 M 1、M 2与点N 1、N 2，则三角形面积之比21212211ON ON OM OM S S N OM N OM ⋅=∆∆.若从点O 所作的不在同一平面内的三条射线OP 、OQ 和OR 上，分别有点P 1、P 2，点Q 1、Q 2和点R 1、R 2，则类似的结论为 .图9—10 图9—1149.（2002京皖春，15）正方形ABCD 的边长是2，E 、F 分别是AB 和CD 的中点，将正方形沿EF 折成直二面角（如图9—11所示）.M 为矩形AEFD 内一点，如果∠MBE =∠MBC ，MB 和平面BCF 所成角的正切值为21，那么点M 到直线EF 的距离为 . 50.（2002北京，15）关于直角AOB 在定平面α内的射影有如下判断：①可能是0°的角；②可能是锐角；③可能是直角；④可能是钝角；⑤可能是180°的角.其中正确判断的序号是（注：把你认为是正确判断的序号都填上）.51.（2002上海春，10）图9—12表示一个正方体表面的一种展开图，图中的四条线段AB 、CD 、EF 和GH 在原正方体中相互异面的有对.图9—1252.（2002上海，4）若正四棱锥的底面边长为23cm，体积为4 cm3，则它的侧面与底面所成的二面角的大小是.53.（2001京皖春，16）已知m、n是直线，α、β、γ是平面，给出下列命题：①若α⊥β，α∩β＝m，n⊥m，则n ⊥α或n⊥β；②若α∥β，α∩γ＝m，β∩γ＝n，则m∥n；③若m不垂直于α，则m不可能垂直于α内的无数条直线；④若α∩β＝m，n∥m且n⊄α，n⊄β，则n∥α且n∥β.其中正确的命题序号是（注：把你认为正确的命题的序号都．填上）.54.（2001春季北京、安徽，13）已知球内接正方体的表面积为S，那么球体积等于．55.（2001全国理，13）若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的侧面积是.56.（2000上海春，9）若两个长方体的长、宽、高分别为5 cm、4 cm、3 cm，把它们两个全等的面重合在一起组成大长方体，则大长方体的对角线最长为_____cm.57.（2000上海春，8）如图9—13，∠BAD＝90°的等腰直角三角形ABD与正三角形CBD所在平面互相垂直，E是BC的中点，则AE与平面BCD所成角的大小为_____.58.（2000年春季北京、安微，18）在空间，下列命题正确的是_____（注：把你认为正确的命题的序号都填上）.①如果两直线a、b分别与直线l平行，那么a∥b.②如果直线a与平面β内的一条直线b平行，那么a∥β.③如果直线a与平面β内的两条直线b、c都垂直，那么a⊥β.④如果平面β内的一条直线a垂直平面γ，那么β⊥γ.59.（2000春季北京、安徽，16）如图9—14是一体积为72的正四面体，连结两个面的重心E、F，则线段EF的长是_____.60.（2000全国，16）如图9—15（1），E、F分别为正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是图9—15（2）的（要求：把可能的图的序号都．填上）.图9—1 图9—15（1）图9—15（2）61.（2000上海，7）命题A：底面为正三角形，且顶点在底面的射影为底面中心的三棱锥是正三棱锥．图9—13命题A 的等价命题B可以是：底面为正三角形，且的三棱锥是正三棱锥．62.（1999全国，18）α、β是两个不同的平面，m 、n 是平面α及β之外的两条不同直线.给出四个论断：①m ⊥n ②α⊥β ③n ⊥β ④m ⊥α以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个．．命题： . 63.（1998全国，18）如图9—16，在直四棱柱A 1B 1C 1D 1—ABCD中，当底面四边形ABCD 满足条件（或任何能推导出这个条件的其他条件，例如ABCD 是正方形、菱形等）时，有A 1C ⊥B 1D 1（注：填上你认为正确的一种条件即可，不必考虑所有可能的情形）.64.（1998上海）棱长为2的正四面体的体积为 .65.（1997全国，19）已知m 、l 是直线，α、β是平面，给出下列命题①若l 垂直于α内的两条相交直线，则l ⊥α②若l 平行于α，则l 平行于α内的所有直线③若m ⊂α，l ⊂β，且l ⊥m ，则α⊥β④若l ⊂β，且l ⊥α，则α⊥β⑤若m ⊂α，l ⊂β，且α∥β，则m ∥l其中正确的命题的序号是_____（注：把你认为正确的命题的序号都填上）.66.（1997上海）圆柱形容器的内壁底半径为5 cm ，两个直径为5 cm 的玻璃小球都浸没于容器的水中，若取出这两个小球，则容器的水面将下降_____ cm.67.（1996上海，18）把半径为3 cm 、中心角为32π的扇形卷成一个圆锥形容器，这个容器的容积为 cm 3（结果保留π）.68.（1996上海，18）如图9—17，在正三角形ABC 中，E 、F 依次是AB 、AC 的中点，AD ⊥BC ，EH ⊥BC ，F Ｇ⊥BC ，D 、H 、G 为垂足，若将正三角形ABC 绕AD 旋转一周所得的圆锥的体积为V ，则其中由阴影部分所产生的旋转体的体积与V 的比值是 .图9—17 图9—1869.（1996全国，19）如图9—18，正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角，则异面直线AD 与BF 所成角的余弦值是_____.70.（1995全国，17）已知圆台上、下底面圆周都在球面上，且下底面过球心，母线与底面所成的角为3π，则圆台的体积与球体积之比为_____.71.（1995上海理）把圆心角为216°，半径为5分米的扇形铁皮焊成一个圆锥形容器（不计焊缝），那么容器的容积是_____.72.（1994全国，19）设圆锥底面圆周上两点A 、B 间的距离为2，圆锥顶点到直线AB图9—16的距离为3，AB和圆锥的轴的距离为1，则该圆锥的体积为_____.73.（1994上海）有一个实心圆锥体的零部件，它的轴截面是边长为10 cm的等边三角形，现在要在其整个表面上镀一层防腐材料，已知每平方厘米的工料价为0.10元，则需要的费用为_____元（π取3.2）.三、解答题74.（2003京春文，19）如图9—19，ABCD—A1B1C1D1是正四棱柱，侧棱长为1，底面边长为2，E是棱BC的中点.（Ⅰ）求三棱锥D1—DBC的体积；（Ⅱ）证明BD1∥平面C1DE；（Ⅲ）求面C1DE与面CDE所成二面角的正切值.图9—1 图9—2075.（2003京春理，19）如图9—20，正四棱柱ABCD—A1B1C1D1中，底面边长为22，侧棱长为4.E，F分别为棱AB，BC的中点，EF∩BD=G.（Ⅰ）求证：平面B1EF⊥平面BDD1B1；（Ⅱ）求点D1到平面B1EF的距离d；（Ⅲ）求三棱锥B1—EFD1的体积V.76.（2002京皖春文，19）在三棱锥S—ABC中，∠SAB=∠SAC=∠ACB=90°，且AC=BC=5，SB=55.（如图9—21）（Ⅰ）证明：SC⊥BC；（Ⅱ）求侧面SBC与底面ABC所成二面角的大小；（Ⅲ）求三棱锥的体积V S－AB C.77.（2002京皖春理，19）在三棱锥S—ABC中，∠SAB=∠SAC=∠ACB=90°，AC=2，BC=13，SB=29.（Ⅰ）证明：SC⊥BC；（Ⅱ）求侧面SBC与底面ABC所成二面角的大小；（Ⅲ）求异面直线SC与AB所成的角的大小（用反三角函数表示）.图9—22 图9—2378.（2002全国文，19）四棱锥P—ABCD的底面是边长为a的正方形，PB⊥面ABCD，图9—21如图9—22所示.（Ⅰ）若面P AD 与面ABCD 所成的二面角为60°，求这个四棱锥的体积；（Ⅱ）证明无论四棱锥的高怎样变化，面P AD 与面PCD 所成的二面角恒大于90°. 79.（2002北京文，18）如图9—23，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，上、下底面矩形的长、宽分别为c ，d 与a ，b ，且a ＞c ，b ＞d ，两底面间的距离为h .（Ⅰ）求侧面ABB 1A 1与底面ABCD 所成二面角的正切值；（Ⅱ）在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是V=6h（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面） 80.（2002北京理，18）如图9—24，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E ，F 两点，上、下底面矩形的长、宽分别为c ，d 与a ，b ，且a ＞c ，b ＞d ，两底面间的距离为h .（Ⅰ）求侧面ABB 1A 1与底面ABCD 所成二面角的大小；（Ⅱ）证明：EF ∥面ABCD ；（Ⅲ）在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是V =6h（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明.（注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面） 81.（2002全国文，22）（Ⅰ）给出两块相同的正三角形纸片（如图（1），图（2）），要求用其中一块剪拼成一个正三棱锥模型，另一块剪拼成一个正三棱柱模型，使它们的全面积都与原三角形的面积相等，请设计一种剪拼方法，分别用虚线标示在图（1）、图（2），并作简要说明；（Ⅱ）试比较你剪拼的正三棱锥与正三棱柱的体积的大小；图9—2582.（2002全国理，18）如图9—26，正方形ABCD 、ABEF 的边长都是1，而且平面ABCD 、ABEF 互相垂直.点M 在AC 上移动，点N 在BF 上移动，若CM =BN =a （0＜a ＜2）.（Ⅰ）求MN 的长；（Ⅱ）当a 为何值时，MN 的长最小；（Ⅲ）当MN 长最小时，求面MNA 与面MNB 所成的二面角α的大小.图9—24图9—26 图9—2783.（2001春季北京、安徽，19）如图9—27，已知VC 是△ABC 所在平面的一条斜线，点N 是V 在平面ABC 上的射影，且在△ABC 的高CD 上.AB ＝a ，VC 与AB 之间的距离为h ，点M ∈V C.（Ⅰ）证明∠MDC 是二面角M —AB —C 的平面角；（Ⅱ）当∠MDC ＝∠CVN 时，证明VC ⊥平面AMB ；（Ⅲ）若∠MDC ＝∠CVN ＝θ（0＜θ＜2），求四面体MABC 的体积.84.（2001上海，19）在棱长为a 的正方体OABC —O ′A ′B ′C ′中，E 、F 分别是棱AB 、BC 上的动点，且AE ＝BF ．（Ⅰ）求证：A ′F ⊥C ′E ；（Ⅱ）当三棱锥B ′—BEF 的体积取得最大值时，求二面角B ′—EF —B 的大小（结果用反三角函数表示）．85.（2001全国理17，文18）如图9—28，在底面是直角梯形的四棱锥S —ABCD 中，∠ABC ＝90°，SA ⊥面ABCD ，SA ＝AB ＝BC ＝1，AD ＝21. （Ⅰ）求四棱锥S —ABCD 的体积；（Ⅱ）求面SCD 与面SBA 所成的二面角的正切值.86.（2000京皖春理20,文21）在直角梯形ABCD 中，如图9—29，∠D ＝∠BAD ＝90°，AD ＝21AB ＝a （如图（1）），将△ADC 沿AC 折起，使D 到D ′，记面ACD ′为α，面ABC 为β，面BCD ′为γ．图9—29（Ⅰ）若二面角α—AC —β为直二面角（如图（2）），求二面角β—BC —γ的大小；（Ⅱ）若二面角α—AB —β为60°（如图（3）），求三棱锥D ′—ABC 的体积．87.（2000全国理，18）如图9—30，已知平行六面体ABCD —A 1B 1C 1D 1的底面ABCD 是菱形，且∠C 1CB ＝∠C 1CD ＝∠BCD ＝60°．（Ⅰ）证明：C 1C ⊥BD ；图9—28（Ⅱ）假定CD ＝2，CC 1＝23，记面C 1BD 为α，面CBD 为β，求二面角α—BD —β的平面角的余弦值；（Ⅲ）当1CC CD的值为多少时，能使A 1C ⊥平面C 1BD ？请给出证明．图9—30 图9—3188.（2000全国文，19）如图9—31，已知平行六面体ABCD —A 1B 1C 1D 1的底面ABCD 是菱形，且∠C 1CB ＝∠C 1CD ＝∠BCD ．（Ⅰ）证明：C 1C ⊥BD ；（Ⅱ）当1CC CD的值为多少时，能使A 1C ⊥平面C 1BD ?请给出证明． 89.（2000上海，18）如图9—32所示四面体ABCD 中，AB 、BC 、BD 两两互相垂直，且AB ＝BC ＝2，E 是AC 中点，异面直线AD 与BE 所成的角大小为arccos 1010，求四面体ABCD 的体积．图9—32 图9—3390.（1999全国文22，理21）如图9—33，已知正四棱柱ABCD —A 1B 1C 1D 1，点E 在棱D 1D 上，截面EAC ∥D 1B ，且面EAC 与底面ABCD 所成的角为45°，AB ＝a .（Ⅰ）求截面EAC 的面积；（Ⅱ）求异面直线A 1B 1与AC 之间的距离；（Ⅲ）求三棱锥B 1－EAC 的体积.91.（1998全国理，23）已知如图9—34，斜三棱柱ABC —A 1B 1C 1的侧面A 1ACC 1与底面ABC 垂直，∠ABC ＝90°，BC ＝2，AC ＝23，且AA 1⊥A 1C ，AA 1＝A 1C.（Ⅰ）求侧棱A 1A 与底面ABC 所成角的大小；（Ⅱ）求侧面A 1ABB 1与底面ABC 所成二面角的大小；（Ⅲ）求顶点C 到侧面A 1ABB 1的距离.图9—34 图9—3592.（1998全国文，23）已知如图9—35，斜三棱柱ABC —A 1B 1C 1的侧面A 1ACC 1与底面ABC 垂直，∠ABC ＝90°，BC ＝2，AC ＝23，且AA 1⊥A 1C ，AA 1＝A 1C.（Ⅰ）求侧棱A 1A 与底面ABC 所成角的大小；（Ⅱ）求侧面A 1ABB 1与底面ABC 所成二面角的大小；（Ⅲ）求侧棱B 1B 和侧面A 1ACC 1的距离.93.（1997全国，23）如图9—36，正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是BB 1、CD 的中点.（Ⅰ）证明：AD ⊥D 1F ；（Ⅱ）求AE 与D 1F 所成的角；（Ⅲ）证明：面AED ⊥面A 1FD 1；（Ⅳ）（理）设AA 1＝2，求三棱锥F —A 1ED 1的体积11ED A F V -. （文）设AA 1＝2，求三棱锥E —AA 1F 的体积F AA E V 1-.图9—36图9—3794.（1997上海理）如图9—37在三棱柱ABC —A ′B ′C ′中，四边形A ′ABB ′是菱形，四边形BCC ′B ′是矩形，C ′B ′⊥A B.（1）求证：平面CA ′B ⊥平面A ′AB ；（2）若C ′B ′=3，AB =4，∠ABB ′=60°，求AC ′与平面BCC ′所成的角的大小（用反三角函数表示）.95.（1996上海，21）如图9—38，在二面角α—l —β中，A 、B ∈α，C 、D ∈l ，ABCD为矩形，P ∈β，P A ⊥α，且P A ＝AD ，M 、N 依次是AB 、PC 的中点.（1）求二面角α—l —β的大小；（2）求证：MN ⊥AB ；（3）求异面直线P A 与MN 所成角的大小.图9—38 图9—3996.（1995全国文24，理23）如图9—39，圆柱的轴截面ABCD 是正方形，点E 在底面的圆周上，AF ⊥DE ，F 是垂足.（Ⅰ）求证：AF ⊥DB ；（Ⅱ）（理）如果圆柱与三棱锥D —ABE 的体积比等于3π，求直线DE 与平面ABCD 所成的角.（文）求点E 到截面ABCD 的距离.97.（1995上海，23）如图9—40，四棱锥P —ABCD 中，底面是一个矩形，AB ＝3，AD ＝1，又P A ⊥AB ，P A ＝4，∠P AD ＝60°.（Ⅰ）求四棱锥P —ABCD 的体积；（Ⅱ）求二面角P —BC —D 的大小（用反三角函数表示）.图9—40 图9—4198.（1994全国，23）如图9—41，已知A 1B 1C 1—ABC 是正三棱柱，D 是AC 中点. （Ⅰ）证明：AB 1∥平面DBC 1；（Ⅱ）（理）假设AB 1⊥BC 1，求以BC 1为棱的DBC 1与CBC 1为面的二面角α的度数. （文）假设AB 1⊥BC 1，BC ＝2，求线段AB 1在侧面B 1BCC 1上的射影长. 99.（1994上海，23）如图9—42在梯形ABCD 中，AD ∥BC ， ∠ABC ＝2，AB ＝a ，AD ＝3a ，且∠ADC ＝arcsin55，又P A ⊥平面ABCD ，P A =a .求（1）二面角P —CD —A 的大小（用反三角函数表示）.（2）点A 到平面PBC 的距离. ●答案解析 1.答案：B解析：将三角形折成三棱锥如图9—43所示.HG 与IJ 为一对异面直线.过点D 分别图9—42图9—43作HG 与IJ 的平行线，即DF 与AD .所以∠ADF 即为所求.因此，HG 与IJ 所成角为60°.评述：本题通过对折叠问题处理考查空间直线与直线的位置关系，在画图过程中正确理解已知图形的关系是关键.通过识图、想图、画图的角度考查了空间想象能力.而对空间图形的处理能力是空间想象力深化的标志，是高考从深层上考查空间想象能力的主要方向.2.答案：D解析：A 选项中，若a ∥M ，b ∥M ，则有a ∥b 或a 与b 相交或a 与b 异面.B 选项中，b 可能在M 内，b 可能与M 平行，b 可能与M 相交.C 选项中须增加a 与b 相交，则l ⊥M . D 选项证明如下：∵a ∥N ，过a 作平面α与N 交于c ，则c ∥a ，∴c ⊥M .故M ⊥N .评述：本题考查直线与直线、直线与平面、平面与平面的基本性质. 3.答案：D解析：垂直于同一平面的两直线必平行，因此选D.评述：判断元素之间的位置关系问题，也可以从元素之间所有关系分析入手，再否定若干选项.如A ，因为α、β有两种位置关系，在α与β相交情况下，仍有α⊥r ，β⊥r .因此，α∥β是错误的.4.答案：A解析：∵CD 在平面BCD 内，AB 是平面BCD 的斜线，由三垂线定理可得A. 5.答案：B 解析：（1）、（4）是正确命题.因为α∥β，l ⊥α，∴l ⊥β. 又m ⊂β，∴l ⊥m .因为l ∥m ，l ⊥α，∴m ⊥α，∴β⊥α. 6.答案：D解析：如图9—44，该旋转体的体积为圆锥C —ADE 与圆锥B —ADE 体积之差又∵求得AB =1∴23133125331πππ=⋅⋅⋅-⋅⋅⋅=-=--ADE B ADE C V V V7.答案：C解析：设该长方体水箱的长、宽、高分别为x 、y 、z ，∴x ·y ·z =4 ∴原长方形中用于制作水箱的部分的长、宽应分别为x +2z ，y +2z （如图9—45中（2）所示）从而通过对各选项的考查，确定C 答案.图9—458.答案：C解析：如图9—46，作出轴截面，设公共底面圆的半径为R ，圆锥的高为h∴V 锥=31πR 2h ，V 半球=21·43πR 3图9—44图9—47∵V 锥=V 半球，∴h =2R ∴tan α=21 ∴cos θ=53411411tan 1tan 122=+-=+-αα 9.答案：C 解析：V 甲=64·34π·（4a ·21）3=61πa 3， S 甲=64·4π·（4a ·21）2=4πa 2 V 乙=34π（a ·21）3=61πa 3，S 乙=4π（a ·21）2=πa 2 ∴V 甲=V 乙，S 甲＞S 乙. 10.答案：C解析：若命题甲成立，命题乙不一定成立，如底面为菱形时. 若命题乙成立，命题甲一定成立. 11.答案：B解析：连结FE 1、FD ，则由正六棱柱相关性质得FE 1∥BC 1. 在△EFD 中，EF =ED =1，∠FED =120°，∴FD =3.在Rt △EFE 1和Rt △EE 1D 中，易得E 1F =E 1D =3.∴△E 1FD 是等边三角形.∴∠FE 1D =60°. ∴BC 1与DE 1所成的角为60°.评述：本题主要考查正六棱柱的性质及异面直线所成的角的求法. 12.答案：D解析：①∵a ∥b ，a ⊥α，∴b ⊥α，又∵b ⊥β，∴α∥β ②∵a ⊥α，α⊥β ∴a ∥β或a ∈β 又∵b ⊥β ∴b ⊥a ③若α∥β，则a ∥b④若α、β相交，则a 、b 可能相交也可能异面，显然D 不对. 13.答案：C解析:展开图可以折成如图9—47的正方体,由图可知①②不正确. ∴③④正确. 14.答案：A 解析：∵S ＝21ab sin θ 图9—47∴21a 2sin60°＝3 ∴a 2＝4，a ＝2，a =2r ∴r ＝ 1 S 全＝2πr ＋πr 2＝2π＋π＝3π 15.答案：D解析：由S 底＝S 侧cos θ可得P 1＝P 2 而P 3＝θθθcos )(2)cos sin (22121S S S S +=+ 又∵2（S 1＋S 2）＝S 底 ∴P 1＝P 2＝P 316.答案：B解析：如图9—48，D 1、D 分别为B 1C 1、BC 中点，连结AD 、D 1C ，设BB 1＝1，则AB ＝2，则AD 为AB 1在平面BC 1上的射影，又32cos ,22,3311====BC BC BC C BD BE∴DE 2＝BE 2＋BD 2－2BE ·BD ·cos C 1BC ＝6132223322131=⋅⋅⋅-+ 而BE 2＋DE 2＝216131=+＝BD 2 ∴∠BED ＝90° ∴AB 1与C 1B 垂直 17.答案：C解析：设圆锥底面半径为r ，母线长为l ，依条件则有2πr ＝πl ，如图9—49∴21=l r ，即∠ASO ＝30°，因此圆锥顶角为60°. 18.答案：A解析：（1）如果a ，b 是平面M 中的两条相交直线，面M ∥α， ∴有a ∥α，b ∥α，但a b ，所以（1）错．（2）如果α∩β＝b ，而a ∥b ，∴有a ∥α，a ∥β，但αβ，所以（2）错．（3）如果α∩β＝b ，而b ⊥γ，∴有β⊥γ，α⊥γ，但αβ，（3）错． 19.答案：C解析：设圆锥的底面半径为R ，则V 圆锥＝32πR 3，V 球＝34πR 3， ∴V 圆锥∶V 球＝1∶2． 20.答案：D解析：设长方体共一顶点的三边长分别为a =1，b ＝2，c ＝3，则对角线l 的长为图9—48图9—49l =6222=++c b a ．21.答案：D解析：如图9—50，由题意知，31πr 2h ＝61πR 2h ， ∴r ＝2R．又△ABO ∽△CAO ，∴R OA OA r =，∴OA 2＝r ·R ＝422,2R OA R =， ∴cos θ＝421=R OA ． 22.答案：A解析：设圆柱的底面半径为r ，高为h ，则由题设知h =2πr . ∴S 全=2πr 2+（2πr ）2=2πr 2（1+2π）.S侧=h 2=4π2r 2，∴ππ221+=侧全S S . 评述：本题考查圆柱的侧面展开图、侧面积和全面积等知识.23.答案：B解析：设水面半径为x cm ，则水面高度为3x cm则由已知得：π·22·6＝31πx 2·3x （3x ）3＝63，3x ＝6.评述：本题重点考查柱体、锥体的体积公式及灵活的运算能力. 24.答案：D解析：由已知得中截面圆的半径r ′＝25+R . 设圆台的母线长为l ，则中截面截圆台所得上面小圆台的母线长l ′＝2l，且上面小圆台的侧面积S ′与圆台侧面积S 之比为1∶3，由圆台侧面积公式得：31)5(21)255(=+⋅++='l R R S S ππ，解得R =25 评述：本题主要考查圆台及其侧面积公式，立足课本，属送分题.图9—5025.答案：D解析：连EB 、E C.四棱锥E —ABCD 的体积V E —ABCD =31·32·2=6.由于AB =2EF ，EF ∥AB ，所以S △EAB =2S △BEF∴V F —EBC =V C —EFB =21V C —ABE =21V E —ABC =21·21V E —ABCD =23 ∴多面体EF —ABCD 的体积V EF —ABCD =V E —ABCD +V F —EBC =6+21523=. 此题也可利用V EF —ABCD ＞V E —ABCD =6.故选D.评述：本题考查多面体体积的计算以及空间想象能力和运算能力. 26.答案：C解析：设圆锥底面半径为r ，母线长为l ，由已知得：πr 2＋πrl ＝3πr 221=⇒l r ， ∴θ＝lr×2π＝π. 评述：本小题考查圆锥的概念、性质及侧面积公式.侧面展开是立体问题平面化的重要手段应引起广大考生的注意. 27.答案：A解析：设该棱台为正棱台来解即可.评述：本题考查棱台的中截面问题.根据选择题的特点本题选用“特例法”来解，此种解法在解选择题时很普遍，如选用特殊值、特殊点、特殊曲线、特殊图形等等.28.答案：B 解析：设球心为O ，由题设知三棱锥O —ABC 是正四面体，且△ABC 的外接圆半径是2，设球半径为R ，则33R ＝2，∴R ＝23. 29.答案：C解析：A 中直线l ⊥β，l α，所以α⊥β，A 为真命题.B 中，在α内取两相交直线，则此二直线平行于β，则α∥β，B 为真命题.D 为两平面平行的性质，为真命题.C 为假命题，l 只有在垂直交线时才有l ⊥β，否则l 不垂直β.故选C.评述：本题考查平面与平面垂直、直线与平面平行的判定和性质. 30.答案：C解析：长方体的对角线长等于球的直径，于是（2R ）2＝32＋42＋52，R 2＝225，则S 球＝4πR 2＝4π·225＝50π. 评述：本题考查长方体、球的有关概念和性质.。

2011-2019年全国卷立体几何真题汇编

2011-2019年全国卷立体几何真题汇编2011年全国卷6.在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的俯视图可以为A. B. C. D.2011年全国卷15.已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,23AB BC ==,则棱锥O ABCD -的体积为_______.2012年全国卷7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为A.6B.9C.12D.182012年全国卷11．已知三棱锥ABC S -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2=SC ,则此棱锥的体积为A.26B.36C.23D.222013年全国一卷6.如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计的厚度，则球的体积为A.35003cm πB.38663cm πC.313723cm πD.320483cm π2013年全国一卷8.某几何体的三视图如图所示，则该几何体的体积为（）A.168π+B ．88π+C ．1616π+D ．816π+2013年全国二卷4.已知,m n 为异面直线,m ^平面a ,n ^平面b ,直线l 满足l m ^,l n ^,l Úa ,l Úb ,则A.//a b 且//l aB.a b ^且l b^C.a 与b 相交，且交线垂直于lD.a 与b 相交,且交线平行于l2013年全国二卷7.一个四面体的顶点在空间直角坐标系O xyz -中的坐标是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为2014年全国一卷12.如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为A.62B.42C.6D.42014年全国二卷6.如图，网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为A .1727B .59C.1027D.132014年全国二卷11.直三棱柱111ABC A B C -中，90BCA ∠=,M ,N 分别是11A B ,11AC 的中点，1BC CA CC ==，则BM 与AN 所成的角的余弦值为A.110B .25C.3010D.222015年全国一卷6.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。

2017年高考数学—立体几何(解答+答案)

2017年高考数学—立体几何（解答+答案）1.（17全国1理18.（12分））如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o .（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠=o ，求二面角A -PB -C 的余弦值.2.（17全国1文18．（12分））如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ,90APD ∠=o ,且四棱锥P-ABCD 的体积为83，求该四棱锥的侧面积.如图，四棱锥P ABCD -中，侧面PAD 为等比三角形且垂直于底面ABCD ，o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD 的中点. （1）证明：直线//CE 平面PAB（2）点M 在棱PC 上，且直线BM 与底面ABCD 所成角为o 45 ，求二面角M AB D --的余弦值4.17全国2文18.(12分)如图，四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面ABCD ，12AB BC AD ==，90BAD ABC ∠=∠=o 。

（1）证明：直线//BC 平面PAD ；（2）若PCD ∆的面积为27，求四棱锥P ABCD -的体积。

如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形．ABDCBD ??，AB BD =．（1）证明：平面ACD ^平面ABC ；（2）过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分．求二面角D AE C --的余弦值．6.（17全国3文19．（12分））如图，四面体ABCD 中，△ABC 是正三角形，AD =CD ．（1）证明：AC ⊥BD ；（2）已知△ACD 是直角三角形，AB =BD ．若E 为棱BD 上与D 不重合的点，且AE ⊥EC ，求四面体ABCE 与四面体ACDE 的体积比．DABCE7.（17北京理（16）（本小题14分））如图，在四棱锥P ABCD -中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，点M 在线段PB 上，//PD 平面,6,4MAC PA PD AB ===（I ）求证：M 为PB 的中点；（II ）求二面角B PD A --的大小；（III ）求直线MC 与平面BDP 所成角的正弦值．8.（17北京文（18）（本小题14分））如图，在三棱锥P ABC -中，,,,2PA AB PA BC AB BC PA AB BC ⊥⊥⊥===，D 为线段AC 的中点，E 为线段PC 上一点．（Ⅰ）求证：PA BD ⊥；（Ⅱ）求证：平面BDE ⊥平面PAC ；（Ⅲ）当//PA 平面BDE 时，求三棱锥E BCD -的体积．9.（17山东理17.）如图，几何体是圆柱的一部分，它是由矩形ABCD （及其内部）以AB 边所在直线为旋转轴旋转120︒得到的，G 是»DF的中点. （Ⅰ）设P 是»CE上的一点，且AP BE ⊥，求CBP ∠的大小；（Ⅱ）当3AB =，2AD =，求二面角E AG C --的大小.10.（17山东文（18）（本小题满分12分））由四棱柱1111ABCD A B C D -截去三棱锥111C B CD -后得到的几何体如图所示，四边形ABCD 为正方形，O 为AC 与BD 的交点，E 为AD 的中点，1A E ⊥平面ABCD, （Ⅰ）证明：1A O ∥平面11B CD ；（Ⅱ）设M 是OD 的中点，证明：平面1A EM ⊥平面11B CD .11.（17天津理（17）（本小题满分13分））如图，在三棱锥P -ABC 中，PA ⊥底面ABC ，90BAC ∠=︒.点D ，E ，N 分别为棱PA ，P C ，BC 的中点，M 是线段AD 的中点，PA =AC =4，AB =2.（Ⅰ）求证：MN ∥平面BDE ；（Ⅱ）求二面角C -EM -N 的正弦值；（Ⅲ）已知点H 在棱PA 上，且直线NH 与直线BE 所成角的余弦值为7，求线段AH 的长.12.（17天津文（17）（本小题满分13分））如图，在四棱锥P ABCD -中，AD ⊥平面PDC ，AD BC ∥，PD PB ⊥，1AD =，3BC =，4CD =，2PD =.（Ⅰ）求异面直线AP 与BC 所成角的余弦值；（Ⅱ）求证：PD ⊥平面PBC ；（Ⅲ）求直线AB 与平面PBC 所成角的正弦值.如图，已知四棱锥P–ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点.（Ⅰ）证明：CE∥平面PAB；（Ⅱ）求直线CE与平面PBC所成角的正弦值.14.（17江苏15.（本小题满分14分））-中，AB⊥AD，BC⊥BD，平如图，在三棱锥A BCD面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD。

历年全国理科数学高考试题立体几何部分精选(含答案)

1.在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的俯视图可以为2.已知矩形ABCD的顶点都在半径为4的球O的球面上，且6,==,则棱锥AB BC-的体积为。

O ABCD3.如图，四棱锥P—ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明：PA⊥BD；(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。

1.D2.3. 解：（Ⅰ）因为60,2DAB AB AD ∠=︒=，由余弦定理得BD =从而BD 2+AD 2= AB 2，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面PAD. 故 PA ⊥BD（Ⅱ）如图，以D 为坐标原点，AD 的长为单位长，射线DA 为x 轴的正半轴建立空间直角坐标系D-xyz ，则()1,0,0A，()0B，()C -，()0,0,1P 。

(1),(1,0,0)AB PB BC =-=-=-uu u v uu v uu u v设平面PAB 的法向量为n=（x ，y ，z ），则0,0,{n AB n PB ⋅=⋅=u u u r u u u r00z =-=因此可取n=设平面PBC 的法向量为m ，则m 0,m 0,{PB BC ⋅=⋅=u u u ru u u r可取m=（0，-1， cos ,m n == 故二面角A-PB-C 的余弦值为1. 正方体ABCD-1111A B C D 中，B 1B 与平面AC 1D 所成角的余弦值为C 232. 已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为俩切点，那么PA PB ∙的最小值为(A) 4- (B)3-+ (C) 4-+3-+3. 已知在半径为2的球面上有A 、B 、C 、D 四点，若AB=CD=2,则四面体ABCD 的体积的最大值为(C)4. 如图，四棱锥S-ABCD 中，SD ⊥底面ABCD ，AB//DC ，AD ⊥DC ，AB=AD=1，DC=SD=2，E 为棱SB 上的一点，平面EDC ⊥平面SBC .（Ⅰ）证明：SE=2EB ；（Ⅱ）求二面角A-DE-C 的大小 .1. D2. D3. B4. 解法一：(Ⅰ)连接BD,取DC 的中点G ，连接BG,由此知 1,DG GC BG ===即ABC ∆为直角三角形，故BC BD ⊥. 又ABCD,BC SD SD ⊥⊥平面故,所以，BC ⊥⊥平面BDS,BC DE .作BK ⊥EC,EDC SBC K ⊥为垂足，因平面平面，故,BK EDC BK DE DE ⊥⊥平面，与平面SBC 内的两条相交直线BK 、BC 都垂直 DE ⊥平面SBC ，DE ⊥EC,DE ⊥SBSB =SD DB DE SB ==-EB SE SB EB ====所以，SE=2EB(Ⅱ) 由1,2,,SA AB SE EB AB SA ===⊥知1,AD=1AE ==又.故ADE ∆为等腰三角形.取ED 中点F,连接AF ,则,AF DE AF ⊥==. 连接FG ，则//,FG EC FG DE ⊥.所以，AFG ∠是二面角A DE C --的平面角.连接AG,A G=,3FG ==, 2221cos 22AF FG AG AFG AF FG +-∠==-,所以，二面角A DE C --的大小为120°. 解法二：以D 为坐标原点，射线DA 为x 轴的正半轴，建立如图所示的直角坐标系D xyz -，设A(1,0,0)，则B(1,1,0),C(0,2,0),S(0,0,2)（Ⅰ）(0,2,-2),(-1,1,0)SC BC ==设平面SBC 的法向量为n=(a, b, c) 由,n SC n BC ⊥⊥，得0,0n SC n BC == 故2b-2c=0,-a+b=0令a=1，则b=c,c=1,n=(1,1,1) 又设SE EB λ= (0)λ>，则2(,,)111E λλλλλ+++ 2(,,),(0,2,0)111DE DC λλλλλ==+++设平面CDE 的法向量m=(x,y,z) 由,m DE m DC ⊥⊥,得0m DE ⊥=，0m DC ⊥= 故20,20111x y zy λλλλλ++==+++. 令2x =，则(2,0,)m λ=-.由平面DEC ⊥平面SBC 得m ⊥n,0,20,2m n λλ=-== 故SE=2EB（Ⅱ）由（Ⅰ）知222(,,)333E ，取DE 的中点F ，则111211(,,),(,,)333333F FA =--，故0FA DE =，由此得FA DE ⊥ 又242(,,)333EC =--，故0EC DE =，由此得EC DE ⊥，向量FA 与EC 的夹角等于二面角A DE C --的平面角于是 1cos(,)2||||FA EC FA EC FA EC ==-所以，二面角A DE C --的大小为120（三）1. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（）（A （B （C (D) 342. 已知二面角l αβ--为60o，动点P 、Q 分别在面α、β内，P 到β，Q 到α的距离为则P 、Q 两点之间距离的最小值为（）(A) (B)2 (C) 3. 直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===, 120BAC ∠=︒，则此球的表面积等于。

2011年高考数学试题分类汇编立体几何

一、选择题1.（重庆理9）高为24的四棱锥S-ABCD 的底面是边长为1的正方形，点S 、A 、B 、C 、D 均在半径为1的同一球面上，则底面ABCD 的中心与顶点S 之间的距离为A ．24 B ．22C ．1D 2【答案】C2.（浙江理4）下列命题中错误的是A ．如果平面αβ⊥平面，那么平面α内一定存在直线平行于平面βB ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βC ．如果平面αγ⊥平面，平面βγ⊥平面，=l αβ⋂，那么l γ⊥平面D ．如果平面αβ⊥平面，那么平面α内所有直线都垂直于平面β【答案】D3.（四川理3）1l ，2l ，3l是空间三条不同的直线，则下列命题正确的是 A ．12l l ⊥，23l l ⊥13//l l ⇒ B ．12l l ⊥，23//l l ⇒13l l ⊥C ．233////l l l ⇒1l ，2l，3l共面D ．1l ，2l ，3l 共点⇒1l ，2l ，3l 共面【答案】B【解析】A 答案还有异面或者相交，C 、D 不一定 4.（陕西理5）某几何体的三视图如图所示，则它的体积是A ．283π-B ．83π-C ．82π-D ．23π【答案】A5.（浙江理3）若某几何体的三视图如图所示，则这个几何体的直观图可以是【答案】D6.（山东理11）右图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正（主）视图、俯视图如下图；②存在四棱柱，其正（主）视图、俯视图如右图；③存在圆柱，其正（主）视图、俯视图如右图．其中真命题的个数是A．3 B．2C．1 D．0【答案】A7.（全国新课标理6）。

在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为【答案】D3 32正视图侧视图俯视图图1 8.（全国大纲理6）已知直二面角α− ι−β，点A ∈α，AC ⊥ι，C 为垂足，B ∈β，BD ⊥ι，D 为垂足．若AB=2，AC=BD=1，则D 到平面ABC 的距离等于A ．23B ．3C ．6D ．1【答案】C9.（全国大纲理11）已知平面α截一球面得圆M ，过圆心M 且与α成060二面角的平面β截该球面得圆N ．若该球面的半径为4，圆M 的面积为4π，则圆N 的面积为 A ．7π B ．9π C ．11π D ．13π 【答案】D10.（湖南理3）设图1是某几何体的三视图，则该几何体的体积为 A ．9122π+ B ．9182π+C ．942π+D ．3618π+【答案】B11.（江西理8）已知1a ，2a ，3a 是三个相互平行的平面．平面1a ，2a之间的距离为1d ，平面2a ，3a 之间的距离为2d ．直线l 与1a ，2a ，3a 分别相交于1p ，2p ，3p ，那么“12P P =23P P ”是“12d d =”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C12.（广东理7）如图1－3，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则该几何体的体积为A．63B．93C．123D．183【答案】B13.（北京理7）某四面体的三视图如图所示，该四面体四个面的面积中，最大的是A．8 B．62C．10 D．82【答案】C14.（安徽理6）一个空间几何体的三视图如图所示，则该几何体的表面积为（A）48（B）32+817（C）48+817（D）80【答案】C15.（辽宁理8）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高三数学立体几何高考题1.（2012年7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A ）6 （B ）9 （C ）12 （D ）182.（2012年8）平面α截球O 的球面所得圆的半径为1，球心O到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π3.(2013年11)某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π4.(2013年15)已知H 是球O 的直径AB 上一点，AH ∶HB ＝1∶2，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为______．5.(2014年8)如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三视图，则这个几何体是（） A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱6.(2014年10)正四棱锥的顶点都在同一球面上．若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4 B ．16π C ．9π D.27π47.(2015年6)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问”积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各位多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米有（）（A ）14斛（B ）22斛（C ）36斛（D ）66斛8.(2015年11)圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为1620π+，则r =( ) （A ）1 （B ）2 （C ）4 （D ）89（2016年7）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是（A ）17π （B ）18π （C ）20π （D ）28π10（2016年11）平面α过正方体ABCD —A 1B 1C 1D 1的顶点A ，11//CB D α平面,ABCD m α=I 平面，11ABB A n α=I 平面，则m ，n 所成角的正弦值为（A ）32 （B ）22 （C ）33 （D ）1311．(2017年6)如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直接AB 与平面MNQ 不平行的是12．（2017年16）已知三棱锥S-ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径。

若平面SCA ⊥平面SCB ，SA =AC ，SB =BC ，三棱锥S-ABC 的体积为9，则球O 的表面积为________。

13(2011年).如图，四棱锥P ABCD -中，底面ABCD 为平行四边形，60DAB ∠=︒，2AB AD =，PD ⊥底面ABCD ．（I ）证明：PA BD ⊥；（II ）设PD=AD=1，求棱锥D-PBC 的高．14.(2012课标全国Ⅰ)如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比。

15. (2013课标全国Ⅰ)如图，三棱柱ABC －A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°. (1)证明：AB ⊥A 1C ；(2)若AB ＝CB ＝2，A 1C ＝6，求三棱柱ABC －A 1B 1C 1的体积．16 (2014课标全国Ⅰ)如图1-1所示，三棱柱ABC -A1B1C1中，点A1在平面ABC内的射影D在AC上，∠ACB＝90°，BC＝1，AC＝CC1＝2.(1)证明：AC1⊥A1B；(2)设直线AA1与平面BCC1B1的距离为3，求二面角A1-AB-C的大小．17.(2015年新课标1)如图四边形ABCD为菱形，G为AC与BD交点，BE ABCD⊥平面，(1)证明：平面AEC⊥平面BED；(2)若120ABC∠=o，,AE EC⊥三棱锥E ACD-的体积为6，求该三棱锥的侧面积.18 (2016年新课标1)如图，已知正三棱锥P -ABC 的侧面是直角三角形，P A =6，顶点P 在平面ABC 内的正投影为点D ，D 在平面P AB 内的正投影为点E ，连结PE 并延长交AB 于点G . （I ）证明：G 是AB 的中点；（II ）在图中作出点E 在平面P AC 内的正投影F （说明作法及理由），并求四面体PDEF 的体积．PABD CGE19(2017年新课标1)如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o （1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ,90APD ∠=o , 且四棱锥P-ABCD 的体积为83，求该四棱锥的侧面积.高三数学立体几何高考题答案1.答案：B2.答案：B3.解析：该几何体为一个半圆柱与一个长方体组成的一个组合体．V 半圆柱＝12π×22×4＝8π， V 长方体＝4×2×2＝16.所以所求体积为16＋8π.故选A. 4.解析：如图，设球O 的半径为R ，则AH ＝23R ， OH ＝3R .又∵π·EH 2＝π，∴EH ＝1. ∵在Rt△OEH 中，R 2＝22+13R ⎛⎫ ⎪⎝⎭，∴R 2＝98.∴S 球＝4πR 2＝9π2.5.答案：B6．A [解析] 如图所示，因为正四棱锥的底面边长为2，所以AE ＝12AC ＝ 2.设球心为O ，球的半径为R ，则OE ＝4－R ，OA ＝R .又因为△AOE 为直角三角形，所以OA 2＝OE 2＋AE 2，即R 2＝(4－R )2＋2，解得R ＝94，所以该球的表面积S ＝4πR 2＝4π⎝⎛⎭⎫942＝81π4. 7.答案：B 8.答案：B9.试题分析：由三视图知：该几何体是78个球，设球的半径为R ，则37428V R 833ππ=⨯=，解得R 2=，所以它的表面积是22734221784πππ⨯⨯+⨯⨯=，故选A ．10试题分析：如图m ,n 所成角的正弦值为3211.答案：A 12答案：36π13解：（Ⅰ）因为60,2DAB AB AD ∠=︒=，由余弦定理得3BD AD = 从而BD 2+AD 2= AB 2，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面P AD. 故 P A ⊥BD（Ⅱ）如图，作DE ⊥PB ，垂足为E 。

已知PD ⊥底面ABCD ，则PD ⊥BC 。

由（Ⅰ）知BD ⊥AD ，又BC//AD ，所以BC ⊥BD 。

故BC ⊥平面PBD ，BC ⊥DE 。

则DE ⊥平面PBC 。

由题设知，PD=1，则BD=3，PB=2，根据BE·PB=PD·BD ，得DE=23，即棱锥D —PBC 的高为.231415．1)证明：取AB 的中点O ，连结OC ，OA 1，A 1B .因为CA ＝CB ，所以OC ⊥AB . 由于AB ＝AA 1，∠BAA 1＝60°，故△AA 1B 为等边三角形，所以OA 1⊥AB .因为OC ∩OA 1＝O ，所以 AB ⊥平面OA 1C . 又A 1C ⊂平面OA 1C ，故AB ⊥A 1C .(2)解：由题设知△ABC 与△AA 1B 都是边长为2的等边三角形，所以OC ＝OA 13又A 1C 6，则A 1C 2＝OC 2＋21OA ，故OA 1⊥OC .因为OC ∩AB ＝O ，所以OA 1⊥平面ABC ，OA 1为三棱柱ABC －A 1B 1C 1的高．又△ABC 的面积S △ABC 3ABC －A 1B 1C 1的体积V ＝S △ABC ×OA 1＝3.P ABDC G E 16．解：方法一：(1)证明：因为A 1D ⊥平面ABC ，A 1D ⊂平面AA 1C 1C ，故平面AA 1C 1C ⊥平面ABC .又BC ⊥AC ，平面AA 1C 1C ∩平面ABC ＝AC ，所以BC ⊥平面AA 1C 1C .连接A 1C ，因为侧面AA 1C 1C 为菱形，故AC 1⊥A 1C . 由三垂线定理得AC 1⊥A 1B .(2)BC ⊥平面AA 1C 1C ，BC ⊂平面BCC 1B 1，故平面AA 1C 1C ⊥平面BCC 1B 1.作A 1E ⊥CC 1，E 为垂足，则A 1E ⊥平面BCC 1B 1.又直线AA 1∥平面BCC 1B 1，因而A 1E 为直线AA 1与平面BCC 1B 1的距离，即A 1E ＝ 3. 因为A 1C 为∠ACC 1的平分线，故A 1D ＝A 1E ＝ 3.作DF ⊥AB ，F 为垂足，连接A 1F .由三垂线定理得A 1F ⊥AB ，故∠A 1FD 为二面角A 1 AB C 的平面角．由AD ＝AA 21－A 1D 2＝1，得D 为AC 中点，所以DF ＝55，tan ∠A 1FD ＝A 1D DF ＝15，所以cos ∠A 1FD ＝14. 所以二面角A 1 AB C 的大小为arccos 14.17、解：（I ）因为四边形ABCD 为菱形，所以AC ⊥BD. 因为BE ⊥平面ABCD,所以AC ⊥BE,故AC ⊥平面BED.又AC ⊂平面AEC,所以平面AEC ⊥平面BED. ……5分（II ）设AB=x ，在菱形ABCD 中，又∠ABC=o120 ，可得 AG=GC=3x ，GB=GD=2x . 因为AE ⊥EC,所以在Rt △AEC 中，可的EG=3x . 由BE ⊥平面ABCD,知△EBG 为直角三角形，可得BE=2x . 由已知得，三棱锥E-ACD 的体积E ACD V -=13×12AC ·GD ·BE=366243x =. 故x =2 ……9分从而可得AE=EC=ED=6.所以△EAC 的面积为3，△EAD 的面积与 △ECD 的面积均为5. 故三棱锥E-ACD 的侧面积为3+25. ……12分18试题分析：（1）ABC PD 底面⊥ΘPD AB ⊥∴E PAB D 内的投影为在ΘPAB DE 平面⊥∴AB DE ⊥∴D PD DE =I ΘPDG AB 平面⊥∴PG AB ⊥∴ 为正三棱柱ABC P -Θ PB PA =∴的中点为中，在AB G PAB ∆∴ （II ）在平面PAB 内，过点E 作PB 的平行线交PA 于点F ，F 即为E 在平面PAC 内的正投影.理由如下：由已知可得PB PA ⊥，⊥PB PC ，又//EF PB ,所以EF PA EF PC ，⊥⊥,因此EF ⊥平面PAC ，即点F 为E 在平面PAC 内的正投影.连结CG ，因为P 在平面ABC 内的正投影为D ，所以D 是正三角形ABC 的中心.由（I ）知，G 是AB 的中点，所以D 在CG 上，故2.3=CD CG由题设可得⊥PC 平面PAB ，⊥DE 平面PAB ，所以//DE PC ，因此21,.33==PE PG DE PC由已知，正三棱锥的侧面是直角三角形且6=PA ，可得2,2 2.==DE PE 在等腰直角三角形EFP 中，可得 2.==EF PF所以四面体PDEF 的体积114222.323=⨯⨯⨯⨯=V19.【解析】（1）由已知90BAP CDP ==︒∠∠，得AB AP ⊥,CD PD ⊥. 由于AB CD ∥，故AB PD ⊥，从而AB ⊥平面PAD . 又AB ⊂平面PAB ，所以平面PAB ⊥平面PAD .（2）在平面PAD 内作PE AD ⊥，垂足为E .由（1）知，AB ⊥平面PAD ，故AB PE ⊥，可得PE ⊥平面ABCD . 设AB x =，则由已知可得2AD x =，22PE x =. 故四棱锥P ABCD -的体积31133P ABCD V AB AD PE x -=⋅⋅=. 由题设得31833x =，故2x =. 从而2PA PD ==，22AD BC ==，22PB PC ==. 可得四棱锥P ABCD -的侧面积为21111sin 606232222PA PD PA AB PD DC BC ⋅+⋅+⋅+︒=+.。