第四章投入产出核算
第四章 投入产出分析

(2)产品产量怎样组合才能达到最优。
本章从生产函数出发,以只包含一种生产要素的生 产函数,考察厂商在短期内的生产规模以及生产的 不同阶段;以包含两种生产要素的生产函数,来考 察厂商在长期内实现最优生产要素组合的均衡条件。
第一节 生产与生产函数
生产函数 生产
• 一定时期内,在 既定的生产技术 水条件下,各种 可行的生产要素 组合和可能达到 的最大产出量之 间的数量关系
第三阶段:L3之外 边际产量MP<0 TP AP
这个阶段由于总产量呈下降趋势,所以单位产品的固定成 本呈上升趋势;又由于平均产量呈下降趋势,所以单位产 品的变动成本也呈上升趋势。两者都呈上升趋势,说明可 变投入要素的数量不能超过OC,否则就会使成本增高。企 业如果在这个阶段组织生产是十分不利的,可变要素投入 量过多,物极必反,效益必然下降。要改变这种不经济的 状况,从管理决策角度,重点是改变前提条件,如生产技 术条件、其他要素投入量等,这些条件发生变化,边际收 益递减规律就不适用了。所以可称为管“条件”阶段
L取某值时的边际产量等于总产量曲 线上该点的切线斜率
MPL实际上是对Q = f(L)取导数含义:总产量曲线上当L 取某值时该点切线的斜率,从图中知B点是总产量曲线上 的拐点(斜率为最大点),边际曲线的顶点B1。 总产量曲线的顶点D→MP曲线上零点D1。
可知:
边际产量为正值时,总产量曲线↑(k>0) 表明增加L→增加产量Q
边际产量为负值时,总产量曲线↓(k<0)
表明增加L→Q↓ 边际产量为0时,总产量为最大(k=0)
表明增加L,Q不变
L取某值时的平均产量等于总产量曲 线上该点与原点的连接线的斜率。
第四章投入产出核算
... 0 ... 0 ... ... ... 1 acn
中间流量模型
ˆ X Aq ˆ A Xq
其中:q ˆ ——以q j 为元素的对角阵
1
投入产出模型分析
一、最终需求变化对各部门生产规模的影响——行模型 二、最终需求变化对各部门之间流量结构的影响——中间 流量模型 三、各部门总产量变化对增加值的影响——列模型 四、大型建设项目投产对最终需求和各部门生产的影响 五、各部门最终需求的变化可能引起的工资(V)、税收(T) 和营业盈余(M)的变化 六、价格变动影响分析
移项整理:
n ai1 ) q1 y1 (1 i 1 n (1 ai 2 ) q2 y 2 i 1 ... n (1 ain ) qn y n i 1
价值模型(2)
写成矩阵形式:
ˆ c ) q y q (I A ˆ c ) 1 y (I A 0 1 ac1 0 1 ac 2 ˆ ( I Ac ) ... ... 0 0 acj aij
n
展开为线形方程组:
a11q1 a12q2 ... a1n qn f1 q1 a q a q ... a q f q 21 1 22 2 2n n 2 2 ... an1q1 an 2 q2 ... ann qn f n qn
七、部门影响力和灵敏度分析
表4-1
中 间 投 入 最 初 投 入
部门1 部门2 部门3 合计 折旧 工资
生产税
盈余 合计 总投入
××年度价值型投入产出表 最终 中间产品 部门1 部门2 部门3 合计 产品 20 10 40 70 120 40 600 100 740 160 10 30 100 140 240 70 640 240 960 520 10 30 15 55 20 40 50 110 40 90 45 175 50 100 30 180 120 260 140 520 190 900 380 1470
《投入产出核算 》课件

投入产出表的矩阵运 算
通过矩阵运算,我们可以计算 出各个产业的投入和产出量, 从而分析经济的总体特征。
投入产出模型的线性 性质
投入产出模型是基于线性关系 假设的,这使得我们可以使用 线性代数方法进行分析与研究。
投入产出分析方法
投入产出模型的应用前景
投入产出核算的局限性
随着数据和计算能力的不断提高, 投入产出模型将在更多领域发挥 作用,为经济决策提供科学依据。
投入产出核算方法也存在局限性, 例如对经济增长的预测和不确定 因素的处理。
1
总产值分析
使用投入产出模型,我们可以计算出各个产业的总产值,评估整体经济发展状况。
2
就业分析
通过投入产出表,我们可以估计各个产业的就业人数,研究经济结构对就业的影 响。
3
产业关联分析
投入产出模型可以帮助我们分析各个产业之间的关联度,揭示不同产业间的相互 依赖关系。
投入产出模型的改进与发展
1
对称性假设
《投入产出核算》PPT课 件
本课程将介绍投入产出核算的基本知识和应用。我们将深入探讨投入产出模 型的构建、数学基础、分析方法以及改进与发展。让我们一起来了解这个令 人着迷的领域!
什么是投入产出核算
投入产出核算是一种经济分析方法,用于衡量不同产业之间的经济联系投入产出模型的构建
基本概念
投入产出模型涉及到生产要 素和最终产品之间的关系, 以及各个产业之间的交互作 用。
构建流程
构建投入产出模型需要收集 和整理大量的数据,并进行 数学建模和计算。
应用领域
投入产出模型广泛应用于经 济政策制定、产业分析、环 境影响评估等领域。
《投入产出核算》课件

投入产出表是反映一定时期内社会再生产过程中,各部门之间相互依存 、相互制约的经济技术联系的报表。
03
投入产出分析
投入产出分析是利用投入产出表提供的数据,对国民经济各部门之间的
经济技术联系进行分析பைடு நூலகம்究的方法。
投入产出核算的目的和意义
目的
投入产出核算是为了全面、系统地反映国民经济的运行 过程,揭示各部门之间的经济技术联系,为宏观经济决 策提供依据。
02
投入产出表
投入产出表的定义和结构
总结词
投入产出表是用于描述一个经济体内部各产业部门之间投入与产出的关系的表格,其结构包括 行和列,行表示投入,列表示产出。
详细描述
投入产出表是一种重要的经济统计工具,它以矩阵形式展示了经济体内部各产业部门之间的投 入产出关系。该表格的行表示生产过程中各种投入的来源,列表示各产业部门的产品去向。通 过投入产出表,可以全面了解一个经济体在生产过程中的投入产出规模、结构和效率。
意义
完全消耗系数反映了部门之间的 直接和间接经济联系,是制定宏 观经济政策和进行经济分析的重 要参数。
影响力系数和感应度系数
定义
影响力系数是指某一产业或部门增加一个单位最终产品时,对其他产业或部门的生产需求 所产生的影响程度。感应度系数是指其他产业或部门增加一个单位最终产品时,某一产业 或部门所受到的生产需求感应程度。
计算方法
影响力系数和感应度系数的计算公式比较复杂,需要用到线性代数的方法。具体可参考相 关教材和文献。
意义
影响力系数和感应度系数是判断产业或部门在经济发展中的地位和作用的重要指标,对于 制定产业发展战略和政策具有重要的指导意义。
生产诱发系数和最终需求依赖度系数
04第四章-投入产出分析

b11 b12 b21 b22 1 ( I A) Y b 1n b2 n y1 x1 j X 1 y 2 x2 j X 2 y x X nj n n
2.中间消耗与增加值的分解 (1)按比例分摊:假定投入是按产值分配的
某产品对某种中间投入的消耗=该中间投入的消耗总
额×某产品产值/企业总产值 (2)按定额分摊:假定投入是按工时分配的 某产品对某种中间投入的消耗=该中间投入的消耗总 额×该产品实际生产工时/企业生产总工时
3.最终产品的分解与调整
根据样本资料推断总体
3.为了获得稳定的投入产出表,可以采用下列方法 (1)采用一定的工艺假设,尽可以“纯化”投入产出 表 (2)用生产资料价格指数调整中间消耗的价格变动
(3)对直接消耗系数给予一定的时间限制
二.完全消耗系数
1.概念 生产产品j对于i的直接或间接消耗之和
直接消耗:
aij
第一轮间接消耗:
a
k 1
n
ik
2.从横向看:中间使用+最终使用=总产出
3.每个部门的总投入=该部门的总产出
第二节 直接消耗系数和完全消耗系数
一.直接消耗系数 1.概念 反映两个部门之间直接存在的投入关系,用每一行业 某一产品的投入数值比该行业的产出数值,可以得到 反映出每生产一单位的j所需要付出的i的数量。
aij
xij
Xj
第四章 投入产出分析
第一节
投入产出核算的基本原理
投入产出法是本世纪30年代美国经济学家列昂惕夫提
出的,根据计量单位的不同,可以分为实物型和价值 型两种,根据时间的不同,分为静态和动态。 Wassily Leontief(1906-1999),美国著名经济学 家和统计学家,投入产出方法的创始人。1931年移居 美国,1936年在《经济统计评论》杂志上发表了《美 国经济系统中投入产出的数量关系》一文,首次提出 投入产出分析法。
第四章投入产出核算
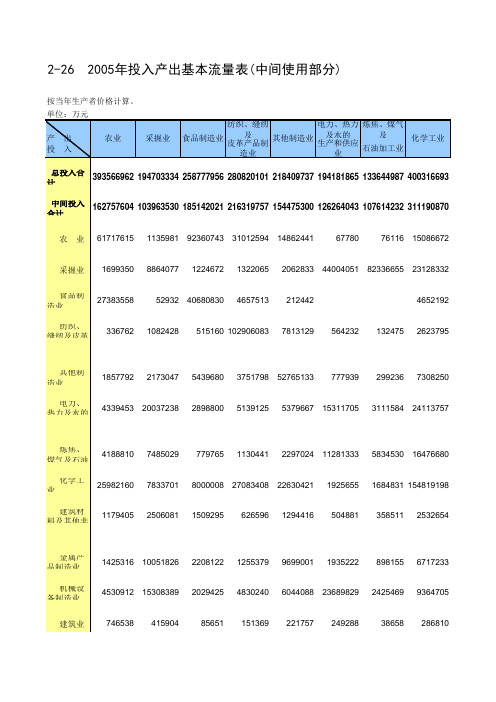
110644539 331608325 720950147 316806564 193915207 173032966 93846013 39472397 257082970
133284
72076 253354 30299716 3534741 18755113 280005
2548066
16048850 49949850 6800131 8601617 2155262 957765 598428
房地产业、租10赁03和74商1务服2务06业2785 5160390 6058597 3106687 651545 588721 6480618
金融保险业4143831 2544852 1613730 2150454 2146328 4562756 660011 3502369 其他服务业4473998 5819133 2554455 3560145 1991051 5142457 1114330 4445117 增加值合计230809359 90739804 73635934 64500343 63934436 67917822 26030755 89125822 劳动者报2酬08972657 20677244 15307413 27503029 18424180 15125189 5278379 26309589 生产税净额1209199 16156095 25664925 10205817 8180562 14305722 8837161 18186699 固定资产折1旧1945295 10777152 7781459 7818374 6657360 22296953 5791297 15272654 营业盈余 8682207 43129313 24882138 18973123 30672334 16189959 6123918 29356880
4第四章投入产出理论
x2=f2(p2,p3,…,pn;w1,w2,…,wm) x3= f3(p2,p3,…,pn;w1,w2,…,wm) ………… …… …… xn= fn(p2,p3,…,pn;w1,w2,…,wm) x1=( y1w1+y2w2+…+ymwm)- ( x2p2+x3p3+,…,+xnpn)
很明显,商品x1的方程不同于商品x1, x2,… ,xn的方程,原因在于,x1被限定 为“一般等价物”,价格p1=1,其他商品价 格可能发生变化,但x1的价格不会发生变化。 x1的方程实际上是预算方程,个人的全部收 入用于购买商品x2,……,xn之后的余额, 就是用于购买x1的收入。
y1=g1(p1,p2,……,pn;w1,w2,……,wm) y2=g2(p1,p2,……,pn;w1,w2,……,wm) …… …… …… …… …… ym=gm(p1,p2,……,pn;w1,w2,……,wm)
以上只是一个人对每种要素的提供量,在经济社 会中,同时作为消费者和要素所有者存在的家庭和个 人有许许多多。用k表示经济社会或模型中家庭或个 人数目,y1表示所有k个家庭或个人提供的要素y1, 用y2表示所有k个家庭或个人提供的要素y2,以此类 推,用ym表示所有k个家庭或个人提供的要素ym的 总数,这样, ym=ym1+ym2+,…,+ymk 其中:ym1,ym2,…,ymk分别代表第一个人 提供的要素ym,第二个人提供的要素ym,以此类推, 第k个人购买的商品ym。
பைடு நூலகம்
在简单的瓦尔拉斯模型中,商品都是最终产品, 没有中间产品。也就是说,商品直接用要素来生产, 每生产一定量的产品,都要使用一定各类的要素。 符号a11表示生产1个单位的第一种商品所用的第一 种要素的数量,a12表示生产一个单位的第二种商 品所用的第一种要素的数量,……,a1n表示生产1 个单位的第n种商品所用的第一种要素的数量。一 般地,aij表示生产1个单位的第j种商品所用的第i 种要素的数量,aij被称为生产系数。生产系数表 示一定技术条件下,生产一个单位商品所用要素数 量。基本假设规定,模型中的生产系数固定不变。 由于模型中共有n种商品,m种要素,所以生产系数 一共m*n个。
第四章投入产出核算
第4章投入产出核算一、思考题1.投入产出核算对部门分类有什么特殊要求, 它与现实经济管理中的部门分类有什么区别与联系?2.试比较直接消耗系数、完全消耗系数、完全需求系数及中间消耗系数的定义及其所反映的经济内容。
3.试述投入产出表各象限所反映的内容。
4.什么是部门工艺假定?采用部门工艺假定会出现什么问题?5.什么是产品工艺假定?采用产品工艺假定会出现什么问题?6.使用表是由哪几个象限构成的?每个象限各反映什么内容?7.投入产出表的主要应用领域有哪些?二、单项选择题.1.投入产出分析法是经济学家()于1936年提出来的A、列昂惕夫B、科普兰C、瓦尔拉D、斯通2.我国第一张表全国规模的价值型投入产出表于()开始编制的。
.A、1973B、1983C、1981D、19883.就全国来说,下列命题不正确的是()A、总投入等于总产出B、中间投入等于中间产出C、总产出即全部物品的产出D、最终使用在价值上于最终产品相等4.描述货物和服务从它们的最初生产者到它们的使用者过程的账户是()。
.A、货物和服务账户B、生产账户C、收入形成账户D、收入使用账户5.投入产出核算中采用产品部门分类,是因为()。
.A、产品部门分类比较简单B、按产业部门分类的投入产出表无意义C、产品部门更能够揭示产品部门之间的生产技术联系D、产业部门分类只适合于行政管理6.在投入产出表的第一象限中,每一个数据都有双重的经济意义,即一方面表示投入,另一方面表示产出,这正符合复式记帐的原理。
这种说法是()。
A、完全正确的B、完全错误的C、可能不正确的D、毫无道理的7.编制投入产出表最合适的估价形式是()。
A、生产价格B、购买价格C、基本价格D、现行价格8.投入产出核算和收入分配核算账户之间有联系,表现在()。
A、部门分类是相同的B、研究的目的是相同的C、投入产出表的第三象限和收入初次分配账户的项目设置和核算总量是接近的D、投入产出表的第二象限和收入二次分配账户的项目设置和核算总量是接近的9.指出正确的命题().A、供给和使用表采用了不同的格式B、供给和使用表也是一种投入产出表C、供给和使用表的行表示产业,列表示产品D、在列中,产品是按照《主产品分类》的规定进行分类的。
第四章投入产出核算
投入产出表 投入产出的数学模型 投入产出法的应用
(四) 投入产出法的产生与发展 1产生的时代背景
(1)由谁提出— (2)时间—1936 (3)诞生标志—列昂剔夫在《经济与统计评
论》杂志上 论文: 《美国在经济体系中的投入产出的数量关系》 2在世界各国的发展 3在我国的应用
二 全国价值型投入产出表式结构
a21
,1
a22
,
.
.
.
.
.
.
a2
n
......
an1,an2 ,.....1. ann
每一列说明生产一个单位的产品,需要消耗各部门 产品的数量。
(二)价值模型
引言:
aij
xij qj
xij aij q j
n
xij y j q j
i 1
1 一般表达式
矩阵的含义 (I A)1
行:
全社会各部门生产一个单位的最终产品需 要i产品的总产品的数量。
列:
生产一个单位的j种最终产品需要全社会 各部门提供的总产品的数量。
三 投入产出的数学模型
(一)产品模型
引言:
1一般表达式
aij
xij qj
n
xij fi qi
j 1
xij aij q j
xij aij q j
a11a12......a1n q1
a21a22
.
.
.
.
.
.a2
n
q2
......
:
an1an
2
第四章 投入产出核算
投入产出核算
第一节 投入产出核算的基本问题 第二节 投入产出表 第三节 投入产出的分析应用
1
第一节 投入产出核算的基本问题
2
一、投入产出核算的几个基本概念 (一)投入产出核算 投入产出核算又称投入产出分析, 又称投入产出分析 投入产出核算又称投入产出分析,是指 主要利用投入产出表来反映部门间生产过程 中所形成的技术经济联系和各种比例关系。 中所形成的技术经济联系和各种比例关系。 投入产出表的产生与发展
14
三、投入产出表的消耗系数
若用第Ⅰ 若用第Ⅰ象限每个部门的中间投入分别 除以本部门的总投入, 除以本部门的总投入,便可得到由全部直接 消耗系数aij组成的直接消耗系数矩阵 组成的直接消耗系数矩阵。 消耗系数 组成的直接消耗系数矩阵。
a11 a 21 A= L a n1 a12 L a1n a 22 L a 2 n L L L a n 2 L a nn
( I − A ) −1 Y = X 表明的是最终产出与总产出的关
系。
19
四、各种消耗系数与产出的联系
2.从列的模型看,直接消耗系数与总产出和增 从列的模型看, 从列的模型看 加值的关系表现为: 加值的关系表现为: a 0 L 0 (I- AC)X=N ,其中
c1 0 Ac = L 0 ac 2 L L L L L 0 0 a cn
29
二、用于研究产业结构的分析和规划 (二)根据投入产出模型进行产业规划 利用投入产出模型进行产业结构规划的 基础是它的行模型
X = ( I − A ) −1Y
若用∆Y代表各产业部门增加的最终需 若用 代表各产业部门增加的最终需 最终使用)数值, 表示 表示∆Y对各产业 求(最终使用)数值,∆X表示 对各产业 部门总产出的影响, 部门总产出的影响,则 −1 ∆ X = ( I − A) ∆ Y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
和全部间接消耗量的总和。 bij 0 bij ai
分析 生产单位甲产品对乙产品的消耗 b31 a31 a32a21 a34a41 a36a65a51
a65 5
a51
6 a36
1甲
3乙
a21 a41
a32 2
a34 4
2完全消耗系数的计算公式
资本形 净出 成总额 口
合 计
产 出
中间 投入
工业 农业 其它
dj
增
vj
加tj值源自sj合计 y j总投入 q j
5249 2233 3717
4690 4660
1500 3045 790
1210
6545
19144
5600
7856 4875
1740 505 7845 19144 5850 415 14121 34461 3873 666 9414 22974
yj fi
j 1
i 1
从全社会看各部门增加值的总和等于全社会最终使用的价值量
注:每一部门的增加值不等于该部门最终产品的价值量
(3) n qi n q j
i 1
j 1
全社会的总产出等于总 投入。 注:每一部门的总产出等于
总投入。
第二节 技术经济系数与投入产出模型 一 直接消耗系数与增加值系数
(三) 完全需要系数(矩阵)(列昂剔夫逆系数矩阵)
1 (I A)1 B I
2元素 tij 完全需要系数
生产单位最终产品 所需要 总产品
3
t11t12 .....t.1n
不同符号的含义解释
xij
qi
f i
qj
f ik
dj vj
Ei
tj
sj
yi
yj
yj dj vj tj sj
( 二) 价值型投入产出表的结构分析
1 四象限划分 1第一象限(中间产品象限)
行方向:某一部门产品提供给其他部门作中间产品
使用的数量。
列方向:某一部门生产过程中消耗其他部门产品的
数量。
2第二象限 (最终使用象限) 3增加值象限(最初投入象限) 4 第四象限 再分配象限 2 横表与竖表划分
(三) 投入产出法的内容
投入产出表 投入产出的数学模型 投入产出法的应用
(四) 投入产出法的产生与发展 1产生的时代背景
(1)由谁提出— (2)时间—1936 (3)诞生标志—列昂剔夫在《经济与统计评
论》杂志上 论文: 《美国在经济体系中的投入产出的数量关系》 2在世界各国的发展 3在我国的应用
二 全国价值型投入产出表式结构
引言: 直接消耗—生产过程中为生产某种产品对有 关各种产品的第一轮消耗。 1直接消耗系数计算:
aij
xij qj
i 1,2...... n A Xqˆ 1
j 1,2...... n
解释:
xij j部门为生产一定数量的总产品 消耗i部门产品的数量. q j j种产品的总产值.
aij j部门生产单位产品消耗 i部门产品的数量
第四章 投入产出核算
第一节 投入产出的结构原理 一 投入产出与部门联系
(一)投入产出法的命名 1 从研究问题的角度命名
得:投入产出法 投入产出技术 投入产出分析
注:三者之间得差别在于该方法是 “方法”、 “技术”、 “分析工具”
2从这种方法说明问题地角度命名 得:部门联系平衡法 产业关联(或部门联系)法
4 中间投入系数
n
acj
aij
i 1
5增加值系数
n
ayj 1 aij i 1
1 acj
0acj 1
二 完全消耗系数与完全需要系数
(一)完全消耗=直接消耗+全部间接消耗
间接消耗—一种产品通过媒介产品对另一种产品的消耗。 第一轮 第二轮 ……
(二) 完全消耗系数
1 bij=直接消耗系数+全部间接消耗系数
(1)
n
nn
bij aij
aik akj
ais ask akj
k 1
s 1 k 1
nnn
ait ats ask akj ......
t 1 s 1 k 1
结论:间接消耗系数等于直接消耗系数的连乘积
一次间接消耗是2个有关直接消耗系数的连乘积 K次间接消耗是K+1个有关直接消耗系数的连乘积
(2)矩阵表达式 B (I A)1 I
①
b11b12 ......b1n
B
b21b22 ......b2n
......
bn1bn2 ......bnn
② 矩阵B的含义
行方向表示:
全社会各部门生产单位最终产品需要消耗i种产品的全部数量
列方向表示:
J部门生产单位最终产品对全社会各部门产品的完全消耗量
(二)对“投入”与“产出”的理解 1 投入 一般意义:
一定时期内(通常为一年)生 产过程中的消耗。
投入产出法中的投入:
除包含上述含义外,还包含各种消耗的来源。 即 哪些部门向本部门提供了产品及提供了多少。
2 产出 一般意义:
是指各种生产活动在一定时期内生产的 成果。
投入产出法中的产出:
不仅指成果的数量,而且指各类成果的分配使用 去向。
(一)全国价值表的基本表式 1表示
中间使用
最终使用
总
12…….n
总消费
资本形 净出 成总额 口
合 计
产 出
1
中间 投入
2 …
xij
增 加 值
合计
总投入
n
dj vj tj sj
yqj j
f f i f ik Ei
i qi
3
例表:
fi 31380
i 1
中 间 使用
最终使用
总
工 业
农 业
其 它 总消费
2、投入产出表中的指标解释
1中间投入(中间消耗) xij
2增加值(最初投入)
dj
=固定资产折旧+劳动者报酬+生产税净额 v j
+营业盈余
3总投入(总产值)q j
生产税净额 =生产税-政府补贴
4中间使用(中间产品) xij
tj sj yj
f 5最终使用(最终产品) f i i f ik Ei
6 总产品 q i
A
a11a12.....a. 1n
a21a22 ......
.
.
.
.
.
a. 2
n
qˆ
1
an1an2 .....a. nn
q1 0......0 1 0, q2 ......0
......
0,0.....q. n
矩阵A的含义
2 :aij的影响因素
生产技术水平
产品消耗结构
价格
3 特性:
aij 1 aij 0
横表—产品表 竖表—价值表
三 全国价值表的平衡关系
1行平衡关系
n
xij f i qi
j 1
i =12….n
2列平衡关系
n
xij y j q j
i 1
j =12…n
3总量平衡关系(推论)
(1)中间使用合计等于中间投入合计
nn
nn
xij xij
i1 j 1
j 1 i1
(2)
n
n
