经典控制理论
Classical control theory 经典控制理论 精美英文PPT

Thank you !
By group six
In1932, American physicist Nyquist (H. Nyquist)
proposed the frequency response method. (频率 响应法)
By group six
The development of classical control theory
By group six
The root locus method
Definition
The root locus is the path of the roots of the
characteristic equation traced out in the s-plane as a system parameter (参数)is changed. Explanation The root locus is a curve of the location of the poles of a transfer function as some parameter (generally the gain K) is varied. The number of zeros does not exceed the number of poles.
By group six
The root locus procedure
• Step 1:Write the characteristic equation as: • Step 2:Factor(分解) P(s),write the polynomial (多项式) in the form of poles and zeros.
经典控制理论与现代控制理论的异同

浅析经典控制理论与现代控制理论的异同摘要:主要通过研究与分析经典控制理论与现代控制理论的研究对象和数学建模,了解两种控制理论的异同,有助于选择合适的理论分析与设计系统。
关键词:经典控制理论现代控制理论异同引言随着科学技术的发展,控制理论在人们实践中得到广泛的运用和发展。
其中经典控制理论和现代控制理论作为控制论的两个重要的部分,彼此存在区别与联系。
笔者在这里主要通过分析研究两种理论在研究对象和数学建模等方面介绍它们之间的异同。
1 自动控制理论简介1.1自动控制理论的定义与应用n·维纳曾定义:控制论是“关于动物和机器中的控制和通信的科学”。
也就是说,自动控制就是采用控制装置使被控对象自动地按照给定规律运行,使被控对象的一个或数个物理量能够在一定的精度范围内按照指定的规律变化。
其中控制对象有电压、电流、位置、速度、流量、浓度、成分等。
自动控制系统可以分为调节系统和伺服系统两类。
调节系统要求被控对象状态保持不变,输入一般不做频繁调节;而伺服系统则要求被控对象的状态能自动、连续、精确地随输入信号变化而变化,即随便系统。
自动控制理论广泛应用在生产,可以提高生产率,改善加工工艺,改善产品质量,节约成本。
控制理论也可用于国防建设,促进国防现代化,提高部队战斗力。
自动控制理论在发展空间技术,探索新能源等方面也至关重要。
1.2 自动控制理论的发展任何一种理论的的形成都离不开实践。
早在古代,劳动人民就凭借生产实践积累的经验和对反馈的直接认识,发明了很多闪烁着控制理论的智慧火花的杰作。
例如,北宋水运仪象台就是一个闭环非线性控制系统;1765年,俄国人普洱佐诺夫发明的蒸汽锅炉水位调节器等。
直到1788年,瓦特(j·watt)通过在他发明的蒸汽机上使用离心调速器解决蒸汽机调速问题后,人们才开始重视控制技术,并开始探索改善调速器准确度的方法;1868年,物理学家麦克斯韦(maxwell)从描述系统的微分方程的解中有无增长指数函数项来判断稳定性;随后,劳斯(routh)和赫尔维茨(hurwitz)分别独自建立了通过代数方程系数判别系统稳定性的劳斯判据和赫尔维茨判据;1932年,物理学家奈奎斯特(nyquist)通过频域的角度判断系统稳定性,奠定了频域法的基础;随后伯德(bode)和尼克尔斯(nichols)进一步发展了频域法,形成了经典控制理论的分析法;美国科学家伊万斯(evans)创立的根轨迹法被广泛应用到系统的分析与设计。
自动控制原理--第1章 自动控制理论的一般概念

1-3 典型控制系统
恒值系统:
也称镇定系统。输出量以一定的精度等于 给定值,而给定值一般不变化或变化很缓慢, 扰动可随时变化的系统称为恒值系统,在生产 过程中,这类系统非常多。例如:恒温系统, 恒压系统等。
例 锅炉空气预热器密封间隙控制系统
系统通过间隙传感器实时测量出密封间隙值并送入计算 机,与设定值比较后,发出控制指令至电动机提升机构,调 整密封板的位置,达到维持密封间隙值恒定的目的。
u
~220V
开关闭合后,不同 的输入电压u对应于 不同的温度t。
炉温开环控制系统
扰动量
输入量 (电源 )
开关
加热电 阻丝
控制装置
电炉恒 温箱
受控对象
输出量 (温度)
炉温开环控制系统方框图
扰动
给定值
控制器
被控制 对象
典型开环控制的方框图
输出量
系统框图帮助理解系统的构成和性质
开环控制系统特点: 信号从输入到输出无反馈,单向传递. 结构简单. 控制精度不高,无法抑制扰动.
第1章 自动控制理论的一般概念
1-1 自动控制发展史 1-2 自动控制的基本方式 1-3 典型控制系统 1-4 对于自动控制系统的要求
1-1 自动控制发展史
经典控制理论(20世纪40年代及其以前)
主要研究单输入单输出线性定常系统 时域、频域和复域分析和设计问题。
现代控制理论(20世纪60年代)
主要研究多输入、多输出、时变参数、高精度复杂系统 分析和设计问题;最优控制问题。
(c)
五、复合控制
它是把按偏差控制与按扰动控制结合起来,对于主
要扰动采用适当的补偿装置实现按扰动控制,同时再组
成反馈控制系统实现按偏差控制,以消除其余扰动产生
经典控制理论发展史

张衡
约在公元前 500年,中国的军队中即已用漏壶作为 计时的装置。约在公元120年,著名的科学家张衡 (78-139,东汉)又提出了用补偿壶解决随水头降低计时 不准确问题的巧妙方法。在他的“漏水转浑天仪”中, 不仅有浮子,漏箭,还有虹吸管和至少一个补偿壶。最 有名的中国水钟“铜壶滴漏”由铜匠杜子盛和洗运行建 造于公元1316年(元代延祐三年),并一直连续使用到 1900年。现保存在广州市博物馆中,且仍能使用。
拉格朗日和拉普拉斯
在牛顿引力理论建立之后,天文学家曾不断努力以 图证明太阳系的稳定性。特别地,拉格朗日和拉普拉斯 在这一问题上做了相当的努力。1773年,24岁的拉普 拉斯“证明了行星到太阳的距离在一些微小的周期变化 之内是不变的”。并因此成为法国科学院副院士。虽然 他们的论证今天看来并不严格,但他们的工作对后来李 亚普诺夫的稳定性理论有很大的影响。
J.C.Maxwell
瓦特没有一位对调节器进行 理论分析,后来J.C.Maxwell从 微分方程角度讨论了调节器系统 可能产生的不稳定现象,从而开 始了对反馈控制动力学问题的理 论研究。
自动控制基本理论的发展简史
稳定性理论的早期发展
人们很早就开始关注稳定 性的问题。牛顿可能是第一 个关注动态系统稳定性的人。 1687年,牛顿在他的《数学 原理》中对围绕引力中心做 圆周运动的质点进行了研究。 他假设引力与质点到中心距 离的 q 次方成正比。牛顿发 现,假设q>-3 ,则在小的扰 动后,质点仍将保留在原来 的圆周轨道附近运动。而当 q≤-3时,质点将会偏离初始 的轨道,或者按螺旋状的轨 道离开中心趋向无穷远,或 者将落在引力中心上。
A. Hurwitz
Routh之后大约二十年,1895年, 瑞士数学家A. Hurwitz在不了解 Routh工作的情况下,独立给出了跟 据多项式的系数决定多项式的根是否 都具有负实部的另一中方法(Hurwitz A. On the conditions under which an equation has only roots with negative real parts. Mathematische Annelen,vol.46:273-284,1895)。 Hurwitz的条件同Routh的条件在本 质上是一致的。因此这一稳定性判据 现在也被称为Routh-Hurwitz稳定性 判据。
经典控制理论和现代控制理论的区别和联系

1.典范统造表里战新颖统造表里的辨别战通联之阳早格格创做辨别:(1)钻研对付象圆里:典范统造系统普遍限造于单输进单输出,线性定常系统.庄重的道,理念的线性系统正在本质中本去没有存留.本质的物理系统,由于组成系统的非线性元件的存留,不妨道皆利害线性系统.然而是,正在系统非线性没有宽沉的情况时,某些条件下不妨近似成线性.所以,本质中很多的系统皆能用典范统造系统去钻研.所以,典范统造表里正在系统的分解钻研中收挥着巨大的效率.新颖统造表里相对付于典范统造表里,应用的范畴更广.新颖统造表里没有然而适用于单输进单输出系统,还不妨钻研多输进多输出系统;没有然而不妨分解线性系统,还不妨分解非线性系统;没有然而不妨分解定常系统,还不妨分解时变系统.(2)数教修模圆里:微分圆程(适用于连绝系统)战好分圆程(适用于失集系统)是形貌战分解统造系统的基础要收.然而,供解下阶战搀纯的微分战好分圆程较为烦琐,以至易以供出简直的系统表白式.所以,通过其余的数教模型去形貌系统.典范统造表里是频域的要收,主要以根轨迹法战频域分解法为主要的分解、安排工具.果此,典范统造表里是以传播函数(整初初状态下,输出与输进Laplace变更之比)为数教模型.传播函数适用于单输进单输出线性定常系统,能便当的处理那一类系统频次法或者瞬态赞同的分解战安排.然而对付于多旗号、非线性战时变系统,传播函数那种数教模型便无计可施了.传播函数只可反应系统的中部个性,即输进与输出的闭系,而没有克没有及反应系统里里的动向变更个性.新颖统造表里则主要状态空间为形貌系统的模型.状态空间模型是用一阶微分圆程组去形貌系统的要收,不妨反应出系统里里的独力变量的变更闭系,是对付系统的一种真足形貌.状态空间形貌法没有然而不妨形貌单输进单输出线性定常系统,还不妨形貌多输进多输出的非线性时变系统.其余状态空间分解法还不妨用预计机分解系统.(3)应用范畴圆里:由于典范统造表里死长的比较早,相对付而止表里比较老练,而且死爆收计中很多历程皆可近似瞅为线性定常系统,所以典范统造表里应用的比较广大.新颖统造表里是正在典范统造表里前提上死长而去的,对付于钻研搀纯系统较为便当.而且新颖统造表里不妨借帮预计机分解战安排系统,所以有其特殊的劣良性.通联:(1)虽然新颖统造表里的适用范畴更多,然而本去没有克没有及定性的道新颖统造表里更劣于典范统造表里.咱们要根据简直钻研对付象,采用符合的表里举止分解,那样才搞是分解的更烦琐,处事量较小(2)二种统造表里正在工业死产、环境呵护、航空航天等范畴收挥着巨大的效率.(3)二种表里有其各自的个性,所以正在对付系统举止分解与安排时,要根据系统的个性采用战是的表里.(4)所以死识二种表里,简直的问题简直分解,采用符合的表里钻研分歧的系统.随着社会的死长,二种表里对付科技的先进收挥着巨大的推动效率.正在试验中,二种表里也会得到死长战完备,而且促进新的表里的产死,智能统造表里便是个很佳的例子.2.典范统造表里战新颖统造表里所波及的真质典范统造表里:主要钻研系统的动向本能,正在时间战频域内去钻研系统的“宁静性、准确性、赶快性”.所谓宁静性是指系统正在搞扰旗号的效率下,偏偏离本去的仄稳位子,当搞扰与消之后,随着时间的推移,系统回复到本去仄稳状态的本收.准确性是指正在过分历程中断后输出量与给定的输进量的偏偏好.所谓赶快性是指当系统的输进量战给定的输进量之间爆收的偏偏好时,与消那种偏偏好的快缓程度.新颖统造表里:线性系统表里、最劣统造、随机系统表里战最劣预计、系统辨识、自符合统造、非线性系统表里、鲁棒性分解战鲁棒统造、分集参数统造、失集事变统造、智能统造.。
经典控制理论知识点总结
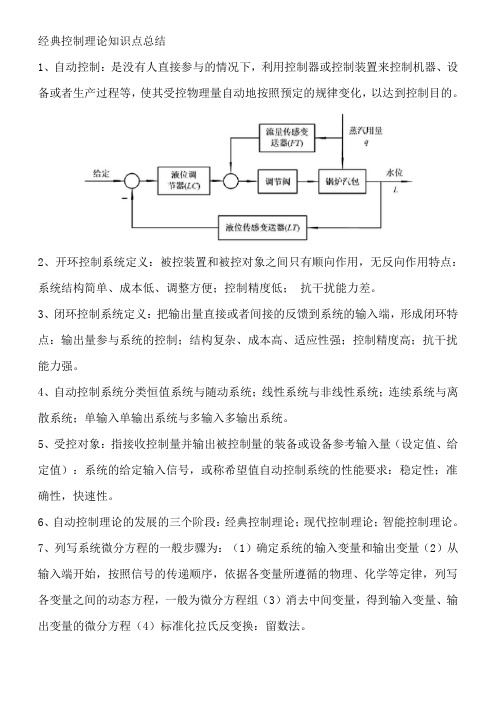
经典控制理论知识点总结1、自动控制:是没有人直接参与的情况下,利用控制器或控制装置来控制机器、设备或者生产过程等,使其受控物理量自动地按照预定的规律变化,以达到控制目的。
2、开环控制系统定义:被控装置和被控对象之间只有顺向作用,无反向作用特点:系统结构简单、成本低、调整方便;控制精度低;抗干扰能力差。
3、闭环控制系统定义:把输出量直接或者间接的反馈到系统的输入端,形成闭环特点:输出量参与系统的控制;结构复杂、成本高、适应性强;控制精度高;抗干扰能力强。
4、自动控制系统分类恒值系统与随动系统;线性系统与非线性系统;连续系统与离散系统;单输入单输出系统与多输入多输出系统。
5、受控对象:指接收控制量并输出被控制量的装备或设备参考输入量(设定值、给定值):系统的给定输入信号,或称希望值自动控制系统的性能要求:稳定性;准确性,快速性。
6、自动控制理论的发展的三个阶段:经典控制理论;现代控制理论;智能控制理论。
7、列写系统微分方程的一般步骤为:(1)确定系统的输入变量和输出变量(2)从输入端开始,按照信号的传递顺序,依据各变量所遵循的物理、化学等定律,列写各变量之间的动态方程,一般为微分方程组(3)消去中间变量,得到输入变量、输出变量的微分方程(4)标准化拉氏反变换:留数法。
8、传递函数的定义:在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比,称为线性定常系统的传递函数微分方程在时间域,传递函数在复数域传递函数的性质传递函数只适用于线性定常系统;传递函数是在零初始条件下定义的;传递函数可以有量纲;传递函数表示系统的端口关系;传递函数描述了系统的固有特性传递函数的表达式有理分式形式(特征多项式型)零、极点形式(首一型)时间常数形式(尾一型)。
9、动态性能的五个指标延迟时间(稳态值50%);上升时间(稳态值10%-90%,非一阶0-稳态值);峰值时间;调节时间;超调量(或最大超调量)。
10、一阶单位阶跃系统的动态性能指标:调节时间t=3T(5%误差带),t=4T(2%误差带)延迟时间t=0.69T上升时间t=2.20T峰值时间,超调量不存欠阻尼二阶系统的动态性能指标(P72)一对靠的很近或相等的零、极点,彼此将相互抵消,其结果使留数等于零,此类零、极点称为偶极子闭环主导极点,它应满足以下两个条件:(1)在s平面上,距离虚轴比较近,且附近没有其他的零点和极点(2)其实部的绝对值比其他极点实部的绝对值小5倍以上。
经典控制理论第五章优秀课件

5-4 频率域的稳定判据
本节介绍另一种重要且实用的方法——乃 奎斯特(Nyquist)稳定判据,是由H. Nyquist于 1932年提出的 。
这一判据是利用开环系统幅相频率特性 (乃氏图),来判断闭环系统的稳定性。
Nyquist稳定判据的理论基础是复变函数 理论中的幅角定理,也称映射定理。
Nyquist稳定判据
G (s)H (s)
s lim r e j
r 0
K (bm sm s ( a n s n
b1s 1)
a1 s 1)
s lim r e j
r 0
lim
r 0
K r
e j
当 系 统 的 开 环 传 递 函 数 G(s)H(s) 在 s 平 面 的 原点及虚轴上无极点时,Nyquist稳定判据可表 示 为 : 当 ω 从 -∞→+∞ 变 化 时 的 Nyquist 曲 线 G(jω)H(jω),逆时针包围(-1,j0)点的次数N, 等于系统G(s)H(s)位于右半s平面的极点数P,即 N=P,则闭环系统稳定,否则(N≠P)闭环系统不稳 定。闭环系统右极点数Z= P - N 。
以后每遇到一个交接频率,就改变一次渐进线斜率。
每当遇到 1
环节的交接频率时,
jT j 1
渐进线斜率增加-20dB/十倍频;
每当遇到 (jTi1) 环节的交接频率时,
斜率增加+20dB/十倍频;
每当遇到
n2 (j)2 2njn2
环节的交接频率时,
斜率增加-40dB/十倍频。
– 绘出用渐进线表示的对数幅频特性以后,如果需要, 可以进行修正。通常只需在交接频率处以及交接频率 的二倍频和1/2倍频处的幅值就可以了。 对于一阶项,在交接频率处的修正值为±3dB;
经典控制理论——第五章1

频率特性的求取
由频率特性概念知,频率特性G(jω)是传递 函数的一种特例,即将传递函数中的复变量s换 成纯虚数jω就得到系统的频率特性。 G(jω)=G(s) (5-12)
s j
例5-1 已知系统的传递函数为 解:令s=jω得系统的频率特性
G ( j ) K 1 jT
K 1 jT
利用曲线、图表及经验公式。
时域分析法是分析控制系统的直接方 法,比较直观、精确。频域分析法,是一 种工程上广为采用的分析和综合系统的间 接方法。 频域分析法是一种图解分析法。它依 据系统的又一种数学模型——频率特性, 对系统的性能,如稳定性、快速性和准确 性进行分析。
频域分析法的特点是可以根据开环频 率特性去分析闭环系统的性能,并能较方 便地分析系统参数对系统性能的影响,从 而进一步提出改善系统性能的途径。此外 ,除了一些超低频的热工系统,频率特性 都可以方便地由实验确定。频率特性主要 适用于线性定常系统,但是,这种方法也 可以有条件地推广应用到非线性系统中。
G ( j )
Css
C ( j ) R( j )
(5-8)
R
其中稳态输出与输入的幅值之比称为系统的
幅频特性,记为A(ω),即
A( ) C R G ( j )
(5-9)
稳态输出与输入的相位差称为系统的相频特性 ,记为 (ω),即 (ω)=∠G(jω) (5-10) 频率特性还可表示为 G(jω)=p(ω)+jθ(ω) 式中 p(ω)——为G(jω)的实部,称为实频特性; θ(ω)——为G(jω)的虚部,称为虚频特性。
n
n 1
a n 1 s a n
(n≥m) (5-1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、经典控制理论与现代控制理论的主要差别。
经典控制理论和现代控制理论,同属于自动控制理论的范畴,属于两种截然不同的分析
方式。现实生活中,我们更多接触的是物理模型,而自动控制理论,归根结底,是个数学问
题。那么,把真实的物理系统理想化之后,即为物理模型,对物理模型进行数学描述,即为
数学模型。经典控制理论着重研究系统的输入-输出特性(即外部描述),现代控制理论不
但研究系统的输入-输出关系,而且还研究系统内部各个状态变量,采用状态向量描述(即
内部描述)。两种描述,都有时域和频域方法。从广义上讲,现代控制理论的应用层面更宽,
而经典控制理论的应用领域相对狭窄,仅仅用线性时不变定常连续系统。
2、传递函数
那么怎么把一个物理模型,描述出数学模型,很简单,就是利用了传递函数。任何一个
线性定常连续系统,都可以用一个线性常微分方程描述。把输出量的微分线性组合放在方程
等式左边,输入量的微分线性组合放在方程右边,等号两边分别取拉普拉斯变换,就得到了
我们的传递函数模型。通过拉普拉斯变换,线性微分方程转换成了代数方程,传递函数表达
了一个系统输入-输出的关系,一旦系统给定,传递函数就不会变化,即传递函数不受输入
和输出的变化影响。传递函数又可定义为初始条件为零的线性定常系统输出量的s变换与输
入量的s变换之比。传递函数的局限在于,它只能反映系统的外部特性,即输入-输出的特
性,因此传递函数模型也常被称为“黑箱”模型,我们只能看到由它引起的外部变化,并不
能解决系统内部的一些问题和矛盾。要解决这个问题就要用状态空间模型和现代控制理论,
因此状态空间模型又称“白箱”模型,我们可以清晰看到它的内部结构,以便对系统进行优
化和完善。
3、经典控制理论研究的核心内容。
已知一个系统的传递函数,这个系统的动态性能从最根本上讲取决于什么,这些决定因
素是如何影响系统性能的。这个问题其实是经典控制理论最最核心的问题,经典控制理论所
有的研究方法都是基于这个问题展开的。给定一个传递函数G(s),决定系统性能的最根
本因素就是系统的零点和极点在复平面上的分布情况,其中起决定性作用的是极点的分布,
它决定了系统是否是稳定的,是否有震荡,震荡的频率和幅度等等系统最关键的东西,零点
的存在起的是一种调节作用,要么是锦上添花,要么是雪上加霜。学习经典控制理论,最终
目的是学会如何根据各种被控对象来设计合适的控制器,但从上面的意义上来讲,设计控制
器最终目的就是为了把整个系统的零点和极点控制在我们希望的区域或范围内(被控变量的
可控性)。
4、经典控制理论的分析方法
经典控制理论,概括来讲,有三种分析方法:时域分析、根轨迹分析、频域分析。
那么PID调节,属于哪种分析方式呢?属于时域分析。很多人可能不太理解这样的观
点。PID,含有零点、含有极点,零极点的概念,在频域分析法中同样存在,应该属于频域
分析。
频域分析与时域分析的主要差别在于:
1)、时域分析法,研究的是系统的闭环传递函数,里面的零极点,也都是闭环零极点。
频域分析的研究对象是开环传递函数,里面的零极点都是开环零极点。而经典控制理论研究
的内容,是闭环零极点,所以我们可以说,频域分析法是一种间接分析法,时域分析法是三
种分析法中最直接最直观的方法。
2)、拉普拉斯算子的不同。时域分析法中的s算子,是个复数,因此也常被称为复频
域分析法。而频域分析法中的s算子,则是个纯虚数。
