第一章 有限元的基本理论
合集下载
第1章有限元法简介
Fix uix k ii 0 F v iy iy 0 0 K = = F jx u jx k ji 0 F jy v jy 0 0
k ij 0 uix 1 v 0 0 iy EA 0 l 1 k jj 0 u jx 0 0 0 v jy
钱学森
钱伟长
胡海昌
杨桂通
徐芝伦
软件名称
简介
MSC/Nastran
LS-Dyna MSC/Dytran MSC/Marc ANSYS FLUENT ABAQUS
著名结构分析程序,最初由NASA研制。
动力学分析程序(大多为显式算法) 非线性分析软件 通用结构分析软件(耦合场分析) 流场分析软件 非线性分析软件(非协调单元,非线性 直接解算方法)
令杆件两端节点分别产生单位位移,可以计算产生这样的单 位位移所需要的力,而力的大小就是刚度系数。 EA 首先取 ui 1,u j 0, 此 时 需 要 压 力 ui。 按 照 局 部 坐 标 系 l EA EA 和力的规定, Fi ui,F j ui, 则 l l EA EA ui l k , k
单元2 3
F3 10N
x
考虑y方向的单元刚度矩阵
Fi k ii k ij ui EA 1 1 ui = u l F u k k 1 1 jj j j ji j
若考虑y方向,则有:
——宏观假设
弹性力学的基本假定
2、线弹性(Linear elastic)
物体的变形与外力作用的关系是线性的, 除去外力,物体可回复原状 ,而且这个关系和 时间无关,也和变形历史无关,称为完全线弹 性材料
第一讲有限元绪论

考虑微段dx,内力 N=q (L-x)
dx的伸长为
Δ(dx) N(x)dx q(L x)dx
EA
x截面上的位移:
x N(x)dx x q(L x)dx q
x2
u 0 EA 0
EA
(Lx )
EA
2
根据几何方程求应变,物理方程求应力。这里
应变
du q ε x dX EA(L X)
实验方法的最大优点是结果真实可靠,通
常被当作产品最终定型的权威性依据。
实验方法也存在不足:
1)实验一定要在样品或样机试制之后才 能进行,成本高、周期长,并且只适合 批量生产的产品。
2)可以获得的数据量有限,无法对设计 提供更多的指导,更无法进行结构优化。
3)受实验手段的限制,有些参数无法测 准。
应力
σx
Eε x
q A
(L X)
有限单元法求解直杆拉伸:
1、离散化
2、外载荷集中到结点上,即把投 影部分的重量作用在结点i上
L1
1
L2
2
Li Li+1
i-1 i i+1
n-1 n
图 2-2
i-1
Li
i q (Li + Li+1)
Li+1
2
i+1
图 2-3
有限单元法求解直杆拉伸:
3、假设线单元上的位移为线性函数
五、数值分析与实验分析的比较
分析方法可分为理论计算和实验两大类。
1、基于实验的分析方法
指通过的实验测试获取需要的性能参数的 方法。这种方法获取不同的性能参数需要采用 不同的测试方法、仪器设备和辅助实验装置。 如:强度实验,可以采用电阻应变片及应变仪、 光弹涂膜或云纹栅、应变涂料等;扭转与弯曲 刚度实验则需要专门的实验台等等。
《有限元分析及应用》课件

受垂直载荷的托架
31
体单元
•线性单元 / 二次单元 –更高阶的单元模拟曲面的精度就越高。
低阶单元
更高阶单元
32
有限元分析的作用
复杂问题的建模简化与特征等效 软件的操作技巧(单元、网格、算法参数控制) 计算结果的评判 二次开发 工程问题的研究 误差控制
36
第二章 有限元分析的力学基础
(3) 研究的基本技巧
采用微小体积元dxdydz的分析方法(针对任意变
形体)
40
2.2 弹性体的基本假设
为突出所处理的问题的实质,并使问题简单化和抽 象化,在弹性力学中,特提出以下几个基本假定。
物质连续性假定: 物质无空隙,可用连续函数来描述 ;
物质均匀性假定: 物体内各个位置的物质具有相同特 性;
0.02 0.04 0.06 0.08
0.1
0.12
X
0.056
0.058
X
0.06
28
Y
Y
0 -0.02 -0.04 -0.06 -0.08
0
-0.001
-0.002
-0.003 0.054
-0.1 0
0.02 0.04 0.06 0.08
0.1
0.12
X
0.056
0.058
X
0.06
29
30
y
dy zy
1 2
zy
z
dz
0
略去微量项,得 yz zy
MY 0 zx xz
MZ 0
xy yx
剪切力互等定律
53
二维问题: 平衡微分方程
x yx X 0
x y xy y Y 0 x y
剪切力互等定律
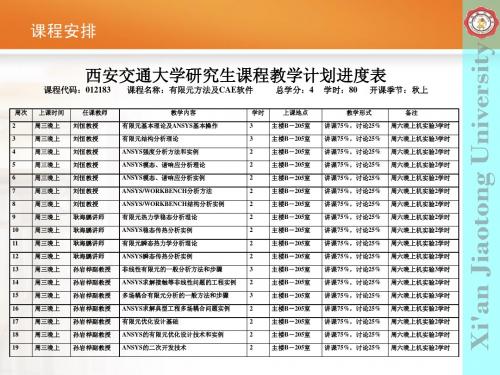
第一课 有限元基本理论及软件介绍(苏研院)
引言——线弹性的五个基本假设
1)物体内的物质连续性假设:物质无空隙,可用连续函数描述;
2)物体内的物质均匀性假设:物体内各个位置的物质具有相同特性 3)物体内的(力学)特性各向同性假设:物体内同一位置的物质在各个 方向上具有相同特性; 4)线性弹性假设:物体的变形与外力作用关系是线性的,外力去除后物 体可恢复原状; 5)小变形假设:物体变形远小于物体的几何尺寸,在建立方程时可略去 高阶小量(二阶以上) 。
教学形式 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25% 讲课75%,讨论25%
求解过程 直接针对原方程;分离变量; 微分->差商;
代换;偏微分方程->常微分 方程;解析或半解析 线性方程; 求解
小;线性方程组 函数的要求及 为简化问题可事先假设解函数,进行变量分离; 试函数满足所有边条;函数连 只满足位移边条; 形式 函数连续性要求高 续性要求高 函数连续要求低
泛函形式
关键点 难易程度 求解精度
考试安排
平时成绩占总成绩40% 2次大作业 闭卷考试占总成绩60% 1、填空; 2、选择; 3、问答题
第一讲 有限元方法概述
引言 偏微分方程 偏微分方程的解 有限元分析的实例 有限元基础知识 有限元中数学原理 各种有限元软件
引言——变形体及其受力情况的描述
基本变量: u 基本方程: 1)材料方面 ==》 ui ij ij
有限元分析基础ppt课件

a. 单元位移函数的项数,至少应等于单元的自由度 数。它的阶数至少包含常数项和一次项。至于高次项要 选取多少项,则应视单元的类型而定。
32
第三章 杆系结构静力分析的有限单元法
b. 单元的刚体位移状态和应变状态应当全部包含在
位移函数中。
c. 单元的位移函数应保证在单元内连续,以及相邻
单元之间的位移协调性。 由单元结点位移,确定待定系数项
17
第二章 结构几何构造分析
②超静定结构——自由度大于零的几何不变结构。其特 性:
a. 超静定结构仅仅满足静力平衡条件的解有无穷多 个,但同时满足结构变形协调条件的解仅有一个。
b. 超静定结构的内力及支反力不仅与载荷有关,而 且与林料的力学性能和截面尺寸有关。
c. 超静定结构在非载荷因素作用下,如温度变化、 支座沉陷、制造误差等而产生的位移会受到多余约束的 限制,结构内必将产生内力。
33
第三章 杆系结构静力分析的有限单元法
3.2.2 梁单元平面弯曲的位移函数
梁单元平面弯曲仅考虑结点的四个位移分
量 i, i , j , j ,由材料力学知,各截面的转角:
v x
故梁单元平面弯曲的位移表达式可分为仅包含四个 待定系数 1, 2, 3, 4的多项式 v(x) 1 2 x 3 x 2 4 x3
全为零。 d. 若静定结构在载荷作用下, 结构中的某一部分
能不依靠于其它部分, 独立地与载荷保持平衡时,则 其它部分的内力为零。
e. 当将一平衡力系作用于静定结构的一个几何不 变部分时,结构的其余部分都无内力产生。
f. 当静定结构中的一个内部几何不变部分上的载 荷作等效变换时,其余部分的内力不变。
g. 当静定结构中的一个内部儿何不变部分作构造 改变时,其余部分的内力不变。
32
第三章 杆系结构静力分析的有限单元法
b. 单元的刚体位移状态和应变状态应当全部包含在
位移函数中。
c. 单元的位移函数应保证在单元内连续,以及相邻
单元之间的位移协调性。 由单元结点位移,确定待定系数项
17
第二章 结构几何构造分析
②超静定结构——自由度大于零的几何不变结构。其特 性:
a. 超静定结构仅仅满足静力平衡条件的解有无穷多 个,但同时满足结构变形协调条件的解仅有一个。
b. 超静定结构的内力及支反力不仅与载荷有关,而 且与林料的力学性能和截面尺寸有关。
c. 超静定结构在非载荷因素作用下,如温度变化、 支座沉陷、制造误差等而产生的位移会受到多余约束的 限制,结构内必将产生内力。
33
第三章 杆系结构静力分析的有限单元法
3.2.2 梁单元平面弯曲的位移函数
梁单元平面弯曲仅考虑结点的四个位移分
量 i, i , j , j ,由材料力学知,各截面的转角:
v x
故梁单元平面弯曲的位移表达式可分为仅包含四个 待定系数 1, 2, 3, 4的多项式 v(x) 1 2 x 3 x 2 4 x3
全为零。 d. 若静定结构在载荷作用下, 结构中的某一部分
能不依靠于其它部分, 独立地与载荷保持平衡时,则 其它部分的内力为零。
e. 当将一平衡力系作用于静定结构的一个几何不 变部分时,结构的其余部分都无内力产生。
f. 当静定结构中的一个内部几何不变部分上的载 荷作等效变换时,其余部分的内力不变。
g. 当静定结构中的一个内部儿何不变部分作构造 改变时,其余部分的内力不变。
有限元基本原理

有限元基本原理
有限元基本原理是一种数值分析方法,用于解决连续介质力学问题。
它将连续物体离散化为有限数量的小单元,通过对这些小单元的力学行为进行建模和分析,来推导出整体结构的力学特性。
有限元分析的步骤如下:
1. 离散化:将结构或物体分割成有限数量的小单元,例如三角形或四边形。
这些小单元被称为有限元素。
2. 建立数学模型:在每个有限元素内,选择适当的数学表达式来描述变形和应力分布。
这些表达式通常基于线性弹性理论或非线性材料模型。
3. 形成刚度矩阵:通过将每个有限元素的刚度矩阵组合起来,形成整体系统的刚度矩阵。
刚度矩阵描述了结构在受力作用下的刚度和变形响应。
4. 施加边界条件:给定结构的边界条件,例如约束和载荷。
这些条件可用于限制结构的自由度和模拟外部加载。
5. 求解方程:将边界条件应用到刚度矩阵上,并求解得到结构的位移和应力分布。
6. 分析结果:利用位移和应力分布,评估结构的强度、刚度、变形等力学特性。
这些结果可以帮助设计师优化结构并预测其
行为。
有限元基本原理的核心思想是将复杂的力学问题转化为小单元内的简单数学表达式,并通过组合这些单元的行为来推导整体结构的力学性能。
这种方法具有广泛的应用领域,包括结构分析、流体力学、热传导等。
有限元分析基础-文档资料

有限元分析基础
2019.8
内容结构
第一章 第二章 第三章 第四章 第五章 第六章 第七章 概述 结构几何构造分析 杆系结构静力分析的有限单元法 平面结构问题的有限单元法 等参元 空间问题的有限单元法 轴对称旋转单元
2
第一章 概述
1.1 有限单元法的概念 1.2 有限单元法基本步骤 1.3 工程实例
21
第二章 结构几何构造分析
② 反对称载荷作用
(a) 变形状态分析
(b) 铲运机工作装置插入工况有限元分析
图1-3 WJD-1.5型电动铲运机
8
第一章 概述
(a) KOMATSU液压挖掘机
(b) 某液压挖掘机动臂限元分析
图1-4 液压挖掘机
9
第一章 概述
图1-5 驾驶室受侧向力应力云图
图1-6 接触问题结构件应力云图
10
第一章 概述
图1-7 液压管路速度场分布云图
18
第二章 结构几何构造分析
对称结构在正对称载荷下,对称轴截面上只能产生 正对称的位移,反对称的位移为零;对称结构在反对称 载荷下,对称轴截面上只有反对称的位移,正对称的位 移为零。
(1) 具有奇数跨的刚架 ① 正对称载荷作用
2.2.3 结构对称性的利用
(a) 对称刚架
(b) 变形状态分析 图2-22对称性利用示意图
图1-8 磨片热应力云图
图1-9 支架自由振动云图
11
第二章 结构几何构造分析
2.1 结构几何构造的必要性 2.2 结构计算基本知识 2.3 结构几何构造分析的自由度与约束2.1 结构几何构造的必要性
结构是用来承受和传递载荷的。如果不计材料的 应变,在其受到任意载荷作用时其形状和位置没有发 生刚体位移时,称之为几何不变结构或几何稳定结构, 反之则称为几何可变结构或几何不稳定结构。几何可 变结构不能承受和传递载荷。对结构进行几何构造分 析也是能够对工程结构作有限单元法分析的必要条件。
2019.8
内容结构
第一章 第二章 第三章 第四章 第五章 第六章 第七章 概述 结构几何构造分析 杆系结构静力分析的有限单元法 平面结构问题的有限单元法 等参元 空间问题的有限单元法 轴对称旋转单元
2
第一章 概述
1.1 有限单元法的概念 1.2 有限单元法基本步骤 1.3 工程实例
21
第二章 结构几何构造分析
② 反对称载荷作用
(a) 变形状态分析
(b) 铲运机工作装置插入工况有限元分析
图1-3 WJD-1.5型电动铲运机
8
第一章 概述
(a) KOMATSU液压挖掘机
(b) 某液压挖掘机动臂限元分析
图1-4 液压挖掘机
9
第一章 概述
图1-5 驾驶室受侧向力应力云图
图1-6 接触问题结构件应力云图
10
第一章 概述
图1-7 液压管路速度场分布云图
18
第二章 结构几何构造分析
对称结构在正对称载荷下,对称轴截面上只能产生 正对称的位移,反对称的位移为零;对称结构在反对称 载荷下,对称轴截面上只有反对称的位移,正对称的位 移为零。
(1) 具有奇数跨的刚架 ① 正对称载荷作用
2.2.3 结构对称性的利用
(a) 对称刚架
(b) 变形状态分析 图2-22对称性利用示意图
图1-8 磨片热应力云图
图1-9 支架自由振动云图
11
第二章 结构几何构造分析
2.1 结构几何构造的必要性 2.2 结构计算基本知识 2.3 结构几何构造分析的自由度与约束2.1 结构几何构造的必要性
结构是用来承受和传递载荷的。如果不计材料的 应变,在其受到任意载荷作用时其形状和位置没有发 生刚体位移时,称之为几何不变结构或几何稳定结构, 反之则称为几何可变结构或几何不稳定结构。几何可 变结构不能承受和传递载荷。对结构进行几何构造分 析也是能够对工程结构作有限单元法分析的必要条件。
《弹性力学与有限元》第1章弹性力学的基础知识

(五)小应变位移假设 物体在外加因素作用下,物体变形产生的位移与物体尺寸相比极其微小,因 而应变分量和转角均远小于 1。这样,在建立物体变形后的平衡方程时,可以不 考虑由于变形引起的物体尺寸和位置的变化;在建立几何方程和物理方程时,可 以略去应变、转角的二次幂或二次乘积以上的项,使得到的基本方程是线性偏微 分方程组。这个假设又称为几何线性的假设。
物体的弹性性质是客观存在的,人类很早就可以利用物体的弹性性质了,比 如在树枝上荡漾,古代的弓箭等等。
了解掌握弹性物体的客观规律,并形成弹性力学这样一门学科,则经过了三 个发展时期:
弹性力学的发展初期。17 世纪开始,主要是通过实践,尤其是通过实验来 探索弹性力学的基本规律。英国的胡克和法国的马略特于 1680 年分别独立地提 出了弹性体的变形和所受外力成正比的定律,后被称为胡克定律。牛顿于 1687 年确立了力学三定律,奠定了力学的发展基础。
《弹性力学与有限元》
第 1 章 弹性力学的基础知识
第 1 章 弹性力学的基础知识
弹性力学(Elastic Mechanics)是固体力学的重要分支,它研究弹性物体在外力 和其它外界因素作用下产生的变形和内力,也称为弹性理论。它是材料力学、结 构力学、塑性力学和某些交叉学科的基础,广泛应用于建筑、机械、化工、航天 等工程领域。
材料力学的研究对象主要是杆状构件(一维弹性杆件),而且常采用一些关 于变形的近似假设,如“平面截面”的假设等等,使得计算简化。
而弹性力学的分析方法在一开始并不考虑平面截面的假设,而是从变形连续 性的观念出发列出几何方程,所谓变形连续性是指在变形前的连续物体在变形后 仍保持连续,物体的任一部分及单元体均保持连续。在保持变形连续的情况下, 平面界面变形以后可能不再保持平面,
