薄膜等厚干涉资料教程
合集下载
13.5 薄膜等厚干涉
§13.5
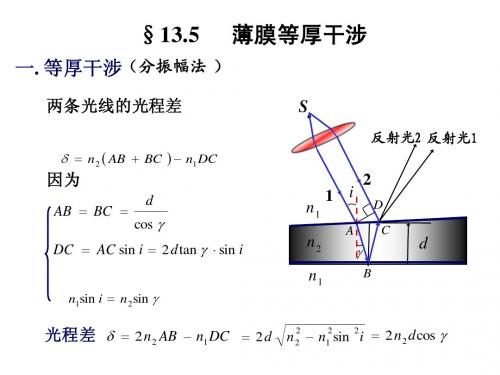
一. 等厚干涉(分振幅法 )
两条光线的光程差
δ = n2 ( AB + BC ) n1DC 因为 d AB = BC = cosγ
薄膜等厚干涉
S
n1 n2 n1
1 i
A
反射光2 反射光1 反射光2 反射光1
2
D
C
DC = ACsini = 2dtanγ sini
n1sin i = n2sin γ
S
r
d
r2 d= 2R
AB
M
O
≈ 2 Rd
R 2 = r 2 + ( R d )2
明纹
r2 λ λ 2 + = 2k ,k = 1,2 ,3,L 2R 2 2
暗纹
r2 λ λ 2 + = (2k + 1) ,k = 0 ,1,2,L 2R 2 2
半径
Rλ r = (2k 1) 2
r = kλR
k = 1,2,3,L明纹
k r = mRλ
2 k
讨论 (1) 测透镜球面的半径 测透镜球面的半径R 可得R 已知 λ, 测 m、rk+m、rk,可得 (2) 测波长 λ 已知R 测出m 可得λ 已知 ,测出 、 rk+m、rk, 可得 (3) 检测透镜的曲率半径误差及其表面平整度 (4) 若接触良好 中央为暗纹 若接触良好,中央为暗纹 中央为暗纹——半波损失 半波损失 (5) 透射图样与反射图样互补 透射图样 图样与反射图样互补
γ
B
d
2 光程差 δ = 2n2 AB n1DC = 2d n2 n12sin 2i = 2n2 dcosγ
光程差 考虑半波损失
2 n2 d cos γ
一. 等厚干涉(分振幅法 )
两条光线的光程差
δ = n2 ( AB + BC ) n1DC 因为 d AB = BC = cosγ
薄膜等厚干涉
S
n1 n2 n1
1 i
A
反射光2 反射光1 反射光2 反射光1
2
D
C
DC = ACsini = 2dtanγ sini
n1sin i = n2sin γ
S
r
d
r2 d= 2R
AB
M
O
≈ 2 Rd
R 2 = r 2 + ( R d )2
明纹
r2 λ λ 2 + = 2k ,k = 1,2 ,3,L 2R 2 2
暗纹
r2 λ λ 2 + = (2k + 1) ,k = 0 ,1,2,L 2R 2 2
半径
Rλ r = (2k 1) 2
r = kλR
k = 1,2,3,L明纹
k r = mRλ
2 k
讨论 (1) 测透镜球面的半径 测透镜球面的半径R 可得R 已知 λ, 测 m、rk+m、rk,可得 (2) 测波长 λ 已知R 测出m 可得λ 已知 ,测出 、 rk+m、rk, 可得 (3) 检测透镜的曲率半径误差及其表面平整度 (4) 若接触良好 中央为暗纹 若接触良好,中央为暗纹 中央为暗纹——半波损失 半波损失 (5) 透射图样与反射图样互补 透射图样 图样与反射图样互补
γ
B
d
2 光程差 δ = 2n2 AB n1DC = 2d n2 n12sin 2i = 2n2 dcosγ
光程差 考虑半波损失
2 n2 d cos γ
物理-薄膜等厚干涉

Collimator
lens
(准直透镜)
E
E1rE2r
半反 半透镜
光学平晶 n 黑色表面
在凸透镜和光学平晶之 间的薄膜产生干涉条纹
二、牛顿环
2、理论分析
C
r2 R2 (R e)2 2R e e2 2R e
极小
极大
R
条件
2nd
0 2
(k
1 2
)0
条件
2nd
0 2
(k
1)0
极小
极大
nG
A e
2)用白光照射,将出现 什么现象?
条纹向中心收缩
e
二、牛顿环
白光牛顿环
二、牛顿环
5、牛顿环的应用 检测透镜球表面质量
标准验规 缺陷透镜
暗纹
二、牛顿环
5、牛顿环的应用
检测透镜球面曲率
通过使用一套精确地球
面测试板或量规(gauges)
,设计者可以利用牛顿环条 纹的条数和规整性来精确测 量新的透镜。
R
极小条件
2nd
0 2
(k
1 2
)0
nG e0
O r
间隙
极小(k 级暗纹的半径)
rk2 k0 R n 2R e0
为了消除间隙 e0 的影响
r2 k k
rk2
k0
R
n
二、牛顿环
4、牛顿环的特征
形状: 一系列同心圆环 条纹间隔分布: 内疏外密 条纹级次分布: 内低外高
讨论
1)若平凸透镜向上平移, 条纹分布如何变化?
楔形膜上时
0
2ne 0 2 (e)
等厚条纹
一、劈尖干涉
2、干涉图样分析
极大的位置: (e) 2ne 0 2 k0
薄膜干涉—等厚条纹

等厚干涉条纹
例3 利用空气劈尖的等厚干涉条纹可以检测工
件表面存在的极小的加工纹路, 在经过精密加
工的工件表面上放一光学平面玻璃,使其间形
(1) 明暗条纹的判据
2e
/2
k
(2k
(k 1,2,3...)
1) / 2 (k 0,1,2...)
明纹 暗纹
由几何关系可知
(R – e)2+r2=R2
R
R2 - 2Re + e2 + r2=R2
e = r2/2R
0
r
e
牛顿环
3.3 牛顿环干涉条纹的特征
r
(k 1 2)R kR
k 1,2,3... k 0,1,2...
L 暗纹 明纹
≈ /2n
e
结论: a.条纹等间距分布
L
e
b.夹角越小,条纹越疏;反之则密。如过大,
条纹将密集到难以分辨,就观察不到干涉条纹了。
劈尖膜
2.3 劈尖干涉条纹的特征
劈尖干涉条纹是一系列明暗相间的、等间 距分布的、平行于棱边的平直条纹。
劈尖干涉条纹
劈尖膜
例1 在半导体元件生产中,为了测定硅片上SiO2薄
劈尖膜
2.3 劈尖干涉条纹的特征
(1)明、暗条纹处的膜厚:
e
(2k
k /
1) / 4n 2n(k
(k 1,2,3...) 0,1,2...)
明纹 暗纹
k 0 e 0 棱边呈现暗纹
k 1
e
/ /
4n 2n
第一级明纹 第一级暗纹
k 2
e
3
/ /
4n n
第二级明纹 第二级暗纹
……
一系列明暗相间的、平行于棱边的平直条纹。
3-02 薄膜干涉(一)——等厚条纹

n
h
第三章:干涉装置 光场的时空相干性 § 2 薄膜干涉(一)——等厚条纹
2.6 薄膜的颜色、增透膜和高反膜 薄膜的颜色:干涉导致不同波长光的反射率不同。 增透膜:
n1 < n < n 2 nh = λ 4 , n1 n n2
例: n1 = 1,
3λ 4 ,
n1 n 2 时完全消光
→ n 0 = 1 . 23
2.2 薄膜表面的等厚条纹(i固定,h变化) 光程差计算:
Q
i1
C
n
A
i
B
P
h
Δ L ( P ) = ( QABP ) − ( QP ) = ( QA ) − ( QP ) + ( ABP ) Δ L ( P ) ≈ 2 nh cos i
第三章:干涉装置 光场的时空相干性 § 2 薄膜干涉(一)——等厚条纹
2 nh cos i = conL ) = − 2 nh sin i δ i + 2 n cos i δ h = 0
第三章:干涉装置 光场的时空相干性 § 2 薄膜干涉(一)——等厚条纹
2.5 等厚干涉条纹的观测方法及倾角的影响 ii)反衬度下降: 眼睛瞳孔限制扩展光源 参与干涉的区域。光源 不同处的 i 不同, h 越 大,反衬度越低。
rk2+ m − rk2 R= mλ
由于半波损失,中心时暗纹。
rk
DP k2 = CP k2 − CD 2 rk2 = R 2 − ( R − h k ) 2 = 2 Rh k − h k2
第三章:干涉装置 光场的时空相干性 § 2 薄膜干涉(一)——等厚条纹
2.5 等厚干涉条纹的观测方法及倾角的影响 严格的等厚干涉要求点光源、正入射。但扩展光源、斜入 射,用眼睛也能观察到干涉现象。主要是眼睛的瞳孔对光 束进行了限制,只是干涉的结果会受到一定的影响。 i) 条纹偏离等厚线: 干涉条纹:
1-8 双光束分振幅薄膜干涉(二)等厚干涉 _投影稿
加热时,待测 材料膨胀,上表 面上升,条纹有 什么变化?
待测材料膨胀后,空气膜变薄,条纹向远离劈棱 的方向移动。 每移动一个条纹,空气膜厚度变化为:h=/2 移过m条,则说明膨胀: h=m(/2)
next next
2
13
14
白光入射薄膜时,条纹如何分布? 白光照射下的肥皂膜
例:检查光学平面的平整度 标准平面 空气 待测平面
next
3、光程差
/ 2 2hn 2 cos i 2 0 0
3
二、劈尖干涉 劈尖:上下表面都是平面的透明体,两表面之间有 一个很小的夹角。 1. 条纹形状
4
上、下表面夹角很小时,在局部可近似认为是平行膜:
0和i2固定,只与h 有关, 同一级条纹出现 在薄膜厚度相同处,故称 等厚条纹。 条纹的特点由薄膜厚h度变化的规律决定。
n2 2n2
21
22
r1 : r2 : r3 : ...... 1 : 2 : 3 : ...... 无额位光程差时, r1 : r2 : r3 : ...... 1 : 3 : 5 : ...... 有额位光程差时,
条纹内疏外密,级次内低外高 透镜上移时: 条纹收缩,中心条纹被吞没。 透镜下移时: 条纹扩展,中心有条纹冒出。 球面半径变化时,条纹如何变化?
25
两个力在竖直方向平衡: d·Fn·cos= g·dm 水平方向满足:d·Fn·sin=2r·dm tan = 2r/g
tan dy dr
26
水旋转时表面为旋转对称曲面,取过水面最低点的 竖直线为y轴,原点o在水盘底面。 取水表面上某一点P处质量为dm的水元。
y
1 2 2 r C 表示水膜的厚度 2 g
22-3 薄膜干涉(等厚干涉)

d
δ = 2d + λ
2
光程差
22-3 薄膜干涉(等厚干涉) 薄膜干涉(等厚干涉) 牛顿环实验装置 显微镜 T L S M半透 半透 半反镜
第二十二章 光的干涉
R
r
d
牛顿环干涉图样
22-3 薄膜干涉(等厚干涉) 薄膜干涉(等厚干涉)
第二十二章 光的干涉
光程差
δ = 2d +
λ
2
明纹 R r d
δ=
第二十二章 光的干涉
4 )半波损失需具体问题具体分析
n n
n1 n3
n2
n1 < n2 < n3
b=
λ
2sin α
α
tan α ≈ sin α =
依题意
λ
2b
4.295mm b= = 0.148mm D 29 λD d = D tan α = = 5.746 × 10−2 mm 2b
d
22-3 薄膜干涉(等厚干涉) 薄膜干涉(等厚干涉) 二
第二十二章 光的干涉
牛顿环 由一块平板玻璃和一平凸透镜组成
22-3 薄膜干涉(等厚干涉) 薄膜干涉(等厚干涉)
第二十二章 光的干涉
k = 3, d 3 = 750 nm
h
r
o R
d
k = 4 , d 4 = 1000 nm
h = 8 . 0 × 10 2 nm 由于 故可观察到四条明纹 . 当 油滴展开时, 油滴展开时,条纹间距变 条纹数减少. 大,条纹数减少
第二十二章 光的干涉
讨 论
明环半径 暗环半径
1 r = (k − )Rλ (k = 1,2,3,L) 2 (k = 0,1,2,L) r = kR λ
薄膜干涉-等条纹[整理后]
![薄膜干涉-等条纹[整理后]](https://img.taocdn.com/s3/m/939af829bb68a98271fefa8f.png)
解:由暗纹条件 = 2ne = (2k+1) /2 (k=0,1,2…)
SiO2
Si
M O
知,第9条暗纹对应于k=8,代入上式得 e = (2k+1) /4n = 1.72(m) 所以SiO2薄膜的厚度为1.72 m。
应用2:检测工件平面的平整度
例2 利用空气劈尖的等厚干涉条纹可以检测工 件表面存在的极小的加工纹路, 在经过精密加 工的工件表面上放一光学平面玻璃,使其间形 成空气劈形膜,用单色光照射玻璃表面,并在 显微镜下观察到干涉条纹, 如图所示,试根据干涉条纹 a 的弯曲方向,判断工件表面 b 是凹的还是凸的;并证明凹 ba 凸深度可用下式求得 :
2k k 1,2,3 2 2n2e 2k 1 k 0,1,2 2
二、劈尖膜 1.装置: 两光学平板玻璃一端接触,另 一端垫一薄纸或细丝 单色、平行光垂直入射 i 0 2 2 2 2e n2 n1 sin i
2n2 e
应用1:测量微小直径,厚度
例1 在半导体元件生产中,为了测定硅片上SiO2薄 膜的厚度,将该膜的一端腐蚀成劈尖状,已知SiO2 的 折射率n =1.46,用波长 =5893埃的钠光照射后,观 察到劈尖上出现9条暗纹,且第9条在劈尖斜坡上端点 M处,Si的折射率为3.42。试求SiO2薄膜的厚度。
ek-1
b ba
h
ek
h
e sin b h sin a
所以:
a h b2
ba
a b
h
ek-1
ek
h
三、牛顿环 1.装置
平板玻璃上放置曲率半径很大的平凸透镜
显微镜 T
L
S
R
SiO2
Si
M O
知,第9条暗纹对应于k=8,代入上式得 e = (2k+1) /4n = 1.72(m) 所以SiO2薄膜的厚度为1.72 m。
应用2:检测工件平面的平整度
例2 利用空气劈尖的等厚干涉条纹可以检测工 件表面存在的极小的加工纹路, 在经过精密加 工的工件表面上放一光学平面玻璃,使其间形 成空气劈形膜,用单色光照射玻璃表面,并在 显微镜下观察到干涉条纹, 如图所示,试根据干涉条纹 a 的弯曲方向,判断工件表面 b 是凹的还是凸的;并证明凹 ba 凸深度可用下式求得 :
2k k 1,2,3 2 2n2e 2k 1 k 0,1,2 2
二、劈尖膜 1.装置: 两光学平板玻璃一端接触,另 一端垫一薄纸或细丝 单色、平行光垂直入射 i 0 2 2 2 2e n2 n1 sin i
2n2 e
应用1:测量微小直径,厚度
例1 在半导体元件生产中,为了测定硅片上SiO2薄 膜的厚度,将该膜的一端腐蚀成劈尖状,已知SiO2 的 折射率n =1.46,用波长 =5893埃的钠光照射后,观 察到劈尖上出现9条暗纹,且第9条在劈尖斜坡上端点 M处,Si的折射率为3.42。试求SiO2薄膜的厚度。
ek-1
b ba
h
ek
h
e sin b h sin a
所以:
a h b2
ba
a b
h
ek-1
ek
h
三、牛顿环 1.装置
平板玻璃上放置曲率半径很大的平凸透镜
显微镜 T
L
S
R
薄膜干涉 等厚干涉和等倾干涉

大学物理
1
相干条件:频率相同、相位差恒定 、光矢量振动方向平行
相干叠加 I P I1 I 2 2 I1I 2 co s
普通光源 相干光: 同一原子的同一次发光
获得相干光的方法 1. 分波阵面法 2. 分振幅法
杨 氏
δ
r2
r1
xd D
双 缝 干 涉
=
2k
λ 2
,
dmax
kλ 2n2
7.2 107
m
(3) 最外暗环逐渐向外扩大,中心点明暗交替变化,
条纹级数逐渐减少
14
二. 等倾干涉(厚度均匀的薄膜)
两条光线的光程差
S
P
L
E
n2 AB BC n1AD
2n2dcos
考虑到有半波损失
δ
2n2dcosγ
λ 2
iD
n1
a
相邻条纹之间距 asinθ
心心
讨论
2
(1) 空气劈尖顶点处是一暗纹 —— 半波损失 dk
2
dk+1
(2) 可测量小角度θ、微位移 x、微小直径 D、波长 λ 等
(3) 测表面不平整度
等厚条纹
平晶
D
待测工件
9
2. 牛顿环
C
R
光程差
L
2d
2
B
r
A O
S d
R 2 r 2 ( R d ) 2 R>>d, 消去d2 d r 2
2
n1 1 i D
n2
AC
d
1
相干条件:频率相同、相位差恒定 、光矢量振动方向平行
相干叠加 I P I1 I 2 2 I1I 2 co s
普通光源 相干光: 同一原子的同一次发光
获得相干光的方法 1. 分波阵面法 2. 分振幅法
杨 氏
δ
r2
r1
xd D
双 缝 干 涉
=
2k
λ 2
,
dmax
kλ 2n2
7.2 107
m
(3) 最外暗环逐渐向外扩大,中心点明暗交替变化,
条纹级数逐渐减少
14
二. 等倾干涉(厚度均匀的薄膜)
两条光线的光程差
S
P
L
E
n2 AB BC n1AD
2n2dcos
考虑到有半波损失
δ
2n2dcosγ
λ 2
iD
n1
a
相邻条纹之间距 asinθ
心心
讨论
2
(1) 空气劈尖顶点处是一暗纹 —— 半波损失 dk
2
dk+1
(2) 可测量小角度θ、微位移 x、微小直径 D、波长 λ 等
(3) 测表面不平整度
等厚条纹
平晶
D
待测工件
9
2. 牛顿环
C
R
光程差
L
2d
2
B
r
A O
S d
R 2 r 2 ( R d ) 2 R>>d, 消去d2 d r 2
2
n1 1 i D
n2
AC
d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) 测波长 λ
已知R,测出m 、 rk+m、rk, 可得λ
样板 待测 透镜
条纹
(3) 检测透镜的曲率半径误差及其表面平整度
(4) 若接触良好,中央为暗纹——半波损失
(5) 透射图样与反射图样互补
二. 等倾干涉
条纹特点
(1) 等倾干涉条纹为一系列同心圆 环;内疏外密;内圆纹的级次比 外圆纹的级次高
D C AsC i n 2 dtsg in
2
n1 1 i D
n2
AC
d
n1
B
n1siinn2sin
22nn22cAdo B ns12 D dC t2 gn2sin2
2n2cdos(1si2n)2
2n2dcos
2
2d n22n12si2ni2 (2kk1)2加减 强弱 k0,1,2....
当n1 n2同理
明暗
纹纹 中中
l
心心
2d2 (2 kk 1加 )2 减 强弱k k 1 0,,2 1,.2.......
2
dk dk+1
同一明条纹或同一暗条纹都对应相同厚度的空气层
讨论
1、干涉特点:在与棱平行的地方空气层厚度处处相等,所以干
涉条纹是平行棱的明暗相间的直条纹 明 暗
2. 光垂直入射时,两相邻条纹对 应的空气层厚度差都等于
2b
解:同一条纹所对应的空气膜厚度是相等的
B点的厚度>C点的厚度
凹厚度每增加时,条纹向下移动一级,
即移动b,现在条纹移动了a,所对应的厚度
变化
b: a:H
2
H a 2b
即可测量工件与标准板的偏差值。
三0
R
干涉特点:中心
疏而边缘密的一
组同心环状条纹。 B
光程差
A
3、对透射光来说,也有干涉现象,无半波损失
2d n22n12si2ni
当反射光相互加强时,透射光将相互减弱,反之亦然,它们互补
4、上面讨论的是单色光,若所用的是复色光,则由于各种波长的 光各自在薄膜表面形成自己的一套干涉条纹,互相错开,因而在 薄膜表面形成彩色的花纹。 5、观察薄膜干涉,对膜的厚度有无限制呢?
Δh
块
块
规
规
等厚条纹的应用
石
待
英
测
环
样
品
干涉膨胀仪
不变,只增减薄膜厚度,则等厚干涉条纹并不改变其条纹
间距,而只发生条纹移动,厚度增加,条纹向棱的方向移动,
即厚度每增加/2 时,条纹向下移动一级,数出条纹移动的数 目,即可测知厚度改变多少。(测量精度达 /10以上)。干涉膨 胀仪就是根据这种原理形成的,用它可以测量很小的固体样品的
若膜的厚度太大,会使光程差 大于光源的相干长度。
尖劈状肥皂膜的干涉图样(左图为倒象)
1. 劈尖干涉
两块平面玻璃片,一端接触,另一端夹一薄纸片,即在两玻 璃片之间形成一劈尖型的空气薄膜,劈尖的夹角 很小(秒数量 级)
当平行单色光垂直玻璃表面入射 时,在空气劈尖上下表面引起的 反射光将形成相干光,
中心 d=0是暗斑。反射光的明暗纹所对应的半径分别为
r k ( 2 k 1 ) R 2k 1 , 2 , 3 ..明 .纹 .. r k kRk 0 , 1 , 2 , 3 ..暗 .纹 ..
rk2mrk2mR
r2 km
rk2
Rm
讨论 (1) 测透镜球面的半径R
已知 , 测 m、rk+m、rk,可得R
热膨胀系数。
薄膜上表面 面上移
k+1
·k
· ·
·
k-1
k
移动后条纹位置 移动前条纹位置
干涉条纹的移动
3.检查工件表面质量
如图,待测工件表面上放一平板
等厚条纹
平晶
玻璃,使其之间形成空气劈尖。以单
色光垂直照射玻璃表面,用显微镜观
察干涉条纹。由于工件表面不平,观
察到的条纹如图,根据条纹的弯曲方
待测工件
向,说明工件表面上的纹路是凹还是 凸?纹路深度或高度可表示为 H a
(2) 膜厚变化时,条纹发生移动。 当薄膜厚度增大时,圆纹从中 心冒出,并向外扩张,条纹变 密
(3) 使用面光源条纹更清楚明亮
(5) 透射光图样与反射光图样互补
PE i
i
n1
d
n2 n1
i
屏幕
i
f
S
L
M
n
观察等倾条纹的实验装置和光路
例 波长550 nm黄绿光对人眼和照像底片最敏感。要使照像机
对此波长反射小,可在照像机镜头上镀一层氟化镁MgF2薄 膜,已知氟化镁的折射率 n=1.38 ,玻璃的折射率n=1.55
实际用途;
1. 测量微小角度或细丝直径
2l
例:将细丝放在两块平面玻璃板之间,
如图,已知用绿光,546 n1m
明暗
l 5 m ,L m 2 c0 ,m 2 l 1 '',D 5 L 1 .5 4 m 4 纹 中 心
纹 中 心
l
D
2
dk dk+1
平晶 平晶
2. 测量长度的微小改变
标 准
待 测
第四节 薄膜等厚干涉
一、薄膜干涉
我们知道,两束光产生干涉的条件(又称相干条件)为:
(1) 频率相同;(2). 相位差恒定;(3). 光矢量振动方向相同
我们讲的薄膜指的是由透明介质形成的厚度很薄的一层介质膜。
S·
反射光2 反射光1
n1 1
i2
D
n2
AC
d
n1
B
S·
反射光2 反射光1
ABBC d
cos
求 氟化镁薄膜的最小厚度
解 两条反射光干涉减弱条件
2 n d(2 k 1 ) k0,1 ,2,
纹纹 中中
l
心心
dk1
dk
2
2
dk dk+1
相邻条纹之间距
lsinθ 2
3. 空气劈尖顶点处是一暗纹,这是半波损失的一个有力证明。
d 0
/2
设劈尖夹角 ,相邻明条纹(或暗条纹)之间距离 l
则
lsindk1dk
.
2
一定 , 大当 l , 小,条 相 纹当 密大 ,时 当 无 ,法 条辨
所以干涉条纹只能尖 在的 很劈尖上看到。
讨论: 1、如果照射到薄膜上的光都是以相同入射角入射,即两光线相 干点的光程差只由薄膜的厚度决定,由此干涉图样中同一条干涉 条纹下面所对应的膜厚是一样,这种条纹称为等厚干涉条纹。
2、对于厚度均匀的平面薄膜来说,光程差是随着光线的倾角(入射 角)而变化,这样不同的干涉明条纹和暗条纹相应的具有不同的倾 角,而同一干涉条纹上的各点都具有同样倾角,这种干涉条纹叫等 倾干涉。
2d
2 R2r2(Rd)2
r
O
S• d
又 R d 所d以 2略去 d, r2 2R
T
L
M A B
dr2
r增加得 增 快加得快,牛 所顿 以环 看越 到来 的越
2 d 2 2 2 r R 2 2 ( 2 k k 1 ) 2 加 减 强 k k 弱 1 0 , , 2 1 , . 2 .......
已知R,测出m 、 rk+m、rk, 可得λ
样板 待测 透镜
条纹
(3) 检测透镜的曲率半径误差及其表面平整度
(4) 若接触良好,中央为暗纹——半波损失
(5) 透射图样与反射图样互补
二. 等倾干涉
条纹特点
(1) 等倾干涉条纹为一系列同心圆 环;内疏外密;内圆纹的级次比 外圆纹的级次高
D C AsC i n 2 dtsg in
2
n1 1 i D
n2
AC
d
n1
B
n1siinn2sin
22nn22cAdo B ns12 D dC t2 gn2sin2
2n2cdos(1si2n)2
2n2dcos
2
2d n22n12si2ni2 (2kk1)2加减 强弱 k0,1,2....
当n1 n2同理
明暗
纹纹 中中
l
心心
2d2 (2 kk 1加 )2 减 强弱k k 1 0,,2 1,.2.......
2
dk dk+1
同一明条纹或同一暗条纹都对应相同厚度的空气层
讨论
1、干涉特点:在与棱平行的地方空气层厚度处处相等,所以干
涉条纹是平行棱的明暗相间的直条纹 明 暗
2. 光垂直入射时,两相邻条纹对 应的空气层厚度差都等于
2b
解:同一条纹所对应的空气膜厚度是相等的
B点的厚度>C点的厚度
凹厚度每增加时,条纹向下移动一级,
即移动b,现在条纹移动了a,所对应的厚度
变化
b: a:H
2
H a 2b
即可测量工件与标准板的偏差值。
三0
R
干涉特点:中心
疏而边缘密的一
组同心环状条纹。 B
光程差
A
3、对透射光来说,也有干涉现象,无半波损失
2d n22n12si2ni
当反射光相互加强时,透射光将相互减弱,反之亦然,它们互补
4、上面讨论的是单色光,若所用的是复色光,则由于各种波长的 光各自在薄膜表面形成自己的一套干涉条纹,互相错开,因而在 薄膜表面形成彩色的花纹。 5、观察薄膜干涉,对膜的厚度有无限制呢?
Δh
块
块
规
规
等厚条纹的应用
石
待
英
测
环
样
品
干涉膨胀仪
不变,只增减薄膜厚度,则等厚干涉条纹并不改变其条纹
间距,而只发生条纹移动,厚度增加,条纹向棱的方向移动,
即厚度每增加/2 时,条纹向下移动一级,数出条纹移动的数 目,即可测知厚度改变多少。(测量精度达 /10以上)。干涉膨 胀仪就是根据这种原理形成的,用它可以测量很小的固体样品的
若膜的厚度太大,会使光程差 大于光源的相干长度。
尖劈状肥皂膜的干涉图样(左图为倒象)
1. 劈尖干涉
两块平面玻璃片,一端接触,另一端夹一薄纸片,即在两玻 璃片之间形成一劈尖型的空气薄膜,劈尖的夹角 很小(秒数量 级)
当平行单色光垂直玻璃表面入射 时,在空气劈尖上下表面引起的 反射光将形成相干光,
中心 d=0是暗斑。反射光的明暗纹所对应的半径分别为
r k ( 2 k 1 ) R 2k 1 , 2 , 3 ..明 .纹 .. r k kRk 0 , 1 , 2 , 3 ..暗 .纹 ..
rk2mrk2mR
r2 km
rk2
Rm
讨论 (1) 测透镜球面的半径R
已知 , 测 m、rk+m、rk,可得R
热膨胀系数。
薄膜上表面 面上移
k+1
·k
· ·
·
k-1
k
移动后条纹位置 移动前条纹位置
干涉条纹的移动
3.检查工件表面质量
如图,待测工件表面上放一平板
等厚条纹
平晶
玻璃,使其之间形成空气劈尖。以单
色光垂直照射玻璃表面,用显微镜观
察干涉条纹。由于工件表面不平,观
察到的条纹如图,根据条纹的弯曲方
待测工件
向,说明工件表面上的纹路是凹还是 凸?纹路深度或高度可表示为 H a
(2) 膜厚变化时,条纹发生移动。 当薄膜厚度增大时,圆纹从中 心冒出,并向外扩张,条纹变 密
(3) 使用面光源条纹更清楚明亮
(5) 透射光图样与反射光图样互补
PE i
i
n1
d
n2 n1
i
屏幕
i
f
S
L
M
n
观察等倾条纹的实验装置和光路
例 波长550 nm黄绿光对人眼和照像底片最敏感。要使照像机
对此波长反射小,可在照像机镜头上镀一层氟化镁MgF2薄 膜,已知氟化镁的折射率 n=1.38 ,玻璃的折射率n=1.55
实际用途;
1. 测量微小角度或细丝直径
2l
例:将细丝放在两块平面玻璃板之间,
如图,已知用绿光,546 n1m
明暗
l 5 m ,L m 2 c0 ,m 2 l 1 '',D 5 L 1 .5 4 m 4 纹 中 心
纹 中 心
l
D
2
dk dk+1
平晶 平晶
2. 测量长度的微小改变
标 准
待 测
第四节 薄膜等厚干涉
一、薄膜干涉
我们知道,两束光产生干涉的条件(又称相干条件)为:
(1) 频率相同;(2). 相位差恒定;(3). 光矢量振动方向相同
我们讲的薄膜指的是由透明介质形成的厚度很薄的一层介质膜。
S·
反射光2 反射光1
n1 1
i2
D
n2
AC
d
n1
B
S·
反射光2 反射光1
ABBC d
cos
求 氟化镁薄膜的最小厚度
解 两条反射光干涉减弱条件
2 n d(2 k 1 ) k0,1 ,2,
纹纹 中中
l
心心
dk1
dk
2
2
dk dk+1
相邻条纹之间距
lsinθ 2
3. 空气劈尖顶点处是一暗纹,这是半波损失的一个有力证明。
d 0
/2
设劈尖夹角 ,相邻明条纹(或暗条纹)之间距离 l
则
lsindk1dk
.
2
一定 , 大当 l , 小,条 相 纹当 密大 ,时 当 无 ,法 条辨
所以干涉条纹只能尖 在的 很劈尖上看到。
讨论: 1、如果照射到薄膜上的光都是以相同入射角入射,即两光线相 干点的光程差只由薄膜的厚度决定,由此干涉图样中同一条干涉 条纹下面所对应的膜厚是一样,这种条纹称为等厚干涉条纹。
2、对于厚度均匀的平面薄膜来说,光程差是随着光线的倾角(入射 角)而变化,这样不同的干涉明条纹和暗条纹相应的具有不同的倾 角,而同一干涉条纹上的各点都具有同样倾角,这种干涉条纹叫等 倾干涉。
2d
2 R2r2(Rd)2
r
O
S• d
又 R d 所d以 2略去 d, r2 2R
T
L
M A B
dr2
r增加得 增 快加得快,牛 所顿 以环 看越 到来 的越
2 d 2 2 2 r R 2 2 ( 2 k k 1 ) 2 加 减 强 k k 弱 1 0 , , 2 1 , . 2 .......
