结构自振周期计算公式
结构基本自振周期计算

W
---风荷载组合系数;一般结构可不考虑,风荷载起控制作用的高层建筑应
采用0.2;
精品课件
3.8.3结构抗震承载力验算
(2)截面抗震验算
S R RE
S---包含地震作用效应的结构构件内力组合的设计值; R---结构构件承载力设计值; RE ---承载力抗震调整系数;
精品课件
3.8.3结构抗震承载力验算
3.4.1能量法
位移: xi(t)Xisi nt()
速度: x (t)Xicots()
mn
当体系振动达到平衡位置时,体系变形
位能为零,体系动能达到最大值Tmax
Tmax12ω2 in1 miXi2
m1
xn (t)
x2 (t) x1 (t )
当体系振动达到振幅最大值时,体系动能为零,
位能达到最大值Umax
无论结构是否有偏心,地震地面运动产生的结构扭 转振动均是存在的。
★扭转作用会加重结构的震害 《规范》规定对质量和刚度明显不均匀、不对称结构 应考虑水平地震作用的扭转效应
精品课件
3.6竖向地震作用
抗震设计中,一般不考虑竖向地震作用的影响 震害表明:
1、在高烈度区,竖向地面运动的影响是明显的 2、竖向地震作用对高层建筑、高耸及大跨结构
3.4结构自振周期及振型的实用计算方法
能量法是根据体求解以剪切型为主的框架结构
mn
xn (t)
设体系作自由振动,任一质点i的位移:
xi(t)Xisi nt()
3.4.1能量法
速度为 x (t)X ico ts()
m1
精品课件
x2 (t) x1 (t )
竖向地震作用。
精品课件
3.8.1地震作用及计算方法
简支梁的周期计算

简支梁的周期计算简支梁是一种较为常见的结构形式,其两个端点可以完全自由地旋转,不受约束。
这种结构梁比较简单,可以用一维振动理论来描述和计算。
简支梁的自由振动方程可以表示为:m* d²u/dt² + k* u = 0其中,m是梁的质量,k是梁的刚度,u是梁的挠度,t是时间。
这是一个二阶线性常微分方程,可以通过解特征方程来得到解析解。
由于此处要求大于1200字,我将分几个方面来详细讲解简支梁的周期计算。
1.导出简支梁的振动方程2.计算简支梁的自然频率3.计算简支梁的周期首先,我们可以从简支梁的振动方程出发,推导得到简支梁的自然频率。
自然频率是梁在自由振动时的频率,是梁固有的特性。
可以用公式表示为:ω=√(k/m)其中,ω是自然频率,k是梁的刚度,m是梁的质量。
接下来,我们可以用自然频率来计算简支梁的周期。
周期是一个完整振动周期所需的时间,可以用公式表示为:T=2π/ω其中,T是周期,ω是自然频率。
对于简支梁,刚度k和质量m可以通过结构的几何形状和材料性质来确定。
例如,对于均匀截面的简支梁,可以用梁的截面面积A、杨氏模量E和长度L来计算刚度k和质量m。
刚度k可以通过以下公式计算:k=3EI/L³其中,E是杨氏模量,I是梁截面的惯性矩,L是梁的长度。
质量m可以通过以下公式计算:m=ρAL其中,ρ是梁的密度,A是梁的截面面积,L是梁的长度。
通过上述方法,我们可以计算出简支梁的自然频率ω和周期T。
需要注意的是,上述计算方法适用于假设简支梁是线性弹性结构的情况。
对于非线性情况,计算方法会有所不同。
此外,简支梁的几何形状和材料特性也会对周期的计算结果产生影响。
在实际工程中,为了保证结构的安全性和可靠性,设计时通常会将简支梁的自然频率控制在一定范围内。
频率过高或过低都可能导致结构出现问题,例如共振或不够刚性。
综上所述,简支梁的周期计算是工程设计中的重要问题。
通过推导梁的振动方程,计算自然频率和周期,可以帮助工程师合理地确定梁的材料和几何形状参数,确保结构的安全性和可靠性。
结构基本自振周期计算分解课件

竖向地震作用
竖向地震作用对高层建筑的影响较大,需要在计算中考虑竖向地震 作用的影响。
地震作用的组合
在计算中,需要考虑不同方向和不同强度地震作用的组合效应,以 更准确地评估结构的抗震性能。
06 结论与展望
本课程总结
01
结构基本自振周期计算是工程结 构分析中的重要环节,本课件详 细介绍了计算方法及其应用。
05 结构基本自振周期计算中 的注意事项
边界条件的处理
固定边界
对于固定边界,需要考虑结构在边界上的刚度,确保边界条件满 足,以减小误差。
弹性边界
对于弹性边界,需要考虑边界的弹性变形,并适当调整结构的刚 度矩阵,以更准确地模拟结构的振动。
支撑条件的模拟
在计算中,需要正确模拟结构的支撑条件,包括支撑刚度和阻尼 等参数,以确保计算结果的准确性。
02
通过案例分析,使学习者更好地 理解计算过程,掌握相关技能。
本课件注重理论与实践相结合, 帮助学习者提高解决实际问题的 能力。
03
本课件内容丰富,条理清晰,适 合作为学习资料或培训教材。
04
未来研究方向
01
深入研究结构基本自振周期的影 响因素,提高计算精度和可靠性
。
03
结合数值模拟和实验研究,进一 步验证和改进计算方法。
高层建筑结构的自振周期计算
总结词:复杂度高
详细描述:高层建筑结构的自振周期计算相对复杂,需要考虑更多的因素,如楼层高度、建筑材料、施工方法等。计算时需 要建立详细的数学模型,并进行数值分析。
大跨度结构的自振周期计算
总结词
跨度大,影响因素多
详细描述
结构基本周期

结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系。
自振周期是结构按某一振型完成一次自由振动所需的时
计特征周期是在抗震设计用的地震影响系数曲线中,反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值;场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期,表示场地土最主要的振动特性。
结构在地震作用下的反应与建筑物的动力特性密切相关,建筑物的自振周期是主要的动力特征,与结
周期相等或接近时,建筑物的震害较为严重。
基本周期应该取决于建筑物的结构形式,各种结构形式都是定数。
结构自振周期是结构在水平作用下的震动周期,是变数。
结构在地震作用下的反应与建筑物的动力特性密切相关,建筑物的自振周期是主要的动力特征,与结构的质量和刚度相关。
经验表明,当建筑物的自振周期与场地的卓越周期相等或接近时,建筑物的震害较为严重。
结构的基本周期可采用结构力学方法计算,对于比较规则的结构,也可以采用近似方法计算:
框架结构 T=()N
框剪结构、框筒结构 T=()N
剪力墙结构、筒中筒结构 T=()N
其中N为结构层数。
也可采用结构分析得到的结构第1平动周期。
自振周期及地震作用计算讲义
n
i
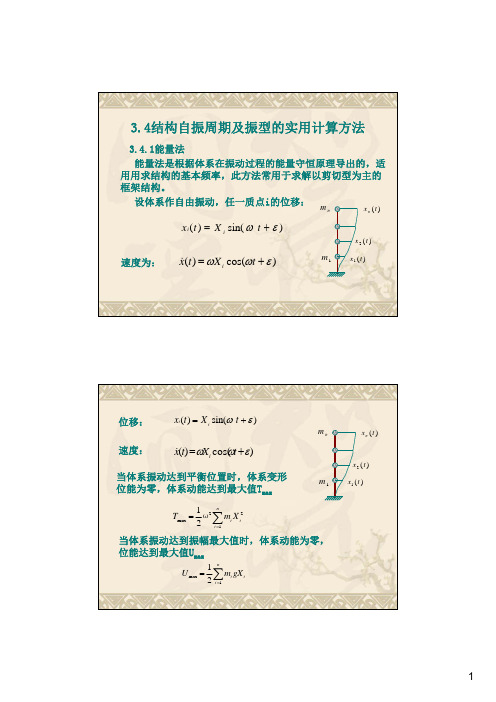
根据能量守恒原理:
g
m
i 1 n i
n
i
Xi
T1
2 i
2
m
i 1
X
1
2
m X
i i 1 n
n
2 i
g
m X
i i 1
2
i
G X
i
n
2 i
G X
i i 1
i 1 n
i
一般假定:将结构重力荷载当成水平荷载作用于质点上 所得的结构弹性曲线为结构的基本振型。
T 1 max 1 2
n
i 1
m i ( 1 x i )
2
mN
xn
M
eq
xm
单质点体系的最大动能为
T 2 max 1 M 2
eq
xm xn
m1 x1
( 1 x m ) 2
x m ---体系按第一振型振动时,相应于折算质点处的最大位移;
T1max
1 n mi (1xi )2 2 i1
ห้องสมุดไป่ตู้
竖向地震作用,烟囱上 抛后下落错位。
9
德阳利森水泥厂生料均化库,受到 竖向地震作用,塔筒上抛后下落。
底部框架底层为薄弱层, 底层墙体叠合塌落。 (9度 区)
10
底部框架结构底层框架叠合塌落(北川11度区)。
中间层叠合塌落(日本阪神大地震)。
11
中间层水平裂缝 中间层水平裂缝。
3.6.1高耸结构及高层建筑的竖向地震作用
台湾省漳化县富贵 名门大楼,16层钢筋混 凝土住宅楼,平面为C 型, 平面不规整,单排 柱框架,柱子间距太大, 数量偏少。
结构基本自振周期计算
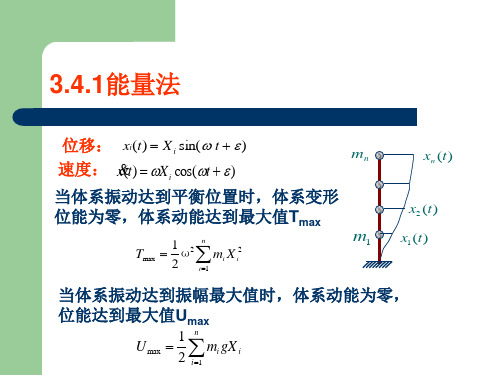
h ---计算楼层层高;
[ e ]---弹性层间位移角限值,按表3.14采用。
3.8.4多遇地震作用下结构抗震变形验算
表3.14弹性层间位移角限值
结构类型 钢筋混凝土框架
钢筋混凝土框架-抗震墙、板柱-抗震墙、框架-核心筒 钢筋混凝土抗震墙、筒中筒 钢筋混凝土框支层 多、高层钢结构
T1 (0.04 ~ 0.05) N
(4)钢-钢筋混凝土混合结构
T1 (0.06 ~ 0.08) N
(5)高层钢结构
T1 (0.08 ~ 0.12) N
3.5结构的扭转地震效应
一、产生扭转地震反应的原因
两方面:建筑自身的原因和地震地面运动的原因。 m 1.建筑结构的偏心
主要原因:结构质量中心与刚度 中心不重合 质心:在水平地震作用下, 惯性力的合力中心 刚心:在水平地震作用下, 结构抗侧力的合力中心
(1)竖向反应谱及竖向振动周期 竖向地震反应谱: 与水平地震反应谱的形状相差不大 竖向反应谱的加速度峰值约为水平反应谱的1/2至2/3。可利用水平地震反应谱进行分析。
V 0.65 H
Ⅰ类场地的竖向和水平平均反应谱
3.6.1高耸结构及高层建筑的竖向地震作用
竖向振动周期: 计算结果表明:高耸结构和高层建筑竖向振动周 期较短,基本周期在0.1~0.2s范围内 小于场地的特征周期Tg 《建筑抗震规范》直接取竖向地震影响系数:
u g (t )
刚心 质心
3.5结构的扭转地震效应
2.地震地面运动存在扭转分量 地震波在地面上各点的波速、周期和相位不同。建 筑结构基底将产生绕竖直轴的转动,结构便会产生扭转 振动。 无论结构是否有偏心,地震地面运动产生的结构扭 转振动均是存在的。 ★扭转作用会加重结构的震害 《规范》规定对质量和刚度明显不均匀、不对称结构 应考虑水平地震作用的扭转效应
几种周期的区分

结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系。
结构基本周期:是指结构按基本振型完成一次自由振动所需的时间。
自振周期T:结构按某一振型完成一次自由振动所需的时间,是结构本身的动力特性,仅与结构的质量m、刚度系数k有关。
设计特征周期:是在抗震设计用的地震影响系数曲线中,反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值;场地卓越周期:是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期,表示场地土最主要的振动特性。
卓越周期按地震记录统计得到,地基土随软硬程度的不同有不同的卓越周期,可划分为四级:一级——稳定基岩,卓越周期是0.1-0.2s,平均为0.15s。
二级——一般土层,卓越周期为0.21-0.4s,平均为0.27s。
三级为松软土层,卓越周期在二级和四级之间。
四级——为异常松软的土层,卓越周期为0.3-0.7s,平均为0.5s.特征周期Tg:即建筑场地自身的周期,是建筑物场地的地震动参数,在地震影响系数曲线中,水平段与下降段交点的横坐标,反映了地震震级,震源机制(包括震源深度)、震中距等地震本身方面的影响,同时也反映了场地的特性;如软弱土层的厚度,类型等场地类别等。
在抗震设计规范中,设计特征周期Tg与场地类别有关:场地类别越高(场地越软),Tg越大;地震震级越大、震中距离越远,Tg越大。
Tg越大,地震影响系数α的平台越宽,对于高层建筑或大跨度结构,基本周期较大,计算的地震作用越大。
剪切波速是指震动横波在土内的传播速度,单位是m/s。
可通过人为激震的方法产生震动波,在相隔一定距离处记录振动信号到达时间,以确定横波在土内的传播速度。
测试方法一般有单孔法、跨孔法等。
剪切波速是抗震区确定场地土类别的主要依据。
地震时,从震源发出的地震波在土层中传播时,经过不同性质地质界面的多次反射,将出现不同周期的地震波。
若某一周期的地震波与地基土层固有周期相近,由于共振的作用,这种地震波的振幅将得到放大,此周期称为卓越周期。
结构周期

1. 结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系:自振周期是结构按某一振型完成一次自由振动所需的时间;基本周期是指结构按基本振型完成一次自由振动所需的时间;设计特征周期是在抗震设计用的地震影响系数曲线中,反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值;场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期,表示场地土最主要的振动特性。
结构在地震作用下的反应与建筑物的动力特性密切相关,建筑物的自振周期是主要的动力特征,与结构的质量和刚度相关。
经验表明,当建筑物的自振周期与场地的卓越周期相等或接近时,建筑物的震害较为严重。
2.经验公式一般情况下,高层钢筋混凝土结构的基本自振周期T1为T1=(0.05~1.10)n(4.3-27)其中:钢筋混凝土框架结构:T1=(0.06~0.09)n(4.3-28)框架-剪力墙结构:T1=(0.06~0.08)n(4.3-29)高层钢结构的基本自振周期T1为T1=(0.10~0.15)n(4.3-30)式中:n——建筑层数。
结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系:结构基本周期、结构自振周期与设计特征周期、场地卓越周期之间的区别和联系:自振周期是结构按某一振型完成一次自由振动所需的时间;基本周期是指结构按基本振型完成一次自由振动所需的时间;设计特征周期是在抗震设计用的地震影响系数曲线中,反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值;场地卓越周期是根据覆盖层厚度H和土层剪切波速VS按公式T0=4H/VS计算的周期,表示场地土最主要的振动特性。
结构在地震作用下的反应与建筑物的动力特性密切相关,建筑物的自振周期是主要的动力特征,与结构的质量和刚度相关。
经验表明,当建筑物的自振周期与场地的卓越周期相等或接近时,建筑物的震害较为严重。
用顶点位移法求自振周期:T=1.7*周期折减系数*(层间侧移开方)折减系数:框架结构取0.6~0.7框剪结构取0.7~0.8抗剪墙取1.0按照行业标准《工程抗震术语标准》(JGJ/97)的有关条文,自振周期:结构按某一振型完成一次自由振动所需的时间。
