结构动力学计算题
结构动力计算习题

160结构动力计算习题一.选择题8-1 体系的动力自由度是指( )。
A .体系中独立的质点位移个数B .体系中结点的个数C .体系中质点的个数D .体系中独立的结点位移的个数 8-2 下列说法中错误的是( )。
A .质点是一个具有质量的几何点;B .大小、方向作用点随时间变化的荷载均为动荷载;C .阻尼是耗散能量的作用;D .加在质点上的惯性力,对质点来说并不存在 8-3 图示体系EI =常数,不计杆件分布质量,动力自由度相同的为( )。
题8-3图A .(a )、(b )、(c )B .(a )、(b )C .(b )、(c )D .(a )、(c ) 8-4图示体系不计杆件分布质量,动力自由度相同的为( )。
(b )(c )题8-4图A .(a )、(b )、(c )B .(a )、(b )C .(b )、(c )D .(a )、(c )8-5 若要提高单自由度体系的自振频率,需要( )。
A .增大体系的刚度B .增大体系的质量C .增大体系的初速度D .增大体系的初位移 8-6不计阻尼影响时,下面说法中错误的是( )。
A .自振周期与初位移、初速度无关;B .自由振动中,当质点位移最大时,质点速度为零;C .自由振动中,质点位移与惯性力同时达到最大值;D .自由振动的振幅与质量、刚度无关 8-7 若结构的自振周期为T ,当受动荷载)(P t F =t F θsin 0作用时,其自振周期T ( )。
A .将延长B .将缩短C .不变D .与荷载频率θ的大小有关8-8 若图(a )、(b )和(c )所示体系的自振周期分别为a T 、b T 和c T ,则它们的关系为( )。
(a)(b)(c)题8-8图A .a T >b T >c TB .a T >c T >b TC .a T <c T <b TD .a T =c T <b T 8-9 振幅计算公式βst y A =中的st y 为( )。
结构的动力计算习题

《结构的动力计算》习题一、判断题1、图示等效体系的关系是:3211111k k k k ++=。
( )2、结构的动力反应只与初始条件及动荷载有关。
( )3、任何动力荷载作用下均可以采用公式:1221-⎪⎪⎭⎫⎝⎛-=ωθβ计算动力系数。
( ) 4、外界感干扰力只影响振幅、不影响体系的自振频率。
( )5、体系的动力自由度数与质点的个数无关、也与结构静定或超静定无关。
( )6、图示体系各杆自重不计、EA =∞,则该体系在初始时刻的干扰力作用下将做竖向振动。
( )二、选择题1、增加单自由度体系的阻尼、但仍保持为低阻尼体系,其结果是( )。
A 、周期变长 B 、周期不变 C 、周期变短 D 、 周期视具体体系而定2、图示两个等效结构,正确的刚度关系是( )。
A 、k=k 1+k 2 B 、21111k k k += C 、21211k k k k k += D 、2112k kk k k +=3、图示体系不计阻尼,平稳阶段最大动位移y max =4Pl 3/7EI ,其最大动力弯矩为( )。
A 、3Pl /7 B 、4Pl /7 C 、12Pl /7 D 、4Pl /21 4、下列哪句话有错误或不够准确()。
第3题图A、在多自由度体系自由振动问题中,主要问题是确定体系的全部自振频率和相应的主振型; B 、多自由度体系的自振频率不止一个,其个数与自由度个数相等;C 、每个自振频率都有自己相应的主振型,主振型就是多自由度体系振动时各质点的位移变化形式;D 、与单自由度体系相同,多自由度体系的自振频率和相应的主振型也是体系本身的固有性质。
5、图示单自由度体系自振周期的关系为( )。
A 、(a)=(c)B 、(a)=(b)C 、(b)=(c)D 、都不相等6、单自由度振动体系中,若质点在杆的中点,各杆EI 、l 相同,其自振周期的大小排列顺序为(A 、(c)>(a)>(b)B 、(c)>(b)>(a) C 、(a)>(b)>(c) D 、(b)>(c)>(a)三、分析计算题1、梁的抗弯刚度为EI2m3、柱的自重不计,求图示刚架的自振频率。
结构动力学试题及答案

结构动力学试题及答案(本文按试题和答案格式进行编写)试题一:1. 请问什么是结构动力学?2. 简述结构动力学的研究对象和主要内容。
3. 结构动力学分析常用的方法有哪些?4. 结构动力学分析中常用的数学模型有哪些?5. 结构动力学的应用领域有哪些?答案一:1. 结构动力学是研究结构在外力作用下的动态响应及其稳定性的学科。
2. 结构动力学的研究对象是各种工程结构,主要内容包括结构的振动、冲击响应、瞬态响应和稳态响应等。
3. 结构动力学分析常用的方法有模态分析法、频率响应分析法、时程分析法等。
4. 结构动力学分析中常用的数学模型有单自由度体系、多自由度体系、连续体系等。
5. 结构动力学的应用领域广泛,包括建筑结构工程、桥梁工程、风力发电机组、地震工程等。
试题二:1. 结构动力学分析中,模态分析的基本原理是什么?2. 简述模态分析的步骤和计算方法。
3. 常用的模态分析软件有哪些?4. 请问什么是结构的固有频率和阻尼比?5. 结构的模态振型对结构动力响应有什么影响?答案二:1. 模态分析是基于结构的振动特性,通过求解结构的固有频率、模态振型和阻尼比等参数,来研究结构的动力响应。
2. 模态分析的步骤包括建立结构有限元模型、求解结构的固有频率和模态振型、计算结构的阻尼比等。
常用的计算方法有有限元法、拉普拉斯变换法等。
3. 常用的模态分析软件有ANSYS、ABAQUS、MSC.NASTRAN等。
4. 结构的固有频率是结构在无外力作用下自由振动的频率,阻尼比是结构振动过程中能量耗散的程度。
5. 结构的模态振型对结构动力响应有很大影响,不同的模态振型会导致不同的振动特性和反应。
试题三:1. 结构动力学分析中,频率响应分析的基本原理是什么?2. 简述频率响应分析的步骤和计算方法。
3. 频率响应分析和模态分析有什么区别?4. 结构的频率响应函数和传递函数有什么区别?5. 频率响应分析在结构设计中的应用有哪些?答案三:1. 频率响应分析是研究结构在单频激励下的响应特性,通过求解结构的频率响应函数,来获得结构的响应。
结构动力学习题
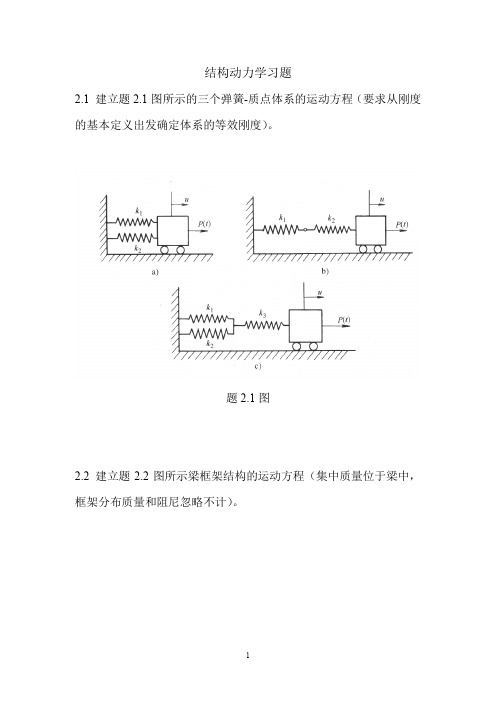
结构动力学习题2.1 建立题2.1图所示的三个弹簧-质点体系的运动方程(要求从刚度的基本定义出发确定体系的等效刚度)。
题2.1图2.2 建立题2.2图所示梁框架结构的运动方程(集中质量位于梁中,框架分布质量和阻尼忽略不计)。
题2.2图2.3 试建立题2.3图所示体系的运动方程,给出体系的广义质量M、广义刚度K、广义阻尼C和广义荷载P(t),其中位移坐标u(t)定义为无重刚杆左端点的竖向位移。
题2.3图2.4 一总质量为m1、长为L的均匀刚性直杆在重力作用下摆动。
一集中质量m2沿杆轴滑动并由一刚度为K2的无质量弹簧与摆轴相连,见题 2.4图。
设体系无摩擦,并考虑大摆角,用图中的广义坐标q1和q2建立体系的运动方程。
弹簧k2的自由长度为b。
题2.4图2.5 如题2.5图所示一质量为m1的质量块可水平运动,其右端与刚度为k的弹簧相连,左端与阻尼系数为c的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连,摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程(坐标原点取静平衡位置)。
题2.5图2.6如题2.6图所示一质量为m1的质量块可水平运动,其上部与一无重刚杆相连,无重刚杆与刚度为k2的弹簧及阻尼系数为c2的阻尼器相连,m1右端与刚度为k1的弹簧相连,左端与阻尼系数为c1的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连,摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程(坐标原点取静平衡位置,假定系统作微幅振动,sinθ=tanθ=θ)。
计算结果要求以刚度矩阵,质量矩阵,阻尼矩阵的形式给出。
3.1单自由度建筑物的重量为900kN,在位移为3.1cm时(t=0)突然释放,使建筑产生自由振动。
如果往复振动的最大位移为2.2cm(t =0.64s),试求:(1)建筑物的刚度k;(2)阻尼比ξ;(3)阻尼系数c。
3.2 单自由度体系的质量、刚度为m=875t,k=3500kN/m,且不考虑阻尼。
结构动力学试题

结构动力学试题一、选择题1. 结构动力学中的“动力响应”是指:A. 结构在静态载荷下的变形B. 结构在动态载荷下的变形C. 结构的自然频率D. 结构的阻尼比2. 单自由度系统的周期公式为:A. T = 2π√(m/k)B. T = 2π√(k/m)C. T = 2π/mD. T = π√(m/k)3. 多自由度系统的振型分解法是基于以下哪个原理?A. 结构的对称性B. 结构的不确定性C. 结构的线性叠加原理D. 结构的能量守恒原理4. 在地震分析中,反应谱方法的主要优点是:A. 考虑了地震动作用的非线性B. 可以处理任意形状的地震波形C. 能够直接给出结构的响应结果D. 适用于快速评估结构的地震安全性5. 结构阻尼比的增大通常会导致:A. 自然频率的提高B. 振幅的减小C. 周期的延长D. 响应的不稳定二、填空题1. 在结构动力学中,________是用来描述结构在动态载荷作用下的运动状态。
2. 动态载荷下,结构的响应可以通过________方法进行求解,该方法基于结构振动的线性叠加原理。
3. 地震波的________特性对结构的响应有显著影响,因此在进行地震分析时需要特别考虑。
4. 结构的阻尼比可以通过________方法进行实验测定,以评估结构的能量耗散能力。
5. 在进行结构动力分析时,通常需要将结构简化为________自由度系统,以便于计算和分析。
三、简答题1. 请简述单自由度系统与多自由度系统的区别及其各自的适用场景。
2. 描述地震波的基本特性,并解释为什么需要对其进行频谱分析。
3. 说明结构阻尼对动力响应的影响,并讨论如何通过设计来提高结构的阻尼性能。
四、计算题1. 一个单自由度系统的质量为500 kg,刚度为2000 N/m。
请计算该系统的自然频率和阻尼比为0.05时的周期。
2. 假设一个结构在地震作用下的最大加速度为0.3g,其中g为重力加速度(9.81 m/s²),请使用反应谱方法计算该结构在自然频率为2Hz时的响应加速度。
结构动力学试题及答案

结构动力学试题及答案一、选择题1. 在结构动力学中,下列哪项不是描述结构动力响应的参数?A. 自然频率B. 阻尼比C. 静力平衡D. 模态阻尼2. 以下哪个不是结构动力学分析中的常用方法?A. 模态分析B. 时域分析C. 频域分析D. 静力分析二、简答题1. 简述结构动力学中模态分析的目的和重要性。
2. 描述阻尼对结构动力响应的影响。
三、计算题1. 假设一个单自由度系统,其质量为m,刚度为k,初始位移为x0,初始速度为v0。
若外力为F(t) = F0 * sin(ωt),求该系统在任意时间t的位移响应。
答案一、选择题1. 正确答案:C. 静力平衡解析:静力平衡是静力学的概念,与结构动力学无关。
2. 正确答案:D. 静力分析解析:静力分析是分析结构在静载荷作用下的响应,而结构动力学分析动态载荷下的结构响应。
二、简答题1. 模态分析的目的在于识别结构的自然振动特性,包括自然频率、阻尼比和模态形状。
它的重要性在于:- 预测结构在动态载荷下的响应。
- 为控制结构的振动提供基础数据。
- 优化设计,提高结构的抗震性能。
2. 阻尼对结构动力响应的影响主要表现在:- 减少振动幅度,提高结构的稳定性。
- 改变系统的自然频率和模态形状。
- 影响系统的动态响应时间。
三、计算题1. 单自由度系统的位移响应可以通过以下步骤求解:- 写出系统的动力学方程:m * d²x/dt² + c * dx/dt + k * x = F(t)- 应用初始条件:x(0) = x0, v(0) = v0- 应用外力:F(t) = F0 * sin(ωt)- 通过傅里叶变换或拉普拉斯变换求解方程。
- 应用逆变换得到位移响应的解析解或数值解。
位移响应的一般形式为:x(t) = X * cos(ωt - φ) + Y *sin(ωt - φ),其中X和Y是与系统参数和初始条件有关的常数,φ是相位角。
具体的数值需要根据系统参数和初始条件进行计算。
结构动力学典型习题及答案

ω
2 2
=
537.287
1/ s2
{X
}1
=
1 1.870
ω1 = 9.885 1/ s ω2 = 23.179 1/ s
{X }2
=
−
1 0.642
ω12 = 7.965EI / ml3
ω
2 2
=
65.53EI
/
ml 3
ω1 = 2.822 EI / ml3
ω2 = 8.095 EI / ml3
m
EI1 = ∞
EI
2m
EI1 = ∞
2EI
y1
2EI
y2
l 2EI
l
X11 = 0.4612; X12 = −4.336
X 21
X 22
{X
}1
=
1 2.168
m2
EI1 = ∞
i2 m1
y2
i2 4m
k11 − m1ω 2 kδ 21
k12
=0
k22 − m2ω 2
EI1 = ∞
i1
i1y1 4m
X11 = 0.5347; X12 = −1.559
0.012ω 4 − 7.62ω 2 + 630 = 0
X 21
X 22
ω12 = 97.713 1/ s2
=1
=1 3l/16 5l/32 l/2
=1
δ
11
=
l3 192EI
ω = 13.856 EI / ml3
δ11
=
l3 EI
ω = EI / ml3
m
EI m y1
y2
EI
l/2 l/2
l/2 l/2
15结构的动力计算--习题

P h 2.5 6
M st
2
2
4
3.75kN m
Mmax Mst 3.751.375 5.156kN m
Ph/4 Ph/4
P Ph/4
Ph/4
Ph/4
Ph/4
动荷幅值弯矩图
Ph/4
动弯矩幅值图
Ph/4
结构力学电子教程
15 结构的动力计算
15.12 图示一个重物W=500N,悬挂在刚度k=4N/mm的弹簧
15.3 求图示体系的自振频率。
解:
1 1 l h h 2 lh2
EI 2
3 3EI
1
m
3EI Mlh2
M
I1=∞ EI
l
h
1
h h M1
结构力学电子教程
15 结构的动力计算
15.5 求图示刚架水平振动的圆频率。
解: k 12EI 3 36EI
h3
h3
k m
36EI 2mh3
18EI mh3
st
Wh3
A
3 2 104
106 16 104 20 103 33
108
9.8
41.74s1
y y0 cost, A y0 0.1cm. v y0 sin t, vmax y0 0.1 41.74 4.174cm / s. a y02 cost, amax y02 0.1 41.742 174.2cm / s2.
0.05534
9.8
1 1 9.035
2 2 0.05534
k mW
g
Psin t
A y(t) max
yst
P k
=9.035
50 =0.11294m=112.94mm 4000
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
无阻尼自由振动计算题(单位:kg、N = kg・m/s2、Pa = N/m2、)无阻尼自由振动运动方程:u(t) = u(0) cos w n t +丝^sinw湛;w n刚度k = F/* (kN/m);自振圆频率3〃= £ = (rad/s);无阻尼体系简谐荷载反应:其中频率比P = 0/w n;17(0) P o /? 1 P o 1u0)=状0)cos w n t + - sin啪 + 9t稳态反应等效静位移四=Po/k = P0/mw n2;稳态反应振幅I/。
= u st R d = y—K I1-P I阻尼c = 2mw n^ (kN * s/m);阻尼比(=—=—— = 有阻尼圆频率c cr 2mw n 2nn ut+nW D = w n y/l-^2;有阻尼自振周期T D=L/房寻有阻尼体系动力方法系数R d= — = u st1/J[1一供]2 + [2〈仞2;拉格朗日方程计算题lagrange方程:,(茶J 一 *" += Q);其中Q)为非有势力对应于广义坐标0/的广义力平面运动刚体的动能T = |mv c2+|/c w2,随质心平移的动能和绕质心转动的动能之和。
细直杆绕质心的转动惯量:J c—,对喘部:J z=■ ^mZ2;圆盘对其质心的转JL£O动惯量:]0— ^mr2o振型叠加法计算题(第一类型)频率方程:\[K] - a)2[M]| = 0得自振频率s由特征方程:([K] - 口2[的){勿=0;设{飕)=1,得到{破)和{泌。
已知条件 1:切}i = [o.644,、{必2 = {-0.601,、切}3={-2.57>、[M]= (0.311.52.可得振型质量:M n =同理可知M 2 = 2.456, M3 = 23.109。
1.5 ) 加已知条件 2: m (0)} = {2.5 }m,位(0)} = {2.25 m/s4.50)-0.6762.47可知 Mi = {0}7[M]{0h = (1 0.644 0.3)1 ・1.5 .2.。
:44"。
2, 0.3 J13.75J 可得振兴坐标表示的初始条件:(1 0.644 0.3)小、{^}i[M]u(0)Qi(0)=1 ・1.5. 2. 1.25 2.5 3.755.915 =3.2825 1.80202(°)=ri(1.25) (1 -0.601 -0.676)1.52.5■2. (3.75)-6.07375 2.456何片网成。
)03(0)=ri (1.25)(1 -2.570 2.470)1.52.52. (3.75)__ 10.1375M 3 =0.43868ri (1.5)(1 0.644 0.3)1.52.252 JU.50)Mi =3.53696.3735 1.8021.25Mi1.8022.456M 2 =-2.47323.10923.1091.802・小、何片网讥。
)91(0)==0.65153由初始条件引起各广义坐标的自由振动q?(t) = Q n (0) cosw n t + ^-^sin w n 结构自由振动反应方程{u°(t)) = Y 切Lq?(t)=切}iq?(t) +切}20珀)+(p3q30t弯曲梁计算题弯矩与曲率关系:M = -£7*^=-£7/;剪力Q = * 等截面梁自由振动偏微分方程:m 空笋+引竺"=0,分成两个方程 d z t d^x 1) 单自由度体系无阻尼自由振动不。
)+ o )2q(t) = 0得解:随时间变化振幅:q(t) = q 处(0) cos wt +迎^sin 切w2) 振动形状方程:拭”3)-。
403)= 0,其中mu )2 = a 4EI ;得解:振动形状通解(边界条件):位移:(p(x) = Asinax + Bcosax + Csinhax + Dcoshax 斜率:0‘(x) = a(bcosax — Bsinax + Ccoshax + Osinhax)弯矩:(p H (x) = a 2 (—bsinax — Bcosax + Csinhax + Dcoshax) 剪力:<p" (x) = a 3 (—bcosax +Bsinax + Ccoshax + £)s inh ax) 悬臂端集中质量边界条件:一端固定,一端自由其边界条件可表示为:1在x = 0处,位移和转角为零0(0) = 0; 0‘(0) = 0;在x = L 处,弯矩:(p H(L) = 0;剪力:El (p ,n(L) = -Ma )2(/)(L);S(o)=倒网讥。
)M2ri (1.5)(1 -0.601 -0.676)1.52.252 J U.50)S(0)=-6.612375 ""2.456-=-2.6923{以网讯0)(1 -2.570 2.470)11.52」U.50)M 3 23.10915.05625 23.109mud 2t1=1a —2.456代入在x = 0处的边界条件可得B + D = O;Q(,+C)=O;即B = -D; A=-C;利用(p" (A) = 0可得9" (L) = a2(—i4sinaL —BcosaL + CsinhaL + DcoshaL) = 0 所以有:/(sinaL + sinhaL) +B(cosaL + cosha,)= 0 ;利用剪力:EI Q ' (L) = —Ma)2(p(L),得到EIa3(—AcosaL + BsinaL + CcoshaL +Z^s inh aZ士以n2 /s in aL +Bcos aL+Cs inh aL士庆osh aL=0£7Q3(_/(COSQ L + coshaL) + B (sinaL— sinhaL))+ Ma)2(A(sinaL — sinhaL) + B(cosaL— coshaL)) = 0刀[—£7Q3(COSQ L + coshoL) + M32(sinaL — sinhoL)]+ 8[£7尸6赢七—sinhaL) + M3? (COSQ L — coshoL)] = 0使A,B不同时为零的条件时联立方程组系数行列式为零sinaL + sinhaL cosaL + coshaL —EIa3(cosaL + coshaL) + Ma>2 (sinaL — sinhaL) Ela3 (sinaL — sinhaL) + Mo)2(cc.\f _ 10 m k chki sin 以一.、加7cos kl \E/a3 ((sinaL)2— (sinhaL)2) + Mo)2 (cosaL — coshaL)(sinaL + sinhaL)+£7Q3((COSQ L)2 + (coshaL)2 + 2 cos aL cosh aL)—Ma)2(sinaL — sinhaL) (cosaL + coshaL) = 0EZa3 [(sinaL)2 + (cosaL)2 + (coshaL)2— (sinhaL)2 + 2 cos aL cosh aL]+ Ma)2 [(cosaL — coshaL)(sinaL + sinhaL)—(sinaL — sinhaL) (cosaL + coshaL)] = 02£7Q3(I + cos aL cosh aL) + 2Ma)2 (cosaL ・ sinhaL — sinaL - coshaL) = 0 , 因为mu)2 = a4 Eh所求频率方程:m(l + cos aL cosh aL) + Ma^cosaL - sinhaL - sinaL -cosha£=0注意:sinh(O) = 0,cosh(0) = 1 ; cosh2t — sinh2 t = 1 ; (cosh*)' = sinhx ; (sinh *)' = coshx2、端部弹性支撑边界条件:(p n (L) = 0 >剪力:El(p‘"(L) = k(p(L);/(sin。
%+ sinhaL) + B(cosaL + cosh 以)=0;EIa3(—AcosaL + BsinaL + CcoshaL + Ds inhaL)= k^AsinaL + BcosaL + CsinhaL + DcoshaL)刀〔—£7Q3(COSQ L + cosh 以)—k(sinaL— sinh。
%)]+ 研£7Q3(sinaL — sinh。
%) —k(cosaL— cosh。
%)] = 0sinaL + sinhaL (cosaL + coshaL) —£7Q3(COSQ L + coshaL) —k (sinaL— sinhaL) El a3 (sinaL — sinhaL) —k^cosaL —=0(sinaL + sinhaL) [El a3 (sinaL — sinhaL) — k(cosaL — coshaL)]—(cosaL + coshaL) [—Ela3 {cosaL + coshaL) — k (sinaL — sinhaL)]=0[EZa3(sin2aL — sinh2 aL) — k^sinaL + sinhaL^cosaL — coshaL)]—[—EIc^^cosaL + coshaL)2— k^cosaL + co shaL) {sinaL — sinhaL')]=0El a3 (sin2 aL — sinh2 aL) + EIa3(cosaL + coshaL)2—k (sinaL + sinhaL) (cosaL — coshaL)+ k^cosaL + coshaL) (sinaL — sinhaL') = 0Elc^^sin2 aL — sinh2 aL +cos2 aL + cosh2 aL + 2 cos aL coshaL)+ k (sinaL + sinhaL) ^coshaL — cosaL)+ k^cosaL + coshaL) (sinaL — sinhaL) = 02£7Q3(I +1 cos aL coshaL) + 2k{sinaLcoshaL — cosaLsinhaL) = 0可矢口:£7Q3(I + cos aL cosh aL) + fc(sinaLcoshaL — cosaLsinhaL) = 03、端部弹性支撑,固定集中质量M边界条件:(p n (L) = 0、剪力:El0〃'O = k(p(L) -。
