幻方数学题九宫格
数阶幻方的编排方法

精心整理奇数阶幻方的编排方法简便易学的编排方法。
一、九子排列法宋朝数学家杨辉在《续古摘奇算法》中,总结“洛书”幻方的编排方法时说:三阶幻方的编排方法是“九子排列,上下对易,左右相更,四维挺出”。
这四个句子是什么意思呢?我们通过下面的一组图来加以理解。
先画出一个3×3的“九宫格”,并在第二列上、下方和第二行左、右边各添加一个虚线格子,把1~9这九个数字按顺序写在如上图所示的三排斜线上,然后上、下对调,左右交换,(因为我123图1)4然后把551下面以五阶幻方为例,再介绍一种奇数阶幻方的编排方法。
步骤如下:①先画出一个5×5(五行五列)的方格,在方格的四周画出凸阶梯式的虚线方格(如下图1)②把1~25这二十五个数按斜行方向从左到右依次填入图中(如上图2);③以3、15、23、11四个数为顶点(实际上就是五阶幻方的四个顶点)画出一个正方形;④把正方形外面凸出的虚线方格中的数按“上移下,下移上;左移右,右移左”的方法,全部平移5格到对应部分的方格中,擦掉虚线格子,就得到一个五阶幻方(见下图)。
这种编排幻方的方法叫“巴舍法”,也叫平移补空法,它和“罗伯法”一样,也适用于一切的奇数阶幻方的编排。
需要提醒大家注意的是,在步骤②中,填写1~25这二十五个数时,可以从左向右上填写,也可以从右向左上填写,或者从上向右下填写,还可以从上向左下填写,其移动后的结果都是一个五阶幻方,同学们可以自己动手试一试。
另外,编排n 阶幻方时,不一定非要从1开始,只要是这些数能构成等差数列就可以了。
练习(一定要完成的哦)1、使用“罗伯法”将4~12编排一个三阶幻方。
2、用“罗伯法”将21、31、32、41、43、61、121、125、127编成一个三阶幻方。
3、使用“巴舍法”将1~49编排一个七阶幻方。
双偶数阶幻方的编排方法一、中心对称交换法例1、用1~16这十六个数编排一个四阶幻方(四行四列)。
【分析与解答】用1至16编排一个四阶幻方,就是把1~16这十六个数填入四行四列的方格34。
有趣的九宫格填数解读

有趣的九宫格填数江苏省泗阳县李口中学沈正中九宫格填数是幻方中最简单的一种填数形式。
如果一个n 2矩阵的每行、每列及两条对角线的所有数之和都相等,且这些数都是从1到 n2的自然数,这样的方阵就称为n 阶幻方。
有关幻方问题的研究在我国已流传了两千多年,这是一类形式独特的填数问题。
九宫格实质上是幻方中n =3时的三阶幻方。
三阶幻方传说最早出现在夏禹时代的“洛书” ,在北周的甄弯注《数术记遗》一书中,记有三阶幻方的填法:九宫内,二四为肩,六八为足,左七右三,戴九履一,五居中央。
我国南宋时期杰出的数学家杨辉,是最早系统研究幻方的数学家。
他曾将幻方命名为“纵横图” (三阶幻方也叫络书或九宫图,并给出了三阶、四阶幻方构造方法的说明,四阶以上幻方,杨辉只画出图形而未留下作法。
但他所画的五阶、六阶乃至十阶幻方全都准确无误。
杨辉在在《续古摘奇算法》中,总结出了三阶幻方构造的方法:“九子斜排(1、2、3,4、5、6,7、8、9),上下对调(1、9),左右相换(7、3),四维挺出(4、2、8、6)。
”意思是:先把l ~9九个数依次斜排(如下图一),再把上l 下9两数对调(如下图二),左7右3两数互换(如下图三),最后把四面的2、4、6、8向外面挺出(如下图四),这样就构造了一个三阶幻方。
1 9 9 42 4 2 4 2 4 9 2 7 53 7 5 3 3 5 7 3 5 7 8 6 8 6 8 6 8 1 6 9 1 1图一图二图三图四三阶幻方的填法不是唯一的,矩阵的第一行与第三行对调,或第一列与第三列对调,可以得出4种填法,将其中的任意一种填法旋转90°,又可以得到另外的4种填法。
例如,将上面图四的第一列与第三列对调,就可以得出前面口诀中的填法。
通常我们把幻方中每行3个数的和称为幻方的幻和,幻方正中心的那个数叫做中心数,中心数也就是这9个数的中位数。
从1到9这9个数的和为:1+2+3+…8+9=45;则三阶幻方每行3个数字之和即幻和为:45÷3=15。
三年级上册趣味数学(8)幻方(九宫格九宫阵)

三年级趣味数学(8)九宫格与阵班级姓名1.在1——9这九个数中,取其中3个不同的数相加,使和为15,你能写出哪些三组数?(例如1,5,9。
1+5+9=15)1+5+9=15 2+4+9=15 3+4+8=15 1+6+8=15 2+5+8=15 3+5+7=15 2+6+7=15 4+5+6=153.探索三阶幻方的特点(1)对角线上三个数之间有什么关系?(2)“十”字形中纵列或横行三个数之间有什么关系? (3)中宫数(最中间的数)与九个数之间有什么关系? (4)研究特殊的等腰三角形数之间的关系。
4.利用掌握三阶幻方的特点制作三阶幻方。
2 9 4 7 5 3 6 1 86 7 2 1 5 9 8 3 48 1 6 3 5 7 4 9 24 3 8 9 5 1 2 7 6 6 1 8 7 5 3 2 9 42 7 6 9 5 1 43 87 22 13 22 16 10 19 4 257 8 12 14 9 4 6 10 1110 21 8 11 13 15 18 5 165.九宫阵(俗称数独)。
将1——9这九个数填入每行、每列、每个九宫格的小方格内。
每个数字在每行、每列、每个九宫格内只能出现一次。
13 15 108 11541057 4 13 981 6 92 3 68 2 95 7 46 47 23 1 982 7 1 68 4 532 5 9 7 3165 7342 48 9 1 73 9 16 8 2 4287 9 81 2 54 96 325 68 5 7 6 41 37 5 9294 8 7 637 1 56 5 3 14 298 5 67 74 1 3 9 8 2 56 52 3147 89。
九宫格的填数
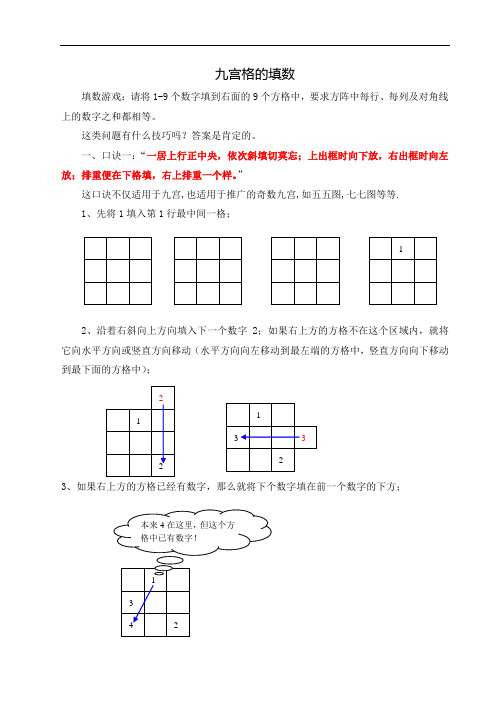
九宫格的填数填数游戏:请将1-9个数字填到右面的9个方格中,要求方阵中每行、每列及对角线上的数字之和都相等。
这类问题有什么技巧吗?答案是肯定的。
一、口诀一:“一居上行正中央,依次斜填切莫忘;上出框时向下放,右出框时向左放;排重便在下格填,右上排重一个样。
”这口诀不仅适用于九宫,也适用于推广的奇数九宫,如五五图,七七图等等. 1、先将1填入第1行最中间一格;2、沿着右斜向上方向填入下一个数字2;如果右上方的方格不在这个区域内,就将它向水平方向或竖直方向移动(水平方向向左移动到最左端的方格中,竖直方向向下移动到最下面的方格中);3、如果右上方的方格已经有数字,那么就将下个数字填在前一个数字的下方;4、如果右上方的方格向左或向右移动都不在区域内,仍然将它填在前一个数字的下方;5、继续以上步骤,就可以完成所有方格数字的填写。
特别注意的是,这种方法不但可以填3×3的方阵,还可以填所有奇数×奇数方阵。
如7×7,9×9方阵等。
二、在《射雕英雄传》中黄蓉曾破解九宫格,口诀:戴九履一,左七右三,二四有肩,六八为足,五居中央。
但是“二四有肩,六八为足“只是提示答案的快捷方法,并不是具体的解法。
三、九宫格填数的决窍(三阶幻方) 活动要求:1、熟练100以内的加法口算。
2、知道两个单数或两个双数相加的和一定是双数,一个单数和一个双数相加的和是单数。
例1: 把1、2、3、4、5、6、7、8、9九个数分别填入右边的九宫格里,使横行、竖行、斜行三个数的和都相等。
1、要解决这个问题,关键是什么?先要求出“和”是多少?怎么求呢?方法是先把所有数的和求出来:1+2+3+4+5+6+7+8+9=45然后因为三行和都相等,所以45/ 3=15 所以各行各列的和是15。
(写在格子旁) 师:接下来再考虑什么?2、中间数是几?是53、然后将凑成10的四对数填在四周,这四对数的填法也很有讲究。
因为“15”是单数,根据: 单数+单数=双数 单数+双数=单数 双数+双数=双数只能把两对双数(2、4、6、8)填在四个角上,并且对角线的和=15,四角可以旋转。
有趣的九宫格填数

有趣的九宫格填数江苏省泗阳县李口中学沈正中九宫格填数是幻方中最简单的一种填数形式.如果一个n2矩阵的每行、每列及两条对角线的所有数之和都相等,且这些数都是从1到 n2的自然数,这样的方阵就称为n阶幻方。
有关幻方问题的研究在我国已流传了两千多年,这是一类形式独特的填数问题。
九宫格实质上是幻方中n=3时的三阶幻方.三阶幻方传说最早出现在夏禹时代的“洛书”,在北周的甄弯注《数术记遗》一书中,记有三阶幻方的填法:九宫内,二四为肩,六八为足,左七右三,戴九履一,五居中央。
我国南宋时期杰出的数学家杨辉,是最早系统研究幻方的数学家。
他曾将幻方命名为“纵横图”(三阶幻方也叫络书或九宫图), 并给出了三阶、四阶幻方构造方法的说明,四阶以上幻方,杨辉只画出图形而未留下作法.但他所画的五阶、六阶乃至十阶幻方全都准确无误。
杨辉在在《续古摘奇算法》中,总结出了三阶幻方构造的方法:“九子斜排(1、2、3,4、5、6,7、8、9),上下对调(1、9),左右相换(7、3),四维挺出(4、2、8、6)。
”意思是:先把l~9九个数依次斜排(如下图一),再把上l下9两数对调(如下图二),左7右3两数互换(如下图三),最后把四面的2、4、6、8向外面挺出(如下图四),这样就构造了一个三阶幻方。
1 994 2 4 2 4 24 927 5 3 75 3 3 57 3 578 686868 1 69 11图一图二图三图四三阶幻方的填法不是唯一的,矩阵的第一行与第三行对调,或第一列与第三列对调,可以得出4种填法,将其中的任意一种填法旋转90°,又可以得到另外的4种填法。
例如,将上面图四的第一列与第三列对调,就可以得出前面口诀中的填法.通常我们把幻方中每行3个数的和称为幻方的幻和,幻方正中心的那个数叫做中心数,中心数也就是这9个数的中位数。
从1到9这9个数的和为:1+2+3+…8+9=45;则三阶幻方每行3个数字之和即幻和为:45÷3=15。
三年级上册趣味数学(8)幻方(九宫格九宫阵)ys

三年级趣味数学(8)
九宫格与阵
班级姓名
1.在1——9这九个数中,取其中3个不同的数相加,使和为15,你能写出哪些三组数?(例如1,5,9。
1+5+9=15)
2.如右图把一个正方形划分为3行3列9个方格,我们俗称“九宫
格”。
每个方格填一个数,使横行、数列以及对角线上三个数的和相
等。
这样的九宫格成为三阶幻方。
把上面的1——9这九个数填入格子中,使横行、数列以及对角线上
三个数相加的和为15,怎样填呢?
3.探索三阶幻方的特点
(1)对角线上三个数之间有什么关系?
(2)“十”字形中纵列或横行三个数之间有什么关系?(3)中宫数(最中间的数)与九个数之间有什么关系?(4)研究特殊的等腰三角形数之间的关系。
4.利用掌握三阶幻方的特点制作三阶幻方。
5.九宫阵(俗称数独)。
将1——9这九个数填入每行、每列、每个九宫格的小方格内。
每个数字在每行、每列、每个九宫格内只能出现一次。
九宫格的解题过程讲解

九宫格的解题过程第1步首先计算每行数字之和。
1-9九个数字之和:1+2+3+4+5+6+7+8+9=45九宫格共有三行,并且每行的数字之和相等,因此45/3=15,即每行数字之和为15。
第2步计算中间格的数字。
考虑第2行,第2列,和2条对角线的数字之和。
它们的总和为 15/4 = 60。
在它们的总和中,中间格子的数字出现了4次,其它位置格子的数字都出现了而且仅出现了1次。
所以,它们的总和=(4×中间格子的数字)+(其它8个数字)=(3×中间格子的数字)+(1-9九个数字之和)因此, 60=3×中间格子的数字+45,中间格子的数字等于5第3步,奇数不能出现在4个角上的格子里。
比如,如果数字9出现在角上的格子里,那么为了保证9所在行或所在列的数字和为15,必须需要4个数字,两两之和必须为6。
1,2,3,4,6,7,8中,只有2和4组成和为6的数字对,找到第2个和为6的数字对是不可能的。
因此,数字9不能出现在4个角上的格子里。
同样道理,1,3,7也不能出现在4个角上的格子里。
第4步,2,4,6,8必须填在4个角上的格子里,并且保证对角线数字和为15。
第5步,将1,3,7,9填入相应的格子里就完成了九宫格填数字任务,注意和为15的条件。
完成了填九宫格的任务后,我们进一步考虑,如果上面九宫格内所有数字都加数字1会发生什么呢?即可不可以用数字2,3,4,5,6,7,8,9,10填九宫格,得到每一行,每一列,每一对角线的三个数字之和都相等的新九宫格呢。
显而易见,上面九宫格每行每列每对角线数字之和为18,奇数3,5,7,9处在4个角上的格子里,中间数6处在中间的格子里。
从1-9和2-10各九个数字所填充的九宫格可以得出下列规律:1)九个数字是由9个相连的整数构成的。
2)九个数字中正中间的数字填在九宫格的中间格子里。
1-9中的5,2-10中的6等。
3)每行每列的数字和等于中间数字的三倍。
九宫格的解题过程

九宫格的解题过程第1步首先计算每行数字之和。
1-9九个数字之和:1+2+3+4+5+6+7+8+9=45九宫格共有三行,并且每行的数字之和相等,因此45/3=15,即每行数字之和为15。
第2步计算中间格的数字。
考虑第2行,第2列,和2条对角线的数字之和。
它们的总和为 15/4 = 60。
在它们的总和中,中间格子的数字出现了4次,其它位置格子的数字都出现了而且仅出现了1次。
所以,它们的总和=(4×中间格子的数字)+(其它8个数字)=(3×中间格子的数字)+(1-9九个数字之和)因此, 60=3×中间格子的数字+45,中间格子的数字等于5第3步,奇数不能出现在4个角上的格子里。
比如,如果数字9出现在角上的格子里,那么为了保证9所在行或所在列的数字和为15,必须需要4个数字,两两之和必须为6。
1,2,3,4,6,7,8中,只有2和4组成和为6的数字对,找到第2个和为6的数字对是不可能的。
因此,数字9不能出现在4个角上的格子里。
同样道理,1,3,7也不能出现在4个角上的格子里。
第4步,2,4,6,8必须填在4个角上的格子里,并且保证对角线数字和为15。
第5步,将1,3,7,9填入相应的格子里就完成了九宫格填数字任务,注意和为15的条件。
完成了填九宫格的任务后,我们进一步考虑,如果上面九宫格内所有数字都加数字1会发生什么呢?即可不可以用数字2,3,4,5,6,7,8,9,10填九宫格,得到每一行,每一列,每一对角线的三个数字之和都相等的新九宫格呢。
显而易见,上面九宫格每行每列每对角线数字之和为18,奇数3,5,7,9处在4个角上的格子里,中间数6处在中间的格子里。
从1-9和2-10各九个数字所填充的九宫格可以得出下列规律:1)九个数字是由9个相连的整数构成的。
2)九个数字中正中间的数字填在九宫格的中间格子里。
1-9中的5,2-10中的6等。
3)每行每列的数字和等于中间数字的三倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幻方数学题九宫格
摘要:
一、幻方数学题九宫格简介
1.幻方概念
2.九宫格与幻方的联系
二、幻方数学题九宫格的历史与起源
1.古代中国对幻方的认识
2.九宫格在古代的应用
三、幻方数学题九宫格的解题方法
1.基础解法
2.高阶解法
3.计算机算法
四、幻方数学题九宫格的现实意义与应用
1.教育领域
2.科学研究领域
3.人工智能领域
正文:
幻方数学题九宫格,顾名思义,是将幻方与九宫格相结合的一种数学题型。
幻方,又称魔方,是一种具有特殊规律的数字排列,例如1-9 的九宫格排列,每个行、列、对角线上的数字和都相等,这就是一个三阶幻方。
而九宫格,又称洛书,是一种由九个数字组成的方格,其数字排列具有特殊的规律和
数学意义。
幻方与九宫格的结合,为数学爱好者提供了一种富有趣味性和挑战性的题目形式。
幻方数学题九宫格的历史源远流长,可以追溯到古代中国。
在古代,我国学者对幻方进行了广泛的研究,并发现了许多有关幻方的规律。
同时,九宫格也在古代得到了广泛的应用,如风水、卜卦等。
这充分展示了我国古代数学的辉煌成就。
幻方数学题九宫格的解题方法有很多,初级解法通常采用暴力穷举法,逐行、逐列、逐对角线检查数字和是否相等。
而高阶解法则涉及到一些高级数学技巧,如行列式、矩阵运算等。
此外,随着计算机技术的发展,人们已经开发出了许多高效的算法来解决幻方数学题九宫格。
幻方数学题九宫格在现实意义和应用方面也具有重要意义。
在教育领域,幻方数学题九宫格可以培养学生的逻辑思维能力和创新思维,激发他们对数学的兴趣。
在科学研究领域,幻方数学题九宫格的研究有助于揭示数字之间的深层规律,推动数学的发展。
此外,在人工智能领域,幻方数学题九宫格也可以作为算法训练的实例,提高计算机的智能水平。
