数据结构 第5章 魔方阵
魔方阵算法及C语言实现

魔方阵算法及C语言实现1 魔方阵概念魔方阵是指由1,2,3……n2填充的,每一行、每一列、对角线之和均相等的方阵,阶数n = 3,4,5…。
魔方阵也称为幻方阵。
例如三阶魔方阵为:魔方阵有什么的规律呢?魔方阵分为奇幻方和偶幻方。
而偶幻方又分为是4的倍数(如4,8,12……)和不是4的倍数(如6,10,14……)两种。
下面分别进行介绍。
2 奇魔方的算法2.1 奇魔方的规律与算法奇魔方(阶数n = 2 * m + 1,m =1,2,3……)规律如下:1.数字1位于方阵中的第一行中间一列;2.数字a(1 < a ≤ n2)所在行数比a-1行数少1,若a-1的行数为1,则a的行数为n;3.数字a(1 < a ≤ n2)所在列数比a-1列数大1,若a-1的列数为n,则a的列数为1;4.如果a-1是n的倍数,则a(1 < a ≤ n2)的行数比a-1行数大1,列数与a-1相同。
2.2 奇魔方算法的C语言实现1 #include <stdio.h> 2// Author: / 3// N为魔方阶数 4#define N 115 6int main()7{8int a[N][N]; 9int i;10 int col,row;1112 col = (N-1)/2;13 row = 0;1415a[row][col] = 1;1617for(i = 2; i <= N*N; i++)18 {19if((i-1)%N == 0 )20 {21 row++;22 }23else24 {25// if row = 0, then row = N-1, or row = row - 126 row--;27 row = (row+N)%N;2829// if col = N, then col = 0, or col = col + 130 col ++;31 col %= N;32 }33 a[row][col] = i;34 }35for(row = 0;row<N;row++)36 {37for(col = 0;col < N; col ++)38{39 printf("%6d",a[row][col]);40 }41printf("\n");42 }43return0;44 }3 偶魔方的算法偶魔方的情况比较特殊,分为阶数n = 4 * m(m =1,2,3……)的情况和阶数n = 4 * m + 2(m = 1,2,3……)情况两种。
魔方阵

问题3.1、n –魔方阵一、提出问题所谓“n – 魔方阵”是指由1至n 这n 个不同整数构成的魔方阵,其魔方常数为n ( n + 1 ) / 2。
例如,5 – 魔方阵和7 – 魔方阵如图3 – 1所示。
易知,这两个魔方阵的魔方常数分别为15和28。
3215415432432152154354321 ,4321765176543254321762176543654321732176547654321 图3 – 1 5 – 魔方阵和7 – 魔方阵n – 魔方阵的数字排列很有规律,若用人工的方法给出并不困难。
现在要求给出:能让计算机自动输出n (≥ 3)为奇数时形如图3 – 1所示的n – 魔方阵的算法。
二、简单分析n – 魔方阵较我们之后将要讨论的奇、偶数阶魔方阵,要简单许多。
观察后不难发现:1.要填入的n 个数字在阵列的每一行和每一列都要出现且仅出现一次,且各行(列)中的数字顺序相同,这里的顺序是指循环顺序,其中数字1接在数字n 的后面。
2.从阵列的行来看,每一行的第一个数字与它上一行正中间的数字相同。
通过对“n – 魔方阵”的分析,下面几个基本问题必须得到解决:◆ 如何确定阵列第一行各个数字?◆ 在填入其他行的数字时如何保证数字原有的顺序不改变同时每一行的第一个数字正好是其上一行正中间的数字?三、设计准备假设我们要构建的是一个n – 魔方阵,为此定义一个有n 行n 列的二维数组。
1.确定阵列第一行各个数字这里我们处理的方法很简单,即可以利用循环方法顺序地在二维数组第一行中填写1,2,3,…,n 这n 个自然数即可。
2.填入其他行的数字,并保证数字原有的顺序不改变同时每一行的第一个数字正好是其上一行正中间的数字要解决这个问题,需借助一个有n + 1单元的一维数组,并对该数组进行若干次“循环左移”处理。
所谓做一次“循环左移”,即指在一维数组中,将第1个数填入第n + 1个单元,第2个数填入第1个单元,……,第n个数填入第n– 1 个单元,最后再将第n + 1个单元中的数填入第n个单元。
魔阵

Page 16
三、单偶阶魔阵的实现
的倍数, 但不是4 的倍数, 注意n 必须大于2 (即n 是2 的倍数, 但不是4 的倍数, 注意n 必须大于2)
单偶阶魔阵的构造基本思想: 单偶阶魔阵的构造基本思想 (1) 将m = n/ 2,则可以分成四个数 , 据段: 据段 1. . m^2 , m^2 + 1. .2*m^2 , 2*m^2 + 1. . 3*m^2 , 3*m^2 + 1. . 4*m^2 ; (2) 采用德拉鲁布算法 分别排出 采用德拉鲁布算法, 分别排出m 阶魔阵A ×m阶魔阵 、B 、C、D 。A 、 阶魔阵 、 B 、C、D 魔阵起始数据分别为 , 、 魔阵起始数据分别为1 m+ 1 , 2*m^2 + 1 , 3*m^2 + 1 ; (3) 将A 、B 、C、D 以图 的形式 、 以图1的形式 合成n× 方阵; 合成 ×n 方阵
图1
Page 17
三、单偶阶魔阵的实现
单偶阶魔阵的构造基本思 想: (4) 将A 、D 方阵中前 m 方阵中前( + 1) / 2 - 1列元素除第 列 列元素除第1 列元素除第 中第( 行不变外, 中第 m + 1) / 2 行不变外 其余分别对应元素交换; 其余分别对应元素交换 (5) 将A 、D 方阵中心元素 交换, 即第( 交换 即第 m+ 1) / 2 行第 ( m + 1) / 2 列; (6) 将B 、C 方阵中后 m 方阵中后( - 1) / 2 - 1 列元素对应交 换。
Page 12
(二)德拉鲁布算法
它是一种构造奇阶方阵的方法, 它是一种构造奇阶方阵的方法,具 体如下: 体如下: 开始,将 放在第一行正中; (1)从1 开始 将1 放在第一行正中; ) (2)接着向右上方移动一格 填入数 )接着向右上方移动一格, 若超出右边(上 界限时, 字, 若超出右边 上 边) 界限时 接至最左边(下边 即行为 列为 下边) 即行为0 列为n 接至最左边 下边 ,即行为 (列为 + 1) 时, 将行改成 (列改为 ; 将行改成n 列改为 列改为1) (3)若右上方已有数字 则向下方一 )若右上方已有数字, 格填数; 格填数 直至数填完n (4)重复 、(3) 直至数填完 ×n )重复(2) 的方阵。 的方阵。
魔方阵

魔方阵,古代又称“纵横图”,是指组成元素为自然数1、2…n的平方的n×n的方阵,其中每个元素值都不相等,且每行、每列以及主、副对角线上各n个元素之和都相等。
如3×3的魔方阵:8 1 63 5 74 9 2魔方阵的排列规律如下:(1)将1放在第一行中间一列;(2)从2开始直到n×n止各数依次按下列规则存放;每一个数存放的行比前一个数的行数减1,列数加1(例如上面的三阶魔方阵,5在4的上一行后一列);(3)如果上一个数的行数为1,则下一个数的行数为n(指最下一行);例如1在第一行,则2应放在最下一行,列数同样加1;(4)当上一个数的列数为n时,下一个数的列数应为1,行数减去1。
例如2在第3行最后一列,则3应放在第二行第一列;(5)如果按上面规则确定的位置上已有数,或上一个数是第一行第n列时,则把下一个数放在上一个数的下面。
例如按上面的规定,4应该放在第1行第2列,但该位置已经被占据,所以4就放在3的下面;一、魔方阵的简介1.何谓矩阵?矩阵就是由方程组的系数及常数所构成的方阵。
把用在解线性方程组上既方便,又直观。
2.何谓n阶方阵?若一个矩阵是由n个横列与n个纵行所构成,共有个小方格,则称这个方阵是一个n阶方阵。
3.何谓魔方阵?4 9 2 3 5 7 8 1 6定义:由n*n个数字所组成的n阶方阵,具有各对角线,各横列与纵行的数字和都相等的性质,称为魔方阵。
而这个相等的和称为魔术数字。
若填入的数字是从1到n*n,称此种魔方阵为n阶正规魔方阵。
4.最早的魔方阵相传古时为了帮助治水专家大禹统治天下,由水中浮出两只庞大动物背上各负有一图,只有大禹才可指挥其中之由龙马负出的为河图,出自黄河;另一由理龟负出的洛书出自洛河。
洛书5.最早的四阶魔方阵最早的四阶方阵刻在印度一所庙宇石上,年代大约是十一世纪。
古代印度人十分崇拜这种幻方,至今从古神殿的遗址,墓碑上常常还可以发现四阶幻方的遗迹。
数据结构课程设计之奇数魔方阵

长沙理工大学《数据结构》课程设计报告田晓辉学院计算机与通信工程专业计算机科学与技术班级计08-01 学号************学生姓名田晓辉指导教师陈倩诒课程成绩完成日期2010年7月10日课程设计成绩评定学院计算机与通信工程专业计算机科学与技术班级计08-01学号200850080110 学生姓名田晓辉指导教师陈倩诒完成日期2010年7月10日指导教师对学生在课程设计中的评价指导教师对课程设计的评定意见课程设计任务书计算机与通信工程学院计算机科学技术专业用C语言解决魔方阵的问题学生姓名:田晓辉指导老师:陈倩诒摘要本课程设计主要解决设计一个n×n的矩阵中填入1到n2的数字(n为奇数),使得每一行、每一列、每条对角线的累加和都相等的问题。
在课程设计中,系统开发平台为Windows 7,程序设计语言采用Visual C++6.0,程序运行平台为Windows 98/2000/XP/7。
在程序设计中,采用了C 语言结构化程序设计思想和过程设计方法,以功能函数为基本结构,对问题中的要求做出了准确的实现。
程序通过调试运行,初步实现了设计目标。
关键词程序设计;C++6.0;结构化;过程设计;功能函数目录1.引言 (1)1.1课程设计目的 (1)1.2课程设计内容 (1)2.设计思路与方案 (2)3.详细实现 (3)3.1数据结构与数据存储表示 (3)3.2功能函数 (3)3.3函数逻辑功能调用图 (5)3.4本程序执行流程图 (6)4.运行环境与结果 (7)4.1程序运行环境 (7)4.2程序运行结果 (7)5.结束语 (9)参考文献 (10)附录源程序代码 (11)1 引言本课程设计主要解决设计一个n×n的方阵中填入1到n2(n为奇数)的数字,使得每一行、每一列、每条对角线上各个数字累加的和都相等的问题。
1.1 课程设计目的通过这次课程设计进一步了解了二维数组的使用方法和一些基本的设计思路。
数据结构实验报告-魔方阵
数据结构与程序设计实验实验报告
哈尔滨工程大学
实验报告三
c. 如果按上述方法找到的位置已填入数据,则在同一列下一行填入下一个数字。
(3). 以3×3魔方阵为例,说明其填数过程,如下图所示。
三阶魔方阵的生成过程
由三阶魔方阵的生成过程可知,某一位置(x,y)的左上角的位置是(x-1,y-1),如果x-1≥0,不用调整,否则将其调整为x-1+m;同理,如果y-1≥0,不用调整,否则将其调整为y-1+m。
所以,位置(x,y)的左上角的位置可以用求模的方法获得,即:
x=(x-1+m)%m
y=(y-1+m)%m
如果所求的位置已经有数据了,将该数据填入同一列下一行的位置。
这里需要注意的是。
此时的x和y已经变成之前的上一行上一列了,如果想变回之前位置的下一行同一列,x需要跨越两行,y需要跨越一列,即:
x=(x+2)%m
printf("%d\t",a[i][j]);
printf("\n");
}
四、界面设计
程序需要获取魔方阵的阶数(包括错误判断),输出结果,均在执行过程中给出提示。
五、运行测试与分析
1. 获取阶数并给出错误提示
2. 获取正确阶数,并输出结果
六、实验收获与思考
本次实验采用的数据结构为二维数组,在使用过程中巩固了学习的知识,在用C语言实现魔方阵算法时对C语言的使用更加熟悉。
七、附录(原程序)。
数据结构 陈雁 第5章 自测练习题参考答案
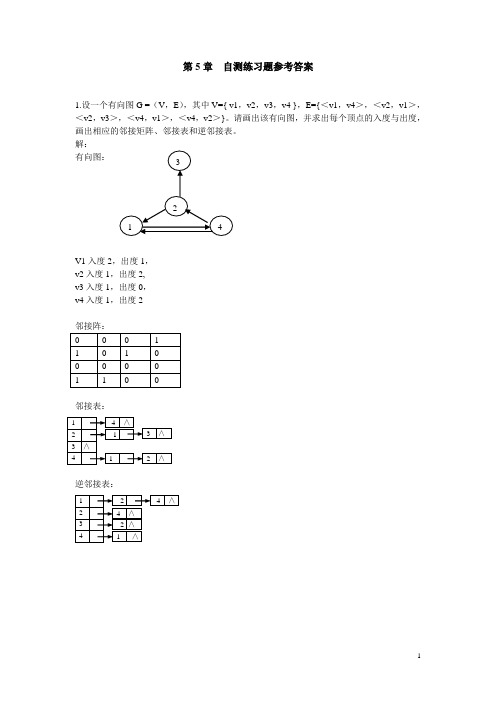
第5章自测练习题参考答案1.设一个有向图G =(V,E),其中V={ v1,v2,v3,v4 },E={<v1,v4>,<v2,v1>,<v2,v3>,<v4,v1>,<v4,v2>}。
请画出该有向图,并求出每个顶点的入度与出度,画出相应的邻接矩阵、邻接表和逆邻接表。
解:有向图:V1入度2,出度1,v2入度1,出度2,v3入度1,出度0,v4入度1,出度2邻接阵:邻接表:逆邻接表:2.分别求出题图5-1从v 2出发按深度优先搜索和广度优先搜索算法遍历得到的顶点序列(假设图的存储结构采用邻接矩阵表示)。
解 :广度优先序列是:v2,v1,v3,v6,v4,v5 深度优先序列是:v2,v1,v3,v4,v5,v63.已知一个有向图的邻接表如题图5-2所示,求出根据深度优先搜索算法从顶点v 1出发遍历得到的顶点序列。
解 :深度优先序列是:v1,v3,v4,v5,v2 广度优先序列是:v1,v3,v2,v4,v54.分别用普里姆和克鲁斯卡尔算法构造题图5-3所示网络的最小生成树。
解 :普里姆算法: (v1,v3) (v3,v4)(v4,v5)(v4,v2) 或 (v5,v2)克鲁斯卡尔算法: (v4,v5)(v2,v4) 或 (v2,v5) (v1,v3) (v3,v4)5.求出题图5-4从顶点v 1到其它各顶点之间的最短路径。
解:(v1-v3 ) 5 (v1-v3-v6) 15 (v1-v3-v6-v4) 19 (v1-v2) 20 (v1-v3-v6-v5) 256.画出题图5-5所示的AOV网所有可能的拓扑有序序列。
并指出应用拓扑排序算法求得的是那一个序列(若选用邻接表作存储结构)?解:(1)所有可能的拓扑有序序列:v1,v4,v2,v5,v3 ,v6v1,v4,v2,v3,v5, v6v1,v4,v5,v2,v3, v6v4,v1,v2,v5,v3, v6v4,v1,v2,v3,v5, v6v4,v1,v5,v2,v3, v6v4,v5,v1,v2,v3, v6(2)根据邻接表,应用拓扑排序算法求得的序列是:v4,v5,v1,v2,v3 v6。
魔方阵

C语言程序求魔方阵如下:(求奇数幻方)代码一:#include <stdio.h>#define N 16 //这里可以修改N的值int main(){int a[N][N]={0},i,j,k,p,m,n;p=1;while(p==1){printf("Enter n(1~%d): ",N-1);/*可以输入小于等于N-1的整数*/ scanf("%d",&n);if((n!=0)&&(n<N)&&(n%2!=0)) p=0;}i=n+1;j=n/2+1; /*建立魔方阵*/a[1][j]=1;for(k=2;k<=n*n;k++){i=i-1;j=j+1;if((i<1)&&(j>n)){i=i+2;j=j-1;}else{if(i<1) i=n;if(j>n) j=1;}if(a[i][j]==0) a[i][j]=k;else{i=i+2;j=j-1;a[i][j]=k;}}for(i=1;i<=n;i++)/*输出魔方阵*/{for(j=1;j<=n;j++)printf("%4d",a[i][j]);}printf("\n");}代码二:(相对于代码一条理更清晰,更简单、更容易理解)将1~n的平方这几个数构成一个n阶魔方阵。
算法:依以下法则,你可以很快的写出奇数阶幻方!当然,这种写法只是其中一个答案,而不是唯一答案。
1)将1填入第一行中间;2)将每个数填在前一个数的右上方。
3)若该位置超出最上行,则改填在最下行的对应位置;4)若该位置超出最右列,则该填在最左列的对应行位置;5)若某元素填在第一行最右列,下一个数填在该数同列的下一行;6)若某数已填好,但其右上角已填了其他数据,则下一个数填在该数同列的下一行位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构
实验报告第五章
实验名称:魔方阵
实验类型:设计性实验
班级:
学号:
姓名:
实验日期:2014年6月7日
1.问题描述
魔方阵是一个古老的智力问题,它要求在一个m×m的矩阵中填入1~m2的数字(m为奇数),使得每一行、每一列、每条对角线的累加和都相等,如图1所示。
基本要求
●输入魔方阵的行数m,要求m为奇数,程序对所输入的m作简单的判
断,如m有错,能给出适当的提示信息。
●实现魔方阵。
●输出魔方阵。
2.数据结构设计
这个问题的数据结构使用数组就可以解决。
3.算法设计
●由1开始填数,将1放在第0行的中间位置。
●将魔方阵想象成上下、左右相接,每次往左上角走一步,会有下列情况:
✧左上角超出上方边界,则在最下边相对应的位置填入下一个数字;
✧左上角超出左边边界,则在最右边相应的位置填入下一个数字;
✧如果按上述方法找到的位置已填入数据,则在同一列下一行填入下
一个数字。
以3×3魔方阵为例,说明其填数过程,如图2所示。
图2 三阶魔方阵的生成过程
由三阶魔方阵的生成过程可知,某一位置(x,y)的左上角的位置是(x-1,y-1),如果x-1≥0,不用调整,否则将其调整为x-1+m;同理,如果y-1≥0,不用调整,否则将其调整为y-1+m。
所以,位置(x,y)的左上角的位置可以用求模的方法获得,即:
x=(x-1+m)%m
y=(y-1+m)%m
如果所求的位置已经有数据了,将该数据填入同一列下一行的位置。
这里需要注意的是。
此时的x和y已经变成之前的上一行上一列了,如果想变回之前位置的下一行同一列,x需要跨越两行,y需要跨越一列,即:
x=(x+2)%m
y=(y+1)%m
4.运行、测试与分析
(1)程序开始运行并输入。
(2)输出结果。
(3)容错检验。
(4)测试其他数据。
5.实验收获及思考
遇到的问题:
输出结果不正确。
解决办法:
因为程序较短,通过肉眼观察程序,发现是数组下标表示错误,一时大意把n维数组的下标范围误认为从1到n,经过修改后,输出结果正常。
实验的收获:
这次试验体会到了解决问题时算法的重要性,一个良好的解法可以使程序大大简化。
附录:
#include<stdio.h>
#include<iostream>
#include<stdlib.h>
using namespace std;
int main()
{
int m;//m是魔方阵的行数
int n=1;//用来递增给每个位置赋值
int x,y;//i是行数,j是列数 cout<<"输入魔方阵的行数:";
while(1)
{
cout<<"输入魔方阵的行数。
";
cin>>m;
if(!(m>=1&&m%2==1)) //检验行数是否是奇数{cout<<"输入有误!请输入正奇数。
"; exit(-2);} int shuzu[m][m]; //建立魔方阵,并且全部元素为0 for(int i=0;i<m;i++)
{
for(int j=0;j<m;j++)
{
shuzu[i][j]=0;
}
}
x=0;
y=(m-1)/2;
shuzu[x][y]=n++;
while(1)
{
x=(x-1+m)%m; //左上移动
y=(y-1+m)%m;
if(!(shuzu[x][y]==0))
{
x=(x+2)%m;
y=(y+1)%m;
}
shuzu[x][y]=n++;
if(n==m*m+1) break;
}
for(int i=0;i<m;i++)
{
for(int j=0;j<m;j++)
{
cout<<shuzu[i][j]<<" ";
}
cout<<endl;
}
}
return 0;
}。
