人教版九年级上册数学期中考试试卷及答案
人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案

6.在二次函数yx22x3中,当 时,y的最大值和最小值分别是()
A.0,4B.0,3C.3,4D.0,0
7.若二次函数 的x与y的部分对应值如下表:
x
-2
-1
0
1
2
3
y
14
7
2
-1
-2
-1
则当 时,y的值为()
A.-1B.2C.7D.14
8.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是()
【分析】由给出的x和y的值可得,抛物线的对称轴为x=2,由抛物线的对称性可知,x=5时y的值与x=﹣1时y的值相等,由此即可求解.
【详解】解:由表格可知,当x=1时,y=﹣1,当x=3时,y=﹣1,
∴由抛物线的对称性可知,抛物线的对称轴为直线x=2,
∴x=5时y的值与x=﹣1时y的值相等,
由表格可知,当x=﹣1时,y=7,
23.如图,AB是⊙O的弦,过点O作OC⊥OA,OC交AB于P,CP=BC,点Q是 上的一点.
(1)求证:BC是⊙O的切线;
(2)已知∠BAO=25°,求∠AQB的度数;
(3)在(2)的条件下,若OA=18,求 的长.
五、解答题(三)(每小题10分,共20分)
24.如图,已知在矩形ABCD中,AD=10cm,AB=4cm,动点P从点A出发,以2cm/s的速度沿AD向终点D移动,设移动时间为 (s).连接PC,以PC为一边作正方形PCEF,连接DE、DF.
人教版2022--2023学年度第一学期期中测试卷
九年级 数学
(满分:120分 时间:100分钟)
人教版九年级上册数学期中考试试卷含答案

人教版九年级上册数学期中考试试题一、单选题1.下列图形中,既是轴对称图形又是中心对称图形的是( )A .三角形B .等边三角形C .平行四边形D .菱形 2.如果(x ﹣y ﹣2)(x ﹣y +1)=0,那么x ﹣y =( )A .2B .﹣1C .2或﹣1D .﹣2或13.如图所示,将△AOB 绕点O 按逆时针方向旋转45°后得到△A'OB',若△AOB =15°,那么△AOB'的度数是( )A .15°B .30°C .45°D .60°4.把方程x 2+x =3(x ﹣2)化成ax 2+bx+c =0的形式,则a ,b ,c 的值分别为( ) A .1,﹣2,2 B .1,﹣3,6 C .1,﹣2,6 D .1,4,6 5.如图,在平面直角坐标系中,点A 坐标为(3,1),则sinα的值为( )A .13BCD 6.函数y =﹣(x ﹣2)2+1的图象可以由函数y =﹣x 2的图象通过( )得到 A .向左平移1个单位,再向上平移2个单位B .向左平移1个单位,再向下平移2个单位 C .向右平移2个单位,再向上平移1个单位D .向右平移2个单位,再向下平移1个单位 7.如图,△ABC△△ADE ,且BC =2DE ,则S 四边形BEDC :S △ABC 的值为( )A .1:4B .3:4C .2:3D .1:28.已知点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3)都在二次函数y =﹣x 2+2x ﹣1的图象上,且x 1<x 2<1<x 3,则下列结论可能成立的是( )A .y 1<y 2<y 3<0B .0<y 1<y 2<y 3C .y 1<y 2<0<y 3D .y 3<y 2<y 1<0二、填空题9.在平面直角坐标系中,点P (﹣2,﹣5)关于原点对称的点的坐标是 ___________________. 10.某商场八月份销售额为100万元,十月份的销售额为121万元,求这个商场九、十月销售额的平均增长率,若设平均增长率为x ,则可列方程为 ___.11.如图AB△CD△EF ,若1=2AC CE ,5DF =,则=BF ______.12.若一元二次方程x 2﹣4x ﹣2=0的两个实数根为m ,n ,则m n mm+的值为 ___. 13.若二次函数y =x 2+3x+c 的图象经过点A (0,c ),过点A 作x 轴的平行线,与抛物线交于点B ,则线段AB 的长为 ___.14.二次函数y =ax 2+bx+c (a≠0)的图象经过(﹣1,0),(0,4),(t ,4)三点,当t≥3时,一元二次方程ax 2+bx+c =n 一定有实数根,则n 的取值范围是 ___.15.如图,△ABC 绕点B 顺时针旋转得到△DBE ,点A 与点D 对应,点C 与点E 对应,DB ,DE 分别与AC 边交于G ,F 两点,连接BF ,若DE 垂直平分BC ,下列结论:△△E =30°;△BF△BE ;△△ABG△△DBF ;△GF•BD =DG•BF .其中结论正确的是 ___.(填序号即可)16.如图,ABC ∆中,65CAB ∠=︒,在同一平面内,将ABC ∆绕点A 旋转到AED ∆的位置,使得DC AB ∥,则BAE ∠等于______.三、解答题17.解方程:(1)x 2+2x ﹣7=0.(2)2x 2﹣3x+1=0.18.如图,已知△ABC 三个顶点的坐标分别是A (2,4),B (1,2),C (4,1).按下列要求画出图形,并回答问题.(1)画出△ABC 绕点O 逆时针旋转90°后得到的△A 1B 1C 1,并写出点A 1坐标.(2)以O 为位似中心,相似比为2,在y 轴左侧将△ABC 放大,得到△A 2B 2C 2,在网格中画出△A 2B 2C 2.19.已知关于x 的方程x 2+kx+k -2=0,证明不论k 为什么实数,这个方程总有两个不相等实数根.20.如图,在△ABC 中,△C =90°,△A =45°,tan△DBC =34,AB =AD 的长.21.已知二次函数y=x2﹣4x+3.(1)在平面直角坐标系xOy中,描出二次函数图像的顶点A,与x轴的交点B、C,并画出此二次函数的图像(不必列表);(2)根据图像,直接写出当x<4时y的取值范围.22.如图,将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,点B与点E对应,点E恰好落在AD边上,BH△CE交于点H,求证:AB=BH.23.如图,在Rt△ACB中,△ACB=90°,点D为AB边上一点,且BC=CD,过D作DE△AB 交AC于E.(1)求证:△CDE△△CAD;(2)若BC=2,CE=1,求AD的长.24.某水果捞店销售一款成本为12元/份的水果捞,若以30元/份的价格出售,每周可售出150份,“十一”黄金周降价促销,若销售单价每降低1元,则每周可多售出15份(销售单价不低于25元/份),设该款水果捞的销售单价为x元/份,“十一”黄金周的销售利润为y元.(1)当销售单价为多少元/份时,“十一”黄金周的销售利润为2880元.(2)当销售单价为多少元/份时,“十一”黄金周的销售利润最大,最大利润为多少元?25.如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点B(0,2),与x轴交于D,C(2,0)两点,点P为抛物线上一动点.(1)求抛物线的解析式.(2)如图1,点P在直线BC下方抛物线上运动,PM△BC交于M,PN△y轴交BC于N,当△PMN的周长最大时,求点P坐标.(3)平面内一点Q(1,1),连接PB,PC,PQ,若PQ恰好平分△BPC,请直接写出点P 的横坐标.26.如图,在平行四边形ABCD中,AD=AC,△ADC=α,点E为射线BA上一动点,且AE<AB,连接DE,将线段DE所在直线绕点D顺时针旋转α交BA延长线于点H,DE所在直线与射线CA交于点G.(1)如图1,当α=60°时,求证:△ADH△△CDG;(2)当α≠60°时,△如图2,连接HG,求证:△ADC△△HDG;△若AB=9,BC=12,AE=3,请直接写出EG的长.参考答案1.D【分析】一个图形沿着某条直线对折,直线两旁的部分能够完全重合的图形称为轴对称图形,这条直线称为对称轴;如果一个图形绕某一点旋转180゜后能够与原来图形重合,则称这个图形为中心对称图形,这个点称为对称中心;根据轴对称图形和中心对称图形的概念完成即可.【详解】A、三角形既不是轴对称图形也不是中心对称图形,故不符合题意;B、等边三角形是轴对称图形,但不是中心对称图形,故不符合题意;C、平行四边形是中心对答图形,但不是轴对称图形,故不符合题意;D、菱形既是轴对称图形,对称轴是两条对角线所在的直线,也是中心对称图形,对称中心是两对角线的交点,故符合题意;故选:D.本题考查了轴对称图形和中心对称图形的概念,关键是理解概念,并知道一些常见图形中哪些是轴对称图形,哪些是中心对称图形.2.C【解析】【分析】由()()210,x y x y ---+=可得:20x y --=或10,x y -+= 从而可得答案.【详解】解:()()210,x y x y ---+=20x y ∴--=或10,x y -+=2x y ∴-=或 1.x y -=-故选:.C【点睛】本题考查的是一元二次方程的解法,掌握因式分解的方法解一元二次方程是解题的关键. 3.B【解析】【分析】根据旋转的性质旋转前后图形全等以及对应边的夹角等于旋转角,进而得出答案即可.【详解】解:△将△AOB 绕点O 按逆时针方向旋转45°后得到△A′OB′,△△A′OA =45°,△AOB =△A′OB′=15°,△△AOB′=△A′OA−△A′OB′=45°−15°=30°,故选:B .【点睛】此题主要考查了旋转的性质,根据旋转的性质得出△A′OA =45°,△AOB =△A′OB′=15°是解题关键.4.C【解析】【分析】将方程x 2+x =3(x ﹣2)化成ax 2+bx+c =0的形式,即可求解.解:把方程x 2+x =3(x ﹣2)化成ax 2+bx+c =0的形式为:2260x x -+= ,△1,2,6a b c ==-= .故选:C【点睛】本题主要考查了一元二次方程的一般式,熟练掌握一元二次方程的一般式是解题的关键. 5.B【解析】【分析】根据正弦函数是对边比斜边,可得答案.【详解】如图:作AB△x 轴于点B ,△点A 坐标为(3,1),△OB=3,AB=1,在RtABO 中,根据勾股定理=△sinα=AB OA = 故选B .【点睛】此题考查锐角三角函数,解题关键在于掌握在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.6.C【解析】【分析】根据函数的平移规律:左加右减,上加下减确定即可得解.函数2(2)1y x =--+的图像可以由函数2y x =-的图像通过右平移2个单位,再向上平移1个单位得到.故选C .【点睛】此题考查的是二次函数的平移,掌握二次函数平移的性质是解题的关键.7.B【解析】【分析】根据相似三角形的性质解答即可.【详解】解:△△ABC△△ADE ,且BC =2DE , △214ADE ABC ED S S BC ⎛⎫== ⎪⎝⎭, △S 四边形BEDC :S △ABC =41344-=, 故选:B .【点睛】此题考查相似三角形的性质,关键是根据相似三角形的面积之比等于相似比的平方解答. 8.A【解析】【分析】判断出二次函数的对称轴为x=1,再根据二次函数的增减性解答.【详解】解:△二次函数y=-x 2+2x -1的对称轴为x=-2b a=1,顶点坐标为(1,0),且在x 轴上,开口向下,△x <1时,y 随x 的增大而增大,△x 1<x 2<1<x 3,△y 1<y 2<0,y 3<0.△下列结论可能成立的是A ,【点睛】本题考查了二次函数图象上点坐标特征,主要利用了二次函数的对称性和增减性,比较简单.9.(2,5)【解析】【分析】根据关于原点对称的两个点,横坐标、纵坐标分别互为相反数即可求解.【详解】解:点P(﹣2,﹣5)关于原点对称的点的坐标是(2,5)故答案为:(2,5)【点睛】本题考查了关于原点对称的两个点的坐标特征,掌握“关于原点对称的点的横坐标、纵坐标分别互为相反数”是解题的关键.10.100(1+x)2=121【解析】【分析】可设平均增长率为x,,则九月份的营业额是100(1+x),十月份的营业额是100(1+x)(1+x),则可以得到方程即可.【详解】解:设平均增长率为x.根据题意得:100(1+x)2=121,故答案为:100(1+x)2=121.【点睛】本题考查数量平均变化率问题.原来的数量为a,平均每次增长或降低的百分率为x的话,经过第一次调整,就调整到a×(1±x),再经过第二次调整就是a(1±x)(1±x)=a(1±x)2.增长用“+”,下降用“−”.11.15 2【解析】【分析】利用平行线分线段成比例定理得到AC CE =BD DF,求出BD 即可. 【详解】解:△AB△CD△EF , △AC CE =BD DF =12 , △DF =5,△BD =52, △BD =DF+BD =5+52=152, 故答案为:152. 【点睛】 本题考查平行线分线段成比例定理,解题的关键是理解三条平行线截两条直线,所得的对应线段成比例.12.-2【解析】【分析】先根据根与系数的关系得到m+n=4,mn=-2,然后利用整体代入的方法计算.【详解】解:根据题意得m+n=4,mn=-2,所以原式=42-=-2. 故答案为:-2.【点睛】本题考查了根与系数的关系:若x 1,x 2是一元二次方程ax 2+bx+c=0(a≠0)的两根时,12b x x a +=-,12c x x a=. 13.3【解析】【分析】运用配方法求出抛物线的对称轴,再根据抛物线的对称性得出点B 的坐标,由此即可求出AB 的长.【详解】解:△22393()24y x x c x c =++=++- △抛物线的对称轴是直线32x =- △过点A 作x 轴的平行线,与抛物线交于点B ,△点A ,B 关于直线32x =-对称,且A (0,c ) △B(-3,c)△0(3)3AB =--=故答案为:3.【点睛】本题主要考查了二次函数的图象与性质,正确求出抛物线对称轴方程是解答本题的关键. 14.254n ≤ 【解析】【分析】根据二次函数y =ax 2+bx+c (a≠0)的图象经过(﹣1,0),(0,4),通过列三元一次方程组并求解,即可得到4b a =+及c 的值;分0a >和0a <两种情况分析;当0a >时,结合二次函数图像的性质,得0t <,不符合题意;当0a <时,结合二次函数平移和一元二次方程的性质,通过求解二元一次方程组和一元一次方程,即可得到答案.【详解】△y =ax 2+bx+c (a≠0)的图象经过(﹣1,0),(0,4)△04a b c c -+=⎧⎨=⎩, △4b a =+根据题意,分0a >和0a <两种情况分析;当0a >时△y =ax 2+bx+c (a≠0)的图象经过(﹣1,0),(0,4)△y =ax 2+bx+c (a≠0)的对称轴02b x a=-< △y =ax 2+bx+c (a≠0)的图象经过(0,4),(t ,4) △0022t b a+=-< △0t <,即和t≥3相矛盾△0a >不符合题意;当0a <时,y =ax 2+bx+c (a≠0)的图象如下图:当0n >时,y =ax 2+bx+c (a≠0)的图象向下平移△随n 增大,y =ax 2+bx+c -n 与x 轴右侧交点向左移动根据题意,y =ax 2+bx+c -n 与x 轴右侧交点的最小值,为3t =时,即()3,0 △322b a=-,即3b a =- △34b a b a =-⎧⎨=+⎩△13a b =-⎧⎨=⎩ △3t =时,y =ax 2+bx+c 最大值为254 △2504n -= △254n =当0n <时,y =ax 2+bx+c (a≠0)的图象向上平移;△随n 减小,y =ax 2+bx+c -n 与x 轴右侧交点向右移动,即当t≥3时,一元二次方程ax 2+bx+c =n 一定有实数根 △254n ≤ 故答案为:254n ≤. 【点睛】 本题考查了二次函数、一元二次方程、三元一次方程组、二元一次方程组的知识;解题的关键是熟练掌握二次函数、一元二次方程的性质,从而完成求解.15.△△△##△△△##△△△##△△△##△△△##△△△【解析】【分析】根据旋转的性质以及等边三角形的判定,得到△BCE是等边三角形,可判断△;由△FBC =30°,推出△FBE=90°,可判断△;由三角形外角的性质推出△DBF=60°-△D<60°,可判断△;证明△AFB△△DFG,利用相似三角形的性质可判断△.【详解】解:连接CE,如图:△△DBE是△ABC绕点B顺时针旋转得到的,△AB=DB,BC=BE,△A=△D,△BEF=△BCF,△DE垂直平分BC,△BF=FC,EB=EC,△EB=BC=EC,即△BCE是等边三角形,且DE平分△BEC,△△BEF=30°,故△正确;△BF=FC,△BEF=△BCF=30°,△CBE=60°,△△FBC=△BCF=30°,△△FBE=△FBC+△CBE=30°+60°=90°,△BF△BE,故△正确;△△FBC=△BCF=30°,DE垂直平分BC,△△CFE=△DFG=△BFE=△AFB=60°,△△A=△D,△△A+△ABG =△D+△DFG,△△ABG=△DFG=60°,而△DBF=△BFE-△D=60°-△D<60°,△△ABG与△DBF不相似,故△不正确;△△AFB=△DFG=60°,又△A=△D,△△AFB△△DFG,△AB BF DG FG=,又AB=DB,△BD BF DG GF=,△GF•BD=DG•BF,故△正确.综上,△△△正确.故答案为:△△△.16.50︒【分析】根据平行线的性质得到△ACD=△CAB=65°,根据旋转变换的性质计算即可.【详解】△DC△AB,△△ACD=△CAB=65°,由旋转的性质可知,AD=AC,△DAE=△CAB=65°,△△ADC=△CAB=65°,△△CAD=50°,△△CAE=15°,△△BAE=50°,故答案为50°.17.(1)x1=-x2=-1-(2)x1=1,x2=1 2【解析】(1)利用配方法求解即可;(2)利用因式分解法求解即可.【详解】解:(1)△x2+2x=7,△x2+2x+1=7+1,即(x+1)2=8,x+1=-解得x1=-,x2=-1-(2)△2x2-3x+1=0,△(x-1)(2x-1)=0,则x-1=0或2x-1=0,解得x1=1,x2=12.18.(1)见解析;A1坐标为(-4,2);(2)见解析【解析】(1)利用旋转变换的性质分别作出A,B的对应点A1,B1即可;(2)直接利用位似图形的性质得出对应点位置进而得出答案.【详解】解:(1)如图所示:A1坐标为(-4,2);(2)如图所示.19.见解析【解析】根据方程的系数结合根的判别式可得出()24120k k ∆=-⨯⨯-> ,由此即可得出该方程总有两个不相等的实数根.【详解】解:在方程x 2+kx+k -2=0中,△()()222412=48240k k k k k ∆=-⨯⨯--+=-+>,△方程x 2+kx+k -2=0不论k 为什么实数,总有两个不相等的实数根.【点睛】本题考查了根的判别式,解决该题型题目时,根据根的判别式的符号确定方程根的情况是关键.20.1【解析】【分析】 先根据等腰直角三角形的性质求出AC 、BC ,再根据tan△DBC =34求出CD ,故可得到AD 的长.【详解】△在△ABC 中,△C =90°,△A =45°,△△ABC 是等腰直角三角形△AB=△BC=AC= 4= △tan△DBC =CD BC =34 △CD=3△AD=AC -CD=1.【点睛】此题主要考查解直角三角形,解题的关键是熟知等腰直角三角形的性质.21.(1)见解析;(2)1y ≥-【解析】【分析】(1)根据配方法将函数解析式化为顶点式,即可得到该函数的顶点坐标;根据函数解析式,可以写出该函数的顶点坐标和图像上的几个点的坐标,从而可以画出相应的函数图像; (2)根据题意可得当4x = 时,3y = ,观察图像,即可写出y 的取值范围.【详解】解:(1)()224321y x x x =-+=--△二次函数图像的顶点()2,1A - ,令0y = ,即2430x x -+=,解得:121,3x x == ,△二次函数图像与x 轴的交点B 、C 为()()1,0,3,0B C ,画出此二次函数的图像如下图所示:(2)当4x = 时,3y = ,观察图像,得:当x <4时,1y ≥- .【点睛】本题考查二次函数的性质、二次函数的图像、二次函数图像上点的坐标特征,利用数形结合的思想解答是解答本题的关键.22.见解析【解析】【分析】根据旋转的性质得到CB=CE ,求得△EBC=△BEC ,根据平行线的性质得到△EBC=△BEA ,再利用AAS 得到△EAB△△EHB ,即可得到AB=BH .【详解】证明:连接BE,△矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,△CB=CE,△△EBC=△BEC,又△AD△BC,△△EBC=△BEA,△△BEA=△BEC,在△EAB和△EHB中,90BAE BHEBEA BECBE BE∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,△△EAB△△EHB(AAS),△AB=BH.【点睛】本题考查了旋转的性质,全等三角形的判定和性质,矩形的性质,正确的作出辅助线是解题的关键.23.(1)见解析(2【解析】【分析】(1)证明△A=△CDE,即可得到△CDE△△CAD;(2)根据相似三角形的性质得到tanA=12,故可求出AC、AE,再在Rt△ADE中求出AD 的长.【详解】(1)△BC=CD,△△B=△BDC△△ACB=90°,DE△AB△△A+△B=△BDC+△CDE=90°△△A+△B=△BDC+△CDE△△A=△CDE又△DCE=△ACD△△CDE△△CAD(2)△△CDE△△CAD△DE CD CE AD CA CD==△tanA=212 DEAD CA==△AC=4,AD=2DE△AE=4-1=3在Rt△ADE中AE2=AD2+DE2△32=(2DE)2+DE2【点睛】此题主要考查相似三角形的判定与性质、解直角三角形,解题的关键是熟知相似三角形的判定定理.24.(1)销售单价为28元/份时,“十一”黄金周的销售利润为2880元.(2)当销售单价为26元/份时,“十一”黄金周的销售利润最大,最大利润为2940元【解析】【分析】(1)根据“总利润=每件商品的利润×销售量”结合黄金周的销售利润为2880元列出方程求解即可;(2)根据“总利润=每件商品的利润×销售量”列出二次函数关系式,经过配方求解即可.【详解】解:(1)设销售单价为x元,根据题意得,(12)[150(30)15]2880x x-+-⨯=整理得,2526720x x -+=解得,128x =,22425x =<(不符合题意,舍去)△销售单价为28元/份时,“十一”黄金周的销售利润为2880元. (2)根据题意得,(12)[150(30)15]y x x =-+-⨯=(12)(60015)x x -- =2157807200x x -+- =215(26)2940x --+ △150a =-< △抛物线开口向下,△25x ≥,对称轴为直线26x = △当26x =时,y 的最大值为2940所以,当销售单价为26元/份时,“十一”黄金周的销售利润最大,最大利润为2940元25.(1)232y x x =-+.(2)(1,0)P ;(3)点P 的横坐标为2【分析】(1)把点B (0,2),C (2,0)代入抛物线解析式,求出b ,c 的值即可;(2)证明PMN ∆是等腰直角三角形,求得PMN 的周长=(1PN +,再求出PN 的最大值即可;(3)求出直线PQ 的解析式为y=x ,联立方程组得232y x y x x =⎧⎨=-+⎩求解即可. 【详解】解:(1)△抛物线y =x 2+bx+c 的图象经过点B (0,2),C (2,0)△=2420c b c ⎧⎨++=⎩解得,32b c =-⎧⎨=⎩ △抛物线的解析式为232y x x =-+. (2)△B (0,2),C (2,0)△BOC ∆是等腰直角三角形 △45OBC ∠=︒ 又PN△y 轴△45PNM OBC ∠=∠=︒ 又PM△BC△PMN ∆是等腰直角三角形△PM MN ==△PMN 的周长=(1MN PM PN PN PN ++=+=△PMN 的周长最大时,PN 最大, 设直线BC 的解析式为y=kx+b 把B (0,2),C (2,0)代入得220b k b =⎧⎨+=⎩解得,12k b =-⎧⎨=⎩△直线BC 的解析式为y=-x+2 设2(,32)P x x x -+ △PN△y 轴△(,2)N x x -+,且点P 在直线BC 的下方△222(2)(32)2(1)1PN x x x x x x =-+--+=-+=--+ △当1x =时,PN 有最大值为1△PMN的周长最大值为1(1⨯=1△(1,0)P(3)△直线BC 的解析式为y=-x+2 当x=1时,y=-1+2=1 △Q (1,1)在直线BC 上, 又B (0,2),C (2,0) △Q (1,1)为线段BC 的中点△PQ 平分△BPC , △BPQ CPQ ∠=∠△PQ 所在直线是线段BC 的垂直平分线, △△OBC 是等腰直角三角形 △直线PQ 的解析式为y=x联立方程组得232y xy x x =⎧⎨=-+⎩解得,1122x y ⎧=+⎪⎨=+⎪⎩2222x y ⎧=⎪⎨=⎪⎩故此时点P的横坐标为226.(1)证明见详解;(2)△证明见详解;△EG或2. 【分析】(1)AD =AC ,△ADC =60°,可证△ACD 为等边三角形,根据四边形ABCD 为平行四边形,可得AB=CD=BC=AD ,△B=△ADC=60°,AD△BC ,可得△HAD=△B=60°=△GCD ,由△GDH=△CDA=60°,可证△HAD =△CDG ,即可证△ADH△△CDG (ASA );(2)△根据AD =AC ,△ADC =α,可得△ACD=△ADC =α,根据四边形ABCD 为平行四边形,可得AD△BC ,可得△HAD=△ADC=α=△GCD ,由△GDH=α=△ADC ,可得△ADH =△CDG 即可;△根据点E 的位置分两种情况,当点E 在AB 上时,过C 作CN△AB 于N ,过G 作GM△AE 于M ,根据四边形ABCD 为平行四边形,AB△DC ,AB=DC=9,AD=BC=12,可证△AGE△△CGD ,得出AG=3,CG=AC -AG=12-3=9,根据等腰三角形三线合一性质可得AN=BN=1922AB =,根据勾股定理=,由GM△CN ,再证△AMG△△ANC ,可求1948AM AN ==,14GM CN ==EM=AE -AM=915388-=,根据勾股定理=,当点E 在BA 延长线上,过C 作CN△AB 于N ,过G 作GM△AE 于M ,由AE△CD ,△GAE△△GCD ,可求GA=6,由GM△CN ,可证△GMA△△CNA ,可得1122GM CN ===,11992224AM AN ==⨯=,EM=AE -AM=3-9344=,根据勾股定理2. 【详解】(1)证明:△AD =AC ,△ADC =60°, △△ACD 为等边三角形, △四边形ABCD 为平行四边形,△AB=CD=BC=AD ,△B=△ADC=60°,AD△BC , △△HAD=△B=60°=△GCD , △△GDH=△CDA=60°,△△HDA+△ADG=△CDG+△ADG=60°, △△HDA =△CDG , 在△ADH 和△CDG 中 ADH CDG AD CDHAD GCD ∠=∠⎧⎪=⎨⎪∠=∠⎩△ADH△△CDG (ASA );(2)△证明:△AD =AC ,△ADC =α, △△ACD=△ADC =α,△四边形ABCD 为平行四边形, △AD△BC ,△△HAD=△ADC=α=△GCD , △△GDH=α=△ADC ,△△ADH+△ADG=△CDG+△ADG=α, △△ADH =△CDG ,△△ADH△△CDG;△解:当点E在AB上时,过C作CN△AB于N,过G作GM△AE于M,△四边形ABCD为平行四边形,AB△DC,AB=DC=9,AD=BC=12,△△EAG=△DCG,△AEG=△CDG,△△AGE△△CGD,△3193 AG AECG CD===,△3CG AG=,△AD=AC=12,△AG+CG=AG+3AG=4AG=12,△AG=3,△CG=AC-AG=12-3=9,△AC=AD=BC,CN△AB,△AN=BN=19 22 AB=,在Rt△BCN中,根据勾股定理,△GM△CN,△△AMG△△ANC,△31124 AM AG GMAN AC CN====,△1948AM AN==,14GM CN==△EM=AE-AM=915388-=,在Rt△MGE 中,根据勾股定理,当点E 在BA 延长线上,过C 作CN△AB 于N ,过G 作GM△AE 于M , △AE△CD ,△△GAE=△GCD ,△GEA=△GDC , △△GAE△△GCD , △3193GA EA GC DC ===, △3GC GA =,△AC=GC -GA=3GA -GA=2GA=12, △GA=6,△AC=AD=BC ,CN△AB , △AN=BN=1922AB =,在Rt△BCN 中,根据勾股定理,△CN△AB , GM△AE , △GM△CN , △△GMA△△CNA , △61122GA GM AM CA CN AN ====,△1122GM CN ==,11992224AM AN ==⨯=, △EM=AE -AM=3-9344=,在Rt△GME 中,根据勾股定理=,△综合EG.2【点睛】本题考查图形旋转性质,平行四边形性质,等边三角形判定与性质,三角形全等判定,三角形相似判定与性质,勾股定理,本题难度角度,利用辅助线画出准确图形,掌握以上知识是解题关键.。
人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案

(3)设⊙C的圆心C在x轴上,半径为2,若直线yx上存在点D,使得半径为1的⊙D上存在点P是⊙C的等直顶点,求圆心C的横坐标的取值范围;
(4)直线y4x4分别和两坐标轴交于E,F两点,若线段EF上的所有点均为⊙O的等直顶点,求⊙O的半径的最大值与最小值.
(1)在如图所示的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?
23.(5分)第二十四届冬季奥林匹克运动会于2022年2月4日至2月20日在北京举行,赛后,越来越多的青少年走向冰场、走进雪场、了解冰雪运动知识.某校开展了一次冬奥知识答题竞赛,七、八年级各有200名学生参加了本次活动,为了解两个年级的答题情况,从两个年级各随机抽取了20名学生的成绩进行调查分析,过程如下(数据不完整).
【解析】
【分析】圆周角定理:在同圆或等圆中,一条弧所对的圆周角是它所对的圆心角的一半,根据圆周角定理即可得出答案.
【详解】解:∵∠ACB=43°,
∴∠AOB=2∠ACB=86°,
故选:C.
【点睛】本题考查的是圆周角定理,掌握圆周角定理求解圆心角或圆周角是解题的关键.
3. C
【解析】
【详解】已知⊙O的半径为5,圆心O到直线l的距离为6,因6>5,即d<r,所以直线l与⊙O的位置关系是相离.
【详解】解:A. 化为一般形式为 , ,该方程有两个不相等的实数根,不符合题意;
B. 化为一般形式为 , ,该方程没有实数根,符合题意;
C. , ,该方程有两个不相等的实数根,不符合题意;
D. ,化为一般形式为 , ,该方程有两个不相等的实数根,不符合题意.
人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案

∴不等式mx+n>ax2+bx+c的解集是:x<-1或x>4.
故答案为:x<-1或x>4.
【点睛】本题主要考查二次函数、一次函数与不等式的关系,数形结合思想的运用是解题关键.
16.24或25##25或24
【解析】
A.2B.3C.-2D.-1
7.a是方程 的一个根,则代数式 的值是()
A. B. C. D.
8.已知抛物线 的对称轴是直线 ,则实数 的值是()
A.2B. C.4D.
9.把二次函数 的图象先向右平移3个单位,再向上平移1个单位后得到一个新图象,则新图象所表示的二次函数的解析式是()
A. B.
C D.
(1)设花圃的一边AD长为x米,请你用含x的代数式表示另一边CD的长为米;
(2)当矩形场地面积为160平方米时,求AD的长.
22.某商品交易会上,某商场销售一批纪念品,进价时每件为38元,按照每件78元销售,平均每天可售出20件,为了扩大销售,增加盈利,商场决定采取适当的降价措施,经调查发现,若每个纪念品降价2元,则平均每天多销售4件.
∴方程ax2+bx+c﹣m=0没有实数根时,
∴抛物线 -m顶点在x轴下方
,
故④正确,
⑤∵对称轴x=﹣1=﹣ ,
∴b=2a,
∵a+b+c<0,
∴3a+c<0,
故⑤正确,
所以正确的选项有②③④⑤,
故选:C.
【点睛】本题考查二次函数图象与系数的关系,一元二次方程根的判别式、抛物线与x轴的交点等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案(含两套题)
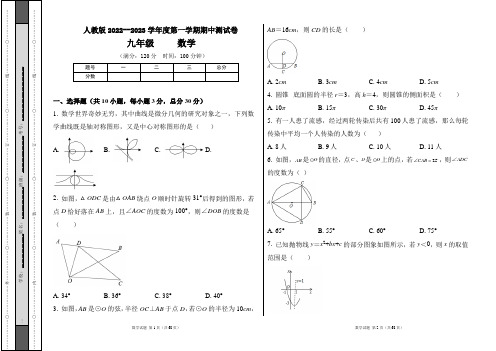
(1)如图1,点E在BC边上.
①依题意补全图1;
②若AB=6,EC=2,求BF的长;
(2)如图2,点E在BC边的延长线上,用等式表示线段BD,BE,BF之间的数量关系.
∴∠ODA=90°,AD=BD=8cm,
在Rt△ODA中,由勾股定理得
OD= cm,
∵OC=10cm,
∴CD=OC-OD=4cm,故选C.
【点睛】本题考查了垂径定理,勾股定理.能根据垂径定理求出AD的长是解题的关键.
4. B
【解析】
【分析】先求圆锥的母线,再根据公式求侧面积.
【详解】由勾股定理得:母线 ,
(1)如图1,MA=6,MB=8,∠NOB=60°,求NB的长;
(2)如图2,过点M作MC⊥AB于点C,P是MN的中点,连接MB,NA,PC,试探究∠MCP,∠NAB,∠MBA之间的数量关系,并证明.
24.(12分)已知:如图1,在平面直角坐标系中,⊙P的圆心 ,半径为5,⊙P与抛物线 的交点A、B、C刚好落在坐标轴上.
三、解答题(共9小题,总分72分)
17.(6分)已知△ABC的顶点A、B、C在格点上,按下列要求在网格中画图.
(1)△ABC绕点C顺时针旋转90°得到△A1B1C;
(2)画△A1B1C关于点O的中心对称图形△A2B2C2.
18.(6分)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
人教版2022--2023学年度第一学期期中测试卷
九年级 数学
(满分:120分 时间:100分钟)
题号
一
二
人教版九年级上册数学期中考试试卷含答案
人教版九年级上册数学期中考试试题一、单选题1.下列图形中,既是轴对称又是中心对称图形的是( )A .B .C .D . 2.下列方程中是一元二次方程的是( )A .21xy +=B .21902x x+-= C .20ax bx c ++= D .20x =3.如图,已知AB∥CD∥EF 且AC∥CE =3∥4,BF =14,则DF 的长为( )A .8B .7C .6D .34.已知二次函数2287y x x =++的图象上有点()12,A y -,()25,B y -,()31,C y -,则1y 、2y 、3y 的大小关系为( )A .123y y y >>B .213y y y >>C .231y y y >>D .311y y y >>5.如图,∥ABC 与∥BEF 位似,点O 是它们的位似中心,其中OE=2OB ,则∥ABC 与∥DEF 的周长之比是( )A .1:2B .1:4C .1:3D .1:96.现要在一个长为40m ,宽为26m 的矩形花园中修建等宽的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为2950m ,那么小道的宽度应是( )A .1mB .1.5mC .2mD .2.5m7.如图,在平面直角坐标系中,线段OA 与x 轴正方向夹角为45︒,且2OA =,若将线段OA 绕点O 沿逆时针方向旋转105︒到线段OA ',则此时点A '的坐标为( )A .1)-B .(-C .(D .(1,8.如图,Rt ABC △中,90C ∠=︒,30A ∠=︒,20AB =,点P 是AC 边上的一个动点,将线段BP 绕点B 顺时针旋转60︒得到线段BQ ,连接CQ ,则在点P 运动过程中,线段CQ 的最小值为( )A .5B .10C .20D .259.已知12x x 、是方程2320x x -+=的两根,则12x x += ,12x x = . A .-3,2 B .-3,-2 C .3 , 2 D .2,310.某数学复习课上,数学老师用几何画板上画出二次函数y =ax 2+bx+c (a≠0)图象如图所示,四名同学根据图象,说出下列结论:李佳:abc <0:王宁:2a ﹣b <0:孙浩:b 2>4ac一帆:点(﹣3,y 1),(1,y 2)都在抛物线上,则有y 1>y 2,你认为其中正确的结论有( )A .4个B .3个C .2个D .1个二、填空题 11.若y =(m ﹣4)x |m |﹣2﹣2x ﹣1是关于x 的二次函数,则m =___.12.已知0是关于x 的一元二次方程22(1)10m x x m -++-=的一个根,则m 的值是______. 13.把抛物线23y x =先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式为_________14.如图,小明为了测量高楼MN 的高度,在离点18N 米的点A 处放了一个平面镜,小明沿NA 方向后退1.5米到点C ,此时从镜子中恰好看到楼顶的点M ,已知小明的眼睛(点B )到地面的高度BC 是1.6米,则高楼MN 的高度是______.15.如图,在ABC 中,108BAC ∠=︒,将ABC 绕点A 按逆时针方向旋转得到AB C ''△.若点B '恰好落在BC 边上,且AB CB ''=,则C '∠的度数为______.16.如图,点A 在数轴的负半轴,点B 在数轴的正半轴,且点A 对应的数是21x -,点B 对应的数是2x x +,已知5AB =,则x 的值为______.17.将二次函数y =x 2﹣5x ﹣6在x 轴上方的图象沿x 轴翻折到x 轴下方,图象的其余部分不变,得到一个新图象,若直线y =2x+b 与这个新图象有3个公共点,则b 的值为_____.三、解答题18.解方程:(1)2531x x x -=+(2)3(21)42x x x +=+19.如图,在平面直角坐标系中,已知ABC 三个顶点的坐标分别为()()()1,2,3,4,2,6A B C ---.(1)画出ABC 绕点A 顺时针旋转90︒后得到的111A B C △,写出点1C 的坐标.(2)以原点O 为位似中心,在网格内画出将111A B C △三条边放大为原来的2倍后得222A B C △,写出点2B 的坐标.20.已知关于x 的方程2(1)2(1)0x m x m -++-=()求证:无论m 取何值时,方程总有实数根;(2)若等腰三角形一边长为4,另两边恰好是此方程的根,求此三角形的另两边长.21.如图,在ABC 中,PC 平分ACB ∠,PB PC =.(1)求证:APC ACB;(2)若2AP=,5PC=,求AC的长.22.如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约53米,铅球落地点在B处,铅球运行中在运动员前4米处(即4OC=)达到最高点,最高点高为3米,已知铅球经过的路线是抛物线.根据图示的直角坐标系回答下列问题.(1)求铅球所经过路线的函数表达式.(2)铅球的落地点离运动员有多远?23.如图,在Rt∥ABC中,∥ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA 边上以5cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4cm/s的速度向点B匀速运动,运动时间为t s(0<t<2),连接PQ.(1)若∥BPQ和∥ABC相似,求t的值;(2)连接AQ,CP,若AQ∥CP,求t的值.24.如图,抛物线2:3L y ax bx=++与x轴交于A、(3,0)B两点(A在B的左侧),与x轴交于A、B两点,且点B坐标为(3,0)与y轴交于点C,已知对称轴1x=.(1)求抛物线L的解析式;(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在OBC内(包括OBC的边界),求h的取值范围:△能否成为以点P为直角(3)设点P是抛物线L上任一点,点Q在直线:3l x=-上,PBQ顶点的等腰直角三角形?若能,求出符合条件的点P的坐标:若不能,请说明理由.25.商场销售某种电子产品,每个进货价为40元,调查发现,当销售价格为60元时,平均每天能销售100个;当销售价每降价1元时,平均每天多售出10个,该商场要想使得这种电子产品的销售利润平均每天达到2240元.(1)每个电子产品的价格应该降价多少元?(2)在平均每天利润不变的情况下,为尽可能赢得市场,需要让利于顾客,该商场应该将该电子产品按照几折优惠销售?(3)当定价为多少时,商场每天销售该电子产品的利润最大?最大利润是多少?∠=,点P是平面内不与点A、C重合的任意一点,连26.在ABC中,CA CB=,ACBα接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD、BD、CP.(1)如图(1),当60α=︒时,BD CP的值是______,直线BD 与直线CP 相交所成的较小角的度数是______. (2)如图(2),当90α=︒时,请求出BD CP的值及直线BD 与直线CP 相交所成的较小角的度数. (3)如图(3),当90α=︒时,若点E 、F 分别是CA 、CB 的中点,点P 在直线EF 上,请直接写出当点C 、P 、D 在同一直线上时AD CP的值.参考答案1.D【解析】【分析】根据轴对称图形与中心对称图形的概念求解.【详解】A 、是轴对称图形,不是中心对称图形,故此选项不符合题意;B 、不是轴对称图形,不是中心对称图形,故此选项不符合题意;C 、是轴对称图形,不是中心对称图形,故此选项不符合题意;D 、是轴对称图形,是中心对称图形,故此选项符合题意;故选:D.【点睛】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.2.D【解析】【分析】根据一元二次方程的定义:含有一个未知数,且未知数的最高次数为2的整式方程是一元二次方程,据此逐项分析即可解题.【详解】解:A、21xy+=含有2个未知数,不是一元二次方程,故A不符合题意;B、2190 2xx+-=含有分式,不是一元二次方程,故B不符合题意;C、20ax bc c++=,当0a=不是一元二次方程,故C不符合题意;D、20x=,是一元二次方程,故D符合题意;故选D.【点睛】本题考查一元二次方程的概念,是基础考点,难度较易,掌握相关知识是解题关键.3.A【解析】【分析】根据平行线分线段成比例定理即可得到结论.【详解】解:由题意:∥AB∥CD∥EF,∥AC∥CE=BD∥DF=3∥4,所以设BD=3x,DF=4x,所以3x+4x=14,即x=2,∥DF=4x=8故答案选:A【点睛】本题考查平行线分线段成比例定理,关键是找出对应的比例线段,写出比例式,用到的知识点是平行线分线段成比例定理.4.C【解析】【分析】先求出二次函数y=2x2+8x+7的图象的对称轴,然后判断出A(-2,y1),B(-5,y2),C(-1,y3)在抛物线上的位置,再求解.【详解】解:∥二次函数y=2x2+8x+7中a=2>0,∥开口向上,对称轴为x=-2,∥A(-2,y1)中x=-2,y1最小,B(-5,y2),点B关于对称轴的对称点B′横坐标是2×(-2)-(-5)=1,则有B′(1,y2),因为在对称轴得右侧,y随x得增大而增大,故y2>y3.∥y2>y3>y1.故选:C.【点睛】此题考查二次函数图象上点的坐标特征,关键是掌握二次函数图象的性质.5.A【解析】【分析】利用位似的性质得∥ABC∥∥DEF,OB:OE= 1:2,然后根据相似三角形的性质解决问题.【详解】解:∥∥ABC与∥DEF位似,点O为位似中心.∥∥ABC∥∥DEF,OB:OE= 1:2,∥∥ABC与∥DEF的周长比是:1:2.故选:A.【点睛】本题主要考查了位似变换,正确掌握位似图形的性质是解题关键.6.A【解析】【分析】设小道的宽度应为x m,则剩余部分可合成长为(40-2x)m,宽为(26-x)m的矩形,根据矩形的面积计算公式,结合种植花草的面积为950m2,即可得出关于x 的一元二次方程,解之取其符合题意的值即可得出结论.【详解】解:设小道的宽度应为x m ,则剩余部分可合成长为(402)m x -,宽为(26)m x -的矩形, 依题意得:(402)(26)950x x --=,解得,11x =,245x =.4540>(不合题意,舍去),1x ∴=.答:小道进出口的宽度应为1米.故选:A .【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键. 7.C【解析】【分析】过点A '作A B x '⊥轴,由旋转可知10545150A Ox ∠=︒+︒='︒,进而可得30A OB '∠=︒,进而根据含30度角的直角三角形的性质求得A B ',勾股定理求得OB ,根据A '在第二象限,即可求得点A '的坐标.【详解】解:如图,过点A '作A B x '⊥轴,由旋转可知10545150A Ox ∠=︒+︒='︒,30A OB '∴∠=︒在Rt A OB '△中,11122A B A O AO ''∴===BO A '在第二象限,A '∴(故选C【点睛】本题考查了坐标与图形,旋转的性质,含30度角的直角三角形的性质,求得30A OB '∠=︒是解题的关键.8.A【解析】【分析】如图,取AB 的中点T ,连接PT ,过点T 作TH∥AC 于H .证明∥TBP∥∥CBQ (SAS ),推出CQ=PT ,根据垂线段最短可知,当点P 与H 重合时,PT 的值最小,最小值=TH=12AT=5.【详解】解:如图,取AB 的中点T ,连接PT ,过点T 作TH∥AC 于H .∥∥ACB=90°,∥A=30°,∥AB=2BC ,∥ABC=60°,∥AT=TB ,∥BC=BT ,∥BP=BQ ,∥CBT=∥PBQ ,∥∥CBT -∥PBC=∥PBQ -∥PBC ,即∥TBP=∥CBQ ,∥∥TBP∥∥CBQ (SAS ),∥CQ=PT ,根据垂线段最短可知,当点P 与H 重合时,PT 的值最小,最小值=TH=12AT=14AB=5,∥CQ 的最小值为5.故选A【点睛】本题考查旋转变换,垂线段最短,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.9.C【解析】【分析】根据一元二次方程根与系数的关系,x 1+x 2=−b a ,12cx x a =即可进行作答.【详解】由一元二次方程x 2-3x+2=0,知a=1,b=-3,c=2,又∥x1、x 2是一元二次方程x 2-3x+2=0的两根,∥x 1+x 2=−b a =3,12cx x a ==2.故选C.【点睛】本题考查一元二次方程的根与系数的关系,熟练掌握关系式是解题的关键.10.B【解析】【分析】根据二次函数的性质结合图象逐项分析可得解.【详解】解:对称轴在左侧,故ab 同号,c <0,故李佳:abc <0正确;函数对称轴:x =2ba -<﹣1,解得:2a <b ,故王宁:2a ﹣b <0正确;函数和x 轴有两个交点,b 2﹣4ac >0,故孙浩:b 2>4ac 正确;x =﹣3时,y 1<0,而x =1时,y 2>0,故一帆:点(﹣3,y 1),(1,y 2)都在抛物线上,则有y 1>y 2错误;故选B .【点睛】主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a 与b 的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.11.﹣4【解析】【分析】直接利用二次函数的定义进而分析得出答案.【详解】解:∥y =(m ﹣4)x |m |﹣2﹣2x ﹣1是关于x 的二次函数,∥|m|﹣2=2,m ﹣4≠0,解得:m =﹣4 .故答案为:﹣4.【点睛】本题考查了二次函数的定义.二次函数的定义:一般地,形如y =ax 2+bx+c (a 、b 、c 是常数,a≠0)的函数叫做二次函数.其中x 、y 是变量,a 、b 、c 是常量,a 是二次项系数,b 是一次项系数,c 是常数项.y =ax 2+bx+c (a 、b 、c 是常数,a≠0)也叫做二次函数的一般形式.12.-1【解析】【分析】把x=0代入已知方程,列出关于m 的新方程,通过解新方程可以求得m 的值.【详解】解:∥x=0是关于x 的一元二次方程22(1)10m x x m -++-=的一个根,∥m 2-1=0且m -1≠0,即m 2=1且m≠1,解得 m=-1.即m 的值是-1.故答案为:-1.【点睛】本题考查了一元二次方程的解的定义.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.13.23(3)2y x =-+【解析】【分析】按照“左加右减,上加下减”的规律得出即可.【详解】解:23y x =先向上平移2个单位,得到232y x =+,再向右平移3个单位23(3)2y x =-+. 得到抛物线的解析式为23(3)2y x =-+.故答案为:23(3)2y x =-+.【点睛】本题考查了抛物线的平移以及抛物线解析式的变化规律,解题的关键是掌握左加右减,上加下减.14.19.2米【解析】【分析】根据相似三角形的判定定理证明BCA ∥MNA △,再利用相似三角形的性质求解即可.【详解】解:由题意得:BC∥CA ,MN∥AN ,∥∥C =∥MNA =90°,由光的反射原理可得:∥BAC =∥MAN ,∥BCA ∥MNA △, ∥BC AC MN AN =,即118.6 1.5MN =, ∥MN =19.2米.故答案为:19.2米.【点睛】本题考查了相似三角形的判定定理与性质,熟练掌握相似三角形的判定定理及性质是解题的关键.15.24︒【解析】【分析】根据旋转可得AB AB '=,由已知条件AB CB ''=,根据等边对等角可得B AC C '∠=∠,AB B B '∠=∠,根据三角形的外角性质可得2AB B C '∠=∠,根据三角形内角和可得1802BAB B '∠=︒-∠,根据108BAC ∠=︒即可求得C '∠的度数【详解】AB CB ''=B AC C '∴∠=∠2AB B C '∴∠=∠将ABC 绕点A 按逆时针方向旋转得到AB C ''△.AB AB '∴=,C C '∠=∠AB B B '∴∠=∠1802BAB B '∴∠=︒-∠1804C =︒-∠108BAC ∠=︒1802BAC CAB B AB C B ''∴∠=∠+∠=∠+︒-∠18041803C C C =∠+︒-∠=︒-∠24C ∴∠=︒24C '∴∠=︒故答案为:24︒【点睛】本题考查了旋转的性质,三角形内角和定理,三角形的外角性质,掌握旋转的性质是解题的关键.16.-2【解析】【分析】根据数轴上点的位置可得2210x x x -<<+,即可得到()2215AB x x x =+--=,由此解方程,再根据210x -<即12x <进行求解即可. 【详解】解:由数轴上点的位置可得2210x x x -<<+,∥()2215AB x x x =+--=即260x x --=,∥()()230+-=x x ,解得3x =或2x =-,∥210x -<即12x <, ∥2x =-,故答案为:-2.【点睛】本题主要考查了数轴上两点的距离,解一元二次方程,解题的关键在于能够熟练掌握数轴上两点的距离以及解一元二次方程的方法.17.﹣12或﹣734. 【解析】【分析】如图所示,过点B 作直线y=2x+b ,将直线向下平移到恰在点C 处相切,则一次函数y=2x+b 在这两个位置时,两个图像有3个交点,即可求解.【详解】解:如图所示:过点B 的直线y =2x+b 与新抛物线有三个公共点,将直线向下平移到恰在点C 处相切,此时与新抛物线也有三个公共点,令y =x 2﹣5x ﹣6=0,解得:x =﹣1或6,即点B 坐标(6,0),将一次函数与二次函数表达式联立得:x 2﹣5x ﹣6=2x+b ,整理得:x 2﹣7x ﹣6﹣b =0, ∥=49﹣4(﹣6﹣b )=0,解得:b =﹣734, 当一次函数过点B 时,将点B 坐标代入:y =2x+b 得:0=12+b ,解得:b =﹣12, 综上,直线y =2x+b 与这个新图象有3个公共点,则b 的值为﹣12或﹣734; 故答案是:﹣12或﹣734. 【点睛】本题考查的是二次函数与坐标轴的交点,涉及到一次函数、根的判别式、翻折的性质等知识点,画出图像确定临界点在图像上的位置是解答本题的关键.18.(1)115x =-,21x =;(2)123x =,212x =- 【解析】【分析】(1)先移项,然后利用因式分解的方法解一元二次方程即可;(2)先去括号,然后移项合并,最后利用因式分解的方法解一元二次方程即可.【详解】解:(1)∥2531x x x -=+,∥25410x x --=,∥()()5110x x +-=, 解得115x =-,21x =; (2)∥3(21)42x x x +=+,∥26342x x x +=+,∥2620x x --=,∥()()21320x x +-=, 解得123x =,212x =-. 【点睛】本题主要考查了解一元二次方程,解题的关键在于能够熟练掌握解一元二次方程的方法. 19.(1)图见解析,1(3,3)C ;(2)图见解析,1(3,3)C【解析】【分析】(1)画出旋转后的对应顶点,再顺次连接即可;根据点的位置,写出坐标即可;(2)根据位似性质,画出放大后的对应顶点,再顺次连接即可;根据点的位置,写出坐标即可;【详解】解:(1)如图,111A B C △为所求作的三角形,1(3,3)C .(2)如图所示,则222A B C △为所求作的三角形,()22,8B .【点睛】本题考查了平面直角坐标系坐标系中画图,涉及到旋转与位似,解题关键是明确旋转和位似的性质,准确进行画图.20.(1)见详解;(2)4和2【解析】【分析】(1)根据方程的系数结合根的判别式,即可得出Δ=(m -3)2∥0,由此即可证出:无论m 取何值,这个方程总有实数根;(2)分腰长为4和底边长度为4两种情况分别求解可得.【详解】解:(1)证明:∥∥=[-(m+1)]2-4×2(m -1)=m 2-6m+9=(m -3)2≥0,∥无论m 取何值,这个方程总有实数根;(2)若腰长为4,将x=4代入原方程,得:16-4(m+1)+2(m -1)=0,解得:m=5,∥原方程为x 2-6x+8=0,解得:x 1=2,x 2=4.组成三角形的三边长度为2、4、4;若底边长为4,则此方程有两个相等实数根,∥∥=0,即m=3,此时方程为x 2-4x+4=0,解得:x 1=x 2=2,由于2+2=4,不能构成三角形,舍去;所以三角形另外两边长度为4和2.【点睛】本题考查了根的判别式、三角形三边关系、等腰三角形的性质以及解一元二次方程,解题的关键是:(1)牢记“当Δ∥0时,方程有实数根”;(2) 分腰长为4和底边长度为4两种情况分别求解.21.(1)见解析;(2)AC 【解析】【分析】(1)利用角平分线及等腰三角形性质,可得出ACP ABC ∠=∠,同时两个三角形有一个公共角,即可得出两个三角形相似;(2)利用(1)中相似三角形的对应边成比例,将已知边代入即可求出答案.【详解】(1)∥PC 平分ACB ∠,PB PC =,∥ACP BCP ∠=∠,BCP ABC ∠=∠,∥ACP ABC ∠=∠.又∥CAP BAC ∠=∠,∥APC ACB ;(2)由(1)可知:APC ACB ,且5PB PC ==,2AP =, ∥257AB AP BP =+=+=,∥AC AP AB AC=, ∥27214AC AB AP =⋅=⨯=,∥AC =【点睛】本题主要考察相似三角形的判定和性质,理解掌握判定定理及性质是解答本题关键. 22.(1)()214312y x =--+;(2)铅球的落地点离运动员有10米远 【解析】(1)根据题意得A 点坐标为(0,53),D 点坐标为(4,3),且D 为抛物线的顶点,故可将抛物线解析式设为顶点式,然后代入A 点坐标求解即可;(2)令0y =,求出x 的值,再根据B 点在x 轴正半轴求出B 点坐标,则OB 的长即为所求.【详解】解:(1)由题意得:A 点坐标为(0,53),D 点坐标为(4,3),且D 为抛物线的顶点, ∥设抛物线的解析式为()243y a x =-+, ∥()250433a =-+, ∥112a =-, ∥抛物线解析式为()214312y x =--+; (2)令0y =,则()2104312x =--+, ∥()2436x -=, 解得10x =或2x =-(因为B 点在x 轴正半轴),∥B 点坐标为(10,0),∥OB=10∥铅球的落地点离运动员有10米远,答:铅球的落地点离运动员有10米远.【点睛】本题主要考查了求二次函数解析式,二次函数与x 轴的交点问题,解题的关键在于能够熟练掌握二次函数的相关知识.23.(1)t的值为1s或3241s;(2)t的值为78s.【解析】(1)根据勾股定理即可得到结论;分两种情况:∥当∥BPQ∥∥BAC时,∥当∥BPQ∥∥BCA 时,根据相似三角形的性质,把BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可;(2)过P作PM∥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,MC=8-4t,根据∥ACQ∥∥CMP,得出AC:CM=CQ:MP,代入计算即可.【详解】解:(1)∥∥ACB=90°,AC=6cm,BC=8cm,(cm),分两种情况讨论:∥当∥BPQ∥∥BAC时,BP BQ BA BC=,∥BP=5t,QC=4t,AB=10,BC=8,∥584 108t t-=,解得,t=1,∥当∥BPQ∥∥BCA时,BP BQ BC BA=,∥584 810t t-=,解得,t=32 41,∥t=1s或3241s时,∥BPQ∥∥BCA;(2)过P作PM∥BC于点M,AQ,CP交于点N,如图所示,则PB=5t,MC=8-4t,∥PM∥BC,∥ACB=90°,∥PM∥AC,∥∥BPM∥∥BAC,∥BP PM BM BA AC BC==,即51068t PM BM ==, ∥PM=3t ,BM=4t ,MC=8-4t ,∥∥NAC+∥NCA=90°,∥PCM+∥NCA=90°,∥∥NAC=∥PCM ,∥∥ACQ=∥PMC ,∥∥ACQ∥∥CMP , ∥AC CQ CM MP =, ∥64843t t t=-, 解得t=78. 【点睛】本题考查了相似三角形的判定与性质,勾股定理,直角三角形的性质,由三角形相似得出对应边成比例是解题的关键.24.(1)2y x 2x 3=-++;(2)24h ≤≤;(3)能,点P 的坐标为:()()1,4,0,3,,⎝⎭⎝⎭【解析】 (1)根据对称性求得A 的坐标,进而待定系数法求二次函数解析式即可;(2)先求得BC 的解析式,再求得抛物线的顶点坐标,根据平移的特点求得h 的范围; (3)根据题意,点P 是抛物线L 上任一点,点Q 在直线:3l x =-上,设2(,23)P m m m -++,(3,)Q n -,分P 点在x 轴的上方和下方两种情况讨论,证明MPQ ≌NBP △,根据6,MN PM PN PM BN =+==分别列出方程,解方程即可求解.【详解】解:(1)抛物线的对称轴为1x =,点B 坐标为(3,0)与y 轴交于点C ,∴(1,0)A -∥抛物线2:3L y ax bx =++过点(1,0),(3,0)A B -∥309330a b a b -+=⎧⎨++=⎩解得12a b =-⎧⎨=⎩ ∴抛物线L 的解析式为:2y x 2x 3=-++(2)抛物线L :2y x 2x 3=-++与y 轴交于点C()0,3C ∴()3,0B设直线BC 的解析式为y kx b =+将()3,0B ,()0,3C 代入303k b b +=⎧⎨=⎩解得13k b =-⎧⎨=⎩∴直线BC 的解析式为3y x =-+()222314y x x x =-++=--+∴顶点坐标为()1,4∴在直线BC 上,1x =时,2y = 平移后所得抛物线的顶点落在OBC 内(包括OBC 的边界),∴当2h =时,抛物线的顶点在直线BC 上,当4h =时,抛物线的顶点在x 轴上,即OB 上∴24h ≤≤(3)能,点P 的坐标为:()()1,4,0,3,,⎝⎭⎝⎭, 根据题意,点P 是抛物线L 上任一点,点Q 在直线:3l x =-上,设2(,23)P m m m -++,(3,)Q n -, ∥当P 点在x 的上方时,过点P 作PM l ⊥于M ,过点B 作BN x ⊥轴交MP 的延长线于点N ,如图,∥PBQ △是以点P 为直角顶点的等腰直角三角形∥90,BPQ BP PQ ∠=︒=∥,PM MQ PN BN ⊥⊥∥90PMQ BNP ∠=∠=︒MPQ BPN NBP BPN ∴∠+∠=∠+∠MPQ NBP ∴∠=∠在MPQ 和NBP △中PMQ BNP MPQ NBP BP PQ ∠=∠⎧⎪∠=∠⎨⎪=⎩∴MPQ ≌NBP △PM BN ∴=223PM BN m m ∴==-++()3,0B ,3PN m ∴=-,6MN PM PN =+=即22336m m m -+++-=解得121,0m m ==(1,4)P ∴或(0,3)∥当P 点在x 轴下方时,过点P 作PM l ⊥于M ,过点B 作BN x ⊥轴交MP 的延长线于点N ,如图,同理可得MPQ ≌NBP △PM BN ∴=()633PM m m ∴=--=+,223BN m m =--则2323m m m +=--解得12m m ==P ∴,⎝⎭⎝⎭综上所述P 的坐标为:()()1,4,0,3,,⎝⎭⎝⎭【点睛】本题考查了二次函数综合,待定系数法求二次函数解析式,二次函数的的平移,等腰直角三角形的性质,全等三角形的性质与判定,坐标与图形,解一元二次方程,第(3)问中,分类讨论,作出辅助线是解题的关键.25.(1)每个电子产品的价格应该降价4元或6元;(2)该商场应该将该电子产品按照九折优惠销售;(3)当x =55时,w 有最大值,最大值为2250元.【解析】【分析】(1)设每个电子产品的价格应该降价x 元,根据每个电子产品的利润乘以销售量,得一元二次方程,求解即可;(2)由(1)所求得的降价额,结合问题的实际意义,可得应降价多少,从而可得打几折优惠;(3)设定价为y 元,商场每天销售该电子产品的利润为w 元,根据题意列出函数关系式,写成顶点式,即可得问题的答案.【详解】解:(1)设每个电子产品的价格应该降价x 元,由题意得:(60﹣x ﹣40)(100+10x )=2240∥(x ﹣4)(x ﹣6)=0∥x 1=4,x 2=6∥每个电子产品的价格应该降价4元或6元.(2)在平均每天利润不变的情况下,为尽可能赢得市场,需要让利于顾客,该商场应该将该电子产品可以降价6元销售:(60﹣6)÷60=0.9∥该商场应该将该电子产品按照九折优惠销售..(3)设定价为y 元,商场每天销售该电子产品的利润为w 元,由题意得:w =(y ﹣40)[100+(60﹣y )×10]=(y ﹣40)(﹣10y+700)=﹣10y 2+1100y ﹣28000=﹣10(y ﹣55)2+2250∥二次项系数为﹣10<0∥当x =55时,w 有最大值,最大值为2250元.【点睛】本题考查了二次函数及一元二次方程在实际问题中的应用,明确成本利润问题的基本关系式及二次函数的性质,是解题的关键.26.(1)1,60︒;(2,45︒;(3)22+【解析】【分析】(1)如图1中,延长CP 交BD 的延长线于E ,设AB 交EC 于点O .证明()CAP BAD SAS ∆≅∆,即可解决问题.(2)如图2中,设BD 交AC 于点O ,BD 交PC 于点E .证明DABPAC ∆∆,即可解决问题.(3)分两种情形:∥如图3﹣1中,当点D 在线段PC 上时,延长AD 交BC 的延长线于H .证明AD DC =即可解决问题;∥如图3﹣2中,当点P 在线段CD 上时,同法可证:DA DC =解决问题.【详解】解:(1)如图1中,延长CP 交BD 的延长线于E ,设AB 交EC 于点O .CA CB =,60ACB ∠=︒ABC ∴是等边三角形60CAB ∴∠=︒由旋转可得PA=PD ,∥APD=60°∥三角形PAD 是等边三角形60PAD CAB ∠=∠=︒,CAP BAD ∴∠=∠,CA BA =,PA DA =,()CAP BAD SAS ∴∆≅∆,PC BD ∴=,ACP ABD ∠=∠,AOC BOE ∠=∠,60BEO CAO ∴∠=∠=︒,1BDPC ∴=,线BD 与直线CP 相交所成的较小角的度数是60︒,故答案为1,60︒.(2)如图2中,,90CA CB ACB =∠=︒,将线段AP 绕点P 逆时针旋转90︒得到线段DP ,45,90,CAB CBA APD PA PD ∴∠=∠=︒∠=︒=,45PAD CAB ︒∴∠=∠=,,PAD CAB ∴△△是等腰直角三角形,,DA BA ∴==PAD DAC DAC CAB ∴∠+∠=∠+∠PAC DAB ∴∠=∠,AB AD AC AP ==DAB PAC ∴∆∆,PCA DBA ∴∠=∠,BDABPC AC ==,GHC AHB ∠=∠,45CGH HAB ︒∴∠=∠=,∴直线BD 与直线CP 相交所成的小角的度数为45︒.(3)如图3﹣1中,当点D 在线段PC 上时,延长AD 交BC 的延长线于H .CE EA =,CF FB =,EF AB ∴∥,45EFC ABC ︒∴∠=∠=,45PAO ︒∠=,PAO OFH ∴∠=∠,POA FOH ∠=∠,H APO ∴∠=∠,90APC ︒∠=,EA EC =,PE EA EC ∴==,EPA EAP BAH ∴∠=∠=∠,H BAH ∴∠=∠,BH BA ∴=,45ADP BDC ︒∠=∠=,90ADB ︒∴∠=,BD AH ∴⊥,AD DH =∴90ACH ∠=︒12DC AH AD ∴== DA DC ∴=,设=AD a ,则DC AD a ==,2PD =,2AD CP ∴==如图3﹣2中,当点P 在线段CD 上时,同法可证:=DA DC ,设=AD a ,则CD AD a ==,2PD =,PC a ∴=,2AD PC ∴== 综上所述,AD PC的值为22 【点睛】本题属于相似形综合题,考查了旋转变换,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.。
人教版九年级上册期中数学试卷(含答案)

人教版九年级上册期中数学试卷练习题一、选择题。
一、方程3x2﹣1=0的一次项系数是()A、﹣1B、0C、3D、1二、方程x(x﹣1)=0的根是()A、x=0B、x=1C、x1=0,x2=1D、x1=0,x2=﹣13、抛物线y=2(x+1)2﹣3的对称轴是()A、直线x=1B、直线x=3C、直线x=﹣1D、直线x=﹣34、下列所述图形中,是中心对称图形的是()A、直角三角形B、平行四边形C、正五边形D、正三角形五、用配方式解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为()A、(x+3)2=1B、(x﹣3)2=1C、(x+3)2=19D、(x﹣3)2=19六、如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使点A′恰好落在AB上,则旋转角度为()A、30°B、45°C、60°D、90°7、若关于x的方程x2+x﹣a+ =0有两个不相等的实数根,则实数a的取值范围是()A、a>2B、a≥2C、a≤2D、a<2八、三角形两边的长是3和4,第三边的长是方程x2﹣12x+35=0的根,则该三角形的周长为()A、14B、12C、12或14D、以上都不对九、设二次函数y=(x﹣3)2﹣4图象的对称轴为直线l,若点M在直线l上,则点M的坐标可能是()A、(1,0)B、(3,0)C、(﹣3,0)D、(0,﹣4)10、二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是()A、函数有最小值B、对称轴是直线x=C、当x<,y随x的增大而减小D、当﹣1<x<2时,y>0二、填空题:1一、把方程2x2﹣1=5x化为一般形式是________.1二、点P(﹣1,2)关于原点对称的点P′的坐标是________.13、若x=﹣1是一元二次方程x2+2x+a=0的一个根,那么a=________.14、请写出一个开口向上,且其图象通过原点的抛物线的解析式________.1五、已知点A(,y1),B(﹣2,y2)都在二次函数y=(x﹣2)2﹣1的图象上,则y1与y2的大小关系是________.1六、如图,△ABC绕点A顺时针旋转45°取得△AB′C′,若∠BAC=90°,AB=AC= ,则图中阴影部份的面积等于________.三、解答题17、解方程:x2﹣3x+2=0.18、已知二次函数y=﹣x2﹣2x,用配方式把该函数化为y=a(x﹣h)2+c的形式,并指出函数图象的对称轴和极点坐标.1九、已知x=1是关于x的一元二次方程x2+3x﹣m=0的一个根,求m的值和方程的另一个根.20、如图,在平面直角坐标系中,已知△ABC的三个极点的坐标别离为(﹣1,1),B(﹣3,1),C(﹣1,4).(1)将△ABC绕点A顺时针旋转90°后取得△AB′C′,请在图中画出△AB′C′.(2)写出点B′、C′的坐标.2一、如图,已知抛物线y=x2+x﹣6与x轴两个交点别离是A、B(点A在点B的左侧).(1)求A、B的坐标;(2)利用函数图象,写出y<0时,x的取值范围.2二、向阳村2021年的人均收入为10000元,2021年人均收入为12100元,若2021年到2021年人均收入的年平均增加率相同.(1)求人均收入的年平均增加率;(2)2021年的人均收入是多少元?23、如图所示,一个农户要建一个矩形猪舍,猪舍的一边利用长为12m的房墙,另外三边用25m长的建筑材料围成,为了方便进出,在垂直于房墙的一边留一个1m宽的门.(1)所围成矩形猪舍的长、宽别离是多少时,猪舍面积为80m2(2)为做好猪舍的卫生防疫,现需要对围成的矩形进行硬底化,若以房墙的长为矩形猪舍一边的长,且已知硬底化的造价为60元/平方米,请你帮忙农户计算矩形猪舍硬底化需要的费用.24、一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F别离在BC、AB、AC上.(1)若设AE=x,则AF=________;(用含x的代数式表示)(2)要使剪出的矩形CDEF的面积最大,点E应选在何处?2五、如图,已知抛物线y=x2+bx+c与x轴交于点A、B,AB=2,与y轴交于点C,对称轴为直线x=2,对称轴交x轴于点M.(1)求抛物线的函数解析式;(2)设P为对称轴上一动点,求△APC周长的最小值;(3)设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为极点的四边形是菱形,则点D的坐标为________.答案解析部份一、<b >选择题。
人教版】九年级上期中数学试卷及答案

人教版】九年级上期中数学试卷及答案九年级(上)期中数学试卷一、选择题:每小题4分,共40分1.下列方程中,是关于x的一元二次方程的是()A。
ax^2+bx+c=0改写:哪一个方程是关于x的一元二次方程?答案:A。
ax^2+bx+c=02.用配方法解方程x^2+8x+9=0,变形后的结果正确的是()A。
(x+4)^2=-7 B。
(x+4)^2=-9 C。
(x+4)^2=7 D。
(x+4)^2=25改写:用配方法解方程x^2+8x+9=0,哪一个变形后的结果是正确的?答案:B。
(x+4)^2=-93.若关于x的一元二次方程x^2-2x+m=0有两个不相等的实数根,则m的取值范围是()A。
m1 D。
m>-1改写:若关于x的一元二次方程x^2-2x+m=0有两个不相等的实数根,那么m的取值范围是什么?答案:B。
m<-14.一元二次方程x^2-x-2=0的解是()A。
x1=1,x2=2 B。
x1=1,x2=-2 C。
x1=-1,x2=-2 D。
x1=-1,x2=2改写:解一元二次方程x^2-x-2=0的答案是什么?答案:A。
x1=1,x2=25.下列标志中,可以看作是轴对称图形的是()A。
B。
C。
3(x+1)^2=2(x+1) D。
2x^2+3x=2x^2-2改写:哪一个标志可以看作是轴对称图形?答案:B.6.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A 顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是()A。
32° B。
64° C。
77° D。
87°改写:如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.如果∠CC′B′=32°,那么∠B的大小是多少?答案:D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版九年级上册数学期中考试试卷及答案考试试卷
第一部分选择题
1. 下面哪组数互质的有:
A. 4, 6
B. 8, 12
C. 9, 15
D. 10, 25
2. 若 a 是一个整数,且a^2 − 7a + 10 = 0,则 a 的值为:
A. 2或5
B. 2或-5
C. 1或5
D. 1或-5
3. 如图,在菱形 ABCD 中,∠ACB = 90°,BD = 12cm,AB = 16cm,连接 BE 垂直于 AC 于点 E,则 BE =
A. 6cm
B. 8cm
C. 10cm
D. 12cm
4. 一个长度为 15cm 的正方形纸片如图,沿着虚线矩形剪去 ABCD
部分,并将纸片折起粘在 EFCD 上,得到三棱柱 ADEFBC。
已知 EF =
5cm,则三棱柱 ADEFBC 的体积为:
A. 75 cm³
B. 60 cm³
C. 55 cm³
D. 50 cm³
5. 下列各数以 14 为公差的等差数列:
A. 4,1,-2,-5,...
B. 10,17,24,31,...
C. 12,6,0,-6,...
D. -3,-7,-11,-15,...
第二部分解答题
1. 若 a:b = 3:2,b:c = 4:5,c:d = 6:7,则 a:b:c:d 等于多少?
2. 已知正方形的边长为 a,求正方形的对角线长。
3. 某体育场的篮球场长 28 米,宽 15 米,每个完整的篮球场地的斜线长度为多少?
4. 描述一个刀最多能切割出几块蛋糕,如图所示(图略),要求每块蛋糕的形状相同且面积相等。
5. 某种果酱的水分含量为 75%,如果有 3L 的果酱,经过蒸发后水分含量下降到 55%,请计算剩余果酱的体积。
参考答案
第一部分选择题
1. A
2. A
3. D
4. A
5. B
第二部分解答题
1. a:b = 3:2,b:c = 4:5,c:d = 6:7,所以 a:b:c:d = 3:2 * 4:5 * 6:7 = 12:10:24:30
2. 根据勾股定理,正方形的对角线长为a√2。
3. 斜线长度为篮球场的对角线长,根据勾股定理,斜线长度为
√(28² + 15²)。
4. 刀最多能切割出的蛋糕块数为刀的切割次数加 1,即为蛋糕的边的个数加 1。
5. 原始果酱中的水分含量为 75%,即 3L 中有 0.25 * 3 = 0.75L 的水分。
剩余果酱的体积为 3L - 0.75L = 2.25L。
希望以上答案能够满足你的需求。
