11--3.1用力矩分配法计算连续梁
第2讲用力矩分配法的计算连续梁和无节点线位移刚架-文档资料

100 0
-57.1 -42.9 -6.1 3.5 2.6
0
0
4 i 4 μ 0 . 571 BC 4 i 3 i 7
对C节点:
S i CB 4
分 配 传 递
0
SCD 3 i
M 0
140
-140 40.3 -40.3
0
3 i 4 i 4 μ 0 .429 μ 0 . 571 CD CB 4 i3 i 4 i 3 i 7
F
A
B 0 .625 0 .375
C 0.5 0.5
D 0 .706 0 .294
E
分 配 传 递
-1500 -469 60.78
1500 -938 -562
-194.5
121.56 72.94
-281 1059 -389 -389
-3000 2118 882
-3000 -882 -28.59
-194.5
练习:力矩分配法计算图示连续梁,作弯矩图。
1000 kN
A
EI
1
EI
2
EI
3
1m
B
10m
10m
10m
作业:P274 1, 2, 5
3. 依次放松各节点,使弯矩平衡(见上表)
4. 绘内力图
A
q 12 kN /m
B
C
D
M
F
0.429 0.571 0.571 0.429
0
0
150 -100
-28.6 -9.2 -12.2 1.8 -0.8 -1.0 140
100 0
-57.1 -42.9 -6.1 3.5 2.6
0
0 0
结构力学——力矩分配法分解

3 . 一般最终的杆端力矩与固端力矩是同量级的,要求精确 到三位有效数字,计算中取4位计算,以保证前三位的 精确度
第三节 多结点力矩分配法
计算的指导思想由两个步骤说明:
固定状态的计算(与单点固定一样)。
即刚臂→荷载→固端力矩→约束力矩;
100k0N
EI
1 EI
2 EI
0.43 0.57 0.57 0.43
-500 -1000
M3B=1000
例题:有支座移动(已知结点线位移)E=200GPa,I = 2500cm4
绘制弯矩图。
A
B
C
D
EI
EI
=1cm
10m
10m
10m
0.429 0.571
0.571 0.429
MF
3000
3000 -1500
2 . 不相邻 点可同时 释放.
例题:用力矩分配法求图示结构弯矩图(利用传递系数的概念) 。
A
EI
10m
1 EI
10m
100k0N 2 EI 3 B 3B是悬臂梁,
转动结点3 时,
10m 1m 悬臂可自由转
0.43 0.57 0.5 0.5 1 0
动,固其转动
MF
1000 刚度为零
或A
MF
100k0N
放松状态的计算(与单点放松不同)。
力矩的分配和传递是在远端约束已知的情况下进行的, 因此,分配单元的相邻结点不应同时放松。每次只能 放松一个结点,同时相邻结点保持固定,所以,整个 放松过程是轮流放松每一个结点来逐步完成的。
第三节 多结点力矩分配法
土木工程力学网上形考专业04全部选择题和判断计算

土木工程力学作业04任务一、单项选择题(共10 道试题,共30 分。
)1. 位移法典型方程实质上是(A )A。
平衡方程B。
位移条件C。
物理关系D。
位移互等定理2 用位移法计算超静定结构时,独立的结点角位移数等于( B )A。
铰结点数B。
刚结点数C。
多余约束数D。
不确定3。
用位移法解超静定结构其基本未知量的数目( A )A。
与结构的形式有关B。
与多余约束的数目有关C。
与结点数有关D. 与杆件数有关4。
用位移法计算超静定结构时,其基本未知量为(D )A. 多余未知力B。
杆端内力C。
杆端弯矩D。
结点位移5。
在位移法计算中规定正的杆端弯矩是(A )A。
绕杆端顺时针转动 B. 绕结点顺时针转动C。
绕杆端逆时针转动D。
使梁的下侧受拉6位移法典型方程中的系数代表在基本体系上产生的( C)A. B. C. 第i个附加约束中的约束反力 D. 第j个附加约束中的约束反力7 位移法基本方程中的自由项,代表荷载在基本体系作用下产生的( C )A. B. C. 第i个附加约束中的约束反力 D。
第j个附加约束中的约束反力8 图示超静定结构结点角位移的个数是( C )A。
2 B。
3 C。
4 D. 59. 图示超静定结构结点角位移的个数是( B )A。
2 B。
3 C. 4 D。
510. 图示超静定结构,结点线位移(独立)的个数是( B )A。
0 B. 1 C. 2 D。
311。
图示超静定结构独立结点角位移的个数是(B)A。
2 B。
3 C。
4 D。
512. 用位移法求解图示结构时,基本未知量的个数是( B)A。
8 B. 10 C。
11 D。
1213。
用位移法求解图示结构时,基本未知量个数是( B )A. 1 B。
2 C. 3 D。
414。
图示结构位移法方程中的系数=(D )A. 11B. 5C. 9 D。
815 图示结构位移法方程中的系数=( C )A. 3 B。
8 C。
15 D。
1316。
图示结构位移法方程中的自由项=( B )A。
结构力学习题集及答案

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.C.M =1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M kM p21y 1y 2**ωω( a )M 17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q11、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
ll l /32 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/l/2219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
ll22、图示结构充满水后,求A 、B 两点的相对水平位移。
结构力学计算题经典(有答案)
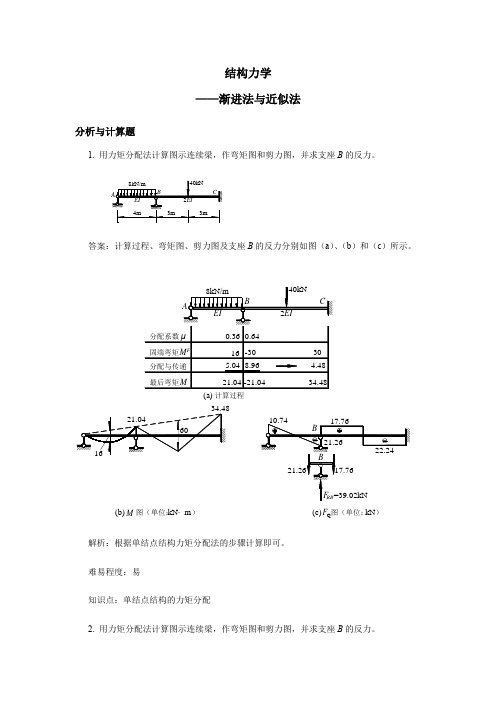
结构力学 ——渐进法与近似法分析与计算题1. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:计算过程、弯矩图、剪力图及支座B 的反力分别如图(a )、(b )和(c )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:易知识点:单结点结构的力矩分配2. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
A60kN 40kN·m EIEI B C4m4m6m(b)M 图(单位: )kN·m 图(单位: )(c)kNQ F (a)计算过程答案:图(a )为求解结点B 约束力矩的受力分析图。
计算过程、弯矩图、剪力图及支座B 的反力分别如图(b )、(c )和(d )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:中知识点:单结点结构的力矩分配3. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:CD 段为静定悬臂梁,将其截开并暴露出截面C 的弯矩,用力矩分配法计算如图(a )所示结构。
弯矩图和剪力图如图(b )、(c )所示。
BCEIN/m2EI m3m3m40kN(b)计算过程F BM (a)图(单位: )(c)M kN·m图(单位: )Q F (d)kN10kN20kN12kN/m ABCDEI 2EI 2m 4m4m解析:根据单结点结构力矩分配法的步骤计算即可。
本题中悬臂段CD 若不切除,则可按B 、C 两个刚结点的结构进行计算。
难易程度:中知识点:单结点结构的力矩分配4. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:AB 段为静定悬臂梁,将其截开并暴露出截面B 的弯矩,用力矩分配法计算过程如图(a )所示。
弯矩图和剪力图图(b )、(c )所示。
kNQ F (c)图(单位: )m M 图(单位: )(b)RB F =63.02kN ( )计算过程(a)mkN·10kN/m 60kN EI 2IB CD2m6m2m解析:根据单结点结构力矩分配法的步骤计算即可。
最新国家开放大学电大《土木工程力学(本科)》形考任务4试题及答案

最新国家开放大学电大《土木工程力学(本科)》形考任务4试题及答案最新国家开放大学电大《土木工程力学(本科)》形考任务4试题及答案形成性考核作业4 一、单项选择题(每小题3分,共30分)题目1 图示刚架在节点集中力偶作用下,弯矩图分布是()选择一项:A. 仅AB杆产生弯矩B. 仅AB、BE杆产生弯矩C. 各杆都产生弯矩D. 各杆都不产生弯矩题目2 位移法典型方程实质上是()选择一项:A. 位移互等定理B. 平衡方程C. 物理关系D. 位移条件题目3 用位移法求解图示结构时,基本未知量个数是()选择一项:A. 2B. 1C. 3D. 4 题目4 图示超静定结构,结点线位移(独立)的个数是()选择一项:A. 1B. 2C. 3D. 0 题目5 下图所示三根梁的EI、杆长相同,它们的固定端的弯矩之间的关系是()选择一项:A. (1)、(2)的固定端弯矩相同B. (2)、(3)的固定端弯矩相同C. 三者的固定端弯矩相同 D. 三者的固定端弯矩不同题目6 欲使图示节点A的转角=0,应在节点A施加的力偶M=()选择一项:题目7 用力矩分配法计算结构得到一个收敛的结果,是因为()。
选择一项:A. 传递系数小于1B. 分配系数小于1C. 分配系数小于1和传递系数小于1同时满足D. 结点上有外力矩作用题目8 下图所示连续梁,欲使A端发生单位转动,需在A端施加的力矩()选择一项:题目9 力矩分配法的直接对象是()选择一项:A. 结点位移B. 杆端弯矩C. 多余未知力D. 未知反力题目10 下图所示连续梁结点B的不平衡力矩为()选择一项:A. —10kN·mB. 18 kN·mC. 46 kN·mD. —28 kN·m 二、判断题(每小题3分,共30分)题目11 位移法的基本方程使用的是平衡条件,该方法只适用于解超静定结构。
选择一项:对错题目12 位移法的基本体系是一组单跨超静定梁。
力矩分配法计算单结点连续梁无侧移刚架介绍课件

结构优化设计:通 过调整结构参数,
优化结构性能
结构稳定性分析: 判断结构是否满足
稳定性要求
结构动力分析:分 析结构在动力荷载
作用下的响应
结构疲劳分析:评 估结构在循环荷载 作用下的疲劳寿命
单结点连续梁无侧移刚架 的计算
单结点连续梁无侧移刚架的结构特点
01
结构形式: 由梁、柱和 结点组成, 梁与柱通过 结点连接
原理:力矩分配法基于虚功原理, 将梁端力矩分配到梁的各个截面 上,从而得到梁的内力。
适用范围:力矩分配法适用于求 解连续梁无侧移刚架的内力,对 于其他类型的结构,需要采用其 他方法进行计算。
力矩分配法的应用
连续梁无侧移刚架 分析:计算支座反 力、内力、位移等
超静定结构分析: 求解超静定结构的
未知力、位移等
01 计算简便:力矩分配法计算过程简单,易于 理解和掌握。
02 精度高:力矩分配法计算结果精确,能够满 足工程实际需要。
03 适用范围广:力矩分配法适用于各种类型的 单结点连续梁无侧移刚架计算。
04 便于优化设计:力矩分配法可以方便地进行结 构优化设计,提高结构的承载能力和稳定性。
力矩分配法在单结点连续梁无侧移刚架计算中的具体步骤
02
受力特点: 梁承受弯矩 和剪力,柱 承受轴力
03
结点类型: 单结点,即 梁与柱在结 点处只有一 个连接点
04
刚架类型: 无侧移刚架, 即梁与柱在 结点处没有 相对位移
单结点连续梁无侧移刚架的计算方法
力矩分配法:将力矩分 配到各个结点,计算结
点的转角和位移
结点平衡方程:根据结 点的平衡条件,建立结
计算方法:力矩分配法
结构特点:单结点、无侧移、刚架 计算步骤:
力矩分配法(两个例题)

h
12
例 试用力矩分配法计算图a所示刚架,并绘M图。
表23-2 杆端弯矩的计算
用力矩分配法计算刚架时,可列成表格进行,(后面)最后弯矩图如图b所示。
h
13
结点 杆端
B
A
C
BA AB AD AC CA
分配系数
0.3 0.3 0.4
固端弯矩
0 60.0 -48.0 0
0
分配和传递
弯矩Biblioteka 0 -3.6 -3.6 -4.8 -2.4
分配系数
{载常数(表22-1)}固端弯矩
{求和}杆端弯矩
0
3i 4i
2i
0 3/7 4/7 1/2
0
90 -60
60
0
-30*3/7 -30*4/7
=-12.9 =-
-需8.要6 -30
17.1
0
77 . -
51.4
1 77 .
h
1
10
试用力矩分配法
计算图所示的连
续梁做出M图
{形常数(表22-2)}
•
h
20
感谢下 载
h
21
• ⑶ 进行第一轮次的分配与传递,从不平衡力矩较大 的结点开始,依次放松各结点,对相应的不平衡力 矩进行分配与传递。
MF
• ⑷ 循环步骤3,直到最后一个节点的传递弯矩小到 可以略去为止。(结束在分配上)
• ⑸ 求最后杆端弯矩,将各杆杆端的固端弯矩与历次 的分配弯矩和历次的传递弯矩代数即为最后弯距。
• ⑹ 作弯矩图(叠加法),必要时根据弯矩图再作剪 力图。
M
S Ak
将所求得的φA代入前式,得
h
所以
6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MB= MPBA+ MPBC= 6kN m
A
-15
15
-9
+
C
(2)放松结点B,即加-6进行分配
3
(2)放松结点B,即加-6进行分配
20kN 6 B -6 0.571 A -1.72 -3.43 0.429 B -2.57 0 2kN/m C
计算转动刚度:
6 B -6
2kN/m C
A
-15
15
0.571
-9
+
0.429 0
A -1.72
-3.43
B -2.57
C
=
0.571 A -15
-1.72 -16.72 16.72 15 -3.43 11.57 11.57
0.429 B -9
-2.57 -11.57 9 B
(3) 合并前面两个过程
C 0 0
(4) 绘弯矩图
M图 (kNm)
3m
3m
←
36 -18 -7.2 -10.8 28.8 -28.8 28.8
→
0 0
例. 用力矩分配法作图示连续梁的弯矩图。
20kN A 3m EI 3m 20kN 6 B -6 A B B 2kN/m EI 6m 2kN/m C C
解:(1)B点加约束
MP
20 6 15kN m AB= 8 MPBA= 15kN m
2 3 0.3 2 3 2 4 1.5 4 1.5 4 AD 0.3 2 3 2 4 1.5 4 100 22 M AD 48kNm 2 5
AB
AC
2 4 0.4 2 3 2 4 1.5 4 1 M AB 30 16 60kNm 8 100 2 32 M DA 72kN m 2 5
AB
B 0.3
AC
0.4 A
AD
0.3 72 -1.8 70.2 D
60 -48 -3.6 -4.8 -3.6 56.4 -4.8 - 51.6 C ↓ -2.4
→ →
56.4 51.6 4.8
70.2
2.4
M图(kNm)
例题
0.8 0.2 B i C l l ql2/12
C
q
i A
-4ql2/60 ql2/60
EI 6m
A
3m
30 EI
3m
m) C M图(kN·
5
三、悬臂部分的处理
M=Pl
1.不管悬臂端,2个刚结点进行分配。 2.切除悬臂端,减少一个刚结点。
注意:此时铰结点处的集中力偶M要产生固端弯矩,近端C处为M,远端B处为M/2。
例题
100kN 30kN/m D
B 4 m i=2 A i=2 C 4 m 3 m 2 m i=1.5
A
-15
15
-9
+
C
设i =EI/l SBA=4i SBC=3i
分配系数: 分配力矩:
BA
4i 0.571 4i 3i
BC
3i 0.429 7i
M BA 0.571 (6) 3.43
M BC 0.429 (6) 2.57
4
20kN
100kNm
i i i
50kNm
12kN/m
4m i 2Δ
4miຫໍສະໝຸດ 4m i Δ练习l
l
11-3
例题
单结点的力矩分配——基本运算
M
i i
4/7 3/7
i i
固端弯矩 分配、传递 杆端弯矩 2M/7 2M/7 ←
-M 4M/7 3M/7 4M/7 3M/7 4M/7 → 0 0
M图
2M/7
3M/7
12kN/m
例题 i 2i
16kN
6m 0.4 0.6 固端弯矩 分配、传递 最后M -36 -3.6 -39.6 39.6
-ql2/60 -ql2/60
ql2/60 ql2/60
ql2/60
M图
-ql2/12 -2ql2/60
7ql2/60
-7ql2/60
A
练习
i
k
Sik=4iik
i
k
Sik=3iik
i
k
Sik=4iik
i
k
Sik=0
i
k
Sik=4iik
i EI=∞ l K
k
Sik=Kl2
i
k
Sik=4iik
练习
4m
