位移法形载常数
形常数和载常数

位移法是计算超静定结构的基本方法之一
图1
如图1所示结构,力法计算,9个基本未知量
位移法计算,1个基本未知量
单跨超静定梁的形常数与载常数
1. 杆端力的正、负号规定
杆端弯矩:对杆件而言,当杆端弯矩绕杆件顺时针方向旋转为正,反之为负。
对结点而言,当杆端弯矩绕结点(或支座)逆时针方向旋转为正,反之为负。
杆端剪力:使所研究的分离体有顺时针转动趋势为正,有逆时针转动趋势为负。
2. 杆端位移的正、负号规定
杆端转角(角位移):以顺时针方向转动为正,反之为负。
杆端相对线位移:指杆件两端垂直于杆轴线方向的相对线位移,正负号则以使整个杆件顺时针方向转动规定为正,反之为负。
3. 等截面梁的形常数
杆端单位位移引起的杆端内力称为形常数•
i=EI/l——线刚度
4. 等截面梁的载常数
荷载引起的杆端内力称为载常数.
下图是在不同支承条件下的载常数和形常数
一端固定一端定向滑动的单跨超静定梁的载常数和形常数。
结构力学—形常数载常数2010

1、形常数:由单位杆端位移引起的杆端力 (只 、形常数: 只 与截面尺寸和材料性质有关的常数)。 与截面尺寸和材料性质有关的常数 。 2、载常数:由荷载引起的杆端力 (只与荷载形 、载常数: 只与荷载形 式有关的常数) 式有关的常数
3、转角位移方程:杆端弯矩的一般公式: 转角位移方程
∆ +M F M AB = 4iθ A + 2iθ B − 6i AB l ∆ F M BA = 2iθ A + 4iθ B − 6i + M BA l
↓↓↓↓↓↓↓↓
QAB
θB
QBA
转角位移方程
MAB P
4、已知杆端弯矩求剪力:取杆 已知杆端弯矩求剪力 件为分离体建立矩平衡方程:
QAB MAB
QAB
M AB + M BA F =− + QAB l
QBA MBA
注:1)MAB,MBA绕杆端顺时 顺时 针转向为正。 针转向为正 F 2) QAB 是荷载引起的固端剪力。
Q’AB
‘
P
0 QAB
+
‘ ’ QBA
0 QBA
∆
MBA MBA
MAB
θA
β
结构力学位移法

R2
R1=0 R2=0
ql
C D
Z1 R1
l
四.位移法典型方程
ql
q
l/2 B
ql
C D
ql B
A r22
q
R2 Z1
R1=0
ql C D
Z2=1
l/2 A
EI=常数
R2=0 R1 R1 r11 Z1 r12 Z 2 R1 P 0
l
C
r21
R2 r21 Z1 r22 Z 2 R2 P 0
r11
3i 3i
EI
r
11
=6i
R1P
ql 2 / 8
R1P
q
R1 P ql 2 / 8
Z1 ql / 48i ql 2 8 MM Z M 1 1 P
2
MP
ql2 / 16
r11
3i
Z1=1 3i
M1
Z1
M
位移法求解过程:
1)确定基本体系和基本未知量 2)建立位移法方程 3)作单位弯矩图和荷载弯矩图 4)求系数和自由项 5)解方程 6)作弯矩图
A
Z1
B
Z1
q
B
C
=
A
B
+
B
ቤተ መጻሕፍቲ ባይዱ
C
Z1
q
A
EI
B
Z1
EI
C
----刚臂,限制转动的约束 R1=0 R1=r11 Z1+ R1P =0
R1
q
A
EI
B
EI
C
r11
3i
B B
ql 8
2
3i
r
位移法知识讲解
§8-1 形常数与载常数 §8-2 位移法Ⅰ—直接平衡法 §8-3 位移法Ⅱ—典型方程法 §8-4 对称性利用 §8-5 支座位移和温度变化时的计算 §8-8 小结
8-1 形常数与载常数
基本构件
形常数 三类基本构件由于杆端单位位移所引起的杆端弯矩和剪力.
载常数 三类基本构件在荷载作用下的杆端弯矩和剪力
8-2位移法Ⅰ——直接平衡法
q=20kN/m
A 4I0 4m
B 5I0 3I0 E
5m
C 4I0 D 3I0
F 4m
4m 6m
MCB 2iBC 1 4iBC 2 MCFB 21 42 41.7
MCD 3iCD 2 3 2
MBE 4iBE 1 3 1
MEB 2iEB 1 1.5 1
MCF 4iCF 2 2 2
将系数和自由项代入方程,解得
35.5
1 3.24 / i 2 0.534 / i
2.9
13
2.1
(4)利用叠加原理,做弯矩图
M图
6.5
1
8-3 位移法Ⅱ——典型方程法
【例题】 试做图示刚架的弯矩图。
FP FP iEI1=∞ i
i EI1=∞i
ll
1 2
基本结构
解 (1)选择基本结构 (2)建立位移法方程
EI
EI
Δ1
Δ2
4m
4m
2m 2m
解 (1)选择基本结构
(2)建立位移法方程 k11 1 k12 2 F1P 0 k21 1 k22 2 F2P 0
基本结构
8-3 位移法Ⅱ——典型方程法
(3)求系数和自由项,解方程
k11 1 1 4i
k21
位移法复习要点

位移法复习要点位移法需要掌握的知识点有:直接平衡法:1. 以结点位移为基本未知量(转角或线位移);2. 以结点作为端点,将结构分解为简单杆件;3. 将杆端内力分为外力单独作用部分(限制位移=加刚臂或链杆)+ 位移单独作用部分,最终结点平衡求位移;外力单独作用部分→载常数;位移单独作用部分→形常数;4. 载常数和形常数都由前一章力法求得,用时可查表。
典型方程法:1. 先锁:基本体系=单跨超静定梁的组合(增加刚臂或链杆来限制位移);2. 后松:将基本结构还原成原结构,依次放松每一个刚臂或链杆;3. 建立位移法典型方程→矩阵位移法求解基本未知量;Δi为基本未知量,即结点位移;kij为刚度系数,第j个结点发生单位位移Δ=1 时第i个结点位移方向所需要的反力;kij=kji →反力互等定理;Fj p基本体系中外荷载引起的结点力;下标i 代表基本未知量方向; j 代表产生力的原因;4. 叠加法求内力:解题步骤(直接平衡法):① 确定结点位移数量和类型(特别是有无侧移);② 拆解杆件,写出杆端力与杆端位移表达式;③ 由结点平衡建立平衡方程;④ 解方程求解结点位移;⑤ 结点位移回代求解杆端力;⑥ 将杆件综合为结构,求最终内力。
Tips:1. 本方法基于以下三个假设:① 忽略杆件轴向变形,即EA→∞;② 变形后的曲杆长度与其弦等长;③ 适用于等截面直杆;2. 注意载常数和形常数形式,若与表中单跨梁的支座或加载方向相反,别忘×负号;3. 拆解的杆件中,端部内力顺时针为正;杆件综合为结构,结点内力逆时针为正;4. 尤其注意每根杆件线刚度的变化;5. 对静定结构求解同样适用。
例1 采用直接平衡法建立位移法方程,计算图1-(a) 所示刚架,绘制结构的弯矩图。
各杆EI为常数1-(a)分析:该刚架共有两个基本未知量,即刚结点B的转角φB和结点B、C的水平位移Δ。
令Δ1=φB,Δ2=Δ,并设Δ1顺时针方向转动,Δ2向右移动。
位移法典型方程
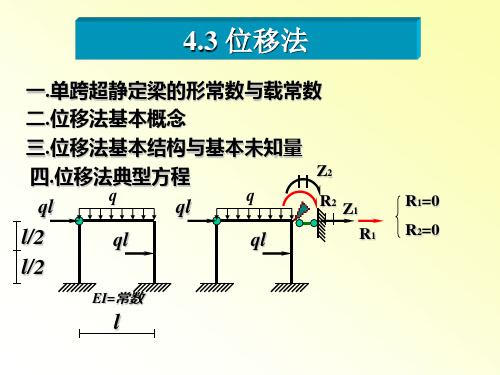
Z1=1
lq ql2 / 8 q
Z1
MP
6i / l 2 r11
3ql / 8 R1 P
练习4:
1)建立位移法基本 体系,列出典型方程
q
EI=常数
2) 求出典型方程中
系数r14, r32,R4P。
l
l
Z1
q
r11Z1 r12 Z2 r13 Z3 r14 Z4 R1P 0 r21Z1 r22 Z2 r23 Z3 r24 Z4 R2P 0 r31Z1 r32 Z2 r33 Z3 r34 Z4 R3P 0 r41Z1 r42 Z2 r43 Z3 r44 Z4 R4P 0
3i / l 2 3i / l 2
r22
12i / l 2 12i / l 2
练习1:
q
作M图,EI=常数
ql2 l
R1=0 r11Z1 R1P 0
r11 8i R1P 3ql 2 / 2 Z1 3ql 2 / 16i
M M1Z1 MP
l
l
l
Z1=1
i
r11
4i M1
r11
i 4i
3i
R2 r21Z1 r22Z2 R2P 0
r22
r11 30i / l 2 r12 r21 9i / l r21
R1P P
r22 11i
R2P 0
r22
Z1 0.044Pl 2 / i
8i
3i / l
12i / l
3i
4i
3i / l 2
3i
24i / l 2
8i
3i / l
Z2 0.036Pl / i R2P
17Pl 2 Z2 414i
EA
形常数和载常数表

形常数和载常数表在结构力学中,形常数和载常数表是非常重要的工具,它们对于分析和计算结构的内力与变形起着关键作用。
首先,让我们来了解一下什么是形常数。
形常数指的是在杆件仅发生单位位移(例如单位转角或单位线位移)时,杆件内部所产生的内力(例如弯矩、剪力等)。
这些内力的大小和分布规律是固定的,只与杆件的几何形状和约束条件有关。
比如说,对于两端固定的梁,当在其中一端发生单位转角时,所产生的弯矩分布就是一种形常数。
通过对各种常见杆件结构的分析和计算,可以得到相应的形常数表。
这些形常数表通常以表格的形式呈现,清晰地列出了不同杆件结构在不同单位位移下的内力值。
接下来,我们再看看载常数。
载常数是指在杆件上作用单位荷载(集中力、均布力等)时,杆件内部所产生的内力。
与形常数类似,载常数也只与杆件的几何形状和约束条件有关。
以简支梁为例,当在梁上作用单位集中力时,梁内产生的弯矩和剪力就是载常数。
同样,各种不同类型的杆件结构在不同单位荷载作用下的载常数也可以整理成表格形式,方便我们在结构分析和计算中直接查阅和使用。
那么,形常数和载常数表有什么实际用途呢?在结构力学的计算中,我们常常需要求解复杂结构在各种荷载作用下的内力和变形。
通过利用形常数和载常数表,可以将复杂的结构分解为简单的杆件单元,然后根据各杆件单元的连接方式和荷载情况,运用叠加原理,快速准确地计算出整个结构的内力和变形。
比如说,对于一个由多个梁和柱组成的框架结构,我们可以先分别确定每个梁和柱的形常数和载常数,然后根据它们在框架中的位置和连接关系,将各个杆件单元的内力和变形进行叠加,从而得到整个框架结构的内力和变形。
在实际工程中,形常数和载常数表的应用非常广泛。
无论是建筑结构的设计、桥梁的建造,还是机械结构的分析,都离不开对形常数和载常数的准确掌握和运用。
然而,需要注意的是,在使用形常数和载常数表时,必须要确保所分析的结构与表中所列的杆件结构类型和约束条件相符。
如果结构存在特殊的情况或者与标准的杆件结构有较大的差异,就不能简单地直接套用形常数和载常数表,而需要进行专门的分析和计算。
位移法基本原理及方法

4i1
20i2
ql 2 12
0
请自行作出 最终M图
1
ql 2 672i
2
ql 2 224i
最终内力: M M11 M 22 M P
例二:用位移法计算图示刚架,并作弯矩图. E=常数.
na 1 nl 1
熟记了“形、载
常数”吗?
kij、RiP
如何求?
单位弯矩图和荷载弯矩图示意图如下:
由形、载常数可得单位和荷载弯矩图如下:
有一(A 点
转角,设为
).
位移法第一种基本思路
利用转角位移 方程可得:
M AD M
M AC
3i
ql 2 8
M AB
4i
FP l 8
M AE
i
FP l 2
在此基础上,由图示结点平衡得 M 0
第一种基本思路
位移法思路(平衡方程法)
以某些结点的位移为基本未知量 将结构拆成若干具有已知力-位移(转角-位移) 关系的单跨梁集合 分析各单跨梁在外因和结点位移共同作用下 的受力 将单跨梁拼装成整体 用平衡条件消除整体和原结构的差别,建立 和位移个数相等的方程 求出基本未知量后,由单跨梁力-位移关系可 得原结构受力
FP x
y
在线性小变形条件下,由叠加原理可得
M
AB
4i A
2i B
6i l
AB
MF AB
M
BA
4i B
2i A
6i l
AB
MF BA
转角位移方程(刚度方程)
Slope-Deflection (Stiffness) Equation其中: i EI 称杆源自的线刚度。lMF AB
,
