人教A版数学必修一—郸城一高高一上学期第三次周练
人教A版数学必修一-第一学期高一单元测试.doc
2011－2012学年度第一学期高一数学单元测试汤阴一中 苏永鹏一、选择题：（本大题共12个小题，每小题3分，共36分）1．已知集合}1,log |{3>==x x y y A ，}0,3|{>==x y y B x，则=⋂B A ( )A ．}310|{<<y yB ．}0|{>y yC ． }131|{<<y y D ．}1|{>y y 2．下列各式中成立的是 （ ）A ．1777()m n m n= B ．4312(3)3-=-C ．33344()x y x y +=+D ．3393=3．下列函数在区间（0，3）上是增函数的是 （ ）A x y 1=B 21x y = C x y )31(= D 1522--=x x y4．若函数()log (01)a f x x a =<<在区间]2,[a a 上的最大值是最小值的3倍，则a 的值为( )A ．42 B ． 22 C ． 41 D ． 21 5．设()x a f x =（a>0，a ≠1），对于任意的正实数x ，y ，都有( )A.()()()f xy f x f y =B. ()()()f xy f x f y =+C.()()()f x y f x f y +=D. ()()()f x y f x f y +=+ 6．下列判断正确的是（ ）A ．35.27.17.1> B ．328.08.0< C ．22ππ< D ．3.03.09.07.1>7．设函数⎪⎩⎪⎨⎧>≤=0,0,)21()(21x x x x f x，若)(a f >1，则a 的取值范围是（ ）A ． (－1,1)B ． ),1(+∞-C ． ),0()2,(+∞⋃--∞D ．),1()0,(+∞⋃-∞ 8．函数lg y x =是( )A ．偶函数，在区间(,0)-∞ 上单调递增B ．偶函数，在区间(,0)-∞上单调递减C ．奇函数，在区间(0,)+∞ 上单调递增D ．奇函数，在区间(0,)+∞上单调递减 9．计算机成本不断降低,若每隔三年计算机价格降为原来的23,则现在价格为8100元的计算机9年后价格为 ( )A ．2400元B ．900元C ．300元D ．3600元10．当10<<a 时,在同一坐标系中,函数x y a y a xlog ==-与的图象是( )A ．B ．C ．D ．11．若01x y <<<，则（ ）A ．33y x <B ．log 3log 3x y >C ．44log log x y >D ．11()()44x y<12．函数y =)12(log 21-x 的定义域为（ ）A ．（21，+∞） B ．［1，+∞) C ．（ 21，1] D ．（－∞，1） 第Ⅱ卷二、填空题：（本大题共4个小题，共16分，把答案填在相应的横线上）13．已知幂函数()y f x =的图象过22,2⎛⎫⎪ ⎪⎝⎭，则()9f ＝_________xy o 1 1 o y x 1 1 o y x1 1 xy 1 1 o14．函数)10(11≠>+=-a a ay x 且，无论a 取何值，函数图像恒过一个定点，则定点坐标为_______15．若函数()y f x =是函数(01)xy a a a =>≠且的反函数，且()y f x =的图象过点（2，1），则()f x =______________16．关于函数22log (23)y x x =-+有以下4个结论:其中正确的有① 定义域为(,3](1,);-∞-⋃+∞ ② 递增区间为[1,);+∞ ③ 最小值为1; ④ 图象恒在x 轴的上方 17．（每小题6分，共12分）计算题：（1）21134320212)12(])2[(])73(2[)25.0(--+-⨯⨯---（2）2(lg5)lg2lg50+⨯18、已知m >1，试比较（lg m ）0．9与（lg m ）0．8的大小．19．(本题满分12分)已知函数()log (1)a f x x =+，()log (1)a g x x =-， 其中(01)a a >≠且,设()()()h x f x g x =-． (1)判断()h x 的奇偶性，并说明理由；(2)若(3)2f =，求使()0h x >成立的x 的集合．20已知函数2lg(21)y ax ax =++：（1）若函数的定义域为R ，求a 的取值范围； （2）若函数的值域为R ，求a 的取值范围.21．（本题满分12分）设函数2()21x f x a =-+, （1）求证：不论a 为何实数()f x 总为增函数;（2）确定a 的值，使()f x 为奇函数及此时()f x 的值域．选做题、已知()(01)xxf x a a a a -=+>≠且 （Ⅰ）证明函数f ( x )的图象关于y 轴对称；（Ⅱ）判断()f x 在(0,)+∞上的单调性，并用定义加以证明； （Ⅲ）当x ∈［1，2］时函数f (x )的最大值为25，求此时a 的值.（Ⅳ）当x ∈［－2，－1］时函数f (x )的最大值为25，求此时a 的值. ）2011－2012学年度第一学期高一数学单元测试答案一、选择题：题号 1 2 3 4 5 6 7 8 9 10 11 12 答案D D B A C D D B A C B C 二、填空题：13．1314．(1,2)15．()f x=2log x16．②③④三、解答题：17．（1）1252-……6分（2）1 ……12分18、解：∵m>1，∴lg m＞0；以下分类为①lg m＞1，②lg m=1；③0＜lg m＜1 三种情形讨论（lg m）0．9与（lg m）0．8的大小．…………2分①当lg m＞1即m＞10时，（lg m）0．9＞（lg m）0．8；…………5分②当lg m=1即m=10时，（lg m）0．9=（lg m）0．8；…………7分③当0＜lg m＜1即1＜m＜10时，（lg m）0．9＜（lg m）0．8．…………10分19．解：(1)由对数的意义，分别得1＋x>0，1－x>0，即x>－1，x<1.∴函数f(x)的定义域为(－1，＋∞)，函数g(x)的定义域为(－∞，1)，∴函数h(x)的定义域为(－1,1)．……3分∵对任意的x∈(－1,1)，－x∈(－1,1)，h(－x)＝f(－x)－g(－x)＝log a(1－x)－log a(1＋x)＝g(x)－f(x)＝－h(x)，∴h(x)是奇函数．……3分(2)由f(3)＝2，得a＝2.此时h(x)＝log2(1＋x)－log2(1－x)，由h(x)>0即log2(1＋x)－log2(1－x)>0，∴log2(1＋x)>log2(1－x)．由1＋x>1－x>0，解得0<x<1.故使h(x)>0成立的x 的集合是{x|0<x<1}． ……12分 20 （过程略）（1） [)0,1 （2）[)1,+∞. 21．解： (1)()f x 的定义域为R, 12x x ∴<,则121222()()2121x x f x f x a a -=--+++=12122(22)(12)(12)x x x x ⋅-++, 12x x <, 1212220,(12)(12)0x x x x ∴-<++>,12()()0,f x f x ∴-<即12()()f x f x <,所以不论a 为何实数()f x 总为增函数．……6分 (2)()f x 为奇函数, ()()f x f x ∴-=-,即222121x x a a --=-+++, 解得: 1.a = 2()1.21x f x ∴=-+ 由以上知2()121x f x =-+, 211x+>,20221x∴<<+, 220,1()121x f x ∴-<-<∴-<<+ 所以()f x 的值域为(1,1).-……12分选做题、解：（Ⅰ）要证明函数f ( x )的图象关于y 轴对称则只须证明函数f ( x )是偶函数…1分∵x ∈R …………2分 由)()(x f a a a ax f x x x x=+=+=--- …………3分∴函数f ( x )是偶函数，即函数f ( x )的图象关于y 轴对称…………4分（Ⅱ）证明：设210x x <<，则12()()f x f x -=21211111112211)1)(()11()()(x x x x x x x x x x x x x a a a a a a a a aaaa x ++----=-+-=+-+（1）当a >1时，由0<12x x <，则x 1+x 2>0，则01>x a 、02>x a 、21x x a a <、121>+x x a ；12()()f x f x -<0即12()()f x f x <；（2）当0<a <1时，由0<12x x <，则x 1+x 2>0，则01>x a、02>x a 、21x x a a >、1021<<+x x a ；12()()f x f x -<0即12()()f x f x <；所以，对于任意a （10≠>a a 且），f (x )在(0,)+∞上都为增函数．（Ⅲ）由（Ⅱ）知f (x )在(0,)+∞上为增函数，则当x ∈［1，2］时，函数f (x )亦为增函数；由于函数f (x )的最大值为25，则f (2)= 25即25122=+a a ，解得2=a ，或22=a （Ⅳ）由（Ⅰ）（Ⅱ）证知f (x ) 是偶函数且在(0,)+∞上为增函数，则知f (x )在)0,(-∞上为减函数；则当x ∈［－2，－1］时，函数f (x )为减函数 由于函数f (x )的最大值为25，则f (－2)= 25即25122=+a a，解得2=a ，或22=a。
人教A版高一数学必修第一册全册复习训练题卷含答案解析(63)
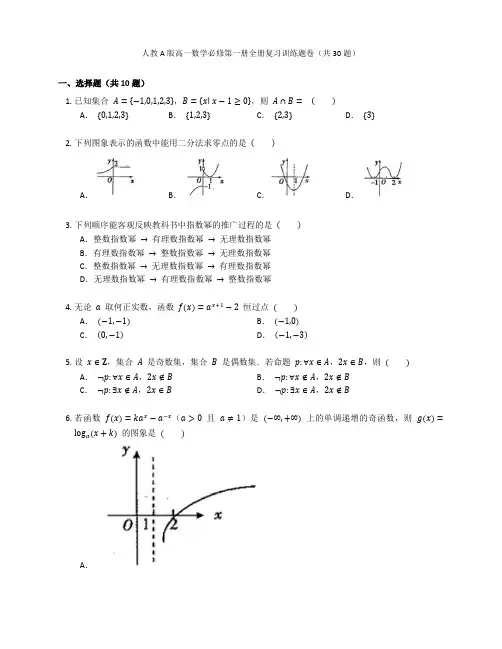
人教A版高一数学必修第一册全册复习训练题卷（共30题）一、选择题（共10题）1.已知集合A={−1,0,1,2,3}，B={x∣ x−1≥0}，则A∩B=( )A．{0,1,2,3}B．{1,2,3}C．{2,3}D．{3}2.下列图象表示的函数中能用二分法求零点的是( )A．B．C．D．3.下列顺序能客观反映教科书中指数幂的推广过程的是( )A．整数指数幂→有理数指数幂→无理数指数幂B．有理数指数幂→整数指数幂→无理数指数幂C．整数指数幂→无理数指数幂→有理数指数幂D．无理数指数幂→有理数指数幂→整数指数幂4.无论a取何正实数，函数f(x)=a x+1−2恒过点( )A．(−1,−1)B．(−1,0)C．(0,−1)D．(−1,−3)5.设x∈Z，集合A是奇数集，集合B是偶数集．若命题p:∀x∈A，2x∈B，则( )A．¬p:∀x∈A，2x∉B B．¬p:∀x∉A，2x∉BC．¬p:∃x∉A，2x∈B D．¬p:∃x∈A，2x∉B6.若函数f(x)=ka x−a−x（a>0且a≠1）是(−∞,+∞)上的单调递增的奇函数，则g(x)=log a(x+k)的图象是( )A．B．C．D．7.已知a,b,c∈R，命题“若a+b+c=3，则a2+b2+c2≥3”的否命题是( )A．若a+b+c≠3，则a2+b2+c2<3B．若a+b+c=3，则a2+b2+c2<3C．若a+b+c≠3，则a2+b2+c2≥3D．若a2+b2+c2≥3，则a+b+c=38.命题“∀x>0，lnx≥1−1x”的否定是( )A．∃x0≤0，lnx0≥1−1x0B．∃x0≤0，lnx0<1−1x0C．∃x0>0，lnx0≥1−1x0D．∃x0>0，lnx0<1−1x09.已知集合A={0,1,2}，集合B={x∣ x>2}，则A∩B=( )A．{2}B．{0,1,2}C．{x∣ x>2}D．∅10.已知集合A={x∣x≥1}，B={−1,0,1,2}，则A⋂B=( )A．{2}B．{1,2}C．{0,1,2}D．{x∣ x≥−1}二、填空题（共10题）11.设函数f(x)={x2+1,x≤12x,x>1，则f(f(3))=．12.本场数学考试时间2小时，请问这段时间时针旋转弧度．13.不等式(x−1)(2−x)≥0的解集是．14.设全集U={−1,0,1,2}，若集合A={−1,0,2}，则∁U A=．15.如果某人x秒内骑车行进了1千米，骑车的速度为y千米/秒，那么y=．16.设集合A={1,3,5,7}，B={x∣ 4≤x≤7}，则A∩B=．17.设集合A={x∣ −1≤x≤2}，B={x∣ 0≤x≤4}，则A∩B=．18.已知偶函数f(x)，且当x∈[0,+∞)时都有(x1−x2)[f(x2)−f(x1)]<0成立，令a=f(−5)，b=f(12)，c=f(−2)，则a，b，c的大小关系是（用“>”连接）．19.已知A={x∣ 2x≤1}，B={−1,0,1}，则A∩B=．20.已知集合M={x∣ x>2}，集合N={x∣ x≤1}，则M∪N=．三、解答题（共10题）21.已知集合A含有两个元素1和a2，若a∈A，求实数a的值．22.求证：cos2(A+B)−sin2(A−B)=cos2Acos2B．23.指数函数的定义．一般地，函数y=a x（a>0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R．问题：为何指数函数的概念中规定a>0且a≠1？24.a，b是实数，比较a2+b2与2(a+b−1)的大小．25.如何记忆一元二次方程根的分布满足的条件？26.用列举法表示下列给定的集合．(1) 大于1且小于6的整数组成的集合A．(2) 方程x2−9=0的实数根组成的集合B．(3) 小于8的质数组成的集合C．(4) 一次函数y=x+3与y=−2x+6的图象的交点组成的集合D．27.初中我们学习过哪些函数？试举几个具体的例子．28.函数的表示方法主要有哪几种？29.已知y=f(x)是定义域为R的奇函数，当x>0时，f(x)=x2−2x．(1) 求函数f(x)的单调递增区间；(2) 若a∈R，函数y=f(x)−a的零点个数为F(a)，求F(a)的解析式．30.一元二次方程、一元二次函数、一元二次不等式有何联系？答案一、选择题（共10题）1. 【答案】B【解析】画数轴，选B．【知识点】交、并、补集运算2. 【答案】C【知识点】二分法求近似零点3. 【答案】A【知识点】幂的概念与运算4. 【答案】A【解析】f(−1)=−1，所以函数f(x)=a x+1−2的图象一定过点(−1,−1)．故选A．【知识点】指数函数及其性质5. 【答案】D【解析】命题p:∀x∈A，2x∈B是一个全称量词命题，其命题的否定¬p应为：∃x∈A，2x∉B．故选D．【知识点】全（特）称命题的否定6. 【答案】C【解析】函数f(x)=ka x−a−x（a>0且a≠1）是奇函数，f(−x)=−f(x)对于任意x∈R 恒成立，即ka−x−a x=a−x−ka x对于任意x∈R恒成立，即(k−1)⋅(a x+a−x)=0对于任意x∈R恒成立，故只能是k=1，此时函数f(x)=a x−a−x，由于这个函数单调递增，故只能是a>1．函数g(x)=log a(x+k)的图象是把函数y=log a x的图象沿x轴左移一个单位得到的．【知识点】对数函数及其性质、函数的奇偶性、指数函数及其性质7. 【答案】A【解析】“a+b+c=3”的否定是“a+b+c≠3”，“a2+b2+c2≥3”的否定是“a2+b2+c2<3”．【知识点】全（特）称命题的否定8. 【答案】D【解析】“∀x>0，lnx≥1−1x ”的否定为∀x>0，lnx≥1−1x不恒成立，即“∃x0>0，lnx0<1−1x0”．故选D ．【知识点】全（特）称命题的否定9. 【答案】D【解析】由题意可知集合 A 表示的三个实数 0，1，2，而集合 B 表示的是大于 2 的所有实数，所以两个集合的交集为空集． 【知识点】交、并、补集运算10. 【答案】B【知识点】交、并、补集运算二、填空题（共10题） 11. 【答案】139【解析】 f (3)=23，f(f (3))=f (23)=49+1=139．【知识点】分段函数12. 【答案】 −π3【知识点】弧度制13. 【答案】 [1,2]【知识点】二次不等式的解法14. 【答案】 {1}【知识点】交、并、补集运算15. 【答案】 x −1【知识点】函数模型的综合应用16. 【答案】 {5,7}【知识点】交、并、补集运算17. 【答案】 [0,2]【知识点】交、并、补集运算18. 【答案】 a >c >b【解析】 x 1,x 2∈[0,+∞)，在 x 1>x 2 时，f (x 2)<f (x 1)，在 x 1<x 2 时，f (x 2)>f (x 1)，由上可知，f (x ) 在 [0,+∞) 上单调递增，由 f (x ) 为偶函数，a =f (−5)=f (5)，c =f (−2)=f (2)， 12<2<5，即 f (12)<f (2)<f (5)， 故 a >c >b ．【知识点】函数的奇偶性、函数的单调性19. 【答案】 {−1,0}【解析】 A =(−∞,12]，B ={−1,0,1}，所以 A ∩B ={−1,0}． 【知识点】交、并、补集运算20. 【答案】 (−∞,1]∪(2,+∞)【知识点】交、并、补集运算三、解答题（共10题）21. 【答案】由题意可知，a =1 或 a 2=a ．（1）若 a =1，则 a 2=1，这与 a 2≠1 相矛盾，故 a ≠1．（2）若 a 2=a ，则 a =0 或 a =1（舍去），又当 a =0 时，A 中含有元素 1 和 0，满足集合中元素的互异性，符合题意． 综上可知，实数 a 的值为 0．【知识点】元素和集合的关系、集合中元素的三个特性22. 【答案】左边=1+cos (2A+2B )2−1−cos (2A−2B )2=cos (2A+2B )+cos (2A−2B )2=12(cos2Acos2B −sin2Asin2B +cos2Acos2B +sin2Asin2B )=cos2Acos2B =右边.所以原等式成立． 【知识点】二倍角公式23. 【答案】①若 a =0，则当 x >0 时，a x =0；当 x ≤0 时，a x 无意义；②若 a <0，则对于 x 的某些数值，可使 a x 无意义．如 (−2)x ，这时对于 x =14，x =12，⋯，在实数范围内函数值不存在； ③若 a =1，则对于任何 x ∈R ，a x =1，是一个常量，没有研究的必要性．【知识点】指数函数及其性质24. 【答案】 a 2+b 2−2(a +b −1)=(a −1)2+(b −1)2≥0，所以 a 2+b 2≥2(a +b −1)． 【知识点】不等式的性质25. 【答案】虽然上述表格中的公式比较复杂，但结合图形理解会比较简单，因此上述公式不要死记硬背，结合图形理解其含义即可． 【知识点】二次不等式的解法26. 【答案】(1) A ={2,3,4,5}．(2) B ={−3,3}． (3) C ={2,3,5,7}． (4) D ={(1,4)}．【知识点】集合的概念27. 【答案】正比例函数 y =x ，一次函数 y =x +1，反比例函数 y =1x ，二次函数 y =x 2．【知识点】函数的相关概念28. 【答案】（1）解析法：解析法是将定义域与值域之间的对应法则用解析式表示．（2）列表法：是将定义域和值域中所有变量的对应法则用表格形式一一列出． （3）图象法：图象法是借助于二维的坐标系刻画两个变量之间的对应法则．【知识点】函数的表示方法29. 【答案】(1) 当 x ∈(−∞,0) 时，−x ∈(0,+∞)，因为 y =f (x ) 是定义域为 R 的奇函数，所以 f (x )=−f (−x )=−[(−x )2−2(−x )]=−x 2−2x ，f (0)=0， 所以 f (x )={x 2−2x,x ≥0,−x 2−2x,x <0.当 x ≥0 时，函数图象开口向上，增区间是 [1,+∞)； 当 x <0 时，函数图象开口向下，增区间是 (−∞,−1]． 所以函数 f (x ) 的单调递增区间是 (−∞,−1]，[1,+∞)．(2) 由（1）可得 f (x ) 的解析式，据此可作出函数 y =f (x ) 的图象，根据图象得，若方程 f (x )=a 恰有 3 个不同的解，则 a 的取值范围是 (−1,1)，此时 F (a )=3，当 a =±1 时，F (a )=2，当 a >1 或 a <−1 时，F (a )=1． 综上可得 F (a )={1,a <−1或a >12,a =±13,−1<a <1．【知识点】函数的单调性、函数的奇偶性、函数的零点分布30. 【答案】（1）一元二次函数与 x 轴的交点为一元二次方程的根；（2）一元二次函数 x 轴上方的部分对应元二次不等式大于 0，下方的部分对应一元二次不等式小于 0；（3）一元二次不等式解集的两个端点恰好为一元二次方程的根．【知识点】二次不等式的解法。
度高中数学 周练卷(一)新人教A版必修1
周练卷(一)(时间:90分钟满分:120分)【选题明细表】知识点、方法题号集合的概念1,2,5,6集合的运算4,7,9,10,13,14,17 由集合的运算求参数15,16,18,19,20 集合间关系3,8,11,121.下列表示:①{0}=∅;②∅∈{0};③∅{0};④0∈∅中,正确的个数为( A )(A)1 (B)2 (C)3 (D)4解析:因为∅是不含有任何元素的集合,所以①错;因为集合与集合之间不是∈关系,所以②错;因为∅是任何非空集合的真子集,所以③对;因为∅中不含任何元素,所以④错.故选A.2.集合A={1,x,y},B={1,x2,2y},若A=B,则实数x的取值集合为( A )(A){} (B){,-}(C){0,} (D){0,,-}解析:集合A={1,x,y},B={1,x2,2y},若A=B,则解得x=1或0,y=0,显然不成立,或解得x=,故实数x的取值集合为{}.故选A.3.设A,B是全集I={1,2,3,4}的子集,A={1,2},则满足A⊆B的B的个数是( B )(A)5 (B)4 (C)3 (D)2解析:A,B是全集I={1,2,3,4}的子集,A={1,2},则满足A⊆B的B为{1,2},{1,2,3},{1,2,4},{1,2,3,4}.故选B.4.若全集U={1,2,3,4,5},A={2,4,5},B={1,2,5},则(∁U A)∩B等于( D )(A){2,5} (B){1,3,4}(C){1,2,4,5} (D){1}解析:因为全集U={1,2,3,4,5},A={2,4,5},B={1,2,5},所以(∁U A)∩B={1,3}∩{1,2,5}={1}.故选D.5.下列各组对象能构成集合的是( B )(A)充分接近的所有实数(B)所有的正方形(C)著名的数学家(D)1,2,3,3,4,4,4,4解析:选项A,C不满足集合的确定性;选项B正方形是确定的,故能构成集合;选项D不满足集合的互异性.故选B.6.若集合A={-1,1},B={0,2},则集合{z|z=2x2+y,x∈A,y∈B}中的元素的个数为( D )(A)5 (B)4 (C)3 (D)2解析:集合A={-1,1},B={0,2},所以集合{z|z=2x2+y,x∈A,y∈B}={2,4},故选D.7.设全集U={(x,y)|y=x+1,x,y∈R},M={(x,y)|=1},则∁U M等于( B )(A) (B){(2,3)} (C)(2,3) (D){2,3}解析:全集U={(x,y)|y=x+1,x,y∈R},M={(x,y)|=1}={(x,y)|y=x+1且x≠2},∁U M={(2,3)}.故选B.8.(2018·秦州区高一期末)设全集U是实数集R,M={x|x>2},N={x|1<x<3},则图中阴影部分所表示的集合是( C )(A){x|2<x<3}(B){x|x<3}(C){x|1<x≤2}(D){x|x≤2}解析:图中阴影部分表示的集合中的元素是在集合N中,但不在集合M中.又M={x|x>2},N={x|1<x<3},所以图中阴影部分表示的集合是(∁U M)∩N={x|x≤2}∩{x|1<x<3}={x|1<x≤2},故选C.9.已知集合M={x|-1<x<1},N={x|x2<2,x∈Z},则( C )(A)M⊆N (B)N⊆M(C)M∩N={0} (D)M∪N=N解析:N={x|x2<2,x∈Z}={-1,0,1},故M∩N={0}.故选C.10.定义集合A-B={x|x∈A且x∉B},若集合M={1,2,3,4,5},集合N={x|x=2k-1,k∈Z},则集合M-N的子集个数为( C )(A)2 (B)3 (C)4 (D)无数个解析:因为M={1,2,3,4,5},N={x|x=2k-1,k∈Z},由新定义A-B={x|x∈A且x∉B},得M-N={2,4},所以M-N的子集为∅,{2},{4},{2,4},共4个.故选C.11.满足M⊆{a1,a2,a3,a4},且M∩{a1,a2,a3}={a1,a2}的集合M的个数是( B )(A)1 (B)2 (C)3 (D)4解析:M∩{a1,a2,a3}={a1,a2},a1∈M,a2∈M,a3∉M,又M⊆{a1,a2,a3,a4},则a4∈M或a4∉M,故M={a1,a2,a4}或M={a1,a2},故选B.12.(2018·黄陵县高二期末)下列六个关系式:①{a,b}⊆{b,a},②{a,b}={b,a},③0=∅,④0∈{0},⑤∅∈{0},⑥⌀⊆{0},其中正确的个数为( C )(A)6个(B)5个(C)4个(D)少于4个解析:根据集合自身是自身的子集,可知①正确;根据集合无序性可知②正确;根据元素与集合只有属于与不属于关系可知③⑤不正确;根据元素与集合之间的关系可知④正确;根据空集是任何集合的子集可知⑥正确.故选C.二、填空题(每小题5分,共20分)13.已知集合A={-1,0,1,2},B={-2,1,2},则A∩B= .解析:因为集合A={-1,0,1,2},B={-2,1,2},所以A∩B={1,2}.答案:{1,2}14.(2018·丽水高二期末)已知全集U={1,2,3,4,5,6,7},集合A={1,2,3},B={2,3,4},则A∩B= ,∁U A= .解析:全集U={1,2,3,4,5,6,7},集合A={1,2,3},B={2,3,4},所以A∩B={2,3};∁U A={4,5,6,7}.答案:{2,3} {4,5,6,7}15.(2018·怀仁县高二期末)已知集合A={x|ax2-3x+2=0}至多有一个元素,则a的取值范围是 .解析:a=0时,ax2-3x+2=0,即x=,A={},符合要求;a≠0时,ax2-3x+2=0至多有一个解,Δ=9-8a≤0,a≥.综上,a的取值范围为{a|a≥或a=0}.答案:{a|a≥或a=0|16.设集合A={x|-3≤x≤2},B={x|2k-1≤x≤2k+1},且A⊇B,则实数k的取值范围是.解析:由题意得解得即-1≤k≤.答案:{k|-1≤k≤}三、解答题(共40分)17.(本小题满分8分)已知全集U={x|x≤4},集合A={x|-2<x<3},B={x|-3≤x≤2},求A∩B,(∁U A)∪B,A∩(∁U B). 解:如图所示,因为A={x|-2<x<3},B={x|-3≤x≤2},所以∁U A={x|x≤-2,或3≤x≤4},∁U B={x|x<-3,或2<x≤4}.A∩B={x|-2<x≤2},(∁U A)∪B={x|x≤2,或3≤x≤4},A∩(∁U B)={x|2<x<3}.18.(本小题满分10分)已知全集U=R,集合A={x|-2≤x≤5},B={x|a+1≤x≤2a-1}且A⊆∁U B,求实数a的取值范围. 解:若B=∅,则a+1>2a-1,则a<2,此时∁U B=R,所以A⊆∁U B;若B≠∅,则a+1≤2a-1,即a≥2,此时∁U B={x|x<a+1,或x>2a-1},由于A⊆∁U B,如图,则a+1>5,所以a>4,所以实数a的取值范围为{a|a<2,或a>4}.19.(本小题满分10分)(2018·张掖高二期末)已知集合A={x|0<2x+a≤3},B={x|-<x<2}.(1)当a=1时,求(∁R B)∪A;(2)若A∩B=A,求实数a的取值范围.解:(1)a=1时,集合A={x|0<2x+1≤3}={x|-<x≤1},B={x|-<x<2},所以∁R B={x|x≤-或x≥2},所以(∁R B)∪A={x|x≤1或x≥2}.(2)若A∩B=A,则A⊆B,因为A={x|0<2x+a≤3}={x|-<x≤},所以解得-1<a≤1,所以实数a的取值范围是{a|-1<a≤1}.20.(本小题满分12分)设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若(∁U A)∩B=∅,求m的值. 解:A={-2,-1},由 (∁U A)∩B=∅得B⊆A,因为方程x2+(m+1)x+m=0的判别式:Δ=(m+1)2-4m=(m-1)2≥0,所以B≠∅,所以B={-1}或B={-2}或B={-1,-2}.①若B={-1},则m=1;②若B={-2},则应有-(m+1)=(-2)+(-2)=-4且m=(-2)·(-2)=4,这两式不能同时成立, 所以B≠{-2};③若B={-1,-2},则应有-(m+1)=(-1)+(-2)=-3且m=(-1)·(-2)=2,得m=2.经检验知m=1和m=2符合条件.所以m=1或m=2.。
新人教A版必修12021学年高中数学周练卷3测评含解析
周练卷(三)一、选择题(每小题5分，共40分)1．函数f(x)＝x2＋3的奇偶性是(B)A．奇函数B．偶函数C．既是奇函数又是偶函数D．既不是奇函数又不是偶函数解析：函数f(x)＝x2＋3的定义域为R，f(－x)＝(－x)2＋3＝x2＋3＝f(x)，所以该函数是偶函数．2．函数f(x)＝x2(x<0)的奇偶性为(D)A．奇函数B．偶函数C．既是奇函数又是偶函数D．非奇非偶函数解析：∵函数f(x)＝x2(x<0)的定义域为(－∞，0)，不关于原点对称，∴函数f(x)＝x2(x<0)为非奇非偶函数.3．下列函数中，既是偶函数又在(－3,0)上单调递减的函数是(C)A．y＝x3B．y＝－x2＋1C．y＝|x|＋1 D．y＝x解析：A项为奇函数；B项为偶函数，但在(－3,0)上单调递增，不合题意；C项，函数是偶函数，当x∈(－3,0)时，y＝－x＋1单调递减，符合题意；D项，函数的定义域为[0，＋∞)，不关于原点对称，所以该函数既不是奇函数也不是偶函数，不合题意．故选C.4．若函数y＝x2－6x－7，则它在[－2,4]上的最大值、最小值分别是(C)A．9，－15 B．12，－15C．9，－16 D．9，－12解析：函数的对称轴为x ＝3，所以当x ＝3时，函数取得最小值为－16， 当x ＝－2时，函数取得最大值为9，故选C.5．设函数f (x )，g (x )的定义域都为R ，且f (x )是奇函数，g (x )是偶函数，则下列结论中正确的是( C )A ．f (x )g (x )是偶函数B ．|f (x )|g (x )是奇函数C ．f (x )|g (x )|是奇函数D ．|f (x )g (x )|是奇函数解析：f (x )为奇函数，g (x )为偶函数，故f (x )g (x )为奇函数，|f (x )|g (x )为偶函数，f (x )|g (x )|为奇函数，|f (x )g (x )|为偶函数，故选C.6．定义在R 上的偶函数f (x )满足：对任意的x 1，x 2∈(－∞，0]，x 1≠x 2，有f (x 2)－f (x 1)x 2－x 1<0，则( B )A ．f (－3)<f (－2)<f (1)B ．f (1)<f (－2)<f (－3)C ．f (－2)<f (1)<f (－3)D ．f (－3)<f (1)<f (－2)解析：由任意的x 1，x 2∈(－∞，0](x 1≠x 2)，f (x 2)－f (x 1)x 2－x 1<0可知函数f (x )在(－∞，0]上单调递减．又因为函数f (x )为R 上的偶函数，所以f (1)＝f (－1)． 而－3<－2<－1，所以f (－3)>f (－2)>f (－1)， 即f (－3)>f (－2)>f (1)．故选B.7．已知f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝x 2－2x ，则f (x )在R 上的表达式是( D )A ．y ＝x (x －2)B ．y ＝x (|x |＋2)C ．y ＝|x |(x －2)D ．y ＝x (|x |－2)解析：由x ≥0时，f (x )＝x 2－2x ，f (x )是定义在R 上的奇函数得，当x <0时，－x >0，f (x )＝－f (－x )＝－(x 2＋2x )＝x (－x －2)．∴f (x )＝⎩⎪⎨⎪⎧x (x －2)，x ≥0，x (－x －2)，x <0，即f (x )＝x (|x |－2)．8．定义在R 上的奇函数f (x )满足f ⎝ ⎛⎭⎪⎫12＝0，且在(0，＋∞)上单调递减，则xf (x )>0的解集为( B )A.⎩⎨⎧⎭⎬⎫xx <－12或x >12B.⎩⎨⎧⎭⎬⎫x －12<x <0或0<x <12C.⎩⎨⎧⎭⎬⎫xx <－12或0<x <12D.⎩⎨⎧⎭⎬⎫x －12<x <0或x >12 解析：结合性质画出f (x )的草图，如图所示．由图象可知x 与f (x )同号的区间为⎝ ⎛⎭⎪⎫－12，0和⎝ ⎛⎭⎪⎫0，12.故选B. 二、填空题(每小题5分，共15分)9．如果函数f (x )＝ax 2＋2x －3在区间(－∞，4)上是单调递增的，则实数a 的取值范围是[－14，0]．解析：若a ＝0，则f (x )＝2x －3，显然函数在区间(－∞，4)上单调递增，符合题意；若a ≠0，则由函数在区间(－∞，4)上单调递增可得a <0，且－22a ≥4，解得－14≤a <0.综上，实数a 的取值范围是[－14，0]．10．已知函数f (x )＝ax 3－bx ＋3(其中a ，b 为常数)，若f (3)＝2 015，则f (－3)＝－2_009.解析：设g (x )＝f (x )－3，则g (x )＝ax 3－bx ， 显然g (x )为R 上的奇函数， 又g (3)＝f (3)－3＝2 015－3＝2 012， 所以g (－3)＝－g (3)， 即f (－3)－3＝－2 012， 解得f (－3)＝－2 009.11．奇函数f (x )在区间[3,10]上是增函数，在区间[3,9]上的最大值为6，最小值为－2，则2f (－9)＋f (－3)＝－10.解析：因为函数在区间[3,10]上是增函数， 所以在区间[3,9]上单调递增．所以函数在区间[3,9]上的最小值为f (3)＝－2，最大值为f (9)＝6. 又因为函数f (x )为奇函数，所以f (－3)＝－f (3)＝2， f (－9)＝－f (9)＝－6.所以2f (－9)＋f (－3)＝2×(－6)＋2＝－10. 三、解答题(共45分)12．(15分)判断下列函数的奇偶性．(1)f (x )＝⎩⎪⎨⎪⎧1，x 是有理数，－1，x 是无理数；(2)f (x )＝x 2＋|x ＋a |＋1.解：(1)f (x )为偶函数．因为x ∈Q 时，－x ∈Q ， 所以f (－x )＝1＝f (x )．同理，x 为无理数时，－x 也为无理数． 所以f (－x )＝－1＝f (x )，所以f (x )为偶函数． (2)①当a ＝0时，f (x )为偶函数．②当a ≠0时，因为对所有x ∈R 而言|x ＋a |≠|－x ＋a |. 所以f (x )既不是奇函数又不是偶函数．13．(15分)已知y ＝f (x )是奇函数，它在(0，＋∞)上是增函数，且f (x )<0，试问F (x )＝1f (x )在(－∞，0)上是增函数还是减函数？证明你的结论．解：F (x )在(－∞，0)上是减函数． 证明如下：任取x 1，x 2∈(－∞，0)，且x 1<x 2，则有－x 1>－x 2>0. 因为y ＝f (x )在(0，＋∞)上是增函数，且f (x )<0， 所以f (－x 2)<f (－x 1)<0，① 又因为f (x )是奇函数，所以f (－x 2)＝－f (x 2)，f (－x 1)＝－f (x 1)，② 由①②得f (x 2)>f (x 1)>0.于是F (x 1)－F (x 2)＝f (x 2)－f (x 1)f (x 1)·f (x 2)>0，即F (x 1)>F (x 2)，所以F (x )＝1f (x )在(－∞，0)上是减函数．14．(15分)已知函数f (x )＝4x ＋ax ＋b (a ，b ∈R )为奇函数． (1)若f (1)＝5，求函数f (x )的解析式；(2)当a ＝－2时，不等式f (x )≤t 在[1,4]上恒成立，求实数t 的最小值．解：因为函数f (x )＝4x ＋ax ＋b (a ，b ∈R )为奇函数， 所以f (－x )＝－f (x )， 即－4x －a x ＋b ＝－4x －ax －b ， 所以b ＝0，(1)f (1)＝4＋a ＋b ＝5，所以a ＝1. 故函数f (x )的解析式为f (x )＝4x ＋1x .(2)a ＝－2，f (x )＝4x －2x .因为函数y ＝4x ，y ＝－2x 在[1,4]上均单调递增， 所以函数f (x )在[1,4]上单调递增， 所以当x ∈[1,4]时，f (x )max ＝f (4)＝312. 因为不等式f (x )≤t 在[1,4]上恒成立， 所以t ≥312，故实数t 的最小值为312.。
人教A版数学必修一—郸城一高高一上学期第三次周练.docx
马鸣风萧萧马鸣风萧萧高中数学学习材料马鸣风萧萧*整理制作2015—2016学年度郸城一高高一上学期第三次周练数学试卷注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分，时间120分钟，满分150分；2.答卷前请将自己姓名，班级，考号在答题卡上准确填涂；3.选择题答案用2B 铅笔涂到答题卡指定位置，非选择题答案用0.5mm 黑色签字笔答题，全部答案均答到答题卡上， 在本试卷上答题无效。
第Ⅰ卷（选择题）一．选择题：本大题共14小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目要求。
1．下列四个关系式中，正确的是A ．{}a ∅∈B ．{}a a ∉C ．{}{},a a b ∈D ．{}b a a ,∈ 2．已知全集U R =，集合21{|2},{|1}2A x xB x x =-<<=<，则()U A B ð= A ．{|2}x x ≥ B ．1{|1}2x x x ≤-≥或C ．{|12}x x x ≤-≥或D ．1{|2}2x x x ≤-≥或3．函数0()(2)f x x =-的定义域为 A. }41|{≤<x x B. }2,41|{≠≤<x x x 且 C. }241|{≠≤≤x ，x x 且 D. }4|{≥x x4．函数()|2|(1)f x x x =-+-的值域为A ．[0,)+∞B ．[2,2]-C ．[0,2]D ．(,2]-∞5. 设全集U ＝R ，集合M ＝{x |－1≤x ≤7}，N ＝{x |y ＝x －2＋2－x }，则下图中阴影表示的集合为A ．{0}B ．{2}C ．φD ．{x |2≤x ≤7} 6．下列所给4个图象中，与所给3件事吻合最好的顺序为（1）我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学； （2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间； （3）我出发太晚后来为了赶时间开始加速行走。
人教A版数学必修一高一数学周考卷(2)参考答案.docx
高一数学周考（2）参考答案1．B 【解析】因为，1{|210}{|}2A x R x x R x =∈+<=∈<-， {|(1)(2)0}{|12}B x R x x x R x =∈+-<=∈-<<，所以，=⋂B A 1{|}{|12}2x R x x R x ∈<-⋂∈-<<=⎪⎭⎫ ⎝⎛--21,1，故选B . 考点：集合的运算，简单不等式解法.2．B【解析】如果对于函数()f x 的定义域内的任何一个x 值，都有()()f x f x =-，那么就称()f x 为偶函数，A 选项的函数是奇函数，B 、C 、D 选项的函数是偶函数，B 选项的函数在()0,+∞是单调递增的，C 选项的二次函数在()0,+∞是单调递减的，D 选项的函数在()0,+∞上是单调递减的.考点：偶函数的判断，函数单调性.3．B【解析】因为{|1}A x x =>，所以{|1}U C A x x =≤，要使()U C A B R =U ，只需1a ≤. 考点：集合的运算.4．A【解析】由0)9()3(2<-+-a f a f ，得)9()3(2a f a f --<-；又奇函数满足)()(x f x f -=-，得)9()3(2-<-a f a f ；因为)(x f 是（-1,1）上的减函数，所以⎪⎩⎪⎨⎧->-<-<-<-<-9319113122a a a a ，解得322<<a .考点：函数的奇偶性、单调性的应用，解不等式（组）.5． D【解析】∵等腰三角形周长为20cm ，腰长为xcm ，底边为ycm ，∴y=20-2x ；又两边之和大于第三边两边之差小于第三边，∴2x>20-2x,x-x<20-2x,解得：5＜x ＜10；因此可知函数解析式为y=20-2x （5＜x ＜10）．选D.考点：函数应用题，建立函数解析式以及函数的定义域.6．(]3,0-【解析】自变量x 满足12030x x ⎧-≥⎨+>⎩，解得30x -<≤，故函数()f x =的定义域为(]3,0-.考点：函数的定义域7．1e【解析】根据题意，由于11f ()ln1e e ==-,因此所求的解析式为11f (-1)e e -==,故可知答案为1e考点：分段函数的求值点评：解决该试题的关键是利用函数的解析式来求解函数值，注意变量的分类讨论。
人教A版数学必修一周练2.docx
周练(二) 函数及其表示(时间：80分钟满分：100分)一、选择题(每小题5分，共40分)1．函数y＝f(x)(f(x)≠0)的图象与x＝1的交点个数是()．A．1 B．2 C．0或1 D．1或2解析结合函数的定义可知，如果f：A→B成立，则任意x∈A，则有唯一确定的B与之对应，由于x＝1不一定是定义域中的数，故x＝1可能与函数y＝f(x)没有交点，故函数f(x)的图象与直线x＝1至多有一个交点．答案 C2．如下图给出的四个对应关系，其中构成映射的是()．A．(1)(2) B．(1)(4)C．(1)(2)(4) D．(3)(4)解析在(2)中，元素1和4没有对应关系，(3)中元素1和2都有两个元素与它们对应，不满足映射的定义；(1)、(4)符合映射定义．故选B. 答案 B3．(2013·汕头高一检测)已知正方形的周长为x ，它的外接圆的半径为y ，则y 关于x 的解析式为( )．A ．y ＝12xB ．y ＝24x C ．y ＝28xD ．y ＝216x解析 正方形的对角线长为24x ，从而外接圆半径为y ＝12×24x ＝28x . 答案 C4．若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，例如解析式为y ＝2x 2＋1，值域为{9}的“孪生函数”三个： (1)y ＝2x 2＋1，x ∈{－2}；(2)y ＝2x 2＋1，x ∈{2}；(3)y ＝2x 2＋1，x ∈{－2,2}． 那么函数解析式为y ＝2x 2＋1，值域为{1,5}的“孪生函数”共有( )．A ．5个B ．4个C ．3个D ．2个 解析 当y ＝1时，x ＝0； 当y ＝5时，x ＝± 2.∴y ＝2x 2＋1，x ∈{}0，2，或x ∈{0，－2}或x ∈{0，2，－2}，则所求的“孪生函数”有3个． 答案 C5．已知f (x )＝⎩⎨⎧2x ，x ＞0，f (x ＋1)，x ≤0，则f ⎝ ⎛⎭⎪⎫43＋f ⎝ ⎛⎭⎪⎫－43的值等于( )．A ．－2B ．4C ．2D ．－4 解析 ∵f ⎝ ⎛⎭⎪⎫43＝2×43＝83，∴f ⎝ ⎛⎭⎪⎫－43＝f ⎝ ⎛⎭⎪⎫－43＋1＝f ⎝ ⎛⎭⎪⎫－13＝f ⎝ ⎛⎭⎪⎫23＝43.∴f ⎝ ⎛⎭⎪⎫43＋f ⎝ ⎛⎭⎪⎫－43＝83＋43＝4.答案 B6．一列货运火车从某站出发，匀加速行驶一段时间后开始匀速行驶，过了一段时间，火车到达下一站停下，装完货以后，火车又匀加速行驶，一段时间后再次匀速行驶．下列图象可以近似地刻画出火车在这段时间内的速度变化情况的是( )．解析 根据题意，知火车从静止开始匀加速行驶，所以只有B 、C 两项符合题意，然后匀速行驶一段时间后又停止了一段时间，所以可以确定选B 项． 答案 B7．若函数f (x )满足关系式f (x )＋2f ⎝ ⎛⎭⎪⎫1x ＝3x ，则f (2)的值为( )．A ．1B ．－1C ．－32 D.32 解析 令x ＝2时，f (2)＋2f ⎝ ⎛⎭⎪⎫12＝6，①令x ＝12时，f ⎝ ⎛⎭⎪⎫12＋2f (2)＝32.②由①、②联立，得f (2)＝－1. 答案 B8．函数f (x )＝⎩⎪⎨⎪⎧x 2－x ＋1，x ＜1，1x，x ＞1，的值域是( )．A.⎣⎢⎡⎭⎪⎫34，＋∞ B ．(0,1) C.⎣⎢⎡⎭⎪⎫34，1 D ．(0，＋∞)解析 f (x )＝x 2－x ＋1＝⎝ ⎛⎭⎪⎫x －122＋34≥34(x ＜1)，当x ＞1时，f (x )＝1x ∈(0,1)，∴f (x )的值域(0,1)∪⎣⎢⎡⎭⎪⎫34，＋∞＝(0，＋∞)．答案 D二、填空题(每小题5分，共20分)9．下列图形是函数y ＝⎩⎨⎧x 2，x <0，x －1，x ≥0，的图象的是________．解析 由于f (0)＝0－1＝－1，所以函数图象过点(0，－1)；当x <0时，y ＝x 2，则函数是开口向上的抛物线在y 轴左侧的部分．因此只有图形③符合． 答案 ③10．已知集合A ＝R ，B ＝{(x ，y )|x ，y ∈R}，f ：A →B 是从A 到B 的映射，f ：x →(x ＋1，x 2＋1)，求B 中元素⎝ ⎛⎭⎪⎫32，54与A 中________对应．解析由题意知⎩⎪⎨⎪⎧x ＋1＝32，x 2＋1＝54，解得x ＝12.答案 1211．若函数f (x )的定义域为[0,4]，则g (x )＝f (2x )x －1的定义域为________． 解析 ∵f (x )的定义域为[0,4]， ∴要使g (x )有意义， 应有⎩⎨⎧0≤2x ≤4，x －1≠0，因此0≤x ≤2，且x ≠1. ∴g (x )的定义域为[0,1)∪(1,2]．答案 [0,1)∪(1,2]12．已知函数f (x )＝⎩⎨⎧－x －1(－1≤x ＜0)，－x ＋1(0＜x ≤1)，则f (x )－f (－x )＞－1的解集为________．解析 (1)当－1≤x ＜0时，f (x )＝－x －1， f (－x )＝x ＋1，∴原不等式化为－x －1－(x ＋1)＞－1，x ＜－12， 因此－1≤x ＜－12.(2)当0＜x ≤1时，f (x )＝－x ＋1，f (－x )＝x －1， ∴原不等式化为 －2x ＋2＞－1，x ＜32. 因此0＜x ≤1.综上(1)、(2)知，原不等式的解集为 [－1，－12)∪(0,1]． 答案 [－1，－12)∪(0,1] 三、解答题(每小题10分，共40分)13．已知f (x )＝⎩⎨⎧x (x ＋4) (x ≥0)，x (x －4) (x <0)，若f (1)＋f (a ＋1)＝5，求a 的值．解 f (1)＝1×(1＋4)＝5， ∵f (1)＋f (a ＋1)＝5，∴f (a ＋1)＝0. 当a ＋1≥0，即a ≥－1时， 有(a ＋1)(a ＋5)＝0， ∴a ＝－1或a ＝－5(舍去)； 当a ＋1<0，即a <－1时，有(a ＋1)(a －3)＝0，无解．综上可知a ＝－1.14．如图所示，函数f (x )的图象是折线段A 、B 、C ，其中A ，B ，C 的坐标分别为(0,4)，(2,0)，(6,4)．(1)求f [f (0)]的值； (2)求函数f (x )的解析式． 解 (1)直接由图中观察，可得 f [f (0)]＝f (4)＝2.(2)设线段AB 所对应的函数解析式为y ＝kx ＋b ，k ≠0， 将⎩⎨⎧ x ＝0，y ＝4，与⎩⎨⎧x ＝2y ＝0代入，得 ⎩⎨⎧4＝b ，0＝2k ＋b .∴⎩⎨⎧b ＝4，k ＝－2. ∴y ＝－2x ＋4(0≤x ≤2)．同理，线段BC 所对应的函数解析式为 y ＝x －2(2＜x ≤6)．因此函数f (x )＝⎩⎨⎧－2x ＋4，0≤x ≤2，x －2，2＜x ≤6.15．已知函数f (x )对任意实数a ，b ，都有f (ab )＝f (a )＋f (b )成立． (1)求f (0)与f (1)的值； (2)求证：f ⎝ ⎛⎭⎪⎫1x ＝－f (x )；(3)若f (2)＝p ，f (3)＝q (p ，q 均为常数)，求f (36)的值． (1)解 令a ＝b ＝0，得f (0)＝f (0)＋f (0)，解得f (0)＝0； 令a ＝1，b ＝0，得f (0)＝f (1)＋f (0)，解得f (1)＝0. (2)证明 令a ＝1x ，b ＝x ，得f (1)＝f ⎝ ⎛⎭⎪⎫1x ＋f (x )＝0，∴f ⎝ ⎛⎭⎪⎫1x ＝－f (x )． (3)解 令a ＝b ＝2，得f (4)＝f (2)＋f (2)＝2p ， 令a ＝b ＝3，得f (9)＝f (3)＋f (3)＝2q ，令a ＝4，b ＝9，得f (36)＝f (4)＋f (9)＝2p ＋2q .16．如图所示，已知底角为45°的等腰梯形ABCD ，底边BC 长为7 cm ，腰长为22cm ，当垂直于底边BC (垂足为F )的直线l 从左至右移动(与梯形ABCD 有公共点)时，直线l 把梯形分成两部分，令BF ＝x ，试写出左边部分的面积y 关于x 的函数解析式，并画出大致图象．解 过点A ，D 分别作AG ⊥BC ，DH ⊥BC ，垂足分别是G ，H . 因为ABCD 是等腰梯形，底角为45°，AB ＝2 2 cm ， 所以BG ＝AG ＝DH ＝HC ＝2 cm ，又BC ＝7 cm ， 所以AD ＝GH ＝3 cm. (1)当点F 在BG 上时， 即x ∈(0,2]时，y ＝12x 2；(2)当点F 在GH 上时，即x ∈(2,5]时，y ＝x ＋(x －2)2×2＝2x －2； (3)当点F 在HC 上时，即x ∈(5,7]时， y ＝S 五边形ABFED ＝S 梯形ABCD －S Rt △CEF ＝12(7＋3)×2－12(7－x )2 ＝－12(x －7)2＋10.综合(1)(2)(3)，得函数解析式为y ＝⎩⎪⎨⎪⎧12x 2，x ∈(0，2]，2x －2，x ∈(2，5]，－12(x －7)2＋10 ，x ∈(5，7].图象如图所示．。
高一数学上学期周练(三)(2021学年)
河南省正阳县２017-20１8学年高一数学上学期周练(三）编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(河南省正阳县2017-20１8学年高一数学上学期周练(三））的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为河南省正阳县2０17-201８学年高一数学上学期周练（三)的全部内容。
2017—２０18学年高一上期数学周练三一.选择题：1。
已知集合Ａ={2,1,0,1,2}--,B=2{|20}x x x +-<,则Ａ∩B＝_＿_____＿___A 。
｛－１,０} B.{0，1｝ C 。
{-1，0,1} D 。
{1,2,0}2．已知集合{|11}M x x =-<，集合2{|230}N x x x =--<,则()R M C N ＝___A 。
{|02}x x <<B 。
{|12}x x -<<C.{|10x x -<≤或23}x ≤< D ．∅3.全集Ｕ＝{-１，-2,－3,－４，０},集合A ＝｛—1,-2,0},集合N=｛—3,—４，0｝,则()U C A B =＿____A 。
{0｝ Ｂ．{—３,－４｝ C ．{—1,—2｝ D 。
∅4．已知集合{|2,}A x x x R =≤∈,B={2,},x x Z ∈则Ａ∩B=________＿__A 。
(0，2） Ｂ.[0，2］ Ｃ。
{0,2｝ D.{0,１,2} ５.已知全集U ＝R,集合{|2,A x x =<-或0}x >，1{|1}B x x =<,则()UC A B =_____A 。
（—2，0) Ｂ.[2,0)- C. ∅ Ｄ。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2015—2016学年度郸城一高高一上学期第三次周练
数学试卷
注息事项:
1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分，时间120分钟，满分150分；
2.答卷前请将自己姓名，班级，考号在答题卡上准确填涂；
3.选择题答案用2B 铅笔涂到答题卡指定位置，非选择题答案用0.5mm 黑色签字笔答题，全部答案均答到答题卡上， 在本试卷上答题无效。
第Ⅰ卷（选择题）
一．选择题：本大题共14小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目要求。
1．下列四个关系式中，正确的是
A ．{}a ∅∈
B ．{}a a ∉
C ．{}{},a a b ∈
D ．{}b a a ,∈
2．已知全集U R =，集合21{|2},{|1}2
A x x
B x x =-<<=<，则()U A B ð= A ．{|2}x x ≥ B ．1{|1}2
x x x ≤-≥或 C ．{|12}x x x ≤-≥或 D ．1{|2}2
x x x ≤-≥或
3．函数0()(2)f x x =-的定义域为 A. }41|{≤<x x B. }2,41|{≠≤<x x x 且
C. }241|{≠≤≤x ，x x 且
D. }4|{≥x x
4．函数()f x =的值域为 A ．[0,)+∞ B ．[2,2]- C ．[0,2] D ．(,2]-∞
5. 设全集U ＝R ，集合M ＝{x |－1≤x ≤7}，N ＝{x |y ＝x －2＋2－x }，则下图中阴影表示的集合为
A ．{0}
B ．{2}
C ．φ
D ．{x |2≤x ≤7}
6．下列所给4个图象中，与所给3件事吻合最好的顺序为
（1）我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；
（2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；
（3）我出发太晚后来为了赶时间开始加速行走。