语音信号处理实验二

合集下载

语音信号处理实验报告实验二

语音信号处理实验报告实验二一、实验目的本次语音信号处理实验的目的是深入了解语音信号的特性，掌握语音信号处理的基本方法和技术，并通过实际操作和数据分析来验证和巩固所学的理论知识。

具体而言，本次实验旨在：1、熟悉语音信号的采集和预处理过程，包括录音设备的使用、音频格式的转换以及噪声去除等操作。

2、掌握语音信号的时域和频域分析方法，能够使用相关工具和算法计算语音信号的短时能量、短时过零率、频谱等特征参数。

3、研究语音信号的编码和解码技术，了解不同编码算法对语音质量和数据压缩率的影响。

4、通过实验，培养我们的动手能力、问题解决能力和团队协作精神，提高我们对语音信号处理领域的兴趣和探索欲望。

二、实验原理（一）语音信号的采集和预处理语音信号的采集通常使用麦克风等设备将声音转换为电信号，然后通过模数转换器（ADC）将模拟信号转换为数字信号。

在采集过程中，可能会引入噪声和干扰，因此需要进行预处理，如滤波、降噪等操作，以提高信号的质量。

（二）语音信号的时域分析时域分析是对语音信号在时间轴上的特征进行分析。

常用的时域参数包括短时能量、短时过零率等。

短时能量反映了语音信号在短时间内的能量分布情况，短时过零率则表示信号在单位时间内穿过零电平的次数，可用于区分清音和浊音。

（三）语音信号的频域分析频域分析是将语音信号从时域转换到频域进行分析。

通过快速傅里叶变换（FFT）可以得到语音信号的频谱，从而了解信号的频率成分和分布情况。

（四）语音信号的编码和解码语音编码的目的是在保证一定语音质量的前提下，尽可能降低编码比特率，以减少存储空间和传输带宽的需求。

常见的编码算法有脉冲编码调制（PCM）、自适应差分脉冲编码调制（ADPCM）等。

三、实验设备和软件1、计算机一台2、音频采集设备（如麦克风）3、音频处理软件（如 Audacity、Matlab 等）四、实验步骤（一）语音信号的采集使用麦克风和音频采集软件录制一段语音，保存为常见的音频格式（如 WAV）。

语音信号处理试验教程

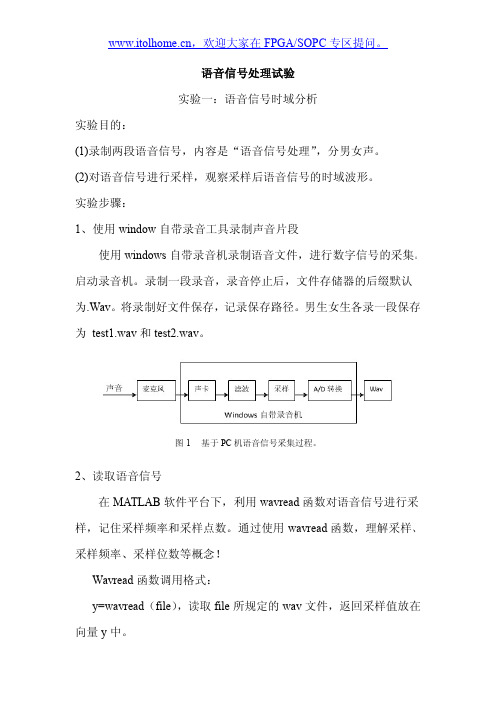
语音信号处理试验实验一：语音信号时域分析实验目的：(1)录制两段语音信号，内容是“语音信号处理”，分男女声。

(2)对语音信号进行采样，观察采样后语音信号的时域波形。

实验步骤：1、使用window自带录音工具录制声音片段使用windows自带录音机录制语音文件，进行数字信号的采集。

启动录音机。

录制一段录音，录音停止后，文件存储器的后缀默认为.Wav。

将录制好文件保存，记录保存路径。

男生女生各录一段保存为test1.wav和test2.wav。

图1基于PC机语音信号采集过程。

2、读取语音信号在MATLAB软件平台下，利用wavread函数对语音信号进行采样，记住采样频率和采样点数。

通过使用wavread函数，理解采样、采样频率、采样位数等概念！Wavread函数调用格式：y=wavread（file），读取file所规定的wav文件，返回采样值放在向量y中。

[y，fs，nbits]=wavread（file），采样值放在向量y中，fs表示采样频率（hz），nbits表示采样位数。

y=wavread（file，N），读取前N点的采样值放在向量y中。

y=wavread（file，[N1，N2]）,读取从N1到N2点的采样值放在向量y中。

3、编程获取语音信号的抽样频率和采样位数。

语音信号为test1.wav和test2.wav，内容为“语音信号处理”，两端语音保存到工作空间work文件夹下。

在M文件中分别输入以下程序，可以分两次输入便于观察。

[y1,fs1,nbits1]=wavread('test1.wav')[y2,fs2,nbits2]=wavread('test2.wav')结果如下图所示根据结果可知：两端语音信号的采样频率为44100HZ，采样位数为16。

4、语音信号的时域分析语音信号的时域分析就是分析和提取语音信号的时域参数。

进行语音分析时，最先接触到并且夜市最直观的是它的时域波形。

语音信号处理实验报告

语音信号处理实验报告——语音信号分析实验一．实验目的及原理语音信号分析是语音信号处理的前提和基础，只有分析出可表示语音信号本质特征的参数，才有可能利用这些参数进行高效的语音通信、语音合成和语音识别等处理，并且语音合成的音质好坏和语音识别率的高低，都取决于对语音信号分析的准确性和精确性。

贯穿语音分析全过程的是“短时分析技术”。

因为从整体来看，语音信号的特性及表征其本质特征的参数均是随时间变化的，所以它是一个非平稳态过程，但是在一个短时间范围内（一般认为在10~30ms的时间内），其特性基本保持不变，即相对稳定，可将其看做一个准稳态过程，即语音信号具有短时平稳性。

所以要将语音信号分帧来分析其特征参数，帧长一般取为10ms~30ms。

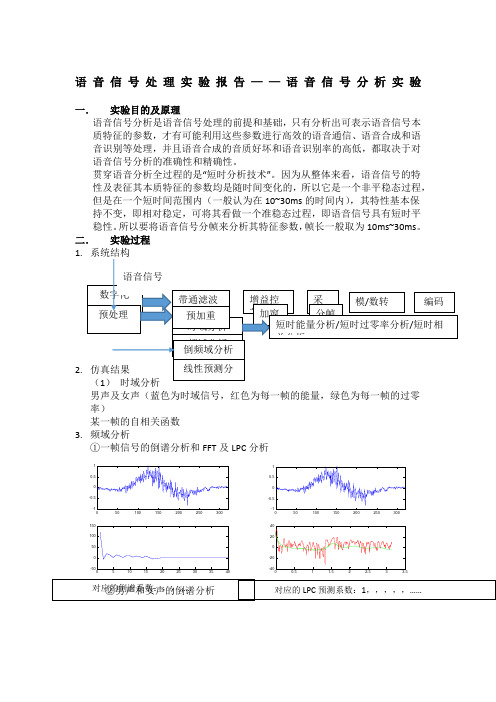
二．实验过程1.2.男声及女声（蓝色为时域信号，红色为每一帧的能量，绿色为每一帧的过零率）某一帧的自相关函数3.频域分析①一帧信号的倒谱分析和FFT及LPC分析②男声和女声的倒谱分析对应的倒谱系数：，，……对应的LPC预测系数：1，，，，，……原语音波形一帧语音波形一帧语音的倒谱③浊音和清音的倒谱分析④浊音和清音的FFT分析和LPC分析（红色为FFT图像，绿色为LPC图像）三．实验结果分析1.时域分析实验中采用的是汉明窗，窗的长度对能否由短时能量反应语音信号的变化起着决定性影响。

这里窗长合适，En能够反应语音信号幅度变化。

同时，从图像可以看出，En可以作为区分浊音和清音的特征参数。

短时过零率表示一帧语音中语音信号波形穿过横轴（零电平）的次数。

从图中可以看出，短时能量和过零率可以近似为互补的情况，短时能量大的地方过零率小，短时能量小的地方过零率较大。

从浊音和清音的时域分析可以看出，清音过零率高，浊音过零率低。

从男声女声的时域信号对比图中可以看出，女音信号在高频率分布得更多，女声信号在高频段的能量分布更多，并且女声有较高的过零率，这是因为语音信号中的高频段有较高的过零率。

2.频域分析这里对信号进行快速傅里叶变换（FFT），可以发现，当窗口函数不同，傅里叶变换的结果也不相同。

语音信号处理实验讲义

sum=0;
for m=1:N
sum=sum+b1(m)*b1(m+k-1);
end
A(k)=sum;
end
for k=1:320
A1(k)=A(k)/A(1);
end
%画图
figure(1)
subplot(3,1,1)
plot(A1);
xlabel('延时k')
ylabel('R(k)')
legend('N=320')
e=fra(256,128,x);
ee=e(20,:);
subplot(2,2,1)
ee1=ee/max(ee);
plot(ee1)
xlabel('样点数')
ylabel('幅度')
title('原始语音')
axis([0,256,-1.5,1.5])
%矩形窗傅立叶变换
r=fft(ee,1024);
axis([0,320,-0.5,1])
图2-2 修正的自相关函数（参加自相关运算的点数N取不同值）
四、思考题
1、自相关函数的作用是什么？互相关函数的作用是什么？
2、浊音信号分别加矩形窗和汉明窗时自相关函数有什么不同？
3、清音信号的自相关函数和浊音信号的有什么区别？
实验三语音信号频域特征分析
一、实验目的
plot(s2)
title('一帧语音信号');
xlabel('样点数');
ylabel('幅度');
axis([0,320,-1,1]);
subplot(3,1,2)

数字语音信号处理教案

数字语音信号处理实验指导书前言语音信号处理是研究用数字信号处理技术和语音学知识对语音信号进行处理的新兴的学科，是目前发展最为迅速的信息科学研究领域的核心技术之一。

通过语音传递信息是人类最重要、最有效、最常用和最方便的交换信息形式。

同时，语言也是人与机器之间进行通信的重要工具，它是一种理想的人机通信方式，因而可为信息处理系统建立良好的人机交互环境，进一步推动计算机和其他智能机器的应用，提高社会的信息化程度。

语音信号处理是一门新兴的学科，同时又是综合性的多学科领域和涉及面很广的交叉学科。

虽然从事这一领域研究的人员主要来自信号与信息处理及计算机应用等学科，但是它与语音学、语言学、声学、认知科学、生理学、心理学等许多学科也有非常密切的联系。

20世纪60年代中期形成的一系列数字信号处理的理论和算法，如数字滤波器、快速傅立叶变换（FFT）等是语音信号数字处理的理论和技术基础。

随着信息科学技术的飞速发展，语音信号处理取得了重大的进展：进入70年代之后，提出了用于语音信号的信息压缩和特征提取的线性预测技术（LPC），并已成为语音信号处理最强有力的工具，广泛应用于语音信号的分析、合成及各个应用领域，以及用于输入语音与参考样本之间时间匹配的动态规划方法；80年代初一种新的基于聚类分析的高效数据压缩技术—矢量量化（VQ）应用于语音信号处理中；而用隐马尔可夫模型（HMM）描述语音信号过程的产生是80年代语音信号处理技术的重大发展，目前HMM已构成了现代语音识别研究的重要基石。

近年来人工神经网络(ANN)的研究取得了迅速发展，语音信号处理的各项课题是促进其发展的重要动力之一，同时，它的许多成果也体现在有关语音信号处理的各项技术之中。

为了深入理解语音信号数字处理的基础理论、算法原理、研究方法和难点，根据数字语音信号处理教学大纲，结合课程建设的需求，我们编写了本实验参考书。

本本参考书针对教学大纲规定的四个研究设计型实验，每个实验给出了参考程序，目的是起一个抛砖引玉的作用，学生在学习过程中，可以针对某一个实验进行延伸的创新学习，比如说，语音端点的检测、语音共振峰提取、基于HMM或DTW的有限词汇或大词汇的特定人、非特定人的语音识别、识别率的提高（如何提高有噪环境下的识别率）、以及编码问题等，同时在学习中还可深入思考如何将有关的方法在嵌入式系统或DSP 下的实现问题等。

《语音信号处理》实验2-基音周期估计

华南理工大学《语音信号处理》实验报告实验名称：基音周期估计姓名：学号：班级：10级电信5班日期：2013年5 月15日1.实验目的本次试验的目的是通过matlab编程，验证课本中基音周期估计的方法，本实验采用的方法是自相关法。

2. 实验原理1、基音周期基音是发浊音时声带震动所引起的周期性，而基音周期是指声带震动频率的倒数。

基音周期是语音信号的重要的参数之一，它描述语音激励源的一个重要特征，基音周期信息在多个领域有着广泛的应用，如语音识别、说话人识别、语音分析与综合以及低码率语音编码，发音系统疾病诊断、听觉残障者的语音指导等。

因为汉语是一种有调语言，基音的变化模式称为声调，它携带着非常重要的具有辨意作用的信息，有区别意义的功能，所以，基音的提取和估计对汉语更是一个十分重要的问题。

由于人的声道的易变性及其声道持征的因人而异，而基音周期的范围又很宽，而同—个人在不同情态下发音的基音周期也不同，加之基音周期还受到单词发音音调的影响，因而基音周期的精确检测实际上是一件比较困难的事情。

基音提取的主要困难反映在：①声门激励信号并不是一个完全周期的序列，在语音的头、尾部并不具有声带振动那样的周期性，有些清音和浊音的过渡帧是很难准确地判断是周期性还是非周期性的。

②声道共振峰有时会严重影响激励信号的谐波结构，所以，从语音信号中直接取出仅和声带振动有关的激励信号的信息并不容易。

③语音信号本身是准周期性的(即音调是有变化的)，而且其波形的峰值点或过零点受共振峰的结构、噪声等的影响。

④基音周期变化范围大，从老年男性的50Hz到儿童和女性的450Hz，接近三个倍频程，给基音检测带来了一定的困难。

由于这些困难，所以迄今为止尚未找到一个完善的方法可以对于各类人群(包括男、女、儿童及不向语种)、各类应用领域和各种环境条件情况下都能获得满意的检测结果。

尽管基音检测有许多困难，但因为它的重要性，基音的检测提取一直是一个研究的课题，为此提出了各种各样的基音检测算法，如自相关函数(ACF)法、峰值提取算法(PPA)、平均幅度差函数(AMDF)法、并行处理技术、倒谱法、SIFT、谱图法、小波法等等。

语音信号处理(电气与电子工程学院)

四、实验条件
计算机、高分辨麦克、matlab 及相关软件。五、实验步骤
可以使用已有工作空间文件也可以自己录制一段语音（录制方法见附加内容）
1、听一下 we_be10k（可用 sound） 2、使用函数 specgram_ex3p19.显示语谱图和语音波形。对比调用参数窗长 20ms （200 点）、帧间隔 1ms（10 点）和参数窗长 5ms（50 点）、帧间隔 1ms（10 点）；再对比窗长>20ms 或小于 5ms，以及帧间隔>1ms 时的语谱图说明宽带语谱图、窄带语谱图与时频分辨率的关系及如何得到时频折中。
1-3
在自相关法中
1-1，1-3 变为
P
∑αk rn [i − k ] = rn [i − 0],i = 1, 2,3,...p
k =1
1-4
P
En = Rn [0] − ∑αk Rn [k ]
k =1
1-5
由 1-4 可列出方程组 1-6
⎛ ⎜ ⎜
Rn Rn
[0] [1]
Rn [1] Rn [0]
图2
图3
7
采用 MATLAB 中的录音函数 wavrecord（）进行语音信号的录制。同样，选择三种频率不同的采样率对同一语音信号进行采样，试听回放效果，进行比较。
二、实验涉及的 MATLAB 子函数 Wavrecord 功能：录制语音调用格式： filename=wavrecord(N, fs, ‘dtype’);录制一段 N/fs 秒长度的语音信号，采样率为 fs Hz，缺省值为 11025Hz，dtype 是录制声音的数据类型。具体可通过 help wavrecord 命令查阅。 y=wavrecord(N, fs, ch)；与上面语句不同的是最后一个参数，ch 是指录音的声道，ch 为 1 是单声道，ch 为 2 是双声道。 Wavread 功能：把数据文件的声音数据赋给变量 x。【x，fs，bits】=wavread（’filename’）;把数据文件的声音数据赋给变量 x，同时把 x 的采样频率 fs 和数据的位数 bits 放进 MATLAB 的工作空间。 Sound 功能：将变量 x 的数据转换成 MATLAB 的数据文件保存。调用格式： Sound（x，fs，bits）； Save 功能：将变量 x 的数据转换成 MATLAB 的数据文件保存。调用格式： Save‘filename’x；将数据转换成文件名与‘filename’相同，扩展名为.mat 的数据并保存，以便用 MATLAB 的各种工具进行处理。

语音信号实验二报告

实验二语音信号处理班级：08电子C班姓名：苏清法学号：0815241036（1）语音信号的采集：利用Windows下的录音机，录制一段话音。

然后在Matla软件平台下，利用函数wavread对语音信号进行采样，播放语音信号，并绘制原始语音信号；wavread函数调用格式：y=wavread(file)，读取file所规定的wav文件，返回采样值放在向量y中。

[y,fs,nbits]=wavread(file)，采样值放在向量y中，fs表示采样频率（Hz），nbits表示采样位数。

y=wavread(file,N)，读取前N点的采样值放在向量y中。

y=wavread(file,[N1,N2])，读取从N1点到N2点的采样值放在向量y中。

降采样：利用windows下的录音机录制的音频采样率是固定的fs（=22050），可以选择以下函数实现对语音信号的降采样。

y=x((1:N:length(x))); %对原始信号每隔N个点取一位，即采样率变为原来的1/Ny=resample(yn,L,M); %采样率变为原来的L/M倍y=downsample(yn,N); %%采样率变为原来的1/N倍改变采样率为原来的1/2倍，1/4倍，1/20倍，1/50倍，1/100倍等，分别画出降样前后的信号波形和频谱图，分析采样前后信号的变化Matlab程序如下：（2）重构原信号：降采样后，信号的采样率和采样点数同时变化。

如采样率变为原来的1/2，即对原始信号每隔一个点采样。

如果要恢复原始信号，即信号长度和采样率须变为原来同样大小。

所以，必须对降采样后信号进行插值重构。

对采样后的真实语音信号进行插值重构，滤波，恢复原始信号。

画出插值前后信号的波形以及频谱图，并将重构后信号与原始信号进行比较。

如，对采样率降为原来1/4的降采样后信号插值重构。

Matlab程序如下：（3）对原始信号加入噪声：对原始语音信号加入s=sin(2*pi*f*Ts*n)的噪声，采样后可知Fs = 16000，选择f = 2500，播放加入噪声信号的语音信号，并绘制噪声信号和含噪语音信号；设计频率已知的噪声信号或者用自然噪声信号加在原始语音信号上，构建带噪声信号。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验二语音信号的时域分析一、实验目的在理论学习的基础上，进一步理解和掌握语音信号短时能量、短时过零了分析的意义及基于matlab 的实现方法。

二、实验原理语音是一时变的、非平稳的随机过程，但由于一段时间内(10-30ms)人的声带和声道形状的相对稳定性，可认为其特征是不变的，因而语音的短时谱具有相对稳定性。

在语音分析中可以利用短时谱的这种平稳性，将语音信号分帧。

10～30ms 相对平稳，分析帧长一般为20ms 。

语音信号的分帧是通过可移动的有限长度窗口进行加权的方法来实现的。

几种典型的窗函数有：矩形窗、汉明窗、哈宁窗、布莱克曼窗。

语音信号的能量分析是基于语音信号能量随时间有相当大的变化，特别是清音段的能量一般比浊音段的小得多。

定义短时平均能量[][]∑∑+-=∞-∞=-=-=nN n m m n m n w m x m n w m x E 122)()()()(下图说明了短时能量序列的计算方法，其中窗口采用的是直角窗。

过零就是信号通过零值。

对于连续语音信号，可以考察其时域波形通过时间轴的情况。

而对于离散时间信号，如果相邻的取样值改变符号则称为过零。

由此可以计算过零数，过零数就是样本改变符号的次数。

单位时间内的过零数称为平均过零数。

语音信号x (n )的短时平均过零数定义为()[]()[]()()[]()[]()n w n x n x m n w m x m x Z m n *--=---=∑∞-∞=1sgn sgn 1sgn sgn式中，[]∙sgn 是符号函数，即()[]()()()()⎩⎨⎧<-≥=0101sgn n x n x n x短时平均过零数可应用于语音信号分析中。

发浊音时，尽管声道有若干个共振峰，但由于声门波引起了谱的高频跌落，所以其语音能量约集中干3kHz 以下。

而发清音时．多数能量出现在较高频率上。

既然高频率意味着高的平均过零数，低频率意味着低的平均过零数，那么可以认为浊音时具有较低的平均过零数，而清音时具有较高的平均过零数。

然而这种高低仅是相对而言，没有精确的数值关系。

三、实验步骤1. 语音信号的录音、读入、放音等：利用函数wavread 对语音信号进行采样,记住采样频率和采样点数，给出以下语音的波形图（2.wav ）。

程序：x=wavread('2.wav');Fs=10000; nbits=80;[x,Fs,nbits]=wavread('2.wav'); wavplay(x,10000); soundview(x,10000);2.短时能量分析：(1)首先对语音信号预加重；(2)对预加重后的语音信号进行分帧，帧长取N=256个样值点，帧移取128个样值点；(3)求短时能量。

程序：x=wavread('2.wav');z=filter([1-0.9375],1,x);y=enframe(z,256,128);m1=sum(abs(y),2);m2=sum(y.*y,2);m3=sum(log(y.*y+eps),2);figure(1);subplot(3,1,1),plot(m1)subplot(3,1,2),plot(m2)subplot(3,1,3),plot(m3)3.短时过零率分析：求语音信号的短时过零率。

程序：[x,fs,nbit]=wavread('2.wav');x=x/max(abs(x));len=256;inc=128;tmp1=enframe(x(1:end-1),256,128);tmp2=enframe(x(2:end),256,128);signs=(tmp1.*tmp2)<0;diffs=(tmp1-tmp2)>0.02;zor=sum(signs.*diffs,2)figure;subplot(2,1,1),plot(x)subplot(2,1,2),plot(zor)4.编写程序：参考Matlab有关资料，设计并编写出上述程序。

利用subplot，将语音信号的波形、短时能量、短时过零率放在一张图里进行比较，给出结论，注明语音段和所用窗函数及其宽度。

清音的短时能量小，浊音的短时能量大。

清音的短时过零率大，浊音的短时过零率小。

语音段为第二段，为矩形窗。

5.换一段语音重复上述步骤。

程序：[x,fs,nbit]=wavread('8.wav');soundview(x,10000);z=filter([1-0.9375],1,x);inc=128;len=256;y=enframe(z,len,inc);amp1=sum(abs(y),2);tmp1=enframe(x(1:end-1),256,128);tmp2=enframe(x(2:end),256,128);signs=(tmp1.*tmp2)<0;diffs=(tmp1-tmp2)>0.02;zor=sum(signs.*diffs,2);figure;subplot(3,1,1),plot(x)subplot(3,1,2),plot(amp1)subplot(3,1,3),plot(zor)结果：6.变换帧长观察结果有什么不同。

程序：[x,fs,nbit]=wavread('2.wav'); z=filter([1-0.9375],1,x);inc=128;len=256;y=enframe(z,len,inc);amp1=sum(abs(y),2);tmp1=enframe(x(1:end-1),256,128); tmp2=enframe(x(2:end),256,128); signs=(tmp1.*tmp2)<0;diffs=(tmp1-tmp2)>0.02;zor=sum(signs.*diffs,2);subplot(2,2,1),plot(amp1)title('短时能量（256）')subplot(2,2,2),plot(zor)title('短时过零率（256）')inc1=256;len1=512;y1=enframe(z,len1,inc1);amp11=sum(abs(y1),2);tmp11=enframe(x(1:end-1),512,256);tmp21=enframe(x(2:end),512,256);signs1=(tmp11.*tmp21)<0;diffs1=(tmp11-tmp21)>0.02;zor1=sum(signs1.*diffs1,2);subplot(2,2,3),plot(amp11)title('短时能量（512）')subplot(2,2,4),plot(zor1)title('短时过零率（512）')结果对比：7.（选作）学习语音信号处理工具软件praat(参见教程)，它可以分析、合成、变换语音并为论文著述创建优质图表的计算机程序，Praat程序由阿姆斯特丹大学语音科学研究所(the Institute of Phonetics Sciences of the University of Amsterdam)的Paul Boersma与David Weenink共同开发。

利用它画出波形图，与上述结果比较。

四、实验报告要求报告中要有实验目的、实验原理及步骤、实验程序、实验中得出的图形结果及结论等(清浊音的短时平均能量、短时过零率有什么特点)，注明语音段和所用窗函数及其宽度。

五、思考题1.短时平均能量、短时过零率的主要用途是什么？短时能量的用途：第一，可以区分清音段和浊音段，因为浊音时比清音能量大的多。

第二，可以用来区分声母和韵母的分界，有声和无声的分界，连字的分界等。

第三，作为一种超音段信息，用于语音识别。

短时过零率的用途：第一，初步判断清音和浊音。

第二，与短时能量结合进行端检测。

第三，作为语音频域分析的中间步骤。

2. 窗的宽度（帧长）的改变，对短时能量分析产生怎样的影响？答：语音信号采用短时能量分析时，信号流的处理用分段或分帧来实现，分帧可以用可移动的有限长度窗口进行加权的方法来实现。

窗每次移动的距离如果恰好与窗的宽度相等，相应于各帧语音信号是相互衔接的；如果窗的移动距离比窗宽度要小，那么相邻帧之间将有一部分重叠。