2009-2010 学年度武汉市部分学校九年级元月调研测试数学试卷.doc
2009-2010学年度武汉市部分学校九年级调研测试

2009-2010学年度武汉市部分学校九年级调研测试数学试题武汉市教育科学研究院命制 2010.1.26. 一、选择题(每小题3分,共36分)1、要使式子32+a 在实数范围内有意义,字母a 的取值必须满足( ) A. a ≥0. B. a ≥-23. C. a ≠-23. D. a ≤-23. 2.下列计算① 53⨯=15;②1031003=; ③2723=32;④ 16=4.其中错误的是( ) A . ① B. ② C. ③ D. ④3.在一元二次方程x 2-4x-1=0中,二次项系数和一次项系数分别是( ) A.1 , 4. B.1,-4. C. 1, -1. D. x 2,4x.4.某校九个班进行迎新春大合唱比赛,用抽签的方式确定出场顺序。
签筒中有9根形状、大小完全相同的纸签,上面分别标有出场的序号1,2,3,…,9.下列事件中是必然事件的是( ) A. 某班抽到的序号小于6. B. 某班抽到的序号为0. C. 某班抽到的序号为7. D. 某班抽到的序号大于0.5.在一个口袋中有3个完全相同的小球,把它们分别标号为1,2,3,随机地摸取一个小球然后放回,再随机地摸出一个小球。
则两次取的小球的标号相同的概率为( ) A.31. B. 61 C. 21. D. 91 6.方程x 2-5x-6=0的两根之和为( )A. -6.B. 5C. -5.D. 1.7.下列图案是部分汽车的标志,其中是中心对称图形的是( )A. B. C. D.8.如图,在⊙O 中,弦BE 与CD 相交于点F ,CB,ED 的延长线相交于点A , 若∠A=30°,∠CFE=70°,则∠CDE=( )A. 20°B. 40°.C. 50°.D. 60°9.2009年,甲型H1N1病毒蔓延全球,抗病毒的药物需求量大增。
某制药厂连续两个月加大投入,提高生产量,其中九月份生产35万箱,十一月份生产51万箱。
武汉市2009年初中毕业生学业考试数学试题(含答案).doc

EH ③ = 2;
BE
其中结论正确的是( A .只有①② C.只有③④
④ S△ EDC
=
AH
.
S△ EHC CH
) B.只有①②④ D .①②③④
A
D
H
E
B
C
第Ⅱ卷(非选择题,共 84 分)
二、填空题(共 4 小题,每小题 3 分,共 12 分)
下列各题不需要写出解答过程,请将结论直接填写在答题卷指定的位置.
4500
4000 3500 3000 2500 2000
2622
2936
3255
3587
4140
1500 1000
500 0 2004 年 2005年 2006 年 2007年 2008 年
B.只有②③
C.只有①③
年份 D.①②③
12.在直角梯形 ABCD 中, AD ∥ BC , ∠ABC = 90°,AB = BC ,E 为 AB 边上一点, ∠BCE = 15°,且 AE = AD.连接 DE 交对角线 AC 于 H ,连接 BH .下列结论: ① △ ACD ≌△ ACE ;② △CDE 为等边三角形;
考试科目用 2B 铅笔涂在“答题卡”上.
3.答第Ⅰ卷时,选出每小题答案后,用
2B 铅笔把“答题卡”上对应题目的答案标号
涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,不得答在试题卷上.
4.第Ⅱ卷用钢笔或黑色水性笔直接答在“答题卷”上,答在试题. 卷. 上.无.效. . . . .
预祝你取得优异成绩!
)
A . OM 的长
B. 2OM 的长
C. CD 的长
D. 2CD 的长
D C
D
O
武昌区2010年元月调考九年级数学模拟试卷(word版)

2009——2010学年度上学期期末调研考试九年级数学训练题一、选择题1.x 的取值范围是( )A .1x >B .1x ≥C .1x <D .1x ≤2. 关于x 的一元二次方程225250x x p p -+-+=的一个根为1,则实数p 的值是( ) A .4B .0或2C .1D .1-3.下列运算不正确的是( ) A. 2)43(=6B. 2)3(-=3 C. 4-=-2 D. 2)3(--=314.下列事件:①期末考试小王考了100分;②随机的抽取一张扑克牌,抽到黑桃;③向上抛掷一枚小石头,它最终落了下来;④一个多边形的内角和大于或等于它的外角和,其中是必然事件的有( )A. 1个B. 2个C. 3个D. 4个5.两圆的半径分别是3cm 和5cm ,若两圆的位置关系是相离,则下列圆心距中满足条件的是( ) A. 8cmB. 5cmC. 2cmD. 1cm6.一辆直行的汽车连续通过两个只有红灯与绿灯的路口,其中红灯持续20秒,绿灯持续30秒,则该汽车一路通畅不停的概率是( ) A.52 B.53 C.259 D.25167.如图,将半径为2cm 的圆形纸片折叠后,圆弧恰好经过圆心O ,) A.2cmB.C.D.8.一个正六边形外接圆的半径为3,则它的内切圆半径为( ) A.3 B.233 C.23 D.239.如图所示,小华从一个圆形场地的A 点出发,沿着与半径OA 夹角为α的方向行走,走到场地边缘B 后,再沿着与半径OB 夹角为α的方向折向行走。
按照这种方式,小华第五次走到场地边缘时处于弧AB 上,此时∠AOE =56°,则α的度数是( )。
AA 、52°B 、60°C 、72°D 、76°10.某工程队计划三个月完成一面有475立方的工程,第一个月将完成其中的100立方,以后再每月按x%的增长率加快工程度,但实际工作时,第三个月在第二个月的基础上再增加快了一倍,则根据以上信息可列方程( ),面此时三个月恰好完成工程。
(整理)年元月.

2008----2009学年度 武汉市部分学校九年级调研测试数学试卷武汉市教育科学研究院命制 2009.1.5说明:本试卷分第Ⅰ卷和第Ⅱ卷.第Ⅰ卷为选择题,第Ⅱ为非选择题.全卷满分120分,考试用时120分钟第Ⅰ卷(选择题,共36分)一、选择题(12小题,每小题3分,共36分)1.a 的取值必须满足( )A.0a ≠B.a ≥2C.a ≠2D.a ≤2 2.下列运算不正确的是( )4=5=-110= D.(218=3.如果2是方程20x c -=的一个根,那么c 的值是( )A.4B.-4C.2D.-24.已知两圆的半径为3cm 和1cm ,圆心距为2cm ,则两圆的位置关系是( )A.外离B.外切C.相交D.内切5.有下列事件:①购买一张彩票,中奖;②抛掷一只质地均匀的骰子两次,朝上一面的点数之和一定大于或等于2;③在标准大气压下,水加热到100℃时沸腾;④如果a 、b 为实数,那么a b b a +=+,其中是必然事件的有( ) A.1个 B.2个 C.3个 D.4个6.在奥运会中,双人跳水比赛没有预赛,直接进行决赛,出场顺序由计算机随机决定.2008年8月10日,共有8对选手参赛,“黄金档期”郭晶晶/吴敏霞参赛时被确定为第二个出场的概率为( ) A.18 B.14 C.12 D.387.下列北京奥运项目标志图案中,是中心对称图形为( )A. 柔道B. 赛艇C.田径D.跆拳道8.如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是()A.50°B.40°C.30°D.25°9.2008年10月29日,央行宣布,从10月30日起下调金融机构人民币存款基准利率.其中一年期存款基准利率由现行的3.87%下调至3.60%.11月26日,央行宣布,从11月27日,一年期存款基准利率由现行的 3.60%下调至2.52%.短短一个月,连续两次降息.设平均每次存款基准利率下调的百分率为x,根据以上信息可列方程()A.3.87% 2.52%2x-= B.()23.871 2.52x-=C.()23.87%1% 1.52%x-= D.()22.52%13.87%x+=10.对于一元二次方程20ax bx c++=,下列说话:①若a b c==,那么方程没有实数根;②若b a c=+,则方程必有一根为-1;③若方程有两个不等的实数根,则方程20x bx c++=也有两个不等的实数根.其中正确的是()A.①B.①②C.①③D.②③11.如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O,H分别为边,AB AC的中点,将△ABC绕点B逆时针旋转120°到△11A BC的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为()A.73π4738ππ+ C.π D.43π+12.如图,△ABC的高,CF BG相交于点H,分别延长,CF BG与△ABC的外接圆交于,D E两点.则下列结论:①AD AE=;②AH AE=;③若DE为△ABC的外接圆的直径,则BC AE=;GHF EDCBA1A1ECDAO其中正确的是( )A.①B.①②C.②③D.①②③第Ⅱ卷(非选择题,共84分)二、填空题(4小题,每小题3分,共12分)13.半径为R 的圆内接正六边形的边心距为_______________________. 14.如图是一个中心对称图形,A 为对称中心,若∠C =90°, ∠B =30°,BC =,则BB '的长为__________________________. 15.观察下列各式的规律:①==③=.若=,则a =___________________. 16.为了让国人分享“神七”升空的骄傲,中央电视台在神七发射期间与“问问”网站联合举办“神七我问问”的活动,网友可以自由地提出问题,解答问题,对问题的解答发表评论。
武汉市部分学校九级元月调考数学试卷

武汉市部分学校九级元月调考数学试卷2012-2013学年度武汉市部分学校九年级调研测试数学试卷一、选择题(共IO 小题,每小题3分,共30分) 下列各题中均有四个备选答案,其中有且只有一个正确,请在答题卡上将正确答案的代号 涂黑. 1.要使式子2a 在实数范围内有意义,字母a的取值必须满足A .a≥2 B.a≤2 C .a≠2 D.a≠0 2.车轮要做成圆形,实际上就是根据圆的特征 A .同弧所对的圆周角相等B .直径是圆中最大的弦C .圆上各点到圆心的距离相等D .圆是中心对称图形3.在平面直角坐标系中,点A(l ,3)关于原点O 对称的点A′的坐标为A .(-1,3)B .(1,-3) C.(3,1) D .(-1,-3)4.同时抛掷两枚硬币,正面都朝上的概率为( )A.21B.31C.41D.325.下列式子中,是最简二次根式的是( )A.21B.313C.51D.86.商场举行摸奖促销活动,对于“抽到一等奖的概率为O.1”.下列说法正确的是( ) A.抽10次奖必有一次抽到一等奖 B .抽一次不可能抽到一等奖 . C .抽10次也可能没有抽到一等奖D.抽了9次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖7.方程x 2-7=3x 的根的情况为( )A .有两个不等的实数根B .有两个相等的实数根C .有一个实数根 D.没有实数根 8.收入倍增计划是2012年l1月中国共产党第十八次全国代表大会报告中提出的,“2020年实现国内生产总值和城乡居民人均收入比2010年翻一番”,假设2010年某地城乡居民人 均收人为3万元,到2020年该地城乡居民人均收入达到6万元,设每五年的平均增长率为 a %,下列所列方程中正确的是( )A.3(1+ a %)=6B.3(1+a%)2=6 C.3 +3(1-a %)+3(1+ a %)2=6 D.3(1+2 a %)=6OI ABCBOD9.已知x 1、x 2是方程x 2-5x+l=O 的两根,则x 1+x 2的值为( )A.3B.5C.7 D . 10.如图,点I 和O 分别是△ABC 的内心和外心,则∠A IB 和∠AOB 的关系为( )A .∠AIB=∠AOB B .∠AIB≠∠AOBC .2∠AIB -∠AOB=180°D .2∠AOB -∠AIB=180°二、填空题(共6小题,每小题3分,共18分) ll.计算:248÷6=____12.为了宣传环保,小明写了一篇倡议书,决定用微博转发的方式传播,他设计了如下的传播规则:将倡议书发表在自己的微博上,再邀请II 个好友转发倡议书,每个好友转发倡议书之后,又邀请n 个互不相同的好友转发倡议书,依此类推,已知经过两轮传播后,共有111人参与了传播活动,则n= ____.13.如图,在⊙O 中,半径OA ⊥弦BC ,∠AOB=50°,DBAHFOE则圆周角∠ADC=_____14.如图,正八边形ABCDEFGH 的半径为2,它的面积为____.15.一个扇形的弧长是20πcm ,面积是240πcm 2,则扇形的圆心角是____.16.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性的大小相同,三辆汽车经过这个十字路口,至少有两辆车向左转的概率为____.三、解答题(共8小题,共72分)下列各题需要在答卷指定位置写出文字说明、证DCOAB573420明过程、演算步骤或域出图形.17.(本题6分)解方程:x (2x-5)=4x-10.18.(本题6分)有两个可以自由转动的质地均匀转盘都被分成了3.个全等的扇形,在每一扇形内均标有不同的自然数,如图所示,转 动转盘,两个转盘停止后观察并记录两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向上边的扇形).(l)用列表法或画树形图法求出同时转动两个转盘一次的所 有可能结果;(2)同时转动两个转盘一次,求“记录的两个数字之和为7”的概率.19.(本题6分)如图,两个圆都以点D为圆心.求证:AC =BD;20.(本题7分)已知关于x 的一元二次方程x 2+4x+m=O .图1CAB图2B 1C 1CAOB(1)当m=l 时,请用配方法求方程的根: (2)若方程没有实数根,求m 的取值范围.21.(本题7分)△ABC 为等边三角形,点D 是边AB 的延长线上一点(如图1),以点D 为中心,将△ABC 按顺时针方向旋转一定角度得到△A 1B 1C 1.(1)若旋转后的图形如图2所示,请将△A 1B 1C 1以点D 为中心,按顺时针方向再次旋转同样的角度得到△A 2B 2C 2,在图2中用尺规作出△A 2B 2C 2,请保留作图痕迹,不要求写作法:(2)若将△ABC 按顺时针方向旋转到△A 1B 1C 1的旋转角度为α(0°<α<360°). 且AC∥B 1C 1,直接写出旋转角度α的值为_____22.(本题8分)如图,已知在Rt△ABC 中,∠ACB=90°,BC >AC ,⊙O 为△ABC 的外接圆,以点C 为圆 心,BC 长为半径作弧交CA 的延长线于点D ,交⊙O 于点E ,连接BE 、DE. (l)求∠DEB 的度数;(2)若直线DE 交⊙0于点F ,判断点F 在半圆AB 上的位置,并证明你的结论.FEDOABC23.(本题10分)如图,利用一面墙(墙EF 最长可利用25米),围成一个矩形花园ABCD ,与围墙平行的 一边BC 上要预留3米宽的入口(如图中MN 所示,不用砌墙),用砌46米长的墙的材料,当 矩形的长BC 为多少米时,矩形花园的面积为299平方米.3m25mD C EAB图1ECAD 图2F EAD24.(本题10分)已知等边△ABC,边长为4,点D 从点A 出发,沿AB 运动到点B ,到点B 停止运动.点E 从A 出发,沿AC 的方向在直线AC 上运动.点D 的速度为每秒1个单位,点E 的速度为每秒2个单位,它们同时出发,同时停止.以点E 为圆心,DE 长为半径作圆.设E 点的运动时间为t 秒. (l)如图l ,判断⊙E 与AB 的位置关系,并证明你的结论;(2)如图2,当⊙E 与BC 切于点F 时,求t 的值; (3)以点C 为圆心,CE 长为半径作⊙C ,OC 与射线AC 交于点G .当⊙C 与⊙E 相切时,直接 写出t 的值为____ED OABC25.(本题12分)如图,在边长为1的等边△OA B 中,以边AB 为直径作⊙D ,以D 为圆心似长为半径作圆O,C 为半圆AB 上不与A 、B 重合的一动点,射线AC 交⊙O 于点E,BC=a,AC=b, (1)求证:AE=b+3a (2)求a+b 的最大值;(3)若m 是关于x 的方程:x 2+3ax=b 2+3ab 的一个根,求m 的取值范围.参考答案题1 2 3 4 5 6 7 8 9 10 号A C D CBC A B A C答案11.4212.10 13.25 14.8215.150716.2717.解:2x2-9x+10=0 ………3分∴x 1=2 x 2=25 …………6分 18.解:(1) A 盘 B 盘 0 243 0,3 2,3 4,3 5 0,5 2,5 4,5 70,72,74,7由上表可知转动两个圆盘一次共有9中不同结果…………3分(2)第一问的9中可能性相等,其中“记录的两个数字之和为7”(记为事件A )的结果有3个,∴所求的概率P(A)=93=31………6分19.证明:过点O 作OE ⊥AB 于E ,………1分 在小⊙O 中,∵OE ⊥AB ∴EC=ED ………3分 在大⊙O 中,∵OE ⊥AB ∴EA=EB ………5分 ∴AC=BD ………6分20.(1)当m=1时,x 2+4x+1=0 ………1分x 2+4x+4=3 ,(x+2)2=3,x+2=±3∴x=-2±B2C 2A 2B 1C1A 1C A OBαB 1C 1A1C A O B αB 1C11CAOB3……4分(2)∵x2+4x+m=O ∴42-4m<0,∴m>4 ………7分21.(1)如图……3分(2)60°或240图如下22.证明:(1)连接CE 、BD ,∵∠BDE 与∠ECB 所对的弧都为弧EB∴∠BDE=21∠ECB 同理∠DBE=21∠ECD ∴∠BDE+∠DBE =21∠DCB ………3分∵∠ACB=90°∴∠BDE+∠DBE =45°∴∠DEB=135°………5分(2)由(1)知∠DEB=135°∴∠BEF=45°………6分 ∴弧FB=21弧AB 即F 为弧AB 中点;23.解:设矩形花园BC 的长为x 米,则其宽为21(46-x+3)米,依题意列方程得: 21(46-x+3)x=299,……5分 x 2-49x-498=0, 解这个方程得:x 1=26, x 2=23………8分25<26∴x 1= 26不合题意,舍∴x=23 …………9分答:矩形花园的长为23米; …………10分GEBC D24.解:(1)AB 与⊙E 相切, ………1分 理由如下:过点D 作DM ⊥AC 于点M∵△ABC 为等边三角形∴∠A=60° 在Rt △ADM 中∵AD=t, ∠A=60°∴AM=21t,DM=23t, ∵AE=2t ∴ME=23t,在Rt △DME中,DE2=AM2+EM2=3t2,在Rt △ADE 中,∵AD 2=t 2,AE 2=4t 2,DE 2=3t 2,∴AD 2+DE 2=AE 2∴∠ADE=90°∴AD 与⊙D 相切 …………4分(2)连BE 、EF ,∵BD 、BE 与⊙O 相切∴BE 平分∠ABC∵AB=BC ∴AE=CE ∵AC=4 ∴AE=2,t=1 …………8分(3)t=133832±;当⊙C 与⊙E 相切时,DE=EG=2EC,∵DE=3t,∴EC=23t,有两种情形:第一,当E 在线段AC 上时,AC=AE+EC,∴2t+23t=4,t=133832-……9分GEBC DMH EDOABC第二、当点E 在AC 的延长线上时,AC=AE-EC, 2t-23t=4,t=133832 …….10分25.解:(1)连接BE,∵△ABC 为等边三角形∴∠AOB=60°∴∠AEB=30°∵AB 为直径∴∠ACB=∠BCE=90°,∵BC=a ∴BE=2a,CE=3a,∵AC=b ∴AE=b+3a …………3分(2)过点C 作CH ⊥AB 于H,在Rt △ABC 中,BC=a,AC=b,AB=1∴a 2+b 2=1∴(a+b) 2=a 2+b 2+2ab=1+2ab=1+2CH ·AB=1+2CH≤1+2MD=1+2AD=2 ∴a+b ≤2,故a+b 的最大值为2…………7分(3) x 2+3ax=b 2+3ab ∴x 2- b 2+3ax-3ab=0 (x+b)(x-b)+3a(x-b)=0,(x-b)(x+b+3a)=0∴x=b 或x=-(b+3a)当a=m=b时,m=b=AC<AB=1∴0<m<1 (9)分当m=-(b+3a)时,由(1)知AE=-m,又AB<AE≤2AO=2∴1<-m≤2∴-2≤m<-1…………11分∴m的取值范围为0<m<1或-2≤m<-1。
2009—2010学年度武汉市部分学校九年级四月调考测试

1 2
D.
4 3
第1页 共5页
11、来自某综合市场财务部的报告表明,商场 2009 年 1-4 月份的投资总额一共是 2010 万元.商场 2009 年 第一季度每月利润统计图和 2009 年 1—4 月份利润率统计图如下(利润率=利润 ÷ 投资金额) : 第 10 题图 20 09年1月-4月份 利润 率统计 图
C
甲图
乙图
第6题 第 7 题图 7.分别由五个大小相同的正方形组成的甲﹑乙两个几何体如上图所示,它们的三视图中完全一致的是 ( ) A.主视图 B.左视图 C.俯视图 D.三视图 8、若 x1 、 x2 是一元二次方程 x − 2 x − 3 = 0 的两个根,则 x1 + x2 的值是(
2
)
B. −2 C. 4 D. −3 A. 2 9、古希腊的毕达哥拉斯学派把 1,3,6,10,…,这样的数称为“三角形数” ,把 1,4,9,16,…,这样的数 称为“正方形数”. “三角形数”和“正方形数”之间存在如下图所示的关系:
20 09年第 一季度 每月 利润统 计图 月利 润/万元 135 130 12 5 12 0
0.10 0.05
利润率
0.35 30.0% 0.30
13 0
0.25 26.0% 0.20 20.0% 0.15 25.0%
125 120 115
1月
2月
3月
月份
0.00
1月
2月
3月
4月
月份
根据以上信息,下列判断:①商场 2009 年第一季度中 1 月份投资金额最多;②商场 2009 年第一季度 中 2 月份投资金额最多;③商场 2009 年 4 月份利润比 2 月份的利润略高;④商场计划 2010 年 4 月份的利 润率比去年同期持平,利润不低于去年第一季度的最高值,那么商场 2010 年 4 月份的投资金额至少为 520 万元.其中正确的是( ) A.①② B. ②③ C. ①③④ D. ②③④ 12.如图,在矩形 ABCD 中, AB = 2 BC , E 为 CD 上一点,且 AE = AB , M 为 AE 的中点.下列结论: ① DM = DA ; ② EB 平分 ∠AEC ; E
2010武汉市九年级四月调考数学测试题及答案
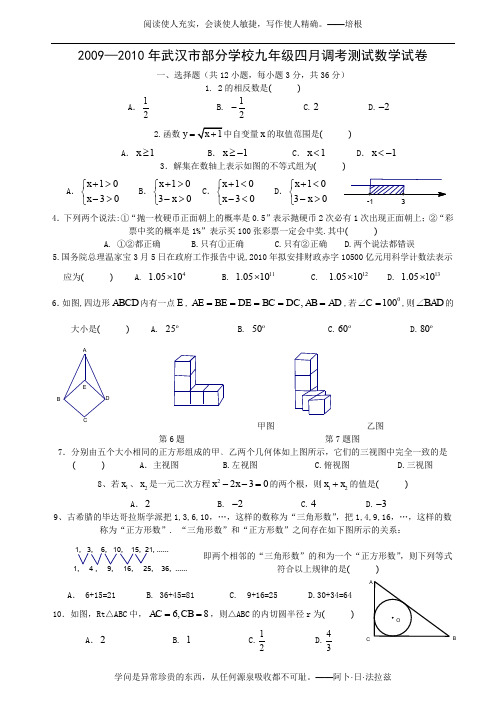
2009—2010年武汉市部分学校九年级四月调考测试数学试卷一、选择题(共12小题,每小题3分,共36分)1. 2的相反数是( )A .12 B. 12- C.2 D.2- 2.函数1y x =+中自变量x 的取值范围是( )A .1x ≥B .1x ≥-C .1x <D .1x <-3.解集在数轴上表示如图的不等式组为( )A .1030x x +>⎧⎨->⎩B .1030x x +>⎧⎨->⎩C .1030x x +<⎧⎨-<⎩D .1030x x +<⎧⎨->⎩4.下列两个说法:①“抛一枚硬币正面朝上的概率是0.5”表示抛硬币2次必有1次出现正面朝上;②“彩票中奖的概率是1%”表示买100张彩票一定会中奖.其中( )A. ①②都正确B.只有①正确C.只有②正确D.两个说法都错误5.国务院总理温家宝3月5日在政府工作报告中说,2010年拟安排财政赤字10500亿元用科学计数法表示应为( ) A. 41.0510⨯ B. 111.0510⨯ C. 121.0510⨯ D. 131.0510⨯6.如图,四边形ABCD 内有一点E ,,AE BE DE BC DC AB AD =====,若0100C ∠=,则BAD ∠的大小是( ) A. 25o B. 50o C.60o D.80o甲图 乙图第6题 第7题图7.分别由五个大小相同的正方形组成的甲﹑乙两个几何体如上图所示,它们的三视图中完全一致的是( ) A .主视图 B.左视图 C.俯视图 D.三视图8、若1x 、2x 是一元二次方程2230x x --=的两个根,则12x x +的值是( )A .2 B. 2- C.4 D.3-9、古希腊的毕达哥拉斯学派把1,3,6,10,…,这样的数称为“三角形数”,把1,4,9,16,…,这样的数称为“正方形数”. “三角形数”和“正方形数”之间存在如下图所示的关系:即两个相邻的“三角形数”的和为一个“正方形数”,则下列等式符合以上规律的是( )A . 6+15=21 B. 36+45=81 C. 9+16=25 D.30+34=6410.如图,Rt △ABC 中,6,8AC CB ==,则△ABC 的内切圆半径r 为( )A .2 B. 1 C.12 D.43EDC B A 1, 4 , 9, 16, 25, 36, ......1, 3, 6, 10, 15, 21, ......B O CA3-1y=x B A o y x 2009年1月-4月份利润率统计图利润率25.0%26.0%30.0%0.0520.0%0.350.250.150.200.100.300.00月份4月3月2月1月1301201252009年第一季度每月利润统计图月利润/万元月份1351301251201153月2月1月11、来自某综合市场财务部的报告表明,商场2009年1-4月份的投资总额一共是2010万元.商场2009年第一季度每月利润统计图和2009年1—4月份利润率统计图如下(利润率=利润÷投资金额): 第10题图根据以上信息,下列判断:①商场2009年第一季度中1月份投资金额最多;②商场2009年第一季度中2月份投资金额最多;③商场2009年4月份利润比2月份的利润略高;④商场计划2010年4月份的利润率比去年同期持平,利润不低于去年第一季度的最高值,那么商场2010年4月份的投资金额至少为520万元.其中正确的是( )A .①② B. ②③ C. ①③④ D. ②③④12.如图,在矩形ABCD 中, 2AB BC =,E 为CD 上一点,且AE AB =,M 为AE 的中点.下列结论:① DM DA =; ② EB 平分AEC ∠ ; ③ABE ADE S S ∆∆=;④22BE AE EC =.其中结论正确的个数是( )A .1 B. 2 C. 3 D. 4二、填空题(共4小题,每小题3分,共12分)13.计算tan30︒= ;23(2)a -= ;2(2)-= .14.小明五次数学考试的成绩如下:84,87,x ,90,95,成绩都为整数,其中x 为中位数,已知这组数据的平均数小于中位数,那么x = .15.在平面直角坐标系中,直线y kx =向右平移2个单位后,刚好经过点(0,4),则不等式24x kx >+的解集为 .16.如图,B 为双曲线(0)k y x x=>上一点,直线AB 平行于y 轴交直线y x =于点A ,若224OB AB -=,则k = .三、解答下列各题(共9小题,共72分)17.(本题满分6分)解方程:2310x x +-=.B CE MA D18. (本题满分6分)先化简,再求值:35(2)242x x x x -÷----,其中33x =-.19. (本题满分6分)在等边ABC ∆中,点D ,E 分别在边BC ,AB 上,且BD AE =. 求证AD CE =.20. (本题满分7分)小聪和小明玩一种摸球游戏:一布袋中有红、黄、白、黑四种颜色的球各一个,它们除颜色外其它都一样.请一人从布袋中摸出两个球来,如果至少有一个红球,则小聪赢,如果没有摸到红球,则小明赢.他们设计了甲、乙两种摸球方案,甲方案:一次摸出两个球;乙方案:摸出一个球后,放回去摇匀,再摸出一个.请你分别利用列表法和画树状图的方法求出甲乙两个方案小聪赢的概率,并判断哪种方案对小聪更有利.21. (本题满分7分)如图,已知网格中每个正方形的边长都是1,图中的阴影图案是由两段以格点为圆心,分别以小正方形的边长和对角线长为半径的圆弧和网格的边围成.(1)填空:图中阴影部分的面积是 ;(2)请你在网格中以阴影图案为基本图案,借助轴对称、平移或旋转设计一个完整的图案(要求至少含有两种图形变换).第21题图EC D B A22. (本题满分8分)如图,AE 是ABC ∆外接圆O 的直径,AD 是ABC ∆的边BC 上的高,EF BC ⊥,F 为垂足.(1)求证:BF CD =;(2)若1CD =,3AD =,6BD =,求O 的直径.23. (本题满分10分)某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x 元,每个月的销售量为y 件.(1)求y 与x 的函数关系式并直接写出自变量x 的取值范围;(2)设每月的销售利润为W ,请直接写出W 与x 的函数关系式;(3)每件商品的售价定位多少元时,每个月可获得最大利润?最大的月利润是多少元?24. (本题满分10分)如图,P 为正方形ABCD 边BC 上任一点,BG AP ⊥于点G ,在AP 的延长线上取点E ,使AG GE =,连接BE ,CE .(1)求证:BE BC =;(2)CBE ∠的平分线交AE 于N 点,连接DN ,求证:2BN DN AN +=;(3)若正方形的边长为2,当P 点为BC 的中点时,请直接写出CE 的长为.(1) (2)D o CE F B A25. (本题满分12分)抛物线2(6)3y a x =+-与x 轴相交于A ,B 两点,与y 轴相交于C ,D 为抛物线的顶点,直线DE x ⊥轴,垂足为E ,23AE DE =.(1)求这个抛物线的解析式;(2)P 为直线DE 上的一动点,以PC 为斜边构造直角三角形,使直角顶点落在x 轴上.若在x 轴上的直角顶点只有一个时,求点P 的坐标;(3)M 为抛物线上的一动点,过M 作直线MN DM ⊥,交直线DE 于N ,当M 点在抛物线的第二象限的部分上运动时,是否存在使点E 三等分线段DN 的情况,若存在,请求出所有符合条件的M 的坐标,若不存在,请说明理由阅读使人充实,会谈使人敏捷,写作使人精确。
湖北武汉武昌梅园中学2010年元月调考九年级模拟试卷--数学

湖北省武汉市武昌区梅园中学2010年元月调考模拟试卷一.选择题(共12小题,每小题3分,共36分) 1.x 的取值范围是( )A .x >1B .x ≥1C .x <1D .x ≤12. 下列计算正确的是( )AB0 C=9 D﹣3 3. 已知关于x 的方程x ²-kx -6=0的一个根为x=3,则实数k 的值为( )A .1B .1-C .2D .2-4. 已知两圆的半径分别为3和5,圆心距为4,则这两圆的位置关系是( )A .内切B .外切C .相交D .外离5. 下面事件:①掷一枚硬币,着地时正面向上;②在标准大气压下,水加热到100℃会沸腾;③买一张福利彩票,开奖后会中奖;④明天会下雨.其中,必然事件有( ) A .1个 B .2个 C .3个 D .4个6. 小明外出游玩,带上棕色、蓝色、淡黄色3件上衣和蓝色、白色2条长裤,他任意拿出1件上衣和1条长裤正好是棕色上衣和蓝色长裤的概率是( ) A .12B .15C .16D .197. 下列图案既是轴对称图形,又是中心对称图形的是( )A .B .C .D .8. 如图,AB 是⊙O 的直径,C ,D 为圆上两点,∠AOC =130°,则∠D 等于( )A .25°B .30°C .35°D .50°ODCB A OC′C A′ADEODCBA9.某市2008年国内生产总值(GDP)比2007年增长了12%,由于受到国际金融危机的影响,预计今年比2008年增长7%,若这两年GDP年平均增长率为x%,则x%满足的关系是()A.12%+7%=x%B.(1+12%)(1+7%)=2(1+x%)C.12%+7%=2x%D.(1+12%)(1+7%)=(1+x%)²10.关于x的一元二次方程ax2+bx+c=0(a≠0)。
下列论断:⑴若a-b+c=0,则它有一根为﹣1;⑵若它有一根为﹣c,则一定有ac-b=﹣1;⑶若b=a+2c,则它一定有两个不相等的实数根;其中正确的是()A.0个B.1个C.2个D.3个11.如图,AC是汽车挡风玻璃前的刮雨刷.如果AO=65㎝,CO=15㎝,当刮雨刷AC绕点O旋转90°时,则刮雨刷AC扫过的面积为()A.25πcm2B.1000πcm2C.25cm2D.1000cm212.如图,PA、PB切⊙O于A、B,PO及其延长线分别交⊙O于C、D,AE为⊙O的直径,连结AB、AC,下列结论:①CB=DE;②∠ABP=∠DOE;③AC平分∠PAB;④∠CAB=∠BAE;其中正确的有()A.①②③B.①②③④C.①②④D.②③④二.填空题(共4小题,每小题3分,共12分)13.若圆内接正三角形的边长为2,则圆的半径为______;14.如图, Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E= 90°,AC=3,DE=5,则OC的长为______;15.观察并分析下列数据,寻找规律:03,﹣第10个数据应是______;第n个数据是______;16.一个小组有若干人,新年互送贺年卡一张,已知全组共互送贺年卡72张,则这个小组的人数为______;三.解答题(共9小题,共72分)17.(本题6分)解方程:x2+4x-2=018. (本题6a 值代入化简结果进行计算;19. (本题6分)如图,已知△ABC ,图中的每个小正方形的边长为1;⑴AC 的长等于______,⑵先将△ABC 向右平移2个单位得到△A B C ''',在图中画出△A B C ''',并写出A 点的对应点A '的坐标是______;⑶再将△ABC 绕点C 按逆时针方向旋转90°后得到△A 1B 1C 1,在图中画出△A 1B 1C 1,并写出A点对应点A 1的坐标是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009~2010 学年度
武汉市部分学校九年级调研测试
说明:本试卷分第Ⅰ卷和第Ⅱ卷.第Ⅰ卷为选择题,第Ⅱ卷为非选择题.全卷满 分 120 分,考试用时 120 分钟.
第Ⅰ卷(选择题 共 36 分)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在答题卷指定位置;
2.每小题选出答案后,用 2B 铅笔在答题卷上将对应的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案,答在试卷上无效;
3.考试结束,监考人员将本试卷和答题卷一并收回.
一.选择题(12 小题,每小题 3 分,共 36 分)
1.要使式子 A .a ≥0
B .a ≥
C .a ≠
D .a ≤
2.下列计算①
②
;
③
; 在实数范围内有意义,字母 a 的取值必须满足
= ;
④ =4.其中错误的是
A .①
B .②
C .③
D .④
3.在一元二次方程 x 2-4x -1=0 中,二次项系数和一次项系数分别为
A .1,4
B .1,-4
C .1,-1
D .x 2,4x
4.某校九个班进行迎新春大合唱比赛,用抽签的方式决定出场顺序.签筒中有
9 根形状、大小的纸签,上面分别标有出场的序号 1、2、3、…,9.下列事件中 是必然的是
A .某班抽到的序号小于 6.
B .某班抽到的序号为 0.
C .某班抽到的序号为 7.
D .某班抽到的序号大于 0.
5.在一个口袋中有3 个完全相同的小球.把它们分别标号为1,2,3,随机地
摸取一个小球然后放回,再随机地摸出一个小球.则两次取的小球的标号相同的
概率为
A.
B.
C.
D.
6.方程x2-5x-6=0 的两根之和为
A.-6
B.5
C.-5
D.1
7.下列图案是部分汽车的标志,其中是中心对称的是
A.
B.
C.
D.
8.如图,在O 中,弦BE 与CD 相交于点F,CB,ED 的延长线相交于点A,若∠A=30°\u65292X∠CFE=70°\u65292X则∠CDE=
A.20°
B.40°
C.50°
D.60°
9.2009 年甲型H1N1 病毒蔓延全球,抗病毒的药物需求量大增.某制药厂连续
两个月加大投入,提高生产量,其中九月份生产35 万箱,十一月份生产51 万箱.设
九月份到十一月份平均每月增长的百分率为x,根据以上信息可以列出的正确的
方程为
A.51(1-x)2=35
B.35(1+x)=51
C.35(1+x)=51(1-x)
D.35(1+x)2=51
10.2009 年7 月22 日上午,长江流域的居民有幸目睹了罕见的日全食天文奇观,
下面是天文爱好者拍摄的三个瞬间,其中白色的圆形是太阳,逐渐覆盖太阳的黑
色圆形是月亮.如果把太阳和月亮的影像视作同一平面中的两个圆,则关于这两
圆的圆心距与两圆的半径之间的关系的下列说法,正确的是
A.三张图片中圆心距都大于两圆的半径之和.
B.第一幅图片中圆心距等于两圆的半径之和.
C.第三幅图片中圆心距小于两圆的半径之差.
D.三张图片中圆心距都大于两圆的半径之差且小于两圆的半径之和.
10.已知b2-4ac>0.下列方程①ax2+bx+c=0;②x2+bx+ac=0;③cx2+bx
+a=0.其中一定有两个不等的实数根的方程有
A.0 个
B.1 个
C.2 个
D.3 个
12.在O 中,弦CD 垂直于直径AB,E 为劣弧一动点(不与点B,C 重合),DE 交弦BC 于点N,AE 交半径OC 于点M,在E 点运动过程中,∠AMC 与∠BNE 的大小关系为
A.∠AMC>∠BNE
B.∠AMC=∠BNE
C.∠AMC<∠BNE
D.随着E 点的运动以上三种关系都有可能.
第Ⅱ卷(选择题共84 分)
注意事项:
用黑色墨水的签字笔或钢笔直接答在答题卷上该题对应答题区域内,答在试卷上
无效.
二.填空题(4 小题,每小题 3 分,共12 分)
13.下列等式呈现某种规律,根据规律直接写出第4 个等式为________
14.在平面直角坐标系中有三个点A(1,2),B(-1,2)和C(1,-2),其中关于
原点O 的对称两点为点________与点________.
15.若正n 边形的一个内角等于它的中心角的1.5 倍,则n=________.
16.不透明的口袋中有黑白围棋子若干颗,已知随机摸出一颗是白棋子的概率为
,若加入10 颗白棋子,随机摸出一颗是白棋子的概率为,口袋中原来有
________颗围棋子.
三.解答题(9 小题,共72 分)
17.(本题满分6)计算:.
18.本题满分6 分)解方程:x2-2 x+=0
19.(本题满分 6 分)在平面直角坐标系中有A(0,1),B(-2,0)两点,将线段
AB 以O 为旋转中心逆时针分别旋转90°\u65292X180°\u65292X270°\u65292X请画出旋转后的图形.
20.(本题满分7 分)如图,直线AB 经过O 上的点C,并且OA=OB,CA=CB,求证直线AB 是O 的切线.
21.(本题满分7 分)现有一块矩形钢板ABCD,长AD=7.5 dm 宽AB=5 dm,采
用如图1 的方式在这块钢板上截除两个正方形得到如图 2 所示的模具模具横纵方
向的长柄等宽(即BE=DF).若模具的面积等于原矩形钢板的面积的一半,求模
具长柄的宽.(参考数据:≈1.41,结果精确到0.1 dm)
22.(本题满分8 分)如图D 为Rt△ABC 斜边AB 上一点,以CD 为直径的圆分别交△ABC 三边于E,F,G 三点,连接FE,FG.
(1)求证:∠EFG=∠B
(2)若AC=2BC=4 ,D 为AE 的中点,求CD 的长.
23.(本题满分10 分)
如图,两个转盘A,B 都被分成了 3 个全等的扇形,在每一扇形内均标有不同的
自然数,固定指针,同时转动转盘A,B,两个转盘停止后观察两个指针所指扇
形内的数字(若指针停在扇形的边线上,当作指向上边的扇形).
(1)用列表法(或树形图)表示两个转盘停止转动后指针所指扇形内的数字的所有
可能结果;
(2)小明每转动一次就记录数据,并算出两数之和,其中“和为7”的频数及频率
如下表:
如果实验继续进行下去,根据上表数据,出现“和为7”的频率将稳定在它的概
率附近,试估计出现“和为7”的概率;
(3)根据(2),若0<x<y,试求x 与y 的值.
24.(本题满分10 分)如图,在等腰△ABC 中,AB=AC,∠ABC=α,在四边
形BDEC 中,DB=DE,∠BDE=2α,M 为CE 的中点,连接AM,DM.
(1)在图中画出△DEM 关于点M 成中心对称的图形.
(2)求证AM DM;
(3)当α=________,AM=DM.
25.(本题满分12 分)
如图,在平面直角坐标系中, D 与坐标分别相交于A(-,0),B( ,0),C(0,3)三点.
(1)求 D 的半径;
(2)E 为优弧一动点(不与A,B,C 三点重合),EN x 轴点N,M 为半径DE
的中点,连接MN,求证∠DMN=3∠MNE;
(3)在(2)的条件下,当∠DMN=45°\u26102X,求E 点的坐标.。
