滚动轴承接触的非线性有限元分析
基于有限元的滚动轴承非线性接触分析
麓 翳
基 于 有 限元 的 滚 动 轴 承 非 线 性 接 触 分析
崔 波 程 珩
太原 00 2 ) 3 0 4 ( 原理工大学 机 械电子工程研 究所 山西 太
摘
要: 基于有 限元 分析软件A ss NY ,对滚 动轴承进 行非 线性接触 分析 ,得到其 受载过程 中的应 力和应 变分布情 况 将 计算结 果同赫 兹解 比较 ,二者较 为接
式 中, :00 3 3 . 6 p, 2
、
y是接 触 区尺寸 ,可 通过 图 表查 出 。对于轴 承钢 可 取值 为 l 。
赫 兹接触 应 力计算 式 表述 如下 : 最 大赫兹 接触 应 力:
p一
考
=
⑤
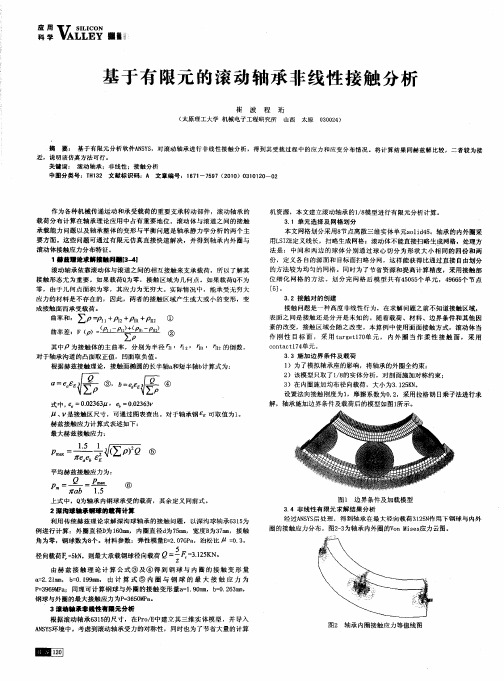
图1 边 界条件 及 加载模 型 3 4 非线性 有 限元 求解结 果分 析
cn at 7单 元 。 ot c 14
其 中 为接触 体 的 主 曲率 ,分 别 为半 径 , h,听2 , 对于轴 承沟 道 的凸面 取正 值 ,凹面 取 负值 。
3 3 施 加边界 条件 及载 荷 .
根 据赫 兹接 触理 论 ,接触 面椭 圆的 长 半轴瘌 短半 轴b 算式为 ; 计 a e£ 1E ③ , b=
本 文 网格划 分 采用 8 节点 离散 三维 实 体单元 s ld5 o i4 。轴承 的 内外 圈采 用 L IE S Z 定义线 长 ,扫略 生成 网格 ;滚 动体 不能 直接 扫略 生成 网格 ,处理 方
法 是 : 中 问 和 两边 的球 体 分 别通 过 球 心 切 分 为 形状 大 小 相 同 的 四份 和 两 份 , 定义 各 自的源 面 和 目标 面扫 略分 网,这 样 能获得 比通过 直接 自由划 分 的 方法 较 为均 匀 的网 格 。同 时为 了节 省 资源 和提 高计 算 精度 ,采 用接 触 部 位 细 化 网 格 的 方 法 。划 分完 网格 后 模 型 共 有 40 5 单元 ,46 5 节 点 5 5个 96 个
滚动轴承力学特性的有限元分析研究

Analytical Research on Mechanical Properties of Rolling Bearings based on Finite Element Method
Candidate Major Supervisor
: Yan Xin : Material Processing Engineering : Prof. Liu Shunhong
学位论文作者签名: 日期: 年 月 日
学位论文版权关保留、使用学位论文的规定,即:学校有权 保留并向国家有关部门或机构送交论文的复印件和电子版,允许论文被查阅和借阅。 本人授权华中科技大学可以将本学位论文的全部或部分内容编入有关数据库进行检 索,可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
The mechanical characteristics and movement characteristics of bearing under the dynamic conditions were analyzed, the stress distribution was similar to static conditions, but also shows a different, the stress is a bit great in the area of the front and the behide of the contact area. The maximal stress may deviate from contact center, and the maximal stress obtained from dynamics analysis is greater than that obtained from statics analysis on the condition of the same load. The movements of the balls were instability, and the velocity of the ball, the motion state and motion trajectory can be obtained at the same
基于ANSYS的滚针轴承的有限元分析

算,本文只考虑滚针与外圈和空心轴的接触情况。忽略滚针之间的互相接触,所以在柱坐标下将滚针进行
了,z方向的位移砜,以约束.
万方数据
中国工程机械学报
第6卷
2.3加载滚针轴承只承受径来自载荷,对空心轴的内表面加载,实际的
载荷是1个变化的值,底部最大,到边缘逐渐减小,基本满足如
下函数关系:Qi=Q1×sinO[6】,其中Q1为最大载荷,①为夹
受载荷,因此只建立下半圈模型进行分析.
选择的单元类型为Solid8node45,轴承材料的弹性模量E=206 GPa,泊松比/2=0.3,将接触区域的
网格细化,共有188 249个单元,398 765个节点.
、
2.2施加边界条件【5】5
将轴承外圈的外表面施加全约束,截面对称约束,对空心轴的端面z向的自由度进行约束.为简化计
3 8 2
罡
:
、
6●5
R
9
目
4
8
2
∞"弱强如”∞M毖%侉引限筋孙∞"船n盯纪瓶 7
7
2
9石2
9
罡
乏
6
\
2
R
翅
9
5
2
9
聊暑:Ⅲ捌琊硎粥拗蟒旧7●Ⅲ6●}眦置弘t 5
图10空心轴径向等效应力分布图
豫.10 Von Mises stress of the hollow shaft
图11外圈径向等效应力分布圈
outer她 rig.11 V抽Mises stress of the
3结论
(1)由计算可知最大的接触应力值为644 MPa,而材料的屈服极限是1 175 MPa,材料满足强度要求. (2)最大接触应力出现在滚针与空心轴的接触面上.滚针在接触面中心的接触应力最大,沿着远离接 触中心的方向,接触应力值逐渐减小到零,整个应力分布曲线呈抛物线状,这与赫兹弹性体接触理论的应 力分布规律是相同的. (3)滚针与空心轴接触时,在滚针的端部出现了“边缘效应”的现象,设计时应该设置减载槽,以消除 “边缘效应”.2端以外应力值分布相对比较均匀.滚针与外圈接触时,因有减载槽,没有在两端出现应力集 中的现象,相反应力值衰减为零. (4)空心轴和外圈在径向方向上的最大等效应力并非出现在接触表面,而是在距接触表面0.256 mm 和O.268 ITIITI处,
高速重载滚动轴承接触应力和变形的有限元分析

一62~机械设计与制造MachineryDesign&Manufacture第10期2008年10月文章编号:100l一3997(2008)10—0062—02高速重载滚动轴承接触应力和变形的有限元分析蒋立冬1应丽霞2(1哈尔滨第七O--研究所传动研究室,哈尔滨150036)(2哈尔滨工程大学机电工程学院,哈尔滨150001)Contactstressanddeformationanalysis0fhigh—speedandheavy.dutyrollingbearingbyFEMJIANGLi-dongI,YINGLi-xia2(1HarbinNo.703ResearchInstituteTransmissionResearchDepartment,Harbin150036,China)(2SchoolofMechatrionicsEngineering,HarbinEngineeringUniversity,Harbin150001,China)【摘要】建立了高速重载滚动轴承接触应力和变形的三维分析模型,在对模型的边界条件进行合理假设的条件下,采用ANSYS软件对滚动轴承的接触应力和变形进行了分析计算,编制了参数化计算程序,方便、直观地得出了轴承内、外圈以及滚动体不同部位的应力和变形。
计算结果与赫兹理论解具有较好的一致性,表明模型的建立以及约束条件的设置准确、合理。
计算结果为滚动轴承的设计和优化提供了依据,计算方法也便于工程应用。
关键词:滚动轴承;有限元分析;接触应力和变形【Abstract]The3Dmodelisestablishedforcontactstressanddeformationanalysisofhigh-speedandheavy-dutyrollingbearing.Withthereasonablehypothesisofboundarycondition,thecontactstressanddeformationofbearingareanalyzedandcalculated.Thefiniteelementcodesareprogrammed,andthein—tut‘tt+ont‘stt。
非线性有限元软件MSC_Marc及其在轴承分析中的应用

非线性有限元软件M SC.M arc 及其在轴承分析中的应用X张业1,2,任成祖1,2,刘远新1,2(1.天津大学先进陶瓷与加工技术教育部重点实验室,天津 300072;2.天津大学东超纳米复合结构陶瓷联合实验室,天津 300072)摘要:介绍了M arc 软件的特点、非线性分析功能及其在接触问题上的应用,并将其应用于圆柱滚子轴承的接触分析。
关键词:M SC.M ar c 软件;接触分析;轴承中图分类号:T P317 文献标识码:A 文章编号:1001-2354(2004)10-0051-031 M ARC 软件简介MA RC Analysis R esearch Cor poration(简称M ARC)始创于1967年,是全球第一家非线性有限元软件公司。
经过三十余年的不懈努力,M ARC 软件得到学术界和工业界的大力推崇和广泛应用,建立了它在全球非线性有限元软件行业的领导者地位。
MA RC 公司的主要产品之一是通用的有限元分析软件M A RC /M ENT A 。
包括求解器M ARC 和前后处理界面M EN T AT 。
图1所示为M ENT AT 与M ARC 程序之间的相互关系。
图1 MENTAT 与MARC 及其输入输出文件求解器M ARC 是软件的核心,软件强大的非线性有限元分析功能就是由求解器完成的。
M ARC 拥有许多对用户开放的子程序,即用户子程序,用户可以根据各自需要编制用户子程序,实现对输入数据的修改、材料本构关系的定义、载荷条件、边界条件、约束条件的变更,甚至扩展M ARC 程序的功能。
M EN T AT 是M A RC 公司有限元分析软件的图形界面,主要由4部分组成:(1)生成有限元网格;(2)交互式输入边界条件、材料参数、几何参数、初始条件、接触条件、定义载荷工况等;(3)进行有限元数值分析和计算;(4)显示计算结果,进行后处理。
由于其易于操作、方便灵活、直观快捷,使用户有更多的时间去关注问题的本质,而不会陷入繁琐的数据准备之中。
钢丝滚道球轴承接触问题有限元分析

根 据 给 定 载 荷 Q 估 算 取 变形产生残余应力 ,致使模型的接触面应力分布与理论 2 9 . 8 4 N / m m 。 [ 4 ] , 建立加载后 的 分析结果有所不同。
模 型如 图 3 所示 。
利 用 AN S YS有 限 元 对
3 结 论
钢 丝滚 道球轴 承的接触 问题计 算是一种非 线性计
[ 2 ] A s t r o p Ar t h u r .Wi r e r a c e b e a r i n g s c u t c o s t s d o w n t o s i z e l J J . M a c h i n e r y a n d P r o d u c t i o n E n g i n e e r i n g , 1 9 7 9 , 1 3 5 ( 3 4 8 4 ) : 3 1 - 3 2 .
以 保 证 切 向 上 位 移 不 受 干
( 3 ) A N S Y S 有 限元软件建立的模型 中的曲线是通过一
Hale Waihona Puke 扰, 在滚珠 1 / 4 球面施加垂直 段段直线拟合而成 ,其计算精度与有效单元格划分 的细 但 对仿真结果影响较小 , 同时由于材料塑性 于 滚 珠 截 面 的 面 载 荷 ,这 里 密程度有关 ,
这个接 触斑 的形状 完全
图 5 滚 珠 与钢 丝 接 触
可 以看 成 是 椭 圆形 状 的 , 按
r a c e b e a r i n g s : U K, 1 1 8 3 3 2 1 l P J . 1 9 7 0 — 0 3 — 0 4 .
H e r t z 理论, 接触变形与接触应 力 的表达 式 简化 嘧 如下 :
该模 型进行非线性接触分析 ,
钢丝滚道球轴承的点接触问题有限元仿真

K  ̄, d t r e a i r tr a l; r a eb l b a i g c n a tp o lm; o -o f r l o tca f i l n e mr J:h e — x s o ay tb e wi rc a l e r ; o t c r b e n n c n ma n a t; nt ee e n o c i e me t
r c alb a ig u e et i peo i r f i u ai gr tr a l sd v l p d Th i u ain wa x cl a eb l e rn s d i a c ran t far a t m ltn o ay tb ewa e eo e . e sm lt se a ty n y c s o p ro me n ANS S I i f u d ta h a m u c ntc te s so c ro u a eo ew ier c , e r d i f Y  ̄ t s o n t em xi m o a tsrs e c u n t s r c ft r a e whi e h t he f h l b e
Smu aino on o tc rb e i r a eb lb ai g i lt fp it na t o lm awi rc al e rn o c p n e b s do nt lm e t to a e nf i ee n h d i e me
S HAN a — io XI o Xi o b a , E Ta
a ay i n lss
1 简介
由钢丝滚道球轴承组成 的轴系具有转动惯量 低、 刚度高 、 精度高 、 误差均化效应 、 制造精度容易 保证 以及轴承与框架温度特性一致等诸多优点 ,
轴承滚子的有限元简化模拟研究

轴承滚子的有限元简化模拟研究文|顾佥随着现代机械工业的精细化发展和计算机软硬件技术的飞速进步,有限元方法已经非常普遍地应用于机械结构设计计算。
在有限元分析中,经常会遇到多个部件之间的非线性连接。
例如,轴承、万向节、铰链等连接结构通常具有复杂的内部接触,如果对每个内部组件都详细建模,就要划分很细致的网格,耗费大量计算时间,因此,在实际的工程应用中,通常会在模型中对它们进行简化处理,以此来提高计算效率。
以轴承为例,目前常用的简化方式是用多组非线性杆单元或者弹簧单元来模拟轴承中的滚动体,将单元属性设置为只受压。
由于去除了滚子的实体网格,滚道与滚子之间也不需要做接触运算,所以这种简化对于计算速度的提升很显著。
但是在这种模拟方式下,如何设置单元的刚度值,才能准确体现轴承滚子的真实刚度,是一个经常让工程师们感到困扰的问题。
通常来说,用实验的方式来获取刚度信息是最准确的方法。
但是对于一些大尺寸的重载轴承,需要制造专门的工装来做实验,成本非常高。
而且实验所得到的结果,一般是一个轴承结构的整体刚度,而不是每个滚子的刚度值,在计算中要把它反算到每个滚子上。
对于一条非线性结果曲线来说,这种反向推导本身就会包含一些误差。
因此,本文尝试用有限元方法来计算和验证轴承滚子的刚度值。
圆柱滚子模拟本文所使用的有限元计算软件为ANSYS 17.2,前处理工具为Hypermesh 14.0。
模型默认单位体系:毫米(mm)、牛顿(N)、秒(s)、开尔文(K)及由此衍生的其他单位。
首先以一款简单的圆柱滚子轴承(其模型如图1所示)为例,该轴承的内径为900mm,滚子直径为75mm,应用于某款直驱型风力发电机组,位于主转轴后侧,是尺寸较大、转速偏低的重载轴承。
由于本文研究的是单个滚子的刚度,因此在有限元建模时,只划分单个滚子的实体单元模型:将轴承内外圈按照截面形状展平,在滚子与滚道之间建立标准接触,取摩擦系数为0.06,将接触位置附近的单元细化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年第23卷第1期测试技术学报V o l.23 N o.1 2009 (总第73期)JOURNAL OF TEST AND M EASURE M ENT TECHNOLOG Y(Sum N o.73)文章编号:167127449(2009)0120023205滚动轴承接触的非线性有限元分析Ξ熊小晋1,张晓昆鸟1,2,熊晓燕1(1.太原理工大学科研处,山西太原030024;2.煤炭科学研究总院太原研究院,山西太原030024)摘 要: 利用M SC.Patran M arc软件建立了滚动轴承的二维有限元分析模型,进行了接触非线性有限元分析,得到接触应力、应变随接触状态的变化情况.当不考虑摩擦接触时,压力与变形间呈现一定的非线性关系.当考虑摩擦接触时,下板面最大等效应力增加,应力分布形状发生改变,最大切向应力发生点向接触部位靠近,说明摩擦因素对接触表面切向应力大小与最大切向应力发生点产生影响.关键词: 滚动轴承;接触力学;摩擦;非线性有限元分析中图分类号: TH133.33 文献标识码:ANon li near FE M Analysis of Con tact Problem of Rolli ng Bear i ngX I ON G X iao jin1,ZHAN G X iaokun1,2,X I ON G X iaoyan1(1.Scientific R esearch D epartm ent,T aiyuan U niversity of T echno logy,T aiyuan030024,Ch ina;2.T aiyuan B ranch,Ch ina Coal R esearch Institute,T aiyuan030024,Ch ina)Abstract: A tw o2di m en si onal fin ite elem en t m odel of ro lling bearing w as develop ed u sing the M SC. Patran M arc softw are.T h rough the non linear FE M analysis of con tact,the changes of con tact stress and strain in differen t con tact states w ere ob tained.W hen neglecting fricti on con tact,there is a certain non2linear relati on sh i p betw een p ressu re and defo r m ati on.W hen con sidering fricti on con tact,the b iggest equ ivalen t stress increases,the shap e of stress distribu ti on changes,and at the sam e ti m e,the b iggest tangen tial stress po in t gets clo se to the con tact part.It is indicated that fricti on can influence the tangen tial stress value and the b iggest tangen tial stress po in t.Key words:ro lling bearing;con tact dynam;fricti on;non linear FE M analysis随着科技与工业的发展,滚动轴承的使用范围越来越广泛.轴承作旋转运动时,其内的滚动体与滚道发生接触,产生各种旋转运动与摩擦,轴承的刚度、承载能力甚至使用寿命主要取决于内部滚动体与滚道之间的接触性质.所以对滚动轴承接触力学问题的研究以及利用有限元法对滚动轴承进行接触非线性分析、解决轴承问题已经成为科研人员研究的重要方向.M SC.Patran M arc兼具M SC.Patran强大的网格划分功能、CAD继承工具和M arc强大的非线性处理功能.它支持多种复杂的材料模型以及材料的试验数据拟合,很容易模拟复杂的接触边界条件以及涉及多种加载历程的问题,尤其是M arc中自适应网格重划分功能可用于精确求解接触变形难题.本文暨利用此软件对滚动轴承进行接触非线性分析,得到滚动轴承接触应力、应变随接触状态的变化情况.Ξ收稿日期:2008204209 基金项目:国家自然科学基金资助项目(50405043);山西省自然科学基金资助项目(200801104322) 作者简介:熊小晋(19662),男,工程师,主要从事动态测试与故障诊断研究.1 接触问题1.1 滚动轴承接触问题滚动轴承接触属于典型的点、线接触问题,而H ertz接触理论在解决两个弹性体点接触的局部应力和变形上有经典解,适用于大部分滚动轴承的应力、应变计算问题.H ertz点接触理论的基本假设有3条[1]:1)接触体是线性弹性体,服从广义胡克(Hooke)定律.2)载荷与表面垂直,即不考虑表面切向应力.3)接触面积尺寸与接触体表面的曲率半径相比很小.H ertz点接触理论的基本计算公式为∑Θ=Θ11+Θ12+Θ21+Θ22,F(Θ)=[(Θ11-Θ12)+(Θ21-Θ22)] ∑Θ,a=a3[3Q2∑Θ(1-Τ21E1+1-Τ22E2)]1 3,b=b3[3Q2∑Θ(1-Τ21E1+1-Τ22E2)]1 3,Ρm ax=32QΠab,式中:∑Θ为曲率和;F(Θ)为曲率差;a,b为接触椭圆长短半轴;Τ1,Τ2为材料泊松比;E1,E2为材料弹性模量;a3,b3为与F(Θ)有关的无量纲量;Ρm ax为最大应力值;Q为法向载荷.H ertz线接触理论的基本计算公式为b=8QΠl∑Θ(1-Τ21E1+1-Τ22E2),Ρm ax=Q∑ΘΠl(1-Τ21E1+1-Τ22E2),式中:b为接触矩形半宽;l为接触物体上的有效接触长度,其余同点接触理论参数.实际上,H ertz接触理论只考虑垂直作用于表面的集中载荷,对于大多数滚动轴承应用场合,润滑条件充分的情况下,可以忽略滚动体与滚道间的摩擦作用,即滚动体与滚道表面上的切向应力与法向应力相比是可以忽略的;但实际上滚动轴承摩擦是不可避免且不可忽略的重要因素,随着对滚动轴承摩擦动力学特性研究的不断深入[2],认识到摩擦动力学特性与接触动力学特性有很强的耦合作用,摩擦特性对接触应力的影响不能忽视.因此,我们在对球轴承进行接触分析时有必要考虑摩擦因素的存在,观测摩擦作用下球轴承的接触特性的变化.1.2 有限元法在接触问题上的应用对于低频的物体运动,如果物体的变形可以忽略,那么运用多刚体方法和刚体接触理论就可以获得想要的结果,但如果考虑物体的高频波动现象且物体变形不可忽略,则有限元法就成为解决接触问题的有效手段;有限元法的基本思想是系统地构造偏微分方程在复杂区域上的近似解,重要特征是能够计算接触区域的变形和构造大规模的简单的线性方程组[3].有限元法可分为两大类,线弹性有限元法和非线性有限元法.线弹性有限元法以理想弹性体为研究对象,所考虑的变形建立在小变形假设的基础上.这类问题中,材料的应力与应变呈线性关系,满足广义胡克定律;应变与位移也呈线性关系.非线性有限元分析中,接触问题属高度边界非线性问题,接触体的变形和接触边界的摩擦作用使得部分边界条件随加载过程改变且不可恢复;接触约束是一类特殊不连续的约束,分析方法必须能够判断接触条件并应用或解除接触约束,M SC.Patran M arc中针对不同的无穿透接触约束方法提供间隙单元、非线性弹簧、接触迭代三种接触算法,其中接触迭代算法是解决所有问题的通用算法.M SC.Patran M arc中采用三种简化的理想模型对摩擦进行数值模拟[4],即:滑动库仑摩擦模型、剪切摩擦模型、粘2滑摩擦模型.其中滑动摩擦模型(包括库仑定理和剪切摩擦定理)可以精确描述滑动摩42测试技术学报2009年第1期擦,但很难模拟纯粹的粘性摩擦;而粘2滑摩擦模型(基于节点力)能够模拟从粘性摩擦到滑动摩擦的摩擦力突变,可模拟真实的粘性摩擦,模型如图1所示.图1中,∃u t 为切向位移增量;a 为乘子(默认值为1.05,用户可自定义大小);Β为滑动摩擦到粘性摩擦的相对位移过渡区域(默认值为10-6,用户可自定义大小);Ε为小常数.图1 阶跃摩擦模型图F ig .1 T he stick 2sli p step fricti onmodel 图2 二维模型图F ig .2 T he graph of two 2di m ensi onal model2 非线性有限元分析2.1 有限元模型由于二维有限元分析模型计算快捷且具有代表性,三维模型可以在二维模型上生成,所以本例中建立二维有限元模型,由球面和下板面组成,考虑到模型对称性的存在,只取右半部如图2所示.边界条件分两种工况:一是球面顶边施加垂直载荷,即对应不考虑切向力状态,球面、下板面左侧边施加水平位移约束,下板面底边施加垂直位移约束;二是在工况一的基础上取消下板面水平位移约束,在下板面右侧边施加水平载荷.模型相关数据为:球面半径5mm ,下板面长度16mm ,宽度2mm ,弹性模量均为2.07×E 11(Pa ),泊松比均为0.3.2.2 结果及分析2.2.1 垂直载荷作用下接触应力及变形球面与下板均设为2D 变形体,不考虑摩擦因素的影响,图3为压力2变形曲线,图4至图6为网格细化计算后应力云纹图.图3 压力2变形曲线F ig .3 T he p ressure 2defo r m ati on curve 图4 接触应力云纹图F ig .4 T he mo ire pattern of contact stress由图3Y 向压力2变形曲线图可知压力与变形间的非线性关系,随着压力载荷增大,Y 向变形速率趋于缓慢,这是因为压力载荷刚开始作用时,接触部位较少,因此接触应力相对较大,所以变形也较大,但随着压力增加,接触部位增大,接触应力相对变小,因此变形也较小,最终呈现非线性趋势.52(总第73期)滚动轴承接触的非线性有限元分析(熊小晋等)由图4可看出,H ertz 接触最先发生在球面和下板接触的顶点上,而且最大接触应力和最大接触变形也发生在此处,接触应力以接触部位为中心对称向两边减小并趋于0.由图5,图6V on M ises 等效应力分布图及X Y 向应力分布图可以看出应力分布以接触部位为中心上下基本对称,并且可以看出最大剪切应力并不是发生在接触部位上,而是发生在接触面下的某个部位,这对我们理解滚动轴承接触疲劳剥落很有帮助.L undberg 等人最初假设最大正交剪切应力首先导致表面下某处裂纹的产生,然后扩展至表面形成滚动轴承的表面剥落现象,而这种假设已经被许多试验所证明是正确的[1].图5 等效应力云纹图F ig .5 T he moire patternof von m ises stress 图6 X Y 向应力云纹图F ig .6 T he stress mo ire patternof the XY directi on图7 接触应力云纹图F ig .7 T he mo ire pattern of contact stress 图8 等效应力云纹图F ig .8 T he mo ire pattern of von m ises stress2.2.2 考虑摩擦因素状态下的接触特性球面顶边施加垂直2D 面压力,下板面右侧边施加水平2D 面压力,不施加下板面X 向位移约束,图9 X Y 向应力云纹图F ig .9 T he stress mo ire pattern of the X Y directi on使下板面与球面有相对运动趋势;球面与下板均设为2D 变形体,考虑摩擦因素影响,采用粘2滑摩擦模型进行摩擦计算,相关参数取默认值,在接触表中设置球面与下板摩擦系数为0.1;提交计算后得到有限元分析结果.从图7可知,接触应力大小及形状改变很小,说明考虑摩擦因素下对接触应力影响不大;将图8,图9与图5,图6进行比较可看出考虑摩擦因素下球面应力分布形状及大小基本没有改变;由于切向力的影响,下板面最大等效应力增加,应力分布形状发生改变,最大剪切应力发生点向接触部位靠近,说明摩擦因素对剪切应力的影响较大.62测试技术学报2009年第1期图10 摩擦应力云图F ig .10 T he mo ire pattern of fricti on stress图11 摩擦应力历程图F ig .11 T he developm ent chart of fricti on stress 图10分别为第6,11,19个增量步摩擦应力云图,从中可看出球面和下板面摩擦云图基本对称,随着载荷增加,摩擦云图向接触部位里侧靠近,且摩擦应力大小相应增加,说明随着载荷增加和相对运动趋势的影响,最大摩擦力发生部位向里侧节点靠近,外侧摩擦力相应减小;这从摩擦应力历程图也可看出,如图11所示,横坐标为下板面顶边节点变化路径,以接触顶点为原坐标,纵坐标为摩擦应力,说明了摩擦应力发生的部位和大小的变化.有许多学者对齿轮齿面摩擦力对接触应力的影响进行过研究[5],并通过实验证明了齿面摩擦力影响的大小与一个无量纲参数S 有关,此参数S 与润滑油粘度、表面卷吸速度、材料综合弹性模量、接触点综合曲率半径及单位载荷有关;鉴于滚动轴承接触与齿轮齿面接触的可比性,我们也可以认为存在这样一个参数,参数的大小决定了滚动轴承接触摩擦力对接触应力的影响程度,这种联系有待于我们在以后的研究中证实.3 总结及展望利用M SC .Patran M arc 强大的非线性处理功能,可以解决静态或动态摩擦条件下的滚动轴承接触非线性问题,并且利用软件丰富的后处理功能可以得到我们想要的结果.本文中建立的二维有限元分析模型在静态摩擦条件下进行分析,由结果可知摩擦因素对滚动轴承接触特性的影响不可忽视;下一步的研究方向是建立三维模型并在动态摩擦条件下进行分析,得到更符合实际情况的结果.参考文献:[1] H arris T A .Ro lling Bearing A nalysis (T h ird Editi on )[M ].John W iley &Sons .Inc .,1991:962128.[2] 赵联春,刘雪峰,曹志飞,等.滚动轴承振动的摩擦动力学特性[C ].洛阳轴承研究所,中国轴承论坛第四届研讨会论文集,洛阳:2006,1072112.[3] 彼得・艾伯哈特,胡斌.现代接触动力学[M ].南京:东南大学出版社,2003.[4] 陈火红,祁鹏.M SC .Patran M arc 培训教程和实例[M ].北京:科学出版社,2004:2362241.[5] 高创宽,周谋,亓秀梅.齿面摩擦力对齿轮接触应力的影响[J ].机械强度,2003,25(6):6422645.Gao Chuangkuan ,Zhou M ou ,Q i X ium ei.Effect of gear too th fricti on fo rce on gear contact stress [J ].Journal of M echanical Strength ,2003,25(6):642~645.(in Ch inese )72(总第73期)滚动轴承接触的非线性有限元分析(熊小晋等)。
