接触问题分析
abaqus接触问题分析

abaqus接触分析1、塑性材料和接触面上都不能用C3D20R和C3D20单元,这可能是你收敛问题的主要原因。
如果需要得到应力,可以使用C3D8I (在所关心的部位要让单元角度尽量接近90度),如果只关心应变和位移,可以使用C3D8R, 几何形状复杂时,可以使用C3D10M。
2、接触对中的sl ave surface应该是材料较软,网格较细的面。
3、接触面之间有微小的距离,定义接触时要设定“Adjust=位置误差限度”,此误差限度要大于接触面之间的距离,否则ABAQU S会认为两个面没有接触:*Contact Pair, interac tion="SOIL PILE SIDE CONTACT", small sliding,adjust=0.2.4、定义tie时也应该设定类似的posit ion toleran ce:*Tie, name=ShaftBo ttom, adjust=yes, positio n toleran ce=0.15、msg文件中出现zeropivot说明ABAQUS无法自动解决过约束问题,例如在桩底部的最外一圈节点上即定义了t ie,又定义了con tact, 出现过约束。
解决方法是在选择tie或c ontact的slave surface时,将类型设为no de region,然后选择区域时不要包含这一圈节点(我附上的文件中没有做这样的修改)。
6、接触定义在哪个分析步取决于你模型的实际物理背景,如果从一开始两个面就是相接触的,就定义在ini tial或你的第一个分析步中;如果是后来才开始接触的,就定义在后面的分析步中。
边界条件也是这样。
7、我在前面上传的文件里用*CONTROL设了允许的迭代次数18,意思是18次迭代不收敛时,才减小时间增量步(ABAQUS默认的值是12)。
第18章接触问题有限元分析技术

第18章接触问题的有限元分析技术第1节基本知识接触问题是一种高度非线性行为,需要较大的计算资源,为了进行准确而有效的计算,理解问题的特性和建立合理的模型是很重要的。
接触问题存在两个较大的难点:其一,在求解问题之前,不知道接触区域,表面之间是接触或分开是未知的、突然变化的,这些随载荷、材料、边界条件和其它因素而定;其二,大多数的接触问题需要计算摩擦,有几种摩擦和模型可供挑选,它们都是非线性的,摩擦使问题的收敛性变得困难。
一、接触问题分类接触问题分为两种基本类型:刚体─柔体的接触和半柔体─柔体的接触。
在刚体─柔体的接触问题中,接触面的一个或多个被当作刚体,(与它接触的变形体相比,有大得多的刚度),一般情况下,一种软材料和一种硬材料接触时,问题可以被假定为刚体─柔体的接触,许多金属成形问题归为此类接触;另一类,柔体─柔体的接触,是一种更普遍的类型,在这种情况下,两个接触体都是变形体(有近似的刚度)。
ANSYS支持三种接触方式:点─点、点─面和平面─面。
每种接触方式使用的接触单元适用于某类问题。
二、接触单元为了给接触问题建模,首先必须认识到模型中的哪些部分可能会相互接触,如果相互作用的其中之一是一点,模型的对立应组元是一个节点。
如果相互作用的其中之一是一个面,模型的对应组元是单元,例如梁单元,壳单元或实体单元。
有限元模型通过指定的接触单元来识别可能的接触匹对,接触单元是覆盖在分析模型接触面之上的一层单元。
下面分类详述ANSYS使用的接触单元和使用它们的过程。
1.点─点接触单元点─点接触单元主要用于模拟点─点的接触行为,为了使用点─点的接触单元,需要预先知道接触位置,这类接触问题只能适用于接触面之间有较小相对滑动的情况(即使在几何非线性情况下)。
如果两个面上的节点一一对应,相对滑动又以忽略不计,两个面挠度(转动)保持小量,那么可以用点─点的接触单元来求解面─面的接触问题,过盈装配问题是一个用点─点的接触单元来模拟面─与的接触问题的典型例子。
球与平面接触问题验证分析

对 本 题 而 言 , R=8mm,F=188.49N, ������1 = 1000N/ ������������2 , ������1 = 0.3,������2 = ∞; 得到理论解:a=1.0096mm, q=88.2904N/������������2 (MPa)
在此做两个分析模型,完整模型和 Cyclic 模型
图 1.完整模型
图 2. Cyclic模型
图 3.完整模型边界条件
将总的载荷 平均施加给 每个循环体
图 4. Cyclic模型边界条件
注意:
①如果是平面对称结构,比如说模型关于某条线或者 某个面对称,在对称线或者面节点加载力时,载荷数 值为整体结构的一半。如下图所示,此题目也可取半
个球进行建模,此时加载力的大小为2 ;
图 9.接触区域内 X 轴坐标最大的节点是 8 号
图 10.8 号节点沿着 X 轴的位移
整体模型算的结果为: 接触半径 a=(1.0242-0.0167)mm=1.0075mm;(误差 0.2%) 最大接触压力 q=87.217MPa(误差 1.2%)
下面是Cyclic模型:
图 11.形变
图 12.Mises 应力
图 13.接触状态
图 14.接触压强(最大 88.355MPa)
图 15.接触区域内 X 轴坐标最大的节点是 735 号
图 16.735 号节点沿着 X 轴向的位移
Cyclic 模型算的结果为: 半径 a=(1.0272-0.0143)=1.0129mm;(误差 0.3%) 最大接触压力 q=88.355MPa(误差 0.07%)
球与平面赫兹接触问题
对于球与平面赫兹接触问题,有如下理论解: 接触半径a =
3
接触分析注意问题

接触分析注意问题1、塑性材料和接触面上都不能用C3D20R和C3D20单元,这可能是你收敛问题的主要原因。
如果需要得到应力,可以使用C3D8I (在所关心的部位要让单元角度尽量接近90度),如果只关心应变和位移,可以使用C3D8R, 几何形状复杂时,可以使用C3D10M。
2、接触对中的slave surface应该是材料较软,网格较细的面。
3、接触面之间有微小的距离,定义接触时要设定“Adjust=位置误差限度“,此误差限度要大于接触面之间的距离,否则ABAQUS 会认为两个面没有接触:*Contact Pair, interaction="SOIL PILE SIDE CONTACT", small sliding, adjust=0.2.4、定义tie时也应该设定类似的position tolerance:*Tie, name=ShaftBottom, adjust=yes, position tolerance=0.1 5、msg文件中出现zero pivot说明ABAQUS无法自动解决过约束问题,例如在桩底部的最外一圈节点上即定义了tie,又定义了contact, 出现过约束。
解决方法是在选择tie或contact的slave surface时,将类型设为node region, 然后选择区域时不要包含这一圈节点(我附上的文件中没有做这样的修改)。
6、接触定义在哪个分析步取决于你模型的实际物理背景,如果从一开始两个面就是相接触的,就定义在initial或你的第一个分析步中;如果是后来才开始接触的,就定义在后面的分析步中。
边界条件也是这样。
7、我在前面上传的文件里用*CONTROL设了允许的迭代次数18,意思是18次迭代不收敛时,才减小时间增量步(ABAQUS默认的值是12)。
一般情况下不必设置此参数,如果在msg文件中看到opening 和closure的数目不断减小(即迭代的趋势是收敛的),但12次迭代仍不足以完全达到收敛,就可以用*CONTROL来增大允许的迭代次数。
接触问题的有限元分析

有限元混合法:以结点位移和接触力为未知量,并 采用有限元形函数插值,将接触区域的位移约束条件和 接触力约束条件均反映到刚度矩阵中去,构成有限元混 合法控制方程
6.1 接触边界的有限元算法
机械分社
6.1 接触边界的有限元算法
机械分社
(2)接触约束算法 2) Lagrange 乘子法与增广Lagrange 乘子法
min U, λ 1 UT K UUT F g U T λ
2
代入
g
U
g0
U
g U U
U
g0
U
GU
K GT U F
G
0
λ
g0
U
Lagrange 乘子法中 接触约束条件可以精 确满足
惩罚函数法对接触约束条件的处理是通过在势能泛函中
增加一个惩罚势能。
p
U
1 2
P T
EP
P
惩罚因子
嵌入深度,是节点位移的函数
接触问题就等价于无约束优化问题:
min U U p U
K K U FF
p
p
6.1 接触边界的有限元算法
机械分社
(2)接触约束算法
1)罚函数方法
K K U FF
机械分社
(1)直接迭代法
在用有限元位移法求解接触问题时,首先假设初始 接触状态形成系统刚度矩阵,求得位移和接触力后,根 据接触条件不断修改接触状态,重新形成刚度矩阵求解, 反复迭代直至收敛。
每次迭代都要重新形成刚度矩阵,求解控制方程, 而实际上接触问题的非线性主要反映在接触边界上,因 此,通常采用静力凝聚技术,使得每次迭代只是对接触 点进行, 大大提高了求解效率。
接触问题分析

引入单边约束条件
线性互补问题
目前,接触问题分析的方法主要还是经典方法,即从各种变 分原理出发,将几何约束和摩擦定律引入泛函,最终获得接触问 题的控制方程。这是由于大型工程结构分析,大多都采用有限元 方法,而经典方法仍然在此框架之内。本章则侧重介绍接触问题 的数学规划解法,主要从可研究的角度考虑。
2018/11/11 5
4)混合(假定x 方向滑动)
Fal Fbl l x, y, z Fax Fax Faz Faz qay qby 0 q q r az bz z
引言(1/5)
接触现象是普遍存在的。实际的工程结构系统往往分成几个非永久性 连在一起的部分,这些部分之间的力靠它们之间的挤压、甚至冲 击来传递。 接触实例:齿轮的齿间啮合;汽(气)轮机及发动机中叶片 与轮盘的榫接;两物体的撞击(动态接触)。 研究现状:简单的弹性接触问题在19世纪末Hertz就已经开始研究, 但只有在有限元方法及计算机出现以后,接触问题的研究才有 了长足发展,并达到实用化程度。 接触问题的特点:属边界非线性问题,边界条件不再是定解条件,而 是待求结果;两接触体间接触面积与压力随外载的变化而变,并 与接触体的刚性有关。这是该问题的特点,也是困难所在。
对以上四方面内容,不少学者进行了研究,提出了不同的理论与 方法,对同一问题,各种理论各有优缺点,尚未达到共识。基于接触 问题的难度、研究的不成熟、加之其实用性,它一直是固体力学研究 的热点。
2018/11/11 2
研究内容浅析:
引言(3/5)
接触模式问题:解决接触面上接触力的传递问题。 点-点(node-to-node)接触模式:将两接触体的接触面分成同样 的网格,使结点组成一一对应的结点对,假定接触力的传递 通过结点对实现,接触面上各局部区域的接触状态也相应地 按结点对来判断。优点-直观、简单、易于编程。缺点-对 于复杂接触面情形,网格结点一一对应不易做到。 点-面(node-to-surface)接触模式:先将两接触体人为地分为主 动体(master body)与被动体(slave body),并假定主动 体网格中的一个结点可与被动体表面上的任意一点(不一定 是网格结点)相接触。优点-两接触体可根据自身情况剖分 网格。缺点-方法较复杂、编程难度大。
《2024年基于ANSYS软件的接触问题分析及在工程中的应用》范文

《基于ANSYS软件的接触问题分析及在工程中的应用》篇一一、引言在当今的工程领域中,接触问题广泛存在于各种复杂的工程结构和系统之中。
如何准确地分析、预测和解决这些接触问题,对于提高工程结构的安全性和可靠性具有重要意义。
ANSYS软件作为一种功能强大的工程仿真软件,其在接触问题的分析和处理上具有显著的优势。
本文将基于ANSYS软件,对接触问题进行分析,并探讨其在工程中的应用。
二、ANSYS软件中的接触问题分析1. 接触问题的基本概念接触问题是一种高度非线性问题,涉及两个或多个物体在接触过程中产生的相互作用。
在工程中,接触问题常常出现在机械、结构、热传导、流体等多个领域。
ANSYS软件通过建立接触对,模拟物体之间的接触行为,从而对接触问题进行精确的分析。
2. ANSYS软件中的接触分析方法ANSYS软件提供了多种接触分析方法,包括面面接触、点面接触、点对点接触等。
针对不同的接触问题,可以选择合适的分析方法。
此外,ANSYS还提供了多种接触算法,如拉格朗日乘子法、罚函数法等,以满足不同问题的需求。
三、ANSYS软件在工程中的应用1. 机械工程中的应用在机械工程中,许多零件在运动过程中会发生接触和摩擦。
利用ANSYS软件对这些接触问题进行精确的分析和模拟,可以帮助工程师优化设计,提高零件的耐用性和可靠性。
例如,齿轮的传动过程涉及复杂的接触问题,通过ANSYS软件的分析和模拟,可以预测齿轮的磨损和疲劳情况,从而优化齿轮的设计和制造过程。
2. 结构工程中的应用在结构工程中,建筑物、桥梁、大坝等结构物在受到外部荷载作用时,可能会发生接触问题。
通过ANSYS软件对这些结构的接触行为进行精确的分析和模拟,可以帮助工程师预测结构的受力情况和变形情况,从而保证结构的安全性。
例如,在桥梁的设计和施工过程中,可以利用ANSYS软件对桥梁的支座、伸缩缝等部位的接触问题进行详细的分析和模拟,以确保桥梁的安全性和稳定性。
3. 热传导和流体领域的应用在热传导和流体领域中,接触问题同样广泛存在。
接触问题分析相关理论
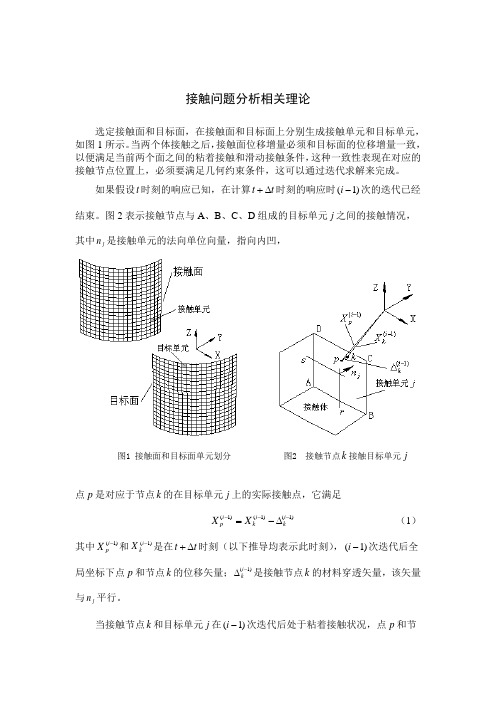
接触问题分析相关理论选定接触面和目标面,在接触面和目标面上分别生成接触单元和目标单元,如图1所示。
当两个体接触之后,接触面位移增量必须和目标面的位移增量一致,以便满足当前两个面之间的粘着接触和滑动接触条件,这种一致性表现在对应的接触节点位置上,必须要满足几何约束条件,这可以通过迭代求解来完成。
如果假设t 时刻的响应已知,在计算t t ∆+时刻的响应时)1(-i 次的迭代已经结束。
图2表示接触节点与A 、B 、C 、D 组成的目标单元j 之间的接触情况,其中j n 是接触单元的法向单位向量,指向内凹,图1 接触面和目标面单元划分 图2 接触节点k 接触目标单元j 点p 是对应于节点k 的在目标单元j 上的实际接触点,它满足)1()1()1(---∆-=i k i k i p X X (1)其中)1(-i p X 和)1(-i k X 是在t t ∆+时刻(以下推导均表示此时刻),)1(-i 次迭代后全局坐标下点p 和节点k 的位移矢量;)1(-∆i k 是接触节点k 的材料穿透矢量,该矢量与j n 平行。
当接触节点k 和目标单元j 在)1(-i 次迭代后处于粘着接触状况,点p 和节点k 在第)(i 次迭代的位移为)()(i ki p X X = (2) 式(2)减去式(1),并以)(i p u ∆和)(i k u ∆表示点p 和节点k 在第)(i 次迭代的位移增量,有)1()()(-∆+∆=∆i k i k i p u u (3)以上是粘着接触下位移协调约束条件。
滑动接触下相应的位移协调约束为][)()()1()()(-T T ∆+∆=∆i k i kj i p j u n u n (4) 并且在粘着和滑动摩擦中都有满足0)1(≥+∆-δi k (5)式中δ为给定的间隙量。
如果在)1(-i 次迭代后节点k 上的压力消除,则在第)(i 次迭代时点p 和节点k 的位移增量互不相关。
在)1(-i 次迭代后,根据外载荷、惯性力和节点力同单元应力的平衡关系可以估计出接触节点所受的力,通过迭代修正可得到符合库仑摩擦律的准确值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
引言( 引言(3/5)
研究内容浅析: 研究内容浅析: 接触模式问题:解决接触面上接触力的传递问题。 接触模式问题:解决接触面上接触力的传递问题。 点-点(node-to-node)接触模式:将两接触体的接触面分成同样 )接触模式: 的网格, 结点组成一一对应的结点对, 的网格,使结点组成一一对应的结点对,假定接触力的传递 通过结点对实现, 通过结点对实现,接触面上各局部区域的接触状态也相应地 按结点对来判断。优点-直观、简单、易于编程。缺点- 按结点对来判断。优点-直观、简单、易于编程。缺点-对 于复杂接触面情形,网格结点一一对应不易做到。 于复杂接触面情形,网格结点一一对应不易做到。 点-面(node-to-surface)接触模式:先将两接触体人为地分为 )接触模式: 主动体( ),并假定主 主动体(master body)与被动体(slave body),并假定主 )与被动体( ), 动体网格中的一个结点可与被动体表面上的任意一点 个结点可与被动体表面上的任意一点( 动体网格中的一个结点可与被动体表面上的任意一点(不一 定是网格结点)相接触。优点- 定是网格结点)相接触。优点-两接触体可根据自身情况剖 分网格。缺点-方法较复杂、编程难度大。 分网格。缺点-方法较复杂、编程难度大。
Hale Waihona Puke (l = x, y , z )
4)混合(假定 方向滑动) ) 假定x 方向滑动)
∆Fal = −∆Fbl ( l = x, y, z ) Fax + ∆Fax = ± µ ( Faz + ∆Faz ) −∆qay + ∆qby = 0 −∆q + ∆q = r az bz z
3)滑移 )
2011-10-19 5
引言( 引言(5/5)
研究内容浅析: 研究内容浅析 (续) 求解方法问题:在这方面,许多科学家倾注了大量的精力。 求解方法问题:在这方面,许多科学家倾注了大量的精力。 经典方法:利用有限元方法,通过迭代进行求解。 经典方法:利用有限元方法,通过迭代进行求解。 数学规划方法: 数学规划方法:利用基于有限元离散的数学规划方法直接求系统 总势能极值(或驻值)问题,其涉及的命题可表述为: 总势能极值(或驻值)问题,其涉及的命题可表述为: 寻求一组位移矢量 {q} ; 二次 引入单边约束条件 使系统总势能 Π 取驻值; 取驻值; 规划 线性互补问题 问题 并满足条件 h ( q ) = 0 。
2011-10-19
8
经典的接触问题求解方法( 经典的接触问题求解方法(3/3)
接触区有限元方程: 接触区有限元方程:
K ∆q = ∆F
静力凝聚 非接触区 凝聚载荷
K * {∆qC } = {∆FL* } + {∆FC }
等效刚度 接触区位移
接触方程! 接触方程!
将定解条件代入, 将定解条件代入,接触方程 就成为定解问题。 就成为定解问题。代入时可 使用间接的接触单元法 接触单元法, 使用间接的接触单元法,也 直接代入。 可直接代入。直接带入时的 计算步骤
经验表明, 经验表明,接触迭代往往只有几步就 可很快收敛,这种试验( )-误 可很快收敛,这种试验(trial)-误 )- )-迭代 差(error)-迭代(iteration)的方 )-迭代( ) 又称为经典方法, 法,又称为经典方法,由于归根到底 求解的仍然是 KU = F 型方程。 型方程。
接触区载荷
2011-10-19 2
引言( 引言(2/5)
研究内容: 研究内容: 接触模式问题:描述两接触体间的力的传递、 接触模式问题:描述两接触体间的力的传递、描述不同载荷 下接触状态的变化; 解决如何描述的问题) 下接触状态的变化;(解决如何描述的问题) 几何约束问题:表示接触面上两物体位移所要满足的条件; 几何约束问题:表示接触面上两物体位移所要满足的条件; 解决到底以什么具体形式来描述、即怎样描述?) (解决到底以什么具体形式来描述、即怎样描述?) 摩擦定律问题: 摩擦定律问题:反映接触面上力与位移或压力与切向力之间 的关系; 的关系; 求解方法问题:建立数学方程并加以求解。 求解方法问题:建立数学方程并加以求解。 对以上四方面内容,不少学者进行了研究, 对以上四方面内容,不少学者进行了研究,提出了不同的理论与 方法,对同一问题,各种理论各有优缺点,尚未达到共识。基于接触 方法,对同一问题,各种理论各有优缺点,尚未达到共识。 问题的难度、研究的不成熟、加之其实用性, 问题的难度、研究的不成熟、加之其实用性,它一直是固体力学研究 的热点。 的热点。
第四章 接触问题分析
目的:以接触问题为例,介绍边界非线性问题。 目的:以接触问题为例,介绍边界非线性问题。 特点:与线性有限元方法比较,边界条件是待求的。 特点:与线性有限元方法比较,边界条件是待求的。 内容: 内容: 引言 经典的接触问题求解方法 数学规划方法求解接触问题
2011-10-19
1
引言( 引言(1/5)
接触现象是普遍存在的。实际的工程结构系统往往分成几个非永久性 接触现象是普遍存在的。实际的工程结构系统往往分成几个非永久性 是普遍存在的 的部分, 连在一起的部分 这些部分之间的力靠它们之间的挤压、 连在一起的部分,这些部分之间的力靠它们之间的挤压、甚至冲 击来传递。 击来传递。 接触实例:齿轮的齿间啮合; 接触实例:齿轮的齿间啮合;汽(气)轮机及发动机中叶片 与轮盘的榫接;两物体的撞击(动态接触)。 与轮盘的榫接;两物体的撞击(动态接触)。 研究现状:简单的弹性接触问题在 世纪末 世纪末Hertz就已经开始研究, 就已经开始研究, 研究现状:简单的弹性接触问题在19世纪末 就已经开始研究 但只有在有限元方法及计算机出现以后, 有限元方法及计算机出现以后 但只有在有限元方法及计算机出现以后,接触问题的研究才有 实用化程度。 了长足发展,并达到实用化程度 了长足发展,并达到实用化程度。 接触问题的特点: 边界非线性问题,边界条件不再是定解条件, 接触问题的特点:属边界非线性问题,边界条件不再是定解条件,而 不再是定解条件 是待求结果;两接触体间接触面积与压力随外载的变化而变 接触面积与压力随外载的变化而变, 是待求结果;两接触体间接触面积与压力随外载的变化而变,并 与接触体的刚性有关。这是该问题的特点,也是困难所在。 与接触体的刚性有关。这是该问题的特点,也是困难所在。
r =0
y
B
x
(切平面) 切平面)
(a) 可能接触区
(b)
接触的A、 两物体 接触的 、B两物体 (a) 可能接触区;(b) 接触区局部坐标系 可能接触区;
r表示接触点对间的间隙 表示接触点对间的间隙
2011-10-19
经典的接触问题求解方法( 经典的接触问题求解方法(2/3)
定解条件: 定解条件: 四类接触状态,对应的定解条件为 四类接触状态,对应的定解条件为: 定解条件 1)开式 ) 2)粘式 )
Fal + ∆Fl = Fbl + ∆Fbl = 0
∆Fal = −∆Fbl ( l = x, y , z ) −∆qal + ∆qbl = 0 ( l = x, y ) −∆q + ∆q = r az bz z
∆F = −∆F ( l = x, y, z ) bl al Fax + ∆Fax = ± µ ( Faz + ∆Faz ) cos θ Fay + ∆Fay = ± µ ( Faz + ∆Faz ) sin θ θ = tan −1 ∆qby − ∆qay ∆qbx − ∆qax −∆qaz + ∆qbz = rz
Trial-Error-Iteration过程: 过程: 过程 Step 1,试求解(trial):假定初始的接触状态,然后 ):假定初始的接触状态 ,试求解( ):假定初始的接触状态, 依此获得相应的定解条件, 依此获得相应的定解条件,以得到新的边界条件并求 同时得到接触力; 解,同时得到接触力; Step 2,计算误差(error):若新得到的接触力与接 ):若新得到的接触力与接 ,计算误差( ): 触位移满足初始假定的接触状态,则为真解。 触位移满足初始假定的接触状态,则为真解。否则转 入Step 3; ; Step 3,迭代(iteration):更新接触状态及相应的定 ):更新接触状态及相应的定 ,迭代( ): 解条件,转入Step 1进行迭代。 进行迭代。 解条件,转入 进行迭代
2011-10-19 6
经典的接触问题求解方法( 经典的接触问题求解方法(1/3)
一般采用三个假设: 一般采用三个假设: 接触表面是凸的、连续的; 接触表面是凸的、连续的; 接触表面服从库仑摩擦定律; 接触表面服从库仑摩擦定律; 接触模式是点-点接触模式。 接触模式是点-点接触模式。
z(法向) 法向)
A
边界的接触状态(判定性条件) 边界的接触状态(判定性条件) 分别为: 分别为:
1)开式(opening)接触:此时 rz ≥ 0 , ) 开式( ) 接触: 即法向间隙大于等于0; 即法向间隙大于等于 ; 2)粘式(cohesive)接触:此时 rz = 0 ) 粘式( ) 接触: 即法向无间隙, ( ∆rx = 0 ,∆ry = 0 ) ;即法向无间隙, 且在一个载荷增量步始末, 且在一个载荷增量步始末,整个切平 面无相对滑动; 面无相对滑动; 3)滑移(sliding)接触:此时 rz = 0 , )滑移( )接触: ∆rx ≠ 0 且 ∆ry ≠ 0 ,即法向无间隙,且 即法向无间隙, 切平面的两个方向均有相对滑动; 切平面的两个方向均有相对滑动; 4)混合(mixed)接触:此时 z )混合( )接触: , ∆ry ∆rx 中一个为0、一个不为0, 与 中一个为 、一个不为 , 即法向无间隙, 即法向无间隙,切平面的一个方向无 相对滑动、而另一个方向有相对滑动。 相对滑动、而另一个方向有相对滑动。 7
2011-10-19 4
