实习9 极射赤平投影之二(1)
极射赤平投影基本作图方法

极射赤平投影基本作图方法§1 极射赤平投影的基本原理一、投影要素1、投影球—以任意长为半径的球,球面即球表面2、赤平面—过投影球球心的水平面3、基圆—赤平面与球面相交的大圆,或称赤平大圆凡过球心的平面与球面相交的大圆,统称为大圆,不过球心的一球面与球面相交所成的圆统称小圆。
4、极射点—球上两极发射点,分上半球投影和下球投影。
二、平面和直线的投影的解析(一)平面投影1、过球心的平面投影任何一个过球心的无限伸展的平面(岩层面、断层面、节理面或轴面等),必然于球面相交成球面大圆,球面大圆与极射点的连线必然穿过赤平面,在赤平面上这些穿透点的连线即为该平面的相应大圆的赤平投影,简称大圆弧。
1)直立大圆(平面)——为基圆直径2)水平大圆(平面)——为基圆本身3)倾斜大圆(平面)——以基圆直径为弧的大圆弧性质:球面大圆投影后在赤平面上仍为一个圆。
2、不过球心的平面投影不过球心的平面与球面相交成直径小于球直径的小圆、球面小圆投影仍为一个小圆。
1)直立小圆(平面)——部分为基圆内一条弧,部位为基圆外一条弧2)水平小圆(平面)——为基圆的同心圆3)倾斜小圆(平面)①全部位于圆基内的小圆②部位于基圆内,部分在基圆外③全部在基圆外性质:1)球面大圆或球面小圆投影在赤平面仍为一个圆2)半径角距相等的球面小圆(即面积相等的小圆),其投影小圆面积不等,近基圆圆心处,远离圆在大。
3)任何过极射点(P)的球面大圆或小圆其赤平投影均为一条直线。
4)球面大圆或小圆在赤平面上的投影圆的圆心(R’)与作图圆心(C)是不重合的;只有水平球面大圆和水平球面小圆投影后,投影圆心(R’)作图圆心(C)与基圆的圆心O点重合,并且投影圆的圆心(R’)与基圆圆心(O)愈远,R’与C分离愈大。
(二)直线投影过球心的直线无限延伸心交于球面两点,称极点。
1、铅直线投影点为基圆圆心2、水平线投影点为基圆直径的两个端点3、倾斜线股影点,一个在基圆内,另一个在基圆外,称对距点,其角距为180°三、投影网:吴尔福网和施密特网(一)吴氏网的结构及成因原理吴氏网的结构:基圆、径几大圆弧、纬向小圆弧、东西、南北经纬线,间距2°,误差±0.5°1、基圆,赤平大圆,代表水平面,0°-360°方位角刻度2、经向大圆弧,由一系列走向SN的,向东或西倾斜,倾角不同(0°-90°),间隔2°的投影大圆弧(代表倾斜平面)组成。
极射赤平投影

为180 °∠40°所决定的平面产状。
N S
20
(7)求平面上的直线产状
例7: 已知平面产状180°∠37°,该平面上一
条直线侧伏向E,侧伏角44°,求直线的倾伏向 和倾伏角。 E 44°
37°
S
21
二、β图解和π图解
β图解是指以褶皱面各切点的切面所作的经向
大圆图解。在理想的圆柱状褶皱中,各个切面交 线互相平行,这些经向大圆交于一点(β),即褶 皱枢纽的投影。非圆柱状褶皱则要分段投影。
7
过球心的的水平线OK的投影是基圆上的一个点K’
过球心的的垂直线OP的投影是圆心O点
8
不过球心的直立平面FGHK投影是一个小圆弧。FH-该面走向
9
不过球心的水平面投影是与基圆平行的小圆
10
过求心的水平面法线OK的
极点K’是投影面的圆心O
过求心的垂直平面法线OK的
极点的投影K点在基圆上
11
(二)、投影网:吴尔福网和施密特网 1、吴氏网的结构及成因原理 吴氏网的结构:基圆、径向大圆弧、纬向小圆弧、 东西、南北经纬线,间距2°,误差±0.5°。 (1)、基圆:赤平大圆,代表水平面,0°360°方位角刻度。 (2)、两条直径:EW,SN。 (3)、经向大圆弧:由一系列走向SN的,向东 或西倾斜,倾角不同(0°-90°),间隔2°的投 影大圆弧(代表倾斜平面)组成。 (4)、纬向小圆“为一系列走向东西、直立小 圆的投影小圆弧组成。他们将SN直径、经向大圆和 基圆等分,每小格为2 °。幻般操作步骤:
预备阶段
①将透明纸蒙在吴氏网上,
②画“+”中心,
③标出E、S、W、N方位(顺钟
向)。
14
(1)、平面的赤平投影 投影步骤(口诀): A、基圆顺钟找倾向; B、东西直径数倾角(由圆周向圆心数); C、径向圆弧拟平面; D、复原归位定投影。 例1: 平面产状 120°∠30°投影 操作如下。
极射赤平投影2 (2)

2、吴尔夫(Wulff)投影网
极射赤平投影学习资料(二)
三、施密特(Schmidt)投影网的解析 1、兰勃特等面积投影
2、施密特(Schmidt)投影网
极射赤平投影学习资料(二)
四、两种赤平投影网的基本特征
极射赤平投影学习资பைடு நூலகம்(二)
要
点
一、解析的缘由 二、吴尔夫(Wulff)投影网的解析 三、施密特(Schmidt)投影网的解析 四、两种赤平投影网的基本特征
极射赤平投影学习资料(二)
一、解析的缘由
极射赤平投影学习资料(二)
二、吴尔夫(Wulff)投影网的解析
1、基本方程 赤平极射投影的基 本原理:平面和球面相 交构成一个圆,球面上 一个圆,它的赤平极射 投影也是一个圆,不论 大圆小圆都是如此。
实习1、晶体的极射赤平投影

图名
班号 学号
1.作磷灰石晶体(2508)晶面的极射持平投影 作磷灰石晶体( 作磷灰石晶体 ) • 测量相邻晶面间的面角(r˄ 、m ˄m) 测量相邻晶面间的面角( m
1 r˄ m m˄ ˄ m 2 3 4 5 6 平均
• 计算各个晶面的极坐标 • 利用吴氏网作晶面的极射赤平投影
二、实习步骤
2.作立方体(3201)所有对称面的极射赤平 作立方体( 作立方体 ) 投影 • 找出立方体的 个对称面 找出立方体的9个对称面 • 分析对称面的分布特点 • 作各个对称面的极射赤平投影图
作立方体3201所有对称面的极射赤平投影作各个对称面的极射赤平投影图三作业格式图名
实习一、 晶体的极射赤平投影实习
一、实习目的
• 学会晶体中各种要素的极射赤平投影 方法。 方法。 • 学会吴氏网的基本使用方法。 学会吴氏网的基本使用方法。 • 归纳极射赤平投影图中各个要素间的 关系。 关系。
二、实习步骤
综合地质课件——极射赤平投影

第七章极射赤平投影
极射赤平投影(Stereographic projection)
极射—从两极点出发
赤平:赤道平面
从两极出发,把线、面投影到赤平面上。
面的投影
线的投影
吴氏网——吴尔福网
吴网氏的操作方法
将透明纸蒙在吴网氏上,描绘基圆及“+”字中心,固定网心,使透明纸能旋转。
(一)平面投影
标绘产状为120°∠30°的平面。
(二)直线投影
标绘产状为300°∠50°的直线。
(二)面的法线投影
标绘产状为300°∠50°的直线的法线。
(四)已知真倾角求视倾角
已知岩层的产状为300°∠40°,求在355 °方
向剖面上该岩层的视倾角。
(五)求两面交线的产状
已知两个倾斜岩层的产状分别为:300°∠40°,和30°∠50°,求两面的交线产状。
(六)两相交直线所决定的面的产状已知两个相交直线的产状分别为:120°∠40°,和200°∠50°,求其所决定面的产状。
(七)求平面上直线产状
已知一平面产状为:180°∠37°,该平面上直
线侧伏向E,侧伏角40°,求直线的倾伏向和
倾伏角。
赤平投影

图 52 平面地质图
5.一个背斜构造两翼产状为 46°∠50°和 344°∠22°,在一个产状为 184°∠80° 的陡壁面上测得该背斜轴迹的侧伏角为 60°W,求该背斜的轴面产状(注意:先作出两翼
43
交线得β,再据作法六作出轴迹的倾伏角,得出轴迹投影点,使β与轴迹点位于同一大圆 弧即为所求) ,并与用两翼顶角平分线和枢纽构成共面的轴面作比较。 (答:枢纽 333°∠ 20°,轴迹 259°∠59°,轴面 257°∠59°—253°∠68°) 。 6. 一背斜在平坦地面上出露的轴迹走向 N20°E, 在横切背斜的河谷中测得坡面为 180 °∠70°,其上轴迹侧伏角 50°E,求该背斜轴面产状。 (答:轴迹倾伏 112°∠46°,轴 面 110°∠46°) 。 7.在中尼边境樟木友谊桥附近,兰晶石黑云母片岩相当于层理的片理产状 310°∠80 °,一组应变滑劈理与褶皱轴面一致,产状为 350°∠36°,求褶皱的枢纽产状及片理面 与应变滑劈理面间的二面角,假定能按照一般劈理与岩层夹角关系来判断岩层正常与倒转 的话,该岩层是正常还是倒转。 (答:β35°∠27°,二面角 54°,倒转) 。 8.一褶皱的石灰岩层产状如下:70°∠61°,318°∠70°,41°∠51°,348°∠55 °,15°∠49°。求①用π图表示的褶皱枢纽的倾伏向和倾伏角,②用β图表示的褶轴的 倾伏向和倾伏角,③褶皱轴面的倾向和倾角(据水平面上轴迹走向正北) ,④轴面上褶轴的 侧伏角。 (答:①24°∠49°,②24°∠49°,③90°∠71°,④54°N) 。 9.一圆柱状背斜的北西翼产状 330°∠45°,北东翼产状 65°∠35°。求①东西向直 立剖面上两翼的视倾角及两翼的翼间角,②横截面(垂直枢纽的剖面)的产状、基本内容 截面上两翼的侧伏角及两翼的翼间角(等于二面角) 。 (答:①北西翼 28,北东翼 32°,翼 间角 118°,②210°∠61°,北西翼 37°W,北东翼 22°E,翼间角 121°) 。
极射赤平投影CAD图解讲解

极射赤平投影CAD图解一、序言岩质边坡稳定性分析方法有许多,但无论是平面滑动的单一楔形断面滑体、单滑块和多滑块分析法,还是楔体滑动的仿平面分析法、楔体分割法、立体分析法、霍克分析法以及《岩土工程勘察规范》(GB50021-94)推荐法等,在计算边坡稳定性系数时,需要知道滑体控制平面(包括结构面和坡面、坡顶面)或直线(包括平面的法线)的地质产状,以及平面与平面、直线与直线、直线与平面间夹角等。
其中平面和直线的产状可以通过现场测量获取,除此之外的几何参数,在没有发明极射赤平投影之前,都是用计算法求得,不仅它们的计算公式复杂,而且计算过程繁琐,也很容易出错。
如果采用极射赤平投影求解边坡稳定性分析所需的几何参数,那就可以简化这些几何参数的计算过程,而且一般情况下只需要在现场测量出各个控制平面的地质产状即可。
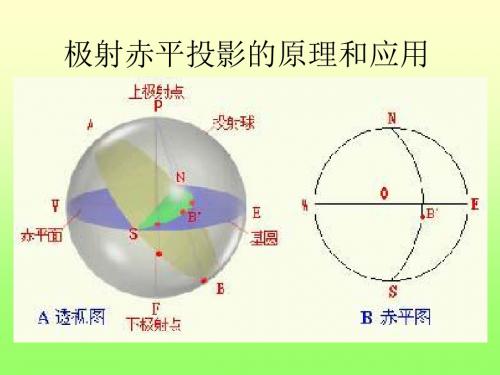
二、极射赤平投影的基本原理(一)投影要素极射赤平投影(以下简称赤平投影)以圆球作为投影工具,其进行投影的各个组成部分称为投影要素,包括:1.投影球(也称投射球):以任意长为半径的球。
2.球面:投影球的表面称为球面。
3.赤平面(也称赤平投影面):过投影球球心的水平面。
4.大圆:通过球心的平面与球面相交而成的圆,统称为大圆(如图一(a)中ASBN、PSFN、NESW),所有大圆的直径相等,且都等于投影球的直径。
当平面直立时,与球面相交成的大圆称为直立大圆(如图一(a)中PSFN);当平面水平时,与球面相交成的大圆称为赤平大圆或基圆(如图一(a)中NESW);当平面倾斜时,与球面相交成的大圆称为倾斜大圆(如图一(a)中ASBN)。
5.小圆:不过球心的平面与球面相而成的圆,统称为小圆(如图一(b)、(c)中AB、CD、FG、PACB)。
当平面直立时,与球面相交成的小圆称为直立小圆(如图一(b)中DC);当平面水平时,与球面相交成的小圆称为水平小圆(如图一(b)中AB);当平面倾斜时,与球面相交成的小圆称为倾斜小圆(如图一(b)中FG或图一(c)中PACB)。
极射赤平投影
求产状为E90°∠40°的平面法线的投影
• 法线的赤平投影 是指平面法线的产状标绘。法线 的投影是极点,平面的投影是圆弧,二者互相垂 直,夹角相差90°。往往用法线的投影代表与其 相对应的平面的投影,这样较为简单。
3.面状要素极点(法线)的投影
应用
• 已知岩层两视倾斜线:80°∠15°、 110°∠32°,求岩层的真倾斜线。
5.两线确定平面(根据视产状求真产状)
应用:褶皱的产状及其测量
褶皱的产状一般用枢纽和轴面的产状表示。
圆柱(筒)状褶皱枢纽与轴面产状的作图法测量
1、β图法求枢纽产状
褶皱枢纽产 状:褶皱两 翼同一褶皱 面的交线求 得。
2、π图法求枢纽的产状
3、轴面产状
一般褶皱则利用枢纽及轴迹确定轴面的连线。 枢纽: 褶皱面上曲率最大点的连线。
• 一切通过球心的 ,延伸后 均会与球面相交,并在球面上形 成大圆和点。以球的北极为发射 点,与球面上的大圆和点相连, 将大圆和点投影到赤道平面上, 这种投影称为极射赤平投影。本 教材采用下半球投影,即只投影 下半球的大圆弧和点。 • 图2为一球体,AC为垂直轴线, BD是水平的东西轴线,FP是水平 的南北轴线,BFDP为过球心的水 平面,即赤平面。
视倾角和真倾角的关系
tgβ = cos ω tgα
• (1)在透明纸上画出两视倾斜线投影为A、 B点; • (2)转动透明纸使A、B两点位于同一大圆 弧上(原因是A、B两点所代表的线就在岩 层层面上) • (3)在EW直径上数圆周至凸弧间的角距, 即为真倾角(40°);再由透明纸上指北 针标记顺时针数至凸弧中心所对基圆的方 位角则为岩层的真倾向
• 直线的投影方法 (图3)设一直线向 东倾伏、倾伏角 40°,此线交下半 球面于G点。以A为 发射点,球面上的 G点在赤平面上的 投影为H。 、D的方位角即 直线的倾伏向。同 理,一条直线向南 西倾伏、倾伏角 20°,此线交下半 球面于J点,其赤平 投影为K。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
﹡
旋转复原
﹡
2012-5-4
构造地质学—郝建民主讲 构造地质学 郝建民主讲
24
四、求相交两直线所构成的平面产状
∠36º, 例:两直线产状为180 ∠20 和120 ∠36 ,求所构成的平面产状 两直线产状为180º∠20 120º∠36 180 ∠20º和
投影前的准备工作: 投影前的准备工作: 透明纸放在投影网上,用铅笔标记一个“ 1. 透明纸放在投影网上,用铅笔标记一个“+” 以注明 投影网中心;再用一5 5mm的透明胶带贴在透明纸上 的透明胶带贴在透明纸上( 投影网中心;再用一5×5mm的透明胶带贴在透明纸上( 贴在 投影网中心所在部位) 投影网中心所在部位) 。 2. 将透明纸上的“+”标记与投影网对准,用图钉或大 将透明纸上的“ 标记与投影网对准, 标记与投影网对准 头针沿中心扎下去并固定在桌面上, 头针沿中心扎下去并固定在桌面上,此时透明纸能绕图钉 投影网中心)作水平方向的旋转。 (投影网中心)作水平方向的旋转。 用铅笔在透明纸上描下投影网的基圆(圆周) 3. 用铅笔在透明纸上描下投影网的基圆(圆周),并在 上端0 处注记一箭头,箭头指向投影网上0 的刻度处。 上端0°处注记一箭头,箭头指向投影网上0°的刻度处。
通过该点描绘经向大圆弧 9
构造地质学—郝建民主讲 构造地质学 郝建民主讲
作产状为120 ∠36º 作产状为120º ∠36 平面的赤平投影 120
旋转复原
●
●
透明纸转回原来的方位
最后效果
2012-5-4
构造地质学—郝建民主讲 构造地质学 郝建民主讲
10
重复一次—— 重复一次 • 例:一平面产状120 ° ∠ 36 °。 一平面产状120 • (1)将透明纸上指北标记与吴氏网上 N重合 , 以N为 将透明纸上指北标记与吴氏网上N重合, 顺时针数至120 得一点为倾向, 120° 0°; 顺时针数至 120° 得一点为倾向 , 与倾向垂直 过圆心的直径为平面的走向; 过圆心的直径为平面的走向; • (2) 转动透明纸使 120° 倾向的该点移至东西直径 转动透明纸使120 120° 由圆周向圆心数36 36° 得一点, 上 , 由圆周向圆心数 36° , 得一点 , 通过该点描 绘经向大圆弧 ; • (3) 把透明纸的指光标记转回到原来的指北方向 , 把透明纸的指光标记转回到原来的指北方向, 此时弧凸所指方向及凸度大小即为平面120 此时弧凸所指方向及凸度大小即为平面 120 °∠ 36 °的产状 。
2012-5-4 构造地质学—郝建民主讲 构造地质学 郝建民主讲 3
• 赤平投影口诀 • 口诀1: 直立为直径;倾斜为圆弧; 口诀1 直立为直径;倾斜为圆弧; 水平为基圆; 平面过球心) 水平为基圆;(平面过球心) • 口诀2: 直立为弧口向外;倾斜为 口诀2 直立为弧口向外; 圆半径小;水平小圆同心套; 圆半径小;水平小圆同心套;平面 过极直线短;(平面不过球心) ;(平面不过球心 过极直线短;(平面不过球心) • 口诀3: 垂线端点重心点;平线直 口诀3 垂线端点重心点; 径两端点;斜线圆内一个点; 径两端点;斜线圆内一个点; • 口诀4:平面投影为线;直线投影为 口诀4 平面投影为线; 点;
2012-5-4
构造地质学—郝建民主讲 构造地质学 郝建民主讲
11
旋转复原 确定倾向
●
●
确定倾 角 一平面产状120 一平面产状120 ° ∠ 36 °的投影 构造地质学—郝建民主讲 构造地质学 郝建民主讲
2012-5-4
12
二、直线的赤平投影
例:作直线产状330 ∠40 作直线产状330º ∠40º 330
·
·
·
╋
·
·
╋
·
·
画基圆、标注ESWN方位及十字中心 画基圆、标注ESWN方位及十字中心 ESWN 2012-5-4
透明纸效果, 透明纸效果,每次作图前的准 备工作( 备工作( 度数可省略 ) 7
构造地质学—郝建民主讲 构造地质学 郝建民主讲
作产状为120 ∠36º 作产状为120º ∠36 平面的赤平投影 120
旋转复原 确定倾伏向
确定倾伏角
2012-5-4
构造地质学—郝建民主讲 构造地质学 郝建民主讲
18
三、法线的赤平投影 •
是指平面法线的产状。 是指平面法线的产状。平面及其法线的投影常常互为使 只要注意到二者互相垂直,夹角相差90 90° 这样, 用 , 只要注意到二者互相垂直, 夹角相差90° , 这样 , 投 影操作就比较容易。由于法线投影是极点,平面投影是圆弧, 影操作就比较容易。由于法线投影是极点,平面投影是圆弧, 所以往往用法线投影代表与其相对应的平面投影,就较为简 所以往往用法线投影代表与其相对应的平面投影, 单。 求一平面产状90 90° 40° 例:求一平面产状90°∠40°的法线投影 。 透明纸上指北标记与网上N重合, (1) 透明纸上指北标记与网上N 重合 , 以N 为 0° 顺时针数 90° 正好在东西直径的E 至 90° , 正好在东西直径的 E 点 , 过该点由圆周向圆内数 40° 为平面倾斜线产状的投影。若继续数90 90° 40°, 得D′ 点, 为平面倾斜线产状的投影。 若继续数90° , 显然已越过圆心进入相反倾向, 显然已越过圆心进入相反倾向, 得 F′ 点, 该点即为该平面 法线产状; 法线产状; 也可沿90 的反方向即以圆心向反倾向数至40 90° 40° (2)也可沿90°的反方向即以圆心向反倾向数至40°即得 线 产状 因为从圆 周数起 数起 正好 该 法 线产状 。 因为从圆周 数起 和从 圆心 反 向 数起正 好 差 90° 90° 。 上述单一面、线的投影方法是利用赤平投影研究线与线、 上述单一面 、 线的投影方法是利用赤平投影研究线与线、 线与面、面与面相互关系的基础方法。 线与面、面与面相互关系的基础方法。
2012-5-4
构造地质学—郝建民主讲 构造地质学 郝建民主讲
16
确定倾伏向
●
旋转复原
●
●
确定倾伏角
2012-5-4
一直线产状330 一直线产状330 °∠40 °的投影 构造地质学—郝建民主讲 构造地质学 郝建民主讲
17
又例:产状为124° 63° 又例:产状为124°∠63°的直线的赤平投影 124
构造地质学—郝建民主讲 构造地质学 郝建民主讲
求一平面产状90 ∠40 求一平面产状90º∠40 的法线投影 90 ∠40º的法线投影
●
●
2012-5-4
最后效果 构造地质学—郝建民主讲 构造地质学 郝建民主讲
23
又例: 投影走向35 35° 倾向南东、倾角25 又例: 投影走向35°、倾向南东、倾角25 的平面( °的平面(125 ° ∠25 °)及其法线
自圆周向圆心数20 的角距 自圆周向圆心数20º的角距,投点 20 的角距, 26
构造地质学—郝建民主讲 构造地质学 郝建民主讲 19
• •
• •
2012-5-4
透视图
投影图
● ●
产状为90 °∠40 °平面的法线投影 产状为90 关键:法线和平面垂直,倾向相反(90°),倾角互余。 关键:法线和平面垂直,倾向相反(90°),倾角互余。 倾角互余
2012-5-4 构造地质学—郝建民主讲 构造地质学 郝建民主讲 20
详细操作步骤—— 详细操作步骤 求一平面产状90 ∠40º的法线投影 90º∠40 例:求一平面产状90 ∠40 的法线投影
●ቤተ መጻሕፍቲ ባይዱ
透明纸 2012-5-4
基圆上90 , 为该平面的倾向; 基圆上90º, 为该平面的倾向;该点正 90 好位于东西直径上, 好位于东西直径上,不用旋转 构造地质学—郝建民主讲 构造地质学 郝建民主讲 21
●
透明纸 2012-5-4
基圆上180 为直线 基圆上180º为直线a的倾伏向 180 为直线a 25 构造地质学—郝建民主讲 构造地质学 郝建民主讲
两直线产状为180 ∠20 120º∠36 ∠36º, 两直线产状为180º∠20 和120 ∠36 ,求所构成的平面产状 180 ∠20º和
●
●
转动纸, 180 点移至东西直径上 转动纸,使180º点移至东西直径上 2012-5-4
2012-5-4 构造地质学—郝建民主讲 构造地质学 郝建民主讲 4
投影步骤(口诀5 投影步骤(口诀5): A、基圆顺钟找倾向; 基圆顺钟找倾向; 顺钟找倾向 B、东西直径数倾角(由圆周向圆心数); 东西直径数倾角(由圆周向圆心数); 直径数倾角 C、径向圆弧拟平面; 径向圆弧拟平面; 圆弧 D、复原归位定投影。 复原归位定投影。 归位定投影
确定倾向
●
●
基圆上120 , 基圆上120º,为该平面的倾向 120 2012-5-4
转动纸, 120 转动纸,使120º 点移至东西直径上 8
构造地质学—郝建民主讲 构造地质学 郝建民主讲
作产状为120 ∠36º 作产状为120º ∠36 平面的赤平投影 120 确定倾 角
●
由圆周向圆心数36 的角距, 由圆周向圆心数36º 的角距,投点 36 2012-5-4
求一平面产状90 ∠40 求一平面产状90º∠40 的法线投影 90 ∠40º的法线投影
●
●
●
由圆周向圆心数40 的角距 投点, 由圆周向圆心数40º的角距,投点,通 40 的角距, 过此点描绘的经向大圆弧表示该平面 2012-5-4
若通过此点继续数90 角距, 若通过此点继续数90º 角距,得另 90 一点, 一点,该点即为该平面的法线产状 22
2012-5-4 构造地质学—郝建民主讲 构造地质学 郝建民主讲 5
一、平面的赤平投影
例:作产状为120 ∠36 平面的赤平投影 作产状为120º ∠36º 120
