20181125小学奥数练习卷(知识点:三视图与展开图)含答案解析
五年级立体几何拓展----三视图专属奥数讲义

学科教师辅导讲义一.三视图在观察物体的时候,我们往往可以从不同的角度进行观察.角度不同,看到的风景就会不同.比如:我们可以从正面看,上面看,左面看,看到的图形分别称为正视图,俯视图和左视图.并且容易发现:正面看和后面看,上面看和下面看,左面看和右面看得到的图形是知识图谱错题回顾三视图知识精讲相同的.对于较复杂的立体图形,通过三视图法往往可以很方便地计算出表面积. 二.正方体的展开图我们采用不同的剪开方法,共可以得到下面11种展开图.三.长方体的展开图观察上图可以发现,长方体的展开图由6个长方形组成,相对面的面积相等,即上面=下面=长×宽,左面=右面=宽×高,前面=后面=长×高. 四.判断图形折叠后能否围成长方体或正方体的方法.判断一个图形折叠后能否围成正方体或长方体,首先,要依据它们各自展开图的特点判断;其次,可以运用空间想象或实际操作进一步判断.重难点:展开图、三视图及三视图求个数和表面积.高宽长右面左面 后面下面 前面 上面上 后 前右左下 展开后由上、下、左、右、前、后六个正方形面组成,这六个正方形面的面积都相等.三点剖析题模精选题模一:展开图与对立面例1.1.1 一个正方体的六个面上分别写着A ,B ,C ,D ,E ,F 六个字母.请你根据图中的三种摆放情况,判断每个字母的对面是______________,______________,______________【答案】 B 与D 相对,E 与A 相对,C 与F 相对 【解析】 由于正方体的6个面上写了6个不同的字母,那么每个字母在正方体的面上只能出现1次,如果2个字母在相邻的面上出现,那么它们一定不能相对.第一步,先看前2种摆放情况:在这2种摆放情况中,只有字母B 出现了2次,那么由第一种摆放可知,B 不与A 相对,也不与F 相对;由第二种摆放可知,B 不与C 相对,也不与E 相对.那么在所有的字母中,B 只能与D 相对.第二步,再看后2种摆放情况:在这2种摆放情况中,只有字母E 出现了2次,那么由第二种摆放可知,E 不与B 相对,也不与C 相对;由第三种摆放可知,E 不与D 相对,也不与F 相对.那么在所有的字母中,E 只能与A 相对.正方体有三个对面,因B 与D 相对,E 与A 相对,那么第三组对面上一定是C 与F 相对.例1.1.2 图中的四个正方体标字母的方式是完全相同的,请你利用图中已知的信息,判断A 、B 、C 的对面分别标的是哪个字母?【答案】 A 的对面标有D ,B 的对面标有F ,C 的对面标有E【解析】 由已知条件,标有C ,D 的两个面不能相对,那么或A 的对面标有D ,或B 的对面标有D .如果标有D ,A 的两个面相对,那么“标有C ,D 的两个面不能相对”,“标有E ,A 的两个面也不能相对”这两个条件都可以满足.注意到当D 在朝右的面,E 在朝上的面时,F 在朝前的面上,那么只能是标有E ,C 的两个面相对,而标有F ,B 的两个面相对.经检验,这种情况满足题目要求.如果标有D ,B 的两个面相对,那么由于标有E ,A 的两个面也不能相对,于是标有A 的对面就是标有F 的面,而标有C 的对面就是标有E 的面.此时D 在朝后的面上,E 在朝左的面上,F 在朝下的面上.我们把六面体旋转,把D 转到朝右的面,并把E 转到朝上的面,此时朝前的面上标的是A ,而朝后的面上标的是F ,与题意不符.A BC综上所述,满足题意的答案只有一个:A 的对面标有D ,B 的对面标有F ,C 的对面标有E .例1.1.3 如图,第1个方格内放着一个正方体木块,木块六个面上分别写着ABCDEF 六个字母.其中A 与D 相对,B 与E 相对,C 与F 相对.现在将木块标有字母A 的那个面朝上,标有字母D 的那个面朝下放在第1个方格内,然后让木块按照箭头指向,沿着图中方格滚动,当木块滚到21格时,木块向上的面上写的是哪个字母?【答案】 字母A【解析】 发现木块向左滚4格后,各个面上标的字母与初始时的情况完全一致.那么木块朝其它方向滚时也有类似的情况,即木块向任意方向连滚4格,它的各个面上标的字母不变. 所以木块向左滚4格到第5格时,各个面上标的字母与在第1格时的情况完全一致.再向下滚4格到第9格,再向右滚4格到第13格,再向下滚4格到第17格,最后向左滚4格到第21格,每次都是朝同一方向滚4格,因此在第5格,第9格,第13格,第17格,第21格木块向上的面上总是写的字母A .例1.1.4 如图,在一个正方体的表面上写着1~6这6个自然数,并且1对着4,2对着5,3对着6.现在将正方体的一些棱剪开,使它的表面展开图如图所示.如果只知道1和2所在的面,那么6应该在哪个面上(写出字母代号)?【答案】 A【解析】 对于立方体展开图,我们可以把任一个面当作底面,把它还原成立方体的表面.如图1,观察虚线圈住的部分,可以发现写有1,A ,B 的三个面两两相邻;再观察图2的虚线圈住的部分,发现写有A ,B ,C 的三个面也两两相邻.此时,写有1的面与A 面,B 面都相邻,C 面也与A 面,B 面都相邻,因此写有1的面与C 面相对,即C 面上写的是4.图11 AB C 2D图2 1 AB C 2D1与C 相对,C 面上写的是41 AB C 2D 3 12观察图3中的虚线圈住的部分,容易看出写有2的面与B 面相对,因此B 面上写的是5.则立方体展开图就如图4所示.还剩下A 面与D 面上的数字没有确定,这两个面上分别写有3和6.由于写有1的面,写有5的面与A 面两两相邻,把这三个面还原到立方体中.在图2所示的立方体中,5与2相对,在立方体朝左的侧面上;1在朝前的侧面上.在展开图中以写有1的面为朝前的侧面,A 面为下底面,则写有5的面恰好在朝左的侧面上.此时写有1的面,写有5的面都对齐了,而原立方体中下底面写有数字6,因此A 面上就是6.例1.1.5 下图是正方体,四边形APQC 是表示用平面截正方体的截面,截面的线表现在展开图的哪里呢?把大致的图形在右面展开图里画出来.【答案】 见解析【解析】 截线在展开图中如图所示:例1.1.6 右图是一个立体图形的平面展开图,图中的每个小方格都是边长为1的正方形.现在将其沿实线...折叠,还原成原来的立体图形,那么立体图形的体积等于_________.P图31 AB 4 2D2与B 相对, B 面上写的是5图41 A5 4 2DA . 3B . 4C . 5D . 6【答案】B【解析】 根据实线还原,体积为4. 题模二:三视图求表面积例1.2.1 下图是由5个相同的正方体木块搭成的,从上面看到的图形是( ).A . A 图B . B 图C . C 图D . D 图【答案】C【解析】 5个在原图均已看到,易知C 符合要求.例1.2.2 右图是由18个棱长为1cm 的小正方形拼成的立体图形,它的表面积是( )平方厘米.A . 44B . 46C . 48D . 50【答案】C【解析】 从正面、左面、上面分别可看见8、7、9块,故表面积为()21879248cm ⨯++⨯=.例1.2.3 右图中的一些积木是由16块棱长为2cm 的正方体堆成的,它的表面积是________2cm .【答案】 200【解析】 从前到后的3面依次有2块、5块、7块,因此还剩162572---=块,为可看D.B .C .A .见的1块与其下方的1块.由此易知正视图、俯视图、左视图分别能看到7块、9块、8块,此外离我们最近的2块有两个面从6个方向均无法看到,综上共可看到()7982250++⨯+=个面,表面积为22250200cm ⨯=.例 1.2.4 图中的立体是由大小相同的若干单位正方体积木搭成的.这样的积木一共有多少块?画出它的三视图,表面积是多少?【答案】 37;三视图如下图所示;102【解析】 将此图分为从左到右的5层,分别有16、9、5、6、1块,故共有16956137++++=块.三视图见答案,分别可看见17、15、16块,其中左视图有3块“被遮挡”,因此表面积为()17151632102+++⨯=⎡⎤⎣⎦.例1.2.5 图中的立体图形由11个棱长为1的立方块搭成,这个立体图形的表面积为_______.【答案】34【解析】 按一定的顺序,从不同的角度来看这个立体图形的表面的面积. 题模三:已知三视图反推个数例1.3.1 这个图形最少是由( )个正方体整齐堆放而成的.正视图 俯视图 左视图A.12B.13C.14D.15【答案】B【解析】从上面看下去,最少需要:122412113++++++=.例1.3.2此图是某几何体从正面和左面看到的图形.若该几何体是由若干个棱长为1的正方体垒成的,则这个几何体的体积最小是________.【答案】6【解析】根据正视图,理论上最少需要6块.而6块可以构造出来,例如,其俯视图如下图所示.因此,体积最小为3166⨯=.例 1.3.3一个立体图形,从前面,上面,右边三个方向看到的图形都如图所示,是一个样的,那么该立体图形最多由__________块小立方体组成.【答案】23【解析】按由上到下逐层分析,各层的小立方体数目分别不超过1个、4个、8个、10个,所以该立体图形最多由23个小立方体组成.例 1.3.4有一些大小相同的正方形木块堆成一堆,从上往下看是图3-1,从前往后看是图3-2,从左往右看是图3-3,那么这堆木块最多有多少块?最少有多少块?从正面看从左面看1 412212【答案】 16,13【解析】 43416+⨯=块,424113+⨯+=块.这堆木块最多有16块,最少有13块.例1.3.5 地上有一堆小立方体,从上面看时如图1所示,从前面看时如图2所示,从左边看时如图3所示.这一堆立方体一共有几个?如果每个小立方体的棱长为1厘米,那么这堆立方体所堆成的立体图形表面积为多少平方厘米?【答案】 10个;42平方厘米【解析】 采用在俯视图上标数的方法来求解,只要知道俯视图上的每格有几块小立方体,就可以很轻松的得到这堆立方体所形成的立体图形的样子.首先从俯视图很容易看出,有3个格子里是没有小立方体的,而其他6个格子里至少有一个小立方体.如下图,将所得信息填入俯视图中.结合俯视图和主视图,不难看出,有两格只有1块小立方体.将所得信息填入俯视图中.同样的,结合俯视图和左视图,又可以知道有一格只有1块小立方体.将所得信息填入俯视图中.从前面看图1图2图3我们来继续考虑,左视图中最左边一排有2块小立方体,所以俯视图左上角处有2块小立方体.将所得信息填入俯视图中.同理,主视图最右边一排有2块小立方体,所以俯视图最右边中间处有2块小立方体.将所得信息填入俯视图中.不难看出,俯视图中最后剩下的那块有3个小立方体,所以俯视图中每格的小立方体数如下:于是这一堆立方体一共有21321110+++++=个. 接着很容易得到这个立体图形的样子,如下图.上下各能看到6个面,前后各能看到6个面,左右各能看到6个面,同时注意到立体图形的中间共有6个会互相遮挡的面,所以表面积是()2666642⨯+++=平方厘米.从左边看随堂练习随练1.1将一正方体纸盒沿右图所示的粗实线剪开,展开成平面图,其展开图的形状为().A.A图B.B图C.C图D.D图【答案】B【解析】竖向只剪了1刀,故前、后、左、右四个面应在一条线上,排除A、D.易知上、下两面不在一条线上,排除C,故选B.随练1.2水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如下图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面.则“祝”、“你”、“前”分别表示正方体的________________________.【答案】后面、上面、左面【解析】易知你、程相对,前、锦相对,祝、似相对,因此“祝”、“你”、“前”分别表示正方体的后面、上面、左面.随练1.3小明把五颗完全相同的骰子拼摆成一排(如图),那么这五颗骰子底面上的点数之和是__________.【答案】16【解析】根据已知推出(4,5)(1,3)(2,6)互为对立面,所以这五颗骰子底面上的点数之和是++++=.6152216随练1.4右图是由八个相同的小正方体组成而成的几何体,则从正面观察,得到的平面图形是__________.序号)【答案】 ②【解析】 从正面看到图②,从上面看到图①,从右面看到图③.所以正确答案是图②.随练1.5 由棱长为1的正方体搭成如图所示的图形,共有__________个正方体,它的表面积是__________.【答案】 10;34【解析】 第一层有8个,第二层有2个,共10个.其三视图分别能看到4、5、8个,故表面积为()11458234⨯⨯++⨯=.随练1.6 如图,有9个边长为1米的正方体,如图所示堆成一个立体图形.该立体图形的表面积等于__________平方米.【答案】 38【解析】 利用三视图.从前面、右面、上面看依次如图所示.所以该立体图形的表面积是()26672138++⨯⨯=平方米.随练1.7 如图6,用若干个棱长为1的小正方体堆成一个大的几何体,这个几何体的表面积(含底面积)是__________.① ② ③ ④【答案】 90【解析】 根据三视图,大的几何体的表面积等于正视图面积+俯视图面积+右视图面积的2倍,所以是()21415162190++⨯⨯=.随练 1.8 用棱长是1厘米的小立方体拼成如图所示的立体图形,这个图形的表面积是__________平方厘米.【答案】 46平方厘米【解析】 如图1,从立体图形上方和下方看去,看到的都是9块小正方形.面积是9平方厘米.从四个侧面看去,看到的是图2形式的7块小正方形,面积是7平方厘米. 所以立体图形的表面积为927446⨯+⨯=平方厘米.随练1.9 把若干个棱长为1厘米的小正方体木块搭成一个图形,从上面和前面看到的都是如图所示的情形,这个图形最多需要__________个这样的小正方体,最少需要__________个这样的小正方体.【答案】 9;7【解析】 由从上方看到的结果可知第一层必有5个,且第二层至多5个;由从前面看到的结果可知共有2层,且第二层至少2个.再结合两个视图可知第二层至多4个.综上,最多9个,最少7个.图1图2 图6自我总结课后作业作业1一个数学玩具的包装盒是正方体,其表面展开图如下.现在每方格内都填上相应的数字.已知将这个表面展开图沿虚线折成正方体后,相对面的两数之和为“3”,则填在A、B、C内的三个数字依次是_____________.【答案】3,1,2【解析】正方体的平面展开图中,相对面之间一定隔着一个正方形,所以在此正方体上与“A”相对的面上的数是“0”.与“B”相对的面上的数是“2”.与“C”相对的面上的数是“1”.所以A、B、C内的三个数字依次是3,1,2.作业2把1至6各一个分别写在正方形的六个面上,每个面只写一个数字,且1与4相对,2与5相对,3与6相对,从某个角度看到的三个面上的数字如图(a)所示,从另一个角度看到的三个面如图(b)所示,那么图(b)中的“?”代表的数字是___________.A.2B.3C.4D.5【答案】A【解析】如图,4对面是1,所以在图a中把4翻到底面,顶部变成了1,如图b,而5对面是2,所以当6转到正面时,5在左侧,右侧自然是2了,故答案是2..作业3 下图由一个正五边形,五个长方形,五个等边三角形组成,它是一个立体图形的平面展开图,那么这个立体图形有__________条棱.【答案】 20【解析】 此立体图形,示意图如上:共20条棱.作业4 用若干个棱长为1cm 的小正方体码放成如图所示的立体,则这个立体的表面积(含下底面面积)等于___________2cm .【答案】 60【解析】 根据三视图,我们可知,此立体图形的前面与后面,左面与右面,上面与下面的表面积分别相等.所以我们只要知道前面有11个正方形,右面有8个正方形,上面有11个面,就可求出它露在外面的面共计()11811260++⨯=个正方形,所以它的表面积是2260160cm ⨯=.作业5 如图,把19个边长为1厘米正方体重叠起来堆成如图所示的立方体,这个立方体的表面积是______平方厘米.【答案】 54【解析】 从上下左右前后六个方向看,分别可以看到9、9、8、8、10、10个小正方形面,所以总的表面积为54平方厘米.作业6 图中的立体是由大小相同的若干单位正方体积木搭成的.这样的积木一共有多少块?画出它的三视图,表面积是多少?【答案】 30;三视图如下图所示;76【解析】 将此图分为从左到右的4层,分别有11、7、5、7块,故共有1175730+++=块.三视图见答案,分别可看见13、12、11块,其中左视图有2块“被遮挡”,因此表面积为()1312112276+++⨯=⎡⎤⎣⎦.作业7 由若干个相同的正方体木块搭成的立体,从正面和左面看到的图形都是右图,搭这样的立体,最少用( )个这样的木块.A . 4B . 5C . 6D . 8【答案】A【解析】 按如图方式摆放即可. 正视图 俯视图 左视图作业8 由若干个棱长为1的正方体堆成的立体图形,其正视图、俯视图和左视图如下所示,请问这个立体图形体积是________.【答案】 5【解析】 由正视图和左视图可知共两层,且顶层只有1块,由俯视图可知底层有4块,故共有5块,体积为5.作业9 一仓库里堆放着若干个完全相同的正方体货箱,这堆货箱的三视图如图所示,这堆真方体货箱共有______________个.【答案】 9【解析】 俯视图确定基座,分析每块上的高度.正视图 俯视图 左视图。
三视图与展开图重点难点考点真题(word+答案)

专题三视图与展开图1.视图:当我们从某一角度观察一个实物时,所看到的图像叫做物体的一个视图。
2.物体的三视图特指主视图、俯视图、左视图。
(1)主视图:从物体的前面向后面投射所得的视图称主视图,能反映物体的前面形状。
(2)俯视图:从物体的上面向下面投射所得的视图称俯视图,能反映物体的上面形状。
(3)左视图:从物体的左面向右面投射所得的视图称左视图,能反映物体的左面形状,有时也叫做侧视图。
物体的三视图实际上是物体在三个不同方向的正投影.正投影面上的正投影就是主视图,水平投影面上的正投影就是俯视图,侧投影面上的正投影就是左视图在画三视图时,三个三视图不要随意乱放,应做到俯视图在主视图的下方,左视图在主视图的右边,三个视图之间保持:长对正,高平齐,宽相等。
3.展开图:平面图形有三角形、四边形、圆等.立体图形有棱柱、棱锥、圆柱、圆锥、球等.把立体图形按一定的方式展开就会得到平面图形,把平面图形按一定的途径进行折叠就会得到相应的立体图形。
【例题1】(2019•四川省达州市)如图是由7个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的左视图是()A.B.C.D.【例题2】(2019•甘肃)已知某几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的左视图的面积为.专题知识回顾专题典型题考法及解析【例题3】(2019•江苏连云港)一个几何体的侧面展开图如图所示,则该几何体的底面是()A.B.C.D.专题典型训练题一、选择题1.(2019广东深圳)下列哪个图形是正方体的展开图()A.B.C.D.2.(2019•山东省济宁市)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是()A.B.C.D.3.(2019•浙江宁波)如图,下列关于物体的主视图画法正确的是()A.B.C.D.4. (2019安徽)一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是()A.B.C.D.5.(2019湖北省鄂州市)如图是由7个小正方体组合成的几何体,则其左视图为()A.B.C.D.6.(2019•山东临沂)如图所示,正三棱柱的左视图()A.B.C.D.7.(2019湖北仙桃)如图所示的正六棱柱的主视图是()8.(2019山东东营)如图所示是一个几何体的三视图,如果一只蚂蚁从这个几何体的点B出发,沿表面爬到AC的中点D处,则最短路线长为()A.B C.3 D.9.(2019年广西柳州市)如图,这是一个机械零部件,该零部件的左视图是()A.B.C.D.10.(2019贵州省安顺市)如图,该立体图形的俯视图是()A.B.C.D.11. (2019黑龙江大庆)一个"粮仓"的三视图如图所示(单位:m),则它的体积是( )A.21πm3B30πm3 C.45πm3 D.63πm312.(2019辽宁本溪)如图所示,该几何体的左视图是()13.(2019广西桂林)一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积为()A.πB.2πC.3πD.1)π+14.(2019湖南益阳)下列几何体中,其侧面展开图为扇形的是()A.B.C.D.15.(2019•黑龙江省齐齐哈尔市)如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图视图,则搭建这个几何体所需要的小正方体的个数至少为()A.5B.6C.7D.816.(2019江苏镇江)一个物体如图所示,它的俯视图是()17.(2019•山东潍坊)如图是由10个同样大小的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的三视图描述正确的是()A.俯视图不变,左视图不变B.主视图改变,左视图改变C.俯视图不变,主视图不变D.主视图改变,俯视图改变18.(2019四川泸州)下列立体图形中,俯视图是三角形的是()19.(2019•湖北省随州市)如图是一个几何体的三视图,则这个几何体的表面积为()A. B. C. D.20.(2019•四川省绵阳市)下列几何体中,主视图是三角形的是()A B C D二、填空题21. (2019•河北省)图2是图1中长方体的三视图,若用S表示面积,S主=x2+2x,S左=x2+x,则S俯=()A .x 2+3x +2B .x 2+2C .x 2+2x +1D .2x 2+3x22.(2019•广西贵港)如图,在扇形OAB 中,半径OA 与OB 的夹角为120°,点A 与点B 的距离为2,若扇形OAB恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为.23.(2019•山东青岛)如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若 干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以 取走 个小立方块.24.(2019湖南郴州)已知某几何体的三视图如图,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形,则该几何体的侧面展开图的面积是 .(结果保留π)25.(2019北京市) 在如图所示的几何体中,其三视图中有矩形的是_______.(写出所有正确答案的序号)第11题图③圆锥②圆柱①长方体26.(2019湖北荆州)如图①,已知正方体ABCD﹣A1B1C1D1的棱长为4cm,E,F,G分别是AB,AA1,AD的中点,截面EFG将这个正方体切去一个角后得到一个新的几何体(如图②),则图②中阴影部分的面积为cm2.27.(2019•黑龙江省绥化市)用一个圆心角为120°的扇形作一个圆锥的侧面,若这个圆锥的底面半径恰好等于4,则这个圆锥的母线长为.专题三视图与展开图1.视图:当我们从某一角度观察一个实物时,所看到的图像叫做物体的一个视图。
20181125小学奥数练习卷(知识点:染色问题)含答案解析

小学奥数练习卷(知识点:染色问题)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)一.选择题(共5小题)1.连接正方形ABCD的对角线,并将四个顶点分别染成红色或黄色,将顶点颜色全相同的三角形称为同色三角形,则图中有同色三角形的染色方法共有()A.12B.17C.22D.102.由210块小正方体构成5×6×7的长方体,如果将其表面涂成红色,那么其中一面涂红的小正方体有()块,两面涂红的小正方体有()块.A.92,48B.94,48C.90,50D.94,463.一个由边长为1的小正方形组成的n×n的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个角上的小正方形不全同色,那么正整数n的最大值是()A.3B.4C.5D.64.如图,一块草地被开垦出11块正六边形耕地,菲菲在这些耕地内种植向日葵、豌豆射手、闪电芦苇、冰冻西瓜4种植物,如果相邻的耕地种植的植物不能相同,她有()种不同的种植办法.(相邻耕地是指有公共边,每块耕地内只能种植一种植物)A.6912B.6144C.4608D.42245.将一个大三角形分割成36 个小三角形,并且将其中一部分小三角形涂成红色,另一部分涂成蓝色,并且使得两个有公共边的三角形的颜色不同,如果红色的三角形比蓝色的多,那么多()个.A.1B.4C.6D.7第Ⅱ卷(非选择题)二.填空题(共37小题)6.把一个正方体的表面积全涂成黑色,然后切成27个小正方体(如图),那么两面是黑色的小正方体共有个.7.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则最少需要种颜色.8.一个长方体的棱长都是整数,表面涂上色后,切成棱长为1的正方体,若没有颜色的小正方体共有12个,则一面有色的正方体最少有个.9.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则最少需要种颜色.10.一个宝库有9个藏宝室,成九宫格状排列,但只有一个进口和一个出口分别开在如图所示的藏宝室,每个藏宝室至多只能进去一次,相邻的藏宝室之间都有门相通,每个藏宝室中的宝贝价值已标在图中,大盗买通守护,夜间进入宝库,他能带走的宝物价值最多是.11.如图是一个由26个相同的小正方体堆成的几何体,它的底层由5×4个小正方体构成,如果把它的外表面(包括底面)全部涂成红色,那么当这个几何体被拆开后,有3个面是红色的小正方体有块.12.如图所示,用64个棱长为1的小立方体组成一个棱长为4的大立方体,再从上到下取走4个小立方体(图中阴影部分).将剩余立体图形的内外表面都染成红色,那么恰有两个面染色的小立方体共有个.13.一个5×5的方格由25个1×1的小方格组成,每个小方格都被分成四个相同的等腰直角三角形,其中三个被涂成了黑色(如图a所示).小正方形的边如果位于黑色部分,就称为黑边,反之就是白边.在5×5的方格内,相邻(有公共边)小方格的公共边必须是同色的,那么5×5方格的四条长边(如图b 所示)上最少有条黑边.14.将一个8×8×8的立方体的三个面染红色,三个面染蓝色(要求任意三个有公共顶点的面不能全都染同一种颜色),然后将其切割成512个1×1×1的小立方体.这512个小立方体中,有个小立方体上既有红色面又有蓝色面.15.如图,5×5的方格中有三个小方格已经染黑.现在要将一个1×3的白长方形(不能选已经染黑的方格)染黑,要求其不能与已经染黑的方格产生公共边或者公共点.有种选法.16.这是一个由72个相同小四边形组成的图形,有一些四边形被病毒感染变成黑色.当某个健康的小四边形(白色),其周围至少有两个相邻的小四边形被感染时,则该四边形也将被感染变黑,依次扩散开来.那么至少再增加个病毒源(即黑色小四边形),可以使整个大图形都被感染.(相邻是指两个小四边形有公共边).17.将一个4×4×4的立方体切割成64个1×1×1的小立方体,然后将其中16个1×1×1的小立方体染成红色,要求与任意一条棱平行的4个小立方体中,都正好有1个小正方体被染成红色,不同的染色方法有种(旋转后相同的染色方法也视为不同的染色方法).18.小明想要对图中的每个小三角形进行染色,要求任意一个三角形的三边都是一条染红色、一条染绿色、一条染蓝色.图中给出了某些边的颜色,则AB边应该染色.19.如图是一个被挖空的长方体,每个洞都是贯穿的,如果把它丢进染缸里,4个面染色的小正方体比3个面染色的小正方体多个.20.如图,一个长方形的表格有8列,将数字1,2,…按一定顺序填入表格中(从左往右填,等一行填满后进入下一行,还是从左往右填),一个学生先将填有数字1的格子涂黑,接下来跳过1个格子,将填有数字3的格子涂黑;接下来跳过2个格子,将填有数字6的格子涂黑;接下来跳过3个格子,将填有数字10的格子涂黑.依此类推,直到所有列都含有至少一个黑格为止(不再继续涂黑了).那么,他涂黑的最后一个格子里的数字为.21.将1,2,3,4,5填入如图表格中(表中的字母和数字用来标注行、列或者小方格,比如D3就表示D行3列那个白色小方格),要求每行每列上的五个数互不相同,接下来给出一些提示:(1)第4列的黑色小方格内的数之和为9;(2)第C行的黑色小方格内的数之和为7;(3)第2列的白色小方格内的数之和为8;(4)第B行的黑色小方格内的数之和小于第D行的黑色小方格内的数之和.则D4中填的数字为.22.图中的网格是由6个相同的小正方形构成,将其中4个小正方形涂上灰色,要求每行每列都有涂色的小正方形,经旋转后两种涂色的网格相同,则视为相同的涂法,那么有种不同的涂色方法.23.如图所示的多面体叫做正二十面体,是5个柏拉图立体(正多面体)中的一个,这个多面体由20个面(正三角形)围成,现将这20个面着色,要求有共同棱的两个面染有不同的颜色,则至少需要种颜色.24.由一些顶点和边构成的图形称为一个图,对一个图用不同颜色给顶点染色,要求具有相同边的两个顶点染不同的颜色.称为图的点染色,图的点染色通常要研究的问题是完成染色所需要的最少的颜色数,这个数称为图的色数.如图的图称为皮特森图,皮特森图的色数为.25.一块长、宽、高分别为15cm、12cm、9cm的长方体木块表面涂上红色后,将它切成大小相等的正方体且没有废料,至少可以切块,其中六个面都没有涂上红色的正方体有块.26.把一个棱长为n的大正方体表面涂上红色,然后切成n3个棱长为1的小正方体,经统计,恰好有一面涂红色的小正方体数量刚好是有三面涂红色的小正方体的12倍,那么n=.27.七个正方形拼成如图,我们要对其中的若干个正方形进行涂色,要求:(1)至少涂其中的两个正方形;(2)相邻正方形不能同时被涂色(有公共边或者公共顶点的正方形称为相邻正方形).那么,有种不同的涂色方法.28.我们有27个1×1×1的小立方体,将其拼成一个3×3×3的大立方体,其中的一些小立方体的某些面被涂成了灰色,最后拼成的大立方体如图所示,那么,六个面都是白色的小立方体最多有个.29.图2的8×8表格中共含有168个如图1的“T”形.现对图2中的每个小方格染成黑色或白色;如果一个“T”形中黑白小方格各2个,则称这个“T”形为“和谐”的;那么对图2的各种染色方案,“和谐”的“T”形至多有个.30.将图中的边染色,要求有共同顶点的两个相邻的边染不同的颜色,则至少需要中颜色.31.四个黑色1×1×1的正方体和四个白色1×1×1的正方体可以组成种不同的2×2×2的正方体(经过旋转得到相同的正方体视为同一种惰况).32.一个大正方形表面涂上红色后,按如图方式切成27个小正方形,这些小正方形中,恰好有三个面涂有红色的有个.33.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则至少需要种颜色.34.有9个表面涂有红漆的正方体,它们的棱长分别是2,3,4,…,9,10.将这些正方体都锯成棱长是1 的小正方体,在得到的小正方体中,至少有一个面是红色的有个.35.用1024个棱长是1的小正方体组成体积是1024的一个长方体.将这个长方体的六个面都涂上颜色,则六个面都没有涂色的小正方体最多有个.36.如图是64个小正方体组成的大正方体,把它的表面全部涂上绿色,请回答:三面涂上绿色的小正方体有个.没有涂上绿色的小正方体有个.两面涂上绿色的小正方体有个.37.将图中的圆圈染色.要求有连线的两个相邻的圆圈染不同的颜色,则最少需要种颜色.38.36个相同的小正方体叠成如图所示的长方体,取走A、B、C三个小正方体后,在这个几何体的整个表面涂满红漆,其中有个正方体是三面有漆的.39.x是一个正整数,将x×4×5的长方体的表面涂满红色后,锯成棱长全部是1的小正方体.这些正方体中,至少有一面是红色的小正方体有110个.那么,x=.40.由四个完全相同的正方体堆积成如图所示的立体,则立体的表面上(包括底面)所有黑点的总数至少是个.41.把一个大长方体表面涂满红色后,分割成若干个同样大小的长方体,其中只有两个面涂上红色的小长方体恰好是12块,那么可以把这个大长方体分割成个小长方体.A.20个B.27个C.32个D.42个.42.如图是一个变形的红十字一共分为六块区域.现在要用n种颜色对其染色,要求相邻的两块区域(有公共边的两块区域称为相邻)染成不同的颜色.如果颜色能反复使用,那么一共有种不同的染色方法(用n表示).三.解答题(共8小题)43.将图中的O分别涂成红色、黄色或绿色,要求有线段相连的两个相邻O涂不同的颜色,共有多少种不同的涂法?44.7×7的方格黑白染色,如果黑格比白格少的列的个数为m,黑格比白格多的行的个数为n,求m+n的最大值.45.如图是一个等边三角形,等分为4个小的等边三角形,用红和黄两种颜色涂染它们的顶点,要求每个顶点必须涂色,且只能涂一种颜色.涂完后,如果经过旋转,等边三角形的涂色相同,则认为是相同的涂色,则共有多少种不同的涂法?46.三阶魔方的国际标准配色:白顶黄底,绿前蓝后,橙左红右.现在规定:白色═1,黄色═2,绿色═3,蓝色═4,橙色═5,红色═6.一个复原状态三阶魔方放在桌面上(如图1所示),今天这个魔方按照动态图片的方式打乱,最终变成图2的形态.此时图片中可以看到7个角块,那么看不到的那一个角块儿中与桌面完全接触的颜色代码是.47.用红、绿、蓝三种颜色涂正八面体(如图)的八个面,要求相邻面涂不同的颜色(有一条公共棱的面称为相邻面),一共有多少种不同的涂色方法?(旋转后相同的视为同一种涂色方法)48.下面是一张把4×6的方格纸去掉两个角所得的图形.(1)请把其中的一些格子涂上阴影,使得每个1×2小长方形(不论横竖)的2个方格中都恰有1个阴影方格和1个空白方格;(2)能否用11个1×2小长方形恰好拼满这张方格纸?如果能,请给出一种方法;如果不能,请说明理由.49.将每个最简分数(其中m,n 互质的非零自然数)染成红色或蓝色,染色规则如下:(1)将1染成红色;(2)相差为1的两个数颜色不同,(3)不为1的数与其倒数颜色不同.问:和分别染成什么颜色?50.在给你的卡纸上画有分别由1、2、3、4、5、6、7、8个小正三角形组成的8块拼板,并涂上黑、白两种颜色.(1)请你把这8块拼板剪下并拼成图1所示大的正三角形,且小三角形间的黑、白两种颜色必须相间.请在图1中用粗线条直接画出拼法,并标上每块拼板的标号.(2)图1的三角形金字塔我们称其为边长为6的金字塔(计每个小正三角形的边长为1).图1金字塔中有个如图2所示的菱形.(注意,只要和图2中的形状一样即可,可旋转.)(3)是否存在整数n,使得边长为n的金字塔中菱形的个数为2012202201220132如果存在,请求出n;如果不存在,请证明.参考答案与试题解析一.选择题(共5小题)1.连接正方形ABCD的对角线,并将四个顶点分别染成红色或黄色,将顶点颜色全相同的三角形称为同色三角形,则图中有同色三角形的染色方法共有()A.12B.17C.22D.10【分析】本题考察染色问题.【解答】解:全部为红色或全部为黄色,2种;三红一黄或者三黄一红,4×2=8种,所以有同色三角形的染色方法有2+8=10(种),故选:D.【点评】本题只需简单分类进行枚举即可.2.由210块小正方体构成5×6×7的长方体,如果将其表面涂成红色,那么其中一面涂红的小正方体有()块,两面涂红的小正方体有()块.A.92,48B.94,48C.90,50D.94,46【分析】根据立体图形切拼可知:三个面均为红色的是各顶点处的小正方体,在各棱处,除去顶点处的正方体的有两面红色,在每个面上,除去棱上的正方体都是一面红色,所有的小正方体的个数减去有红色的小正方体的个数即是没有涂色的小正方体.根据上面的结论,即可求得答案.【解答】解:一面涂红的小正方体在每个面的中间,有:5﹣2=3(块),6﹣2=4(块),7﹣2=5(块)(3×4+3×5+4×5)×2=47×2=94(块)两面涂红的小正方体在12条棱的中间部分(除去顶点),有:(3+4+5)×4=12×4=48(块)答:其中一面涂红的小正方体有94块,两面涂红的小正方体有48块.故选:B.【点评】关键是理解正方体表面涂色的特点,知道切割后的小正方体涂色面的排列特点.注意数形结合与正方体表面涂色的特点的应用.3.一个由边长为1的小正方形组成的n×n的方格网,用白色或黑色对每个小正方形涂色,要求满足在任意矩形的4个角上的小正方形不全同色,那么正整数n的最大值是()A.3B.4C.5D.6【分析】此题要充分利用抽屉原理和假设推理.根据题目所给的选项不妨选一个中间的数5为假设n的值,进行一步步地推理,进而推出与题目要求矛盾.从而得出n的取值范围,即得出答案.【解答】解:①假设n=5,(由抽屉原理知)第一行中至少有3个格子颜色相同.不妨设前3格为黑色(如图1).在这3个黑格下方可以分割为4个横着的3×1的长方形,若其中有一个中有2个黑格(如图2),则存在着图中的粗线长方形4个角上的小正方形都是黑格;所以这4个横着的3×1的长方形中,每个至多1个黑格.②假设这4个横着的3×1的长方形中,有两个对应格子颜色都一样(如图3),则一样存在图中的粗线长方形4个角上的小正方形都是白格;而3×1的长方形中至多1个黑格的只有如图4的这4种.如果这4种都存在的话如图5,则同样存在图中粗线长方形4个角上的小正方形都是白格;这均与题目要求的矛盾.所以,n<5,正整数n的最大值是4.而图6给出了n=4的一种构造.故选:B.【点评】对于选择题(特别是类似本题的),我们可以用题目选项所给答案进行推理,而选项正确的答案.4.如图,一块草地被开垦出11块正六边形耕地,菲菲在这些耕地内种植向日葵、豌豆射手、闪电芦苇、冰冻西瓜4种植物,如果相邻的耕地种植的植物不能相同,她有()种不同的种植办法.(相邻耕地是指有公共边,每块耕地内只能种植一种植物)A.6912B.6144C.4608D.4224【分析】由题意,菲菲在这些耕地内种植向日葵、豌豆射手、闪电芦苇、冰冻西瓜4种植物,相邻的耕地种植的植物不能相同,如图所示,发现阴影六边形一圈是关键,中间选好种后,求出中间一圈3×25×[3×24﹣(3×23﹣3×2×1)]=66,即可得出结论.【解答】解:如图所示发现阴影六边形一圈是关键,中间选好种后,周围一圈3种植物,3×25﹣(A、F同色,相当于5个围一圈),5个围一圈=3×24﹣(4个围一圈),4个围一圈=3×23﹣(3个围一圈),3个围一圈=3×2×1=6,中间一圈3×25×[3×24﹣(3×23﹣3×2×1)]=66,所以总共有4×66×24=4224(种)故选:D.【点评】本题考查染色问题.分情况讨论,发现阴影六边形一圈是关键.5.将一个大三角形分割成36 个小三角形,并且将其中一部分小三角形涂成红色,另一部分涂成蓝色,并且使得两个有公共边的三角形的颜色不同,如果红色的三角形比蓝色的多,那么多()个.A.1B.4C.6D.7【分析】按题目要求来涂色的话,只有1 种涂法:红色比蓝色多:(1+2+3+4+5+6)﹣(1+2+3+4+5)=6个.【解答】解:根据分析,按题目要求来涂色的话,只有1 种涂法,如图:红色比蓝色多:(1+2+3+4+5+6)﹣(1+2+3+4+5)=6个.故选:C.【点评】本题考查染色问题,突破点是:逆向思维,推出按题意要求来染色只有一种符合条件,从而得出红色比蓝色的个数.二.填空题(共37小题)6.把一个正方体的表面积全涂成黑色,然后切成27个小正方体(如图),那么两面是黑色的小正方体共有12个.【分析】根据正方体表面涂色的特点,分别得出切割后的小正方体涂色面的排列特点:(1)三面涂色的在每个顶点处;(2)两面涂色的在每条棱长上(除去顶点处的小正方体);(3)一面涂色的都在每个面上(除去棱长上的小正方体);(4)没有涂色的都在内部.【解答】解:两面涂色的在每条棱长上(除去顶点处的小正方体),有:(3﹣2)×12=12(个)故答案为:12.【点评】解决此类问题的关键是抓住:三面涂色的在顶点处;两面涂色的在每条棱长的中间上;一面涂色的在每个面的中心上;没有涂色的在内部.7.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则最少需要4种颜色.【分析】要保证使用的颜色最少,则两个相邻的圆圈的颜色要尽可能多的相同,尝试2种颜色和3种颜色都不行,需要4种颜色,据此解答即可.【解答】解:尝试2种颜色和3种颜色都不行,需要4种颜色,如下图:【点评】本题考查染色问题.8.一个长方体的棱长都是整数,表面涂上色后,切成棱长为1的正方体,若没有颜色的小正方体共有12个,则一面有色的正方体最少有32个.【分析】设把表面涂色的小正方形去了,得到的长方体的长、宽、高分别为a、b、c,由题意abc=12,分有四种情形求解即可.【解答】解:设把表面涂色的小正方形去了,得到的长方体的长、宽、高分别为a、b、c,由题意abc=12,有四种情形:①1×1×12时,一面有色的正方体有2(1×1+1×12+1×12)=50个,②1×2×6时,一面有色的正方体有2(1×2+1×6+2×6)=40个,③1×3×4时,一面有色的正方体有2(1×3+1×4+3×4)=38个,④2×2×3时,一面有色的正方体有2×(2×2+2×3+2×3)=32个,综上所述,一面有色的正方体最少有32个.故答案为32.【点评】本题考查染色问题,记住长方体(a×b×c)的染色规律:①3面染色的有8个(与长方体的顶点有关);②2面染色的有4[(a﹣2)+(b﹣2)+(c ﹣2)]个(与长方体的棱长有关);③1面染色的有2[(a﹣2)(b﹣2)+(a ﹣2)(c﹣2)+(b﹣2)(c﹣2)]个(与长方体的表面积有关);④0面染色的有(a﹣2)(b﹣2)(c﹣2)个(与长方体的体积有关);9.将图中的圆圈染色,要求有连线的两个相邻的圆圈染不同的颜色,则最少需要2种颜色.【分析】可以用不同的字母或数字表示不同的颜色,在图中进行标示,本题要求是有线段相连的两个圆圈颜色不同.【解答】解:用字母A、B、C…表示不同的颜色,先在左上角的圆圈填入A,为了使用的颜色种类尽量少,下一步在与它相连的三个圆圈都填入B,最后得到下面的涂色方法:共使用了2种颜色.故本题答案为:2.【点评】简单涂色类题目可以用标字母的方法,方便分析和解答.10.一个宝库有9个藏宝室,成九宫格状排列,但只有一个进口和一个出口分别开在如图所示的藏宝室,每个藏宝室至多只能进去一次,相邻的藏宝室之间都有门相通,每个藏宝室中的宝贝价值已标在图中,大盗买通守护,夜间进入宝库,他能带走的宝物价值最多是39.【分析】本题首先能想到根据染色问题进行分析,可将房间黑白相间染色,根据进口和出口所染颜色不同可知大盗应该经过了偶数个房间,因此最多经过8个房间,据此解答.【解答】解:借助染色解题,给3×3的方格黑白相同染色(如图),进口为黑格,若全部走完9个方格,出口应为黑格,而图中出口为白格,故至少有一个黑格不能走到,标数最小的(进口除外)应为6,即标6的房间无法进入,所以大盗能带走的宝物最多是45﹣6=39.故答案为:39.【点评】本题的突破口在于能用染色的方法进行解题,难度较大.11.如图是一个由26个相同的小正方体堆成的几何体,它的底层由5×4个小正方体构成,如果把它的外表面(包括底面)全部涂成红色,那么当这个几何体被拆开后,有3个面是红色的小正方体有14块.【分析】首先分析染色的方法,3个面的红色的上层的角块和下层的边块是符合条件的.【解答】解:依题意可知:第一层的共有4个角满足条件.第二层的4个角是4面红色,去掉所有的角块其余的符合条件.分别是3+2+3+2=10(个);共10+4=14(个);故答案为:14【点评】本题考查对染色问题的理解和运用,关键是底面边长不同计算时要分开计算.同时注意底面是涂色的,问题解决.12.如图所示,用64个棱长为1的小立方体组成一个棱长为4的大立方体,再从上到下取走4个小立方体(图中阴影部分).将剩余立体图形的内外表面都染成红色,那么恰有两个面染色的小立方体共有28个.【分析】首先分析棱上的小块,面上的除了空心通道以外其他是没有的,空心通道的数字计算出来相加即可.【解答】解:依题意可知:在大正方体的棱上的,上下各有6个,侧面棱上8个,棱上共20个.空心通道产生的上下各有2个,通道内有4个共8个.共20+8=28(个).故答案为:28.【点评】本题考查对染色问题的理解和运用,关键问题是从棱上分析再分析空心通道即可,问题解决.13.一个5×5的方格由25个1×1的小方格组成,每个小方格都被分成四个相同的等腰直角三角形,其中三个被涂成了黑色(如图a所示).小正方形的边如果位于黑色部分,就称为黑边,反之就是白边.在5×5的方格内,相邻(有公共边)小方格的公共边必须是同色的,那么5×5方格的四条长边(如图b 所示)上最少有5条黑边.【分析】由题意,角上的小方格每个有2条边在外面,故其中至少有1条是黑边,这样5×5方格的四条长边上,黑边不少于1×4=4条.再判断内部的黑边的条数为偶数,则四条长边上的黑边的条数为奇数,所以5×5方格的四条长边上,黑边不少于5条.【解答】解:由题意,角上的小方格每个有2条边在外面,故其中至少有1条是黑边,这样5×5方格的四条长边上,黑边不少于1×4=4条.每个小方格有3条黑边,5×5=25个小方格一共有3×25=75条黑边,而在5×5方格内,相邻(有公共边)小方格的公共边必须是同色的,故内部的黑边的条数为偶数,则四条长边上的黑边的条数为奇数,所以5×5方格的四条长边上,黑边不少于5条,如图所示为5×5方格的四条长边上有5条黑边的例子,综上所述,5×5方格的四条长边(如图b所示)上最少有5条黑边.故答案为5.。
20181125小学奥数练习卷(知识点:燕尾定理)含答案解析

小学奥数练习卷(知识点:燕尾定理)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)一.填空题(共7小题)1.如图,正方形ABCD被分成了面积相同的8个三角形,如果DG=5,那么正方形ABCD面积是.2.如图,在△ABC中,BD=AD,EF=3,FC=2,△ADH与△AGC的面积和等于四边形EFGH的面积,那么BE的长是.3.如图,在△ABC中,AE:EB=1:3,CD=BC,AD与CE交于F,若△AFC面积为24平方厘米,则△DEF的面积是平方厘米.4.在平行四边形ABCD中,三角形DCE的面积5.4平方厘米,则阴影部分的面积是.5.如图中的三角形ABC面积为1,AD=BD,AE=CE,EF=CF,BE和DC交于点G,交DF于点H,则三角形DGH的面积是.6.如图,BD:DC=2:3,AE:CE=5:3,则AF:BF=.7.如图,BD、CF将长方形ABCD分成4块,△DEF的面积是4平方厘米,△CED 的面积是6平方厘米,则四边形ABEF的面积是平方厘米.第Ⅱ卷(非选择题)二.计算题(共1小题)8.计算:3×232+456=760×5﹣2880=805÷7=45+255÷5=三.解答题(共15小题)9.如图,在三角形ABC中,AF=2BF,CE=3AE,CD=2BD,连接CF交DE于P点,求的值.10.梯形ABCD中,AE与DC平行,S△ABE=15,S△BCF=.11.如图,三角形ABC中,AF:FB=BD:DC=CE:AE=4:3,且三角形ABC的面积是74,求三角形GHI的面积.12.如图在△ABC中,==,求的值.13.三角形ABC中,∠C是直角,已知AC=2,CD=2,CB=3,AM=BM,那么三角形AMN(阴影部分)的面积是多少?14.如图,AE=DE,BC=3BD,三角形ABC的面积是30平方分米,求阴影部分的面积.15.如图所示,正方形ABCD的面积为9平方厘米,正方形EFGH的面积为36平方厘米,边BC落在EH上.已知三角形AGC的面积为6.75平方厘米,求三角形ABE的面积.16.如图,△ABC中,E是AD的中点,已知△ABC的面积是2,△BEF的面积是,求△AEF的面积.17.如图,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,四边形BGHF的面积是多少平方厘米?18.如图,BD:DC=2:3,AE:CE=5:3,则AF:BF=.19.如图,长方形ABCD 的面积是2平方厘米,EC=2DE,F是DG的中点.阴影部分的面积是多少平方厘米?20.三角形ABC是等腰直角三角形,直角边AB=2cm,求阴影部分的面积.21.如图,S△BDF=3cm2,S△CDF=5cm2,S△CEF=4cm2,求△ABC的面积.22.如图,在三角形ABC中,CE=2AE,F是AD的中点,三角形ABC的面积是1,那么阴影部分的面积是多少?23.如图,在三角形ABC中,AE=ED,D点是BC的四等分点,阴影部分的面积占三角形ABC面积的几分之几?参考答案与试题解析一.填空题(共7小题)1.如图,正方形ABCD被分成了面积相同的8个三角形,如果DG=5,那么正方形ABCD面积是64.【分析】如图,过G点做MO平行AD,交CD、AB分别于点M、O,过点F做FN⊥BC于N.设正方形面积为“1”,则正方形边长为1,根据正方形ABCD被分成了面积相同的8个三角形,可求出BI、HA的长度,再根据四边形FGHI 是平行四边形,求出FG、GO、GM的长度,在直角三角形GMD中,根据勾股定理求出DG的长度,最后根据如果DG=5,求出正方形的边长,最后算出面积.【解答】解:如图,过G点做MO平行AD,交CD、AB分别于点M、O,过点F 做FN⊥BC于N.设正方形面积为“1”,则正方形边长为1,图中每个小三角形的面积都是,所以BI=HA=,又因为四边形FGHI是平行四边形,所以HI=FG=,GO=GM=,FN=,在直角三角形GMD中,MG=,MD5=1﹣﹣=,根据勾股定理DG==,所以正方形的边长是5÷=8,正方形面积=8×8=64.故答案为:64.【点评】本题难度较大,解题关键是作辅助线求出正方形的边长.2.如图,在△ABC中,BD=AD,EF=3,FC=2,△ADH与△AGC的面积和等于四边形EFGH的面积,那么BE的长是1.【分析】因为BD=AD,根据燕尾定理可得,S△ADC=S△ABC,又因为△ADH与△AGC的面积和等于四边形EFGH的面积,S△AHG是公共部分,所以S△AEF=S △ADC=S△ABC,那么S△ABE+S△AFC=1﹣S△ABC=S△ABC,又因为S△ABE+S△AFC的和与S△AEF等高,所以BE+FC=EF,又EF=3,FC=2,所以BE+2=3,则BE=1,问题得解.【解答】解:因为BD=AD,根据燕尾定理可得,S△ADC=S△ABC,S△ADH+S△AGC=S四边形EFGH,所以S△ADH+S△AGC+S△AHG=S四边形EFGH+S△AHG,即:S△AEF=S△ADC=S △ABC,S△ABE+S△AFC=1﹣S△ABC=S△ABC,又因为S△ABE+S△AFC的和与S△AEF等高,所以BE+FC=EF,又因为∵EF=3,FC=2,BE+2=3,BE=1;故答案为:1.【点评】本题关键是利用S△AHG是S△AEF和S△ADC的公共部分,得出S△AEF=S △ADC=S△ABC.3.如图,在△ABC中,AE:EB=1:3,CD=BC,AD与CE交于F,若△AFC面积为24平方厘米,则△DEF的面积是12平方厘米.【分析】连接BF,因为AE:EB=1:3,根据燕尾定律可得,S△BCF=3S△ACF=72平方厘米,然后分别求出S△CDF 和AF:FD=1:1;然后再求出S△AEF即可求出△DEF的面积.【解答】解:连接BF,因为AE:EB=1:3,根据燕尾定律可得,S△BCF=3S△ACF=3×24=72平方厘米,又因为CD=BC,所以,S△CDF=S△BCF=×72=24平方厘米,所以,S△ACF=S△CDF=24平方厘米,所以,AF:FD=1:1,同理,因为CD=BC,根据燕尾定律可得,S△ABF=2S△ACF=2×24=48平方厘米,又因为,AE:EB=1:3,所以,S△AEF=S△ABF=×48=12平方厘米,由于AF:FD=1:1,所以S=S△AEF=12平方厘米;△DEF故答案为:12.【点评】本题多次用到了燕尾定律,关键是求出AF:FD=1:1.4.在平行四边形ABCD中,三角形DCE的面积5.4平方厘米,则阴影部分的面积是 5.4平方厘米.【分析】根据图形和平行四边形与三角形的面积公式可知:三角形ABE的面积+三角形DCE的面积=平行四边形ABCD面积的一半,三角形BEF的面积(即阴影面积)+三角形ABE的面积=平行四边形ABCD面积的一半,依此可知阴影面积=三角形DCE的面积,从而求解.【解答】解:由于三角形ABE的面积+三角形DCE的面积=平行四边形ABCD面积的一半,三角形BEF的面积(即阴影面积)+三角形ABE的面积=平行四边形ABCD面积的一半,所以阴影面积=三角形DCE的面积=5.4平方厘米.故答案为:5.4平方厘米.【点评】考查了组合图形的面积计算,本题的难点是根据三角形的面积是与它等底等高的平行四边形面积的一半,得出:阴影面积=三角形DCE的面积.5.如图中的三角形ABC面积为1,AD=BD,AE=CE,EF=CF,BE和DC交于点G,交DF于点H,则三角形DGH的面积是.【分析】连接DE 和HC ,根据D 、E 都是中点,以及中位线定理可得DG :GC=1:2,可以求出△DGE 的面积,再根据燕尾定理可得S △DHE =S △DHC ,然后进一步解答即可.【解答】解:连接DE 和HC ,因为,AD=BD ,AE=CE ,所以DE 是△ABC 的中位线,所以,DG :GC=1:2,S △DGE =×S △DCE =××S △DCA =××S △ABC =×S △ABC ,因为,S △ABC =1,所以,S △DGE =;因为,EF=CF ,根据燕尾定理可得S △DHE =S △DHC ,又因为,DG :GC=1:2,所以,S △DHE =S DGH ×(1+2)=S △DGH ×3,所以,S △DGH =×S △DGE =×=;答:三角形DGH 的面积是.故答案为:.【点评】本题考查了燕尾定理和中位线定理的综合应用,关键是求出△DGH 的面积占△DGE 的面积的几分之几.6.如图,BD :DC=2:3,AE :CE=5:3,则AF :BF= 5:2 .【分析】本题考察燕尾定理的应用.AF :BF 可以通过S △ACG :S △BCG 求得,利用BD 与DC 的比可以得到S △ABG 和S △ACG 的比,同理,AE 与CE 的比可以得到S △ABG 和S △BCG 的比.【解答】解:根据燕尾定理有S △ABG :S △ACG =BD :DC=2:3=10:15,同理,S △ABG :S △BCG =AE :CE=5:3=10:6,所以S △ACG :S △BCG =15:6=5:2,所以AF :BF=5:2.故填:5:2.【点评】本题关键在于利用燕尾定理把三角形的面积比和线段的比进行统一,互相转化.7.如图,BD 、CF 将长方形ABCD 分成4块,△DEF 的面积是4平方厘米,△CED 的面积是6平方厘米,则四边形ABEF 的面积是 11 平方厘米.【分析】由蝴蝶定理得,S △BEF =S △CED =6,再由共高定理得S △BEF ×S △CDE =S △EDF ×S △BCE ,求得 S △BCE =6×6÷4=9,由此求出长方形ABCD 的面积的一半,即6+9=15,然后再减去△DEF 的面积4平方厘米即可.【解答】解:根据题干分析可得:根据蝴蝶定理可得:S △BEF =S △CED =6(平方厘米),再由共高定理可得:S △BEF ×S △CDE =S △EDF ×S △BCE ,又因为△DEF 的面积是4平方厘米,△CED 的面积是6平方厘米,则,S △BCE =6×6÷4=9(平方厘米),所以长方形ABCD 的面积的一半是:6+9=15(平方厘米),所以四边形ABEF 的面积是:15﹣4=11(平方厘米);故答案为:11.【点评】此题主要考查利用蝴蝶定理和共高定理解决实际问题的灵活应用.二.计算题(共1小题)8.计算:3×232+456=760×5﹣2880=805÷7=45+255÷5=【分析】计算四则混合运算时,要按照运算顺序,先算乘除,后算加减,同一级运算,按从左到右的运算顺序计算.【解答】解:(1)3×232+456=696+456=1152(2)760×5﹣2880=3800﹣2880=920(3)805÷7=115(4)45+255÷5=45+51=96【点评】计算四则混合运算时,要注意按照运算顺序计算.三.解答题(共15小题)9.如图,在三角形ABC中,AF=2BF,CE=3AE,CD=2BD,连接CF交DE于P点,求的值.【分析】如图,连接DF,根据已知推出△BFD≌△BAC,推出∠BDF=∠BCA,求出DF∥CA,=,求出=,=,根据平行线分线段成比例定理得出即可.【解答】解:连接DF,因为AF=2BF,CD=2BD,所以==,因为∠B=∠B,所以△BFD≌△BAC,所以∠BDF=∠BCA,所以DF∥CA,=,因为CE=3AE ,所以=, 所以=,因为DF ∥CA ,所以==.【点评】本题考查了平行线分线段成比例定理,相似三角形的性质和判定的应用,主要考查学生的推理能力,题目较好,有一定的难度.10.梯形ABCD 中,AE 与DC 平行,S △ABE =15,S △BCF = 15 .【分析】连接DE ,因为AE 与DC 平行,根据等底(EF )同高的两个三角形的面积相等,得出S △DEF =S △CEF ,再根据等底(AD )同高的两个三角形的面积相等,得出 S △ABD =S △AED ,所以,S △ABD ﹣S △AFD =S △AED ﹣S △AFD ,即S △ABF =S △DEF ,所以S △ABF =S △CEF ,由此即可得出答案.【解答】解:连接DE ,因为AE 与DC 平行,根据等底(EF )同高的两个三角形的面积相等,得出S △DEF =S △CEF ,再根据等底(AD )同高的两个三角形的面积相等,得出 S △ABD =S △AED , 所以,S △ABD ﹣S △AFD =S △AED ﹣S △AFD ,即S △ABF =S △DEF ,所以S △ABF =S △CEF ,那么S △ABF +S BEF =S △CEF +S BEF ,即S △ABE =S △BCF =15,故答案为:15.【点评】此题主要考查了蝴蝶定理的应用(即在梯形里,等底同高的两个三角形的面积相等).11.如图,三角形ABC中,AF:FB=BD:DC=CE:AE=4:3,且三角形ABC的面积是74,求三角形GHI的面积.【分析】本题考察三角形的面积计算.考虑到△HIG的面积不能直接求,可以计算出△AGC、△BIC、△BAH的面积,再用整体减去这三部分,剩余的就是△GHI的面积,依此解答.【解答】解:如图,连接BG,设△AGC的面积为12份,根据燕尾定理,S△AGC:S△BGC=AF:FB=4:3=12:9,S△AGB:S△AGC=BD:DC=4:3=16:12,得△BGC的面积为9份,△ABG的面积为16份,则△ABC的面积为9+12+16=37(份),因此△AGC的面积为74÷37×12=24,同理连接AI、CH得△ABH的面积为74÷37×12=24,△BIC的面积为74÷37×12=24,所以△GHI的面积为74﹣24×3=2.【点评】本题关键在于利用燕尾定理求出围在△GHI外部的三个三角形的面积,利用整体法进行计算即可.12.如图在△ABC 中,==,求的值.【分析】本题考察燕尾定理的应用.连接BG ,借助燕尾定理计算出△AGC 占整个图形面积的几分之几,再利用同样的方法连接AI 与CH ,求出△ABH 和△BIC 占整个图形面积的几分之几,最后用整个图形减去这三块后,再除以整个图形的面积即可.【解答】解:如图,连接BG ,设S △BGC =1份,根据燕尾定理S △AGC :S △BGC =AF :FB=3:1,同理,S △ABG :S △AGC =BD :DC=3:1,得S △AGC =3份,S △ABG =9份,则S △ABC =13(份),因此=,同理连接AI 、CH 得=,=,所以==.【点评】本题难度较大,需要学生对燕尾定理较为熟练的应用.13.三角形ABC 中,∠C 是直角,已知AC=2,CD=2,CB=3,AM=BM ,那么三角形AMN (阴影部分)的面积是多少?【分析】作MG∥CB交AD于G,利用中位线的知识求出GM的长,再利用相似三角形的知识,求出MN:CN=GM:BD=1:4,最后再根据高一定时,三角形的面积与底成正比的关系,求出S△AMN 与S△ACM的比,即可求出三角形AMN(阴影部分)的面积是多少.【解答】解:作MG∥CB交AD于G,由题意可知BD=BC﹣CD=3﹣2=1,因为AM=MB,所以=,GM=,所以==,因为△NGM∽△NDC==,S△ABC=2×3÷2=3所以S△ACM=S△ABC=,根据高一定,三角形的面积和底成正比得:S△AMN:S ACM=MN:MC=1:(1+4)=1:5,所以阴=S△ACM=×=,答:三角形AMN(阴影部分)的面积是.【点评】此题主要考了相似三角形的性质和高一定时,三角形的面积与底成正比的关系的灵活应用.14.如图,AE=DE ,BC=3BD ,三角形ABC 的面积是30平方分米,求阴影部分的面积.【分析】连接BE ,设S △BED =1份,根据BC=3BD 以及等高定理求出S △CED =2份,根据AE=DE ,求得阴影部分的面积=S △ACF ,再根据燕尾定理求出AF :BF=2:3,然后再进一步解答即可.【解答】解:连接BE ,设S △BED =1份,因为BC=3BD ,所以△BED 与△CED 等高,所以,S △BED :S △CED =1:2,所以,S △CED =2份,所以,S △BCE =1+2=3份又因为AE=DE ,所以,S △ACE =S △CED =2份,根据燕尾定律可得:AF :BF=S △ACE :S △BCE =2:3,又因为:阴影部分的面积=S △AEF +S △CED =S △AEF +S △ACE =S △ACF ,又因为,△ACF 与△BCF 等高,三角形ABC 的面积是30平方分米,所以阴影部分的面积=S △ACF =30×=12(平方分米);答:阴影部分的面积是12平方分米.【点评】本题考查了燕尾定律和等高定理的灵活应用,关键是求出AF :BF=2:3.15.如图所示,正方形ABCD 的面积为9平方厘米,正方形EFGH 的面积为36平方厘米,边BC 落在EH 上.已知三角形AGC 的面积为6.75平方厘米,求三角形ABE 的面积.【分析】连接EG ,则AC ∥CE ,根据蝴蝶定理可得,S △AEO =S △CGO ,则S △ACE =S △AGC =6.75平方厘米,因为S △ABC =9÷2=4.5平方厘米,所以S △ABE =6.75﹣4.5=2.25平方厘米.【解答】解:连接EG ,则AC ∥CE ,根据蝴蝶定理可得,S △AEO =S △CGO ,则,S △AEO +S △ACO =S △AGC ,又因为三角形AGC 的面积为6.75平方厘米,则S △ACE =S △AGC =6.75平方厘米,因为S △ABC =9÷2=4.5平方厘米,所以S △ABE =6.75﹣4.5=2.25平方厘米.答:三角形ABE 的面积2.25平方厘米.【点评】本题考查了蝴蝶定理的灵活应用,关键是通过转化求出△ACE 的面积.16.如图,△ABC 中,E 是AD 的中点,已知△ABC 的面积是2,△BEF 的面积是,求△AEF 的面积.【分析】因为E是AD的中点,根据等高定理可得:S△ABE=S△BED,S△ACE=S△CED,所以,S△ABE +S△ACE=S△CED+S△BED=S△BCE,因为△ABC的面积是2,所以S△BCE=2×=1,由于△BEF的面积是,所以S△BCF=1+=,同理求出S△ACF=1﹣=,再根据燕尾定律可得AF:FB=:=1:2,再进一步解答即可.【解答】解:因为E是AD的中点,根据等高定理可得:S△ABE=S△BED,S△ACE=S△CED,所以,S△ABE +S△ACE=S△CED+S△BED=S△BCE,因为△ABC的面积是2,所以S△BCE=S△ABE+S△ACE=2×=1,由于△BEF的面积是,所以S△BCF=1+=,同理求出S△ACF=1﹣=,根据燕尾定律可得AF:FB=:=1:2,所以,S△AEF=S△BEF×=×=;答:△AEF的面积是.【点评】本题考查了等高定理和燕尾定律的综合应用,关键是求出AF:FB=1:2.17.如图,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,四边形BGHF的面积是多少平方厘米?【分析】连接BH,然后根据沙漏模型得BG:GD=1:2,然后根据燕尾定理分析各部分之间的关系.【解答】解:连接BH ,然后根据沙漏模型得BG :GD=1:2根据燕尾定理得S △CBH :S △CDH =1:2因为DF 是中线,所以S △DBH :S △CDH =1:1如果把S △CBH 看成一份,那整个正方形可以看成(2+2+1)×2=10(份) 120÷10=12(平方厘米)所以阴影面积=12÷2+12×2÷3=14(平方厘米)答:阴影部分的面积是14平方厘米.【点评】此题主要考查了沙漏模型和燕尾定理.18.如图,BD :DC=2:3,AE :CE=5:3,则AF :BF= 5:2 .【分析】S △ABG :S △ACG =BD :DC=2:3;S △ABG :S △BCG =AE :CE=5:3,据此求解.【解答】解:根据燕尾定理有S △ABG :S △ACG =BD :DC=2:3=10:15S △ABG :S △BCG =AE :CE=5:3=10:6S △ACG :S △BCG =15:6=5:2故填5:2.【点评】此题主要考查燕尾定理.19.如图,长方形ABCD 的面积是2平方厘米,EC=2DE ,F 是DG 的中点.阴影部分的面积是多少平方厘米?【分析】根据燕尾定理解答,连接F、C两点,因为F是DG的中点,那么△CFG 与△CFD的面积相等,并且等于△CDG面积的一半,即长方形ABCD面积的四分之一,又因为EC=2DE,那么△CFE的面积等于△EDF的两倍,所以阴影部分的面积即是2÷4×平方厘米.【解答】解:连接F、C两点,=1,设S△EFD因为EC=2DE,根据燕尾定理,那么△CFE的面积等于△EDF的两倍,=2,即,S△CFES△CFD=2+1=3,又因为F是DG的中点,根据燕尾定理,那么S△CFG=阴影部分的面积是2+3=5,S=3+3=6,△CDG并且等于△CDG面积的一半,即长方形ABCD面积的四分之一,所以阴影部分的面积即是:2÷4×=(平方厘米);答:阴影部分的面积是平方厘米.【点评】本题考查了燕尾定理的灵活应用,关键是表示出阴影部分的面积对应的份数.20.三角形ABC是等腰直角三角形,直角边AB=2cm,求阴影部分的面积.【分析】用两个扇形的面积和减去三角形的面积就得到阴影部分的面积.【解答】解:π×22÷4﹣2×2÷2=1.14(平方厘米)答:阴影部分的面积是1.14平方厘米.【点评】此题采用转化法,将两个扇形合并成一个圆心角90°的扇形.21.如图,S△BDF=3cm2,S△CDF=5cm2,S△CEF=4cm2,求△ABC的面积.【分析】根据燕尾定律,因为(S△BDF +S△CDF):S△CEF=(3+5):4=2:1,所以BF:FE=2:1,则S△ABF:S△AFE=2:1;再根据燕尾定律,S△BDF:S△CDF=S△ABF:S△ACF=S△ABF :(S△AFE+S△EFC)=3:5,然后设S△ABF=2x,那么S△AFE=x,可列比例式为2x:(x+4)=3:5,解比例式求出S△ABF 和S△AFE的面积,然后用加法即可求出△ABC的面积.【解答】解:因为(S△BDF +S△CDF):S△CEF=(3+5):4=2:1,所以BF:FE=2:1,则S△ABF :S△AFE=2:1,根据燕尾定律,S△BDF :S△CDF=S△ABF:S△ACF=S△ABF:(S△AFE+S△EFC)=3:5,所以,设S△ABF=2x,那么S△AFE=x,可得:2x:(x+4)=3:510+x=3x+12x=则:S△ABF=×2=3(cm2)所以,△ABC的面积是:3+5+4+3+=17(cm2)答:△ABC的面积是17cm2.【点评】本题考查了燕尾定律的灵活应用,关键是根据燕尾定律求出S△ABF 与S△ACF的面积比.22.如图,在三角形ABC中,CE=2AE,F是AD的中点,三角形ABC的面积是1,那么阴影部分的面积是多少?【分析】连接CF,因为CE=2AE,所以==,同理,=,设S△AEF=1份,那么S△CEF=2份,因为F是AD的中点,S△CFD=S△ACF=S△AEF+S=1+2=3份,同理,,又因为==,所以△CEF=S△ABF=3份,这样S△ABC=1+2+3+3+3=12份;然后根据阴,所以S△BDF影部分的份数是2+3=5份,在解答即可.【解答】解:连接CF,因为CE=2AE,根据燕尾定理,所以= =,同理,=,=1份,那么S△CEF=2份,设S△AEF因为F是AD的中点,S=S△ACF=S△AEF+S△CEF=1+2=3份,△CFD同理,,又因为==,所以,所以S=S△ABF=3份,△BDF=1+2+3+3+3=12份,这样S△ABC阴影部分的份数是:2+3=5份,5÷12=,即1×=.【点评】本题考查了利用燕尾定律求组合图形的面积.23.如图,在三角形ABC中,AE=ED,D点是BC的四等分点,阴影部分的面积占三角形ABC面积的几分之几?=1,S△BDE=S△ABE=3,则,所以,S 【分析】连接CE,设S△CDE=,,据此解答.△AEF=1,【解答】解:连接CE,设S△CDE因为AE=ED,S=1,△ACED点是BC的四等分点,=S△ABE=3,根据燕尾模型可得:S△BDE则,所以,S=,△AEF.【点评】本题考查了燕尾定律的灵活应用.。
20181125小学奥数练习卷(知识点:数阵图中找规律)含答案解析

小学奥数练习卷(知识点:数阵图中找规律)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)一.选择题(共1小题)1.把自然数按如图所示的方法排列,那么排在第10行第5列的数是()A.79B.87C.94D.101第Ⅱ卷(非选择题)二.填空题(共42小题)2.如图,将1至400这400个自然数填入下面的三角形中,每个小三角形内填有一个数,“1”所处的位置为第1行,“2、3、4”所处的位置为第2行,那么第8行中间数是.3.如图,按照表中规律把自然数填入表格,那么2016所在的行号和列号的和是.4.观察下面数表中的规律,可知x=.5.沿着虚线将如图划分为若干“中环块”(表格内每个小正方形的面积均为1),任意两个相邻“中环块”的面积均不同(如果两个“中环块”有至少一条公共边,就称为相邻“中环块”).图中标了一些数字,每个数字都表示其所在“中环块”的面积.每个“中环块”中可能不含数字,可能含有一个数字,也可能含有多个相同的数字.每列中都画有两个圆圈,其中一个圆圈在表格中,另一个在表格下方.在表格内的圆圈中填上圆圈所在“中环块”的面积,并把这个数字填在与之同列的表格下方圆圈内.最后,表格下方的七个圆圈从左至右构成一个七位数,这个七位数为.6.在下面“而”字型数阵图的圆圈内填入适当的数字(数字可以重复使用),使得每条直线上的数字之和都相等,那么左下角的圆圈内应填.7.将日期5月2日中的5称为“月”,2称为“日”,把2016年1月1日至12月31日中的所有“日”按顺序填入下表,那么,12这个数在左数第三列中出现了次.8.在空格里填入数字1~6,使得每行、每列和每宫数字都不重复,并且两个灰色正方形中相同位置的数字完全相同,那么,五位数是.9.如图,把从1开始的自然数按一定规律排列起来,如图46在这个数表的第a 行,第b列,那么a×b=.10.所有自然数如图排列,数300位于字母的下面.11.在空格内填入1﹣6,使得每行和每列的数字都不重复.图中相同符号所占的两格数字组合相同,数字顺序不确定,那么最后一行前五个数字按从左到右的顺序组成的五位数是.12.图中三角形数表中第4行第5列是.13.将1~9这9个数分别填入图中的圆圈内,使得每个三角(共7个)的3个顶点上的数之和都等于15.现在已经填好了其中的3个,则标有“☆”的圆圈内应填.14.观察下面的三角形数表,第10行的所有数字之和是.15.在空格里填入数字1~6,使得每行、每列和每宫数字不重复.盘面外的数字表示斜线方向所有格的和.那么,第四行从左往右的前5个数字组成的五位数是.16.如图,6×6的正方形表格被粗线分成了9个粗线框,每个粗线框有N个格子就在这N个格子中分别填入1~N的数字,要求每个数字和其周围相邻(包括对角相邻)的数字都不相同.那么,四位数=.17.(如图1)6×6的方格中,每行每列2、0、1、5四个数字各出现一次,空格把每行每列的数字隔成四位数、三位数、两位数或者一位数.右边和下面的数表示该行或列里的几个数字之和,0不能作为多位数的首位.(图2是一个1、2、3、0四个数字各出现一次的例子)那么,大正方形两条对角线上所有数字之和是.18.我们可以将全体正整数和正分数按照下图所示的方法,从1开始,一层一层地“生长”出来:是第一层:第二层是,;第三层是,,,,…按照这个规律,在层.19.观察下表中的数的规律,可知第8行中,从左向右第5个数是.20.如图的9个圆圈间,连有10条直线,每条直线上有3个圆圈,甲先乙后轮流选择一个未被选择的圆圈;如果谁选的圆圈中有3个在同一直线上,谁就获胜.现在,甲选择了“1”,乙接着可选择“5”.甲要获胜,接下来的一步能够选择的编号总乘积是.21.从左上角开始,沿着轨道出现的数字依次是1,2,3,1,2,3,…每行和每列的数字都是1个1,1个2,1个3(另外两个格子不填),那么,第四行的5个数字从左至右组成的五位数是(没有数字的格子看作0)22.从左上角开始,沿着轨道出现的数字依次是1,2,3,1,2,3,…每行和每列的数字都是1个1,1个2,1个3(另外两个空不填),那么,第三行的5个位置从左到右组成的五位数是.(如果是没有数字的位置则写0)23.我们可以将全体正整数和正分数按照如图所示的方法,从1开始,一层一层地“生长”出来;是第一层;第二层是,,第三层是,,,,…按照这个规律,在第层.24.在空格内填入数字1﹣6,使得每行每列数字不重复,黑点两边的数是两倍的关系,白点两边的数差为1.那么第四行所填数字从左往右前5位组成的五位数是.25.如图,用小正方形摆成下列图形,按摆放规律,第25个图形需要小正方形个.26.若如图中方框里填上不同的正偶数后,每个正方形顶点方框内的四个数之和都相等,这个和的最小值是.27.请在下面的“木”字形数阵图中填入0~9各1个,满足4条直线的和都等于15,那么“☆”位置上的数是.28.古希腊的数学家们将自然数按以下方式与多边形联系起来,定义了多边形数:三边形数:1,3,6,10,15,…四边形数:1,4,9,16,25,…五边形数:1,5,12,22,35,…六边形数:1,6,15,28,45,……则按照上面的顺序,第6个七边形数为.29.在下面的数表中,上、下两行都是等差数列,上、下对应的两数中,大数减去小数的差,最小是.5 10 15 20…1430 1435 14402013 2006 1999 1992…18 11 4.30.如图数阵的数字是按一定的规律排列的,其中第201行左起第3个数字是31.观察上边数阵中各行数字的和的规律,根据这个规律,则第10行中各数的和等于.32.将1至5分别填入图中的圆圈内,使得两条线段上3个数的和相等.那么,共有种不同的填法.33.对自然数按如下操作:是3的倍数则除以3,不是3 的倍数则加1,直至出现1才停止.如果这样的操作进行了5次恰停止.开始的数有个.34.将1﹣16填入4×4的表格中,要求同一行右面的比左面的大;同一列下面的比上面的大.其中4和13已经填好,其余14个整数有种不同的填法.35.有16名学生,他们做成一个4×4的方阵,某次考试中他们的得分互不相同,得分公布后,每位同学都将自己的成绩与相邻的同学(相邻指前、后、左、右,如坐在角上的同学只有2人与他相邻)进行比较,如果最多只有1名同学的成绩高于他,那么他会认为自己是“幸福的”.则最多有名同学会认为自己是“幸福的”.36.将1﹣9填入3×3的表格中,要求同一行右面的数字比左面的数大;同一列下面的数比上面的数大,其中1,4,9已经填好,那么其余6个整数有种不同的填法.37.图1的3×3表格中已经填好了数,选择一个格为起点,如果对这个黑格和与它相邻的白格中所填数进行加减乘除中的一次运算(计算时大数在前),计算结果是与白格相邻的另一个黑格所填数的整数倍,就能经过这个白格走到下一个黑格.要求每个格子恰好进过一次.(例如图2中,从7经过8可以走到5,并且图2中箭头走向是一种正确走法)请在图1中找出正确的走法.若图1中正确走法的前3个格子所填数依次为A,B,C,那么三位数=.38.分别姓赵、钱、孙、李、周、吴、王的七位同学站成一排,按下列方式依次报数:报“l998”的是姓的同学.39.有一串数如图排列,第50行的最后一个数是.40.如图,圆点组成了一系列图形,每个图形的圆点个数依次为:1,3,6,10,15….按这样排列,圆点个数为105的是第个图形.41.如图是一个由数字组成的三角形,它的组成有着一定的规律,第九行从左往右第7个数是.42.观察下列九个数字1,2,3,4,5,6,7,8,9的排列方式.第一行:1 2 3 4 5 6 7 8 9第二行:2 3 4 1 6 7 5 9 8第三行:3 4 1 2 7 5 6 8 9…按以上规律排列,第一行的排列方式,从第一行起到100行,一共能出现次.43.观察下图,?代表的数是.三.解答题(共7小题)44.自然数如图的规则排列:求:(1)上起第10行,左起第13列的数;(2)数127应排在上起第几行,左起第几列?45.如图,把从1开始的自然数按照一定的顺序排列成数表,如果这个数表有31行31列,那么这个数表中的第1行第1列的数是.46.古希腊数学家们将一些自然数按照以下方式与正方形联系起来:并将这些数称为正方形数.1770年,法国数学家拉格朗日证明:任何一个自然数都可以表示为最多4个正方形数的和.比如2=1+1,7=1+1+1+4等.请将80表示为最多4个正方形数的和的所有可能情形.47.如图,将1、2、3…按规律排成一个沙漏型的数表,那么,(1)下5行从左向右数的第5个数是多少?(2)上6行最左边的数是多少?(3)2016排在哪一行的从左向右数的第多少个?48.把从1开始的自然数按照如图方式排列(如图只给出了这个数表的一部分).如果我们认为1在第0行第0列,6在第上2行第0列,12在第0行第左2列,19在第下2行第右1列.请问:(1)在第上2行第右3列的数是多少?(2)自然数2014在第几行第几列?(要求写出方向)(3)从1开始向上数100个数(1算作第1个,向后依次是2,6,14…),那么,这100个数的和是多少?49.如图,将1、2、3…按规律排成一个沙漏型的数表,那么,(1)下5行从左向右数的第5个数是多少?(2)上6行最左边的数是多少?(3)2013排在哪一行的从左向右数的第多少个?50.观察下列图形的规律,然后填空:参考答案与试题解析一.选择题(共1小题)1.把自然数按如图所示的方法排列,那么排在第10行第5列的数是()A.79B.87C.94D.101【分析】从表中可知排列的规律是以左上角为顶点的一个等腰三角形,斜着的每组数的个数是1,2,3,4,5…,那么第10行的第一列就应在斜行的第14行上,求出斜行第14行的最后一个数,再减4即可.据此解答.【解答】解:根据以上分析知第14斜行的最后一个数是:1+2+3+ (14)=(14+1)+(13+2)+…+(8+7),=15×7,=105,105﹣4=101.故选:D.【点评】本题的关键是求出第10行第5列的数,在斜行的第几行上,然后再进行计算.二.填空题(共42小题)2.如图,将1至400这400个自然数填入下面的三角形中,每个小三角形内填有一个数,“1”所处的位置为第1行,“2、3、4”所处的位置为第2行,那么第8行中间数是57.【分析】根据图形知第n行的最后一个数为n×n,可得第8行第1个数为7×7+1,第8行最后一个数为8×8,从而得出第8行中间数为.【解答】解:由图可知,第1行的数为1,第2行最后一个数为2×2=4,第3行最后一个数为3×3=9,…所以第7行最后一个数为7×7=49,第8行第1个数为49+1=50,第8行最后一个数为8×8=64,则第8行中间数是=57,故答案为:57.【点评】本题主要考查数阵图中找规律,根据图形得出第n行的最后一个数为n ×n是解题的关键.3.如图,按照表中规律把自然数填入表格,那么2016所在的行号和列号的和是54.【分析】观察数阵图中对角线上的数字2、6、12、20…,其特点是每个数字恰好是两个相邻自然数的乘积,并且,从对角线上的这个数往左边数,依次增加1,往上边数,依次减少1.另外,最顶层一排数字:1、4、9、16…全是完全平方数.因此,只要确定2016这个数对应的对角线上的数字就可以解决问题了.【解答】解:注意到对角线上的数字:2=1×2、6=2×3、12=3×4、20=4×5…,这些数字的最上方的数字1、4、9、16…为完全平方数,比2016小的完全平方数为1936=44×44,因此,从1936这个数字竖着往下数到底得到对角线上的数字为44×45=1980,1980在第45行第45列,从1980往左数36次得到2016,45﹣36=9,因此2016在第45行第9列.所以45+9=54.故答案为54.【点评】本题为数阵图中找规律的题目,主要考查同学们对数阵图中数字排列规律的观察能力以及对特殊位置上的数字结构的识别能力.解答本题的关键是观察并识别出对角线上的数字和最顶部数字的特征.4.观察下面数表中的规律,可知x=45.【分析】每一行最后一个数为完全平方数,当完全平方数为a2时,前面的数字分别为a,3a,5a,7a,据此规律解答即可.【解答】解:根据分析可得,81=92,所以,x=9×5=45;故答案为:45.【点评】一般地说,数表中的规律,应抓住以下几点来考虑问题:(1)数表中前后数的变化和特征;(3)数表中上下数的变化和特征;然后再利用这个规律,解决问题.5.沿着虚线将如图划分为若干“中环块”(表格内每个小正方形的面积均为1),任意两个相邻“中环块”的面积均不同(如果两个“中环块”有至少一条公共边,就称为相邻“中环块”).图中标了一些数字,每个数字都表示其所在“中环块”的面积.每个“中环块”中可能不含数字,可能含有一个数字,也可能含有多个相同的数字.每列中都画有两个圆圈,其中一个圆圈在表格中,另一个在表格下方.在表格内的圆圈中填上圆圈所在“中环块”的面积,并把这个数字填在与之同列的表格下方圆圈内.最后,表格下方的七个圆圈从左至右构成一个七位数,这个七位数为4251257.【分析】由题意得,图中标了一些数字,每个数字都表示其所在“中环块”的面积,并且表格内每个小正方形的面积均为1,所以中环块内的一旦一个小正方形中被标为n的话就表示这个中环块由n个小正方形构成,并且,每个小正方形上面都是标示着n.(n=0,1,2…),因此,题目的要求就是通过题目中所给的一系列的数字将题目中所空出来的部分补全,从最大的数字7开始入手.【解答】解:由题意得,图中标了一些数字,每个数字都表示其所在“中环块”的面积,并且表格内每个小正方形的面积均为1,所以中环块内的一旦一个小正方形中被标为n的话就表示这个中环块由n个小正方形构成,并且,每个小正方形上面都是标示着n.(n=0,1,2…)因此,题目的要求就是通过题目中所给的一系列的数字将题目中所空出来的部分补全.先从最大的数字7开始入手.考虑右下角填数字5,结合任意两个相邻“中环块”的面积均不同,填右边数字4,填下方数字3,填数字5,左上角填入4,中间填2,接着填入3,填入3,2剩下的部分填1,2,所以这个七位数为4251257,故答案为4251257.【点评】本题考查数阵图中找规律,考查新定义,考查学生分析解决问题的能力,正确理解题意是关键.6.在下面“而”字型数阵图的圆圈内填入适当的数字(数字可以重复使用),使得每条直线上的数字之和都相等,那么左下角的圆圈内应填7.【分析】因为每条直线上的数字之和都相等,所以左下角的圆圈内应填2+0+1+6﹣2=7;【解答】解:因为每条直线上的数字之和都相等,所以左下角的圆圈内应填2+0+1+6﹣2=7,故答案为7.【点评】本题考查数阵图中找规律,解题的关键是理解题意,根据每条直线上的数字之和都相等,即可解决问题.7.将日期5月2日中的5称为“月”,2称为“日”,把2016年1月1日至12月31日中的所有“日”按顺序填入下表,那么,12这个数在左数第三列中出现了三次.【分析】2016年的“日”只有29,30,31三种,由于一行有十个数,所以当1个月有30“日”时,12所在的列不变,一个月有29“日”时,12所在的列往前移动一列,一个月有31“日”时,12所在的列往后移动一列,由下表可知,2月份12第一次出现在第五行第三列,2016年2月份有29日,所以3月份12在第二列;2106年3月份有31日,所以4月份12在第三列,2016年4月份30日,所以5月份12在第三列,2016年5月份有31日,所以6月份12在第四列,由此即可解决问题.【解答】解:2016年的“日”只有29,30,31三种,由于一行有十个数,所以当1个月有30“日”时,12所在的列不变,一个月有29“日”时,12所在的列往前移动一列,一个月有31“日”时,12所在的列往后移动一列,由下表可知,2月份12第一次出现在第五行第三列,2016年2月份有29日,所以3月份12在第二列;2106年3月份有31日,所以4月份12在第三列,2016年4月份30日,所以5月份12在第三列,2016年5月份有31日,所以6月份12在第四列,…再往后最多往后移动四列,所以第三列不会出现12了,一共出现三次.故答案为三.【点评】本题考查数阵图中找规律,解题的关键是理解题意,熟悉年历的变化规律.8.在空格里填入数字1~6,使得每行、每列和每宫数字都不重复,并且两个灰色正方形中相同位置的数字完全相同,那么,五位数是12346.【分析】由题意每宫数字都不重复,A、B只能是1和2或2和1,F、G只能是4和1或1和4,由此作出假设,即可解决问题.【解答】解:由题意每宫数字都不重复,A、B只能是1和2或2和1,F、G只能是4和1或1和4,再根据每行、每列和每宫数字都不重复,可知A为1,B为2,F为4,G为1,由此可以得出如图的结论,所以五位数是12346,故答案为12346.【点评】本题考查数阵图中找规律,解题的关键是学会全面观察、勤于思考就一定能抓住规律,解决问题.9.如图,把从1开始的自然数按一定规律排列起来,如图46在这个数表的第a 行,第b列,那么a×b=156.【分析】由表得出每行4个数且第n行的第1个数位于第n列,由46÷4=11 (2)知46位于第12行第2个数,即第13列,据此可得答案.【解答】解:由表可知,每行4个数,且第n行的第1个数位于第n列,46÷4=11…2,则46位于第12行,第2个数,即第13列,a×b=12×13=156,故答案为:156.【点评】本题主要考查数阵图中找规律,根据表格得出每行4个数且第n行的第1个数位于第n列是解题的关键.10.所有自然数如图排列,数300位于字母D的下面.【分析】观察数阵可知每7个数一个循环周期,用300除以7求出商和余数,然后根据余数即可确定数300位于哪个字母的下面.【解答】解:每一循环周期中的相对应的数除以7的余数都相同.因为300÷7=42…6,所以300与6位于同一列,所以,数300应在D字母下面.故答案为:D.【点评】本题考查了数阵图中找规律的问题,关键是明确每一循环周期中的相对应的数除以7的余数都相同.11.在空格内填入1﹣6,使得每行和每列的数字都不重复.图中相同符号所占的两格数字组合相同,数字顺序不确定,那么最后一行前五个数字按从左到右的顺序组成的五位数是46123.【分析】首先是第二行第二列的数字只能是5,第三行第四列只能是6.根据题意即可求解.【解答】解:依题意可知:首先是第二行第二列的数字只能是5,第三行第四列只能是6.继续推理可知答案如图所示:故答案为:46123.【点评】本题考查对数阵图的理解和运用,突破口就是第二行第二列的数字只能是5,第三行第四列只能是6.问题解决.12.图中三角形数表中第4行第5列是63.【分析】首先分析衡行是二次等差数列.数列也是二次等差数列.继续分析求解即可.【解答】解:依题意可知:第四行的首个数字是19,这是一个二次等差的等差数列.19+8=27.27+10=37.37+12=49.49+14=63.故答案为:63【点评】本题考查对数阵图规律的理解和运用,关键是找到二次等差数列的关系.问题解决.13.将1~9这9个数分别填入图中的圆圈内,使得每个三角(共7个)的3个顶点上的数之和都等于15.现在已经填好了其中的3个,则标有“☆”的圆圈内应填7.【分析】根据每个三角形(共7个)的3个顶点上的数之和都等于15,求出E,C,B,即可求出标有“☆”的圆圈内应填的数字.【解答】解:图中共有7 个三角形,每个三角形的 3 个顶点数的和都是15.E=15﹣9﹣4=2,C=15﹣1﹣9=5,B=15﹣4﹣C=6,★=15﹣B﹣E=7.故答案为7.【点评】本题考查数阵图,考查学生的计算能力,正确运用每个三角形(共7个)的3个顶点上的数之和都等于15是关键.14.观察下面的三角形数表,第10行的所有数字之和是256.【分析】观察规律,推出第十行的数字为10个13,9个14,由此即可解决问题.【解答】解:因为第10行的前面有1+3+5+…+17=81个数,又因为1+2+…+12=78,所以第十行的19个数为,10个13,9个14,所以第10行的所有数字之和是130+9×14=256.故答案为256.【点评】本题考查数阵图中找规律,解题的关键是学会全面观察、勤于思考就一定能抓住规律,解决问题.15.在空格里填入数字1~6,使得每行、每列和每宫数字不重复.盘面外的数字表示斜线方向所有格的和.那么,第四行从左往右的前5个数字组成的五位数是35126.【分析】首先确定四个角上的数字,盘面外的数字7和5,可以确定相应的数字,再用类似的方法,即可解决问题.【解答】解:首先确定四个角上的数字,盘面外的数字7和5,可以确定相应的数字,再用类似的方法,即可得出图中的结论.所以第四行从左往右的前5个数字组成的五位数是35126.故答案为35126.【点评】本题考查数阵图中找规律,解题的关键是学会全面观察、勤于思考就一定能抓住规律,解决问题.16.如图,6×6的正方形表格被粗线分成了9个粗线框,每个粗线框有N个格子就在这N个格子中分别填入1~N的数字,要求每个数字和其周围相邻(包括对角相邻)的数字都不相同.那么,四位数=3521.【分析】由题意一个格只能填1,2个格只能填1,2,三个格只能填1,2,3.且和周围8个数均不相同,用此方法,先确定1格,2格,3格的数字,由此即可解决问题.【解答】解:由题意一个格只能填1,2个格只能填1,2,三个格只能填1,2,3.且和周围8个数均不相同,用此方法,先确定1格,2格,3格的数字,可得如图所示的答案.∴四位数=3521,故答案为3521.【点评】本题考查数阵图中找规律,解题的关键是学会全面观察、勤于思考就一定能抓住规律,解决问题.17.(如图1)6×6的方格中,每行每列2、0、1、5四个数字各出现一次,空格把每行每列的数字隔成四位数、三位数、两位数或者一位数.右边和下面的数表示该行或列里的几个数字之和,0不能作为多位数的首位.(图2是一个1、2、3、0四个数字各出现一次的例子)那么,大正方形两条对角线上所有数字之和是18.【分析】观察第五行,第三列可知,521,152或150必须邻,再根据第一行可知,2015必须相邻,由此可以确定第一行,第五行,第三列(如图所示),由此即可解决问题.【解答】解:观察第五行,第三列可知,521,152或150必须邻,再根据第一行可知,2015必须相邻,由此可以确定第一行,第五行,第三列(如图所示),再结合题意,认真思考,即可得出图中结论.因为5+5+5+1+2=18,故答案为18.【点评】本题考查数阵图中找规律,只要全面观察,勤于思考就一定能抓住规律,解决问题.18.我们可以将全体正整数和正分数按照下图所示的方法,从1开始,一层一层地“生长”出来:是第一层:第二层是,;第三层是,,,,…按照这个规律,在8层.【分析】找到数阵图规律数阵图的规律是上边数字的乘积是下方的数字.同时发现的和是8,在相乘的分数中8即是小数3分子又是大数5的分母.继续推理即可.【解答】解:依题意可知:根据数阵图规律可知;;;;数阵图的规律是上边数字的乘积是下方的数字.同时发现的和是8,在相乘的分数中8即是小数3分子又是大数5的分母.那么对应相乘的数字就是,他们之前的是数字积是.那么与相乘的就是前一个数字就是.所以×=,×=.×=;在第三层,后面的数字为,,,,.故答案为:8【点评】本题考查对数阵图的理解和运用,关键问题是找到数阵图规律,问题解决.19.观察下表中的数的规律,可知第8行中,从左向右第5个数是54.【分析】由图形中数字的排列得出第n行的最后一个数为n×n,从而知第7行最后一个数为7×7、第8行中,从左向右第5个数为7×7+5.【解答】解:由图可知,第1行的数为1,第2行的最后一个数为2×2=4,第3行的最后一个数为3×3=9,…所以第7行最后一个数为7×7=49,则第8行第1个数为49+1=50,第5个数为50+4=54,故答案为:54.【点评】本题主要考查数阵图中找规律,根据数字排列规律得出第n行的最后一个数为n×n是解题的关键.20.如图的9个圆圈间,连有10条直线,每条直线上有3个圆圈,甲先乙后轮流选择一个未被选择的圆圈;如果谁选的圆圈中有3个在同一直线上,谁就获胜.现在,甲选择了“1”,乙接着可选择“5”.甲要获胜,接下来的一步能够选择的编号总乘积是504.。
三视图练习题含答案
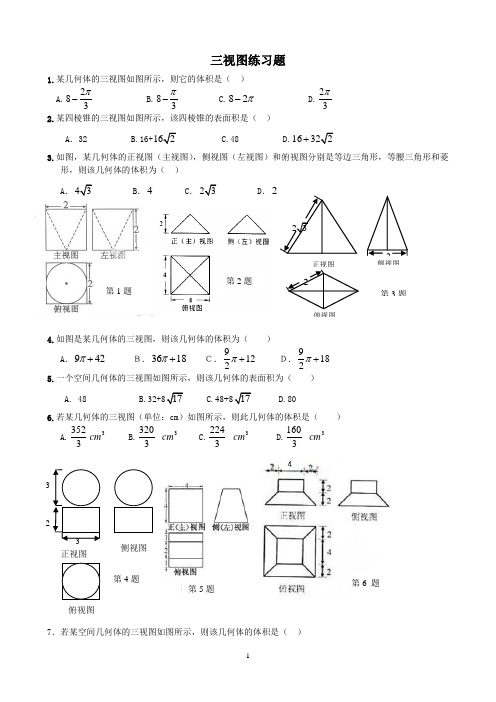
23正视图侧视图2俯视图2第3题三视图练习题1.某几何体的三视图如图所示,则它的体积是( ) A.283π-B.83π-C.π28-D.23π 2.某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32 B.16+162 C.48 D.16322+3.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为( ) A .43 B .4 C .23 D .24.如图是某几何体的三视图,则该几何体的体积为( )A .942π+ B.3618π+ C.9122π+ D.9182π+ 5.一个空间几何体的三视图如图所示,则该几何体的表面积为( )A. 48B.32+817C.48+817D.806.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( ) A.35233cm B.3203 3cm C.2243 3cm D.16033cm7.若某空间几何体的三视图如图所示,则该几何体的体积是( )3 32正视图侧视图俯视图第4题第5题第1题 第2题第6 题A.2B.1C.23D.138.某几何体的三视图如图所示,则该几何体的体积为( )A.π816+B. π88+C. π1616+D. π168+ 9. 某四棱台的三视图如图所示,则该四棱台的体积是( ) A.4 B.314 C.316D.610. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为如图所示的直角三角形,则该三棱锥的体积为( ) A .1 B .3 C .4D .511. 一个几何体的三视图如图所示,则这个几何体的体积为( )A .(8)36π+ B .(82)36π+ C .(6)36π+ D .(92)36π+12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )A .1B .2C .3D .413.某几何体的三视图如图所示,则其体积为______.14.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于______3cm . 15.某几何体的三视图如图所示,则该几何体的体积是______.第7题第8题第9题第10题3122第11题 211俯视图正视图13第12题16.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是 17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是 .18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.20.一个正方体的内切球与它的外接球的体积比是( ).A .1∶33B .1∶22C .1∶383D .1∶4221.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半,且AB =BC =CA =2,则球表面积是( ) A.π964 B. π38 C. π4 D. π91622. P 、A 、B 、C 是球O 面上的四点,且PA 、PB 、PC 的两两垂直,PA=PB=PC=9,则球心O 到截面ABC 的距离为23.半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为 ( ) A. 4 B.3 C.2.5 D. 224.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________.第17题 24 3正视图 侧视图 俯视图第18题 第15题第14题第13题第16题 第19题25. 当圆锥的侧面积与底面积的比值是2时,圆锥的轴截面的顶角等于 26.一平面截一球得到直径是6的圆面,球心到这个平面的距离是4,则该球的体积为 27.一个正四面体的棱长为2,四个顶点在同一个球面上,则此球的表面积为 28.已知一个三棱锥ABC P -的三条侧棱PC PB PA ,,两两垂直,且长度分别为2,3,4,则 该棱锥的外接球的表面积为29.已知用斜二测画法得到的正方形的直观图的面积为218,则原来正方形的面积为 30.正三棱锥的高为1,底面边长为62,正三棱锥内有一个球与其四个面相切.求该棱锥的表面积与体积,内切球的半径.31. 在球心同侧有相距cm 9的两个平行截面,它们的面积分别为249cm π和2400cm π.求球的表面积.32. 球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点,其中18=AB ,24=BC 、30=AC ,球心到这个截面的距离为球半径的一半,求球的表面积.答案1.A2.B3.C4.D5.C6.B7.B8.A9.B 10.A 11.A 12.A 13.3π 14.24 15.1616-π 16.1 17.67π 18.29π 19. 20+8220.A 21.A 22.233 23.B 24. 2 25.︒9026.3500π 27.π628.π29 29.72 30. 3629+32 26-31.2500π 32.π1200。
20181125小学奥数练习卷(知识点:圆)含答案解析
小学奥数练习卷(知识点:圆)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)一.选择题(共4小题)1.如图,从甲地到乙地,A、B两条路都是由半圆形组成的,甲乙两地的中点恰好是O点,这两条路的长度()A.路线A长B.路线B长C.同样长D.无法比较2.如图,长方形的ABCD,长4,宽2,分别以A、C为圆心,以4、2为半径,画圆弧和圆弧,则阴影部分面积是()(π=3.14)A.8.265B.7.5C.6.7D.5.73.如图所示,有两个大小相等的正方形,它们的边平行,并且覆盖在一个半径为3厘米的圆上.阴影的总面积是()平方厘米.(π取3)A.9B.10C.15D.184.淘气用一张正方形纸剪下了一个最大的圆(如图甲),笑笑用一张圆形纸剪下了七个相等的最大圆(如图乙),在这两种剪法中,哪种剪法的利用率最高?(利用率指的是剪下的圆形面积和占原来图形面积的百分率)下面几种说法中正确的是()A.淘气的剪法利用率高B.笑笑的剪法利用率高C.两种剪法利用率一样D.无法判断第Ⅱ卷(非选择题)二.填空题(共41小题)5.如图,直角三角ABC的直角边AB是圆的直径,且AB=40厘米,如果阴影(I)的面积比阴影(II)的面积小92平方厘米,则BC=.6.正方形ABCD的边长为4,DCEF为梯形,圆周率π取3.14,那么,阴影部分的面积是.7.八段圆弧围成如图阴影部分,其中四段圆弧的圆心在一个正方形的四个顶点处,另外四段圆弧的圆心在这个正方形四条边的中点处.这八段圆弧的半径相同,正方形的对角线长度为1,那么阴影部分的面积之和为(答案保留π)8.如图中长方形的长是5厘米,宽是4厘米.阴影部分的周长是厘米.(π取3.14)9.如图,阴影部分的面积是平方厘米.(单位:厘米)10.如图,正方形ABCD的边长为10,以A为圆心10为半径作弧交AC于E,以B为圆心10为半径作弧交BD于F,以C为圆心10为半径作弧交AC于G,以D为圆心10为半径作弧交BD于H,那么,图中阴影部分的面积是.(π取3.14)11.如图,正方形ABCD边长为40厘米,其中M、N、P、Q为所在的中点:分别以正方形的顶点为圆心,以边长的一半为半径做直角扇形,那么形成图中阴影部分的面积是平方厘米.(π 取3.14)12.如图所示的图案由半圆构成,已知最大的圆的半径R=3,则阴影部分图形的周长为,面积为(圆周率用π表示)13.如图是一个对称的四角星形,其中四个顶点构成一个正方形,另外四个顶点在一个圆周上,正方形的边长为10厘米,阴影部分面积是正方形面积的,那么圆的半径为厘米.14.如图,一个半径为10的圆内接两个正方形,这两个正方形重叠的部分刚好构成一个正八边形,那么这个正八边形的面积与图中阴影部分的面积差为.(π取3.14)15.如图,正方形边长为80厘米,O为正方形中心,A为OB中点,在正方形内以A点为圆心,OA为半径的圆,以B点为圆心,OB为半径的圆与正方形的一边围成了一个特殊的图形.将这个图形绕O点顺时针旋转三次能够得到一个风车的形状.那么这个风车(阴影部分)的面积是平方厘米.(π取3.14)16.如图所示,已知最大的圆的直径是100cm,则最小的圆的直径是cm.17.在如图所示的10×12的网格图中,猴子KING的图片是由若干圆弧和线段组成,其中最大的圆的半径是4,图中阴影部分的面积是.(圆周率π取3)18.如图,正方形内接于半圆,圆内接于正方形,已知半圆面积为100,那么,图中阴影部分的面积是.19.如图所示的网格图中,猴子KING的图片是由若干个圆弧和线段组成,其中最大的圆的半径是4,则阴影部分的面积是.【圆周率取3】20.如图,圆0的直径AB与CD互相垂直,AB=20厘米,以C为圆心,CA为半径画弧AB,则阴影部分面积是平方厘米.21.如图,有四种大小不同的圆,直径从小到大依次为5、10、15、20厘米.那么,图中阴影部分面积之和是平方厘米.(π取3.14)22.如图,半径为4厘米的两个圆如图放置,长方形中两块阴影部分面积相等,A、B两点为两圆圆心,那么AB的长度为厘米.(π取3)23.埃及人擅长数学,他们很早之前就发明了个计算圆的面积的公式:S=()2.其中,d是圆的直径.在这个公式当中,相当于将圆周率π取值为(保留两位小数).24.如图所示,△ABC为等腰直角三角形,以斜边AB为直径的半圆周长为15.42厘米,那么分别以AC,BC为直径的两个半圆形(阴影部分)面积之和为平方厘米.(π取3.14)25.如图中的曲线是由半径分别为2,3,4厘米的三个圆周组成,如取π=3,则图中黑色阴影部分的面积是平方厘米.26.如图中阴影部分的面积与空白部分的面积比是.(取π=3)27.如图,以点O为圆心,r和R(r<R)为半径,分别作两个圆,介于这两圆之间的部分称为圆环.已知,阴影部分的面积为60平方厘米,则圆环的面积是平方厘米(π取值3.14).28.如图,若大圆的半径为6,则阴影部分的面积为(答案保留π).29.如图所示,圆的半径是10厘米,圆内部的弧都过此圆的圆心,且此圆的圆周恰好被弧六等分,那么,阴影部分的周长是厘米.(圆周率取3)30.如图,在面积为10000平方厘米的长方形中剪去一个大半圆和两个相等的小半圆,那么余下部分(图中阴影)面积是平方厘米.(π取3.14)31.在荷兰的小镇卡茨林赫弗尔2013年6月建成了一个由三个半圆组成的城市雕塑,三个半圆的直径分别为24.2m,19.3m,4.9m.这个雕塑的原始图形来自于阿基米德《引理集》中的鞋匠刀形(Arbelos),即图中的阴影部分所示的图形.那么该城市雕塑中的鞋匠刀形的周长为(圆周率用π表示).32.如图,已知圆的半径是10厘米,六条直径将圆十二等分,那么,阴影面积之和是平方厘米.(π取3.14)33.在边长为300厘米的正方形中,如图放置了两个直角扇形和一个半圆,那么两块阴影部分的面积差是平方厘米,两块阴影部分的周长差是厘米.(π取3.14)34.如图所示的7个圆相切于一点,若圆的半径分别是(单位:分米):1,2,3,4,5,6,7,则图中阴影部分的面积是平方米.(π取3)35.如图中的曲线是由半径分别为2,3,4厘米的三个圆周组成.如果π=3,则图中黑色阴影部分的面积是平方厘米.36.如图,分别以长方形的一条长边的两个顶点为圆心,以长方形的宽为半径作圆,若图中的两个阴影部分的面积相等,则此长方形的长和宽的比值是.37.如图,圆的半径是6分米,正六边形的六个顶点均在圆上,则阴影部分面积为.(其中π取3.14)38.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米.AB长40厘米,BC长为厘米(π取3.14).39.如图,取π=3,则阴影部分的面积是.40.如图所示,一个圆AOB,半径是10厘米,绕A点顺时针旋转90度,扫过的面积(即整个图形的面积)是平方厘米.(π=3 )41.一个圆A的周长与面积的数值相等,另一个圆B的半径是圆A半径的4倍,则圆B的面积为平方厘米(本题中所有的单位都是厘米,答案保留π).42.如图所示,已知大圆的半径为2,则阴影部分Ⅱ的面积为(用圆周率π表示).43.如图所示,已知大圆的半径为2,则阴影部分I与II的面积之和为(圆周率用π表示).44.如图,一个直径为1厘米的圆绕边长为2厘米的正方形滚动一周后回到原来的位置.在这个过程中,圆面覆盖过的区域(阴影部分)的面积是平方厘米.(π取3)45.如图,圆P的直径OA是圆O的半径,OA⊥BC,OA=10,则阴影部分的面积是.(π取3)三.解答题(共5小题)46.图中扇形半径都是4厘米,求阴影部分的面积.47.三角形ABC为直角三角形,AB是圆的直径,并且AB=20厘米,如果阴影1的面积比阴影2的面积大19平方厘米,那么BC的长度是多少厘米?48.求阴影部分面积(单位:厘米).圆内接正方形(如图)的面积是10平方厘米,求阴影部分面积.49.如图,三个圆的半径分别为1厘米、2厘米、3厘米,AB和CD垂直且过这三个圆的共有圆心O,图中阴影部分面积与非阴影部分面积之比是.50.有一根6厘米长的绳子,它的一端固定在长是2厘米、宽是1厘米的长方形的一个顶点A处(如图),让绳子另一端C与边AB在一条线上,然后把它按顺时针方向绕长方形一周,绳子扫过的面积是多少?参考答案与试题解析一.选择题(共4小题)1.如图,从甲地到乙地,A、B两条路都是由半圆形组成的,甲乙两地的中点恰好是O点,这两条路的长度()A.路线A长B.路线B长C.同样长D.无法比较【分析】由图知道小圆的直径是大圆的半径,利用圆的周长公式C=2πr或πd分别求出半圆弧长,即可分别求得两个路径的长,然后进行比较即可.【解答】解:设小圆的直径为d,则大圆的半径为d,A路线的长度为:2πd÷2=πd,B路线的长度为:πd÷2+πd÷2=πd;所以A、B两条路的长度一样长.故选:C.【点评】本题主要是灵活利用圆的周长公式解决问题.2.如图,长方形的ABCD,长4,宽2,分别以A、C为圆心,以4、2为半径,画圆弧和圆弧,则阴影部分面积是()(π=3.14)A.8.265B.7.5C.6.7D.5.7【分析】根据图形,可知阴影部分面积=扇形ABE的面积﹣△DEF的面积﹣(长方形ABCD的面积﹣扇形BCF的面积),代入数据,即可得出结论.【解答】解:由题意,阴影部分面积=扇形ABE的面积﹣△DEF的面积﹣(长方形ABCD的面积﹣扇形BCF的面积)=﹣﹣(4×2﹣)=5.7,故选:D.【点评】本题考查阴影面积的计算,考查扇形的面积公式,确定阴影部分面积=扇形ABE的面积﹣△DEF的面积﹣(长方形ABCD的面积﹣扇形BCF的面积)是关键.3.如图所示,有两个大小相等的正方形,它们的边平行,并且覆盖在一个半径为3厘米的圆上.阴影的总面积是()平方厘米.(π取3)A.9B.10C.15D.18【分析】如图连接BD、AC.根据S阴=S圆﹣S正方形ABCD计算即可.【解答】解:如图连接BD、AC.∵四边形ABCD是正方形,AC=BD=6,∴S阴=S圆﹣S正方形ABCD=π•32﹣×6×6=27﹣18=9,故选:A.【点评】本题考查圆的面积公式、正方形的面积公式等知识,记住正方形的面积等于边长的平方,也可以等于对角线乘积的一半.4.淘气用一张正方形纸剪下了一个最大的圆(如图甲),笑笑用一张圆形纸剪下了七个相等的最大圆(如图乙),在这两种剪法中,哪种剪法的利用率最高?(利用率指的是剪下的圆形面积和占原来图形面积的百分率)下面几种说法中正确的是()A.淘气的剪法利用率高B.笑笑的剪法利用率高C.两种剪法利用率一样D.无法判断【分析】要求两个人的利用率情况,因为淘气是用正方形纸剪下了一个最大的圆(如图甲),笑笑用一张圆形纸剪下了七个相等的最大圆(如图乙),假设正方形的边长是9厘米,则能求出圆的面积,进而再比较即可.【解答】解:设正方形的边长是9厘米,则正方形的面积是:9×9=81(平方厘米)淘气:圆的半径是9÷2=4.5(厘米)用的材料的面积是3.14×4.52=3.14×20.25=63.585(平方厘米);63.585÷81=0.785=78.5%;笑笑:大圆的直径是9厘米,小圆的半径是9÷3÷2=1.5(厘米),3.14×1.52×7=3.14×2.25×7=49.455(平方厘米);49.455÷63.585≈0.778=77.8%;78.5%>77.8%.答:淘气的利用率高.故选:A.【点评】此题考查的目的是理解掌握百分率的意义及应用以及圆的面积公式的运用,利用赋值法,通过计算后进行比较即可.二.填空题(共41小题)5.如图,直角三角ABC的直角边AB是圆的直径,且AB=40厘米,如果阴影(I)的面积比阴影(II)的面积小92平方厘米,则BC=36厘米.【分析】由图可知:阴影(I)+空白=半圆,阴影(II)+空白=直角三角形ABC,由此可知半圆的面积比直角三角形ABC的面积少92平方厘米,据此分析解答即可.【解答】解:3.14×(40÷2)2÷2=628(平方厘米)628+92=720(平方厘米)720×2÷40=36(厘米)故填:36厘米【点评】本题考查的是圆和三角形面积公式的灵活运用,关键是要理解半圆的面积比直角三角形ABC的面积少92平方厘米,据此分析解答即可.6.正方形ABCD的边长为4,DCEF为梯形,圆周率π取3.14,那么,阴影部分的面积是4.【分析】由题意,阴影部分由两部分组成,左半部分面积为﹣=2π﹣4,右半部分面积为﹣=8﹣2π,即可求出阴影部分的面积.【解答】解:由题意,阴影部分由两部分组成,左半部分面积为﹣=2π﹣4,右半部分面积为﹣=8﹣2π,所以阴影部分的面积是2π﹣4+8﹣2π=4,故答案为4.【点评】本题考查阴影面积的计算,考查扇形的面积公式,考查学生的计算能力,属于中档题.7.八段圆弧围成如图阴影部分,其中四段圆弧的圆心在一个正方形的四个顶点处,另外四段圆弧的圆心在这个正方形四条边的中点处.这八段圆弧的半径相同,正方形的对角线长度为1,那么阴影部分的面积之和为π﹣(答案保留π)【分析】设正中间的阴影部分的面积为a,旁边小是阴影部分的面积为b.想办法求出a、b的值即可解决问题.【解答】解:设正中间的阴影部分的面积为a,旁边小是阴影部分的面积为b.由题意圆的半径为,b=正方形EFGH的面积﹣圆面积=﹣π,4a+b=π,∴4a=π﹣,∴阴影部分的面积=8a+b=π﹣+﹣π=π﹣,故答案为π﹣.【点评】本题考查圆、正方形的面积等知识,学会利用未知数,构建方程解决问题是解题的关键.8.如图中长方形的长是5厘米,宽是4厘米.阴影部分的周长是20.28厘米.(π取3.14)【分析】根据题意可得,阴影部分的周长=圆周长的一半+长方形的两条长+长方形的宽;据此解答即可.【解答】解:3.14×4÷2+5×2+4=6.28+10+4=20.28(厘米)答:阴影部分的周长是20.28厘米.故答案为:20.28.【点评】本题属于求组合图形周长的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的周长和,然后根据周长公式解答即可.9.如图,阴影部分的面积是19.26平方厘米.(单位:厘米)【分析】如图:把①部分补到②部分,则阴影部分的面积=扇形的面积﹣直角边是6厘米的三角形面积的一半,运用圆的面积公式和三角形的面积公式解答即可.【解答】解:3.14×62÷4﹣6×6÷2÷2=28.26﹣9=19.26(平方厘米)答:阴影部分的面积是19.26平方厘米.故答案为:19.26.【点评】这类问题,要根据图形特点进行割补,寻求问题突破点.10.如图,正方形ABCD的边长为10,以A为圆心10为半径作弧交AC于E,以B为圆心10为半径作弧交BD于F,以C为圆心10为半径作弧交AC于G,以D为圆心10为半径作弧交BD于H,那么,图中阴影部分的面积是57.(π取3.14)=S扇形AOB﹣S△AOB即可求解.【分析】弄清楚S阴影部分BOE【解答】解:如图所示,设AC、BD的交点为O在图中,∠BAO=45°、OA 2=OB 2=;=S扇形AOB﹣S△AOB=×πr2﹣×OA×OB=(×π×102﹣)则:S阴影部分BOE=;=57.整个阴影部分面积=4S阴影部分BOE故:应该填57.【点评】此类题主要弄清部分或全部阴影部分面积的组成即可.11.如图,正方形ABCD边长为40厘米,其中M、N、P、Q为所在的中点:分别以正方形的顶点为圆心,以边长的一半为半径做直角扇形,那么形成图中阴影部分的面积是344平方厘米.(π 取3.14)【分析】从图中可以求出看出:阴影部分面积=正方形ABCD的面积﹣四个四分之一圆的面积=正方形ABCD的面积﹣1个圆的面积【解答】解:小圆的半径=20厘米;一个小圆的面积=πγ2=1256平方厘米;阴影部分面积=正方形ABCD的面积﹣1个圆的面积=40×40﹣1256=344平方厘米.故:应该填344.【点评】找出阴影部分面积的等量关系即可.12.如图所示的图案由半圆构成,已知最大的圆的半径R=3,则阴影部分图形的周长为21π,面积为(圆周率用π表示)【分析】由题意,阴影部分图形的周长由两部分组成,外周是以3为半径的大圆,内周是5个以为半径的圆的一半与10个以为半径的圆;面积为大圆面积减去5个半圆的面积.【解答】解:由题意,阴影部分图形的周长由两部分组成,外周是以3为半径的大圆,周长为2π×3=6π,内周是5个以为半径的圆的一半,周长为2π××=π,10个以为半径的圆,周长为2π××=π,所以阴影部分图形的周长为6π+π+π=21π;面积为大圆面积减去5个半圆的面积,即=,故答案为:21π;.【点评】本题考查不规则图形的周长与面积的计算,考查分割法的运用,正确分割是关键.13.如图是一个对称的四角星形,其中四个顶点构成一个正方形,另外四个顶点在一个圆周上,正方形的边长为10厘米,阴影部分面积是正方形面积的,那么圆的半径为厘米.【分析】如图所示,△AOB面积是阴影部分面积的,是正方形面积的,即=厘米2,求出三角形的高,即可求出圆的半径.【解答】解:如图所示,△AOB面积是阴影部分面积的,是正方形面积的,即=厘米2,由于OA=,所以△AOB的高为h==,因为∠AOB=45°,所以OB=h=,即圆的半径为厘米,故答案为.【点评】本题考查圆的半径,考查图形面积的计算,正确求出三角形的高是关键.14.如图,一个半径为10的圆内接两个正方形,这两个正方形重叠的部分刚好构成一个正八边形,那么这个正八边形的面积与图中阴影部分的面积差为86.(π取3.14)【分析】只要证明S八边形﹣S阴=S正方形﹣S圆+S正方形即可解决问题.【解答】解:由图象可知,S圆﹣S正方形=S阴+4•S小三角形,∴S阴=S圆﹣S正方形﹣4•S小三角形,∵S八边形=S正方形﹣4•S小三角形,∴S八边形﹣S阴=(S正方形﹣4•S小三角形)﹣(S圆﹣S正方形﹣4•S小三角形)=S正方形﹣S圆+S正方形=2××202﹣π•102=86.故答案为86.【点评】本题考查圆、正方形的性质、正八边形的性质等知识,解题的关键是灵活运用分割法,得出S八边形﹣S阴=S正方形﹣S圆+S正方形.15.如图,正方形边长为80厘米,O为正方形中心,A为OB中点,在正方形内以A点为圆心,OA为半径的圆,以B点为圆心,OB为半径的圆与正方形的一边围成了一个特殊的图形.将这个图形绕O点顺时针旋转三次能够得到一个风车的形状.那么这个风车(阴影部分)的面积是912平方厘米.(π取3.14)【分析】首先分析其中一部分的阴影面积等于扇形面积减去小圆的面积再减去小三角形的面积即可.图中三角形OBC的面积为80×80÷4=1600(平方厘米).可得出OB2=1600.OB2=3200.继续计算即可.【解答】解:依题意可知:图中三角形OBC的面积为80×80÷4=1600(平方厘米).可得出OB2=1600.OB2=3200.∵∠OBC=45°.八分之一的圆的面积为πOB2=400×3.14=1256(平方厘米).OA2==800.四分之一的圆的面积为:πOA2=628(平方厘米).小三角形的面积是整个三角形OBC的四分之一.1600÷4=400(平方厘米).一个小阴影的面积为:1256﹣628﹣400=228(平方厘米).整个阴影面积为:228×4=912(平方厘米).故答案为:912【点评】本题考查对圆的理解和运用,关键是找到阴影面积转换成标准图形的面积差,问题解决.16.如图所示,已知最大的圆的直径是100cm,则最小的圆的直径是50cm.【分析】可以利用勾股定理先求得最大正方形的边长,再求得第二大圆的半径,然后再求得第二大的正方形的边长,从而最后求得最小圆的半径.【解答】解:根据分析,如图,先求最大的正方形的边长,由勾股定理,得:AC2+OC2=OA2⇒=OC2;=×⇒OD=故最小圆的直径==50(cm)故答案是:50.【点评】本题考查了圆的直径,突破点是:利用圆的半径和正方形的边长以及勾股定理求得圆的半径.17.在如图所示的10×12的网格图中,猴子KING的图片是由若干圆弧和线段组成,其中最大的圆的半径是4,图中阴影部分的面积是21.5.(圆周率π取3)【分析】按题意,可以将猴子KING的图中空白部分分割,而阴影部分的面积可以用圆的面积减去中间空白部分的面积,中间空白部分由一个长方形和两个半圆,以及两个圆组成.【解答】解:由图可知,圆的直径有8个方格,故可得:每个小方格的边长=8÷8=1,a和b部分的面积=2××π×12===4.5;c和d部分的面积==4π=4×3=12;矩形的面积=2×5=10;最大的圆的面积=π×42=16×3=48,故阴影部分的面积=最大的圆的面积﹣a和b部分的面积﹣c和d部分的面积﹣c 和d之间的矩形的面积=48﹣4.5﹣12﹣10=21.5.故答案是:21.5.【点评】本题考查了圆的面积,突破点是:利用大圆的面积减去中间空白部分的面积即可求得阴影部分的面积.18.如图,正方形内接于半圆,圆内接于正方形,已知半圆面积为100,那么,图中阴影部分的面积是40.【分析】按题意,设小圆半径为a,可以利用勾股定理得到小圆面积和半圆面积的关系:a2+(2a)2=r2,解得:,进而求得阴影部分的面积.【解答】解:根据分析,πr2=100,可得πr2=200,设小圆的半径为a,则根据勾股定理可得:a2+(2a)2=r2,解得:,故阴影部分的面积=πa2===40.故答案是:40.【点评】本题考查了圆的面积,突破点是:利用勾股定理求得圆的半径,再求得圆的面积.19.如图所示的网格图中,猴子KING的图片是由若干个圆弧和线段组成,其中最大的圆的半径是4,则阴影部分的面积是21.5.【圆周率取3】【分析】首先计算最大圆的面积然后与空白部分的面积做差即可.【解答】解:依题意可知:小方格的长度是8个小格代表8,那么每一个就是1.大圆的面积为:4×4×3=48.空格部分的面积分为半径为2的圆,和半径为1的圆的1.5倍和2×5的长方形.空格的面积为3×2×2+3×1×1.5+2×5=26.5那么阴影的面积为:48﹣26.5=21.5【点评】本题考查圆的面积的理解和运用,关键问题是求出圆中空白的部分面积做差即可,问题解决.20.如图,圆0的直径AB与CD互相垂直,AB=20厘米,以C为圆心,CA为半径画弧AB,则阴影部分面积是100平方厘米.【分析】按题意,利用已知,阴影部分的面积等于半圆的面积减去弓形的面积.【解答】解:根据分析,连接AC,BC,因为AB为直径,且AB与CD互相垂直,则有:AC2+BC2=AB2=(2OA)2∴AC=BC=OA=(厘米);易知,阴影部分的面积=半圆ADB的面积﹣AEB的面积,S AEBO=S AEBC﹣S△ACB=×π×(10)2﹣=﹣100=50π﹣100;阴影部分的面积=﹣(50π﹣100)=100,故答案是:100.【点评】本题考查了圆的面积,突破点是:阴影部分的面积可以用半圆的面积减去弓形的面积.21.如图,有四种大小不同的圆,直径从小到大依次为5、10、15、20厘米.那么,图中阴影部分面积之和是314平方厘米.(π取3.14)【分析】首先分析阴影的面积和空白部分的面积部分有对称性,结合起来正好是最大圆的面积即可求解.【解答】解:依题意可知:阴影部分的面积和为最大的圆的面积.最大的圆的半径为20÷2=10(厘米);面积为:πr2=100π=314(平方厘米)故答案为:314【点评】本题是考察对圆面积的理解和认识,关键的是找到对称图案,面积和正好是一个大圆的面积.问题解决.22.如图,半径为4厘米的两个圆如图放置,长方形中两块阴影部分面积相等,A、B两点为两圆圆心,那么AB的长度为6厘米.(π取3)【分析】首先将阴影部分平分变成2个长方形,然后发现圆的四分之一的面积和一个小长方形的面积是相等的,即可列出等式.【解答】解:依题意可知:圆的面积为=12.圆的面积和一个小长方形的面积是相等的,两个长方形的面积是24平方厘米.24÷4=6.故答案为:6【点评】本题考查对圆的理解与认识,关键的问题是找到题中的相等的量.问题解决.23.埃及人擅长数学,他们很早之前就发明了个计算圆的面积的公式:S=()2.其中,d是圆的直径.在这个公式当中,相当于将圆周率π取值为 3.16(保留两位小数).【分析】因为d=2r,代入S=()2可得圆周率π的取值.【解答】解:因为d=2r,所以S=()2==所以,π=≈3.16.故答案为:3.16.【点评】本题考查了求圆周率的值,关键是利用代入法解答.24.如图所示,△ABC为等腰直角三角形,以斜边AB为直径的半圆周长为15.42厘米,那么分别以AC,BC为直径的两个半圆形(阴影部分)面积之和为14.13平方厘米.(π取3.14)【分析】根据题意分析,半圆的周长计算公式为:πr+2r;以斜边AB为直径的半圆周长为15.42厘米,可得AB=6;然后根据题意中:△ABC为等腰直角三角形,可知:AC=BC=3;以AC,BC为直径的两个半圆形(阴影部分)面积之和就是一个圆的面积.利用圆的面积公式,即可解答.【解答】解:根据题意分析:半圆的周长计算公式为:πr+2r;以斜边AB为直径的半圆周长为15.42厘米;(π+2)×r=15.42;解得:r=3;AB=2r=6;已知:“△ABC为等腰直角三角形”,根据勾股定理,AC=BC=3;以AC,BC为直径的两个半圆形(阴影部分)面积之和就是一个圆的面积;根据圆的面积公式,以AC,BC为直径的两个半圆形(阴影部分)面积之和=π×()2=14.13平方厘米;故答案为:14.13平方厘米.【点评】解题关键利用半圆的周长计算公式解得AB的长度,再根据等腰直角三角形,解得AC与BC的长度,以AC,BC为直径的两个半圆形(阴影部分)面积之和即可解答.本题主要考查半圆的周长公式,等腰直角三角形的勾股定理,圆的面积公式等.25.如图中的曲线是由半径分别为2,3,4厘米的三个圆周组成,如取π=3,则图中黑色阴影部分的面积是21.25平方厘米.【分析】根据题意可知,图中阴影部分的面积为三个圆再加上一个边长为1的正方形,最后减去一个空白的三角形即可解答.【解答】解:根据题意可知:图中阴影部分的面积为三个圆再加上一个边长为1的正方形,最后减去一个空白的三角形.可列式为:π×(2×2+3×3+4×4)+1﹣×3×1=21.25(平方厘米).故答案为:图中黑色阴影部分的面积是21.25平方厘米.【点评】解题关键将图中阴影部分拆分清楚,利用圆面积公式,正方形面积公式,三角形面积公式等即可解答.26.如图中阴影部分的面积与空白部分的面积比是1:3.(取π=3)【分析】根据图形分析,空白部分面积为两个圆的面积,阴影部分的面积为长方形面积减去两个圆的面积即可.求出两者的面积,比值即可解答.。
完整七年级上册三视图与展开练习

一、选择题: 1、下面右边的图形是由 8 个棱长为 1 个单位的小立方体组成的立体图形,这个立体图形的左视图是( )7、某同学把下图所示的几何体的三种视图画出如下(不考虑尺寸);在这三种视图中,其正确的是:( )A 、①②,B 、①③,C 、②③,D 、② 三视图与展开图3、 4、 A. B. c. 某工艺品由一个长方体和球组成(右图),则其俯视图是 (6、C . D.某几何体的三视图如左图所示,则此几何体A .正三棱柱B .圆柱C .长方体5、图所示的物体,从左面看得到的图是(2A.A .B . D .8、由若干个同样大小的正方体堆积成一个实物,不同侧面观察到如图8所示的投影图,则构成该实物的小正方体个13、如图是正方体的展开图,则原正方体相对两个面上的数字和最小的是( ).数为A. 6 ()B. 7C. 8D. 9 田田俯视图 左聊图 主视图9、某超市货架上摆放着“康师傅”红烧肉面,如图1是它们的三视图,则货架上的“康师傅”红烧肉面至少有A. 8 桶B. 9 桶C. 10 桶D.11 桶 10、 图2中几何体的正视图是( ) 11、由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数A 、6个B 、7个C 、8个D 、9个俯视图 (第12题) 12、 A 、7如图是一些相同的小正方体构成的几何体的正视图和左视图,在这个几何体中,小正方体的个数不可能是(B 、8C 、9D 、10 A. 414、B. 6C. 7D.8 16、 下列几何体,正(主)视图是三角形的是俯视图主视图 左视图图1 主视图 左视图15、 右图所示是一个三棱柱纸盒,在下面四个图中,只有一个是这个纸盒的展开图,那么这个展开图是(如图所示,右面水杯的俯视图是()A .B .C .D . 17、 有一实物如图所示,它的主视图是( ) 1 O HE A B C D18、骰子是一种特别的数字立方体,它符合规则:相对两面的点数之和总是7.下面四幅图中可以折成符合规则的骰子 的是19、一个画家有14个边长为1m 的正方体,他在地面上把它们摆成如图所示的形式,然后他把露 出的表面都涂上颜色,那么被涂上颜色的总面积为()A. 19m 2B. 21m 2C. 33m 2D. 34m 220、如图,以Rt△ABC 为直角边AC 所在直线为轴,将AABC 旋转一周所形成的几何体的俯视图是)21、下面的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的左视图是( )有6个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是( )23、想一想:将左边的图形折成一个立方体,右边的四个立方体哪一个是由左边的图形折成的()C 22、A 主视图的面积最大 C 俯视图的面积最大B 左视图的面积最大D 三个视图的面积一样大Be(A ) 回 (匚) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,从上面看
形状是
,小强摆这个立体图形至少要用
个小正方体, 至多要
用
个小正方体.
11.如图是一个正方体的平面展开图, 每个面上的小图形都表示一个数. 已知这
个正方体中相对的两个面上,每个小图形所表示的数的和相等,那么
1 个□=
个☆.
12.从三个方向看立方图, X 对面的字母是
,Y 对面的字母是
.H
对
中的数字表示该位置上小立方块的个数,那么该几何体的从正面看到的图形
为( )
A.
B.
C.
D.
7.桌子上有一些棋子,棋子分黑白两色,小明把从正面、左面和上面三个方向
看到的情况画了下来(如图) ,那么桌子上共有(
)枚棋子.
A.10
B.12
C.14
评卷人 得 分
第Ⅱ卷(非选择题)
D.16
二.填空题(共 36 小题)
正方体积木.
19.一个正方体的 6 个面分别标着 A、B、C、D、E、F 六个字母,从 3 个不同角
度看正方体如图所示,字母 C 的对面是字母
.
20.用 2 个边长为单位长度的小正方形(单位正方形)可以构成 2﹣联方,这就 是常说的多米诺.显然,经过平移旋转、对称等变换,能够重合的多米诺应
该看成是同一个,因此,多米诺只有一个:
A.8
B.9
C.10
D.11
5.图中的方格纸中有五个编号为 1, 2, 3, 4, 5 的小正方形,将其中的两个涂
上阴影,与图中阴影部分正好组成正方体的展开图,这两个正方形的编号可 以是( )
A.1,2
B.2,3
C.3,4
D.4,5
6.如图表示一个由相同小立方块搭成的几何体的从上面看到的图形,小正方形
面
的
字
母
是
.
13.将一个正方形纸片沿虚线向上对折, 再向右对折后得到一个正方形, 然后剪
下一个角(如图),将这个纸片展开后的形状应该是
.பைடு நூலகம்
14.如图是一个正方体的平面展开图,若该正方体相对的两个面上的数值相等,
则 a﹣ b× c 的值是
.
15.将如图这个展开图围成一个正方体后,与红色的面相对的面是
色.
开图对应的,这个正方体是(
)
A.
B.
C.
D.
3.沿一个纸立方体的边缘,按照图中所示的线切开,平放在桌面上.那么下面
是它展开后的形状是(
)
A.
B.
C.
D.
4.从一张大方格纸上剪下 5 个相连的方格(只有一个公共顶点的两个方格不算
相连),要使剪下的图形可折叠为一个无盖的正方体,则共可以剪出(
)
种不同的图形(经过旋转或翻转相同的图形视为同一种) .
小学奥数练习卷(知识点:三视图与展开图)
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人 得 分
第Ⅰ卷(选择题)
一.选择题(共 7 小题)
1.找一找,下面(
)组的形体侧面展开不是长方形.
A.①②③
B.②③
C.①④
D.②④
2.如图,图是一个正方体的展开图,下图的四个正方体中只有一个是和这个展
.同理,用 3 个单位正方
形构成的不同的 3﹣联方只有 2 个:
.用 4 个单位正方形构成
的不同的 4﹣联方有 5 个. 那么,用 5 个单位正方形构成的 5﹣联方有
16.如图, 是某几何体从正面和左面看到的图形, 若该几何体是由若干个棱长为
1 的正方形垒成的,则这个几何体的体积最小是
.
17.一仓库里堆放着若干个完全相同的正方体货箱, 这堆货箱的三视图如图所示,
这堆正方体货箱共有
个.
18.小胖用一些相同的正方体积木搭成了一个模型, 然后从不同的方向进行观察,
看到的情况如图,那么小胖一共用了
8.两个同样大小的正方体形状的积木.每个正方体上相对的两个面上写的数之
和都等于 9.现将两个正方体并列放置.看得见的五个面上的数字如图所示,
则看不见的七个面上的数的和等于
.
9.李明用小正方体(由图)拼搭图形,至少要准备
个这样的小正方体才
能拼搭成一个从上面、正面、侧面看到的都是 “田”字的立体图形.
10.小强用同样的小正方体摆立体图形,从正面看形状是
