材料热力学作业第7章答案
热学第七章课后习题答案

热学第七章课后习题答案热学是物理学中的重要分支,研究的是热现象和热能转化。
在热学的学习过程中,课后习题是巩固知识和检验理解的重要途径。
本文将为大家提供热学第七章课后习题的答案,并结合相关理论进行解析,帮助读者更好地理解和掌握热学知识。
1. 问题:一个物体的质量是10kg,温度为20℃,求它的内能。
答案:内能可以通过公式Q = mcΔT来计算,其中Q表示内能,m表示物体的质量,c表示物体的比热容,ΔT表示温度的变化。
根据题目中的条件,我们可以得知温度变化ΔT = 20℃-0℃=20℃,物体的比热容c可以通过查表得到,假设为c = 4.18J/(g·℃)。
将这些数据代入公式中,可以得到内能Q = 10kg × 4.18J/(g·℃) × 20℃ = 836J。
2. 问题:一个物体的内能为500J,质量为2kg,求它的温度变化。
答案:根据上一题的公式Q = mcΔT,可以得到温度变化ΔT = Q/(mc)。
将题目中的数据代入公式中,可以得到ΔT = 500J/(2kg × 4.18J/(g·℃)) = 59.81℃。
因此,物体的温度变化为59.81℃。
3. 问题:一个物体的质量为5kg,温度由20℃升高到50℃,求它的内能变化。
答案:内能变化可以通过公式ΔQ = mcΔT来计算,其中ΔQ表示内能变化。
根据题目中的条件,我们可以得到温度变化ΔT = 50℃-20℃=30℃,物体的比热容c可以通过查表得到,假设为c =4.18J/(g·℃)。
将这些数据代入公式中,可以得到内能变化ΔQ= 5kg × 4.18J/(g·℃) × 30℃ = 627J。
因此,物体的内能变化为627J。
4. 问题:一个物体的质量为2kg,内能为300J,求它的温度。
答案:根据上一题的公式ΔQ = mcΔT,可以得到温度变化ΔT = ΔQ/(mc)。
CH7题解-热力学基础

2.
M M PV RT PdV VdP RdT (1)等压(dP 0) (2)等容(dV 0) (3)等温(dT 0)
3.
TN2 210K
TO2 240K
4.
x 0
x2
kT m
Physics of universit19. (B)
20. (B)
21. 2d 2 P 不变 P C T kT (B)
22. (D)
23. (C) 24. (B)
大学物理习题_刘晓旭制作
Physics of university_LXX
二、填空题
1.
M P PV RT V RT M (1)成反比地减少 (2)成正比地增大
气体动理论 一、选择题
2 p1V1
1.
T2 V1 p1V1 p2V2 T1 V2 T1 T2
2 p2V2
( B)
2.
m1T1 m2T2 m PV RT M M 1V1 M 2V2
1 M 1 2 M 2
大学物理习题_刘晓旭制作
( A)
Physics of university_LXX
3.
TA : TB : TC 1 : 4 :16 2 2 2 v A : vB : vC 1 : 2 : 4 TA : TB : TC 1 : 4 :16 PA : PB : PC 1 : 4 :16 P nkT 3kT 3RT v m
vp 2 RT 同温度下,v p ~ v p ( H 2 ) 2000m / s v p (o2 ) 500m / s 1
工程热力学第7章答案
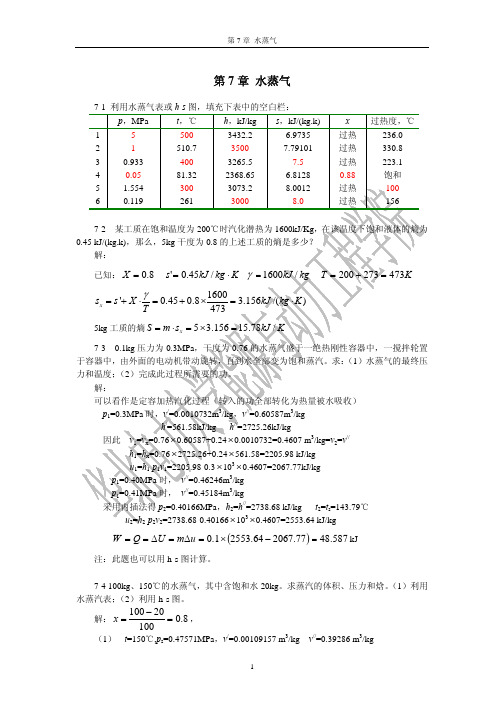
m=3.48 吨/小时
7-10 水蒸气进入汽轮机时 p1=10MPa,t1=450℃,排出汽轮机时 p2=8kPa,假设蒸汽在汽 轮机内的膨胀是可逆绝热的,且忽略入口和出口的动能差,汽轮机输出功率为 100MW,求
3
第 7 章 水蒸气
解:
已知: X = 0.8 s' = 0.45kJ / kg ⋅ K γ = 1600kJ / kg T = 200 + 273 = 473K
sx
=
s '+
X
⋅γ T
=
0.45 + 0.8× 1600 473
= 3.156kJ
/(kg ⋅ K )
5kg 工质的熵 S = m ⋅ sx = 5× 3.156 = 15.78kJ / K
p1=0.40MPa 时, v//=0.46246m3/kg p1=0.41MPa 时, v//=0.45184m3/kg 采用内插法得 p2=0.40166MPa,h2=h//=2738.68 kJ/kg t2=ts=143.79℃
u2=h2-p2v2=2738.68-0.40166 × 103 × 0.4607=2553.64 kJ/kg
∴湿饱和状态 x = h − h ' = 1134.3 − 417.5 = 31.78% h ''− h ' 2675 − 417.5
s''= 7.359kJ / kg ⋅ K
s'= 1.303kJ / kg ⋅ K
sx = 1.303 + 0.3178× (7.359 −1.303) = 3.228kJ / kg ⋅ K
7-8章小结及部分习题解答解析

a v 2a N v0 N
v0 v 2v0
k
1m 2
0
v2
f
(v)d
v
1 2
m
a [
N v0
v v0 2
0
vdv +
2v0 v0
(-v
2
v
+
2
v0
v
2
)dv]
1m 2
a N v0
[ v4 4
+
[-
1 4
(16v04
v04 )]
2 3
v0
(8v03
v03)]
7 12
mv02
P20-1 解:
变了多少? 解:
W P(V2 V1) 500(J)
E Q W 1.21103(J)
8-10一压强8-为101.0105 Pa ,体积为 1.0103 m3 的氧气 自 00 C加热到 1000 C,问:(1)当压强不变时需要多
少热量?当体积不变时,需要多少热量?(2)在等压
或等体过程中各作了多少功 ?
解: 过程 DA(等体过程)
QDA
EDA
m M
CV
(TA
TD )
P
A
QAB
T1
300K
QDA
B
D
QBC
T2 200KC
0.32 5 8.31(300 200)
V1 QCD V2 V
0.032 2
2.08104 (J)
过程 AB(等温过程)
QAB
m M
RT1
ln V2 V1
1.73104 (J)
CV .m (TC TB )
3 2
R(TC
工程热力学第七章 习题解答

第七章 习题解答7-2 ()10.1762.60.927772575.56x h x h xh '''=-+=⨯+⨯= kJ kg()10.1 2.13820.9 6.5847 6.104x s x s xs '''=-+=⨯+⨯=kJ kg K ⋅ 0.90.19430.17487x v xv ''==⨯= 3m2575.5610000.174872400.69 x x x u h Pv =-=-⨯=kJ kg 查h-s 图,2575x h =kJ kg , 6.14x s =kJ kg K ⋅,0.175x v =3m257510000.1752400x x x u h pv =-=-⨯=kJ kg 7-3 ⑴ 定容过程:()2121q u h h v p p ==---()()110.850.0010.85 1.69 1.437v x v xv '''=-+=-⨯+⨯= 3m kg ()()1110.85417.60.852675.12336.46h x h xh '''=-+=-⨯+⨯=kJ kg 查h-s 图:22925h =kJ kg()29252336.46 1.437150100517q ∴=--⨯-=kJ kg ⑵ 查h-s 图:1 6.45s =kJ kg ,27.7s = kJ kg工质吸热,熵增加为:1217.7 6.45 1.25s s s =-=-= kJ kg热源放热,熵减少为:205170.411000273q s T =-=-=-+ kJ kg 孤立系统的熵增为:12 1.250.410.84iso s s s =+=-= kJ kg7-4 (1) 1.556 MPa p =,30.20.1 m 2x v == 30.12714 m v ''=,0.10.7865''0.12714x v x v ≈== (2)()10.2135852.40.78652791.4 2377.4 kJ/kgx h x h xh '''=-+=⨯+⨯=(3) 20.7865 1.573v m m x =⋅=⨯= kg'' 1.5730.127140.2v v m v =⋅=⨯=3m (4)()[]10 1.5732377.483.860.2 1.5563118.2 kJv x q m h h v p p =---⎡⎤⎣⎦=⨯--⨯=7-5 (1) 定压过程:()21W p V V =-查附表3:10.001v =3m 20.090v = 3m kg()30000.0900.0012534W =⨯-⨯= kJ (2) 定压过程:21q h h h ==-查附表3:1852.93h =kJ kg 23114.4h =k J k g()3114.4852.9324522.9q =-⨯=kJ7-624v d c m v xmv π''''⋅≥=2440.9515000.194336003600 3.14xmv d π''⨯⨯⨯≥=⨯ ∴0.06258 m d ≥7-7 湿蒸汽中其加热作用的仅为干饱和蒸汽:()air p xm h h m c T '''-=⋅∆ ()()4000 1.293 1.00512.00306.6kg h 0.942725.5561.4m ⨯⨯⨯-==-7-8 充满饱和水的容器比较危险 7-9 ()11221x x x mv m v m v =+()112221210.3748120.80.19430.83830.27274m v m x v x m m ''''+⨯+⨯⨯===+⨯()312''30.8380.272740.6857 m x V mv m m xv ==+=⨯⨯=()11222x x x Q mu mu m u =--()()()11112222x x x x x m h pv m h p v m h p v =-----()32762.90.838697.10.1627000.8380.27274=⨯+⨯-⨯⨯()()2748.55000.37481227770.8762.610000.80.1943--⨯-⨯+-⨯⨯193.7 kJ =-7-10 查附表3:12886h =kJ kg 23387h = kJ kg10.012v =3m 20.018v =3m k g2133872886501q h h =-=-=kJ kg 21501 h h h ∆=-=kJ kg()()21501180000.0180.012393u q p v v ∆=--=-⨯-=kJ kg 7-11 ()1查 h-s 图:0.816x = 2118k J k gx h = 6.94x s =kJ kg 13325h =k J k g33x t =℃ 1211833251207t x w h h h =-∆=-=-=- kJ kg()2()0.25273331130.5t t w w '=+⨯+=- kJkg7-12 查表 t=25℃,1104h = kJ kg查h-s 图:22708h = kJ kg 20.136v =3m k g33046h =kJ kg 30.184v =3mk g (1) ()31B Q m h h η⋅⋅=-煤()1000030401040.6984143029400η⨯-∴==⨯(2) ()()46321030402708 3.3210Q m h h =-=-=⨯kJ()3232=U m h h p v v ∆---⎡⎤⎣⎦()46103040270814000.1840.136 2.5610=⋅---=⨯⎡⎤⎣⎦kJ 7-13 (1) 由附表2:20t =℃时,183.86h =kJ kg100t =℃时,22675.71h =kJ kg由 ()1221p y m c t m h h ⋅⋅∆=-,得:()()()21212675.7183.862001001503650180 1.079p y h h m m c t --⨯⨯===⋅-⨯kg h7-14 节流前后焓相等,查h-s 图:0.968x =7-15 (1) 查附表3得 10.0010053v '=m 3/kg 128.191v ''= m 3/kg 137.72h '= kJ/kg 2560.6h ''= kJ/kg ()10.928.1910.10.0010053252380.0010053x xv x v v n v v '''+-⨯+⨯====''(2)()211 0.92560.60.1137.72137.722180.6 kJ/kgq h h h xh x h h ''''=∆=-=+--=⨯+⨯-=。
材料基础-第七章热力学及其相图x

(a+β )片状共晶 400 × 图7-9 Pb-Sn 二元合金的共晶显微组织 图中黑色为Pb的 a相,白色为Sn的β相 , a 相、β相呈片层状相间分布,称片层状共晶。
3)合金III的结晶过程(wsn=50%) 合金III的成分在M、E点之间,称为亚共晶 合金。图7-10为其冷却曲线及组织变化。 当缓冷到 1 点时,结晶出一次晶 a 相,温度 在1、2点之间为匀晶反应。温度降到2点共晶温 度tE时,液相L具有共晶成分E,发生共晶反应。 共晶反应后的组织为a+(a+β)共晶。 随温度下降,a相成分沿MF线改变,此时匀 晶和共晶中的a相都要析出βII,室温组织为 a+(a +β)共晶+β II ,显微组织见图7-11。 图中黑色粗大树枝状组织为一次晶a相,粗 黑色间的白色颗粒状组织为二次晶 βII ,其余黑 白相间部分为共晶组织(a+β)共晶。
(7-1) 式表示,自由度越小,平衡共存相就 越大。 自由度f 为零时,(7-1)式变为: P=C+2 (7-2)
再压力给定去掉一个自由度,(7-2)式变为 :
P=C+1
(7-3)
表明系统中平衡相数最多比组元数多一个
一元系:C=1,P=2,最多二相平衡共存。
例如,纯Fe结晶时,同时存在的平衡共存相 仅为液相和固相。
7.2 相图建立的基本方法
1.相图 相图是用图解方法描述在平衡条件下相的 状态和转变与成分、温度、压力的相互关系。 相图有二元相图、三元相图和多元相图。 二元相图是相图的基础,应用最广泛。通 过相图分析,可以了解: (1)不同条件下材料的相转变及相平衡的状态; (2)预测材料的性能; (3)为新材料研制提供依据。
共晶反应完成后,在温度下降过程中,a 固溶体和 β 固溶体分别沿 MF 线和 NG 线不断变化, 合金II从a相中析出二次晶βII,从β相中析出二 次晶aII,可用杠杆定律计算。 由于aII和βII量小,在组织中不易分辨,一 般不予区别。 所以,合金II在结晶过程中的反应为共晶 反应+二次析出,其室温组织为(a+β)共晶, 其形态见图7-9。
热力学统计物理课后习题答案

热⼒学统计物理课后习题答案第七章玻⽿兹曼统计222 Un y n z ,( n x ,n y ,n z 0, 1, 2,)有 P3 V上述结论对于玻尔兹曼分布,玻⾊分布和费⽶分布都成⽴。
证明:处在边长为L 的⽴⽅体中,⾮相对论粒⼦的能量本征值为个量⼦数。
7. 2根据公式Pa iiL证明,对于极端相对论粒⼦V2 2 22 12n z ,n x ,n y ,n z0, 1, 2,有 P1 Ucp cn x n y3VL上述结论对于玻尔兹曼分布,玻⾊分布和费⽶分布都成⽴。
证明:处在边长为 L 的⽴⽅体中,极端相对论粒⼦的能量本征值为2 2 2 2 12n x ,n y ,n zCL "x⼭n x ,n y ,n z 0, 1, 2, -------(1)为书写简便,我们将上式简记为aV ----------------- -——(2)其中V=L 3是系统的体积,常量 a2 2 22 c n xn yn z‘2 ,并以单⼀指标 i 代表 n x ,n y ,n z 个量⼦数。
7. 1试根据公式a i—证明,对于⾮相对论粒⼦VP 2 1 2m 2m2 nx2 2P 21 2n x ,n y ,n z2m 2m L2 nx2 2n y n z ( n x ,n y ,n z 0, 1, 2,) (1)为书写简便,我们将上式简记为aV(2)其中V=L 3是系统的体积,常量(2 )2 2n x 2myn ;,并以单⼀指标I 代表 n x ,n y ,n z由(2)式可得」-aV 353(3)代⼊压强公式,a i2 3Va i2U 3 V(4)式中Ui上述证明未涉及分布的具体表达式,都成⽴。
注:(4 )式只适⽤于粒⼦仅有平移运动的情形。
如果粒⼦还有其他的⾃由度,式( U 仅指平动内能。
a i i是系统的内能。
因此上述结论对于玻尔兹曼分布,玻⾊分布和费⽶分布4)中的由(2)式可得L1aV 43 V31 I 3 V -------- (3)代⼊压强公式,有Pa I -IV1 a I I3V I1 U (4 )- (4⼃式中Ua , II 是系统的内能。
材料热力学 第7章 两个重要的熔体模型之双亚点阵模型

双亚点阵模型(Two sublattice model)是 20世纪 70年代开始应用的模型, 并立即在间隙式固溶体(Interstitial solid solution)和线性化合物(Linear compound)的相平衡计算方面发挥了明显的优势。
模型虽然也把要处理的对象(固溶体或线性化合物)划分为两个亚点阵, 但Bragg-Williams模型中亚点阵的含义完全不同。一是双亚点阵模型的 两个亚点阵的结点数目可以相同,也可以完全不同;另一是两个亚点 阵的性质完全不同,每种组元只能进入一种亚点阵,而不能进入另一 种亚点阵。所以这种模型更像是由两类亚点阵组成的一种“化合物”。 一般用这样一个分子式MaNc来描述两个亚点阵所构成的“化合物”。 这里Ma是一个亚点阵;而Nc是另一个亚点阵。a和c表示两个亚点阵的 结点数的比例。
双亚点阵模型的摩尔自由能
双亚点阵模型的化学势及活度
组元AaVac的化学势:
yc+yva=1
c
1 c
0
G
AaCc
a c
0G
A
I CVa
1 2yC
RT ln yc 1 yc
(1)结点点阵 Fe及代位式溶质如Cr、Mn、Mo 等进入这种亚点阵。
(2)空隙点阵 C及间隙式溶质如N、O、H等进 入这种亚点阵,但会有大量的八面体空隙处于未填 充的空位状态。
双亚点阵模型对间隙固溶体成分的描述
3
双亚点阵模型对线性化合物成分的描述
双亚点阵模型的混合熵
仍以每种亚点阵各有两类结点的铁素体为例对混合熵进行分 析: 用“两类结点”,而不是用“两类原子”,是因为把未被填充 的空隙也看做一类结点,也会对混合熵做出贡献。 实体原子亚点阵上是Fe和Cr,空隙亚点阵上是C和未填充的空 隙,其具体的分子式为:(Fe,Cr)1(C,Va)3。 这类问题的通式是MaNc。两个亚点阵中都有两类结点,因此都 要产生混合熵。 如前所述,固溶体的混合熵为两个亚点阵混合熵之和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业07
1. 成分为x α的α相脱溶析出中间相δ,请图解表示(均相)形核驱动力和相变驱动力,并用化学位形式写出形核驱动力和相变驱动力的表达式。
形核的驱动力为: ))1(())1((//αδαδδαδδαδδαμμμμA B A B m
x x x x G -+--+=∆→ 相变驱动力: ])1([])1([//ααααδααδααδααμμμμB B B B m x x x x G -+--+=∆+→
))(1()(//α
δαααδααμμμμA A B B x x --+-=
2.试用摩尔自由能-成分图说明,为什么碳素钢在淬火之后回火时,渗碳体的粒子越细,其周围的铁素体中的碳含量越高?
[解]
如右图所示,给出了铁素体α(母
相)和大块的渗碳体Fe 3C (以β表示)
的Gibbs 自由能曲线,及其两相平衡
成分。
半径为r 的渗碳体粒子的
Gibbs 自由能曲线以βr 表示。
⇒
当渗碳体粒子的r 越小,其比表面积越大,比表面能也越大,因而渗碳体粒子的Gibbs 自由能越大(即越正,往上移),渗碳体粒子的Gibbs 自由能曲线与母相铁素体α的Gibbs 自由能曲线的公切线切点随着r 的减小往右移(即C 的平衡成分右移)。
公切线切点对应两相平衡的成分点;故渗碳体的粒子越细,其周围的铁素体中的碳含量越高。
3.已知α、β、γ、δ相的自由能-成分曲线如下图所示,从热力学角度判断浓度为C 0的γ相及δ相的优先析出相,并说明理由,同时指出在所示温度下的平衡相(稳定相)及其浓度
4. 指出固溶体调幅分解与形核(脱溶)分解两之间的的主要区别。
参考解: Spinodal分解是扩散型连续相变之一,相变时不需要形核,直接由浓度起伏导致固溶体发生分解,长大成为新相。
而形核(脱溶)分解······
5. 为什么过饱和固溶体经恰当时效处理后,其强度比它具有室温平衡组织下的强度要高?什么样的合金具有明显的时效强化效果?把固溶处理后的合金冷加工一定量后再进行时效,请讨论冷加工的影响。
参考解:
(1)时效处理后:第二相沉淀(弥散强化)
(2)均相化处理温度的固溶度与时效处理温度的固溶度差值大的合金具有明显的时效强化效果
(3)把固溶处理后的合金冷加工一定量后再进行时效,因冷加工使合金材料的位错等晶体缺陷的增加而使得第二相沉淀的相变驱动力增大,•••••••••
6.如下图所示,设含η相的硬质合金烧结体(WC + Co + η)的成分在A点。
若在1430ºC 渗碳气氛下进行渗C处理(即渗C梯度烧结),请图解标示渗C处理后的硬质合金表层成分的位置,并写出梯度烧结后表层的物相组成,说明渗C梯度烧结前后的表层材料力学性能的差异(注:η相为脆性相)。
经渗C梯度烧结后,表层硬质合金的成分位置将从A点变化至B点,表层的物相组成变为WC + Co,η相消失。
渗C梯度烧结前,硬质合金烧结体(WC + Co + η) 表层材料与内部一样硬而脆;但在渗C梯度烧结后,表层材料变得韧性好,因而能有效地抑制表面超硬涂层裂纹的扩展。
