【配套K12】江苏省宿迁市高中数学 第12课时 直线和平面垂直的性质导学案 苏教版必修2
《直线与平面垂直的性质》教案、导学案、课后作业

《8.6.2 直线与平面垂直》教案第2课时直线与平面垂直的性质【教材分析】在直线与平面的位置关系中,垂直是一种非常重要的关系,本节内容既是直线与直线垂直关系延续和提高,也是后续研究平面与平面垂直的基础,既巩固了前面所学的内容,又为后面内容的学习做了知识上和方法上的准备,在教材中起着承前启后的作用。
【教学目标与核心素养】课程目标1.理解直线和平面垂直的性质定理并能运用其解决相关问题.2.通过对空间距离的理解和应用,培养学生的空间转化能力和逻辑推理能力.数学学科素养1.逻辑推理:探究归纳直线和平面垂直的性质定理,线线垂直与线面垂直转化;2.数学运算:求空间点面、线面、面面距离.3.直观想象:题中几何体的点、线、面的位置关系.【教学重点和难点】重点:直线和平面垂直的性质定理.难点:直线和平面垂直的性质定理的应用.【教学过程】一、情景导入问题1:长方体ABCD—A1B1C1D1中,棱AA1、BB1、CC1、DD1所在直线都垂直于平面ABCD,它们之间是有什么位置关系?问题2:已知直线a⊥α 、b⊥α、那么直线a、b一定平行吗?要求:让学生自由发言,教师不做判断。
而是引导学生进一步观察.研探.二、预习课本,引入新课阅读课本153-155页,思考并完成以下问题1、垂直与同一条直线的两条直线有什么位置关系?2、与线面垂直有关的结论有哪些?3、怎样定义直线与平面的距离、平面与平面的距离?要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、新知探究1、直线与平面平行的性质定理常用结论:(1)过一点有且仅有一条直线与已知平面垂直.(2)已知a⊥α.若平面α外的直线b与直线a垂直,则b//α.(3)已知a⊥α.β//α,则a⊥β.2、距离(1)直线与平面的距离:一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离.(2)平面与平面的距离:两个平面平行时,其中一个平面内任意一点到另一个平面的距离.四、典例分析、举一反三题型一直线与平面垂直的性质定理的应用例1 如图所示,在正方体ABCD-A1B1C1D1中,M是AB上的一点,N是A1C的中点,MN⊥平面A1DC.求证:(1)MN∥AD1;(2)M 是AB 的中点. 【答案】证明见解析【解析】(1)因为ABCD-A 1B 1C 1D 1为正方体,所以AD 1⊥A 1D.又因为CD ⊥平面ADD 1A 1,AD 1⊂平面ADD 1A 1,所以CD ⊥AD 1. 因为A 1D∩CD=D,所以AD 1⊥平面A 1DC. 又因为MN ⊥平面A 1DC,所以MN ∥AD 1. (2)设AD 1∩A 1D=O,连接ON,在△A 1DC 中, A 1O=OD,A 1N=NC.所以ONCDAB,即ON ∥AM.又因为MN ∥OA,所以四边形AMNO 为平行四边形,所以ON=AM. 因为ON=AB,所以AM=AB,即M 是AB 的中点.解题技巧(证明两条直线平行的常见方法) (1)公理4:平行于同一条直线的两条直线平行;(2)线面平行的性质定理:如果一条直线与一个平面平行,那么经过这条直线的任一平面与此平面的交线与该直线平行;(3)面面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行;(4)线面垂直的性质定理:垂直于同一个平面的两条直线平行. 跟踪训练一1、如图,已知平面α∩平面β=l ,EA ⊥α,垂足为A ,EB ⊥β,B 为垂足,直线a ⊂β,a ⊥AB.求证:a ∥l .12121212【答案】证明见解析【解析】因为EB⊥β,a⊂β,所以EB⊥a. 又因为a⊥AB,AB∩EB=B,所以a⊥平面ABE.因为α∩β=l,所以l⊂α,l⊂β.因为EA⊥α,EB⊥β,所以EA⊥l,EB⊥l. 又因为EA∩EB=E,所以l⊥平面ABE.所以a∥l.题型二空间中的距离问题例2 如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.若AE=A1E,AB=3,求四棱锥E-BB1C1C的体积.【答案】18.【解析】由长方体ABCD-A1B1C1D1,可知B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,所以B1C1⊥BE,因为BE⊥EC1,B1C1∩EC1=C1,所以BE⊥平面EB1C1,所以∠BEB1=90°,由题设可知Rt△ABE≌Rt△A1B1 E,所以∠AEB=∠A1EB1=45°,所以AE=AB=3,AA1=2AE=6,因为在长方体ABCD-A1B1C1D1中,AA1∥平面BB1C1C,E∈AA1,AB⊥平面BB1C1C,所以E到平面BB1C1C的距离即为点A到平面BB1C1C的距离,AB=3,所以四棱锥E-BB1C1C的体积V=13×3×6×3=18.解题技巧 (空间中距离的转化)(1)利用线面、面面平行转化:利用线面距、面面距的定义,转化为直线或平面上的另一点到平面的距离.(2)利用中点转化:如果条件中具有中点条件,将一个点到平面的距离,借助中点(等分点),转化为另一点到平面的距离.(3)通过换底转化:一是直接换底,以方便求几何体的高;二是将底面扩展(分割),以方便求底面积和高.跟踪训练二1、如图,四棱锥P-ABCD中,PA⊥菱形ABCD所在的平面,∠ABC=60°,E 是BC的中点,M是PD的中点.(1)求证:AE⊥平面PAD.(2)若AB=AP=2,求三棱锥P-ACM的体积.【答案】(1)证明见解析,(2)√33.【解析】解析 (1)连接AC,因为底面ABCD为菱形,∠ABC=60°,所以△ABC为正三角形,因为E是BC的中点,所以AE⊥BC,因为AD∥BC,所以AE⊥AD,因为PA⊥平面ABCD,AE⊂平面ABCD,所以PA⊥AE,又因为PA∩AD=A,所以AE⊥平面PAD.(2)因为AB=AP=2,则AD=2,AE=√3,所以VP-ACM =VC-PAM= 13S△PAM·AE= 13×12×12×2×2×√3=√33五、课堂小结让学生总结本节课所学主要知识及解题技巧六、板书设计七、作业课本155页练习,162页习题8.6的13、14、15、16题.【教学反思】通过本节课性质定理的学习,使学生进一步了解线线垂直和线面垂直时刻相互转化的,即空间问题和平面问题可以相互转化.《8.6.2 直线与平面垂直》教案第2课时直线与平面垂直的性质【学习目标】知识目标1.理解直线和平面垂直的性质定理并能运用其解决相关问题.2.通过对空间距离的理解和应用,培养学生的空间转化能力和逻辑推理能力.核心素养1.逻辑推理:探究归纳直线和平面垂直的性质定理,线线垂直与线面垂直转化;2.数学运算:求空间点面、线面、面面距离.3.直观想象:题中几何体的点、线、面的位置关系.【学习重点】:直线和平面垂直的性质定理.【学习难点】:直线和平面垂直的性质定理的应用.【学习过程】一、预习导入阅读课本153-155页,填写。
高中数学 直线、平面垂直的定义与判定导学案 苏教版必修2

直线与平面垂直的定义与判定一学习要求:掌握直线与平面垂直的定义,理解直线与平面垂直的判定定理,并会用定义和判定定理证明直线与平面垂直的关系.二学习重点:直线与平面垂直的判定定理.学习难点:判定定理的应用.三学习过程:1 知识链接:(1). 复习直线与平面平行的判定定理及性质定理.(2). 讨论:日常生活中有哪些现象给人以直线与平面垂直的感觉?(竖直站立的人与地面、旗杆与地面、生日蛋糕与蜡烛┅)2 .直线与平面垂直的定义:(1)引入:观察旗杆与它在地面的影子的位置关系:随着时间的变化,影子在移动,这是变的一面,那么不变的一面是什么呢?(2)定义:如果_______________________________ ,则直线l与平面α⊥. l叫做平面α的垂线,α叫做直线l的垂面,它们互相垂直,记作lα的唯一公共点P叫做垂足.(线线垂直→线面垂直)问题 1 如果一条直线与平面内无数条直线垂直,那么这条直线与平面垂直吗?举例说明。
问题2 在空间:(1)过一点有几条直线与已知平面垂直?(2)过一点有几个平面与已知直线垂直?结论:问题3:给定一条直线和一个平面,如何判定它们是否垂直?例1 求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面。
已知:a∥b,a⊥α求证:b⊥α学生依图,联系直线与平面垂直的定义,尝试写出证明过程:3.直线与平面垂直的判定:(1)实验:将一张矩形纸片对折后略为展开,竖立在桌面上,观察折痕与桌面有怎样的位置关系?进而,你能得出什么结论?(2)判定定理:如果________________________________________,则这条直线与该平面垂直.符号语言:若l⊥m,l⊥n,m∩n=B,m⊂α,n⊂α,则l⊥α说明:对于判定定理注意二点.一是判定定理的条件中,“平面内的两条相交直线”是关键性词语,一定要记准、用对.二是要判断一条已知直线和一个平面是否垂直,取决于在这个平面内能否找出两条相交直线和已知直线垂直,至于这两条相交直线是否和已知直线有公共点,这是无关紧要的.问题4:以下命题中,正确命题的序号为______________.①若一条直线垂直于平面内的两条直线,则这条直线垂直于这个平面;②若一条直线垂直于一个平面内的无数条直线,则这条直线垂直于这个平面;③若一条直线平行于一个平面,则垂直于这个平面的直线必定垂直于这条直线;④若一条直线垂直于一个平面,则垂直于这条直线的另一直线必垂直于这个平面.问题5:如图,在长方体''''ABCD A B C D 中,与平面''B C CB 垂直的直线有 ;与直线'AA 垂直的平面有 .例2 在正方体ABCD-A'B'C'D'中,求证:AC ┴BD'.例3在△ABC 中,∠B=90°,SA ⊥面ABC ,AM ⊥SC ,AN ⊥SB 垂足分别为N 、M ,求证:AN ⊥BC ,MN ⊥SC四.课时小结:1.定义中的“任何一条直线”这一词语,它与“所有直线”是同义语、定义是说这条直线和平面内所有直线垂直.2.和平面垂直的直线是直线和平面相交的一种特殊形式.3.注意两个结论:过一点有且只有一条直线和已知平面垂直.过一点有且只有一个平面和已知直线垂直.4.判定直线和平面是否垂直,本节课给出了三种方法:(1)定义 强调“任何一条直线”;(2)例1的结论 符合“两条平行线中一条垂直于平面”特征;(3)判定定理 必须是“两条相交直线”.五 当堂检测:1.判断题(1)l ⊥α⇒l 与α相交( )(2)m ⊂α,n ⊂α,l ⊥m ,l ⊥n ⇒l ⊥α( )(3)l ∥m ,m ∥n ,l ⊥α⇒n ⊥α( )2. 如图,已知AP O ⊥ 所在平面,AB 为O 的直径,C 是圆周上的任意, 过点A 作AE PC ⊥于点E. 求证:AE ⊥平面PBC.六 课后作业1 课本P34页练习32 课本P36页习题73 课本P37页习题8。
直线与平面垂直的导学案

直线与平面垂直的判定学案【教学目标】知识与技能1、掌握直线与平面垂直的定义及判定定理.2、使学生掌握判定直线与平面垂直的方法.过程与方法培养学生的几何直观能力,使他们在直观感知,操作确认的基础上学会归纳概括结论情感、态度与价值观在体验数学美的过程中激发学生学习兴趣,从而培养学生勤于思考、勤于动手的良好品质.培养学生学会从“感性认识”到“理性认识”过程中获取新知.重点:直线与平面垂直的定义及判定定理.难点:直线与平面垂直的定义及判定定理和线面角的求法.一创设情景直观感知请同学们想一下旗杆与地面、大桥桥柱与水面是什么位置关系?二探究新知探究一直线与平面垂直的定义思考:当太阳的角度发生变化时,旗杆与它的影子的位置关系会发生变化吗?总结:如何定义直线与平面垂直?________________________________________________________________探究二思考:除定义外,有没有比较方便可行的方法来判断一条直线与一个平面垂直呢?活动:请同学们合作完成课本的学生活动折纸实验总结:直线与平面垂直的判定定理:探究三阅读课本第指出下图所体现的知识三尝试应用如图,在三棱锥V-ABC中,VA=VC,AB=BC, K是AC的中点.求证:AC⊥平面VKB.四典例示范例1 如图,已知a∥b、a⊥α.求证:b⊥α.例2、如图,正方体ABCD-中,求(1)直线AB和平面所成的角。
(2)直线AB和平面所成的角。
AVBCKa bA BCDA BCD五 达标检测(你一定可以做的很好!相信自己!)1在下图的长方体中,请列举与平面ABCD 垂直的直线。
并说明这些直线有怎样的位置关系?2 如图,圆O 所在一平面为 a,AB 是圆O 的直径,C 是圆周上一点, 且PA ⊥平面a 求证:B C ⊥平面PAC3.如图:正方体ABCD-ABCD 中,求:(1)AC 与面ABCD 所成的角(2)AC 与面BBDD 所成的角(3)AC 与面BBCC 所成的角 (4)AC 与面ABCD 所成的角六 课堂小结请同学们锻炼一下自己的概括能力吧!B A ′C ′D ′B A C D P A B C OA B C DA BCD。
苏教版数学高一《直线与平面垂直》 同步导学案

3、需要老师重点讲解的问题是___________________________________________
4、我的建议___________________________________________________________
已知: 求证:
分析:直接证明a∥b比较困难,我们考虑采用反证法证明.
2、直线与平面的距离
如果一条直线和一个平面平行,这条直线上任意一点到这个平面的距离,叫做_______
3、线面所成角
观察如图所示的长方体ABCD-A1B1C1D1
(1)直线AA1和平面ABCD是什么关系?
(2)直线A1B、A1C、A1D和平面ABCD的位置关系?
说明:
1.若直线垂直平面,则直线和平面所成的角为________
2.若直线和平面平行,或直线在平面内,则直线和平面所成的角为___________,直线和平面所成角的取值范围为___________。
b.预习检测题
《突破课堂》P31 1ห้องสมุดไป่ตู้2、5
c.预习提高题
《突破课堂》P31 3;《突破课堂》P32 1、2、
四、预习的展示与总结
五、教师精讲点拨典型例题
例1如图,P是△ABC所在平面外的一点,PA⊥PB,PB⊥PC,PC⊥PA,H是△ABC的垂心,求证:PH⊥平面ABC.
解题思路:线线垂直 线面垂直 线线垂直
例2已知直线 平面 ,求证:直线 上各点到平面 的距离相等.
例3
在正方体ABCD-A’B’C’D’中,求:
(3)直线A1B、A1C、A1D与点B、C、D它们又如何命名呢?
高中数学-《直线、平面垂直的判定及其性质》导学案

《直线、平面垂直的判定及其性质》导学案【学习目标】(1)使学生掌握直线和平面垂直的定义及判定定理;(2)培养学生的几何直观能力,使他们在直观感知,操作确认的基础上学会归纳、概括结论;(3)使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”“两个平面互相垂直”的概念;(4)使学生掌握两个平面垂直的判定定理;(5)使学生理会“类比归纳”思想在数学问题解决上的作用【重点难点】重点:直线与平面垂直的定义和判定定理的探究;平面与平面垂直的判定;难点:如何度量二面角的大小【学法指导】实物观察,类比归纳,语言表达【知识链接】空间点、直线、平面之间的位置关系【学习过程】一.预习自学1.线面垂直定义:如果一条直线l和平面α内的,我们就说直线l和平面α互相垂直,记作,其中直线l叫做平面的垂线,平面α叫做直线l的 , 直线与平面的交点叫做垂足.2.直线与平面垂直的判定定理:3.平面的斜线:4.直线和平面所成的角:5.二面角:6.二面角的平面角:7.面面垂直两个平面垂直的定义:两个平面相交,如果它们所成的二面角是,就说这两个平面互相垂直.记作两平面垂直的判定定理:8.直线和平面垂直的性质定理:9.两平面垂直的性质定理:二.典型例题例1. 已知PA ⊥⊙O 所在的平面,AB 是⊙O 的直径,C 是⊙O 上任意一点,过A 点作AE ⊥PC 于点E ,求证:AE ⊥平面PBC点评:证明直线与平面垂直的常用方法有:利用线面垂直的定义;利用线面垂直的判定定理;利用“若直线a ∥直线b ,直线a ⊥平面α,则直线b ⊥平面α”例2.在正方体ABCD —A 1B 1C 1 D 1中, 求AC 1与面ADD 1 A 1所成的角的正弦值为 .例3.在直三棱柱ABC —A 1B 1C 1中,B 1C 1=A 1C 1,A 1B ⊥AC 1,求证:A 1B ⊥B 1C例4.在正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是BB 1,CD 的中点 (1)求证:AD ⊥D 1F ;(2)求AE 与D 1F 所成的角;(3)证明平面AED ⊥平面A 1FD 1例5.正四棱锥P-ABCD 中,AB =4,高为2,求二面角P-BC -D 的大小.三.课堂检测1.若直线a 与平面α不垂直,那么在平面α内与直线a 垂直的直线 ( ) A .只有一条 B .有无数条 C .所有直线 D .不存在A O E P CD A 1C 1DD A B COE P 2.经过平面α外一点和平面α内一点与平面α垂直的平面有 ( )A .0个B .1个C .无数个D .1个或无数个 3.已知直线m ⊥平面α,直线⊂n 平面β,下列说法正确的有 ( )①若n m ⊥则,//βα ②若βα⊥,则m //n ③若m //n ,则βα⊥④若,//m n αβ⊥则A .1个B .2个C .3个D .4个4.下列命题,其中正确的命题有①直线上有两点到平面的距离相等,则此直线与平面平行②夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面 ③直线m ⊥平面α,直线n ⊥m ,则n ∥α④a 、b 是异面直线,则存在唯一的平面α,使它与a 、b 都平行且与a 、b 距离相等 ⑤直线l 垂直于平面α内的无数条直线,则l ⊥α5.在正方形SG 1G 2G 3中,E 、F 分别是G 1G 2、G 2G 3的中点,D 是EF 的中点,沿SE 、SF 及EF 把这个正方形折成一个四面体,使G 1、G 2、G 3三点重合,重合后的点记为G ,那么,在四面体S —EFG 中必有A. SG ⊥平面EFGB. SD ⊥平面EFGC. FG ⊥平面SEFD. GD ⊥平面SEF6.在直四棱柱ABCD —A 1B 1C 1D 1中,当底面四边形ABCD 满足条件_______时,有A 1C ⊥B 1D 17.在三棱锥S —ABC 中,N 是S 在底面ABC 上的射影,且N 在△ABC 的AB 边的高CD 上,点M ∈SC ,截面MAB 和底面ABC 所成的二面角M —AB —C 等于∠NSC ,求证:SC ⊥截面MAB 8.如图,ABCD 是正方形,O 是正方形的中心,PO ⊥底面ABCD ,E 是五.课外作业1.已知直线a 、b 和平面βα,,下列命题中错误的是( ) A .若αα⊥⊥b a b a 则,,//B .若b a b a //,//,,则βαβα⊥⊥C .若b a b a //,//,//,//则βαβαD .若b a b a ⊥⊥⊥⊥则,,,βαβα2. A 、B 是二面角α—l —β的棱l 上两点,P 是面β内一点,PB ⊥l 于点B ,PA 和l 所成的角为450,PA 和面α所成的角为300,则二面角α—l —β 的大小为( )A .45B .30C .600D .7503.若直线l 与平面所成角为3π,直线a 在平面内,且与直线l 异面,则直线l 与直线a 所成的角的取值范围是( ) A .⎥⎦⎤⎢⎣⎡π32 0,B .⎥⎦⎤⎢⎣⎡3π 0,C .⎥⎦⎤⎢⎣⎡2π 3π,D .⎥⎦⎤⎢⎣⎡π32 3π,4.在正方体ABCD —A 1B 1C 1D 1中,M 为CC 1的中点,AC 交BD 于点O ,求证:A 1O ⊥平面MBD.5.在正方体ABCD —A 1B 1C 1D 1中,E 、F 、G 分别是BC 、CD 、CC 1的中点. 求证:面EFG ⊥面AA 1C 1C .6.如图,在正三棱锥S —ABC 中,E 、F 分别是侧棱SA 、SB 的中点,且平面CEF ⊥平面SAB . (1)若G 为EF 的中点,求证:CG ⊥平面SAB ;(2)求此三棱锥的侧面积与底面积的比值.7.在四棱锥P —ABCD 中,底面ABCD 是矩形,AB =2,BC =a ,又侧棱PA ⊥底面ABCD (1)当a 为何值时,BD ⊥平面PAC ?试证明你的结论; (2)当a =4时,求证:BC 边上存在一点M ,使得PM ⊥DM ;(3)若在BC 边上至少存在一点M ,使PM ⊥DM ,求a 的取值范围.2.3 直线、平面垂直的判定及其性质答案二.典型例题例3例4.(2)900 例5. 450三.课堂检测1.B2.D3.B4.②④5.A6. AC BD⊥五.课外作业1.C2.A3.C 6.(2)32a= (2)M为中点时(3)4a≥。
高中数学直线、平面垂直的判定及其性质导学案

直线、平面垂直的判定及其性质[考纲要求] 1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理.2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题. [知识梳理]1.直线与平面垂直 (1)直线和平面垂直的定义如果一条直线l 与平面α内的__任意一条__直线都垂直,就说直线l 与平面α互相垂直. (2)判定定理与性质定理⎭⎪⎬⎪⎫__a ,b ⊂α____a ∩b =O ____l ⊥a ____l ⊥b __⇒l ⊥α⎭⎪⎬⎪⎫__a ⊥α____b ⊥α__⇒a∥b(1)平面与平面垂直的定义两个平面相交,如果它们所成的二面角是__直二面角__,就说这两个平面互相垂直. (2)判定定理和性质定理⎭⎪⎬⎪⎫__l ⊂β____l ⊥α__⇒α⊥β 题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)直线l与平面α内的无数条直线都垂直,则l⊥α.( ×)(2)垂直于同一个平面的两平面平行.( ×)(3)直线a⊥α,b⊥α,则a∥b.( √)(4)若α⊥β,a⊥β,则a∥α.( ×)(5)若直线a⊥平面α,直线b∥α,则直线a与b垂直.( √)(6)若平面α内的一条直线垂直于平面β内的无数条直线,则α⊥β.( ×)题组二教材改编2.下列命题中错误的是( )A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βB.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γD.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β答案 D解析对于D,若平面α⊥平面β,则平面α内的直线可能不垂直于平面β,即与平面β的关系还可以是斜交、平行或在平面β内,其他选项均是正确的.3.在三棱锥P-ABC中,点P在平面ABC中的射影为点O.(1)若PA=PB=PC,则点O是△ABC的________心;(2)若PA⊥PB,PB⊥PC,PC⊥PA,则点O是△ABC的________心.答案(1)外(2)垂解析(1)如图1,连接OA,OB,OC,OP,在Rt△POA,Rt△POB和Rt△POC中,PA=PC=PB,所以OA=OB=OC,即O为△ABC的外心.(2)如图2,延长AO,BO,CO分别交BC,AC,AB于H,D,G.∵PC⊥PA,PB⊥PC,PA∩PB=P,∴PC⊥平面PAB,又AB⊂平面PAB,∴PC⊥AB,∵AB⊥PO,PO∩PC=P,∴AB⊥平面PGC,又CG⊂平面PGC,∴AB⊥CG,即CG为△ABC边AB上的高.同理可证BD,AH分别为△ABC边AC,BC上的高,即O为△ABC的垂心.题组三易错自纠4.(2017·湖南六校联考)已知m和n是两条不同的直线,α和β是两个不重合的平面,下列给出的条件中一定能推出m⊥β的是( )A.α⊥β且m⊂αB.α⊥β且m∥αC.m∥n且n⊥βD.m⊥n且α∥β答案 C解析由线面垂直的判定定理,可知C正确.5.如图所示,在正方体ABCD—A1B1C1D1中,点O,M,N分别是线段BD,DD1,D1C1的中点,则直线OM与AC,MN的位置关系是( )A.与AC,MN均垂直B.与AC垂直,与MN不垂直C.与AC不垂直,与MN垂直D.与AC,MN均不垂直答案 A解析因为DD1⊥平面ABCD,所以AC⊥DD1,又因为AC⊥BD,DD1∩BD=D,所以AC⊥平面BDD1B1,因为OM⊂平面BDD1B1,所以OM⊥AC.设正方体的棱长为2,则OM=1+2=3,MN=1+1=2,ON=1+4=5,所以OM2+MN2=ON2,所以OM⊥MN.故选A.6.如图所示,AB是半圆O的直径,VA垂直于半圆O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )A.MN∥ABB.平面VAC⊥平面VBCC.MN与BC所成的角为45°D.OC⊥平面VAC答案 B解析由题意得BC⊥AC,因为VA⊥平面ABC,BC⊂平面ABC,所以VA⊥BC.因为AC∩VA=A,所以BC⊥平面VAC.因为BC⊂平面VBC,所以平面VAC⊥平面VBC.故选B.【考点突破】考点一、线面垂直的判定与性质【例1】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:(1)CD⊥AE;(2)PD⊥平面ABE.[解析] (1)在四棱锥P-ABCD中,∵PA⊥底面ABCD,CD⊂平面ABCD,∴PA⊥CD,又∵AC⊥CD,且PA∩AC=A,∴CD⊥平面PAC.而AE⊂平面PAC,∴CD⊥AE.(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.∵E是PC的中点,∴AE⊥PC.由(1)知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.而PD⊂平面PCD,∴AE⊥PD.∵PA⊥底面ABCD,AB⊂平面ABCD,∴PA⊥AB.又∵AB⊥AD,且PA∩AD=A,∴AB⊥平面PAD,而PD⊂平面PAD,∴AB⊥PD.又∵AB∩AE=A,∴PD⊥平面ABE.【类题通法】1.证明直线和平面垂直的常用方法有:(1)判定定理;(2)垂直于平面的传递性(a∥b,a⊥α⇒b⊥α);(3)面面平行的性质(a⊥α,α∥β⇒a⊥β);(4)面面垂直的性质.2.证明线面垂直的核心是证线线垂直,而证明线线垂直则需借助线面垂直的性质.因此,判定定理与性质定理的合理转化是证明线面垂直的基本思想. 【对点训练】如图,在三棱锥A BCD 中,AB ⊥平面BCD ,CD ⊥BD . (1)求证:CD ⊥平面ABD ;(2)若AB =BD =CD =1,M 为AD 中点,求三棱锥A MBC 的体积.[解析] (1)因为AB ⊥平面BCD ,CD ⊂平面BCD , 所以AB ⊥CD .又因为CD ⊥BD ,AB ∩BD =B ,AB ⊂平面ABD ,BD ⊂平面ABD ,所以CD ⊥平面ABD .(2)由AB ⊥平面BCD ,得AB ⊥BD . 又AB =BD =1,所以S △ABD =12×12=12.因为M 是AD 的中点,所以S △ABM =12S △ABD =14.根据(1)知,CD ⊥平面ABD , 则三棱锥C ABM 的高h =CD =1, 故V A MBC =V C ABM =13S △ABM ·h =112.考点二、面面垂直的判定与性质【例2】如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD . (1)证明:平面AEC ⊥平面BED ;(2)若∠ABC =120°,AE ⊥EC ,三棱锥E ACD 的体积为63,求该三棱锥的侧面积.[解析] (1)因为四边形ABCD 为菱形,所以AC ⊥BD . 因为BE ⊥平面ABCD ,所以AC ⊥BE .故AC ⊥平面BED . 又AC ⊂平面AEC , 所以平面AEC ⊥平面BED . (2)设AB =x ,在菱形ABCD 中, 由∠ABC =120°,可得AG =GC =32x ,GB =GD =x 2. 因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =32x . 由BE ⊥平面ABCD ,知△EBG 为直角三角形, 可得BE =22x . 由已知得,三棱锥E ACD 的体积V 三棱锥E ACD =13×12·AC ·GD ·BE =624x 3=63, 故x =2.从而可得AE =EC =ED = 6.所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为 5. 故三棱锥E ACD 的侧面积为3+2 5. 【类题通法】1.面面垂直的证明的两种思路:(1)用面面垂直的判定定理,即先证明其中一个平面经过另一个平面的一条垂线; (2)用面面垂直的定义,即证明两个平面所成的二面角是直二面角,把证明面面垂直的问题转化为证明平面角为直角的问题.2.垂直问题的转化关系:【对点训练】如图,在四棱锥P -ABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°. (1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,∠APD =90°,且四棱锥P -ABCD 的体积为83,求该四棱锥的侧面积.[解析] (1)由已知∠BAP =∠CDP =90°,得AB ⊥PA ,CD ⊥PD . 由于AB ∥CD ,故AB ⊥PD .又PA ∩PD =P ,PA ,PD ⊂平面PAD ,从而AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2)如图,在平面PAD 内作PE ⊥AD ,垂足为E .由(1)知,AB ⊥平面PAD ,故AB ⊥PE ,又AB ∩AD =A ,可得PE ⊥平面ABCD . 设AB =x ,则由已知可得AD =2x ,PE =22x , 故四棱锥P -ABCD 的体积V P -ABCD =13AB ·AD ·PE =13x 3.由题设得13x 3=83,故x =2.从而结合已知可得PA =PD =AB =DC =2,AD =BC =22,PB =PC =22, 可得四棱锥P -ABCD 的侧面积为12PA ·PD +12PA ·AB +12PD ·DC +12BC 2sin 60°=6+2 3. 【作业】全品作业本。
江苏省宿迁市高中数学 第12课时 直线和平面垂直的性质

第12课 课题:直线与平面垂直的性质【学习目标】通过直观感知、操作确认、归纳出:一条直线与一个平面内两条相交直线垂直,则这条直线此平面与此平面垂直 【问题情境】1. 直线与平面垂直的性质:如果一条直线垂直一个平面,则这条直线垂直这个平面内的 直线。
2. 直线与平面垂直的性质定理:垂直于同一个平面的两条直线 。
符号语言:3. 如果一条直线和一个平面平行,这条直线上任意一点到这个平面的距离,叫做 。
4. 有关垂直的证题思路:线面垂直⇔线线垂直。
【合作探究】1. 若,,a b a αα⊥⊥∥c ,则b 与c 的位置关系是 。
2. 对于平面α和共面的直线m 、n ,下列命题是真命题的是 。
①若m α⊥,m n ⊥,则n ∥α ②若m ∥α,n ∥α,则n ∥m ③若,m n α⊂∥α,则n ∥m3. 设a 、b 是两条异面直线,下列命题中正确的是 。
(1)有一平面与a,b 都垂直。
(2)有且仅有一条直线与a,b 都垂直。
(3)过直线a 有且仅有一平面与b 平行。
(4)过空间中任一点必可以作一直线与a,b 都相交。
【交流展示】例1. 已知直线//l 平面α,求证:直线l 上各点到平面α的距离相等例2. 已知四棱锥P-ABCD 的底面是矩形,PA ⊥AB,PA ⊥AC,M,N 分别是AB,PC 的中点, (1)证明:BC ⊥面PAB ;(2)求证:MN ⊥AB 。
AP BCD MN例3.已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥, 求证:AD ⊥面SBC .【学以致用】1. 已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,平行则四边形ABCD 一定是 .2.已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1)1//C O 面11AB D ;(2 )1AC ⊥面11AB D .3.如图,已知空间四边形ABCD 的边BC=AC,AD=BD,BE ⊥CD, E 为垂足,作AH ⊥BE 于H , 求证:AH ⊥平面BCDSDCBAD 1ODBAC 1B 1A 1C AB CDEH4. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
直线与平面垂直的判定导学案
2.3.1直线与平面垂直的判定1、认真研读课本6467p p -的内容,完成课前预习,熟记有关知识概念。
2、对不理解的内容和存在的问题先标注,准备课内小组探究,答疑解惑。
【学习目标】1、掌握并会应用直线与平面垂直的定义,理解直线与平面垂直的判定. 2、了解斜线在平面上的射影与直线和平面所成的角。
【预习案】1、直线与平面垂直的定义3、直线与平面所成的角 作出图: 叫做这个平面的斜线; 叫做斜足。
叫做斜线在这个平面上的射影; 叫做这条直线和这个平面所成的角。
范围 ;90︒时,直线与平面 ;0︒时,直线与平面 。
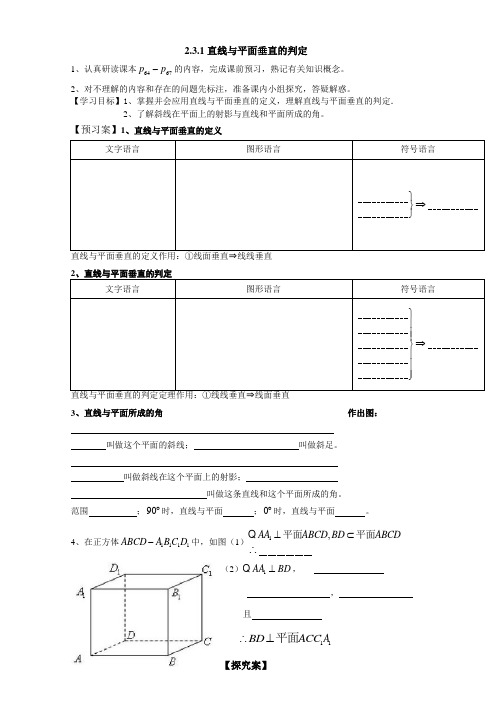
4、在正方体1111ABCD A BC D -中,如图(1)1,AA ABCD BD ABCD⊥⊂∴平面平面(2)1AA BD ⊥ ,,且11A BD ACC ∴⊥平面【探究案】探究一: 如图,已知//,a b a α⊥ ,求证:b a ⊥ 。
探究二: 如图,在三棱锥V-ABC 中 ,VA =VC,AB =BC,K 是AC 的中点。
求证:(1)AC ⊥平面VKB (2)VB ⊥AC【练习案】1已知直线,a b 和平面α,下列推理错误的是( )A 、a a b b αα⊥⎫⇒⊥⎬⊂⎭B 、//a b a b αα⊥⎫⇒⊥⎬⎭C 、//a b a a b ααα⊥⎫⇒⊂⎬⊥⎭或 D 、//a a b b αα⎫⇒⊥⎬⊂⎭2、过ABC 所在的平面α外的一点P ,作PO α⊥,垂足是O ,连接,,PA PB PC 。
(1)若,90PA PB PC C ==∠=︒,则点O 是AB 的 点。
(2)若,PA PB PC ==,则点O 是ABC 的 心。
(3)若,,,PA PB PB PC PC PA ⊥⊥⊥则点O 是ABC 的 心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12课 课题:直线与平面垂直的性质
【学习目标】通过直观感知、操作确认、归纳出:一条直线与一个平面内两条相交直线垂直,则这条直线此平面与此平面垂直 【问题情境】
1. 直线与平面垂直的性质:
如果一条直线垂直一个平面,则这条直线垂直这个平面内的 直线。
2. 直线与平面垂直的性质定理:垂直于同一个平面的两条直线 。
符号语言:
3. 如果一条直线和一个平面平行,这条直线上任意一点到这个平面的距离,叫做 。
4. 有关垂直的证题思路:线面垂直⇔线线垂直。
【合作探究】
1. 若,,a b a αα⊥⊥∥c ,则b 与c 的位置关系是 。
2. 对于平面α和共面的直线m 、n ,下列命题是真命题的是 。
①若m α⊥,m n ⊥,则n ∥α ②若m ∥α,n ∥α,则n ∥m ③若,m n α⊂∥α,则n ∥m
3. 设a 、b 是两条异面直线,下列命题中正确的是 。
(1)有一平面与a,b 都垂直。
(2)有且仅有一条直线与a,b 都垂直。
(3)过直线a 有且仅有一平面与b 平行。
(4)过空间中任一点必可以作一直线与a,b 都相交。
【交流展示】
例1. 已知直线//l 平面α,求证:直线l 上各点到平面α的距离相等
例2. 已知四棱锥P-ABCD 的底面是矩形,PA ⊥AB,PA ⊥AC,M,N 分别是AB,PC 的中点, (1)证明:BC ⊥面PAB ;(2)求证:MN ⊥AB 。
P C
D N
例3.已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥, 求证:AD ⊥面SBC .
【学以致用】
1. 已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,平行则四边形ABCD 一定是 .
2.已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.
求证:(1)1//C O 面11AB D ;
(2 )1
AC ⊥面11AB D .
3.如图,已知空间四边形ABCD 的边BC=AC,AD=BD,BE ⊥CD, E 为垂足,作AH ⊥BE 于H , 求证:AH ⊥平面BCD
S
D
C
B
A
D 1
O
D
B
A
C 1
B 1
A 1
C A
B
C
D E
H
4. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,
AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点P到平面PBC的距离。
参考答案
1.菱形
2. 证明:(1)连接A1C1,设A1C1∩B1D1=O1,连接AO1,
∵ABCD﹣A1B1C1D1是正方体,
∴A1ACC1是平行四边形,
∴A1C1∥AC且A1C1=AC,
又O1,O分别是A1C1,AC的中点,
∴O1C1∥AO且O1C1=AO,
∴AOC1O是平行四边形,
∴C1O∥AO1,AO1∥面AB1D1,
∴C1O∥面AB1D1;
(2)∵CC1⊥面A1B1C1D1∴CC1⊥B1D1,
又∵A1C1⊥B1D1,∴B1D1⊥面A1C1C,即A1C⊥B1D1,
∵A1B⊥AB1,BC⊥AB1,又A1B∩BC=B,
A1B⊥平面A1BC,又A1C?平面A1BC,
∴A1C⊥AB1,又D1B1∩AB1=B1,
∴A1C⊥面AB1D1
3. 解:如图,取AB中点F,连接CF,DF;
∵BC=AC,AD=BD,∴AB⊥CF,AB⊥DF,CF∩DF=F;
∴AB⊥平面CDF,CD⊂平面CDF;
∴CD⊥AB,CD⊥BE,BE∩AB=B;
∴CD⊥平面ABE,AH⊂平面ABE;
∴CD⊥AH,即AH⊥CD,又AH⊥BE,BE∩CD=E;
∴AH⊥平面BCD.
4. :(1)证明:因为PD⊥平面ABCD,BC平面ABCD,所以PD⊥BC.
由∠BCD=90 0,得CD⊥BC,
又PD DC=D,PD、DC平面PCD,
所以BC⊥平面PCD.
因为PC平面PCD,故PC⊥BC.
(2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等.又点A到平面PBC的距离等于E到平面PBC的距离的2倍.由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,因为PD=DC,PF=FC,所以DF⊥PC,
所以DF⊥平面PBC于F.易知DF=,故点A到平面PBC的距离等于
.。
