弹性模量
弹性模量定义

弹性模量定义弹性模量又名弹性模型,是线性弹性材料的质量特性,可表示材料在受力后所反映的抗变形能力。
它是衡量材料弹性特性的重要参数及材料分析的重要参照,也是力学工程中最常用的参数之一。
弹性模量定义:当外力作用于弹性体时,弹性体可以出现变形并存在有限的应变,此时作用于弹性体的外力称为弹性模量。
弹性模量可以表示为一个定义常数,即外力(N/m2)除以对应的变形量(m),表示为:E=F/u其中,E为弹性模量,单位是N/m2;F为外力,单位是N;u为变形量,单位是m。
弹性模量广泛应用于工程领域,其可以帮助工程师正确估算所选材料的抗变形能力,从而避免材料受外力作用下出现过大变形,从而造成损坏。
不同物质的弹性模量有显著的差异。
从普通的结构材料如水泥,钢筋和木材的弹性模量来看,它们的弹性模量都在几GPa以下,硬塑料的弹性模量介于几GPa到几十GPa之间,而硬质合金的弹性模量可高达九十GPa,晶体的弹性模量可以达到几百GPa。
这些物质之间弹性模量的大小取决于其宏观结构特性,因此,通过改变这些物质的宏观结构参数,可以改变它们的弹性模量。
此外,不同材料的热膨胀系数也会影响弹性模量,热膨胀系数越大,材料越容易受到外力的影响,因此其弹性模量也会变小。
常见材料的热膨胀系数介于0.9×10-6/℃到1.8×10-6/℃之间,而金属材料的热膨胀系数比一般材料高几个数量级,因此在使用金属时需要考虑它的变形量。
最后,由于各种不同材料的特性,弹性模量还受到温度的影响。
当温度升高时,材料的结构变弱,弹性模量会相应降低;相反,当温度降低时,材料的弹性模量会相应增加。
因此,材料在不同温度下应用,其弹性模量也会不同,工程师应根据应用场景来估算材料弹性模量。
总而言之,弹性模量是衡量材料弹性特性的重要参数,它是材料分析和力学工程中最常用的参数之一。
它受到很多因素的影响,因此在使用材料时,要根据应用场景正确估算其弹性模量,以免材料受外力作用而出现过大变形,从而造成损害。
弹性力学中的弹性模量

弹性力学中的弹性模量弹性力学是物理学中的一个重要分支,研究物体在受力作用下的弹性变形和恢复行为。
而弹性模量则是衡量物体弹性变形程度的指标。
本文将介绍弹性模量的定义、计算方法以及应用领域。
一、定义弹性模量(Elastic modulus),又称为杨氏模量或弹性系数,是用来衡量物质在受力后发生弹性变形时的抵抗能力。
它是指物体在受到外力作用下,单位面积内产生的应力与应变之比。
弹性模量用E表示,单位一般为帕斯卡(Pa)。
二、计算方法根据胡克定律,弹性模量可以通过应力和应变的关系得到。
在拉伸应力情况下,弹性模量的计算公式为:E = σ / ε其中,E表示弹性模量,σ表示物体所受拉伸应力,ε表示物体的线性应变。
在压缩应力情况下,弹性模量的计算公式为:E = σ / ε其中,E表示弹性模量,σ表示物体所受压缩应力,ε表示物体的线性应变。
三、应用领域弹性模量广泛应用于各个领域,特别在材料科学和工程领域有着重要的作用。
1. 材料工程:弹性模量是评价材料性能的重要参数之一,可以帮助工程师选择适当的材料。
比如在建筑工程中,选择合适的材料可以确保结构安全,弹性模量的大小决定了材料的刚性和强度。
2. 地质学:在地质学领域,弹性模量可以帮助研究地壳的弹性特性和变形机制,对于地震活动和地质灾害的预测和防范具有重要意义。
3. 机械工程:在机械设计和制造中,弹性模量可以用来计算和预测材料的变形和破坏情况。
它影响着机械零件的耐力和寿命。
4. 生物医学工程:在生物医学工程领域,弹性模量被用来研究和评估人体组织的弹性性质,如骨骼、关节等。
这对于人工器官和假肢的设计和制造具有重要的参考价值。
5. 材料科学:弹性模量还被应用于研究材料的力学性能、疲劳行为、温度和湿度对材料性能的影响等方面。
它对于材料的功能设计和改进起到重要的指导作用。
总结:弹性模量是弹性力学中的重要参数,它是衡量物体抵抗变形的能力的指标。
通过计算弹性模量,我们可以了解材料的刚性和强度,评估结构和材料的性能,为工程和科学研究提供理论和实践基础。
弹性模量

材料的“模量”一般前面要加说明语,如弹性模量、压缩模量、剪切模量、截面模量等。
这些都是与变形有关的一种指标。
杨氏模量(Young's Modulus):杨氏模量就是弹性模量,这是材料力学里的一个概念。
对于线弹性材料有公式σ(正应力)=Eε(正应变)成立,式中σ为正应力,ε为正应变,E为弹性模量,是与材料有关的常数,与材料本身的性质有关。
杨(ThomasYoung1773~1829)在材料力学方面,研究了剪形变,认为剪应力是一种弹性形变。
1807年,提出弹性模量的定义,为此后人称弹性模量为杨氏模量。
钢的杨氏模量大约为2×1011N·m-2,铜的是1.1×1011 N·m-2。
弹性模量(Elastic Modulus)E:弹性模量E是指材料在弹性变形范围内(即在比例极限内),作用于材料上的纵向应力与纵向应变的比例常数。
也常指材料所受应力如拉伸,压缩,弯曲,扭曲,剪切等)与材料产生的相应应变之比。
弹性模量是表征晶体中原子间结合力强弱的物理量,故是组织结构不敏感参数。
在工程上,弹性模量则是材料刚度的度量,是物体变形难易程度的表征。
弹性模量E在比例极限内,应力与材料相应的应变之比。
对于有些材料在弹性范围内应力-应变曲线不符合直线关系的,则可根据需要可以取切线弹性模量、割线弹性模量等人为定义的办法来代替它的弹性模量值。
根据不同的受力情况,分别有相应的拉伸弹性模量modulus of elasticity for tension (杨氏模量)、剪切弹性模量shear modulus of elasticity (刚性模量)、体积弹性模量、压缩弹性模量等。
剪切模量G(Shear Modulus):剪切模量是指剪切应力与剪切应变之比。
剪切模数G=剪切弹性模量G=切变弹性模量G 切变弹性模量G,材料的基本物理特性参数之一,与杨氏(压缩、拉伸)弹性模量E、泊桑比ν并列为材料的三项基本物理特性参数,在材料力学、弹性力学中有广泛的应用。
弹性模量详细介绍
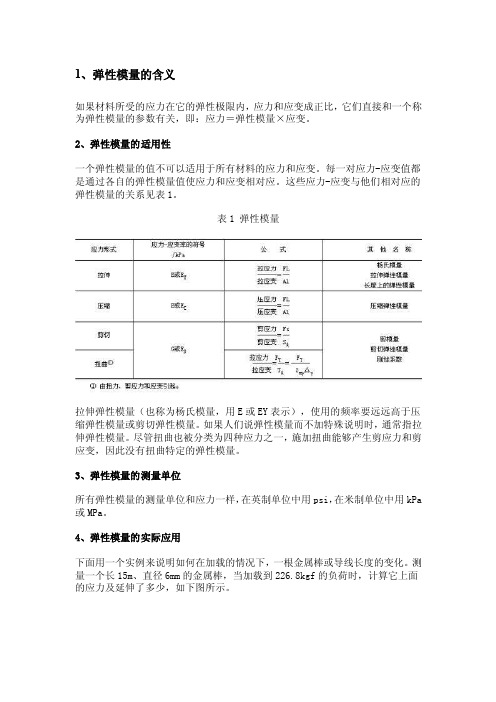
1、弹性模量的含义如果材料所受的应力在它的弹性极限内,应力和应变成正比,它们直接和一个称为弹性模量的参数有关,即:应力=弹性模量×应变。
2、弹性模量的适用性一个弹性模量的值不可以适用于所有材料的应力和应变。
每一对应力-应变值都是通过各自的弹性模量值使应力和应变相对应。
这些应力-应变与他们相对应的弹性模量的关系见表1。
表1 弹性模量拉伸弹性模量(也称为杨氏模量,用E或EY表示),使用的频率要远远高于压缩弹性模量或剪切弹性模量。
如果人们说弹性模量而不加特殊说明时,通常指拉伸弹性模量。
尽管扭曲也被分类为四种应力之一,施加扭曲能够产生剪应力和剪应变,因此没有扭曲特定的弹性模量。
3、弹性模量的测量单位所有弹性模量的测量单位和应力一样,在英制单位中用psi,在米制单位中用kPa 或MPa。
4、弹性模量的实际应用下面用一个实例来说明如何在加载的情况下,一根金属棒或导线长度的变化。
测量一个长15m、直径6mm的金属棒,当加载到226.8kgf的负荷时,计算它上面的应力及延伸了多少,如下图所示。
只要给出应力和应变的数值,就可以用该公式计算出其他的参数。
5、常用金属的弹性模量下图是常用金属的弹性模量。
6、压缩弹性模量和拉伸弹性模量的区别从技术方面讲,压缩弹性模量和拉伸弹性模量都要通过压力和拉力来计算。
然而在工程应用中,对金属材料来说,压缩弹性模量和拉伸弹性模量在应力状态下具有相同的意义。
拉伸试验较压缩试验方便。
因此,一般测定拉伸时的弹性模量并将该数值作为对金属的拉伸和压缩弹性模量。
非金属材料(如砖、石头、混凝土等)拉伸强度低,但压缩强度高,无法进行拉伸试验。
所以这些材料的弹性模量用压缩试验测得。
7、弹性模量的重要性有如下两个原因。
①弹性模量E提供了材料准确的刚性数据,能使人们准确地比较两个物体的刚度,如图8所示。
②弹性模量E还应用于横梁、柱体应力和应变的公式,要进行这些计算必须知道E的数值。
弹性模量决定于材料的原子间的作用力,只与材料成分有关,与组织结构变化无关.各种合金钢的强度悬殊很大,但弹性模量差不多.金属的合金化及热处理方法对弹性模量影响很小.。
弹性模量定义与公式

弹性模量开放分类:基本物理概念工程力学物理学自然科学“弹性模量”的一般定义是:应力除以应变,即弹性变形区的应力-应变曲线的斜率:其中λ是弹性模量,【stress应力】是引起受力区变形的力,【strain应变】是应力引起的变化与物体原始状态的比,通俗的讲对弹性体施加一个外界作用,弹性体会发生形状的改变称为“应变”。
材料在弹性变形阶段,其应力和应变成正比例关系(即胡克定律),其比例系数称为弹性模量。
弹性模量的单位是达因每平方厘米。
“弹性模量”是描述物质弹性的一个物理量,是一个总称,包括“杨氏模量”、“剪切模量”、“体积模量”等。
所以,“弹性模量”和“体积模量”是包含关系。
编辑摘要基本信息编辑信息模块中文名:弹性模量其他外文名:Elastic Modulus 定义:应力除以应变类型:定律定义/弹性模量编辑混凝土弹性模量测定仪图册弹性模量modulusofelasticity,又称弹性系数,杨氏模量。
弹性材料的一种最重要、最具特征的力学性质。
是物体变形难易程度的表征。
用E表示。
定义为理想材料在小形变时应力与相应的应变之比。
根据不同的受力情况,分别有相应的拉伸弹性模量(杨氏模量)、剪切弹性模量(刚性模量)、体积弹性模量等。
它是一个材料常数,表征材料抵抗弹性变形的能力,其数值大小反映该材料弹性变形的难易程度。
对一般材料而言,该值比较稳定,但就高聚物而言则对温度和加载速率等条件的依赖性较明显。
对于有些材料在弹性范围内应力-应变曲线不符合直线关系的,则可根据需要可以取切线弹性模量、割线弹性模量等人为定义的办法来代替它的弹性模量值。
线应变/弹性模量编辑弹性模量图册对一根细杆施加一个拉力F,这个拉力除以杆的截面积S,称为“线应力”,杆的伸长量dL 除以原长L,称为“线应变”。
线应力除以线应变就等于杨氏模量E=( F/S)/(dL/L)剪切应变:对一块弹性体施加一个侧向的力f(通常是摩擦力),弹性体会由方形变成菱形,这个形变的角度a称为“剪切应变”,相应的力f除以受力面积S称为“剪切应力”。
弹性模量概念与公式

弹性模量开放分类:“弹性模量”的一样概念是:应力除以应变,即弹性变形区的应力-应变曲线的斜率:其中λ是弹性模量,【stress 应力】是引发受力区变形的力,【strain应变】是应力引发的转变与物体原始状态的比,通俗的讲对弹性体施加一个外界作用,弹性体会发生形状的改变称为“应变”。
材料在弹性变形时期,其应力和应变成正比例关系(即胡克定律),其比例系数称为弹性模量。
弹性模量的单位是达因每平方厘米。
“弹性模量”是描述物质弹性的一个物理量,是一个总称,包括“杨氏模量”、“剪切模量”、“体积模量”等。
因此,“弹性模量”和“体积模量”是包括关系。
大体信息中文名:弹性模量其他外文名:Elastic Modulus定义:应力除以应变类型:定律目录• 1• 2• 3• 4• 5• 6概念/弹性模量混凝土弹性模量测定仪弹性模量modulusofelasticity,又称弹性系数,杨氏模量。
弹性材料的一种最重要、最具特征的力学性质。
是物体变形难易程度的表征。
用E表示。
定义为理想材料在小形变时应力与相应的应变之比。
根据不同的受力情况,分别有相应的(杨氏模量)、(刚性模量)、等。
它是一个材料常数,表征材料抗击弹性变形的能力,其数值大小反映该材料弹性变形的难易程度。
对一般材料而言,该值比较稳定,但就高聚物而言则对温度和加载速率等条件的依赖性较明显。
对于有些材料在弹性范围内应力-应变曲线不符合直线关系的,则可根据需要可以取切线弹性模量、割线弹性模量等人为定义的办法来代替它的弹性模量值。
线应变/弹性模量弹性模量对一根细杆施加一个拉力F,那个拉力除以杆的截面积S,称为“线应力”,杆的伸长量dL除以原长L,称为“线应变”。
线应力除以线应变就等于E=( F/S)/(dL/L)剪切应变:对一块弹性体施加一个侧向的力f(通常是摩擦力),弹性体会由方形变成菱形,这个形变的角度a称为“剪切应变”,相应的力f除以受力面积S称为“剪切应力”。
弹性模量定义与公式

弹性模量定义与公式弹性模量定义与公式弹性模量开放分类:基本物理概念⼯程⼒学物理学⾃然科学弹性模量”的⼀般定义是:应⼒除以应变,即弹性变形区的应⼒⼀应变曲线的斜率:其中⼊是弹性模量,【stress应⼒】是引起受⼒区变形的⼒,【strain应变】是应⼒引起的变化与物体原始状态的⽐,通俗的讲对弹性体施加⼀个外界作⽤,弹性体会发⽣形状的改变称为应变”材料在弹性变形阶段,其应⼒和应变成正⽐例关系(即胡克定律),其⽐例系数称为弹性模量。
弹性模量的单位是达因每平⽅厘⽶。
弹性模量”是描述物质弹性的⼀个物理量,是⼀个总称,包括杨⽒模量” 剪切模量”、体积模量”等。
所以,弹性模量”和体积模量”是包含关系。
编辑摘要基本信息编辑信息模块中⽂名:弹性模量其他外⽂名:Elastic Modulus定义:应⼒除以应变类型:定律⽬录1定义2线应变3体积应变4意义5说明6单位指标定义/弹性模量编辑弹性模量modulusofelasticity ,⼜称弹性系数,杨⽒模量。
弹性材料的⼀种最重要、最具特征的⼒学性质。
是物体变形难易程度的表征。
⽤E表⽰。
定义为理想材料在⼩形变时应⼒与相应的应变之⽐。
根据不同的受⼒情况,分别有相应的拉伸弹性模量(杨⽒模量)、剪切弹性模量(刚性模量)、体积弹性模量等。
它是⼀个材料常数,表征材料抵抗弹性变形的能⼒,其数值⼤⼩反映该材料弹性变形的难易程度。
对⼀般材料⽽⾔,该值⽐较稳定,但就⾼聚物⽽⾔则对温度和加载速率等条件的依赖性较明显。
对于有些材料在弹性范围内应⼒-应变曲线不符合直线关系的,则可根据需要可以取切线弹性模量、割线弹性模量等⼈为定义的办法来代替它的弹性模量值。
线应变/弹性模量编辑对⼀根细杆施加⼀个拉⼒F,这个拉⼒除以杆的截⾯积S,称为"线应⼒”,杆的伸长量dL除以原长L,称为“线应变”。
线应⼒除以线应变就等于杨⽒模量E=(F/S)/(dL/L)剪切应变:对⼀块弹性体施加⼀个侧向的⼒f (通常是摩擦⼒),弹性体会由⽅形变成菱形,这个形变的⾓度a称为“剪切应变”,相应的⼒f除以受⼒⾯积S称为“剪切应⼒”。
材料的弹性模量

材料的弹性模量
弹性模量,又称弹性常数、线弹性系数或弹性系数,是一种力学参数,它表示了物体
对力作用时变形量和应力大小之间的相关关系,可以用来衡量两种或多种材料之间的弹性
特性和刚度,通常以牛顿每米(N / m2)为单位。
弹性模量是描述物体弹性特性和刚度的重要物理参数,它可以了解物质的无损力学性
能和破坏的机械性能。
它的公式表达为:
E=\frac{\sigma}{\varepsilon},
其中E代表弹性模量;σ(sigma)是应力;δ(delta)是应变。
弹性模量有三种:竖直弹性模量(E1)、侧向弹性模量(E2)和横向弹性模量(E3),它们反映物体在竖直抗压、侧向抗拉或压缩、以及横向抗弯方面的弹性性能,因此,它们
可以用来比较不同材料的刚度和弹性。
不同材料的弹性模量具有不同的值,对它们的估计和测定也有不同的方法。
例如,金
属材料的弹性模量一般通过静态加载实验定值,木质材料的弹性模量可以通过动态法和静
力学加载法定值,而橡胶材料的弹性模量则可以通过热疲劳法定值。
弹性模量对于材料工程学家而言,是材料设计中重要而有用的参数,它可以帮助他们
更准确地预测材料在受到不同外力作用时,所发生的应变和强度变化,从而改善部件的性
能和安全性。
