弹性模量及泊松比计算公式
ANSYS中几个概念解释 杨氏模量、弹性模量、剪切模量、体积模量、强度、刚度,泊松比
（ -dV ）除以原来的体积 V 称为“体积应变”，体积应力除以体积应变就等于体积模量：
p=K （ -dV/V ）
注：液体只有体积模量，其他弹性模量都为零，所以就用弹性模量代指体积模量。
一般弹性体应变都非常小， 即体积的改变量和原来的体积相比， 是一个很小的数。 在这
种情况下，体积相对改变量和密度相对改变量仅仅正负相反，大小是相同的，例如：体积减
弹性模量 E 是在比例极限内， 应力与材料相应的应变之比。 对于有些材料在弹性范围内
应力 - 应变曲线不符合直线关系的，则可根据需要可以取切线弹性模量、割线弹性模量等人
为定义的办法来代替它的弹性模量值。 根据不同的受力情况， 有相应的拉伸弹性模量 （杨氏
模量）、剪切弹性模量（刚性模量） 、体积弹性模量、压缩弹性模量等。
性模量。体积模量是一个比较稳定的材料常数。因为在各向均压下材料的体积总是变小的，
故 K 值永为正值，单位 MPa。体积模量的倒数称为体积柔量。体积模量和拉伸模量、泊松
比之间有关系：
E=3K （ 1-。2 μ）
压缩模量（ CompressionModulus
）——
压缩模量指压应力与压缩应变之比。
储能模量 E' ——
如某种材料的抗拉强度、 抗剪强度是指这种材料在单位面积上能承受的最大拉力、
剪力，
与材料的形状无关。
拉伸强度和拉伸模量的比较： ○1 单位都是 MPa 或 GPa ；○2 拉伸强度是指材料在拉伸过
程中最大可以承受的应力，而拉伸模量是指材料在拉伸时的弹性。
刚度——
刚度（即硬度） 指某种构件或结构抵抗变形的能力， 是衡量材料产生弹性变形难易程度
的指标， 主要指引起单位变形时所需要的应力。 一般是针对构件或结构而言的。 它的大小不
弹性参数测定实验报告(3篇)
第1篇一、实验目的1. 熟悉弹性参数测定的基本原理和方法；2. 掌握测定材料的弹性模量、泊松比等弹性参数的实验步骤；3. 培养实验操作技能和数据分析能力。
二、实验原理弹性参数是描述材料在受力后发生形变与应力之间关系的物理量。
本实验采用拉伸试验方法测定材料的弹性模量和泊松比。
1. 弹性模量（E）：在弹性范围内，应力（σ）与应变成正比，比值称为材料的弹性模量。
其计算公式为：E = σ / ε其中，σ为应力，ε为应变成分。
2. 泊松比（μ）：在弹性范围内，横向应变（εt）与纵向应变（εl）之比称为泊松比。
其计算公式为：μ = εt / εl三、实验仪器与材料1. 仪器：材料试验机、游标卡尺、引伸计、应变仪、万能试验机、数据采集器等；2. 材料：低碳钢拉伸试件、标准试样、引伸计、应变仪等。
四、实验步骤1. 准备工作：将试样安装到材料试验机上，调整好试验机夹具，检查实验设备是否正常；2. 预拉伸：对试样进行预拉伸，以消除试样在安装过程中产生的残余应力；3. 拉伸试验：按照规定的拉伸速率对试样进行拉伸，记录拉伸过程中的应力、应变等数据；4. 数据处理：根据实验数据，计算弹性模量和泊松比；5. 结果分析：对比实验结果与理论值，分析误差产生的原因。
五、实验结果与分析1. 弹性模量（E）的计算结果：E1 = 2.05×105 MPaE2 = 2.00×105 MPaE3 = 2.03×105 MPa平均弹性模量E = (E1 + E2 + E3) / 3 = 2.01×105 MPa2. 泊松比（μ）的计算结果：μ1 = 0.296μ2 = 0.293μ3 = 0.295平均泊松比μ = (μ1 +μ2 + μ3) / 3 = 0.2943. 结果分析：实验结果与理论值较为接近，说明本实验方法能够有效测定材料的弹性参数。
实验过程中，由于试样安装、试验机夹具等因素的影响，导致实验结果存在一定的误差。
材料的泊松比
材料的泊松比
泊松比是材料力学中的一个重要概念，主要用于描述材料在受到外力作用时的变形行为。
泊松比是指在一个材料中，当沿着一个方向施加拉伸力时，材料沿着垂直方向会发生
压缩的程度。
其公式表达如下：
μ= -ε ₂ /ε₁
其中，μ为泊松比，ε₁为沿着拉伸方向的应变，ε ₂为垂直于拉伸方向的应变。
泊
松比的数值一般位于0.1~0.5之间，具体数值取决于材料的种类和材料内部微观结构。
泊松比的值越小，说明材料在受力时越难进行压缩变形，具有较好的刚性。
例如，玻璃、石英、陶瓷等材料的泊松比一般较小，具有较好的刚性和硬度。
而泊松比较高的材料，如钢铁、铜、铝等，受力时较容易产生压缩变形，弹性模量较小，具有较好的韧性和延展性。
泊松比的值还与材料的塑性变形有关。
在材料受力过程中，当材料的应力超过材料产
生塑性变形的极限时，材料会发生塑性变形。
塑性变形后，材料的压缩变形会增大，泊松
比也会随之变大。
因此，泊松比在材料塑性变形方面也具有一定的指示意义。
总的来说，泊松比对于材料在受力过程中的变形行为具有重要的指示意义，它不仅反
映了材料的刚塑性特性，还可以用于材料强度和韧性的评价和选择。
当设计和制造材料产
品时，考虑到泊松比的因素，可使产品更加稳定、坚固和耐用。
常用材料弹性模量及泊松比
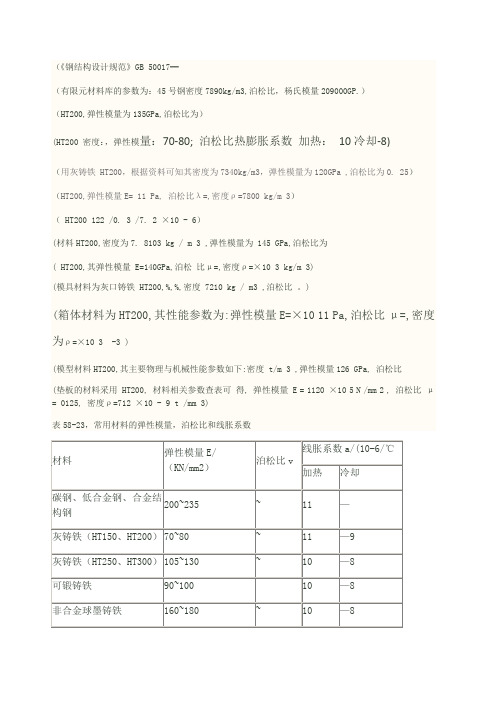
（《钢结构设计规范》GB 50017━（有限元材料库的参数为：45号钢密度7890kg/m3,泊松比，杨氏模量209000GP.）（HT200,弹性模量为135GPa,泊松比为）(HT200 密度：，弹性模量：70-80; 泊松比热膨胀系数加热：10冷却-8)（用灰铸铁 HT200，根据资料可知其密度为7340kg/m3，弹性模量为120GPa ,泊松比为0. 25）（HT200,弹性模量E= 11 Pa, 泊松比λ=,密度ρ=7800 kg/m 3）（ HT200 122 /0. 3 /7. 2 ×10 - 6）(材料HT200,密度为7. 8103 kg / m 3 ,弹性模量为 145 GPa,泊松比为( HT200,其弹性模量 E=140GPa,泊松比μ=,密度ρ=×10 3 kg/m 3)(模具材料为灰口铸铁 HT200,%,%,密度 7210 kg / m3 ,泊松比。
)(箱体材料为HT200,其性能参数为:弹性模量E=×10 11 Pa,泊松比μ=,密度为ρ=×10 3 -3 )(模型材料HT200,其主要物理与机械性能参数如下:密度 t/m 3 ,弹性模量126 GPa, 泊松比(垫板的材料采用 HT200, 材料相关参数查表可得, 弹性模量 E = 1120 ×10 5 N /mm 2 , 泊松比μ= 0125, 密度ρ=712 ×10 - 9 t /mm 3)表58-23，常用材料的弹性模量，泊松比和线胀系数常用弹性模量及泊松比━━━━━━━━━━━━━━━━━━名称弹性模量E 切变模量G 泊松比μ GPa GPa──────────────────镍铬钢 206合金钢 206碳钢 196-206 79铸钢 172-202球墨铸铁 140-154 73-76灰铸铁 113-157 44白口铸铁 113-157 44冷拔纯铜 127 48轧制磷青铜 113 41轧制纯铜 108 39轧制锰青铜 108 39铸铝青铜 103 41冷拔黄铜 89-97 34-36 轧制锌 82 31硬铝合金 70 26轧制铝 68 25-26铅 17 7玻璃 55 22混凝土 14-23纵纹木材横纹木材橡胶电木尼龙可锻铸铁 152拔制铝线 69大理石 55花岗石 48 石灰石 41 尼龙1010夹布酚醛塑料石棉酚醛塑料高压聚乙烯低压聚乙烯聚丙烯。
泊松比弹性模量计算公式
泊松比弹性模量计算公式泊松比弹性模量是材料力学性能的重要参数之一，它描述了材料在受力时的变形特性。
泊松比弹性模量的计算公式是一个重要的工具，可以帮助工程师和科学家预测材料在不同条件下的力学行为。
本文将介绍泊松比弹性模量的计算公式及其应用。
泊松比弹性模量的定义。
泊松比弹性模量是描述材料在受力时横向变形与纵向变形之间的关系的一个参数。
它的定义如下：ν = -ε横向/ε纵向。
其中，ν表示泊松比，ε横向表示材料在受力时横向变形，ε纵向表示材料在受力时纵向变形。
泊松比的取值范围一般在0到0.5之间，其中0表示材料在受力时不会发生横向变形，0.5表示材料在受力时会发生与纵向变形相等的横向变形。
泊松比弹性模量的计算公式。
泊松比弹性模量的计算公式可以通过材料的弹性模量和泊松比来表示，其公式如下：E = 2G(1+ν)。
其中，E表示材料的弹性模量，G表示材料的剪切模量，ν表示泊松比。
通过这个公式，我们可以通过材料的弹性模量和泊松比来计算得到材料的泊松比弹性模量。
这个公式的推导过程涉及到材料力学的一些基本原理，这里不做详细介绍。
泊松比弹性模量的应用。
泊松比弹性模量的计算公式在工程实践中有着广泛的应用。
首先，它可以帮助工程师预测材料在受力时的变形情况，从而指导工程设计和材料选择。
其次，泊松比弹性模量的计算公式也可以用于材料的弹性性能评估和比较。
通过计算得到材料的泊松比弹性模量，可以对不同材料进行性能对比，从而选择最适合的材料来满足工程需求。
此外，泊松比弹性模量的计算公式还可以用于材料的数值模拟和仿真。
在工程设计和科学研究中，通过数值模拟和仿真可以预测材料在不同条件下的力学行为，从而指导实际工程和科研工作。
泊松比弹性模量的计算公式为这些模拟和仿真提供了重要的参数，有助于提高模拟和仿真的准确性和可靠性。
总结。
泊松比弹性模量的计算公式是描述材料力学性能的重要工具，它可以帮助工程师和科学家预测材料在受力时的变形特性。
通过材料的弹性模量和泊松比，我们可以计算得到材料的泊松比弹性模量，从而指导工程设计、材料选择和科学研究。
[新版]各类模量的关系、泊松比的取值
![[新版]各类模量的关系、泊松比的取值](https://img.taocdn.com/s3/m/6d8d53e0bb0d4a7302768e9951e79b8968026828.png)
土的变形模量与压缩模量的关系土的变形模量和压缩模量，是判断土的压缩性和计算地基压缩变形量的重要指标。
为了建立变形模量和压缩模量的关系，在地基设计中，常需测量土的侧压力系数0K 和侧膨胀系数（泊松比）μ。
侧压力系数0K ：是指侧向压力x σ与竖向压力z σ之比值，即：0K ＝x σ/zσ土的侧膨胀系数（泊松比）μ：是指在侧向自由膨胀条件下受压时，侧向膨胀的应变x ε与竖向压缩的应变z ε之比值，即：μ＝x ε/z ε 根据材料力学广义胡克定律推导求得0K 和μ的相互关系：0K ＝μ/(1－μ)或μ=0K /（1＋0K ）土的侧压力系数可由专门仪器测得，但侧膨胀系数不易直接测定，可根据土的侧压力系数，按上式求得。
在土的压密变形阶段，假定土为弹性材料，则可根据材料力学理论，推导出变形模量0E 和压缩模量S E 之间的关系。
数值计算时应用土体的变形模量。
令β＝2121μμ--则0E ＝β×SE 当μ＝0～0.5时，β＝1～0，即0E /S E 的比值在0～1之间变化，即一般0E 小于S E 。
但很多情况下0E /S E 都大于1。
其原因为：一方面是土不是真正的弹性体，并具有结构性；另一方面就是土的结构影响；三是两种试验的要求不同。
注：0E 与S E 之间的关系是理论关系，实际上，由于各种因素的影响，0E 值可能是β×S E 值的几倍，一般来说，土愈坚硬则倍数愈大，而软土的0E 值与β×S E 值比较。
弹性模量E指材料在弹性变形范围内（即在比例极限内），作用于材料上的纵向应力与纵向应变的比例常数。
也常指材料所受应力（如拉伸，压缩，弯曲，扭曲，剪切等）与材料产生的相应应变之比。
对均质土体而言，弹性模量与压缩模量之间有如下关系： ()11(12)S E E μμμ-=+-，或(1)(12)1S E E μμμ+-=-2211S E μμ⎛⎫=- ⎪-⎝⎭上海地区土体的弹性模量一般为压缩模量的3～5倍，即：3~5S E E =变形模量0E土的变形模量是通过现场载荷试验求得的压缩性指标，即在部分侧限条件下，其应力增量与相应的应变增量的比值（土的变形模量是土体在无侧限条件下应力与应变之比值），由于土体不是理想的弹性体，故称为变形模量。
泊松比、弹性模量
泊松比法国数学家 Simeom Denis Poisson 为名在材料的比例极限内，由均匀分布的纵向应力所引起的横向应变与相应的纵向应变之比的绝对值。
比如，一杆受拉伸时，其轴向伸长伴随着横向收缩(反之亦然)，而横向应变 e' 与轴向应变 e 之比称为泊松比 V。
材料的泊松比一般通过试验方法测定。
·泊松比poisson’s ratio 在材料的比例极限内，由均匀分布的纵向应力所引起的横向应变与相应的纵向应变之比的绝对值。
注：超过比例极限时，泊松比随应力变化而变化，实际上已不是泊松比。
此时若记录泊松比，应指出测应力值。
对于各向异性材料，泊松比随施加应力的方向变化。
弹性模量材料在外力作用下发生变形。
当外力较小时，产生弹性变形。
弹性变形是可逆变形，卸载时，变形消失并恢复原状。
在弹性变形范围内，其应力与应变之间保持线性函数关系，即服从虎克(Hooke)定律：式中E为正弹性模量，G为切变模量。
它们之间存在如下关系：弹性模量是表征晶体中原子间结合力强弱的物理量，故是组织结构不敏感参数。
在工程上，弹性模量则是材料刚度的度量。
实际上，理想的弹性体是不存在的，多数工程材料弹性变形时，可能出现加载线与卸载线不重合、应变滞后于应力变化等弹性不完整性。
弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等。
对非晶体，甚至对某些多晶体，在较小的应力时，可能会出现粘弹性现象。
粘弹性变形是既与时间有关，又具有可恢复的弹性变形，即具有弹性和粘性变形量方面特征。
粘弹性变形是高分子材料的重要力学特性之一。
当施加的应力超过弹性极限时，材料发生塑性变形，即产生不可逆的永久变形。
通过塑性变形，不但可使材料获得预期的外形尺寸，而且可使材料内部组织和性能产生变化。
单晶体塑性变形的两个基本方式为滑移和孪生。
滑移和孪生都是切应变，而且只有当外加切应力分量大于晶体的临界分切应力tC时才能开始。
然而，滑移是不均匀切变，孪生为均匀切变。
杨氏模量、弹性模量、剪切模量、体积模量、强度、刚度,泊松比
杨氏模量、弹性模量、剪切模量、体积模量、强度、刚度，泊松比“模量”可以理解为是一种标准量或指标。
材料的“模量”一般前面要加说明语，如弹性模量、压缩模量、剪切模量、截面模量等。
这些都是与变形有关的一种指标。
杨氏模量（Young'sModulus）——杨氏模量就是弹性模量，这是材料力学里的一个概念。
对于线弹性材料有公式σ（正应力）＝Eε（正应变）成立，式中σ为正应力，ε为正应变，E为弹性模量，是与材料有关的常数，与材料本身的性质有关。
杨（ThomasYoung1773～1829）在材料力学方面，研究了剪形变，认为剪应力是一种弹性形变。
1807年，提出弹性模量的定义，为此后人称弹性模量为杨氏模量。
钢的杨氏模量大约为2×1011N∙m-2，C30混凝土是3.00×1010N∙m-2。
弹性模量（ElasticModulus）E——弹性模量E是指材料在弹性变形范围内，作用于材料上的纵向应力与纵向应变的比例常数。
也常指材料所受应力（如拉伸，压缩，弯曲，剪切等）与材料产生的相应应变之比。
弹性模量是表征晶体中原子间结合力强弱的物理量，故是组织结构不敏感参数。
在工程上，弹性模量则是材料刚度的度量，是物体变形难易程度的表征。
弹性模量E是在比例极限内，应力与材料相应的应变之比。
对于有些材料在弹性范围内应力-应变曲线不符合直线关系的，则可根据需要可以取切线弹性模量、割线弹性模量等人为定义的办法来代替它的弹性模量值。
根据不同的受力情况，有相应的拉伸弹性模量（杨氏模量）、剪切弹性模量（刚性模量）、体积弹性模量、压缩弹性模量等。
剪切模量G（ShearModulus）——剪切模量是指剪切应力与剪切应变之比，它表征材料抵抗切应变的能力。
模量大，则表示材料的刚性强。
剪切模数G是材料的基本物理特性参数之一，可表示材料剪切变形的难易程度；与杨氏（压缩、拉伸）弹性模量E、泊桑比ν并列为材料的三项基本物理特性参数，在材料力学、弹性力学中有广泛的应用。
(整理)几个基本常数弹性模量-泊松比-应力应变曲线.
全应力-应变曲线测量岩石的应力应变曲线一般可以有两中试验机：一种是，柔性试验机，使用这种试验机测量时，容易发发生“岩爆”现象，导致试验中不能得到峰值以后的应力应变信息。
另种是，刚性试验机，这种试验机刚度比较高，有“让压”的特点，就不会有“岩爆”现象发生，可以得到全应力-应变曲线用以研究岩石破裂的性质。
刚度矩阵的物理意义：单元刚度矩阵的物理意义，一句话概括说来就是各个节点在广义力的作用下节点的位移变化量。
强度是零件的抗应力程度，反映的是什么时候断裂，破损等刚度反映的是变形大小，就是零件受力后的变形。
刚度矩阵和柔度矩阵的物理意义:一般将刚度矩阵记为[D]，柔度矩阵为[C]，二者互为逆矩阵。
[C]矩阵中任一元素Cij的物理意义为：当微小单元体上仅作用有j方向的单位应力增加，而其他方向无应力增量时，i方向的应变增量分量就等于Cij。
[D]矩阵中任一元素Dij的物理意义为：要使微小单元体只在j方向发生单位应变，而其他方向不允许发生应变，则必须造成某种应力组合，在这种应力组合中，i方向应力分量为Dij。
对于各向异性材料，[D]和[C]都是非对称矩阵，从机理上来说是合理的，然而它给数学模型带来复杂性，也增加了有限元计算的困难。
从工程实用的角度来考虑，往往忽略这种非对称性，而处理为对称矩阵。
物理概念：杨氏模量和泊松比在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E，也叫杨氏模量。
而横向应变与纵向应变之比值称为泊松比μ，也叫横向变性系数，它是反映材料横向变形的弹性常数。
杨氏模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量，它是沿纵向的弹性模量。
1807年因英国医生兼物理学家托马斯·杨(ThomasYoung, 1773-1829) 所得到的结果而命名。
根据胡克定律，在物体的弹性限度内，应力与应变成正比，比值被称为材料的杨氏模量，它是表征材料性质的一个物理量，仅取决于材料本身的物理性质。
岩石变行试验(泊松比及弹性模量)
参考文献： 1．中华人民共和国国家标准 GB/T50266-99 工程岩体试验方法标准，P15。 中国计划出版社。 2．中华人民共和国国土资源部，地发［1986］760 号，岩石物理力学性质试验 规程 DY-17P89。地质出版社。 3．高等学校教材《岩体力学》 。地质出版社。 4．大理石资源地质工作暂行要求及参考资料，国家建筑材料工业局地质公司。
试验二
（一） 目的与意义
岩石变形试验（弹性模量及泊松比）
本试验的目的是测定规则形状的岩石试样在单轴压力作
用下的纵向、横向变形量，绘制应力—应变曲线，从而求得岩石弹性模量和泊松 比，即：岩石弹性模量用 E 表示，泊松比用μ表示。 目前在工程实践中，弹性模量和泊松比是最常用的岩石变形指标。 国内外岩石双指标分类原则，采用 E50（割线模量）作为统一衡量岩石变形 性质的指标。 （一）定义 弹性模量：岩石在压缩或拉伸条件下，压应力或拉应力与纵向应变之比。也 就是岩石在无侧压条件下压应力增量与弹性应变增量的比值。 泊松比：在压缩或拉伸条件下，横向应变与纵向应变之比，也就是岩石在允 许侧向自由膨胀条件下，轴向受压时，轴向应变与侧向应变的比值，又称侧膨胀 系数。 （三）基本原理 是将电阻应变片用粘结剂牢固的贴在试件表面上， 试件受到外力作用，应变 片也发生了变化（拉长或缩短） ，也就是电阻值发生了变化。同过电桥装置，把 机械量——变形转化成电量（电阻值的变化） ，这个变化量经放大器放大后通过 A/D 转换，就可以直接读出应变值。 国际岩石力学学会，实验室和现场标准化委员会建议， 电阻丝长度应大于组 成岩石试件矿物的最大颗粒或斑晶 10 倍以上， 我们采用的是 120 欧姆， 12×4mm 电阻应变片。测量片和补偿片电阻值差值不得超过 0.2 欧姆。 （四）测试方法 测变形的方法很多，有机械测微表法（千分表、百分表） ，杠杆引伸仪法， 电位差传感器法，静态电阻应变仪法。 前三种方法的仪器仪表构造简单轻巧， 使用方便， 但所测得的数据都是岩石 的变形量，而不是应变，需要将变形量换算成应变。它适用于大批量生产任务， 特别是软弱岩石， 具有较大的含水量或饱水状态下的岩石变形试验， 不适合粘贴 电阻应变片。
泊松比模量等
泊松比、模量等1、泊松比法国数学家Simeom Denis Poisson 为名。
在材料的比例极限内，由均匀分布的纵向应力所引起的横向应变与相应的纵向应变之比的绝对值。
比如，一杆受拉伸时，其轴向伸长伴随着横向收缩(反之亦然)，而横向应变e' 与轴向应变 e 之比称为泊松比V。
材料的泊松比一般通过试验方法测定。
可以这样记忆：空气的泊松比为0，水的泊松比为0.5，中间的可以推出。
2、弹性模量英文名称：Elastic Modulus，又称Y oung 's Modulus（杨氏模量）定义：材料在弹性变形阶段，其应力和应变成正比例关系（即符合胡克定律），其比例系数称为弹性模量。
单位：达因每平方厘米。
意义：弹性模量可视为衡量材料产生弹性变形难易程度的指标，其值越大，使材料发生一定弹性变形的应力也越大，即材料刚度越大，亦即在一定应力作用下，发生弹性变形越小。
弹性模量E是指材料在外力作用下产生单位弹性变形所需要的应力。
它是反映材料抵抗弹性变形能力的指标，相当于普通弹簧中的刚度。
说明:又称杨氏模量。
弹性材料的一种最重要、最具特征的力学性质。
是物体弹性t变形难易程度的表征。
用E表示。
定义为理想材料有小形变时应力与相应的应变之比。
E以单位面积上承受的力表示，单位为牛/米^2。
模量的性质依赖于形变的性质。
剪切形变时的模量称为剪切模量，用G表示；压缩形变时的模量称为压缩模量，用K表示。
模量的倒数称为柔量，用J表示。
拉伸试验中得到的屈服极限бb和强度极限бS ，反映了材料对力的作用的承受能力，而延伸率δ 或截面收缩率ψ，反映了材料缩性变形的能力，为了表示材料在弹性范围内抵抗变形的难易程度，在实际工程结构中，材料弹性模量E的意义通常是以零件的刚度体现出来的，这是因为一旦零件按应力设计定型，在弹性变形范围内的服役过程中，是以其所受负荷而产生的变形量来判断其刚度的。
一般按引起单为应变的负荷为该零件的刚度，例如，在拉压构件中其刚度为：式中A0为零件的横截面积。
常用材料弹性模量及泊松比
常用材料弹性模量及泊松比材料的弹性模量和泊松比是工程和材料科学中非常重要的概念。
了解这些数据，就像是拿到了打开材料世界大门的钥匙。
今天，我们就来聊聊这些常用材料的弹性模量及泊松比。
一、弹性模量的定义弹性模量，简单来说，就是材料抵抗变形的能力。
就像一根橡皮筋，拉扯它的时候，它会变长，但放手后又会回到原来的样子。
弹性模量高的材料，比如钢，能承受很大的力而不变形，像个坚韧的战士。
而弹性模量低的材料，比如泡沫，轻轻一捏就会变形，真是脆弱得很。
1.1 拉伸模量拉伸模量是指材料在拉伸时的弹性特性。
这个数值越高，材料在承受拉力时的形变就越小。
钢铁的拉伸模量大约在200 GPa左右，想象一下，它可以承受多大的力量而不屈服。
木材的拉伸模量就低多了，通常在10-20 GPa之间，适合用来建造轻型结构，灵活而富有生命力。
1.2 压缩模量压缩模量则是指材料在压缩时的表现。
像是沙子，放在一只手中，轻轻一握，它就会变形，但放开又会回到原来的样子。
混凝土的压缩模量非常高，约为30 GPa，这是因为它能在建筑中承受巨大的负荷。
与之相对的是泡沫，压缩模量极低，轻轻一捏，立马变形，几乎无法承受重量。
二、泊松比的定义泊松比，听起来有点复杂，其实就是材料在一个方向受力时，另一个方向的变形情况。
比如，当你用力拉伸一根橡皮筋，它不仅会变长，还会变细。
泊松比就是用来描述这种现象的。
2.1 泊松比的计算泊松比的计算方法也很简单，等于材料在一个方向上的应变与另一个方向上的应变的比值。
比如，钢的泊松比大约是0.3，这意味着当它被拉长时，横向的收缩程度是其纵向拉伸的30%。
这就是为什么钢在建筑中被广泛使用，它的各项性能都很均衡。
2.2 不同材料的泊松比每种材料的泊松比都不同，木材的泊松比一般在0.2到0.4之间，稍微有些差异，但在建筑应用中也足够实用。
泡沫的泊松比则接近于0，受力时几乎不收缩，完全是个“厚脸皮”的材料，适合用在包装和保护上。
2.3 泊松比的实际应用泊松比在实际工程中也有很多应用。
电测法测定材料的弹性模量和泊松比
（3）按规定格式写出实验报告。报告中应有各类表格、曲线和原始数据。
（4）试运行 扭动手轮，加载至接近最大荷载值，然后卸载至初荷载以下。观察试验台和 应变仪是否处于正常工作状态。
（5）正式实验 加载至初荷载，记下荷载值以及两个应变仪读数 ε r 、 ε r′ 。以后每增加一 级荷载就记录一次荷载值及相应的应变仪读数 ε r 、 ε r′ ，直至最终荷载。以上步骤重复 3 遍。
三、 预习要求
a) 预习本节实验内容和材料力学书上的相关内容。 b) 阅读并熟悉电测法基本原理和电阻应变仪的使用操作。
四、实验原理和方法
材料在比例极限范围内，应力和应变呈线性关系，即：σ = Eε
比例系数 E 称为材料的弹性模量，可由下式计算，即： E = σ ε
（2－1）
设试件的初始横截面面积为 Ao ，在轴向拉力 F 作用下，横截面上的正应力为：
电测法测定材料的弹性模量和泊松比
弹性模量 E 和泊松比 µ 是各种材料的基本力学参数，测试工作十分重要，测试方法也
很多，如杠杆引伸仪法、电测法、自动检测法，本次实验用的是电测法。
一、 实验目的
在比例极限内，验证虎克定律，用应变电测法测定材料的弹性模量 E 和泊松比 µ 。
二、 实验仪器设备和试样
a) 多功能组合实验台 b) 静态电阻应变仪 c) 游标卡尺 d) 矩形长方体扁试件
（1）测量试件 在试件的工作段上测量横截面尺寸，并计算试件的初始横截面面积 Ao
（2）拟定实验方案
①确定试件允许达到的最大应变值（取材料屈服点σ S 的 70%～80%）及所需的最大载荷值。
②根据初荷载和最大荷载值以及其间至少应有 5 级加载的原则，确定每级荷载的大小。
（3）准备工作 把试件安装在试验台上的夹头内，调整试验台，按图的接线接到两台应变 仪上。
泊松比与弹性模量关系
泊松比与弹性模量关系引言泊松比（Poisson’s ratio）和弹性模量（elastic modulus）是材料力学性质的重要参数，用于描述材料在受到外界力作用时的变形行为。
泊松比和弹性模量之间存在着一定的关系，本文将对这两个参数的概念及其关系进行介绍和解析。
泊松比的定义和计算方法泊松比表示材料在拉伸或压缩过程中，横向收缩或膨胀的程度。
它是一个无量纲的参数，通常用希腊字母ν（nu）表示。
泊松比的计算公式如下：ν = -ε / εl其中，ν为泊松比，ε为材料在拉伸或压缩过程中的横向应变，εl为材料在同一过程中的纵向应变。
泊松比的取值范围一般在0到0.5之间，但也有一些特殊材料的泊松比范围可能大于0.5。
弹性模量的定义和计算方法弹性模量表示材料在受力作用下的变形程度，是一个描绘材料刚性程度的指标，常用符号为E（Elastic modulus）。
弹性模量的计算公式如下：E = σ / ε其中，E为弹性模量，σ为材料的应力，ε为材料的应变。
弹性模量是一个常量，可以通过力学实验或者模拟计算来确定。
泊松比与弹性模量的关系泊松比和弹性模量之间存在一种简单的数学关系，可以通过以下公式来表达：E = 2G(1 + ν)其中，E为弹性模量，G为剪切模量，ν为泊松比。
由上述公式可以看出，泊松比和弹性模量之间的关系是通过剪切模量相互联系的。
剪切模量表示材料在剪切变形时所需要的力和变形之间的比例关系。
这个公式表明，剪切模量对泊松比和弹性模量之间的关系起到了重要的作用。
剪切模量与泊松比的关系剪切模量和泊松比之间的关系可以通过以下公式来表达：G = E / (2(1 + ν))其中，G为剪切模量，E为弹性模量，ν为泊松比。
由上述公式可以看出，剪切模量与泊松比和弹性模量之间的关系也是密切相关的。
剪切模量是材料刚度的另一种度量方式，表示材料抵抗剪切变形的能力。
结论泊松比和弹性模量是描述材料力学性质的重要参数，它们之间存在着一定的关系。
测量金属材料的弹性模量和泊松比--浏览
测量金属材料的弹性模量和泊松比一、实验目的1、测定低碳钢弹性模量E 和泊松比µ。
2、学习掌握电测法的基本原理和电阻应变仪的操作。
3、熟悉测量电桥的应用。
掌握应变片在测量电桥中的各种接线方法。
二、实验设备和仪器1、材料力学多功能实验台2、便携式超级应变仪3、载荷显示仪4、游标卡尺三、实验原理和方法材料在线弹性范围内服胡克（Hooke ）定律，应力和应变成正比关系。
单向拉伸时，其形式为：σ=E ε （式1）式中E 为弹性模量。
在σ-ε曲线上，E 由弹性阶段直线的斜率确定，它表征材料抵抗弹性变形的能力。
E 越大，产生一定变形所需的应力越大。
工程上常把EA 称作杆件材料的抗拉（压）刚度。
E 是弹性元件选材的重要依据，是力学计算中的一个重要参量。
0PL E A Lσ==ε （式2）试件轴向拉伸时，产生纵向伸长，横向收缩。
实验表明在弹性范围内，横向应变ε’与轴向应变ε，二者之比为一常数，其绝对值称为横向变形系数或称为泊松比，用µ来表示，即µ=ε'ε（式3）本实验采用电测法来测量E、µ。
试件采用矩形截面试件，布片方式，如图1。
在试件中央截面上，沿前后两面的轴线方向分别对称地布有一对轴向应变片R1、R1’，以测量轴向应变ε，一对横向应变片R2、R2’以测量横向应变ε’。
图1 拉伸试件及布片图1、测弹性模量E由于实验装置和安装初始状态的不稳定性，拉伸曲线的初始阶段往往是非线性的。
为了尽可能减少测量误差，实验宜从初载P0（P≠0）开始，与P 0对应的应变仪读数εd可预调到零，也可设定一个初读数。
采用增量法，分级加载，分别测量在各相同载荷增量ΔP作用下，产生的应变增量Δε，并求Δε的平均值。
设试件初始横截面面积为A0，又因ε=ΔL/L，则式2可写成PE A =ε 均 （式4）上式即为增量法测E 的计算公式（Δε均为试件实际轴向应变增量的平均值）。
增量法可以验证力与变形之间的线性关系。
各种模量的关系、泊松比的取值
土的变形模量与压缩模量的关系土的变形模量和压缩模量，是判断土的压缩性和计算地基压缩变形量的重要指标。
为了建立变形模量和压缩模量的关系，在地基设计中，常需测量土的侧压力系数0K 和侧膨胀系数（泊松比）μ。
侧压力系数0K ：是指侧向压力x σ与竖向压力z σ之比值，即：0K ＝x σ/z σ 土的侧膨胀系数（泊松比）μ：是指在侧向自由膨胀条件下受压时，侧向膨胀的应变x ε与竖向压缩的应变z ε之比值，即：μ＝x ε/z ε根据材料力学广义胡克定律推导求得0K 和μ的相互关系：0K ＝μ/(1－μ)或μ=0K /（1＋0K ）土的侧压力系数可由专门仪器测得，但侧膨胀系数不易直接测定，可根据土的侧压力系数，按上式求得。
在土的压密变形阶段，假定土为弹性材料，则可根据材料力学理论，推导出变形模量0E 和压缩模量S E 之间的关系。
数值计算时应用土体的变形模量。
令β＝2121μμ--则0E ＝β×S E当μ＝0～0.5时，β＝1～0，即0E /S E 的比值在0～1之间变化，即一般0E 小于S E 。
但很多情况下0E /S E 都大于1。
其原因为：一方面是土不是真正的弹性体，并具有结构性；另一方面就是土的结构影响；三是两种试验的要求不同。
注：0E 与S E 之间的关系是理论关系，实际上，由于各种因素的影响，0E 值可能是β×S E 值的几倍，一般来说，土愈坚硬则倍数愈大，而软土的0E 值与β×S E 值比较。
弹性模量E指材料在弹性变形范围内（即在比例极限内），作用于材料上的纵向应力与纵向应变的比例常数。
也常指材料所受应力（如拉伸，压缩，弯曲，扭曲，剪切等）与材料产生的相应应变之比。
对均质土体而言，弹性模量与压缩模量之间有如下关系：()11(12)S E E μμμ-=+-，或(1)(12)1S E E μμμ+-=-2211S E μμ⎛⎫=- ⎪-⎝⎭上海地区土体的弹性模量一般为压缩模量的3～5倍，即：3~5S E E =变形模量0E土的变形模量是通过现场载荷试验求得的压缩性指标，即在部分侧限条件下，其应力增量与相应的应变增量的比值（土的变形模量是土体在无侧限条件下应力与应变之比值），由于土体不是理想的弹性体，故称为变形模量。
弹性模量E和泊松比
拉伸试验中得到的屈服极限бb和强度极限бS，反映了材料对力的作用的承受能力，而延伸率δ或截面收缩率ψ，反映了材料缩性变行的能力，为了表示材料在弹性范围内抵抗变行的难易程度，在实际工程结构中，材料弹性模量E的意义通常是以零件的刚度体现出来的，这是因为一旦零件按应力设计定型，在弹性变形范围内的服役过程中，是以其所受负荷而产生的变性量来判断其刚度的。
一般按引起单为应变的负荷为该零件的刚度，例如，在拉压构件中其刚度为：式中 A0为零件的横截面积。
由上式可见，要想提高零件的刚度E A0,亦即要减少零件的弹性变形，可选用高弹性模量的材料和适当加大承载的横截面积，刚度的重要性在于它决定了零件服役时稳定性，对细长杆件和薄壁构件尤为重要。
因此，构件的理论分析和设计计算来说，弹性模量E是经常要用到的一个重要力学性能指标。
在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E，也叫杨氏模量。
横向应变与纵向应变之比值称为泊松比µ，也叫横向变性系数，它是反映材料横向变形的弹性常数。
因此金属才料拉伸时弹性模量E地测定是材料力学最主要最基本的一个实验，下面用电测法测定低碳钢弹性模量E和泊松比µ。
(一）(一）试验目的1．1．用电测方法测定低碳钢的弹性模量E及泊松比µ；2．2．验证虎克定律；3．3．掌握电测方法的组桥原理与应用。
(二）(二）试验原理1．测定材料弹性模量E一般采用比例极限内的拉伸试验，材料在比例极限内服从虎克定律，其荷载与变形关系为：（1）若已知载荷ΔP及试件尺寸，只要测得试件伸长ΔL即可得出弹性模量E。
（2）由于本试验采用电测法测量，其反映变形测试的数据为应变增量，即（3）所以（2）成为:（4）式中：ΔP——载荷增量，kN；A0-----试件的横截面面积，cm为了验证力与变形的线性关心，采用增量法逐级加载，分别测量在相同载荷增量ΔP 作用下试件所产生的应变增量Δε。
(整理)几个基本常数弹性模量-泊松比-应力应变曲线.
全应力-应变曲线测量岩石的应力应变曲线一般可以有两中试验机：一种是，柔性试验机，使用这种试验机测量时，容易发发生“岩爆”现象，导致试验中不能得到峰值以后的应力应变信息。
另种是，刚性试验机，这种试验机刚度比较高，有“让压”的特点，就不会有“岩爆”现象发生，可以得到全应力-应变曲线用以研究岩石破裂的性质。
刚度矩阵的物理意义：单元刚度矩阵的物理意义，一句话概括说来就是各个节点在广义力的作用下节点的位移变化量。
强度是零件的抗应力程度，反映的是什么时候断裂，破损等刚度反映的是变形大小，就是零件受力后的变形。
刚度矩阵和柔度矩阵的物理意义:一般将刚度矩阵记为[D]，柔度矩阵为[C]，二者互为逆矩阵。
[C]矩阵中任一元素Cij的物理意义为：当微小单元体上仅作用有j方向的单位应力增加，而其他方向无应力增量时，i方向的应变增量分量就等于Cij。
[D]矩阵中任一元素Dij的物理意义为：要使微小单元体只在j方向发生单位应变，而其他方向不允许发生应变，则必须造成某种应力组合，在这种应力组合中，i方向应力分量为Dij。
对于各向异性材料，[D]和[C]都是非对称矩阵，从机理上来说是合理的，然而它给数学模型带来复杂性，也增加了有限元计算的困难。
从工程实用的角度来考虑，往往忽略这种非对称性，而处理为对称矩阵。
物理概念：杨氏模量和泊松比在弹性范围内大多数材料服从虎克定律，即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E，也叫杨氏模量。
而横向应变与纵向应变之比值称为泊松比μ，也叫横向变性系数，它是反映材料横向变形的弹性常数。
杨氏模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量，它是沿纵向的弹性模量。
1807年因英国医生兼物理学家托马斯·杨(ThomasYoung, 1773-1829) 所得到的结果而命名。
根据胡克定律，在物体的弹性限度内，应力与应变成正比，比值被称为材料的杨氏模量，它是表征材料性质的一个物理量，仅取决于材料本身的物理性质。