模拟电子技术第1章
模拟电子技术第1章PPT课件

多数载流子——自由电子 施主离子
少数载流子—— 空穴
7
8
2. P型半导体
在本征半导体中掺入三价杂质元素,如硼、镓等。
硅原子
+4
空穴
+4
硼原子
+4
8
电子空穴对
空穴
+4 +4
P型半导体
- - --
+3 +4
- - --
- - --
+4 +4
受主离子
多数载流子—— 空穴 少数载流子——自由电子 9
杂质半导体的示意图
(1) 稳定电压UZ ——
在规定的稳压管反向工作电流IZ下UZ,所对应的Iz反min 向工作电u压。
(2) 动态电阻rZ ——
△I
rZ =U /I
rZ愈小,反映稳压管的击穿特性△愈U 陡。
I zmax
(3) 最小稳定工作 电流IZmin——
保证稳压管击穿所对应的电流,若IZ<IZmin则不能稳压。
(4) 最大稳定工作电流IZmax——
17
EW
R
18
(2) 扩散电容CD
当外加正向电压
不同时,PN结两 + 侧堆积的少子的 数量及浓度梯度 也不同,这就相 当电容的充放电 过程。
P区 耗 尽 层 N 区 -
P 区中电子 浓度分布
N 区中空穴 浓度分布
极间电容(结电容)
Ln
Lp
x
电容效应在交流信号作用下才会明显表现出来
18
19
1.2 半导体二极管
30
31
四、稳压二极管
稳压二极管是应用在反向击穿区的特殊二极管
பைடு நூலகம்
第1章—02-半导体二极管-sw

六、发光二极管 发光二极管
将电能转换成光能的特殊半导体器件。 1.定义:将电能转换成光能的特殊半导体器件。 定义: 2.类型 类型 普通发光二极管 红外发光二极管 …… 直流驱动电路 交流驱动电路
3.常用驱动电路: 常用驱动电路:
4.工作原理: 管子加正向电压时 在正向电流激发下, 4.工作原理:当管子加正向电压时,在正向电流激发下, 工作原理 管子发光,属电致发光。 管子发光,属电致发光。 注意:发光二极管在加正向电压时才发光。 注意:发光二极管在加正向电压时才发光。
模拟电子技术基础 第1章 常用半导体器件
电子系 2010年9月 Electronic Department Sep. 2010
第一章 常用半导体器件
1.1、半导体的基础知识 1.1、 1.2、半导体二极管 1.2、 1.3、 1.3、晶体三极管 1.4、 1.4、场效应管
1.2 半导体二极管
一、二极管的组成 二、二极管的伏安特性及电流方程 三、二极管的等效电路 四、二极管的主要参数 五、稳压二极管 六、发光二极管 七、光电二极管 八、其他二极管 九、二极管的应用
ui=0时直流电源作用 时直流电源作用
∆u D U T 根据电流方程,rd = ≈ ∆iD ID
小信号作用 Q越高,rd越小。 越高, 越小。 越高 静态电流
四、二极管的主要参数
• • • • 最大整流电流I 最大整流电流 F:最大平均值 最大反向工作电压U 最大反向工作电压 R:最大瞬时值 反向电流 IR:即IS 最高工作频率f 最高工作频率 M:因PN结有电容效应 结有电容效应 结电容为扩散电容( 与势垒电容( 之和。 结电容为扩散电容(Cd)与势垒电容(Cb)之和。
uL
+
模电课件-第1章-精选文档

直(交)流→交(直)流。
(5)信号发生电路:产生正弦、三角、矩形波等。 (6)直流电源:将交流电转换成不同输出电压和电流的 直流电。
33 MHz
目录
Analog Electronics
1
导言
33 MHz
2 运算放大器 3 二极管及其基本电路 4 晶体三极管及放大电路基础 5 场效应管放大电路 6 模拟集成电路 7 反馈放大电路 8 信号的运算和滤波 9 波形的发生与变换电路 10 直流稳压电源
信号的 信号的 信号的
信号的
提取
传感器 接收器
预处理
隔离、滤波 放大、阻抗 变换
加工
运算、转 换、比较
执行
功率放大 A/D转换
33 MHz
图1.2.1电子信息系统示意图
Analog Electronics
1.2.3
电子信息系统中的模拟电路
信号的 预处理 信号的 加工 信号的 执行
信号的 提取
(1)放大电路:用于信号的电压、电流或功率放大。 (2)滤波电路:用于信号的提取、变换或抗干扰。
Analog Electronics
模拟电子技术基本教程 Fundamentals of Analog Electronics 华成英 主编
33 MHz
Analog Electronics 1. 电子技术的发展简史
电子技术诞生的历史虽短,但深入的领域却是最深最广, 它不仅是现代化社会的重要标志,而且成为人类探索宇宙宏观 世界和微观世界的物质技术基础。 1904年第一只电子器件发明以来,世界电子技术经历了 电子管、晶体管和集成电路等重要发展阶段。
《模拟电子技术》(第3版)课件与教案 第1章
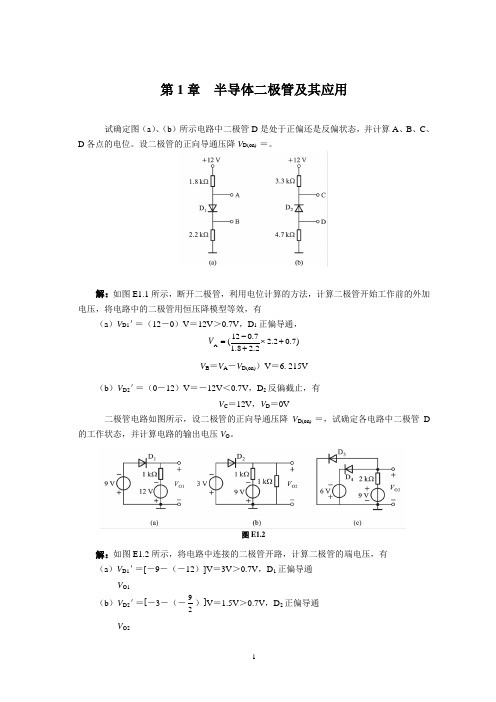
第1章 半导体二极管及其应用试确定图(a )、(b )所示电路中二极管D 是处于正偏还是反偏状态,并计算A 、B 、C 、D 各点的电位。
设二极管的正向导通压降V D(on) =。
解:如图E1.1所示,断开二极管,利用电位计算的方法,计算二极管开始工作前的外加电压,将电路中的二极管用恒压降模型等效,有(a )V D1'=(12-0)V =12V >0.7V ,D 1正偏导通,)7.02.22.28.17.012(A +⨯+-=VV B =V A -V D(on))V =6. 215V(b )V D2'=(0-12)V =-12V <0.7V ,D 2反偏截止,有V C =12V ,V D =0V二极管电路如图所示,设二极管的正向导通压降V D(on) =,试确定各电路中二极管D 的工作状态,并计算电路的输出电压V O 。
解:如图E1.2所示,将电路中连接的二极管开路,计算二极管的端电压,有 (a )V D1'=[-9-(-12)]V =3V >0.7V ,D 1正偏导通V O1(b )V D2'=[-3-(-29)]V =1.5V >0.7V ,D 2正偏导通V O2图E1.2(c)V D3'=9V>0.7V,V D4'=[9-(-6)]V=15V>0.7V,V D4'>V D3',D4首先导通。
D4导通后,V D3''=(0.7-6)V=-5.3V<,D3反偏截止,V O3。
二极管电路如图所示,设二极管是理想的,输入信号v i=10sinωt V,试画出输出信号v O的波形。
图E1.3解:如图E1.3所示电路,二极管的工作状态取决于电路中的输入信号v i的变化。
(a)当v i<0时,D1反偏截止,v O1=0;当v i>0时,D1正偏导通,v O1=v i。
(b)当v i<0时,D2反偏截止,v O2=v i;当v i>0时,D2正偏导通,v O2=0。
(c)当v i<0时,D3正偏导通,v O3=v i;当v i>0时,D3反偏截止,v O3=0。
模拟电子技术第1章 数字电路基础

于其进位规则为“逢十六进一”,故称为十六进制,常用大写字母“H”表示。十六进制按
权展开式为:
n1
(N)16 =
ai 16i
im
式中,ai 为十六进制数的任意一个数码;n 表示整数部分数位,m 表示小数部分数位;下标
16(或 H)表示十六进制数。例如
(5D.6A)H =5×161+13×160+6×16-1+10×16-2
(2)二进制数与十六进制数的相互转换 由表 1-1 可知制数与十六进制数之间
进行转换时通常采用分组等值法。 具体操作以小数点为基准,向左或者向右将二进制数按 4 位一组进行分组(当不足 4 位时,
按整数部分从高位、小数部分从低位的原则予以补 0 处理),然后用对应十六进制数代替各组的 二进制数,即可得等值的十六进制数。反之,将十六进制数的每个数码用相应的 4 位二进制数代 替,并去除高、低位无效的 0,所得结果即为等值二进制数。
1.2.2 编码
利用二进制数表示图形、文字、符号和数字等信息的过程称为编码(Encode),编码的结果 称为代码(Code)。例如,发送邮件时收/发信人的 E-mail、因特网上计算机主机的 IP 地址等, 就是生活中常见的编码实例。
进制数。例如:
(110.01)B =1×22+1×21+0×20+0×2-1+1×2-2
【十六进制】十六进制(Hexadecimal System)是数字电路中另一种常用数制,包含 0~9、A、B、
C、D、E、F 十六个数码,其中 A、B、C、D、E、F 依次表示十进制数 10~15,所以基数为 16。由
(3)十进制数转换为二进制数 十进制数转换为二进制数需要将整数部分和小数部分分别进行转换。通常整数部分采用除 2 反序取余法进行转换,小数部分采用乘 2 顺序取整法进行转换。 具体操作:将给定的十进制整数部分依次除以 2,按反序的原则取余数即为等值二进制数; 十进制小数部分依次乘以 2,按顺序的原则取整数即为等值二进制数。当小数部分不能精确转换 为二进制小数时,可根据精度要求,保留几位小数。 此外,利用二进制数作桥梁,可以方便地将十进制数转换为十六进制数。
精品文档-模拟电子技术(江晓安)(第三版)-第1章

第一章 半导体器件
图 1 – 5 P型半导体的共价键结构
第一章 半导体器件
1.2PN 结
1.2.1 异型半导体接触现象 在P型和N型半导体的交界面两侧, 由于电子和空穴的
浓度相差悬殊, 因而将产生扩散运动。 电子由N区向P区扩 散; 空穴由P区向N区扩散。 由于它们均是带电粒子(离 子), 因而电子由N区向P区扩散的同时, 在交界面N区剩下 不能移动(不参与导电)的带正电的杂质离子; 空穴由P区向 N区扩散的同时, 在交界面P区剩下不能移动(不参与导电) 的带负电的杂质离子, 于是形成了空间电荷区。 在P区和N 区的交界处形成了电场(称为自建场)。 在此电场 作用下, 载流子将作漂移运, 其运动方向正好与扩散运动方 向相反, 阻止扩散运动。 电荷扩散得越多, 电场越强, 因而 漂移运动越强, 对扩散的阻力越大。 当达到平衡时, 扩散运 动的作用与漂移运动的作用相等, 通过界面的载流子总数为 0, 即PN结的电流为0。 此时在PN区交界处形成一个缺 少载流子的高阻区, 我们称为阻挡层(又称为耗尽层)。 上述 过程如图1-6(a)、 (b)所示。
所谓“齐纳”击穿, 是指当PN结两边掺入高浓度的杂 质时, 其阻挡层宽度很小, 即使外加反向电压不太高(一般为 几伏), 在PN结内就可形成很强的电场(可达2×106 V/cm), 将共价键的价电子直接拉出来, 产生电子-空穴对, 使反向电 流急剧增加, 出现击穿现象。
第一章 半导体器件
对硅材料的PN结, 击穿电压UB大于7V时通常是 雪崩击穿, 小于4V时通常是齐纳击穿;UB在4V和7V之间 时两种击穿均有。由于击穿破坏了PN结的单向导电特性, 因而一般使用时应避免出现击穿现象。
CT
dQ dU
S W
第一章 半导体器件
模拟电子技术第一章 习题与答案

第一章习题与答案1.什么是PN结的偏置?PN结正向偏置与反向偏置时各有什么特点?答:二极管(PN结)阳极接电源正极,阴极接电源负极,这种情况称二极管正向偏置,简称正偏,此时二极管处于导通状态,流过二极管电流称作正向电流。
二极管阳极接电源负极,阴极接正极,二极管处于反向偏置,简称反偏,此时二极管处于截止状态,流过二极管电流称为反向饱和电流。
把二极管正向偏置导通、反向偏置截止的这种特性称之为单向导电性。
2.锗二极管与硅二极管的死区电压、正向压降、反向饱和电流各为多少?答:锗管死区电压约为0.1V,硅管死区电压约为0.5V。
硅二极管的正向压降约0.6~0.8 V;锗二极管约0.2~0.3V。
硅管的反向电流比锗管小,硅管约为1uA,锗管可达几百uA。
3.为什么二极管可以当作一个开关来使用?答:二极管在正向电压作用下电阻很小,处于导通状态,相当于一只接通的开关;在反向电压作用下,电阻很大,处于截止状态,如同一只断开的开关。
4.普通二极管与稳压管有何异同?普通二极管有稳压性能吗?答:普通二极管的主要特性是单向导电性,也就是在正向电压的作用下,导通电阻很小;而在反向电压作用下导通电阻极大或无穷大。
稳压二极管的稳压原理:稳压二极管的特点就是加反向电压击穿后,其两端的电压基本保持不变。
而普通二极管反向击穿后就损坏了。
这样,当把稳压管接入电路以后,若由于电源电压发生波动,或其它原因造成电路中各点电压变动时,负载两端的电压将基本保持不变。
因此,普通二极管在未击穿的条件下具有稳压性能。
5.选用二极管时主要考虑哪些参数?这些参数的含义是什么?答:正向电流IF:在额定功率下,允许通过二极管的电流值。
正向电压降VF:二极管通过额定正向电流时,在两极间所产生的电压降。
最大整流电流(平均值)IOM:在半波整流连续工作的情况下,允许的最大半波电流的平均值。
反向击穿电压VB:二极管反向电流急剧增大到出现击穿现象时的反向电压值。
正向反向峰值电压VRM:二极管正常工作时所允许的反向电压峰值。
第1章模拟电子技术(李雅轩)

结。如图1.1.1(b)所示。
在PN结的P区一侧带负电,N区一侧带正电。PN结便 产生了内电场,内电场的方向从N区指向P区。内电场对扩散 运动起到阻碍作用, 电子和空穴的扩散运动随着内电场的加强 而逐步减弱,直至停止。在界面处形成稳定的空间电荷区,如 图1.1.1(b)所示。
第1章 半导体元件及其特征
(五) 实训报告 (1) 整理数据, 填好表格。
(2) 根据测试结果,用方格坐标描绘二极管正、反向特性 曲线和三极管输入、输出特性曲线。
(3) 通过输出特性曲线,在UCE=6 V, IB=60μA的工作点上求 取共发射极直流电流放大系数 和交流电流放大系数β。 (六) 思考题
(1) 如果要测试硅二极管的正向特性,应如何较合理地安 排测试点,为什么?
实表 1.4三极管的输入特性 UBE/V 0 0.10 0.30 0.50 0.55 0.60 0.65 0.70 0.75 0.80
Uce=0V IB/MA
Uce=2V
第1章 半导体元件及其特征 实表1.5 三极管的输出特性
0
0.20
0.50
1
5
10
0 20 40 60 80 100 120
第1章 半导体元件及其特征
量和损坏情况。
(六) 实训报告 (1) 将测得数据进行分析整理, 填入实表1.1。
实表 1.1正、 反向电阻测量值 二极管类型 万用表电阻挡 正向电阻 反向电阻 2AP型 R×100(Ω) R×1K (Ω) 2CP型 R×100(Ω) R×1K (Ω)
1章 半导体元件及其特征
(2) 根据测量结果, 总结出一般晶体二极管正向电阻、 反 向电阻的范围。 (七) 思考题 通过实训, 你能否回答下列问题? (1) 能否用万用表测量大功率三极管? 测量时使用哪一挡, 为什么? (2) 为什么用万用表不同电阻挡测二极管的正向(或反向) 电阻值时,测得的阻值不同? (3) 用万用表测得的晶体二极管的正、反向电阻是直流电 阻还是交流电阻?用万用表R×10(Ω)挡和R×1k(Ω)挡去测量同 一个二极管的正向电阻时,所得的结果是否相同?为什么?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章数字电路基础n数字技术的发展及应用n模拟信号与数字信号n数制n码制n基本逻辑运算n测验1.1 数字技术的发展及应用20世纪90年代开始,整个社会进入数字化、信息化、知识化时代,数字技术与国民经济和社会生活的关系日益密切。
计算机、计算机网络、通信、电视及音像传媒、自动控制、医疗、测量等无一不纳入数字技术并获得较大技术进步。
例:Internet 、程控电话、移动通信、可视电话、会议电视、数字电视、数字相机、VCD 、DVD等等。
数字技术的发展及应用数字通信系统:抗干扰能力强保密性好容量大数字化测量:精度高功能完备具有数控测试功能实现测试自动化智能化计算机:最具代表性的数字系统具有极强的信息处理和控制能力数字设备:精度高、功能完备、智能化数字器件发展概况分立元件40~50s :中小规模集成电路(SSI 、MSI)60s :大规模、超大规模集成电路(LSI 、VLSI)70s :80s : 专用集成电路(ASIC)晶体管逻辑、算术运算、显示器件等存储器、微处理器等可编程逻辑器件PLD1.2 模拟信号与数字信号n模拟信号n数字信号n二值数字信号的两种形式n数字波形及其主要参数n数字信息n习题与答案1. 模拟信号模拟信号: 时间和数值上都是连续变化的物理量正弦波信号三角波信号2. 数字信号数字信号: 时间和数值上都是离散的信号时间上离散---信号只在时间坐标的离散点上发生变化数值上离散---各离散点上的信号数值是量化的(某个最小单位的整倍数)3. 二值数字信号的两种形式电位(平)型:脉冲型:4. 数字波形及其参数除周期T和频率f外,数字波形还有以下主要参数(1)脉冲宽度t w:表示脉冲作用的时间(2)占空比q:表示脉冲宽度占整个周期的比例(2)上升时间t r:从脉冲幅值的10%上升到90%所需要的时间(3)下降时间t f:从脉冲幅值的90%下降到10%所需要的时间数字波形及其参数5. 数字信息字母、字符、数字、图形、影象、声音等都是信息数字信息:最常用的数字信息是一种二值信息,它只有0 、1 两种数值或特征值。
例如:字母A 用ASCII码表示为1000001字符& 用ASCII码表示为0100110数值8 用二进制表示为10000 和1:抽象化了的符号可以表示数值0 和1,例如在二进制数中;可以表示具有二值特征的事物、变量的状态。
如:开关的闭合与断开、条件的出现与不出现、灯的亮与熄灭等;在数字电路中,表示电平的高低1.3 数制n进位计数制的一般表示n二进制n八进制和十六进制n二进制与十进制之间的相互转换n习题与答案1. 进位计数制的一般表示并列表示法: (N)R =(a n-1 a n-2 ······a 1 a 0 . a -1 a -2 ······a -m )R∑−−==1n mi RiiR )R a ((N):多项式表示法式中:m —小数部分位数n —整数部分位数R —基数a i —不同数位的数值,0~R 中的任意一个R i —位权几种常用的进位数制DB B N )375.3(2121202121)011.11()(32101=×+×+×+×+×==−−−DO O N )5.651(8483818281)4.1213()(10123=×+×+×+×+×==−DH H B A AB N )2742(166161116101661616)6()(012012=×+×+×=×+×+×==012108106101)168()(×+×+×==D D N 例如:2. 二进制展开式:mm n n n n B a a a a a a N −−−−−−−−+⋅⋅⋅++++⋅⋅⋅++=222222)(1100112211二进制的多项式形式:1,02a (N)1n mi iiB ∈=∑−−=a 运算规则:逢二进一二进制的形成基于数字系统的构成,实现对性能和成本的综合考虑。
二进制的数符0和1比较容易用具有两个稳定状态的电路或器件来表示。
如:三极管的截止与饱和、电路电压的高低、电流的有无、开关的通断等。
二进制数的运算加:0 + 0 = 00 + 1 = 11 + 0 = 1向高位的进位减:0 -0 = 01 -0 = 11 -1 = 00 -向高位的借位乘:0 ×0 = 00 ×1 = 01 ×0 = 01 ×1 = 1除:0 ÷1 = 01 ÷1 = 1二进制数的运算举例1 0 1+ 1 1 01 0 1 1a. 1 1 . 0 1+ 1 0 1 . 1 11 0 0 1 . 0 0b.1 0 0 1-0 1 1 00 0 1 1c.1 1 0 . 0 1+ 1 0 0 . 1 01 0 1 0 . 1 1d.1 1 0 0×1 0 1 00 0 0 01 1 0 0 0 0 0 0 1 1 0 0 1 1 1 1 0 0 0e.1 0 1 0 11 0 0 0√1 0 1 0 1 0 0 01 0 0 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0f.3. 八进制和十六进制八进制:7,6,5,4,3,2,1,08a (N)1n m i ii O ∈=∑−−=a 十六进制:FE D C B A a ,,,,,,9~061a (N)1n mi iiH ∈=∑−−=八进制和十六进制的基数分别是8和16,并且:8=23,16=24;所以它们与二进制之间具有整倍数的关系。
八、十六进制与二进制间的转换转换方法:(N)B →(N)O 、(N)H将二进制数从小数点开始,分别向左、右按3位或4位分组,不足3位或4位的则需在最高位或最低位补0,最后将每组用对应的八进制数或十六进制数代替。
(257.0554)O =(10101111.0001011011)B =(AF.16C)H例如:八进制:2 5 7 0 5 5 4二进制:0 1 0 1 0 1 1 1 1 . 0 0 0 1 0 1 1 0 1 1 0 0十六进制:A F 1 6 C4. 二进制数与十进制数间的转换(N)B→(N)D :将(N)B写成按权展开的多项式,按十进制规则求各乘积项的积并相加。
(N)D→(N)B :需将整数部分和小数部分分别转换,然后合成。
整数部分:除2取余小数部分:乘2取整十进制数转二进制数实例例:(58.625)D →(N)B整数部分小数部分2 58 0 . 6252 29 ——余0 ×22 14 ——余1 1. 2502 7 ——余0 ×223 ——余1 0. 5002 1 ——余1 ×20 ——余1 1. 000低位高位0.10.100.101所以:(58)D =(111010)B (0.625)D =(0.101)B(58.625)D =(111010.101)B几种进制数之间的对应关系1.4 码制n带符号数的代码表示n数码和字符的代码表示n习题与答案1.4.1 带符号数的代码表示n真值与机器数n原码n反码n补码1. 真值与机器数真值: (N1)B=+1011,(N2)B=-1011机器中,0和1只是数值的表示,无法标示“+”、“-”。
机器数:约定“+”、“-”符号数值化表示为:“0”——“+”“1”——“-”上述N1和N2在机器数中表示为:0 1 0 1 1N11 1 0 1 1N22. 原码构成方式:首位为符号位,“0”—“+”、“1”—“-”,其余各位为数值位例:(N1)B =+10011 (N2)B=-01010(N1)原=010011 (N2)原=101010特点:简单、直观,但是原码的减法运算过程复杂,需要先判断数值大小,再进行运算,最后判断结果的符号位。
整数的原码表示:对n 位整数,N=±N n-1 N n-2······N 1 N 0N 2N 2(N)2N 0Nnn原n≤<−−=<≤例如:N=+1101 (N) 原=01101N=-1101 (N) 原=2n -N=10000-(-1101)=10000+1101=11101小数的原码表示:对m 位小数,N=±0.N -1 N -2······N -mN 1N 1(N)1N 0N原≤<−−=<≤例如:N=+0.1101 (N) 原=0.1101N=-0.1101 (N) 原=1-N=1-(-0.1101)=1+0.1101=1.11012. 反码首位为符号位:“0”—正数、“1”—负数数值部分:正数反码的数值与原码的数值相同负数反码的数值是原码的数值按位求反整数的反码表示:对n 位整数N=±N n-1 N n-2······N 1 N 0N 2N1)2((N)2N 0N n1n n≤<−+−=<≤+反例如:N=+1101 (N) 反=01101N=-1101 (N) 反=(25-1)-N=(100000-1)-1101=11111-1101=10010小数部分的反码表示对m 位小数,N=±0.N -1 N -2······N -mN 1N)2(2(N)1N 0N m≤<−+−=<≤−反例如:N=+0.1101 (N) 反=0.1101N=-0.1101 (N) 反= (2-2-4)+N= (10.0000-0.0001)-0.1101= 1.0010反码运算:运算规则:a. 符号位参加运算,若符号位产生进位,该进位加至和数的最低位—循环进位b. 运算结果中,若符号位为0,即为正数的反码,与原码相同;若符号位为1,则为负数的反码,对结果再求反方得到原码。
反码运算举例N1=0.1100 N2=0.0010(N1+N2)反= N1反+N2反=0.1100+0.0010=0.1110(N1-N2)反= N1反-N2反=0.1100+1.1101=0.10100 . 1 1 0 0+ 1 . 1 1 0 10 . 1 0 1 0= 0.1010,其真值为N1-N2=0.1010所以:(N1-N2)反3. 补码首位为符号位:“0”—正数、“1”—负数数值部分:正数的补码与原码、反码相同负数的补码是原码的数值按位求反再加1整数的补码表示:对n 位整数N=±N n-1 N n-2······N 1 N 0N 21(N)N 2(N)2N 0N n1n n≤<−+=+=<≤+反补例如:N=+1101 (N) 补=01101N=-1101 (N) 补=25-N =100000-1101=10000-1101=10011小数的补码表示对m 位小数,N=±0.N -1 N -2······N -mN 1N22(N)(N)1N 0N m反≤<−+=+=<≤−补例如:N=+0.1101 (N) 补=0.1101N=-0.1101 (N) 补= 2+N= 10.0000-0.1101= 1.0011补码运算:运算规则:a. 符号位参加运算,若符号位产生进位,该进位舍去;b. 运算结果中,若符号位为0,即为正数的补码,与原码相同;若符号位为1,则为负数的补码,要获得原码则应再次求补。
