2018届河北省保定市高三第一次模拟考试文科数学试题Word版含答案
(完整word版)2018-2019高三第一次模拟试题文科数学

高三年级第一次模拟考试60分.在每小题给出的四个选项中,有且合 题目要畚考公式:样本败据x lt 鬲的标准差 尸¥门如一訝+他— 英叩丘为样車屮均数柱体的体积公式Y=*其中/为底!ftl 曲积・h 为海341(1)复数 I ~i = (A) 1+2i (B) 1-2i(C) 2-i (D) 2+i⑵函数的定义域为(A) (-1,2) (B) (0, 2] (C) (0, 2) (D) (-1,2] ⑶ 己知命题p :办I 砒+ llX ,则了为 锥体的体积公式v=*h 乩中$为底面面枳,h 为商 耶的親血祝*休枳公式$=4庆,評It 中月为球的半牲(A) (C)函数|;宀林匚阴的图象可以由函数'尸沁酬的图象 (A) 64 (B) 31 (C) 32 (D) 63(7) 已知某几何体的三视图如图所示,则其表面积为 (A)右+4观(B)「(C) 2 (D) 8一、选择题:本大题共12小题,毎小题5〕 分,共 只有一 项 符(B)(D)(A) (C)向左平移个单位得到JL个单位得到(B)向右平移3个单位得到 向左平移设变量x 、y 满足约束条件 ⑸ (A) 3 (B) 2 (C) 1 (D) 5(D)向右平移个单位得到g+2y —2 鼻(h[2x +工一7冬6则的最小值为(6)等比数列{an }的公比a>1,血,则-血+口 $+他"卜彌=(8) 算法如图,若输入 m=210,n= 119,则输出的n 为 (A) 2 (B) 3 (C) 7 (D) 11(9) 在 中,/恥C 权」,AB=2, AC=3,则 = (A) 10 (B)-10(C) -4 (D) 4(10) 点A 、B 、C D 均在同一球面上,其中 的体积为(11) 已知何m 2 '黑⑴-代2侧集合」「等于D |『工=对止卡(B)卜: (12) 抛物线 的焦点为F,点A 、B 、C 在此抛物线上,点A 坐标为(1,2).若点F 恰为 的重心,则直线 BC 的方程为 (A)龙卄一0 (B): tT '■(C)Ly=0 (D) | It \.■二、填空题:本大题共 4小题,每小题5分,共20分.(13) 班主任为了对本班学生的考试成绩进行分析,从全班 50名同学中按男生、女生用分层 抽样的方法随机地抽取一个容量为 10的样本进行分析•己知抽取的样本中男生人数为 6,则班内女生人数为 ________ .Lif ]町= :—(14) 函数.文+】(X 〉0)的值域是 _________ .(15) 在数列1禺1中,尙=1,如 厂% = 2门丨,则数列的通项 □」= _________ .—7 --- F ------(16) —P 尺的一个顶点P ( 7,12)在双曲线 产 3上,另外两顶点 F1、F2为该双曲线是正三角形,AD 丄平面 AD=2AB=6则该球(D)(C) 卜 j(—Ak 土(D)(A) (B) 15 (C)的左、右焦点,则屮八几的内心的横坐标为 __________ .三、解答题:本大题共 6小题,共70分.解答应写出文字说明、证明过程或演算步骤 (17) (本小题满分12分)在厶ABC 中,角A 、B C 的对边分别为a 、b 、c, A=2B,呦占」5 ' (I ) 求cosC 的值;[c\(II)求的值•(18) (本小题满分12分)某媒体对“男女同龄退休”这一公众关注的问题进行了民意调查, 右表是在某单位得到的数据(人数)•(I )能否有90%以上的把握认为对这一问题的看法与性别有关?(II)从反对“男女同龄退休”的甲、 乙等6名男士中选出2人进行陈述,求甲、乙至少有- 人被选出的概率.反对 合计|男 5 6 H 1 女II1 3 "14 合计 16925(19) (本小题满分12分)如图,在三棱柱.A 尅匚 "Q 中,CC1丄底面ABC 底面是边长为2的正三角形,M N 、G 分别是棱CC1 AB, BC 的中点. (I ) 求证:CN//平面AMB1 (II)若X 严2迄,求证:平面AMG.(20) (本小题满分12 分)X'设函数:「—L(I )当a=0时,求曲线在点(1, f(1))处的切线 方程;P(K 2^k) 0.25 Od U 0J0 kL323 2.072 2.706__ ,讯耐一比严 ____(a+附:(II )讨论f(x)的单调性•(21) (本小题满分12分)中心在原点0,焦点F1、F2在x 轴上的椭圆E 经过点C(2, 2),且 ―二◎土::(I) 求椭圆E 的方程;(II) 垂直于0C 的直线I 与椭圆E 交于A B 两点,当以AB 为直径的圆P 与y 轴相切时,求 直线I 的方程和圆P 的方程•请考生在第(22)、( 23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分 •作答时用2B 铅笔在答题卡上把所选题目对应的题号涂黑 •(22) (本小题满分10分)选修4-1:几何证明选讲如图,AB 是圆0的直径,以B 为圆心的圆B 与圆0的一个交点为P.过点A 作直线交圆Q 于 点交圆B 于点M N. (I )求证:QM=QNi110(II)设圆0的半径为2,圆B 的半径为1,当AM= 时,求MN 的长.(23) (本小题满分10分)选修4-4:坐标系与参数 方程 以直角坐标系的原点 O 为极点,x 轴正半轴为极轴,.已知直线I 的参数方程为 (t 为参数,(I )求曲线C 的直角坐标方程;(II)设直线I 与曲线C 相交于A B 两点,当a 变化时,求|AB|的最小值.(24) (本小题满分10分)选修4-5:不等式选讲 设曲线C 的极坐标方程为2cos 0 L朋& *并在两种坐标系中取相同的长度单位(I) 求不等式的解集S;(II) 若关于x不等式应总=1我=;『;:纂釧有解,求参数t的取值范围(18) 解: 由此可知,有90%的把握认为对这一问题的看法与性别有关.…5分(H)记反对“男女同龄退休”的6男士为ai , i = 1, 2,…,6,其中甲、乙分别为a2,从中选出2人的不同情形为: a1a2, a1a3, a1a4, a1a5, a1a6, a2a3, a2a4, a2a5 , a2a6, a3a4, a3a5, a3a6 , a4a5, a4a6, a5a6,…9分共15种可能,其中甲、乙至少有1人的情形有9种,93 所求概率为P = .…12分(19)解:(I)设 AB1的中点为 P ,连结NP 、MP1 1•/ CM^ — A1 , NP^— A1 , • CM^ NP,2 2文科数学参考答案 一、 选择题: A 卷: ADCDC B 卷: BCDAB 二、 填空题: (13) 20 三、 解答题: (17)解:DACB ADDCAB(14) BB CA(-1,1)(15) n2(16) 1(I): B =(0,亍),••• cosB = 1— s in 2B =•/ A = 2B ,「.4si nA = 2si nBcosB = , cosA = cos2B = 1 — 2si n2B = 5 , ••• cosC = cos[ —(A + B)] = — cos(A + B) = si nAsi nB — cosAcosB =— 2.525 'sinC =1 — cos2C=11 .525 ,根据由正弦定理,c si nC 11b sinB 5…12分(I) K2= 25 X (5 X 3— 6 X11)216 X 9X 11 X 142.932 > 2.706 a1 ,• CNPK是平行四边形,• CN// MP•/ CN平面AMB1 MP平面AMB1 • CN//平面AMB1 …4分(n)v cc 仏平面 ABC •••平面 CC1B1E L 平面 ABC , •/ AG 丄 BC, • AGL 平面 CC1B1B • B1M L AG •/ CC1 丄平面 ABC 平面 A1B1C1 //平面 ABC •- CC L AC, CC1 丄 B1C1 ,在 Rt △ MCA 中 , AM k CM 即 AC2= 6. 同理,B1M=6.•/ BB1/ CC1, • BB1 丄平面 ABC •- BB1 丄 AB, • AB1= B1B2+ AB2= C1C2+ AB2= 2.3 , • AM2+ B1M2= AB2, • B1ML AM 又 AG A AM= A , • B1ML 平面 AMG (20)解:, , x2 x(x — 2) (I)当 a = 0 时,f(x) = , f (x)=—亠exex1 1f(i) =T ,f (i) =-^,曲线y = f(x)在点(1 , f(1))处的切线方程为(2x — a)ex — (x2 — ax 土 a)ex e2x(1 )若 a = 2,贝U f (x) w 0 , f(x)在(一a , +s )单调递减. …7 分(2 )若 a v 2,贝 U…10分 …12分1y =肓(x — 1) +(x — 2)(x — a)exA Bf (x)当x€ ( —a , a)或x€ (2 , +a )时,f (x) v 0,当x € (a , 2)时,f (x) > 0 , 此时f(x)在(—a , a)和(2 , +a )单调递减,在(a , 2)单调递增.(3)若a> 2,贝U当x€ ( —a , 2)或x€ (a , +a )时,f (x) v 0,当x € (2 , a)时,f (x) >0 , 此时f(x)在(—a , 2)和(a , +a )单调递减,在(2 , a)单调递增. …12分x2 y2(21)解:(I)设椭圆E的方程为02+ b2 = 1 (a>b> 0),贝y a2+ b2记c= ,a2—b2 ,不妨设F1( — c , 0) , F2(c , 0),则C f1= ( —c—2, —2) , C f2= (c —2, —2),则C f1 • C f2= 8 —c2 = 2 , c2 = 6,即a2 —b2= 6.由①、②得a2= 12, b2= 6. 当m= 3时,直线I 方程为y =— x + 3, 此时,x1 + x2 = 4,圆心为(2 , 1),半径为2,圆P 的方程为(x — 2)2 + (y — 1)2 = 4; 同理,当 m=— 3时,直线I 方程为y = — x — 3,圆P 的方程为(x + 2)2 + (y + 1)2 = 4. …12分 (22)解:(I)连结 BM BN BQ BP. •/ B 为小圆的圆心,••• BM= BN 又••• AB 为大圆的直径,• BQL MN , •- QM= QN …4 分 (n)v AB 为大圆的直径,•/ APB= 90 , • AP 为圆B 的切线,• AP2= AM- AN …6分 由已知 AB= 4, PB= 1 , AP2= AB2- PB2= 15,所以曲线C 的直角坐标方程为 y2= 2x .(n)将直线l 的参数方程代入 y2 = 2x ,得t2sin2 a — 2tcos a — 1= 0.所以椭圆E 的方程为 x2 y2 i2+ 6 = 1. (也可通过2a = iCFlI + |C ?2|求出a ) (n)依题意,直线 0C 斜率为1,由此设直线I 的方程为y = — X + m 代入椭圆 E 方程,得 3x2 — 4m 灶2m2- 12= 0. 由△= 16m2- 12(2m2 — 12) = 8(18 — m2),得 m2< 18. 4m 2m2— 12 记 A(x1 , y1)、B(x2 , y2),贝U x1 + x2=^ , x1x2 = -—. 3 3 x1 + x2 圆P 的圆心为(一_, y1 + y2 2 ),半径r = 当圆P 与y 轴相切时, x1 + x2 r = 1 2 1, 2x1x2 = (x1 + x2)2 4 2(2m2 — 12)= 3 = 4m2 —,m2= 9v 18. …10分 (I)由 2cos 0 p = sinr v ,得(p sin 0 )2 = 2 p cos 0, …6分 7 6设A、B两点对应的参数分别为t1、t2,则4C0S2 a 4 2 + = ------------------------ sin4 a sin2 a sin2 a当a =—亍时,|AB|取最小值2 .…10分 (24)解:—x + 3, x v — 3,(I) f(x) = — 3x — 3,— 3<x < 0,x — 3, x >0.如图,函数y = f(x)的图象与直线 y = 7相交于横坐标为 x1 =— 4,x2 = 10的两点, 由此得 S = [ — 4, 10].\ :I…6分(n)由(I )知,f (x )的最小值为一3,则不等式 f(x) + |2t —3| < 0有解必须且只需—3 + |2t — 3| < 0,解得0W t < 3,所以t 的取值范围是[0 , 3]. t1 + t2 = 2C0S a sin2 at1t2 sin2 a :.|AB| = |t1 - t2| = (t1 + t2)2 - 4t1t2 …10分。
2018届河北省模拟试题(一)数学(文)试卷(含答案)

2018年河北省衡水金卷普通高等学校招生全国统一考试模拟试题(一)文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2|20M x x x =-≤,{}|3N x N x =∈<,则M N =I ( ) A .{}1,2B .{}0,1,2C .{}0,1,2,3D .{}1,2,32.若sin cos 0θθ⋅<,tan 0sin θθ>,则角θ是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角3.已知复数11z i =-,22z a i =+(其中i 为虚数单位,a R ∈),若12z z ⋅a 的值为( ) A .1B .1-C .1±D .04.已知向量(4sin ,1cos )a αα=-r ,(1,2)b =-r,若2a b ⋅=-r r ,则22sin cos 2sin cos αααα=-( )A .1B .1-C .27-D .12-5.已知函数()f x 是定义在R 上的偶函数,且()f x 在区间(0,)+∞上单调递增,记21(log )5a f =-,0.5(2)b f -=-,4(log 9)c f =,则a ,b ,c 的大小关系为( )A .b c a <<B .a b c <<C .c a b <<D .b a c <<6.《九章算术》卷第六《均输》中,有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何?”若将这五人从上到下分别记为甲、乙、丙、丁、戊,且五人所得依次成等差数列,则乙与丙两人共分得( ) A .83钱 B .72钱 C .136钱 D .3钱7.已知双曲线C :22221x y a b-=(0a >,0b >)的左右焦点分别为1F ,2F ,双曲线C 与圆222x y c +=(222c a b =+)在第一象限交于点A ,且12||3||AF AF =,则双曲线C 的离心率是( ) A .31+B .21+C .3D .28.已知一几何体的正视图、侧视图如图所示,则该几何体的俯视图不可能是( )9.定义运算*a b 为执行如图所示的程序框图输出的S 值,则23231313(sin )*(cos )2*(log 3log 4)1212ππ+⋅的值为( )A .174B .52124+C .2sin412π+ D .522sin212π+10.已知函数2()f x x ax b =++有两个零点1x ,2x ,且满足110x -<<,201x <<,则22b a -+的取值范围为( )A .2(2,)3--B .1(1,)3--C .11(,)23-D .1(1,)3-11.已知抛物线C :28y x =的焦点为F ,准线为l ,过点F 作直线PQ 分别交抛物线C 与直线l 于点P ,Q (如图所示),若||1||3PF QF =,则||FQ =( )A .83B .4C .8D .1212.当0x >时,函数()y k x a =-(1k >)的图象总在曲线2x xy e=的上方,则实数a 的最大整数值为( ) A .1-B .2-C .3-D .0第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.四张扑克牌上分别写有“战”“狼”“2”“火”这四个文字,则随机从这四张牌中抽取两张,恰好抽中的两张牌能拼成“战狼”二字的概率为 .14.如图,在三棱柱111ABC A B C -中,1CC ⊥底面ABC ,D 是AB 的中点,90ACB ∠=︒,1AC BC CC ==,过点D 、C 作截面交1BB 于点E ,若点E 恰好是1BB 的中点,则直线1AC 与DE所成角的余弦值为 .15.已知自主招生考试中,甲、乙、丙三人都恰好报考了清华大学、北京大学中的某一所大学,三人分别给出了以下说法:甲说:“我报考了清华大学,乙也报考了清华大学,丙报考了北京大学.” 乙说:“我报考了清华大学,甲说得不完全对.” 丙说:“我报考了北京大学,乙说得对.”已知甲、乙、丙三人中恰好有1人说得不对,则报考了北京大学的是 .16.已知数列{}n a 的前n 项和为n S ,且满足11a =,22a =,121n n n S a a +++=-(*n N ∈),记121(1)(1)n n n n a b a a +++=--,数列{}n b 的前n 项和为n T ,若对*n N ∀∈,n k T >恒成立,则k 的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,且满足222(2)()2cos a c a b c abc C --+=. (1)求角B 的大小;(2)若ABC ∆的面积为3,2b =,求ABC ∆的周长.18.为了弘扬民族文化,某中学举行了“我爱国学,传诵经典”考试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.(1)若该所中学共有2000名学生,试利用样本估计全校这次考试中优秀生人数;(2)(i )试估计这次参加考试的学生的平均成绩(同一组数据用该组区间的中点值作代表); (ii )若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人赠送一套国学经典学籍,试求恰好抽中2名优秀生的概率.19.如图,直角梯形ABCD 与梯形EFCD 全等,其中////AB CD EF ,112AD AB CD ===,且ED ⊥平面ABCD ,点G 是CD 的中点.(1)求证:平面//BCF 平面AGE ; (2)求平面BCF 与平面AGE 的距离.20.已知椭圆C :22221(0)x y a b a b +=>>的左右焦点分别为1F ,2F ,离心率12e =,短轴长为23.(1)求椭圆C 的标准方程;(2)过2F 的直线l 与椭圆C 交于不同的两点A ,B ,则1F AB ∆的面积是否存在最大值?若存在,求出这个最大值及直线l 的方程;若不存在,请说明理由.21.已知函数()xf x ax be =-,且函数()f x 的图象在点(0,(0))f 处的切线斜率为1a -. (1)求b 的值,并求函数()f x 的最值; (2)当[]1,1a e ∈+时,求证:()f x x ≤.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知直线l的参数方程为1,22x y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为4cos ρθ=,直线l 与圆C 交于A ,B 两点.(1)求圆C 的参数方程和直线l 的普通方程; (2)求AOB ∆的面积. 23.选修4-5:不等式选讲已知函数()|21||1|f x x x =-++. (1)解不等式()3f x ≤;(2)若函数()()|1|g x f x x =++,不等式()|1|g x k ≤-有解,求实数k 的取值范围.2018年普通高等学校招生全国统一考试模拟试题文数(一)答案一、选择题1-5:BDCAA 6-10:CADAA 11、12:CA二、填空题13.16甲、丙 16.[1,)+∞三、解答题17.解:(1)∵222(2)()2cos a c a b c abc C --+=,∴222(2)cos 2a c b a c b C ac+--⨯=, ∴(2)cos cos a c B b C -=,由正弦定理,得2sin cos sin cos sin cos A B C B B C -=, ∴2sin cos sin()sin A B B C A =+=,∵sin 0A ≠,∴60B =︒.(2)∵1sin 2ABC S ac B ∆== ∴4ac =,由余弦定理,得2222cos60b a c ac =+-︒2()3a c ac =+-, 即216()a c =+, ∴4a c +=,∴ABC ∆的周长为6a b c ++=.18.解:(1)由直方图可知,样本中数据落在[]80,100的频率为0.20.10.3+=, 则估计全校这次考试中优秀生人数为20000.3600⨯=. (2)(i )设样本数据的平均数为x ,则450.05550.15650.2750.3850.2950.172.5x =⨯+⨯+⨯+⨯+⨯+⨯=, 则估计所有参加考试的学生的平均成绩为72.5.(ii )由分层抽样知识可知,成绩在[70,80),[80,90),[]90,100间分别抽取了3人,2人,1人. 记成绩在[70,80)的3人为a ,b ,c ,成绩在[80,90)的2人为d ,e ,成绩在[]90,100的1人为f , 则从这6人中抽取3人的所有可能结果有(,,)a b c ,(,,)a b d ,(,,)a b e ,(,,)a b f ,(,,)a c d ,(,,)a c e ,(,,)a c f ,(,,)a d e ,(,,)a d f ,(,,)a e f ,(,,)b c d ,(,,)b c e ,(,,)b c f ,(,,)b d e ,(,,)b d f ,(,,)b e f ,(,,)c d e ,(,,)c d f ,(,,)c e f ,(,,)d e f 共20种,其中恰好抽中2名优秀生的结果有(,,)a d e ,(,,)b d e ,(,,)c d e ,(,,)a d f ,(,,)b d f ,(,,)c d f ,(,,)a e f ,(,,)b e f ,(,,)c e f 共9种,所以恰好抽中2名优秀生的概率为920P =. 19.解:(1)∵//AB CD ,12AB CD =,G 是CD 的中点, ∴四边形ABCG 为平行四边形,∴//BC AG , 又∵AG ⊂平面AEG ,BC ⊄平面AEG ,∴//BC 平面AEG ,∵直角梯形ABCD 与梯形EFCD 全等,////EF CD AB , ∴EF AB =,∴四边形ABFE 为平行四边形, ∴//BF AE ,又∵AE ⊂平面AEG ,BF ⊄平面AEG , ∴//BF 平面AEG , ∵BF BC B =I ,∴平面BCF //平面AGE .(2)设点C 到平面AGE 的距离为d ,易知AE EG AG ===由C AGE E ACG V V --=, 得21111sin 603232AE d CG AD DE ⨯⨯⨯︒⨯=⨯⨯⨯⨯,即2sin 603CG AD DE d AE ⨯⨯==⨯︒, ∵平面//BCF 平面AGE , ∴平面BCF 与平面AGE20.解:(1)根据题意,得2221,2,b c a a b c ⎧=⎪⎪=⎨⎪⎪=+⎩解得24a =,23b =,21c =,∴椭圆C 的标准方程为22143x y +=. (2)设11(,)A x y ,22(,)B x y ,不妨设10y >,20y <, 由题知,直线l 的斜率不为零,可设直线l 的方程为1x my =+,由221,1,43x my x y =+⎧⎪⎨+=⎪⎩得22(34)690m y my ++-=,则122634m y y m +=-+,122934y y m =-+,∴112121||()2F ABS F F y y ∆=-=,t =,可知1t ≥,则221m t =-,∴1212121313F AB t S t t t∆==++, 令1()3f t t t =+,则21'()3f t t=-,当1t ≥时,'()0f t >,即()f t 在区间[1,)+∞上单调递增, ∴()(1)4f t f ≥=,∴13F AB S ∆≤,即当1t =,0m =时,1F AB ∆的面积取得最大值3, 此时直线l 的方程为1x =.21.解:(1)由题得,'()xf x a be =-, 根据题意,得'(0)1f a b a =-=-,∴1b =, ∴'()xf x a e =-.当0a ≤时,'()0f x <,()f x 在R 上单调递减,()f x 没有最值; 当0a >时,令'()0f x <,得ln x a >,令'()0f x >,得ln x a <, ∴()f x 在区间(,ln )a -∞上单调递增,在区间(ln ,)a +∞上单调递减,∴()f x 在ln x a =处取得唯一的极大值,即为最大值,且max ()(ln )ln f x f a a a a ==-. 综上所述,当0a ≤时,()f x 没有最值;当0a >时,()f x 的最大值为ln a a a -,无最小值.(2)要证()f x x ≤,即证(1)x a x e -≤,令()(1)x F x e a x =--,当1a =时,()0x F x e =>,∴(1)x a x e -≤成立;当11a e <≤+时,ln(1)'()(1)x x a F x e a e e -=--=-,当ln(1)x a <-时,'()0F x <;当ln(1)x a >-时,'()0F x >,∴()F x 在区间(,ln(1))a -∞-上单调递减,在区间(ln(1),)a -+∞上单调递增, ∴[]ln(1)()(ln(1))(1)ln(1)(1)1ln(1)a F x F a ea a a a -≥-=---=---.∵11a e <≤+,∴10a ->,[]1ln(1)1ln (1)10a e --≥-+-=,∴()0F x ≥,即(1)x a x e -≤成立,故原不等式成立.22.解:(1)由4cos ρθ=,得24cos ρρθ=,将cos x ρθ=,sin y ρθ=代入,可得2240x y x +-=,∴圆C 的直角坐标方程为22(2)4x y -+=, ∴圆C 的参数方程为22cos ,2sin x y ϕϕ=+⎧⎨=⎩(ϕ为参数), 由直线l 的参数方程,可得直线l 的普通方程为10x y --=.(2)将直线l 的参数方程代入圆C :22(2)4x y -+=,整理得230t -=, 设A ,B 对应的参数分别为1t ,2t ,∴12t t +=123t t =-,则12||||AB t t =-==.又点O 到直线l的距离2d ==∴11||2222AOB S AB d ∆=⋅==. 23.解:(1)由题得,3,1,1()2,1,213,,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩则不等式()3f x ≤, 即为1,33x x ≤-⎧⎨-≤⎩或11,223x x ⎧-<<⎪⎨⎪-≤⎩或1,233,x x ⎧≥⎪⎨⎪≤⎩ 解得11x -≤≤,即原不等式的解集为{}|11x x -≤≤.(2)由题得,()()|1||21||22||2122|3g x f x x x x x x =++=-++≥---=, 当且仅当(21)(22)0x x -+≤时取等号,所以不等式()|1|g x k ≤-有解等价于|1|3k -≥,解得4k ≥或2k ≤-, 即实数k 的取值范围为(,2][4,)-∞-+∞U .。
保定市2018年高三第一次模拟考试文数 (1)

从上述 5 次成绩中任意抽取 2 次 , 求恰有一次两人
( ) 试比较甲 ㊁ 乙二人谁的成绩更稳定 ; 1 ( ) 在一次考试中若两人成绩之差的 绝 对 值 不 大 于 2, 则 称 两 人 2 实力相当 文 科 数 学 试 题 第 3 页 (共 4 页 )
1 0 0
的概率.
1 9 . ( 1 2 分) 如图 , 四 棱 台 A1B1 C D1 - A B C D 中 ,A1A ʅ 底 面 1
, 且a , 已知数列 { 满足 :2 a a a a nȡ2, nɪN * ) a . n} n= n+1 + n-1 ( 1 =1 2 =2 ( ) 求数列 { 的通项公式 ; 1 a n}
组织的计算机技能大赛 , 两人以往 5 次的比赛成绩统计如下 :( 满分 1 0 0 分 , 单位 : 分 )
是奇函数 A .f( x)
的最小正周期为 2 C .f( x) π
的一条对称轴为直线 x=π B .f( x) 4
2 2 x y ) 的左顶点为 A, 虚轴长为 8, 右焦点为 F, 且 ☉F 与 1 1 . 已知双曲线 - 2 =1 ( b>0 9 b
π, π) 在( 上为减函数 D .f( x) 4 2
ң
D .
1 0 1 2 -2 3
1 0 2 2 -2 3
A .0
B .2 0 1 8
C .4 0 3 6
D .4 0 3 7
A . 3+6 2+2 6
4 1 0 . 已知向量 a= ( s i n
D .5 3+4 6
ң ң x) = a㊃ b, 则下列说法正确的是 f(
ң x, 4 x) , 向 量b ,函数 c o s =( 1, 1) 2 2
2018届保定一模数学答案

数学一模答案(理科)一、选择题: DABBB ACDCD DB二、填空题: 13、-1 14、甲 15、9 16、3 三、解答题:17、解:(1)由112-++=n n n a a a (*∈≥N n n ,2)知数列{}n a 为等差数列,且首项为1,公差为112=-a a ,所以n a n = 3分 (2)方法一 ∵n n b n nb )1(21+=+ ∴n b n b n n ⋅=++2111(1≥n ),∴数列⎭⎬⎫⎩⎨⎧n b n 是以111=b 为首项,21为公比的等比数列, 5分 1-21n n n b ⎪⎭⎫ ⎝⎛=,从而1-2n n nb = 7分方法二∵n n b n nb )1(21+=+ ∴nn b b n n 1211+⋅=+ ∴112232112122223)2(21)1(2----=⨯⋅⨯⋅⋅--⋅-=⋅⋅⋅⋅n n n n n n n n n n b b b b b b b b ΛΛ 即12-=n n nb 7分12210221232221--+-++++=n n n n n T Λn n n nn T 22123222121132+-++++=-Λ 9分 ∴n n n n T 221212112112-++++=-Λ n n nn n 222221121-1+-=--=11分 所以1224-+-=n n n T 12分18、解:打5,6,7,8折的概率分别为61231=⨯,31232=⨯,31,61 3分 (1)事件A 为“三位顾客中恰有两位顾客打6折”所以923231)(223=⋅⎪⎭⎫ ⎝⎛=C A P 5分(2)X 的可能取值为2000,2200,2400,2600,2800,3000,3200 6分3616161)2000(=⨯==X P 9123161)2200(=⨯⨯==X P 7分92313123161)2400(=⨯+⨯⨯==X P18536102616123131)2600(==⨯⨯+⨯⨯==X P92261313131)2800(=⨯⨯+⨯==X P 9分9123161)3000(=⨯⨯==X P10分36320093000928001826009240092200362000⨯+⨯+⨯+⨯+⨯+⨯+⨯=)(X E2600=元 12分19、(1)证明:连接1AC∵ABCD D C B A -1111为四棱台,四边形1111D C B A ∽四边形ABCD ∴ACC A AB B A 111121==,由AC=2得,111=C A 2分 又∵⊥A A 1底面ABCD ,∴四边形11ACC A 为直角梯形,可求得21=A C又2=AC ,M 为1CC 的中点,所以C C AM 1⊥ 4分 又∵平面11ACC A ⊥平面11CDD C ,平面11ACC A ⋂平面11CDD C C C 1= ∴⊥AM 平面11CDD C ,⊂D D 1平面11CDD C∴D D AM 1⊥ 5分(2)解:在ABC ∆中,32=AB ,2=AC ,030=∠ABC ,利用余弦定理可求得,4=BC 或2=BC ,由于BC AC ≠,所以4=BC从而222BC AC AB =+,知AC AB ⊥ 6分3616161)3200(=⨯==X P如图,以A 为原点建立空间直角坐标系()000,,A ,()0032,,B ,()020,,C ,()3101,,C ,⎪⎪⎭⎫⎝⎛23230,,M 7分 由于⊥AM 平面11CDD C ,所以平面11CDD C 的法向量为⎪⎪⎭⎫ ⎝⎛=23230,, 8分设平面11BCC B 的法向量为()z y x ,,=()0232,,-=,()3101,,-=CC ,⎪⎩⎪⎨⎧=⋅=⋅001CC ⎪⎩⎪⎨⎧=+-=+-⇒030232z y y x 设3=y ,所以()131,,= 10分5523523233=⨯+==∴sin m AM =u r u u u u r ,,即二面角111D CC B --的正弦值为5. 12分 20、解:(1)由21=a c 得2243b a = 1分 把点⎪⎭⎫ ⎝⎛-231,代入椭圆方程为149122=+b a ,∴139122=+aa 得42=a 3分 32=∴b ,椭圆的标准方程为13422=+y x 4分 (2)①由(1)知13422=+y x ,c=14214241)413)1()1(22222-=+-=-+-=+-=x x x x x y x (而x -=4=2为定值. 6分②设()m Q ,4若0=m ,则NF MF +4=若0≠m ,因为()02,-A ,()02,B 直线QA :()26+=x my ,直线QB :()22-=x m y 由()⎪⎪⎩⎪⎪⎨⎧=++=1342622y x x m y 整理得()010844272222=-+++m x m x m ∴()222710842m m x M +-=-,得2227542mm x M ++-= 8分 由()⎪⎪⎩⎪⎪⎨⎧=+-=1342222y x x m y 整理得()0124432222=-+-+m x m x m ∴2231242mm x N +-=⋅,得22362m m x N +-= 9分 由①知()M x MF -=421,()N x NF -=421 10分 ∴⎪⎪⎭⎫⎝⎛+-+++--=+-=+22223622754221424m m m m x x NF MF N M 2422248484481308130m m m m m ⎛⎫⎪⎛⎫=-=- ⎪ ⎪++⎝⎭ ⎪++⎝⎭11分 ∵188128122=≥+mm (当且仅当92=m 即3±=m 时取等号)∴130814822≤++mm ,即NF MF +的最小值为3. 12分21、解:(1)()0)1(1)2()1()1(1)(222>++-+=+-+-='x x x x a x x ax x a x x f 1分 令1)2()(2+-+=x a x x p①当02≥-a 即2≤a 时,p(x)>1,故0)(>'x f 恒成立,所以)(x f 在()∞+,0上单调递增;②当04)2(2≤--=∆a 即40≤≤a 时,()0f x '≥恒成立,所以)(x f 在()∞+,0上单调递增;③当4>a 时,由于0)(='x f 的两根为02422>-±-=aa a x 所以)(x f 在⎪⎪⎭⎫ ⎝⎛---24202a a a ,,⎪⎪⎭⎫ ⎝⎛∞+-+-,2422a a a 为增函数,在⎪⎪⎭⎫⎝⎛-+----24224222a a a a a a ,为减函数. 5分 综上:4≤a 时,函数)(x f 在()∞+,0为增函数; 4>a 时,函数)(x f 在⎪⎪⎭⎫ ⎝⎛---24202a a a ,,⎪⎪⎭⎫⎝⎛∞+-+-,2422a a a 为增函数,在⎪⎪⎭⎫⎝⎛-+----24224222a a a a a a ,为减函数. 6分 (2)由(1)知4>a ,且221-=+a x x ,121=x x 7分1ln 1ln )()(22211121+-++-=+∴x ax x x ax x x f x f ()()a x x x ax x ax x x -=+++++-=11)1()1(ln 21122121 8分而)2(22ln 1222222ln 22221---=+--⋅--=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+a a a a a a a f x x f 9分 ∴()()2222ln 2222ln 222121+--=++--=+-⎪⎭⎫⎝⎛+a a a a a x f x f x x f 10分 设()2222ln+--=aa a h (4>a ) 则()()022*******<--=-⋅-='a a a a h所以()a h 在()∞+,4上为减函数,又()04=h ,所以()0<a h 所以2)()()2(2121x f x f x x f +<+ 12分 22、(1)解:直线l 和圆2C 的普通方程分别为0=+-b y x ,4)2(22=++y x 3分Θ090=∠AOB ,∴直线l 过圆2C 的圆心)0,2(2-C ,所以02=+-b ,2=b 5分(2)证明:曲线)0(:21>=a ay x C ,可知直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+-=t y t x 22222(t为参数)代入曲线1C 得042222212=+⎪⎪⎭⎫⎝⎛+-t a t 8分04212>+=∆a a 恒成立 设M 、N 两点对应的参数分别为1t 、2t ,则821421==⋅t t 9分 所以82122=⋅=⋅t t N C M C 为定值. 10分 23、解:(1)1101122->+⇒>+-+x x x x ,①211112<<-⇒⎩⎨⎧->+-≥x x x x ,②φ⇒⎩⎨⎧->---<1112x x x 所以,不等式的解集为{}21|<<-x x 5分 (2)1)(+++=m x x x g 111+=+++-≥+++-=m m x x m x x 当且仅当()()01≥++⋅-m x x 时取等号,∴011=++m得2-=m 7分 【另:()1(1)g x x x m x x m =+++=+---,由)(x g 表示x 轴上的数x 到0与1m --的距离之和,且)(x g 在[0,1]之间取最小值,所以11m --=,解得2m =- 7分】 ∴()1,g x x x =+- 故当()1,2x ∈-时⎪⎩⎪⎨⎧-+-=12112)(x x x g 211001<<≤≤<<-x x x 9分所以)(x g 在()1,2x ∈-时的值域为[)3,1. 10分数学一模答案(文科)一、选择题: DABBB ACDCD DB二、填空题: 13、22± 14、甲 15、9 16、0(30)6π或三、解答题:17、解:(1)由112-++=n n n a a a (*∈≥N n n ,2)知数列{}n a 为等差数列,且首项为1,公差为112=-a a ,所以n a n = 3分 (2)方法一 ∵n n b n nb )1(21+=+ ∴n b n b n n ⋅=++2111(1≥n ),∴数列⎭⎬⎫⎩⎨⎧n b n 是以111=b 为首项,21为公比的等比数列, 5分 1-21n n n b ⎪⎭⎫ ⎝⎛=,从而1-2n n nb = 7分方法二∵n n b n nb )1(21+=+ ∴nn b b n n 1211+⋅=+ ∴112232112122223)2(21)1(2----=⨯⋅⨯⋅⋅--⋅-=⋅⋅⋅⋅n n n n n n n n n n b b b b b b b b ΛΛ 即12-=n n nb 7分12210221232221--+-++++=n n n n n T Λn n n nn T 22123222121132+-++++=-Λ 9分 ∴n n n n T 221212112112-++++=-Λ n n nn n 222221121-1+-=--=11分 所以1224-+-=n n n T 12分18、解:(1)∵90=甲x ,90=乙x , 2分6.312=甲s ,502=乙s ,乙甲22s s< 5分∴甲的成绩更稳定 6分 (2)考试有5次,任选2次,基本事件有(87,100)和(87,80),(87,100)和(84,85),(87,100)和(100,95),(87,100)和(92,90),(87,80)和(84,85),(87,80)和(100,95),(87,80)和(92,90),(84,85)和(100,95),(84,85)和(92,90),(100,95)和(92,90)共10个, 8分 其中符合条件的事件有(87,100)和(84,85),(87,100)和(92,90), (87,80)和(84,85),(87,80)和(92,90),(84,85)和(100,95),(100,95)和(92,90)共有6个, 10分 则5次考试,任取2次,恰有一次两人“实力相当”的概率为53106= 12分另法:这5次考试中,分数差的绝对值分别为13,7,1,5,2,则从中任取两次,分差绝对值的情况为(13,7),(13,1),(13,5),(13,2),(7,1),(7,5),(7,2),(1,5),(1,2),(5,2) 共10种……8分其中符合条件的情况有(13,1),(13,2),(7,1),(7,2),(1,5),(5,2)共6种情况……10分则5次考试,任取2次,恰有一次两人“实力相当”的概率为53106= 12分 19、(1)证明:连接1AC∵ABCD D C B A -1111为四棱台,四边形1111D C B A ∽四边形ABCD ∴ACC A AB B A 111121==,由AC=2得,111=C A 2分 又∵⊥A A 1底面ABCD ,∴四边形11ACC A 为直角梯形,可求得21=A C又2=AC ,M 为1CC 的中点,所以C C AM 1⊥ 4分 又∵平面11ACC A ⊥平面11CDD C ,平面11ACC A ⋂平面11CDD C C C 1= ∴⊥AM 平面11CDD C ,⊂D D 1平面11CDD C∴D D AM 1⊥ 6分 (2)解:方法1:在ABC ∆中,32=AB ,2=AC ,030=∠ABC ,利用余弦定理可求得,4=BC 或2=BC ,由于BC AC ≠,所以4=BC从而222BC AC AB =+,知AC AB ⊥ 7分D A又∵⊥A A 1底面ABCD ,则平面⊥11ACC A 底面ABCD ,AC 为交线∴⊥AB 平面11ACC A ,所以1CC AB ⊥,由(1)知1CC AM ⊥,A AM AB =⋂ ∴⊥1CC 平面ABM (连接BM ), 9分 ∴平面⊥ABM 平面11BCC B ,过点A 作BM AN ⊥,交BM 于点N则⊥AN 平面11BCC B , 10分 在ABM Rt ∆中可求得3=AM ,15=BM ,所以5152=AN , 11分 所以,点A 到平面11BCC B 的距离为5152. 12分 方法2:在ABC ∆中,32=AB ,2=AC ,030=∠ABC ,利用余弦定理可求得,4=BC 或2=BC , 由于BC AC ≠,所以4=BC从而222BC AC AB =+,知AC AB ⊥ 7分又∵⊥A A 1底面ABCD ,则平面⊥11ACC A 底面ABCD ,AC 为交线 ∴⊥AB 平面11ACC A , ∴三棱锥2323221311=⨯⨯⨯⨯=-ACC B V 8分 在梯形11BCC B 中,4261111====BC C C C B B B ,,,利用平面几何知识可求得梯形的高为215, 10分 设点A 到平面11BCC B 的距离为h , ∴22154213111==⨯⨯⨯⨯=--ACC B BCC A V h V ,解得5152=h 11分所以,点A 到平面11BCC B 的距离为5152. 12分 20、解:(1)由21=a c 得2243b a = 1分把点⎪⎭⎫ ⎝⎛-231,代入椭圆方程为149122=+b a ,∴139122=+aa 得42=a 3分 32=∴b ,椭圆的标准方程为13422=+y x 4分 (2)①由(1)知13422=+y x ,c=14214241)413)1()1(22222-=+-=-+-=+-=x x x x x y x (而x -=4=2为定值. 6分 ②直线m x y +=21与椭圆C 联立,⎪⎪⎩⎪⎪⎨⎧=++=1342122y x m x y 得0322=-++m mx x ()03422>--=∆m m 22<<-⇒m 设⎪⎭⎫ ⎝⎛+m x x A 1121,,⎪⎭⎫ ⎝⎛+m x x B 2221,,则m x x -=+21,3221-=⋅m x x 8分 由①知)4(211x AF -=,)4(212x BF -= 9分 ∴242421m x x BF AF +=+-=+,MF = 10分 ∵AF ,MF ,BF 成等差数列 ∴MF BF AF 2=+ 即12242+=+m m 解得512=m 或34-=m 11分 又因为22<<-m ,所以34-=m 12分 21、解:(1)因为2221)(x a x x a x f -=-='()0≠x …………………1分 ①若)(,0)(0x f x f a ∴>'≤,在(,0),(0,)-∞+∞为增函数…………………2分②若0>a ,则a x a x a x x f >-<⇒>-⇒>'或00)(2a x a a x x f <<-⇒<-⇒<'00)(2()0≠x∴函数)(x f 的单调递增区间为()a -∞-,,()∞+,a , 单调递减区间为()0,a -,()a ,0 5分 (2)方法1:令1ln )()()(--+=-=x xa x x g x f x h ()0>x 22211)(xa x x x x a x h --=--=' 设=)(x p 02=--a x x 的正根为0x ,所以0020=--a x x∵011)1(<-=--=a a p ,∴10>x 8分 )(x h 在()00x ,上为减函数,在()∞+,0x 上为增函数 2ln 21ln 1ln )()(000002000000min --=---+=--+==x x x x x x x x x a x x h x h 10分 令2ln 2)(--=x x x F ()1>x01212)(>-=-='xx x x F 恒成立,所以)(x F 在()∞+,1上为增函数 又∵0202)1(=--=F ,∴0)(>x F ,即0)(min >x h所以,当()∞+∈,0x 时,)()(x g x f > 12分 方法2:∵0>a ,0>x ∴x xa x >+7分 令1ln )(--=x x x p ()0>x ,x x x x p 111)(-=-=' 1010)(>⇒>-⇒>'x x x p∴函数)(x p 在()10,上为减函数,在()∞+,1上为增函数 ∴0)1()(min ==p x p ,0)(≥x p 恒成立,即1ln +≥x x 11分所以,当()∞+∈,0x 时,)()(x g x f >. 12分 22、(1)解:直线l 和圆2C 的普通方程分别为0=+-b y x ,4)2(22=++y x 3分 Θ090=∠AOB ,∴直线l 过圆2C 的圆心)0,2(2-C ,所以02=+-b ,2=b 5分(2)证明:曲线)0(:21>=a ay x C ,可知直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+-=t y t x 22222(t 为参数)代入曲线1C 得042222212=+⎪⎪⎭⎫ ⎝⎛+-t a t 8分 04212>+=∆a a 恒成立 设M 、N 两点对应的参数分别为1t 、2t ,则821421==⋅t t 9分 所以82122=⋅=⋅t t N C M C 为定值. 10分23、解:(1)1101122->+⇒>+-+x x x x , ①211112<<-⇒⎩⎨⎧->+-≥x x x x ,②φ⇒⎩⎨⎧->---<1112x x x 所以,不等式的解集为{}21|<<-x x 5分(2)1)(+++=m x x x g 111+=+++-≥+++-=m m x x m x x当且仅当()()01≥++⋅-m x x 时取等号,∴011=++m得2-=m 7分 【另:()1(1)g x x x m x x m =+++=+---,由)(x g 表示x 轴上的数x 到0与1m --的距离之和,且)(x g 在[0,1]之间取最小值,所以11m --=,解得2m =- 7分】 ∴()1,g x x x =+- 故当()1,2x ∈-时⎪⎩⎪⎨⎧-+-=12112)(x x x g 211001<<≤≤<<-x x x 9分所以)(x g 在()1,2x ∈-时的值域为[)3,1. 10分。
2018年河北省保定市第一中学高三数学文月考试题含解析

2018年河北省保定市第一中学高三数学文月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知双曲线的左、右焦点分别为、,若上存在一点满足,且的面积为3,则该双曲线的离心率为()A.B. C.2 D.3参考答案:B2. 设,满足,若函数取得最大值4,则实数=()A.2B. 3C.4D.参考答案:A略3. 在数列中,若,且对所有满足,则=()A. B. C. D.参考答案:B4. =( )A. -1 B 1 C. –i D . i参考答案:A5. 已知向量=,=,若⊥,则||=()A. B. C.D.参考答案:B6. 已知函数f(x)=﹣x2+2ax+1﹣a在区间[0,1]上的最大值为2,则a的值为( ) A.2 B.﹣1或﹣3 C.2或﹣3 D.﹣1或2参考答案:D【考点】二次函数在闭区间上的最值.【专题】函数的性质及应用.【分析】利用二次项系数为﹣1,函数f(x)=﹣x2+2ax+1﹣a的图象的开口方向是向下,对称轴为x=a,因此需要按对称轴与区间的关系进行分类讨论.【解答】解:函数f(x)=﹣x2+2ax+1﹣a的对称轴为x=a,图象开口向下,①当a≤0时,函数f(x)=﹣x2+2ax+1﹣a在区间[0,1]是减函数,∴f max(x)=f(0)=1﹣a,由1﹣a=2,得a=﹣1,②当0<a≤1时,函数f(x)=﹣x2+2ax+1﹣a在区间[0,a]是增函数,在[a,1]上是减函数,∴f max(x)=f(a)=﹣a2+2a2+1﹣a=a2﹣a+1,由a2﹣a+1=2,解得a=或a=,∵0<a≤1,∴两个值都不满足;③当a>1时,函数f(x)=﹣x2+2ax+1﹣a在区间[0,1]是增函数,∴fmax(x)=f(1)=﹣1+2a+1﹣a=a,∴a=2综上可知,a=﹣1或a=2.故选:D.【点评】本题考查二次函数在闭区间上的最值问题,考查了数形结合、分类讨论的数学思想.也可以利用回代验证法判断选项.7. 已知函数的定义域是值域是[0,1],则满足条件的整数数对共有()A.2个 B.5个 C.6个 D.无数个参考答案:B8. 中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数n除以正整数m后的余数为r,则记为,例如.现将该问题设计一个程序框图,执行该程序框图,则输出的n等于()A.21 B.22 C. 23 D.24参考答案:C从21开始,输出的数是除以3余2,除以5余3,满足条件的是23,故选C.9. 已知y=f(2x)的定义域为[-1,1],则y=f(log2x)的定义域为( )A.[-1,1] B.[,2] C.[1,2] D.[,4]参考答案:D10. 已知函数,将图象上所有点的横坐标缩短到原来的倍,纵坐标保持不变,得到函数的图象.若,则的最小值为()A. B. π C. 2π D. 4π参考答案:A【分析】用辅助角公式,将化为正弦型三角函数,利用图像变换关系求出,再结合函数图像和性质,即可求解.【详解】,所以,故的周期为,且.因为,所以,或,所以,所以.故选:A【点睛】本题考查函数恒等变换以及图像变换求函数式,考查三角函数的图像及性质,属于中档题.二、填空题:本大题共7小题,每小题4分,共28分11. 已知椭圆的左、右两个焦点分别为、,若经过的直线与椭圆相交于、两点,则△的周长等于 .参考答案:略12. (几何证明选做题)如图△ABC中BC=6,以BC为直径的半圆分别交AB、AC于E、F,若AC=2AE,则EF=参考答案:313. 已知数列是公差为的等差数列,且成等比数列,则。
河北省保定市2018-2019上学期高三数学(文科)10月摸底考试试卷及答案

河北省保定市 2019 届高三摸底考试数学(文)试题说明:1.本试卷分第Ⅰ卷 ( 选择题 ) 和第Ⅱ卷 ( 非选择题 ) 两部分,满分 150 分,考试时间 120 分钟.2.答第Ⅰ卷前,考生务势必自己的姓名、学号、学校、考试科目用铅笔涂写在答题卡上.第Ⅰ卷 ( 选择题共 60 分)一、选择题 ( 本大题共 12 小题,每题 5 分,共 60 分.在每题给出的四个选项中,只有一项为哪一项切合题目要求的. ) 1.设 a , b ∈R ,则“ a + b1= 2- 1”是“ A .充分不用要条件 C .充要条件ab =- 2”的B .必需不充分条件D .既不充分也不用要条件2.函数 f ( x)2sin( x) 在其定义域上是2A .奇函数B .偶函数C .既非奇函数也非偶函数D .不可以确立3.已知等比数列 { a n }中, 有a 3a 114a 7 ,数列{b n } 是等差数列,且 b 7a 7 , 则b 5b 9 等于A .2B . 4C . 6D . 84.若函数 f (x)| x 2 |a的图象对于原点对称,则 f( a) =4 x 223B .—3C . 1D .一 1A .335.已知数列 { a n } 知足 a 12,a n a n 12n ,则 a 1 a 2 a 3 a 4 a 5 a 6 =A .8B . 10C . 15D . 216.已知 sin cos 3且 04 , 则 cossin 的值是A .18B .11D .—1C .32427.已知向量 a (2,1),b( 1, k), 若a (2a b), 则k 等于A .6B .- 6C . 12D .- 128.已知 f( x) 是定义在 R 上的不恒为零的函数,且对于随意的 a 、 b ∈R ,知足f( ab) = af( b)+ bf( a) , f( 2) = 2,令 a n f (2 n ) ( n N * )则数列 { a n } 的通项公式为2n。
(全优试卷)河北省保定市高三第一次模拟考试数学(文)试题Word版含答案
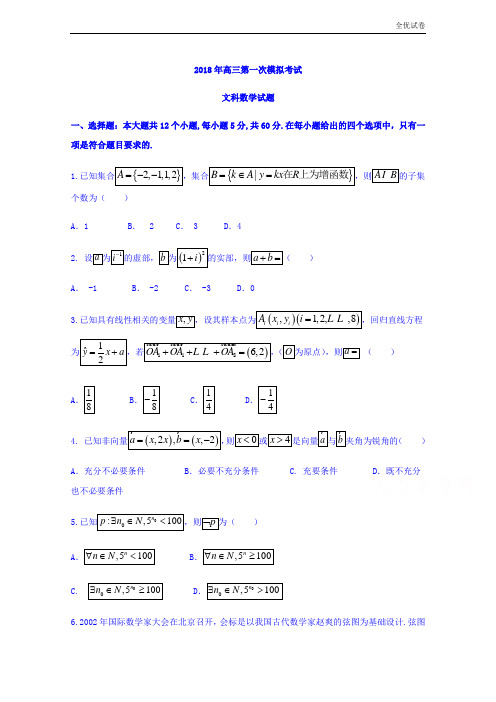
2018年高三第一次模拟考试文科数学试题一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2,1,1,2A =--,集合{}|B k A y kx R =∈=在上为增函数,则A B I 的子集个数为( )A .1B . 2C . 3D .42. 设a 为1i -的虚部,b 为()21i +的实部,则a b +=( )A . -1B . -2C . -3D .03.已知具有线性相关的变量,x y ,设其样本点为()(),1,2,,8i i i A x y i =L L ,回归直线方程为1ˆ2y x a =+,若()1186,2OA OA OA +++=u u u r u u u r u u u u r L L ,(O 为原点),则a = ( )A .18 B .18- C .14 D .14- 4. 已知非向量()(),2,,2a x x b x ==-r r,则0x <或4x >是向量a r 与b r 夹角为锐角的( )A .充分不必要条件B .必要不充分条件 C. 充要条件 D .既不充分也不必要条件5.已知00:,5100np n N ∃∈<,则p ⌝为( )A .,5100nn N ∀∈< B .,5100nn N ∀∈≥C. 00,5100nn N ∃∈≥ D .00,5100n n N ∃∈>6.2002年国际数学家大会在北京召开,会标是以我国古代数学家赵爽的弦图为基础设计.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的边长为2,大正方形的边长为10,直角三角形中较小的锐角为θ,则sin cos 23ππθθ⎛⎫⎛⎫+-+= ⎪ ⎪⎝⎭⎝⎭( )A .43310+ B .43310- C. 43310-+ D .43310-- 7.如图所示的程序框图中,输出的S 为 ( )A .99223-B .100223- C. 101223- D .102223-8. 已知函数()f x 既是二次函数又是幂函数,函数()g x 是R 上的奇函数,函数()()()11g x h x f x =++,则()()()()()()()()()201820172016101201620172018h h h h h h h h h ++++++-+-+-+-=L L ( )A.0 B. 2018 C. 4036 D.40379. 如图是某几何体的三视图,则该几何体的表面积为()A.36226++ B.36246++ C. 6346+D.5346+10. 已知向量44sin,cos22x xa⎛⎫= ⎪⎝⎭r,向量()1,1b=r,函数()f x a b=r rg,则下列说法正确的是()A.()f x是奇函数 B.()f x的一条对称轴为直线4xπ=C. ()f x的最小正周期为2π D.()f x在,42ππ⎛⎫⎪⎝⎭上为减函数11.已知双曲线()222109x ybb-=>的左顶点为A,虚轴长为8,右焦点为F,且Fe与双曲线的渐近线相切,若过点A作Fe的两条切线,切点分别为,M N,则MN=()A.8 B.42 C. 23 D.4312.定义在R上的偶函数()f x满足()()1f x f x+=-,当[]0,1x∈时,()21f x x=-+,设函数()()11132xg x x-⎛⎫=-<<⎪⎝⎭,则函数()f x与()g x的图象所有交点的横坐标之和为()A.2 B.4 C. 6 D.8二、填空题:本题共4小题,每小题5分,满分20分,将答案填在答题纸上13.3,则14.甲、乙、丙三个各自独立地做同一道数学题,当他们都把自己的答案公布出来之后,甲说:我做错了;乙说:丙做对了;丙说:我做错了.在一旁的老师看到他们的答案并听取了他们的意见后说:“你们三个人中有一个人做对了,有一个说对了.”请问他们三个人中做对了的是.15.的最小值为.16.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17. 已知数列{}n a 满足:()1122,n n n a a a n n N ++-=+≥∈,且121,2aa ==.(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足()*1121,n n n n a b a b n n N ++=≥∈gg ,且11b=.求数列{}n b 的通项公式,并求其前n 项和n T .18.某大学导师计划从自己所培养的研究生甲、乙两人中选一人,参加雄安新区某部门组织的计算机技能大赛,两人以往5次的比赛成绩统计如下:(满分100分,单位:分). 第一次 第二次 第三次 第四次 第五次 甲的成绩 87 87 84 100 92 乙的成绩10080859590(1)试比较甲、乙二人谁的成绩更稳定;(2)在一次考试中若两人成绩之差的绝对值不大于2,则称两人“实力相当”.若从上述5次成绩中任意抽取2次,求恰有一次两人“实力相当”的概率. 19. 如图,四棱台1111A B C D ABCD -中,1A A ⊥底面111,3,23,2ABCD A B A A AB AC ====,平面11A ACC ⊥平面11,C CDD M 为1C C 的中点.(1)证明:1AM D D ⊥;(2)若030ABC ∠=,且AC BC ≠,求点A 到平面11B BCC 的距离.20.(1(2若.21.(1(2:当(二)选考题:共10分.请考生在22、23两题中任选一题作答,并用2B 铅笔将答题卡上所选题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分;不涂,按本选考题的首题进行评分.22.,(1(2.23.(1(2.试卷答案一、选择题1-5: DABBB 6-10: ACDCD 11、12:DB二、填空题甲30°)三、解答题17.解:(11(218.解:(1∴甲的成绩更稳定;(2)考试有5次,任选210个,6个,则5次考试,任取2 另法:这5次考试中,分数差的绝对值分别为13,7,1,5,2,则从中任取两次,分差绝对10种,6种情况,则5次考试,任取219.(1)证明:连接1AC ,∵1111A B C D ABCD -为四棱台,四边形1111A B C D :四边形ABCD ,∴111112A B ACAB AC==,由2AC =得,111AC =, 又∵1A A ⊥底面ABCD ,∴四边形11A ACC 为直角梯形,可求得12C A =,又2,AC M =为1CC 的中点,所以1AM C C ⊥,又∵平面11A ACC ⊥平面11C CDD ,平面11A ACC ⋂平面111C CDD C C =,∴AM ⊥平面111,C CDD D D ⊂平面11C CDD ,∴1AM D D ⊥; (2)解:在ABC ∆中,023,2,30AB AC ABC ==∠=,利用余弦定理可求得,4BC =或2BC =,由于AC BC ≠,所以4BC =,从而222AB AC BC +=,知AB AC ⊥,又∵1A A ⊥底面ABCD ,则平面11A ACC ⊥底面,ABCD AC 为交线,∴AB ⊥平面11A ACC ,所以1AB CC ⊥,由(1)知1,AM CC AB AM A ⊥⋂=,,20.解:(1(2)由(121.解:(1(222.(1(2.23.解:(1(2。
河北省保定市2018-2019上学期高三数学(文科)10月摸底考试试卷及答案

河北省保定市2019届高三摸底考试数学(文)试题说明:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.2.答第Ⅰ卷前,考生务必将自己的姓名、学号、学校、考试科目用铅笔涂写在答题卡上.第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设a ,b ∈R ,则“a +b 1=2-1”是“ab =-2”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.函数()2sin()2f x x π=+在其定义域上是A .奇函数B .偶函数C .既非奇函数也非偶函数D .不能确定 3.已知等比数列3117{},4,{}n n a a a a b =中有数列是等差数列,且7759,b a b b =+则等于A .2B .4C .6D .8 4.若函数()f x =的图象关于原点对称,则f (2a )=A .3B .—3C .1D .一1 5.已知数列11123456{}2,2,n n n n a a a a a a a a a a +==+++++满足则=A .8B .10C .15D .21 6.已知3sin cos 0,cos sin 84πααααα=<<-且则的值是 A .13 B .12 C .14- D .—127.已知向量(2,1),(1,),(2),a b k a a b k ==-⊥-若则等于A .6B .-6C .12D .-128.已知f (x )是定义在R 上的不恒为零的函数,且对于任意的a 、b ∈R ,满足 f (ab )=af (b )+bf (a ),f (2)=2,令*(2)(){}2n n n n f a n N a =∈则数列的通项公式为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018届河北省保定市高三第一次模拟考试文科数学试题一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2,1,1,2A =--,集合{}|B k A y kx R =∈=在上为增函数,则A B 的子集个数为( ) A .1 B . 2 C . 3 D .42. 设a 为1i -的虚部,b 为()21i +的实部,则a b +=( )A . -1B . -2C . -3D .03.已知具有线性相关的变量,x y ,设其样本点为()(),1,2,,8i i i A x y i = ,回归直线方程为1ˆ2yx a =+,若()1186,2OA OA OA +++=,(O 为原点),则a = ( )A .18 B .18- C .14 D .14- 4. 已知非向量()(),2,,2a x x b x ==-,则0x <或4x >是向量a 与b 夹角为锐角的( )A .充分不必要条件B .必要不充分条件 C. 充要条件 D .既不充分也不必要条件 5.已知00:,5100np n N ∃∈<,则p ⌝为( )A .,5100n n N ∀∈<B .,5100n n N ∀∈≥ C. 00,5100nn N ∃∈≥ D .00,5100nn N ∃∈>6.2002年国际数学家大会在北京召开,会标是以我国古代数学家赵爽的弦图为基础设计.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的边长为2,大正方形的边长为10,直角三角形中较小的锐角为θ,则sin cos 23ππθθ⎛⎫⎛⎫+-+= ⎪ ⎪⎝⎭⎝⎭( )A .43310+ B .43310- C. 43310-+ D .43310--7.如图所示的程序框图中,输出的S 为 ( )A .99223-B .100223- C. 101223- D .102223-8. 已知函数()f x 既是二次函数又是幂函数,函数()g x 是R 上的奇函数,函数()()()11g x h x f x =++,则()()()()()()()()()201820172016101201620172018h h h h h h h h h ++++++-+-+-+-= ( )A .0B . 2018 C. 4036 D .4037 9. 如图是某几何体的三视图,则该几何体的表面积为( )A .36226++B .36246++ C. 6346+ D .5346+10. 已知向量44sin ,cos 22x x a ⎛⎫= ⎪⎝⎭ ,向量()1,1b = ,函数()f x a b = ,则下列说法正确的是( )A .()f x 是奇函数B .()f x 的一条对称轴为直线4x π=C. ()f x 的最小正周期为2π D .()f x 在,42ππ⎛⎫⎪⎝⎭上为减函数 11.已知双曲线()222109x y b b -=>的左顶点为A ,虚轴长为8,右焦点为F ,且F 与双曲线的渐近线相切,若过点A 作F 的两条切线,切点分别为,M N ,则MN = ( ) A .8 B .42 C. 23 D .4312.定义在R 上的偶函数()f x 满足()()1f x f x +=-,当[]0,1x ∈时,()21f x x =-+,设函数()()11132x g x x -⎛⎫=-<< ⎪⎝⎭,则函数()f x 与()g x 的图象所有交点的横坐标之和为( )A .2B .4 C. 6 D .8二、填空题:本题共4小题,每小题5分,满分20分,将答案填在答题纸上13.抛物线的顶点在原点,焦点在x 轴上,抛物线上的点()2,P a -到焦点的距离为3,则a = . 14.甲、乙、丙三个各自独立地做同一道数学题,当他们都把自己的答案公布出来之后, 甲说:我做错了; 乙说:丙做对了; 丙说:我做错了.在一旁的老师看到他们的答案并听取了他们的意见后说:“你们三个人中有一个人做对了,有一个说对了.” 请问他们三个人中做对了的是 .15.已知实数,x y 满足2202200x y x y x y --≥⎧⎪++≥⎨⎪-≥⎩,若32z x y =-取得最小值时的最优解(),x y 满足()20ax by ab +=>,则4a bab+的最小值为 . 16.已知,,a b c 分别为ABC ∆的三个内角,,A B C 的对边,3,2a b ==,且227cosB a 4ac b bc =-+,则B = .三、解答题 :共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17. 已知数列{}n a 满足:()1122,n n n a a a n n N ++-=+≥∈,且121,2a a ==.(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足()*1121,n n n n a b a b n n N ++=≥∈,且11b =.求数列{}n b 的通项公式,并求其前n 项和n T .18.某大学导师计划从自己所培养的研究生甲、乙两人中选一人,参加雄安新区某部门组织的计算机技能大赛,两人以往5次的比赛成绩统计如下:(满分100分,单位:分). 第一次 第二次 第三次 第四次 第五次 甲的成绩 87 87 84 100 92 乙的成绩10080859590(1)试比较甲、乙二人谁的成绩更稳定;(2)在一次考试中若两人成绩之差的绝对值不大于2,则称两人“实力相当”.若从上述5次成绩中任意抽取2次,求恰有一次两人“实力相当”的概率.19. 如图,四棱台1111A BC D ABCD -中,1A A ⊥底面111,3,23,2ABCD AB A A AB AC ====,平面11A ACC ⊥平面11,C CDD M 为1C C 的中点. (1)证明:1AM D D ⊥;(2)若030ABC ∠=,且AC BC ≠,求点A 到平面11B BCC 的距离.20. 椭圆()2222:10x y C a b a b +=>>的离心率为12,且过点31,2⎛⎫- ⎪⎝⎭.(1)求椭圆C 的方程;(2)设(),P x y 为椭圆C 上任一点,F 为其右焦点,点P '满足()4,0PP x '=-.①证明:PP PF'为定值;②设直线12y x m =+与椭圆C 有两个不同的交点A B 、,与y 轴交于点M .若,,AF MF BF 成等差数列,求m 的值. 21. 已知函数()a f x x x=+. (1)判断函数()f x 的单调性;(2)设函数()ln 1g x x =+,证明:当 ()0,x ∈+∞且0a >时,()()f x g x >.(二)选考题:共10分.请考生在22、23两题中任选一题作答,并用2B 铅笔将答题卡上所选题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分;不涂,按本选考题的首题进行评分.22.在平面直角坐标系xOy 中,曲线1C 的参数方程为21x t y t a =⎧⎪⎨=⎪⎩(t 为参数,0a >),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,直线:cos sin 0l b ρθρθ-+=与2:4cos C ρθ=- 相交于A B 、两点,且090AOB ∠=. (1)求b 的值;(2)直线l 与曲线1C 相交于M N 、,证明:22C M C N (2C 为圆心)为定值. 23. 已知函数()1f x x =+.(1)解关于x 的不等式()210f x x -+>;(2)若函数()()()1g x f x f x m =-++,当且仅当01x ≤≤时,()g x 取得最小值,求()1,2x ∈-时,函数()g x 的值域.试卷答案一、选择题1-5: DABBB 6-10: ACDCD 11、12:DB二、填空题13. 22± 14. 甲 15. 9 16.6π(或30°) 三、解答题17.解:(1)由()*1122,n n n a a a n n N +-=+≥∈知数列{}n a 为等差数列,且首项为1,公差为211a a -=,所以n a n =; (2)∵()121n n nb n b +=+, ∴()11112n n b b n n n +=≥+ ,∴数列n b n ⎧⎫⎨⎬⎩⎭是以111b =为首项,12为公比的等比数列, 112n n b n -⎛⎫= ⎪⎝⎭,从而12n n n b -=,01221123122222n n n n n T ---=+++++ ,23111231222222n n nn n T --=+++++ , ∴2111111122121222222212nn n n n nn n n T --+=++++-=-=-- , 所以1242n n n T -+=-.18.解:(1)∵90,90x x ==甲乙,2231.6,50S S ==甲乙, 22S S <甲乙, ∴甲的成绩更稳定;(2)考试有5次,任选2次,基本事件有()87,100和()87,80,()87,100和()84,85,()87,100和()100,95,()87,100和()92,90,()87,80和()84,85,()87,80和()100,95,()87,80和()92,90,()84,85和()100,95,()84,85和()92,90,()100,95和()92,90共10个,其中符合条件的事件有()87,100和()84,85,()87,100和()92,90,()87,80和()84,85,()87,80和()92,90,()84,85和()100,95,()100,95和()92,90共有6个,则5次考试,任取2次,恰有一次两人“实力相当”的概率为63105=, 另法:这5次考试中,分数差的绝对值分别为13,7,1,5,2,则从中任取两次,分差绝对值的情况为()()()()()()()()()()13,7,13,1,13,5,13,2,7,1,7,5,7,2,1,5,1,2,5,2共10种,其中符合条件的情况有()()()()()()13,1,13,2,7,1,7,2,1,5,5,2共6种情况, 则5次考试,任取2次,恰有一次两人“实力相当”的概率为63105=. 19.(1)证明:连接1AC ,∵1111A BC D ABCD -为四棱台,四边形1111A B C D 四边形ABCD , ∴111112A B ACAB AC==,由2AC =得,111AC =, 又∵1A A ⊥底面ABCD ,∴四边形11A ACC 为直角梯形,可求得12C A =, 又2,AC M =为1CC 的中点,所以1AM C C ⊥,又∵平面11A ACC ⊥平面11C CDD ,平面11A ACC ⋂平面111C CDD C C =,∴AM ⊥平面111,C CDD D D ⊂平面11C CDD , ∴1AM D D ⊥; (2)解:在ABC ∆中,023,2,30AB AC ABC ==∠=,利用余弦定理可求得,4BC =或2BC =,由于AC BC ≠,所以4BC =,从而222AB AC BC +=,知AB AC ⊥,又∵1A A ⊥底面ABCD ,则平面11A ACC ⊥底面,ABCD AC 为交线,∴AB ⊥平面11A ACC ,所以1AB CC ⊥,由(1)知1,AM CC AB AM A ⊥⋂=, ∴1CC ⊥平面ABM (连接BM ),∴平面ABM ⊥平面11B BCC ,过点A 作AN BM ⊥,交BM 于点N , 则AN ⊥平面11B BCC ,在Rt ABM ∆中可求得3,15AM BM ==,所以2155AN =, 所以,点A 到平面11B BCC 的距离为2155. 20.解:(1)由12c a =得2234a b =, 把点31,2⎛⎫- ⎪⎝⎭代入椭圆方程为221914a b +=,∴221913a a+=得24a =, ∴23b =,椭圆的标准方程为22143x y +=; (2)由(1)知221,143x y c +==,()()22222111131244442x PF x y x x x x ⎛⎫=-+=--=-+=- ⎪⎝⎭ ,而4PP x '=-,∴2PP PF'= 为定值;②直线12y x m =+与椭圆C 联立,2212143y x m x y ⎧=+⎪⎪⎨⎪+=⎪⎩得2230x mx m ++-=, ()2243022m m m ∆=-->⇒-<<,设112211,,,22A x x m B x x m ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,则21212,3x x m x x m +=-=- , 由①知()()12114,422AF x BF x =-=-, ∴21244,122x x mAF BF MF m ++=-=+=+, ∵,,AF MF BF 成等差数列,∴2AF BF MF +=,即24212m m +=+解得125m =或43m =-, 又因为22m -<<,所以43m =-.21.解:(1)因为()()22210a x af x x x x-'=-=≠, ①若()0,0a f x '≤>,∴()f x 在()(),0,0,-∞+∞为增函数; ②若0a >,则()200f x x a x a '>⇒->⇒<-或x a >()()2000f x x a a x a x '<⇒-<⇒-<<≠,∴函数()f x 的单调递增区间为()(),,,a a -∞-+∞,单调递减区间为()(),0,0,a a -;(2)令()()()()ln 10a h x f x g x x x x x =-=+-->,()22211a x x ah x x x x--'=--=, 设()20p x x x a =--=的正根为0x ,所以2000x x a --=,∵()1110p a a =--=-<,∴01x >,。
