冯巧玲版自控原理习题6-7解答
自动控制原理第二版6-7-8章习题及详解

第6章习题及详解6-1 试求图6-93所示电路的频率特性表达式,并指出哪些电路的低频段增益大于高频段增益。
(a ) (b )R R(c ) (d )图6-93 习题6-1图解:(a )1112121212++++ωωCj R R R R Cj R R R R ;(b )()11212+++ωωCj R R Cj R ;(c )1155434314368++⎪⎪⎭⎫ ⎝⎛+++ωωCj R Cj R R R R R R R R R R ;(d ) 117767647613++++ωωCj R Cj R R R R R R R R R ;(a )和(c )低频段增益小于高频段增益;(b )和(d )低频段增益大于高频段增益。
6-2 若系统单位脉冲响应为t t e e t g 35.0)(--+=,试确定系统的频率特性。
解:315.011)(+++=s s s G ,故315.011)(+++=ωωωj j j G 6-3 已知单位反馈系统的开环传递函数为11)(+=s s G 试根据式(6-11)频率特性的定义求闭环系统在输入信号()sin(30)2cos(545)r t t t =+︒--︒作用下的稳态输出。
解:先求得闭环传递函数21)(+=s s T 。
(1)1=ω,447.055211)1(==+=j j T ,︒-=-=∠56.2621arctan )1(j T 。
(2)5=ω,186.02929251)5(==+=j j T ,︒-=-=∠20.6825arctan )5(j T 。
故)2.1135cos(372.0)44.3sin(447.0)(︒--︒+=∞→t t t y t 。
6-4 某对象传递函数为s e Ts s G τ-+=11)( 试求:(1)?该对象在输入()sin()u t t ω=作用下输出的表达式,并指出哪部分是瞬态分量; (2)?分析T 和τ增大对瞬态分量和稳态分量的影响;(3)?很多化工过程对象的T 和τ都很大,通过实验方法测定对象的频率特性需要很长时间,试解释其原因。
40096-自动控制原理-参考答案
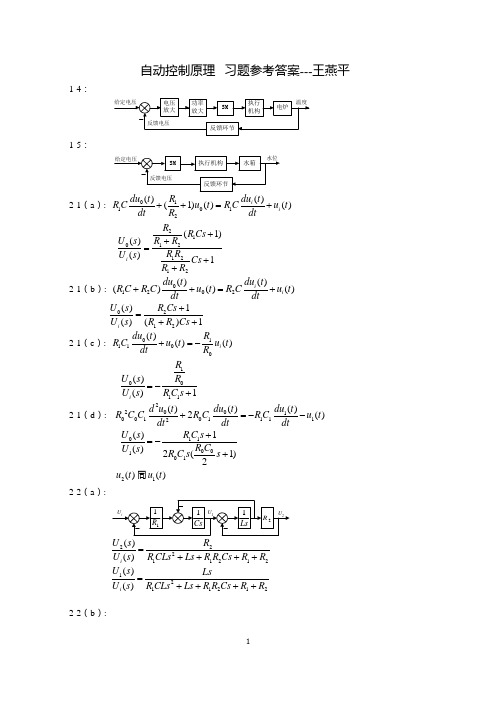
自动控制原理 习题参考答案---王燕平1-4:1-5:2-1(a ): 011012()()(1)()()i i du t du t RR Cu t R C u t dt R dt++=+ 210121212(1)()()1i R R Cs U s R R R R U s Cs R R ++=++2-1(b ): 01202()()()()()i i du t du t R C R C u t R C u t dt dt++=+0212()1()()1i U s R Cs U s R R Cs +=++ 2-1(c ): 011100()()()i du t RR C u t u t dt R +=-10011()()1i R U s R U s R C s =-+ 2-1(d ): 22001001011112()()()2()d u t du t du t R C C R C R C u t dt dt dt+=-- 01100101()1()2(1)2U s R C s R C U s R C s s +=-+2()u t 同1()u t2-2(a ):22211212()()i U s R U s R CLs Ls R R Cs R R =++++1211212()()i U s Ls U s R CLs Ls R R Cs R R =++++2-2(b ):221122112212()1()1i U s U s R C R C s R C s R C s R C s =++++ 12221122112212()()1i U s R C sU s R C R C s R C s R C s R C s =++++2-3:1232151234()()m r m m m K K K K L s U s T s s K K K s K K K K K =+++2-4(a ):123421232121()()()()()()1()()()()()()()()G s G s G s C s G s R s G s H s G s G s H s G s G s H s =++++2-4(b ):1223()()()()1()()G s G s C s R s G s G s -=- 2-4(c :)123412134223121342()()()()()()1()()()()()()()()()()()()()()G s G s G s G s C s R s G s G s H s G s G s H s G s G s G s G s H s G s G s H s =++++2-4(d ):21212112()2()()()()()1()()3()()G s G s G s G s C s R s G s G s G s G s +-=+-+2-5同2-2 2-6同2-3 2-7同2-4 2-8:112123112312()()()()()1()()()()()()()()G s G s G s C s R s G s G s G s G s G s G s G s G s -=+++- 223123223112312()()()()()()()()1()()()()()()()()G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s ++=+++-2-9:24341242434()()()()()()()()()1()()()()()()G s G s G s G s G s G s G s C s R s G s G s H s G s G s H s ++=++42434()()()1()()()()()()G s C s N s G s G s H s G s G s H s =++12424341()()()()()()1()()()()()()G s G s G s H s E s R s G s G s H s G s G s H s -=++42434()()()()1()()()()()()G s H s C s N s G s G s H s G s G s H s =-++2-10(a ):123421421234()()()()()()1()()()()()()()()G s G s G s G s C s R s G s H s G s H s G s G s G s G s =+++2-10(b ):1212()()()()1()()G s G s C s R s G s G s =+ 312412()()()()()()1()()G s G s G s G s C s N s G s G s +=+ 3-5:(1)系统稳定 (2)系统不稳定 (3)系统不稳定3-6:(1)系统不稳定,有2个不稳定根 (2)系统稳定 (3)系统稳定 3-7 : 015K << 3-8 : 1100D K +>3-9:若0.1f K =,则时间常数为0.1,调节时间为0.3;若使调节时间为0.1,则0.3f K = 3-10: (1) 2100()10100s s s Φ=++ (2) 10n ω=,0.5ξ= (3)50()1 1.15sin(8.6760)t c t e t -=-+(4)%16.3%σ=,0.6s t =3-11: 33.67n ω=,0.36ξ=3-12: (1) 0.216D K =,%22.4%σ=, 2.4s t = (2)0D K =,%60.5%σ=,7.31s t = (3)影响:改善了系统性能 3-13:(1) 2()1()0.5()()=2ss ss ss P r t t e r t t e r t t e K ====∞==∞时,;时,;时,; (2) 2()1()0()0.4()=2.5ss ss ss V r t t e r t t e r t t e K ======∞时,;时,;时,; (3)系统不稳定 3-14: 单位阶跃信号作为输入信号时,系统稳态误差为0的条件是:00a b =单位斜坡信号作为输入信号时,系统稳态误差为0的条件是:0011,a b a b ==3-15:(1)系统稳态的条件是:01K << (2)0.5K =,%81.7%σ=,15.4s t = 3-16:(1)11,()1()0.1ss K r t t e ===时,(2)当1n ()1()0.099ss n t t K e ==-时,找不到使 4-1:图略(1)系统开环极点为:0、-0.25、-3,系统开环零点为:-0.5 系统根轨迹增益为:*/2K 系统开环增益为:*/3K(2)系统开环极点为:0、-0.25、-1+j1.4、-1-j1.4,系统开环零点为:-1、-1 系统根轨迹增益为:*/4K 系统开环增益为:*/3K(3)系统开环极点为:0、-0.25、-0.5,系统无开环零点 系统根轨迹增益为:*/8K 系统开环增益为:*K (4)系统开环极点为: -0.25、-3、-2.2、-0.1+j0.67、-0.1 -j0.67,系统开环零点为:-0.5, 系统根轨迹增益为:*/2K 系统开环增益为:*/3K4-2:(1)分离点为-0.88 (2)分离点为-0.89 (3)分离点为-0.29和-1.71 4-3:(1)根轨迹与虚轴的交点为:j2.4和-j2.4,对应的K*为2844-3:(2)根轨迹与虚轴的交点为:j6.6和-j6.6,对应的K*为7304-4略 4-5:4-6:4-7:(1)系统为结构不稳定系统,无论K*如何取值,系统都无法稳定。
自动控制原理习题及答案(冯巧玲)

第二章习题及答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t F ,位移)(t x 和电压)(t u r 为输入量;位移)(t y 和电压)(t u c 为输出量;k (弹性系数),f (阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解(a )以平衡状态为基点,对质块m 进行受力分析(不再考虑重力影响),如图解2-1(a)所示。
根据牛顿定理可写出22)()(dtyd m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++(b )如图解2-1(b)所示,取A,B 两点分别进行受力分析。
对A 点有 )()(111dtdydt dx f x x k -=- (1) 对B 点有 y k dtdydt dx f 21)(=- (2) 联立式(1)、(2)可得:dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= (3) 2)()(R s Uc s I =(4) 联立式(3)、(4),可解得:CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为:r r c c u CR dt du u R CR R R dt du 121211+=++ (d) 由图解2-1(d )可写出[]Css I s I s I R s U c R R r 1)()()()(++= (5) )()(1)(s RI s RI Css I c R c -= (6) []Css I s I R s I s U c R c c 1)()()()(++= (7)联立式(5)、(6)、(7),消去中间变量)(s I C 和)(s I R ,可得:1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++ 2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统(即有相同形式的数学模型)。
自控原理习题解答(第六章)

答6 43
1 1 G s Hs e s , G j H j e j90 s M 1, 1 1, 1 2 1 2.57(rad) -147.32 2 - 147.32 180
G j H j tg tg 0.1 - tg 0.2 tg 2 0 : M 5, 0
: M 0, 90 90 90 90 180
答6 41 3.MAT LAB 画法
5s 1 G s Hs 3 2 0.04s 0.62s 2.3s 1 num 0 0 5 1; den 0.04 0.62 2.3 1; nyquistnum, den
5 [答6 ( 31 ) ]已知:x t sin t 30;G 0 s s 1 5 jtg-1 5 5 5 6 G s s 1 ; G j e 2 5 s6 j 6 36 1 s 1 5 5 M G j 1 0.822 1 36 37 -1 1 G j 1 tg 9.46 6 2 1 ; 2 1 9.46 30 20.54 yt 0.822sint 20.54
0型系统 终点:
5s 1 G s Hs 0.1s 10.2s 12s 1
k,0 5,0 起点:
切于n m 90 3 1 90 180, 终止于原点 Z P N 0 0 0, 稳定 因有零点,故奈氏曲线 有凹凸。
41Leabharlann k 12 2 T 2 1 24
6-2 已知一蒸汽过热器的传递函数为
夏超英自动控制原理678章答案

自动控制原理习题详解(下册 夏超英主编 科学出版社)第六章 习题解答6-1证明RC 无源超前校正环节111,111s Ts s z T Ts s p s Tαααα+++==>+++ 最大超前相角为1arcsin 1m αϕα-=+采用半对数坐标时最大超前相角所对应的频率位于两个转折频率的中间或等于零、极点乘积的平方根,即m ω==解:RC 无源超前校正环节的频率特性为1,11j j z T j p j Tωωααωω++=>++ 相频特性为()arctan arctan T Tωωϕωα=-根据三角函数的基本公式有2222()arctanarctan 1T T T T T T ωωωαωαϕωωαωα--==++ 从0d d ϕω=推出220T T d T dtωαωαω-⎛⎫ ⎪+⎝⎭=即()()220T T T ααω--=得极值的必要条件m ω==证毕。
6-2某单位反馈控制系统的设计指标为调节时间0.1s t ≤秒,超调量%16%σ≤,斜坡输入下的稳态误差0.05ssv e ≤。
(a )试问系统开环频率特性的低频段需要满足什么要求?中频段需要满足什么要求?(b )在s 平面内绘制出能满足设计要求的系统主导极点所在的区域。
解:(a )从静态特性考虑,斜坡输入下的稳态误差0.05ssv e ≤,要求开环传递函数至少有1个积分环节,速度误差系数20v k >,即开环频率特性的低频段的斜率为20dB dec -,在低频段特性或它的延长线上()26L dB ω≥,或者开环传递函数至少有2个积分环节,开环频率特性的低频段的斜率为40dB dec -。
从动态特性考虑,系统中频段特性斜率为20dB dec -且占据一定的中频宽度,调节时间0.1s t ≤秒,超调量%16%σ≤,要求0.5ξ≥, 3.50.135n ξω≥=,取0.5ξ=,则70n ω≥,转换成对中频段特性对幅值穿越频率和相角裕度的要求为5552c arctgarctg ωωγ≥==≥==(b )在s 平面内绘制出满足设计要求的系统主导极点的区域如下图所示。
自动控制原理第二版 冯巧玲 北航第一章习题及答案

《自动控制原理》习题解答郑州轻工业学院电气信息工程学院第一章习题及答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a ,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:d a ↔,c b ↔;(2)系统方框图如图解1-1 所示。
1-2 题1-2图是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理,并画出系统方框图。
题1-2图 仓库大门自动开闭控制系统解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。
与此同时,和大门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开启位置。
反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离开闭自动控制。
系统方框图如图解1-2所示。
1-3 题1-3图为工业炉温自动控制系统的工作原理图。
分析系统的工作原理,指出被控对象、被控量和给定量,画出系统方框图。
题1-3图 炉温自动控制系统原理图解 加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u 的平方成正比,c u 增高,炉温就上升,c u 的高低由调压器滑动触点的位置所控制,该触点由可逆转的直流电动机驱动。
炉子的实际温度用热电偶测量,输出电压f u 。
f u 作为系统的反馈电压与给定电压r u 进行比较,得出偏差电压e u ,经电压放大器、功率放大器放大成a u 后,作为控制电动机的电枢电压。
在正常情况下,炉温等于某个期望值T °C ,热电偶的输出电压f u 正好等于给定电压r u 。
此时,0=-=f r e u u u ,故01==a u u ,可逆电动机不转动,调压器的滑动触点停留在某个合适的位置上,使c u 保持一定的数值。
这时,炉子散失的热量正好等于从加热器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
自控原理习题答案(陈铁牛版)

《自动控制原理》习题答案普通高等教育“十一五”国家级规划教材全国高等专科教育自动化类专业规划教材《自动控制原理》习题答案主编:陈铁牛机械工业出版社第一章习题答案1-11-21-3闭环控制系统主要由被控对象,给定装置,比较、放大装置,执行装置,测量和变送装置,校正装置等组成。
被控对象:指要进行控制的设备和过程。
给定装置:设定与被控量相对应给定量的装置。
比较、放大装置:对给定量与测量值进行运算,并将偏差量进行放大的装置。
执行装置:直接作用于控制对象的传动装置和调节机构。
测量和变送装置:检测被控量并进行转换用以和给定量比较的装置。
校正装置:用以改善原系统控制性能的装置。
题1-4 答:(图略)题1-5 答:该系统是随动系统。
(图略) 题1-6 答:(图略)第二章习题答案题2-1 解:(1)F(s)=12s 1+-Ts T(2)F(s)=0.5)421(2+-s s(3)F(s)=428+⋅s e s sπ(4)F(s)=25)1(12+++s s(5)F(s)=32412ss s ++ 题2-2 解:(1) f(t)=1+cost+5sint (2) f(t)=e -4t(cost-4sint)(3) f(t)=t t t te e e 101091811811----- (4) f(t)= -tt t te e e ----+-3118195214(5) f(t)= -tt e e t 4181312123--+++题2-3 解:a)dtdu u C R dt du R R c c r 22111=++)( b)r c c u CR dt du R R u C R dt du R R 1r 12112111+=++)( c) r r r c c c u dtdu C R C R dtu d C C R R u dtdu C R C R C R dtu d C C R R +++=++++)()(1211222121122111222121 题2-4 解:a) G(s)=1)(212++s T T sT (T 1=R 1C, T 2=R 2C )b) G(s)=1)(1212+++s T T s T (T 1=R 1C, T 2=R 2C )c) G(s)= 1)(1)(32122131221+++++++s T T T s T T s T T s T T (T 1=R 1C 1, T 2=R 1C 2, T 3=R 2C 1, T 4=R 2C 2 ) 题2-5 解:(图略) 题2-6 解:33)(+=Φs s 题2-7 解:a) ksf ms s +-=Φ21)(b) )()()(1))(1)(()(21221s G s G s G s G s G s +++=Φc) )()(1)())()(()(31321s G s G s G s G s G s ++=Φd) )()()()(1))()()(323121s G s G s G s G s G s G s -+-=Φe) G(s)=[G 1(s)- G 2(s)]G 3(s)f) )()()()()()()()()()(1)()()()()(43213243214321s G s G s G s G s G s G s G s G s G s G s G s G s G s G s +-++=Φg) )()()()()()()()(1)()()()(43213212321s G s G s G s G s G s G s G s G s G s G s G s -+-=Φ题2-8 解:102310)1()()(k k s s T Ts k k s R s C ⋅++++⋅=1023101)1()()(k k s s T Ts k k s N s C ⋅++++⋅=1023102)1()()(k k s s T Ts s T k k s N s C ⋅++++⋅⋅⋅= 题2-9 解:)()()()(1)()()(4321111s G s G s G s G s G s R s C +=)()()()(1)()()(4321222s G s G s G s G s G s R s C +=)()()()(1)()()()()(432142121s G s G s G s G s G s G s G s R s C +=)()()()(1)()()(4321412s G s G s G s G s G s R s C += 题2-10 解:(1)3212321)()(k k k s k k k s R s C +=3212032143)()()(k k k s s G k k k s k k s N s C +⋅+= (2) 2140)(k k sk s G ⋅-= 题2-11 解:122212211111)()1()()(z z s T s T T C s T T s T k k s s m m d e L ⋅++⋅+++⋅=ΘΘ(T 1=R 1C, T 2=R 2C, T d =L a /R a , T m =GD 2R a /375C e C m )第三章 习题答案3-1. s T 15=(取5%误差带) 3-2. 1.0=H K K=2 3-3.当系统参数为:2.0=ξ,15-=s n ω时,指标计算为:%7.52%222.0114.32.01===-⨯---e eξξπσs t ns 352.033=⨯==ξωs t n p 641.02.01514.3122=-⨯=-=ξωπ当系统参数为:0.1=ξ,15-=s n ω时,系统为临界阻尼状态,系统无超调,此时有:st ns 95.057.10.145.67.145.6=-⨯=-=ωξ3-4.当110-=s K 时,代入上式得:110-=s n ω,5.0=ξ,此时的性能指标为:%3.16%225.0114.35.01===-⨯---e eξξπσs t ns 6.0105.033=⨯==ξωs t n p 36.05.011014.3122=-⨯=-=ξωπ当120-=s K 时,代入上式得:11.14-=s n ω,35.0=ξ,此时的性能指标为:%5.30%2235.0114.335.01===-⨯---e eξξπσs t ns 6.01.1435.033=⨯==ξω由本题计算的结果可知:当系统的开环放大倍数增大时,其阻尼比减小,系统相对稳定性变差,系统峰值时间变短,超调量增大,响应变快,但由于振荡加剧,调节时间不一定短,本题中的调节时间一样大。
自控原理习题解答(第六章)(课堂PPT)

2
900 2 1 2025 2 1
yt Gj 0.8sin0.1t Gj
3.2 0.8
sin 0.1t 2tg130 0.1 tg1 45 0.1
900 0.12 1 2025 0.12 1
2.56 sin0.1t 143.13 77.47
10 21.25
0.056sin0.1t 220.6
1
GjHj
5 12
1 0.12 1 0.22 1 22
GjHj tg1 tg1 0.1- tg1 0.2 tg1 2
0 : M 5, 0
: M 0, 90 90 90 90 180
13
答6 41 3.MATLAB画法
GsHs
0.04s3
5s 1 0.62s2
kT1s 1
T2s 1
k
T1s
1
T2
1 s
1
R1 R2
k
R2 R1 R2
, T1
R1C, T2
R1R 2C R1 R2
T1 T2 , k 1
1
1 T1
2
1 T2
22
L dB
1
2
90 45
0
1
2
- 45
- 90
23
答6 5b
E0 s Ei s
R2
1 Cs
1 R 2 R1 Cs
R1
R
R1C1s 1R 2C2s 1 2C2s 1R 2C1s 1 R1C2s
R1C1s 1R 2C2s 1 R1C1R 2C2s 2 R1C1 R 2C2 R1C2
s
1
Tas 1Tbs 1 Ta Tbs 2 Ta Tb Ta Tb
