江西省南昌市八一中学高一数学文理分科考试试题
最新版高一数学上学期文理分科考试试题及答案(新人教A版 第106套)

南昌市八一中学高一文理分科考试数学试卷(考试时间120分钟,试卷满分150分)一、选择题:(本大题共10小题,每小题5分,共50分,在每一小题给出的四个选项中,只有一项是符合题目要求的,答案填写在答题卷上.) 1.已知全集U=R ,集合A={x| 23x -≤≤},B={ x| 1x <-或4x >},则()u A C B = ( ) A . {x| 24x -≤<} B .{ x| 3x ≤或4x ≥} C .{x| 21x -≤<-} D .{x| 13x -≤≤} 2.方程125x x -+=的根所在的区间是( ) A 、(0,1) B 、(1,2) C 、(2,3)D 、(3,4)3.为了得到函数y=sin(2x-6π)的图像,可以将函数y=cos2x 的图像( ) A .向右平移6π B . 向右平移3π C . 向左平移6π D .向左平移3π4.3log 21=a ,2log 31=b ,3.0)21(=c ,则 ( )A a <b <cB a <c <bC b <c <aD b <a <c5.在△ABC 中,如果sinA =2sinCcosB ,那么这个三角形是A .锐角三角形B .直角三角形C .等腰三角形D .等边三角形6.若f(x)= 3,[1,0)1(),[0,1]3x x x x ⎧∈-⎪⎨-∈⎪⎩,则3[(log 2)]f f 的值为( )A..12- D .2-7、函数b x A x f +ϕ+ω=)sin()(图象如右图,则)(x f 的解析式与++=)1()0(f f S )(f )(f 20122+⋯+的值分别为( )A . 12sin 21)(+π=x x f , 2013=SB . 12sin 21)(+π=x x f ,212013=SC .12sin 21)(+π=x x f , 2012=SD .12sin 21)(+π=x x f , 212012=S8.函数122log sin(2)3y x π=-的一个单调递减区间是 ( )A . (,)612ππ-B . (,)126ππ-C . (,)63ππD . 25(,)36ππ9.设()f x 是定义在R 上以2为周期的奇函数,若(0,1)x ∈,12()log (1)f x x =-,则()f x在(1,2)上( )A.单调递增,且()0f x >B.单调递减,且()0f x >C.单调递增,且()0f x <D.单调递减,且()0f x < 10.设曲线x b x a x f sin cos )(+=的一条对称轴为5π=x ,则曲线)10(x f y -=π的一个对称点为( )A.⎪⎭⎫ ⎝⎛-0,5π B. ⎪⎭⎫ ⎝⎛0,103π C. ⎪⎭⎫ ⎝⎛0,52π D. ⎪⎭⎫⎝⎛-0,107π 二、填空题:(本大题共5小题,每小题5分,共25分,答案填写在答题卷上.)11、设)x (f 是定义在R 上的奇函数,当0≤x 时,x x )x (f -=22,则)(f 1= .12、已知扇形的周长是10cm ,面积是4cm 2,则扇形的中心角的弧度数是________13、函数3x x y +=的值域是.14.定义运算⎩⎨⎧>≤=*)(,)(,b a b b a a b a ,如:121=*,则函数x x x f cos sin )(*=的值域为15、下面有五个命题:①终边在y 轴上的角的集合是{β|β=Z k ,k ∈+22ππ}.②设一扇形的弧长为4cm ,面积为4cm 2,则这个扇形的圆心角的弧度数是2. ③函数x cos x sin y 44-=的最小正周期是2π. ④的图象为了得到x sin y 23=,只需把函数.)x sin(y 6323ππ的图象向右平移+=⑤函数上,在⎪⎭⎫⎢⎣⎡----=2πππ)x tan(y 是增函数. 所有正确命题的序号是 . (把你认为正确命题的序号都填上)三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤) 16、(本小题满分12分)(1)求值: (2)化简:17.(本题12分)已知:10103)cos(,55sin ,2,2-=-=<-<<<αβαπαβππαπ(1)求βcos 值; (2)求角β的值.3tan()cos(2)sin()2.cos()sin()ππαπαααππα---+----3556331103252718lg )log (log log log ++⋅++-18.(本小题12分) 已知函数)x sin()x (f 6221πω++=(其中01ω<<), 若直线3x π=是函数)x (f 图象的一条对称轴.(1)求ω及最小正周期; (2)求函数()f x ,[]ππ,x -∈的单调减区间.19.(本小题12分)已知函数()log (1)x a f x a =-(0a >且1a ≠). (1)求函数()f x 的定义域;(2)若()1f x >,求x 的取值范围.20.(本小题13分) 已知二次函数()()y f x x =∈R 的图象过点(0,-3),且0)(>x f 的解集)3,1(.(Ⅰ)求)(x f 的解析式; (Ⅱ)求函数]2,0[),(sin π∈=x x f y 的最值.21.(本题14分)已知函数2()2sin ()21,4f x x x x R π=+-∈.(1)函数()()h x f x t =+的图象关于点(,0)6π-对称,且(0,)t π∈,求t 的值;(2)[,],()342x f x m ππ∈-<恒有成立,求实数m 的取值范围.2012-2013学年度高一文理分科考试数学试题参考答案11、3- 12.12; 13、[)+∞,0 ; 14.,22,1⎥⎦⎤⎢⎣⎡- 15. (2)(4) 三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤) 16 解:(1)原式36log 5log 3log )2(5633313+⋅++=-- ……… 3分31321++-=……… 6分 (2)原式=αααααsin cos )cos (cos tan ⋅--⋅⋅- ……… 9分 = -1 ……… 12分17.略解:(1)55sin =α,552cos -=α 10103)cos(-=-αβ,1010)sin(=-αβ23=22])cos[(cos ==+-= ααββ…………….6分 (2) πβπ2<< πβ47=∴…………….12分181)解:由题可知:)z k (k ∈+=+⋅2632ππππω故有k 2321+=ω 又2110=∴<<ωω ………3分ππ2621=++=∴T )x sin()x (f 周期 ……… 6分(2)≤+≤+622πππx k ππk 223+∴≤≤+x k ππ23ππk 234+ ……… 8分 ⎥⎦⎤⎢⎣⎡++=ππππk ,k A 23423设,[]ππ,B -=⎥⎦⎤⎢⎣⎡⋃⎥⎦⎤⎢⎣⎡--=⋂ππππ,,B A 332则 ……… 10分⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--ππππ,,)x (f 332和的单调减区间为故 .……… 12分 19.解:(1)要使函数()f x 有意义必须10x a ->时,即1xa >…………………………1分 ①若1a >,则0x >……………………………………………………………………3分 ②若01a <<,则0x <………………………………………………………………5分 ∴当1a >时,函数()f x 的定义域为:{}0x x |>;当01a <<时,函数()f x 的定义域为:{}0x x |<………………………………6分 (2)()1f x >,即log (1)1x a a ->……………………………………………………7分 ①当1a >,则0x >,且1xa a ->…………………………………………………8分 ∴log (1)a x a >+………………………………………………………………………9分 ②当01a <<时,则0x <,且1xa a -<…………………………………………10分log (1)0a a x +<<…………………………………………………………………11分 ∴综上当1a >时,x 的取值范围是(log (1),)a a ++∞,当01a <<时,x 的取值范围是(log (1),0)a a +…………………………………12分 20.(本小题13分)解:(Ⅰ)由题意可设二次函数f(x)=a(x-1)(x-3)(a<0) …….2分当x=0时,y=-3,即有-3=a(-1)(-3), 解得a=-1, ……4分f(x)= -(x-1)(x-3)=342-+-x x , )(x f 的解析式为)(x f =342-+-x x . …….6分(Ⅱ)y=f(sinx)=3sin 4sin 2-+-x x =()12sin 2+--x . …….9分 [0,]2x π∈ ,sin [0,1]x ∴∈,则当sinx=0时,y 有最小值-3; 当sinx=1时,y 有最大值0. …….13分)z k (k ,k X sin y ,x X ∈⎥⎦⎤⎢⎣⎡+++=+=πππππ22322216的单调减区间为则设21.解:(Ⅰ)∵2()2sin ()211cos(2)2142f x x x x x ππ=+--=-+-∴ ()()2sin(22)3h x f x t x t π=+=+-,∴()h x 的图象的对称中心为 ……………………………… 4分又已知点(,0)6π-为()h x 的图象的一个对称中心,∴()23k t k Z ππ=+∈ 而(0,)t π∈,∴3t π=或56π. …………………………………………7分 (Ⅱ)若[,]42x ππ∈时,22[,]363x πππ-∈, ………………………9分 ()[1,2]f x ∈,由()33()3f x m m f x m -<⇒-<<+……………………………12分∴3132m m -<⎧⎨+>⎩,解得14m -<<, 即m 的取值范围是(1,4)-.…………… 14分。
江西省南昌市八一中学2021-2104学年高一数学文理分科测试试题(1)

高一文理分科测试数学试题第I 卷一、选择题(本大题共10小题,每题5分,共50分.在每题给出的四个选项中只有一项为哪一项符合题目要求的)1. 设集合A= {}}13,04x x x B xx ->=<-⎧⎨⎩,那么AB=( )A.∅B.(3,4)C.(-2,1)D.(4+∞)2.当10<<a 时,在同一坐标系中,函数x y a y a xlog ==-与的图象是( )A .B .C .D .3.函数)34(log )(221+-=x x x f 的递增区间是( )A .),(1∞-B .),(∞+3C .),(2∞-D .),(∞+2 4.在等差数列{}n a 中,假设24681080a a a a a ++++=,那么7812a a -的值为( ) A .4B .6C .10D . 85.如图,执行程序框图后,输出的结果为( )A .8B .10C .12D .32 6.阅读以下程序: INPUT x IF x< 0 THEN y=x ﹡x-3﹡x+5 ELSEy=(x -1) ﹡ (x -1) END IF PRINT y END假设输出y=9, 那么输入的x 值应该是( ) A .-1 B .4或-1 C .4 D .2或-2 7、假设0,0x y >>,且281x y+=,那么xy 有( )第5题图 A .最小值64 B .最大值64 C .最小值164 D .最大值12xy1 1oxy o 1 1 o y x1 1 oyx 1 18.假设对任意x ∈R ,不等式|x |≥ax 恒成立,那么实数a 的取值范围是( )A .a <-1B .D .a ≥1C .| a |<1| a |≤19.一个均匀的正方体玩具,各面上别离标有数字-1,-2,-3,1,2,3,持续掷两次,向上一面的数字别离为a ,b ,那么向量(a ,b )与(1,-1)的夹角为锐角的概率是( ) A .512 B .712 C .13 D .1210、如图,质点p 在半径为2的圆周上逆时针运动,其初始位置为0p (2,2-),角速度为1,那么点p 到x 轴距离d 关于时刻t 的函数图像大致为 ( )第II 卷二、填空题(此题共有5小题,每题填对得5分,此题总分值25分.)11. 某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h ,不然视为违规扣分,某天有1000辆汽车通过了该路段,通过雷达测速取得这些汽车运行时速的频率散布直方图,如下图,那么违规扣分的汽车大约为_____辆。
江西省南昌市八一中学2012-2013学年高一上学期文理分科考试数学试题Word版含答案

南昌市八一中学高一文理分科考试数学试卷(考试时间120分钟,试卷满分150分)一、选择题:(本大题共10小题,每小题5分,共50分,在每一小题给出的四个选项中,只有一项是符合题目要求的,答案填写在答题卷上.) 1.已知全集U=R ,集合A={x| 23x -≤≤},B={ x| 1x <-或4x >},则()u A C B =( )A . {x| 24x -≤<}B .{ x| 3x ≤或4x ≥}C .{x| 21x -≤<-}D .{x| 13x -≤≤} 2.方程125x x -+=的根所在的区间是( )A 、(0,1)B 、(1,2)C 、(2,3)D 、(3,4)3.为了得到函数y=sin(2x- 6π)的图像,可以将函数y=cos2x 的图像( )A .向右平移6πB . 向右平移3πC . 向左平移6πD .向左平移3π4.3log 21=a ,2log 31=b ,3.0)21(=c ,则 ( )A a <b <cB a <c <bC b <c <aD b <a <c5.在△ABC 中,如果sinA =2sinCcosB ,那么这个三角形是A .锐角三角形B .直角三角形C .等腰三角形D .等边三角形6.若f(x)= 3,[1,0)1(),[0,1]3x x x x ⎧∈-⎪⎨-∈⎪⎩,则3[(log 2)]f f 的值为( )AB..12- D .2-7、函数b x A x f +ϕ+ω=)sin()(图象如右图,则)(x f 的解析式与++=)1()0(f f S )(f )(f 20122+⋯+的值分别为( )A . 12sin 21)(+π=x x f , 2013=SB . 12sin 21)(+π=x x f ,212013=SC .12sin 21)(+π=x x f , 2012=SD .12sin 21)(+π=x x f ,212012=S8.函数122log sin(2)3y x π=-的一个单调递减区间是 ( ) A . (,)612ππ- B . (,)126ππ- C . (,)63ππ D . 25(,)36ππ9.设()f x 是定义在R 上以2为周期的奇函数,若(0,1)x ∈,12()log (1)f x x =-,则()f x 在(1,2)上( )A.单调递增,且()0f x >B.单调递减,且()0f x >C.单调递增,且()0f x <D.单调递减,且()0f x < 10.设曲线x b x a x f sin cos )(+=的一条对称轴为5π=x ,则曲线)10(x f y -=π的一个对称点为( )A.⎪⎭⎫ ⎝⎛-0,5πB. ⎪⎭⎫ ⎝⎛0,103πC. ⎪⎭⎫⎝⎛0,52π D. ⎪⎭⎫⎝⎛-0,107π 二、填空题:(本大题共5小题,每小题5分,共25分,答案填写在答题卷上.) 11、设)x (f 是定义在R 上的奇函数,当0≤x 时,x x )x (f -=22,则)(f 1= . 12、已知扇形的周长是10cm ,面积是4cm 2,则扇形的中心角的弧度数是________ 13、函数3x x y +=的值域是.14.定义运算⎩⎨⎧>≤=*)(,)(,b a b b a a b a ,如:121=*,则函数x x x f cos sin )(*=的值域为15、下面有五个命题:①终边在y 轴上的角的集合是{β|β=Z k ,k ∈+22ππ}.②设一扇形的弧长为4cm ,面积为4cm 2,则这个扇形的圆心角的弧度数是2. ③函数x cos x sin y 44-=的最小正周期是2π.④的图象为了得到x sin y 23=,只需把函数.)x sin(y 6323ππ的图象向右平移+=⑤函数上,在⎪⎭⎫⎢⎣⎡----=2πππ)x tan(y 是增函数.所有正确命题的序号是 . (把你认为正确命题的序号都填上)三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤) 16、(本小题满分12分)(1)求值: (2)化简:3tan()cos(2)sin()2.cos()sin()ππαπαααππα---+----3556331103252718lg )log (log log log ++⋅++-17.(本题12分)已知:10103)cos(,55sin ,2,2-=-=<-<<<αβαπαβππαπ(1)求βcos 值; (2)求角β的值.18.(本小题12分) 已知函数)x sin()x (f 6221πω++=(其中01ω<<), 若直线3x π=是函数)x (f 图象的一条对称轴.(1)求ω及最小正周期; (2)求函数()f x ,[]ππ,x -∈的单调减区间.19.(本小题12分)已知函数()log (1)x a f x a =-(0a >且1a ≠). (1)求函数()f x 的定义域;(2)若()1f x >,求x 的取值范围.20.(本小题13分) 已知二次函数()()y f x x =∈R 的图象过点(0,-3),且0)(>x f 的解集)3,1(.(Ⅰ)求)(x f 的解析式;(Ⅱ)求函数]2,0[),(sin π∈=x x f y 的最值.21.(本题14分)已知函数2()2sin ()21,4f x x x x R π=+-∈.(1)函数()()h x f x t =+的图象关于点(,0)6π-对称,且(0,)t π∈,求t 的值;(2)[,],()342x f x m ππ∈-<恒有成立,求实数m 的取值范围.2012-2013学年度高一文理分科考试数学试题参考答案11、3- 12.12; 13、[)+∞,0 ; 14.,22,1⎥⎦⎤⎢⎣⎡- 15. (2)(4) 三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤) 16 解:(1)原式36log 5log 3log )2(5633313+⋅++=-- ……… 3分31321++-=……… 6分 (2)原式=αααααsin cos )cos (cos tan ⋅--⋅⋅- ……… 9分 = -1 ……… 12分17.略解:(1)55sin =α,552cos -=α10103)cos(-=-αβ,1010)sin(=-αβ22])cos[(cos ==+-= ααββ…………….6分(2) πβπ2<< πβ47=∴…………….12分181)解:由题可知:)z k (k ∈+=+⋅2632ππππω故有k 2321+=ω 又2110=∴<<ωω ………3分ππ2621=++=∴T )x sin()x (f 周期 ……… 6分(2)≤+≤+622πππx k ππk 223+∴≤≤+x k ππ23ππk 234+ ……… 8分 ⎥⎦⎤⎢⎣⎡++=ππππk ,k A 23423设,[]ππ,B -=⎥⎦⎤⎢⎣⎡⋃⎥⎦⎤⎢⎣⎡--=⋂ππππ,,B A 332则 ……… 10分⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--ππππ,,)x (f 332和的单调减区间为故 .……… 12分 19.解:(1)要使函数()f x 有意义必须10x a ->时,即1xa >…………………………1分 ①若1a >,则0x >……………………………………………………………………3分 ②若01a <<,则0x <………………………………………………………………5分)z k (k ,k X sin y ,x X ∈⎥⎦⎤⎢⎣⎡+++=+=πππππ22322216的单调减区间为则设23=∴当1a >时,函数()f x 的定义域为:{}0x x |>;当01a <<时,函数()f x 的定义域为:{}0x x |<………………………………6分(2)()1f x >,即log (1)1xa a ->……………………………………………………7分①当1a >,则0x >,且1xa a ->…………………………………………………8分 ∴log (1)a x a >+………………………………………………………………………9分 ②当01a <<时,则0x <,且1xa a -<…………………………………………10分log (1)0a a x +<<…………………………………………………………………11分 ∴综上当1a >时,x 的取值范围是(log (1),)a a ++∞,当01a <<时,x 的取值范围是(log (1),0)a a +…………………………………12分 20.(本小题13分)解:(Ⅰ)由题意可设二次函数f(x)=a(x-1)(x-3)(a<0) …….2分 当x=0时,y=-3,即有-3=a(-1)(-3), 解得a=-1, ……4分 f(x)= -(x-1)(x-3)=342-+-x x ,)(x f 的解析式为)(x f =342-+-x x . …….6分 (Ⅱ)y=f(sinx)=3sin 4sin 2-+-x x =()12sin 2+--x . …….9分[0,]2x π∈, sin [0,1]x ∴∈,则当sinx=0时,y 有最小值-3; 当sinx=1时,y 有最大值0. …….13分 21.解:(Ⅰ)∵2()2sin ()211cos(2)2142f x x x x x ππ=+-=-+-∴ ()()2sin(22)3h x f x t x t π=+=+-,∴()h x 的图象的对称中心为 ……………………………… 4分又已知点(,0)6π-为()h x 的图象的一个对称中心,∴()23k t k Z ππ=+∈而(0,)t π∈,∴3t π=或56π. …………………………………………7分(Ⅱ)若[,]42x ππ∈时,22[,]363x πππ-∈, ………………………9分()[1,2]f x ∈,由()33()3f x m m f x m -<⇒-<<+……………………………12分∴3132m m -<⎧⎨+>⎩,解得14m -<<, 即m 的取值范围是(1,4)-.…………… 14分。
江西省南昌市八一中学2020-2021学年第一学期期末测试卷高一数学

江西省南昌市八一中学2020-2021学年第一学期期末测试卷高一数学(总分150分)一、选择题(每小题5分,共60分)1. 以下各角中,是第二象限角的为( )A. 83π-B. 76π-C. 76πD. 53π 2. 已知扇形的周长为8cm ,圆心角为2弧度,则该扇形的面积为( )A. 24cmB. 26cmC. 28cmD. 216cm3. 给出下列命题:①两个具有公共终点的向量,一定是共线向量②两个向量不能比较大小,但是它们的模能比较大小③0a λ=(λ为实数),则λ必为零 ④λ,μ为实数,若a b λμ=,则a 与b 共线其中正确的命题的个数是( )A. 1B. 2C. 3D. 44. 已知O ,A ,B ,C 为同一平面内的四个点,若20AC CB +=,则向量OC 等于( )A. 2133OA OB -B. 1233OA OB -+ C. 2OA OB -+ D. 2OA OB - 5. 已知3log 5a =,ln 2b =, 1.11.5c -=,则a ,b ,c 的大小关系是( )A. b c a <<B. b a c <<C. a c b <<D. a b c <<6. 已知函数()sin f x x x =,设7a f π⎛⎫= ⎪⎝⎭,6b f π⎛⎫= ⎪⎝⎭,3c f π⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系是( )A. c b a >>B. b a c >>C. c a b >>D. a c b >>7. 已知1sin 34πα⎛⎫-= ⎪⎝⎭,则cos 2=3πα⎛⎫+ ⎪⎝⎭( ) A. 58 B. 78- C. 58- D. 788. []0,2x π∈,y =) A. 02π⎡⎫⎪⎢⎣⎭, B. 2ππ⎛⎤ ⎥⎝⎦, C. 32ππ⎡⎫⎪⎢⎣⎭, D. 322ππ⎛⎤ ⎥⎝⎦, 9. 已知函数()3cos 223f x x π⎛⎫=+ ⎪⎝⎭,则下列关于函数()f x 的说法正确的是( ) A. 将()f x 图像向左平移12π个单位可得到3sin 22y x =的图像 B. 将()f x 图像向右平移6π个单位,所得图像关于()0,0对称 C. 56x π=是函数()f x 的一条对称轴 D. 最小正周期为2π 10. 函数()1=sin 23x f x x ⎛⎫- ⎪⎝⎭在504π⎡⎤⎢⎥⎣⎦,上的零点个数为( ) A. 2 B. 4 C. 5 D. 611. 已知sin sin 35παα⎛⎫++=- ⎪⎝⎭,则8cos 3πα⎛⎫+ ⎪⎝⎭等于( ) A. 45- B. 35- C. 35 D. 4512. 已知sin cos sin cos θθθθ+=,则角θ所在的区间可能是( )A. 42ππ⎛⎫⎪⎝⎭, B. 324ππ⎛⎫ ⎪⎝⎭, C. 54ππ⎛⎫ ⎪⎝⎭, D. 24ππ⎛⎫-- ⎪⎝⎭,二、填空题(每题5分,共20分)13. 已知函数()()2,21,2x xf xf x x-⎧⎪=⎨-⎪⎩<≥,则()2f=14. 已知sin cos1αβ+=,cos sin0αβ+=,则()sinαβ+=15. 若6xπ=是函数()3sin2sin2f x x a x=+的一条对称轴,则函数()f x的最大值是16. 设0ω>,若函数()2sinf x xω=在34ππ⎡⎤-⎢⎥⎣⎦,上单调递增,则ω的取值范围是三、解答题(17题10分,18至22题每题12分,共80分)17. 如图所示,设M,N,P是ABC△三边上的点,且13BM BC=,13CN CA=,13AP AB=,若=AB a,AC b=,试用a,b将NP,MN表示出来18.(1)已知方程()()sin32cos4απαπ-=-,()()()sin5cos232sin sin2παπαπαα-+-⎛⎫---⎪⎝⎭的值(2)已知tanα,1tanα是关于x的方程2230x kx k-+-=的两个实根,且732παπ<<,求cos sinαα+的值19. 已知函数()()sin f x A x B ωϕ=++的部分图像如图所示,其中0A >,0ω>,2πϕ<(1)求函数()f x 的表达式(2)将函数()f x 的图像先向右平移4π个单位长度,再向下平移2个单位长度后,得到函数()g x 的图像,求()g x 的最小值和()g x 取最小值时x 的取值集合20. 已知()2cos 55αβ+=1tan 7β=,且α,02πβ⎛⎫∈ ⎪⎝⎭, (1)求22cos sin sin cos ββββ-+的值 (2)求2αβ+的值21. 已知函数())211sin cos 31cos cos 222f x x x x x =⋅--- (1)求函数()f x 的单调递增区间(2)将函数()f x 的图像上每一点的横坐标伸长原来的两倍,纵坐标保持不变,得到函数()g x 的图像,若方程()0g x +=在[]0,x π∈上有两个不相等的实数解1x ,2x ,求实数m 的取值范围,并求12x x +的值22. 定义在D 上的函数()f x ,如果满足:对任意x D ∈,存在常数0M ≥,都有()f x M ≤成立,则称()f x 是D 上的有界函数,其中M 称为函数()f x 的一个上界,已知函数()11=124x xf x a ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,()121log 1ax g x x -=- (1)若函数()g x 为奇函数,求实数a 的值 (2)在(1)的条件下,求函数()g x 再区间739⎡⎤⎢⎥⎣⎦,上的所有上界构成的集合 (3)若函数()f x 在[)0+∞,上是以5为上界的有界函数,求实数a 的取值范围。
江西省南昌市八一中学2020-2021学年度高一10月份数学考试试题

一、单选题
1. 已知集合
,
,则
=( )
A.
B.
C.
D.
2. 设集合
,
,则图中阴影部分表示的集合是( )
A.
B.
C.
D.
3. 函数
的定义域是( )
A.
B.
C.
D.
4. 下列函数中,与函数
相同的函数是( )
A.
B.
C.
D.
5. 设函数
的最大值
的解析式.
22. 已知函数
是定义域为
上的奇函数,且
.
(1)求
的解析式;
(2)判断并用定义证明
(3)若实数 满足
的单调性; ,求实数 的范围.
,则
的值为( )
A.
B.
C.
D.
6. 已知
,
,
,则
的大小关系为( )
A.
B.
C.
D.
7. 已知
,则
()
A.
B.
C.
D.
8. 已知函数 A.
是幂函数,且在 B.
上是减函数,则实数 C.
()
D. 或
9. 若二次函数
在
A.
一定为奇函数
C.
一定为奇函数
ቤተ መጻሕፍቲ ባይዱ
处取最大值,则( )
B.
一定为偶函数
D.
一定为偶函数
10. 在如图所示的图象中,二次函数 A.
总收益为
元,当月产量超过400台时,总收益为80000元.(注:利润=总收益-总成本)
(1)将利润表示为月产量 的函数
江西省南昌市八一中学高一数学下学期5月开学考试试题

江西省南昌市八一中学2022-2021学年高一数学下学期5月开学考试试题一、选择题:共12小题,每题5分,共60分.在每个小题给出的四个选项中,只有一项为哪一项符合题目要求的.1.410︒角的终边落在〔 〕 A .第一象限 B .第二象限 C .第三象限 D .第四象限2.假设扇形的面积为38π、半径为1,那么扇形的圆心角为〔 〕 A .32π B .34π C .38π D .316π 3.tan 3θ=,那么3cos(2)2πθ+=〔 〕 A .-45B .-35C .35D .454.设函数()cos()3f x x π=+,那么以下结论错误的选项是〔 〕A .()f x 的一个周期为2π-B .()y f x =的图像最新直线83x π=对称 C .()f x π+的一个零点为6x π=D .()f x 在(,)2ππ单调递减5.a 是实数,那么函数()1sin f x a ax =+的图象不可能是〔 〕A .B .C .D .6.在ABC ∆中,tan tan 33tan A B A B ++=,那么C 等于〔 〕 A .6π B .4π C .3π D .23π7.函数sin(2)3y x π=+的图象可由x y 2cos =的图象如何得到〔 〕A .向左平移12π个单位B .向右平移12π个单位C .向左平移6π个单位 D .向右平移6π个单位8.,αβ都是锐角,cos 510αβ==,那么αβ+=〔 〕 A .45︒ B .135︒C .45︒或135︒D .不能确定9,22cos 131b =︒-,c = 〕 A.c a b << B.b c a << C.a b c << D.b a c <<10.函数()sin cos ()f x x a x a R =+∈图象的一条对称轴是6x π=,那么a 的值为〔 〕A .5B C .3D 11.函数1()sin()cos()363f x x x ππ=++-的最大值是〔 〕 A .43 B .23C .1D .1312.函数()sin()(0)6f x x πωω=+>在区间2[,]43ππ-上单调递增,那么ω的取值范围为〔 〕 A .80,3⎛⎤ ⎥⎝⎦B .10,2⎛⎤ ⎥⎝⎦C .18,23⎡⎤⎢⎥⎣⎦D .8,23⎡⎤⎢⎥⎣⎦二、填空题:本大题共4小题,每题5分,共20分.13.在平面直角坐标系xoy 中,角α与角β均以ox 为始边,它们的终边最新y 轴对称.假设1sin ,cos()3ααβ=-=. 14.3sin 0652ππϕϕ⎛⎫⎛⎫-=<< ⎪ ⎪⎝⎭⎝⎭,那么cos ϕ=. 15.1sin 1cos 2x x +=-,那么cos sin 1x x -的值是.16.函数()cos2sin f x x x =+,假设对任意实数x ,恒有()()()12ff x f αα≤≤,那么()12cos αα-=.三、解答题:本大题共6小题,共70分. 解容许写出文字说明、证明过程或演算步骤.17.函数2()21f x x ax =-+.〔1〕假设函数()f x 的增区间是(2,)-+∞,求实数a ;〔2〕假设函数()f x 在区间(1,1)-和(1,3)上分别各有一个零点,求实数a 的取值范围.18.函数()22sin cos 3f x x x x π⎛⎫=-- ⎪⎝⎭. 〔1〕求()f x 的最小正周期;〔2〕求()f x 在[]0,π上单调递增区间.19.如图,在平面直角坐标系xoy 中,以ox 轴为始边做两个锐角,αβ,它们的终边分别与单位圆相交于,A B 两点,,A B 的横坐标分别为10〔1〕求tan()αβ+的值;〔2〕求2αβ+的值.20.函数()()2log a f x ax x =-.〔1〕假设12a =,求()f x 的单调区间; 〔2〕假设()f x 在区间[]2,4上是增函数,求实数a 的取值范围.21.函数()21ax b f x x +=+是定义域为()1,1-上的奇函数,且()112f = 〔1〕求()f x 的解析式;〔2〕假设实数t 满足()()2110f t f t -+-<,求实数t 的范围.BD22.如图,在Rt ABC ∆中,2C π∠=,且ABC AED EAD ∠=∠=∠,假设1CD =,求BE的长.高一数学参考答案一: A 、B 、C 、D 、D C 、B 、B 、A 、D A 、B 二:13、79- 1415、12 16、14- 三:17、解析:〔1〕二次函数2()21f x x ax =-+,对称轴x a =,由题意2a =-〔2〕(1)01210(1)01210(3)09610f a f a f a ⎧->++>⎧⎪⎪<⇒-+<⎨⎨⎪⎪>-+>⎩⎩,所以:51,3a ⎛⎫∈ ⎪⎝⎭.18、解析:(1)由题意,函数3()2sin 2sin 222f x x x x =+-=1sin 2222x x + sin 23x π⎛⎫=+ ⎪⎝⎭,所以()f x 的最小正周期为22T ππ==.(2)令222232k x k πππππ-≤+≤+,k Z ∈,得51212k x k ππππ-≤≤+,k Z ∈, 由[0,]x π∈,得()f x 在[0,]π上单调递增区间为0,12π⎡⎤⎢⎥⎣⎦,7,12ππ⎡⎤⎢⎥⎣⎦. 19、解析:(1)由得:cos αβ==,所以sin αβ==那么1tan 7,tan 2αβ==,故172tan()31172αβ++==--⨯; (2)132tan(2)tan(2)tan()111(3)2αβαβαββ-++=+=++==---⨯, 由,(0,)2παβ∈,知32(0,)2παβ+∈,所以324παβ+=.20、解析:(1)当12a =时,()2121log 2f x x x ⎛⎫=- ⎪⎝⎭,由2102x x ->,得220x x ->,解得0x <或2x >,所以函数的定义域为()(),02,-∞+∞,利用复合函数单调性可得函数的增区间为(),0-∞,减区间为()2,+∞。
2021-2022学年江西省南昌市八一中学高一(上)月考数学试卷(10月份)(解析版)

2021-2022学年江西省南昌市八一中学高一(上)月考数学试卷(10月份)一、单选题(每小题5分)1.下列给出的命题正确的是()A.高中数学课本中的难题可以构成集合B.有理数集Q是最大的数集C.空集是任何非空集合的真子集D.自然数集N中最小的数是12.已知集合M={x|x>4或x<1},N=[﹣1,+∞),则M∩N=()A.(﹣∞,+∞)B.(﹣1,1)∪(4,+∞)C.∅D.[﹣1,1)∪(4,+∞)3.命题“∃x∈R,x≤0”的否定是()A.∀x∈R,x≤0B.∀x∈R,x>0C.∃x∈R,x<0D.∃x∈R,x>0 4.已知集合A={x∈N*|x2﹣2x﹣3<0},B={x|ax+2=0},若A∩B=B,则实数a的取值集合为()A.{﹣1,﹣2}B.{﹣1,0}C.{﹣2,0,1}D.{﹣2,﹣1,0} 5.不等式(x+2)(5﹣x)<0的解集为()A.{x|x>5}B.{x|x<﹣2}C.{x|x<﹣2或x>5}D.{x|﹣2<x<5} 6.已知集合P={x|x=},Q={x|x=},则()A.P=Q B.P⫋Q C.P⫌Q D.P∩Q=∅7.已知函数y=ax2+bx+c,如果a>b>c且a+b+c=0,则它的图象可能是()A.B.C.D.8.某年级先后举办了数学、历史、音乐的讲座,其中有85人听了数学讲座,70人听了历史讲座,61人听了音乐讲座,16人同时听了数学、历史讲座,12人同时听了数学、音乐讲座,9人同时听了历史、音乐讲座,还有5人听了全部讲座.则听讲座的人数为()A.181B.182C.183D.1849.若x∈A,则,就称A是伙伴关系集合,集合的所有非空子集中,具有伙伴关系的集合的个数为()A.1B.3C.5D.710.已知实数a>0,b>0,且满足ab﹣a﹣2b﹣2=0,则(a+1)(b+2)的最小值为()A.24B.3+13C.9+13D.25二、多选题(每小题全对5分一个,少选2分一个,错选0分)11.下列说法正确的有()A.若a>b,则>B.若a>b,则a3>b3C.若ab=1,则a+b≥2D.若a2+b2=1,则ab≤12.已知关于x的不等式ax2+bx+c>0的解集为(﹣∞,﹣2)∪(3,+∞),则()A.a>0B.不等式bx+c>0的解集是{x|x<﹣6}C.a+b+c>0D.不等式cx2﹣bx+a<0的解集为三、填空题(每小题5分)13.满足M⊆{a,b,c,d},且M∩{a,b,c}={a,b}的集合M有个.14.如图为由电池、开关和灯泡组成的电路,假定所有零件均能正常工作,则电路中“开关K1和K2有且只有一个闭合”是“灯泡L亮”的条件.(填“充分不必要”、“必要不充分”“充要”“既不充分也不必要”)15.若命题“∃x∈R,x2﹣2ax+1≤0”是假命题,则实数a的取值范围的解集是.16.中国南宋大数学家秦九韶提出了“三斜求积术”,即已知三角形的三条边长分别为a,b,c,则三角形的面积S可由公式S=求得,其中p为三角形周长的一半,这个公式也被称为海伦﹣秦九韶公式,现有一个三角形的边长满足a=6,b+c =10,则此三角形面积的最大值为.四、解答题(17题10分一个,其它12分一个)17.已知集合A={x|﹣2a+3≤x<4a},B={x|﹣3≤x+1≤6}.(1)若a=2,求A∩B,(∁R A)∩(∁R B);(2)若A∩B=A,求a的取值范围.18.已知二次函数当有最大值,且它的图象与x轴有两个交点,两个交点的距离为5,求这个二次函数的解析式.19.已知集合A={x|2a+1≤x<3a+5},B={x|3≤x≤32},若x∈A是x∈B的充分不必要条件,求a的取值范围.20.已知1≤a﹣b≤2且2≤a+b≤4,求4a﹣2b的取值范围.21.已知函数f(x)=ax2﹣(2a+1)x+2.(1)当a=2时,解关于x的不等式f(x)≤0;(2)若a>0,解关于x的不等式f(x)≤0.22.(1)已知0<x<1,求x(4﹣3x)取得最大值时x的值?(2)已知x<,求f(x)=4x﹣2+的最大值?(3)函数y=(x>1)的最小值为多少?参考答案一、单选题(每小题5分一个)1.下列给出的命题正确的是()A.高中数学课本中的难题可以构成集合B.有理数集Q是最大的数集C.空集是任何非空集合的真子集D.自然数集N中最小的数是1【分析】利用集合的含义与性质即可判断出.解:A、难题不具有确定性,不能构造集合,故本选项错误;B、实数集R就比有理数集Q大,故本选项错误;C、空集是任何非空集合的真子集,故本选项正确;D、自然数集N中最小的数是0,故本选项错误;故选:C.2.已知集合M={x|x>4或x<1},N=[﹣1,+∞),则M∩N=()A.(﹣∞,+∞)B.(﹣1,1)∪(4,+∞)C.∅D.[﹣1,1)∪(4,+∞)【分析】根据集合的交集运算,即可求出M∩N.解:∵集合M={x|x>4或x<1},N=[﹣1,+∞),∴M∩N={x|﹣1≤x<1或x>4},故选:D.3.命题“∃x∈R,x≤0”的否定是()A.∀x∈R,x≤0B.∀x∈R,x>0C.∃x∈R,x<0D.∃x∈R,x>0【分析】直接利用特称命题的否定是全称命题,写出全称命题即可.解:因为特称命题的否定是全称命题,所以“∃x∈R,x≤0”的否定是:“∀x∈R,x>0”.故选:B.4.已知集合A={x∈N*|x2﹣2x﹣3<0},B={x|ax+2=0},若A∩B=B,则实数a的取值集合为()A.{﹣1,﹣2}B.{﹣1,0}C.{﹣2,0,1}D.{﹣2,﹣1,0}【分析】先求出集合A,由A∩B=B,得B⊆A,再分类讨论a的值即可.解:A={x∈N+|x2﹣2x﹣3<0}={x∈N+|﹣1<x<3}={1,2},∵A∩B=B,∴B⊆A,①当a=0时,集合B={x|ax+2=0}=∅,满足B⊆A,当a≠0时,集合B={x|ax+2=0}={﹣},由B⊆A,A={1,2}得,﹣=1,或﹣=2,解得a=﹣2,或a=﹣1,综上由a的取值构成的集合为{0,﹣2,﹣1},故选:D.5.不等式(x+2)(5﹣x)<0的解集为()A.{x|x>5}B.{x|x<﹣2}C.{x|x<﹣2或x>5}D.{x|﹣2<x<5}【分析】先把不等式(x+2)(5﹣x)<0化为(x+2)(x﹣5)>0,再求不等式的解集即可.解:∵(x+2)(5﹣x)<0,∴(x+2)(x﹣5)>0,∴x<﹣2或x>5,∴不等式的解集为{x|x<﹣2或x>5}.故选:C.6.已知集合P={x|x=},Q={x|x=},则()A.P=Q B.P⫋Q C.P⫌Q D.P∩Q=∅【分析】由集合的交集及集合的表示得:P={x|x=,k∈Z},Q={x|x=,k∈Z},即P∩Q=∅,得解解:P={x|x=,k∈Z},Q={x|x=,k∈Z},即P∩Q=∅,故选:D.7.已知函数y=ax2+bx+c,如果a>b>c且a+b+c=0,则它的图象可能是()A.B.C.D.【分析】逐一对选项进行分析,得出与已知条件的矛盾即为错误选项.解:对于B,由图可知,抛物线开口向下,故a<0,因为a>b>c,所以a,b,c均为负值,与a+b+c=0矛盾,故B错误;对于C,由图可知,a>0,ax2+bx+c=0两根分别为0,1,所以c=0,﹣=1,即a=﹣b>0,所以b<0,与a>b>c矛盾,故C错误;对于D,由图象可知a<0,ax2+bx+c=0两根均为正数,所以﹣>0,即<0,所以b>0,与已知a>b>c矛盾,故D错误;故选:A.8.某年级先后举办了数学、历史、音乐的讲座,其中有85人听了数学讲座,70人听了历史讲座,61人听了音乐讲座,16人同时听了数学、历史讲座,12人同时听了数学、音乐讲座,9人同时听了历史、音乐讲座,还有5人听了全部讲座.则听讲座的人数为()A.181B.182C.183D.184【分析】设全班同学是全集U,听数学讲座的人组成集合A,听历史讲座的人组成集合B,听音乐讲座的人组成集合C,根据题意,用韦恩图表示出各部分的人数,即可求出解:设全班同学是全集U,听数学讲座的人组成集合A,听历史讲座的人组成集合B,听音乐讲座的人组成集合C,根据题意,用韦恩图表示,如图所示:,由韦恩图可知,听讲座的人数为62+7+5+11+4+50+45=184(人),故选:D.9.若x∈A,则,就称A是伙伴关系集合,集合的所有非空子集中,具有伙伴关系的集合的个数为()A.1B.3C.5D.7【分析】根据新定义求出集合A中的元素可为﹣1,1,然后写出非空子集,即可得个数.解:∵﹣1∈A时,则A;1∈A时,则∈A,∴集合M={﹣1,0,,,1,2}的所有满足新定义的元素有2个,那么A={﹣1}或A={1}或A={﹣1,1},故选:B.10.已知实数a>0,b>0,且满足ab﹣a﹣2b﹣2=0,则(a+1)(b+2)的最小值为()A.24B.3+13C.9+13D.25【分析】根据等式ab﹣a﹣2b﹣2=0表示出b,求出a的范围,然后将(a+1)(b+2)中的b消去,再利用基本不等式可求出(a+1)(b+2)的最小值.解:因为ab﹣a﹣2b﹣2=0,所以b=,又a>0,b>0,所以>0,解得a>2,又b==1+,所以(a+1)(b+2)=ab+2a+b+2=a+2b+2+2a+b+2=3a+3b+4=3a++7=3(a﹣2)++13≥,当且仅当3(a﹣2)=即a=4时等号成立,即(a+1)(b+2)的最小值为25.故选:D.二、多选题(每小题全对5分一个,少选2分一个,错选0分)11.下列说法正确的有()A.若a>b,则>B.若a>b,则a3>b3C.若ab=1,则a+b≥2D.若a2+b2=1,则ab≤【分析】根据各选项的条件利用特殊值或不等式的基本性质,分别判断即可.解:A.根据a>b,取a=0,b=﹣1,则>不成立,故A不正确;B.若a>b,则根据不等式的性质可知,a3>b3,故B正确;C.根据ab=1,取a=b=﹣1,则a+b≥2不成立,故C不正确;D.根据a2+b2=1,可得1=a2+b2≥2ab,∴ab≤,故D正确.故选:BD.12.已知关于x的不等式ax2+bx+c>0的解集为(﹣∞,﹣2)∪(3,+∞),则()A.a>0B.不等式bx+c>0的解集是{x|x<﹣6}C.a+b+c>0D.不等式cx2﹣bx+a<0的解集为【分析】由题意可知,﹣2和3是方程ax2+bx+c=0的两根,且a>0,再结合韦达定理可得b=﹣a,c=﹣6a,代入选项B和D,解不等式即可;当x=1时,有a+b+c<0,从而判断选项C.解:由题意可知,﹣2和3是方程ax2+bx+c=0的两根,且a>0,∴﹣2+3=,(﹣2)×3=,∴b=﹣a,c=﹣6a,a>0,即选项A正确;不等式bx+c>0等价于a(x+6)<0,∴x<﹣6,即选项B正确;∵不等式ax2+bx+c>0的解集为(﹣∞,﹣2)∪(3,+∞),∴当x=1时,有a+b+c<0,即选项C错误;不等式cx2﹣bx+a<0等价于a(6x2﹣x﹣1)>0,即a(3x+1)(2x﹣1)>0,∴x<或x>,即选项D正确.故选:ABD.三、填空题(每小题5分)13.满足M⊆{a,b,c,d},且M∩{a,b,c}={a,b}的集合M有2个.【分析】利用子集、交集定义直接求解.解:满足M⊆{a,b,c,d},且M∩{a,b,c}={a,b}的集合M有:{a,b},{a,b,d},∴满足M⊆{a,b,c,d},且M∩{a,b,c}={a,b}的集合M有2个.故答案为:2.14.如图为由电池、开关和灯泡组成的电路,假定所有零件均能正常工作,则电路中“开关K1和K2有且只有一个闭合”是“灯泡L亮”的充分不必要条件.(填“充分不必要”、“必要不充分”“充要”“既不充分也不必要”)【分析】根据线路图,利用充分条件和必要条件的定义进行判断.由于两个开关为并联电路,即可得到关系.解:由条件知这两个开关为并联电路,当开关K1与K2合至少有一个闭合,则灯泡亮,所以“开关K1和K2有且只有一个闭合”是“灯泡L亮”的充分不必要条件.故答案为:充分不必要.15.若命题“∃x∈R,x2﹣2ax+1≤0”是假命题,则实数a的取值范围的解集是(﹣1,1).【分析】根据题意,分析可得命题的否定:∀x∈R,x2﹣2ax+1>0是真命题,结合二次函数的性质分析可得答案.解:根据题意,命题“∃x∈R,x2﹣2ax+1≤0”是假命题,则其否定:∀x∈R,x2﹣2ax+1>0是真命题,必有△=4a2﹣4<0,解可得:﹣1<a<1,即a的取值范围为(﹣1,1);故答案为:(﹣1,1).16.中国南宋大数学家秦九韶提出了“三斜求积术”,即已知三角形的三条边长分别为a,b,c,则三角形的面积S可由公式S=求得,其中p为三角形周长的一半,这个公式也被称为海伦﹣秦九韶公式,现有一个三角形的边长满足a=6,b+c =10,则此三角形面积的最大值为12.【分析】由题意,计算p的值,代入S2中,利用基本不等式求出它的最小值.解:由a=6,b+c=10,得p=(a+b+c)=×(6+10)=8;所以S2=8×(8﹣6)×(8﹣b)(8﹣c)=16[bc﹣8(b+c)+64]=16(bc﹣16)≤16×[﹣16]=16×(25﹣16)=144,当且仅当b=c=5时取等号.所以S≤12.故答案为:12.四、解答题(17题10分一个,其它12分一个)17.已知集合A={x|﹣2a+3≤x<4a},B={x|﹣3≤x+1≤6}.(1)若a=2,求A∩B,(∁R A)∩(∁R B);(2)若A∩B=A,求a的取值范围.【分析】(1)可求出B=[﹣4,5],a=2时,求出集合A,然后进行交集、补集的运算即可;(2)根据A∩B=A可得出A⊆B,从而可讨论A是否为空集:A=∅时,﹣2a+3≥4a;A ≠∅时,,解出a的范围即可.解:B=[﹣4,5];(1)a=2时,A=[﹣1,8),∴A∩B=[﹣1,5],∁R A=(﹣∞,﹣1)∪[8,+∞),∁R B=(﹣∞,﹣4)∪(5,+∞),(∁R A)∩(∁R B)=(﹣∞,﹣4)∪[8,+∞);(2)∵A∩B=A,∴A⊆B,∴①A=∅时,﹣2a+3≥4a,解得;②A≠∅时,,解得,综上得,a的取值范围为.18.已知二次函数当有最大值,且它的图象与x轴有两个交点,两个交点的距离为5,求这个二次函数的解析式.【分析】由题意可以得到二次函数的图象的顶点坐标为,与x轴的交点坐标为(﹣2,0),(3,0),设解析式为y=a(x+2)(x﹣3),把顶点坐标代入即可求解.解:由题意得,二次函数与x轴的交点坐标是(﹣2,0),(3,0),设二次函数的解析式为y=a(x+2)(x﹣3),把代入得,,解得a=﹣2,∴y=﹣2x2+2x+12.19.已知集合A={x|2a+1≤x<3a+5},B={x|3≤x≤32},若x∈A是x∈B的充分不必要条件,求a的取值范围.【分析】根据集合的包含关系得到关于a的不等式组,解出即可.解:由题意得A⊊B,当A=∅时,2a+1≥3a+5,解得a≤﹣4,当A≠∅时,,解得1≤a≤9,综上所述,a的取值范围为(﹣∞,﹣4]∪[1,9].20.已知1≤a﹣b≤2且2≤a+b≤4,求4a﹣2b的取值范围.【分析】令4a﹣2b=λ(a﹣b)+μ(a+b)(λ,μ∈R),展开后利用系数相等求得λ与μ的值,再由已知结合不等式的性质求解.解:令4a﹣2b=λ(a﹣b)+μ(a+b)(λ,μ∈R),则4a﹣2b=(λ+μ)a+(μ﹣λ)b,∴,解得,故4a﹣2b=3(a﹣b)+(a+b),∵1≤a﹣b≤2,∴3≤3(a﹣b)≤6.又∵2≤a+b≤4,∴5≤4a﹣2b≤10,故4a﹣2b的取值范围是[5,10].21.已知函数f(x)=ax2﹣(2a+1)x+2.(1)当a=2时,解关于x的不等式f(x)≤0;(2)若a>0,解关于x的不等式f(x)≤0.【分析】(1)a=2时不等式化为2x2﹣5x+2≤0,求出解集即可;(2)不等式f(x)≤0可化为ax2﹣(2a+1)x+2≤0,讨论a的取值,求出对应不等式的解集.解:(1)当a=2时f(x)≤0可化为2x2﹣5x+2≤0,可得(2x﹣1)(x﹣2)≤0,解得,∴f(x)≤0的解集为;(2)不等式f(x)≤0可化为ax2﹣(2a+1)x+2≤0,a>0时,则不等式为a(x﹣)(x﹣2)≤0;①当时,有,解不等式得:;②当时,有,解不等式得:x=2;③当时,有,解不等式得:;综上:①时,不等式的解集为;②时,不等式的解集为{x|x=2};③时,不等式的解集为.22.(1)已知0<x<1,求x(4﹣3x)取得最大值时x的值?(2)已知x<,求f(x)=4x﹣2+的最大值?(3)函数y=(x>1)的最小值为多少?【分析】(1)x(4﹣3x)=,然后结合基本不等式即可求解;(2)由f(x)=4x﹣2+=4x﹣5++3=﹣(5﹣4x+)+3,然后结合基本不等式可求;(3)先进行分离,y===(x﹣1)++2,然后结合基本不等式可求.解:(1)因为0<x<1,所以x(4﹣3x)==,当且仅当3x=4﹣3x,即x=时取等号;(2)因为x<,所以4x﹣5<0,所以f(x)=4x﹣2+=4x﹣5++3=﹣(5﹣4x+)+3≤3﹣2=1,当且仅当5﹣4x=,即x=1时取等号,此时f(x)的最大值1;(3)因为x>1,所以x﹣1>0,所以y===(x﹣1)++2,当且仅当x﹣1=,即x=1+时取等号,此时函数取得最小值2+2.。
江西省南昌市八一中学2016-2017学年高一文理分班考试
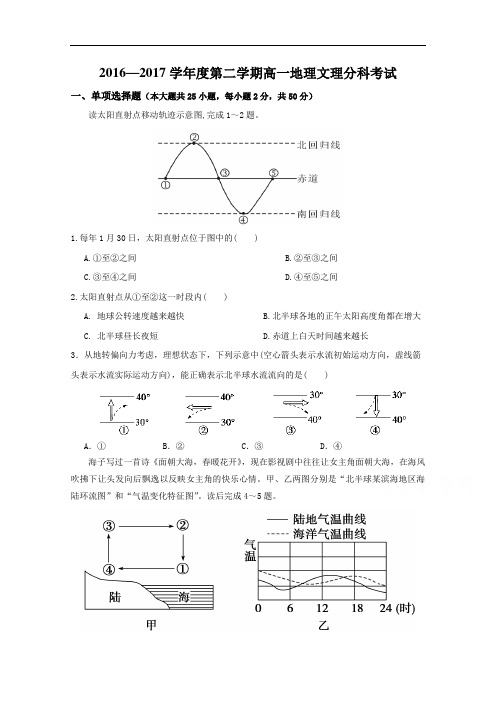
2016—2017学年度第二学期高一地理文理分科考试一、单项选择题(本大题共25小题,每小题2分,共50分)读太阳直射点移动轨迹示意图,完成1~2题。
1.每年1月30日,太阳直射点位于图中的( )A.①至②之间B.②至③之间C.③至④之间D.④至⑤之间2.太阳直射点从①至②这一时段内( )A. 地球公转速度越来越快B.北半球各地的正午太阳高度角都在增大C. 北半球昼长夜短D.赤道上白天时间越来越长3.从地转偏向力考虑,理想状态下,下列示意中(空心箭头表示水流初始运动方向,虚线箭头表示水流实际运动方向),能正确表示北半球水流流向的是( )A.① B.② C.③ D.④海子写过一首诗《面朝大海,春暖花开》,现在影视剧中往往让女主角面朝大海,在海风吹拂下让头发向后飘逸以反映女主角的快乐心情。
甲、乙两图分别是“北半球某滨海地区海陆环流图”和“气温变化特征图”。
读后完成4~5题。
4.甲图中①、②、③、④四处气温最高的是()A.① B.②C.③ D.④5.为了完成女主角头发向后飘逸的场景,如果你是导演,你会选择什么时间段完成拍摄()A.16时至次日8时 B.6时至18时C.18时至次日6时 D.8时至16时读“某日某条经线上部分气压带风带和气流的相关示意图”,回答6~7题。
6.图中②气压带或风带的气流运动方向和性质分别为( )A.上升湿润B.下沉干燥C.由高纬流向低纬干燥D.由低纬流向高纬湿润7.正确表示①②之间风带风向的图是( )下图示意某季节某大洋局部洋流,读图完成8~9题。
8.图示洋流形成的季节是( )A.春季 B.夏季C.秋季 D.冬季9.图中阴影海域渔业资源丰富的主要原因是( )A.离岸风和上升流影响显著 B.刚果河带来较多的营养物质[来源:学|科| C.地处寒、暖流交汇处 D.地处浅海大陆架,光照充足、水温适宜读等温线及地质剖面图,回答10~11题。
10.乙处的地形及地质构造是( )A.山地、背斜B.山地、向斜C.盆地、背斜D.盆地、向斜11.有关岩层沉积的先后顺序是( )①甲处先沉积,乙处后沉积②乙处先沉积,甲处后沉积③上部先沉积,下部后沉积④下部先沉积,上部后沉积A.①②B.③④C.①③D.②④读“我国部分山地垂直带谱”,完成12~13题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015—2016学年度第二学期南昌市八一中学高一文理分科考试高一数学第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项.1.已知全集{}{},|0,|1U R A x x B x x ==≤=≥,则集合()U C AB =( )A .{}|0x x ≥B .{}|1x x ≤C .{}|01x x ≤≤D .{}|01x x << 2.函数()221log f x x x =-+的零点所在区间是( ) A .11,84⎛⎫ ⎪⎝⎭ B .11,42⎛⎫ ⎪⎝⎭ C .1,12⎛⎫⎪⎝⎭D .()1,23. 若程序框图如右图所示,则该程序运行后输出k 的值是( ) A .8 B .7 C .6 D . 54. 若等比数列{}n a 的前n 项和r S n n +=2,则=r ( )A. 2B. 1C. 0D.1-5.设向量m 和n 的夹角为θ,且()()2,2,24,4m n m =-=-,则cos θ的值为( )A .55 B .55- C .15D .0 6.已知函数)sin()(ϕω+=x x f (其中,0>ω2πϕ<)图象相邻对称轴的距离为2π,一个对称中心为)0,6(π-,为了得到x x g ωcos )(=的图象,则只要将)(x f 的图象( )A .向右平移6π个单位 B .向右平移12π个单位C .向左平移6π个单位 D .向左平移12π个单位7.若101a b c >><<,,则 ( )A .c c a b <B .c cab ba < C .log log b a a c b c < D .log log a b c c <8.一个数学兴趣小组有女同学2名,男同学3名,现从这个数学兴趣小组中任选2名同学参加数学竞赛,则参加数学竞赛的2名同学中,女同学人数不少于男同学人数的概率为( )A.310B.25C.35D.710(第3题图)9.甲船在A 处观察到乙船在它的北偏东060的方向,两船相距a 海里,乙船正在向北行驶,若甲船的速度是乙船的3倍,甲船为了尽快追上乙船,应取北偏东θ方向前进,则=θ( )A. 015B. 030C. 045D. 06010.如图所示,茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中有一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是( )A.25B.710C.45D.91011.若,(0,)2παβ∈,3cos()22βα-=,1sin()22αβ-=-,则cos()αβ+的值等于 ( )A.32-B.12- C.12 D.3212.设函数()()21ln 11f x x x=+-+.则使得()()21f x f x >-成立的x 的取值范围是( ) A .1,13⎛⎫ ⎪⎝⎭ B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C .11,33⎛⎫-⎪⎝⎭ D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭第Ⅱ卷二、填空题:(本大题共4小题,每小题5分。
共20分)13.若函数2(2)f x -的定义域是[1-,1],则函数(32)f x +的定义域为________14.函数x x x x y cos sin cos sin ++⋅=取得最大值时,x 的集合为15.ABC ∆中,60,3,2,A AB AC D ===是AC 边的中点,点E 在AB 边上,且12AE EB =,BD 与CE 交于点M ,N 是BC 的中点,则________AM AN =16. 若,a b 是函数2()(0,0)f x x px q p q =-+>>的两个不同的零点,且a ,b ,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p +q 的值等于________三、解答题:(共6小题,70分解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)已知函数()()21,41f x x g x x =+=+的定义域都是集合A ,函数()f x 和()g x 的值域分别是S 和T .(1)若[]1,2A =,求ST ;(2)若[]0,A m =,且S T =,求实数m 的值;18.(本小题满分12分)设函数()22cos 23sin cos f x x x x m ωωω=++(其中0,m R ω>∈),且函数()f x 的图象在y 轴右侧的第一个最高点的横坐标是6π,并过点()0,2. (1)求函数()f x 的解析式; (2)若()0115f x =,0,42x ππ⎡⎤∈⎢⎥⎣⎦,求0cos 2x 的值.19.(本小题满分12分)成等差数列的三个正数的和等于15,并且这三个数分别加上2, 5, 13后成为等比数列{b n }中的b 3,b 4,b 5.(1)求数列{b n }的通项公式;(2)数列{b n }的前n 项和为S n ,求证:数列{S n +54}是等比数列.20.(本小题满分12分)在ABC ∆中,内角A 、B 、C 对应的边长分别为a 、b 、c , 已知21sin cos 2sin a b Ba Bbc C-=-.(1)求角A ;(2)若3a =,求b c +的取值范围.21.(本小题满分12分)设数列}{n a 的前n 项和为n S ,101=a ,1091+=+n n S a .⑴求证:数列}{lg n a 是等差数列. ⑵设n T 是数列13{}(lg )(lg )n n a a +的前n 项和,求使21(5)4n T m m >- 对所有的*∈N n 都成立的最大正整数m 的值.22. (本小题满分12分)已知函数()f x 是定义在[]1,1-上的函数,若对于任意[],1,1x y ∈-,都有()()()f x y f x f y +=+,且x >0时,有()f x >0 ⑴判断函数的奇偶性;⑵判断函数f x ()在[]-11,上是增函数,还是减函数,并证明你的结论;⑶设(1)1f =,若()f x <221m am -+ ,对所有[]1,1x ∈-,[]1,1a ∈-恒成立,求实数m 的取值范围.南昌市八一中学2018届分班考数学试卷参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DCDDADCDBCBA13.⎥⎦⎤⎢⎣⎡--134, 14. ⎭⎬⎫⎩⎨⎧∈+=Z k k x x ,42ππ 15.135 16.9 三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.) 17.解:(1)解:[]1,2A =时,[][]2,5,5,9S T == {}5ST ∴=…………………………………………5 分(2)[]0,A m =时,[]21,1,1,41S m T m ⎡⎤=+=+⎣⎦S T =, 2141m m +=+,且0m >,解得,4m =………………………….10分 (注:0m =没有舍去,扣除1分)18.解:(1)()1cos 23sin 22sin 216f x x x m x m πωωω⎛⎫=+++=+++ ⎪⎝⎭∵ ()f x 的图象在y 轴右侧的第一个最高点的横坐标为6π, ∴ 2ω⋅6π+6π=2π,解得 ω=1 又∵ ()f x 的图象过点(0,2),∴()02f = ,即 2sin 6π+1m +=2, 解得 0m =, ∴()f x =2sin (2x+6π)1+……………………………………6分. (2)由()0115f x =,得2sin(20x +6π)+1=511,即sin(20x +6π)=53,∵4π≤0x ≤2π,∴32π≤20x +6π≤67π, ∴cos(20x +6π)=-)62(sin 102π+-x =-54,cos20x =cos[(20x +6π)-6π]=23 ⋅cos(20x +6π)+21 sin(20x +6π)=23×(-54)+21×53343- ………………………………………12分.19.解:(1)设成等差数列的三个正数分别为a -d ,a ,a +d .依题意,得a -d +a +a +d =15,解得a =5. 所以{b n }中的b 3,b 4,b 5依次为7-d,10,18+d . 依题意,有(7-d )(18+d )=100, 解得d =2或d =-13(舍去).故{b n }的第3项为5,公比为2.由b 3=b 1·22,即5=b 1·22,解得b 1=54.所以{b n }是以54为首项,2为公比的等比数列,其通项公式为b n =54·2n -1=5·2n -3.………6分.(2)数列{b n }的前n 项和S n =541-2n1-2=5·2n -2-54,即S n +54=5·2n -2.所以S 1+54=52, S n +1+54S n +54=5·2n -15·2n -2=2.因此{S n +54}是以52为首项,公比为2的等比数列. ………………………12分.20.(2)由正弦定理得2sin sin sin a b cA B C===,∴2sin b B =,2sin c C = ∴()2sin 2sin 2sin 2sin b c B C B A B +=+=++ .........................................7分2sin 2sin cos 2cos sin B A B A B =++312sin 2cos 2sin 22B B B =+⨯+⨯π3sin 3cos 23sin 6B B B ⎛⎫=+=+ ⎪⎝⎭; ..........................................................9分∵2π0,3B ⎛⎫∈ ⎪⎝⎭,∴ππ5π,666B ⎛⎫+∈ ⎪⎝⎭, .....................................................10分 π1sin ,162B ⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦. .....................................................11分所以(3,23b c ⎤+∈⎦.....................................................12分21且nn n q a a 1011==-,n a n =∴lg . 1)1(lg lg 1=-+=-∴+n n a a n n ,即}{lg n a 是首项为1,公差为1等差数列. ……………. (6分)⑵由⑴知,))1(1321211(3+++⋅+⋅=n n T n=133)1113121211(3+-=+-++-+-n n n .……………………. (9分) 23≥∴n T ,依题意有)5(41232m m ->,解得61<<-m ,…………… (11分)故所求最大正整数m 的值为5 …………………. (12分)22.(1)奇,证明略; (2)单调增,证明略; (3)(,2)(2,)m ∈-∞-+∞∪ (1)令x=y=0,则f (0+0)=f (0)+f (0)∴f(0)=0令y=-x ,则f (x-x )=f (0)=f (x )+f (-x ),∴f(-x )=-f (x ) ∴f(x )是奇函数. .......................3分 (2)函数f (x )在[-1,1]上是增函数.设x 1,x 2∈[-1,1]且x 1<x 则x 2-x 1>0 ∴f(x 1)-f (x 2)=-f (x 2-x 1) 又∵x>0,f (x )>0∴f(x 2-x 1)>0∴f(x 1)-f (x 2)=-f (x 2-x 1)<0即f (x 1)<f (x 2)故由函数单调性定义可知,函数f (x )在[-1,1]上是增函数.(7分)(3)设f (1)=1,若f (x )<221m am -+,对所有x∈[-1,1],a∈[-1,1]恒成立. 则必须221m am -+>1,∀a∈[-1,1]恒成立; 即22>-am m ,∀a∈[-1,1]恒成立令22)(m ma a g +-=必须g(-1)>0g(1)>0即解得:22-<>m m 或故实数m 的取值范围为(,2)(2,)m ∈-∞-+∞∪ …………………. (12分)。
