讲义集合运算的综合应用
高中数学中的集合运算与应用

高中数学中的集合运算与应用在高中数学中,集合运算是一个重要的概念。
集合是数学中的基础概念之一,它是由一些确定的对象组成的整体。
集合运算是指对集合进行各种操作,包括并、交、差和补等。
这些运算在数学中有着广泛的应用,不仅能帮助我们解决实际问题,还能提高我们的逻辑思维能力。
首先,我们来看看集合的基本运算。
并集是指将两个集合中的所有元素合并成一个新的集合。
例如,集合A={1,2,3},集合B={3,4,5},则并集A∪B={1,2,3,4,5}。
并集运算常常用于求两个集合的总体情况,比如统计两个班级的学生总人数。
交集是指两个集合中共有的元素组成的新集合。
例如,集合A={1,2,3},集合B={3,4,5},则交集A∩B={3}。
交集运算常常用于求两个集合的共同特征,比如找出两个班级共同参加的活动。
差集是指从一个集合中减去另一个集合中的元素所得到的新集合。
例如,集合A={1,2,3},集合B={3,4,5},则差集A-B={1,2}。
差集运算常常用于求两个集合之间的差异,比如找出两个班级中只有一个班级参加的活动。
补集是指在某个全集中减去一个集合所得到的新集合。
例如,全集为U={1,2,3,4,5},集合A={1,2,3},则补集A'={4,5}。
补集运算常常用于求某个集合在全集中的补充情况,比如求出某个班级没有参加的活动。
除了基本的集合运算,集合在数学中还有很多应用。
例如,排列组合问题中经常涉及到集合的概念。
排列是指从一组元素中选取若干个元素按照一定的顺序排列的情况。
组合是指从一组元素中选取若干个元素组成的情况,不考虑顺序。
通过集合运算,我们可以方便地求解排列组合问题,提高解题效率。
另外,概率统计中也经常用到集合运算。
概率是指某个事件发生的可能性,而事件可以看作是某个集合。
通过集合运算,我们可以方便地计算事件的概率,帮助我们进行概率统计。
在几何中,集合运算也有着广泛的应用。
例如,平面几何中的图形可以看作是点的集合,通过集合运算我们可以方便地求解图形的性质,比如图形的面积、周长等。
集合论中的集合运算与应用实例

集合论中的集合运算与应用实例集合运算是集合论的基础,通过对不同集合进行运算,我们可以得到新的集合,进而应用于实际问题中。
本文将介绍集合运算的基本概念及其应用实例。
一、集合运算的基本概念集合运算是指对两个或多个集合进行操作,从而得到一个新的集合的过程。
常见的集合运算包括并集、交集、差集和补集。
1. 并集并集是指将两个或多个集合中的元素合并到一个集合中。
用符号"∪"表示。
例如,集合A = {1, 2, 3},集合B = {3, 4, 5},则A∪B = {1, 2, 3, 4, 5}。
2. 交集交集是指两个或多个集合中共同拥有的元素组成的集合。
用符号"∩"表示。
例如,集合A = {1, 2, 3},集合B = {3, 4, 5},则A∩B = {3}。
3. 差集差集是指一个集合中除去与另一个集合相同的元素所得到的集合。
用符号"-"表示。
例如,集合A = {1, 2, 3},集合B = {3, 4, 5},则A-B= {1, 2}。
4. 补集补集是指相对于某个全集而言,除去集合中的元素之外的所有元素所组成的集合。
用符号"\'"表示。
例如,设全集为U,集合A = {1, 2, 3},则A\' = U - A。
二、集合运算的应用实例集合运算在实际问题中有着广泛的应用,下面介绍几个常见的实例。
1. 学生选课情况分析在一所学校,有两个班级,分别是A班和B班。
A班有学生集合A,B班有学生集合B。
为了了解两个班级中有哪些学生同时选了物理课和化学课,可以通过求两个集合的交集来得到结果。
即A班选物理课的学生集合A∩B班选化学课的学生集合B。
2. 地理分布分析假设一个国家有A、B、C、D四个省份,A省有城市集合A,B省有城市集合B,C省有城市集合C,D省有城市集合D。
为了了解哪些城市同时属于A、B、C三个省份,可以通过求三个集合的交集来得到结果,即A∩B∩C。
初中数学教案集合的基本运算与应用

初中数学教案集合的基本运算与应用一、引言数学教学是培养学生逻辑思维和解决问题能力的重要环节。
而教案作为数学教学的指导工具,起到了极为重要的作用。
本文将介绍初中数学教案集合的基本运算与应用,帮助教师更好地指导学生学习。
二、集合与集合运算1. 集合的基本概念集合是由一些元素组成的整体。
可以用高斯括号表示,例如集合A={1, 2, 3}。
其中元素1、2、3属于集合A。
2. 集合的性质- 互异性:集合中的元素各不相同,没有重复的元素。
- 无序性:集合中的元素没有顺序,与元素的排列顺序无关。
- 固定性:集合中的元素是确定的,不会随时间或环境的改变而改变。
3. 集合的运算集合的基本运算包括并集、交集和差集。
- 并集:集合A和集合B的并集,表示为A∪B,是包含了A和B中所有元素的集合。
- 交集:集合A和集合B的交集,表示为A∩B,是包含了A和B 共同元素的集合。
- 差集:集合A和集合B的差集,表示为A-B,是包含了属于A 但不属于B的元素的集合。
三、应用案例1. Venn图的运用利用Venn图可以直观地展示不同集合之间的关系。
例如,有一个集合A表示喜欢篮球的学生,集合B表示喜欢足球的学生,可以通过画出两个圆表示A和B,圆的重叠部分即为同时喜欢篮球和足球的学生。
2. 集合的分类在实际应用中,集合可以按照不同的属性进行分类。
例如,根据学生的性别可以将学生集合分为男生集合和女生集合,根据住址可以将学生集合分为城市学生集合和农村学生集合。
3. 集合的应用集合的应用广泛存在于各个领域。
在概率统计中,集合可以用于表示样本空间和事件,帮助计算概率。
在数学建模中,集合可以用于描述问题中的各个部分和关系,帮助分析和解决问题。
四、教学建议1. 清晰的教学目标在设计数学教案时,应明确教学目标,让学生了解集合的基本概念和运算,并能够灵活应用于实际问题。
2. 合理的教学方法教师可以通过示例、练习和案例分析等方式引导学生掌握集合的基本运算与应用。
第1讲 集合的概念与运算 讲义--高一上学期数学人教A版(2019)必修第一册
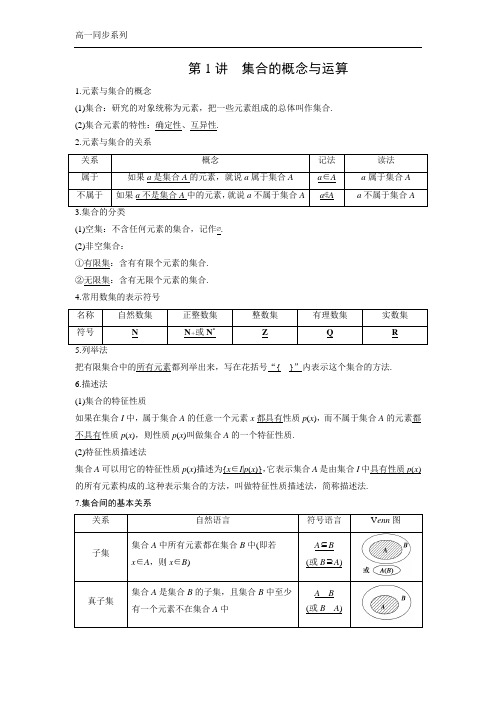
第1讲集合的概念与运算1.元素与集合的概念(1)集合:研究的对象统称为元素,把一些元素组成的总体叫作集合.(2)集合元素的特性:确定性、互异性.2.元素与集合的关系关系概念记法读法属于如果a是集合A的元素,就说a属于集合A a∈A a属于集合A不属于如果a不是集合A中的元素,就说a不属于集合A a∉A a不属于集合A 3.集合的分类(1)空集:不含任何元素的集合,记作∅.(2)非空集合:①有限集:含有有限个元素的集合.②无限集:含有无限个元素的集合.4.常用数集的表示符号名称自然数集正整数集整数集有理数集实数集符号N N+或N*Z Q R5.列举法把有限集合中的所有元素都列举出来,写在花括号“{__}”内表示这个集合的方法.6.描述法(1)集合的特征性质如果在集合I中,属于集合A的任意一个元素x都具有性质p(x),而不属于集合A的元素都不具有性质p(x),则性质p(x)叫做集合A的一个特征性质.(2)特征性质描述法集合A可以用它的特征性质p(x)描述为{x∈I|p(x)},它表示集合A是由集合I中具有性质p(x)的所有元素构成的.这种表示集合的方法,叫做特征性质描述法,简称描述法.7.集合间的基本关系关系自然语言符号语言V enn图子集集合A中所有元素都在集合B中(即若x∈A,则x∈B)A⊆B(或B⊇A)真子集集合A是集合B的子集,且集合B中至少有一个元素不在集合A中A B(或B A)集合相等集合A,B中元素完全相同或集合A,B互为子集A=B子集与真子集的区别与联系:一个集合的真子集一定是其子集,而其子集不一定是其真子集.8.集合的运算(1)如果一个集合包含了我们所要研究的各个集合的全部元素,这样的集合就称为全集,全集通常用字母U表示;集合的并集集合的交集集合的补集图形符号A∪B={x|x∈A,或x∈B}A∩B={x|x∈A,且x∈B}∁U A={x|x∈U,且x∉A}例1(大纲全国,1) 设集合A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则M中元素的个数为()A.3B.4C.5D.6例2 已知集合A={m+2,2m2+m},若3∈A,则m的值为________.[玩转跟踪]1.(新课标全国,1)已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},则B 中所含元素的个数为()A.3B.6C.8D.102.已知集合A是由a-2,2a2+5a,12三个元素组成的,且-3∈A,求实数a.3.(探究与创新)设A为实数集,且满足条件:若a∈A,则11-a∈A(a≠1).求证:(1)若2∈A,则A中必还有另外两个元素;(2)集合A不可能是单元素集.题型二集合的表示方法例3 下面三个集合:A={x|y=x2+1};B={y|y=x2+1};C={(x,y)|y=x2+1}. 问:(1)它们是不是相同的集合?(2)它们各自的含义是什么?例4 已知集合A ={x ∈R |ax 2+2x +1=0},其中a ∈R .若1是集合A 中的一个元素,请用列举法表示集合A .1.已知x ,y 为非零实数,则集合M =⎩⎨⎧m |m =x |x |+y |y |+⎭⎬⎫xy |xy |为( )A.{0,3}B.{1,3}C.{-1,3}D.{1,-3}2.(探究与创新)已知集合A ={x |ax 2-3x -4=0,x ∈R }: (1)若A 中有两个元素,求实数a 的取值范围; (2)若A 中至多有一个元素,求实数a 的取值范围.题型三 集合间的基本关系例5 集合{-1,0,1}共有________个子集. 例6 设集合⎭⎬⎫⎩⎨⎧∈+==Z k k x x M ,412|,⎭⎬⎫⎩⎨⎧∈+==Z k k x x N ,421|,则( ) A .N M =B .NM C .MN D .=N M ∅例7 已知集合A ={x |-3≤x ≤4},B ={x |2m -1<x <m +1},且B ⊆A . 求实数m 的取值范围.1.设M 为非空的数集,M ⊆{1,2,3},且M 中至少含有一个奇数元素,则这样的集合M 共有( ) A .6个B .5个C .4个D .3个2.(2016·山东北镇中学、莱芜一中、德州一中4月联考)定义集合A -B ={x |x ∈A 且x ∉B },若集合M ={1,2,3,4,5},集合N ={x |x =2k -1,k ∈Z },则集合M -N 的子集个数为( ) A.2 B.3C.4D.无数个3.已有集合A ={x |x 2-4x +3=0},B ={x |mx -3=0},且B ⊆A ,求实数m 的集合.题型四 集合的基本运算例8 设集合A ={x |x 2-4x +3<0},B ={x |2x -3>0},则A ∩B =( ) A.⎝⎛⎭⎫-3,-32 B.⎝⎛⎭⎫-3,32 C.⎝⎛⎭⎫1,32 D.⎝⎛⎭⎫32,3 例9 (2015·四川,1)设集合A ={x |(x +1)(x -2)<0},集合B ={x |1<x <3},则A ∪B =( ) A .{x |-1<x <3} B .{x |-1<x <1} C .{x |1<x <2} D .{x |2<x <3} 例10 (1)设全集U =R ,A ={x |x (x +3)<0},B ={x |x <-1},则图中阴影部分表示的集合为( )A .{x |-3<x <-1}B .{x |-3<x <0}C .{x |-1≤x <0}D .{x |x <-3}(2).若集合A ={x |-1≤2x +1≤3},B =⎩⎨⎧⎭⎬⎫x ⎪⎪x -2x ≤0,则A ∩B =( )A.{x |-1≤x <0}B.{x |0<x ≤1}C.{x |0≤x ≤2}D.{x |0≤x ≤1}例11 已知A ={x |2a ≤x ≤a +3},B ={x |x <-1,或x >5},若A ∩B =∅,求实数a 的取值范围.[玩转跟踪]1.若集合P ={x ||x |<3,且x ∈Z },Q ={x |x (x -3)≤0,且x ∈N },则P ∩Q 等于( ) A.{0,1,2} B.{1,2,3} C.{1,2} D.{0,1,2,3}2.如图,I 是全集,M 、P 、S 是I 的3个子集,则阴影部分所表示的集合是( )A.(M ∩P )∩SB.(M ∩P )∪SC.(M ∩P )∩(∁I S )D.(M ∩P )∪(∁I S )3.(探究与创新)已知集合A ={x |-2≤x ≤5},B ={x |2a ≤x ≤a +3},若A ∪B =A ,求实数a 的取值范围.1.已知集合A ={y |y =|x |-1,x ∈R },B ={x |x ≥2},则下列结论正确的是( ) A .-3∈A B .3∉B C .A ∩B =BD .A ∪B =B2.设集合M ={-1,1},N =⎩⎨⎧⎭⎬⎫x ⎪⎪1x<2,则下列结论中正确的是( ) A .N M B .M N C .N ∩M =∅D .M ∪N =R3.(2018·全国Ⅱ)已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为( ) A .9 B .8 C .5 D .44.(2018·济南模拟)设全集U =R ,集合A ={x |x -1≤0},集合B ={x |x 2-x -6<0},则右图中阴影部分表示的集合为( )A .{x |x <3}B .{x |-3<x ≤1}C .{x |x <2}D .{x |-2<x ≤1}5.(2018·潍坊模拟)设集合A =N ,B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x x -3≤0,则A ∩B 等于( ) A .[0,3) B .{1,2} C .{0,1,2}D .{0,1,2,3}6.(2017·全国Ⅱ)设集合A ={1,2,4},B ={x |x 2-4x +m =0}.若A ∩B ={1},则B 等于( ) A .{1,-3} B .{1,0} C .{1,3} D .{1,5}7.已知集合A ={x |-1<x <0},B ={x |x ≤a },若A ⊆B ,则a 的取值范围为( ) A .(-∞,0] B .[0,+∞) C .(-∞,0)D .(0,+∞)8.满足{a ,b }∪B ={a ,b ,c }的集合B 的个数是________.9.设集合A ={-1,1,3},B ={a +2,a 2+4},A ∩B ={3},则实数a 的值为________.10.已知集合M={-2,3x2+3x-4,x2+x-4},若2∈M,则满足条件的实数x组成的集合为________.11.已知全集I={2,3,a2+2a-3},若A={b,2},∁I A={5},求实数a,b.12.已知A={x|x2-3x+2=0},B={x|ax-2=0},且A∪B=A,求实数a组成的集合C.13.设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.(1)分别求A∩B,(∁R B)∪A;(2)已知C={x|a<x<a+1},若C⊆B,求实数a的取值构成的集合.14.已知集合A={x|0<x-a≤5},B={x|-a2<x≤6}.(1)若A∩B=A,求a的取值范围;(2)若A∪B=A,求a的取值范围.。
高考数学讲义:集合的运算(并集)(解析版)

第5讲:集合的运算(并集)【学习目标】1.理解两个集合的并集的含义.会求两个简单集合的并集;2.能使用Venn 图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.【基础知识】一、并集【考点剖析】考点一:并集的求解(基础)例1.若集合{2,1,2}M =--,集合{0,2}N =,则M N 等于()A.{2,1,2}--B.{2,1,0,2}--C.{}2D.{2,1,0}--【答案】B 【详解】因为集合{2,1,2}M =--,集合{0,2}N =,所以{2,1,0,2}M N =-- ,故选:B变式训练1:已知集合{}2,0,1M =-,{}1,0,1,2N =-,则M N = ()A.{}2,1,0,2--B.{}2,0,1-C.{}2,0,1,2-D.{}2,1,0,1,2--【答案】D 【详解】由{}2,0,1M =-,{}1,0,1,2N =-,∴{2,1,0,1,2}M N ⋃=--.故选:D.变式训练2:已知{|7}A x x =∈<N ,{5,6,7,8}B =,则集合A B 中的元素个数为()A.7B.8C.9D.10【答案】C 【详解】{0,1,2,3,4,5,6}A =,{0,1,2,3,4,5,6,7,8}A B = ,共9个元素.故选:C.变式训练3:已知集合A=1{1,2,}2A =,B={}2|,y y x x A =∈,A B = _______________.【答案】11{1,2,,4,}24【详解】因为B={y|y=x2,x∈A}=1144⎧⎫⎨⎬⎩⎭,,,所以A∪B=1112424⎧⎫⎨⎬⎩⎭,,,,.故答案为:1112424⎧⎫⎨⎬⎩⎭,,,,考点二:并集的求解(提升)例2.已知集合{}{}7,27A y y B x x =<=-≤≤,则A B = ()A.{}22x x -≤<B.{}7x x ≤C.{}7x x <D.{}27x x -≤<【答案】B 【详解】{}{}{}77,27A y y x x B x x =<=<=-≤≤,∴A B = {}7x x ≤,故选:B.变式训练1:若集合{0,1,2,3},{13}S T xx ==-<<∣,则S T = ()A.{|13}x x -<<B.{|13}x x -<≤C.{0,1,2}D.{|03}x x <≤【答案】B 【详解】画数轴如图:可看出并集为S T ⋃={|13}x x -<≤故选:B变式训练2:设集合{}{}21,02M x x N x x =-<<=<<,则M N = ()A.{|20}x x -<<B.{|01}x x <<C.{|02}x x <<D.{|22}x x -<<【答案】D 【详解】由{|21}M x x =-<<,{|02}N x x =<<,则{|22}M N x x =-<< 故选:D.变式训练3:设集合13{|}A x x =≤≤,{|24}B x x =<<,则A B = ()A.{|14}x x ≤<B.{|23}x x ≤≤C.{|23}x x <≤D.{|24}x x £<【答案】A 【详解】因为集合13{|}A x x =≤≤,{|24}B x x =<<,所以[13](24)[14)A B == ,,,,故选:A.考点三:并集的求解(拓展)例3.已知集合{|42}M x x =-<<,2{|60}N x x x =--<,则M N =()A.{|43}x x -<<B.{|42}x x -<<-C.{|22}x x -<<D.{|23}x x <<【答案】A 【详解】由题意,集合2{|60}{|23}N x x x x x =--<=-<<,且{|42}M x x =-<<,根据集合并集的概念及运算,可得{|43}M N x x ⋃=-<<.故选:A.变式训练1:若集合{}2270A x x x =-<,{}3B x x =>,则A B = ()A.{}x x >B.732x x ⎧⎫<<⎨⎬⎩⎭C.702x x ⎧⎫<<⎨⎬⎩⎭D.{0x x <或}3x >【答案】A 【详解】(){}727002A x x x x x ⎧⎫=-<=<<⎨⎬⎩⎭,{}3B x x =>,{}0A B x x ∴⋃=>.故选:A.变式训练2:已知集合{}220A x R x x =∈-<,{}14B x R x =∈≤≤,则A B = ()A.{}|04x x <<B.{}04x x <≤C.{}12x x ≤<D.{}24x x <≤【答案】B 【详解】因为{}{}22002A x R x x x R x =∈-<=∈<<,{}14B x R x =∈≤≤,所以{}04A B x x =<≤ .故选:B.变式训练3:已知集合()(){}410A x x x =+-≤,{}2B x x =<,则A B = ()A.{}22x x -<<B.{}21x x -<≤C.{}24x x -<≤D.{}42x x -≤<【答案】D 【详解】由不等式()()410x x +-≤,解得41x -≤≤,即{}41A x x =-≤≤,又因为{}22B x x =-<<,所以{}42A B x x ⋃=-≤<.故选:D.考点四:已知并集求参数例4.设集合{}{}20,2,|40A B x x mx n ==-+=,,若{}0,1,2,3,4A B = ,则m n +的值是()A.1B.3C.5D.7【答案】D 【详解】因为集合{}{}20,2,|40A B x x mx n ==-+=,,{}0,1,2,3,4A B = ,则{}1,3B =,所以,1、3是方程20x mx n -+=的两根,所以,1313mn+=⎧⎨⨯=⎩,因此,437m n +=+=.故选:D.变式训练1:已知集合{}21,A a=,{}1,0,1B =-,若A B B = ,则A 中元素的和为()A.0B.1C.2D.1-【答案】B 【详解】A B B =Q U ,A B ∴⊆,20a ∴=,则0a =,{}1,0A ∴=,因此,集合A 中元素的和为011+=.故选:B.变式训练2:设集合{}24A x Z x =∈≤,{}1,2,B a =,且A B A = ,则实数a 的取值集合为()A.{}2,1,0--B.{}2,1--C.{}1,0-D.{}2,1,1--由题得{}{}242,1,0,1,2A x Z x =∈≤=--,因为{}1,2,B a =,且A B A = ,所以实数a 的取值集合为{}2,1,0--.故选:A变式训练3:已知集合{}2320A x x x =-+=,{}210B x x ax a =-+-=.(1)若A B A = ,求实数a 的值;【答案】(1)2a =或3;【详解】(1)由2320x x -+=得1x =或2,所以{1,2}A =,由210x ax a -+-=得1x =或1a -,所以1,1B a B ∈-∈,因为A B A ⋃=,所以B A ⊆,所以11a -=或2,所以2a =或3;考点五:已知并集求参数范围(基础)例5.已知集合{}2430A x x x =-+<,{}B x x m =>,若{}1A B x x => ,则()A.1m ≥B.13m ≤<C.13m <<D.13m ≤≤【答案】B 【详解】解不等式2430x x -+<可得13x <<,所以{}13A x x =<<,因为{}B x x m =>,{}1A B x x ⋃=>,所以13m ≤<.故选:B.变式训练1:已知集合{|1}A x x =≤,{|}B x x a =≥,且A B R = ,则实数a 的取值范围是()A.1a <B.1a >C.1a ≤D.1a ≥【答案】C 【详解】解:{|1}A x x =≤ ,{|}B x x a =≥,且A B R = ,故选:C.变式训练2:已知集合{}2A x x =>,{}B x x m =<,若A B R = ,则实数m 的取值范围()A.2m ≤B.2m <C.2m ≥D.2m >【答案】D 【详解】因为A B R = ,即集合A 与集合B 包含了所有的实数,那么m>2.故选:D.变式训练3:设集合{}240A x x =-≥,{}20B x x a =+≤,且A B R = ,则a 的取值范围是()A.{|4}x x ≥-B.{|4}x x ≤-C.{|2}x x ≥-D.{|2}x x ≤-【答案】B 【详解】240x -≥,解得:2x ≥或2x -≤,即{2A x x =≥或2}x £-,{|}2aB x x =≤-,A B R = ,22a∴-≥,解得:4a ≤-.故选:B考点六:已知并集关系,求参数范围(提升)例6.已知集合{|25},{|121}A x x B x m x m =-<<=+≤≤-.(1)当3m =时,求A B U ;(2)若A B A = ,求实数m 的取值范围.【答案】(1){|25}A B x x =-<≤ ;(2)3m <.【详解】(1)当3m =时,B 中不等式为45x ≤≤,即{}|45B x x =≤≤,∴{|25}A B x x =-<≤ (2)∵A B A = ,∴B A ⊆,①当B =∅时,121m m +>-,即2m <,此时B A ⊆;②当B ≠∅时,12112215m m m m +≤+⎧⎪+>-⎨⎪-<⎩,即23m ≤<,此时B A ⊆.综上m 的取值范围为3m <.变式训练1:已知集合{}2430A xx x =-+>∣,{4}B x m x m =<≤+∣,若A B R = ,则实数m 的取值范围是()A.{|12}x x -≤<B.{|11}x x -≤<C.{|1}x x <D.{|1}x x ≥-【答案】B 【详解】因为{}2430{|1A xx x x x =-+>=<∣或3}x >,{4}B x m x m =<≤+∣,且A B R = ,所以有143m m <⎧⎨+≥⎩,解得11m -≤<,故选:B.变式训练2:已知集合{}2|3100M x x x =--≤,{}|121N x a x a =+≤≤+.(1)若M N M = ,求实数a 的取值范围.【答案】(1){|2}m m ≤.【详解】(1)(2),M N M N M=∴⊆ ①若N =∅,则121a a +>+,解得0a <,符合题意;②若N ≠∅,则12121512a a a a +≤+⎧⎪+≤⎨⎪+≥-⎩,解得02a ≤≤.综合可得实数a 的取值范围是{|2}m m ≤.变式训练3:已知集合{}121A x a x a =+≤≤+,{}25B x x =-≤≤.(1)若3a =,求A B ;(2)若A B B = ,求实数a 的取值范围.【答案】(1){}27x x -≤≤;(2)2a ≤.【详解】(1)当3a =时,{}47A x x =≤≤,{}25B x x =-≤≤.∴{}27A B x x ⋃=-≤≤(2)由A B B = 得A B ⊆,当A =∅时,211a a +<+,0a <当A ≠∅时,有12215121a a a a +≥-⎧⎪+≤⎨⎪+≤+⎩,解得02a ≤≤综上a 的取值范围为:2a ≤.【过关检测】1、已知集合{3,2,1}A =---,{2,1,0}B =--,则A B = ()A.{3,2,1,0}---B.{3,2,1}---C.{2,1,0}--D.{2,1}--【答案】A 【详解】由{3,2,1}A =---,{2,1,0}B =--,则{3,2,1,0}A B ⋃=---.故选:A2、若集合{}=2,1,1M --,集合{}0,1N =,则M N 等于()A.{}2,1,0,1--B.{}2,1,1--C.{}2,1,0--D.{}1【答案】A 【详解】因为集合{}=2,1,1M --,集合{}0,1N =,所以M N ⋃{}2,1,0,1=--,故选:A3、已知集合{}210,A x x x =-≤∈Z ,{}2,B y y x x A ==∈,则A B = ()A.{2,1,1,2}--B.{2,1,0,1,2}--C.{1,1}-D.{0}【答案】B 【详解】集合{}{}{}210,11,1,0,1A x x x x x x =-≤∈=-≤≤∈=-Z Z ,{}{}2,2,0,2B y y x x A ==∈=-,{}2,1,0,1,2A B ∴=--U ,故选:B.4、已知集合{}2,4,6A =,{}1,3,4,6B =,则A B 中元素的个数是()A.2B.5C.6D.7【答案】B 【详解】由题意得,{}1,2,3,4,6A B = ,显然A B 中元素的个数是5.故选:B.5、若集合{1,3,}A x =,{}2,1B x =,且{1,3,}A B x = ,则满足条件的x 的个数是()A.1B.2C.3D.4【答案】C 【详解】∵{1,3,}A B x = ,{1,3,}A x =,{}2,1B x =,∴23x =或2x x =,解得x =或1x =或0x =,1x =显然不合题意,经检验0x =或故选:C.6、已知集合{}0,1,2A ,{}21,B x x n n A ==-∈,则A B 中元素的个数为()A.1B.3C.4D.5【答案】D【详解】解:{}0,1,2A =,{}1,1,3B =-;∴{}1,0,1,2,3A B ⋃=-;∴A B 中元素的个数为5.故选:D.7、已知集合{}1,0,1A =-,{}2|1,B y y x x A ==+∈,则集合A B 中元素的个数为()A.4B.3C.2D.1【答案】A【详解】当1,0,1x =-,对应2,1,2y =,{}2,1B ∴=,则{}1,0,1,2A B ⋃=-,A B 中有4个元素.故选:A8、满足条件{}{},,,,a b M a b c d = 的所有集合M 的个数是()A.1B.2C.3D.4【答案】D【详解】解:由{}{},,,,a b M a b c d ⋃=,则{},M c d ={},,M a c d =,或{},,M b c d =,或{},,,M a b c d =共4个,故选D.9、已知集合{0,1,2}M =,{}2N x x =<,则M N = ()A.{0}B.{}2x x <C.{0,1}D.{}2x x ≤【答案】D【详解】由题意,集合{0,1,2}M =,{}2N x x =<,根据集合并集的概念及运算,可得{}2M N x x ⋃=≤.故选:D.10、已知集合{}13A x x =<<,{}02B x x =<<,则A B = ()A.{}12x x <<B.{}13x x x <<C.{}02x x <<D.{}03x x <<【答案】D【详解】因为{}13A x x =<<,{}02B x x =<<,所以A B = {}03x x <<故选:D11、已知集合{1},{12}A x x B x x =>=-<<∣∣,则A B = ()A.{1}x x >-∣B.{2}x x <∣C.{11}x x -<<∣D.{12}x x <<∣【答案】A【详解】因为{1},{12}A x x B x x =>=-<<∣∣,所以A B = {1}x x >-∣,故选:A.12、已知集合{}42M x x =-<<,{}(2)(3)0N x x x =+-<,则M N = ()A.{}43x x -<<B.{}42x x -<<-C.{}22x x -<<D.{}23x x <<【答案】A【详解】解:∵{}42M x x =-<<,{}{}(2)(3)023N x x x x x =+-<=-<<,∴{}43M N x x ⋃=-<<,故选:A.13、已知集合{}2230A xx x =--<∣,1{0}2B x x =->∣,则A B = ()A.13{}22x x <<∣B.3{}2x x <∣C.1{1}2x x -<<∣D.{1}xx >-∣【答案】D【详解】解:∵集合{}2323012A xx x x x ⎧⎫=--<=-<<⎨⎩⎭∣∣,11022B x x x x ⎧⎫⎧⎫=->=>⎨⎬⎨⎬⎩⎭⎩⎭∣∣,∴{1}A B xx ⋃=>-∣.故选:D.14、已知集合{}{}2|5140,|5100A x x x B x x =--<=-<,则A B = ()A.{}|27x x -<<B.{}27x x <<C.{}|7x x <D.{}2x x >-【答案】C【详解】解不等式25140x x --<得27x -<<,所以{}27A x x =-<<;解不等式5100x -<得2x <,所以{}2B x x =<,所以{}|7A B x x ⋃=<.故选:C.15、若集合{1,2}A =-,{}240B x x x m =-+=,且{1,2,5}A B =- ,则()A.2B∈B.5B ∉C.1B ∈D.1B-∈【答案】D【详解】依题意,5∈B ,则25200m -+=,解得5m =-,故{1,5}B =-;观察可知,1B -∈,故选:D.16、若集合{1,1}A =-,{|1}B x mx ==,且A B A = ,则m 的值为()A.1或0B.1-或0C.1或1-或0D.1或1-或2【答案】C【详解】,A B A B A⋃=⊆ ∴B ∴=∅;{1}B =-;{1}B =当B =∅时,0m =当{1}B =-时,1m =-当{1}B =时,1m =故m 的值是0;1;1-故选:C.17、已知集合2{|20}A x x x =-≥,{|}B x x a =<,且A B = R ,则实数a 的取值范围是()A.0a <B.0a >C.2a >D.2a ≥【答案】D【详解】由220x x -≥解得0x ≤或2x ≥,则{|0,A x x =≤或}2x ≥,又{|}B x x a =<,若A B = R ,则2a ≥.故选:D .18、已知集合{}2430A x x x =-+=,{}230B x x ax =-+=.(1)若A B B = ,求实数a 的值;【答案】(1)4;【详解】{}2430A x x x =-+=={}1,3,(1)因为A B B ⋃=,所以A B ⊆,所以1和3是230x ax -+=的两个实根,所以13a +=,即4a =.19、设集合{213}A xm x m =-+<<-+∣,{216}B x x =≤+≤∣.(1)若1m =,求A B ;(2)若A B B = ,求实数m 的取值范围.【答案】(1){|15}A B x x =-<≤ ;(2){|0}m m ≤.【详解】解:(1)因为{213}A xm x m =-+<<-+∣,{216}{15}B x x x x =≤+≤=≤≤∣∣,(1)若1m =,{12}A xx =-<<∣,则{|15}A B x x =-<≤ .(2)因为A B B = ,所以A B ⊆,①当A =∅时,213m m -+≥-+,即2m ≤-;②当A ≠∅时,213,211,35,m m m m -+<-+⎧⎪-+≥⎨⎪-+≤⎩解得20m -<≤,综上,实数m 的取值范围是{|0}m m ≤.20、已知集合{}25A x x =-≤≤,{}121B x m x m =+≤≤-.(1)若A B A = ,求实数m 的取值范围;(2)当{},C x x A x Z =∈∈时,求C 的非空真子集的个数;【答案】(1)(],3-∞;(2)254.【详解】(1)A B A =Q U ,B A ∴⊆.①若B =∅,则121m m +>-,解得2m <;②若B ≠∅,则121m m +≤-,可得2m ≥.由B A ⊆可得12215m m +≥-⎧⎨-≤⎩,解得33m -≤≤,此时23m ≤≤.综上所述,实数m 的取值范围是(],3-∞;(2){}{},2,1,0,1,2,3,4,5C x x A x Z =∈∈=-- ,集合C 中共8个元素,因此,集合C 的非空真子集个数为822254-=;21、已知集合{}13A x x =≤≤,集合{}21B x m x m =≤≤-.(1)当1m =-时,求A B ;(2)若A B B = ,求实数m 的取值范围.【答案】(1){}23A B x x =-≤≤ ;(2){}2m m ≤-.【详解】(1)当1m =-时,{}22B x x =-≤≤,又{}13A x x =≤≤,∴{}23A B x x ⋃=-≤≤;(2)∵A B B = ,则A B ⊆,∴B ≠∅,则有:212113m m m m <-⎧⎪≤⎨⎪-≥⎩,解之得:2m ≤-.∴实数m 的取值范围是{}2m m ≤-.。
集合的基本运算与应用

集合的基本运算与应用集合是数学中的一个基本概念,它由一组互不相同的元素组成。
在集合理论中,存在着一些基本的运算,例如并集、交集、差集和补集等。
这些运算不仅在数学中有着重要的作用,也在实际生活中有着广泛的应用。
一、并集并集是指将两个或多个集合中的所有元素放在一起,形成的新集合。
用符号表示为“∪”。
例如,设集合A={1, 2, 3},集合B={3, 4, 5},那么A和B的并集可以表示为A∪B={1, 2, 3, 4, 5}。
并集运算满足交换律和结合律,即A∪B=B∪A,(A∪B)∪C=A∪(B∪C)。
并集运算在实际生活中有很多应用。
比如,在购物时,我们可以将自己选择的商品集合与优惠券的商品集合进行并集运算,得到的新集合即为可以享受优惠的商品。
二、交集交集是指两个或多个集合中共有的元素组成的新集合。
用符号表示为“∩”。
例如,设集合A={1, 2, 3},集合B={3, 4, 5},那么A和B的交集可以表示为A∩B={3}。
交集运算满足交换律和结合律,即A∩B=B∩A,(A∩B)∩C=A∩(B∩C)。
交集运算在实际生活中也有广泛的应用。
比如,在餐厅中,我们可以将自己喜欢的菜品集合与朋友喜欢的菜品集合进行交集运算,得到的新集合即为大家都喜欢的菜品。
三、差集差集是指一个集合减去另一个集合中的元素所得到的新集合。
用符号表示为“-”。
例如,设集合A={1, 2, 3},集合B={3, 4, 5},那么A和B的差集可以表示为A-B={1, 2}。
差集运算不满足交换律和结合律,即A-B≠B-A,(A-B)-C≠A-(B-C)。
差集运算在实际生活中也有重要的应用。
比如,在工作中,我们可以将自己需要完成的任务集合与已完成的任务集合进行差集运算,得到的新集合即为尚未完成的任务。
四、补集补集是指相对于某个全集,除了一个集合中的元素之外,其余的元素组成的新集合。
用符号表示为“'”。
例如,设集合A={1, 2, 3},全集为U={1, 2, 3, 4, 5},那么A的补集可以表示为A'={4, 5}。
集合的运算与应用知识点总结

集合的运算与应用知识点总结在数学中,集合是由一组不同元素组成的整体。
集合的运算是指对集合进行操作和组合的过程,而集合的应用则是指将集合概念应用于实际问题解决的过程。
本文将对集合的运算及其应用知识点进行总结。
一、集合的基本运算1. 并集:表示将两个或多个集合中的所有元素合并在一起,记作A∪B。
例如,A={1, 2, 3},B={2, 3, 4},则A∪B={1, 2, 3, 4}。
2. 交集:表示两个或多个集合中共有的元素,记作A∩B。
例如,A={1, 2, 3},B={2, 3, 4},则A∩B={2, 3}。
3. 差集:表示从一个集合中减去与另一个集合相同元素后的剩余元素,记作A-B。
例如,A={1, 2, 3},B={2, 3, 4},则A-B={1}。
4. 互斥:表示两个集合没有共同元素,记作A⊕B。
例如,A={1, 2, 3},B={4, 5, 6},则A⊕B={1, 2, 3, 4, 5, 6}。
5. 子集:表示一个集合的所有元素都属于另一个集合,记作A⊆B。
例如,A={1, 2},B={1, 2, 3},则A⊆B。
6. 补集:表示在给定的全集中,除了集合中的元素外的其他元素,记作A'。
例如,若全集为U={1, 2, 3, 4, 5},A={1, 2},则A'={3, 4, 5}。
二、集合的应用1. 概率论中的集合运算:在概率论中,集合的运算常用于计算事件的概率。
通过对样本空间的划分,可以将事件表示为集合,并利用集合的运算来计算事件的概率。
例如,在一个拥有6个面的骰子中,我们可以用样本空间Ω={1, 2, 3, 4, 5, 6}表示。
若事件A表示出现的数是一个偶数集合{2, 4, 6},事件B表示出现的数不超过3的集合{1, 2, 3},则可以通过集合运算求得事件A和事件B的交集、并集等,进而计算事件发生的概率。
2. 集合论在数据库中的应用:在数据库中,集合论被广泛应用于数据查询和操作。
《集 合的基本运算》 讲义

《集合的基本运算》讲义一、集合的概念在数学中,集合是把一些确定的、不同的对象看作一个整体,这个整体就叫做集合。
集合中的对象称为元素。
例如,一个班级的所有学生可以组成一个集合,这个集合中的元素就是每个学生;自然数也可以组成一个集合,其元素就是 0、1、2、3……集合通常用大写字母表示,如A、B、C 等;元素用小写字母表示,如 a、b、c 等。
如果一个元素 a 属于集合 A,记作 a∈A;如果一个元素 b 不属于集合 A,记作 b∉A。
二、集合的表示方法1、列举法把集合中的元素一一列举出来,写在大括号内。
例如,集合 A ={1, 2, 3, 4, 5}。
2、描述法用集合所含元素的共同特征来表示集合。
例如,集合 B ={x | x是大于 5 的整数}。
3、图示法(韦恩图)用封闭曲线的内部表示集合。
三、集合间的关系1、子集如果集合 A 中的任意一个元素都是集合 B 中的元素,就说集合 A是集合 B 的子集,记作 A⊆B。
例如,集合 A ={1, 2, 3},集合 B ={1, 2, 3, 4, 5},则 A 是 B 的子集。
2、真子集如果集合 A 是集合 B 的子集,且集合 B 中至少有一个元素不属于集合 A,就说集合 A 是集合 B 的真子集,记作 A⊂B。
例如,集合 A ={1, 2},集合 B ={1, 2, 3},则 A 是 B 的真子集。
3、相等如果集合 A 和集合 B 中的元素完全相同,就说集合 A 和集合 B 相等,记作 A = B。
四、集合的基本运算1、交集由属于集合 A 且属于集合 B 的所有元素组成的集合,称为集合 A与集合 B 的交集,记作A∩B。
例如,集合 A ={1, 2, 3},集合 B ={2, 3, 4},则A∩B ={2, 3}。
用韦恩图表示交集,就是两个集合重叠的部分。
2、并集由属于集合 A 或属于集合 B 的所有元素组成的集合,称为集合 A 与集合 B 的并集,记作 A∪B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
即 矛盾;
综上,a的取值范围是a≤-3.
(3)∵A ( )=A,∴A ,∴A
①若B= ,则 <0 适合;
②若B≠ ,则a=-3时,B= ,A B= ,不合题意;
a>-3,此时需1 B且2 B,将2代入B的方程得a=-1或a=-3(舍去);
将1代入B的方程得a2+2a-2=0
∴a≠-1且a≠-3且a≠-1
(2)由题意知, 或 或 或
根据元素的互异性得 或 即为所求.
考点二:集合的运算
典型例题:
例1.设全集 , 方程 有实数根 , 方程
有实数根 ,求 .
解:当 时, ,即 ;
当 时, 即 ,且 ∴ ,
∴
而对于 , 即 ,∴ .
∴
例2.已知 , 或 .
(1)若 ,求 的取值范围;
(2)若 ,求 的取值范围.
8.已知集合A={x| },B={x| },且A∩B=B,求实数m的取值范围。
9.已知集合 ,若 ,求实数a的值.
10已知全集U=R,A= ,试用列举法表示集合A
11.已知关于x的不等式 <0的解集为M.
(1)当a=4时,求集合M(2)若3∈M且5∈M,求实数a的取值范围.
2.集合中的元素属性具有:
(1)确定性;(2);(3).
3.集合的表示法常用的有、和韦恩图法三种,有限集常用,无限集常用,图示法常用于表示集合之间的相互关系.
二、元素与集合的关系
4.元素与集合是属于和的从属关系,若a是集合A的元素,记作,若a不是集合B的元素,记作.但是要注意元素与集合是相对而言的.
(1)∵A是空集,∴方程mx2-2x+3=0无解.
∴Δ=4-12m<0,即m> .
(2)∵A中只有一个元素,
∴方程mx2-2x+3=0只有一个解.
若m=0,方程为-2x+3=0,只有一解x= ;
若m≠0,则Δ=0,即4-12m=0,m= .
∴m=0或m= .
(3)A中至多只有一个元素包含A中只有一个元素和A是空集两种含义,根据(1)、(2)的结果,
例2.设集合 , , ,求实数a的值.
解:此时只可能 ,易得 或 。
当 时, 符合题意。
当 时, 不符合题意,舍去。
故 。
例3.已知集合A={x|mx2-2x+3=0,m∈R}.
(1)若A是空集,求m的取值范围;
(2)若A中只有一个元素,求m的值;
(3)若A中至多只有一个元素,求m的取值范围.
解:集合A是方程mx2-2x+3=0在实数范围内的解集.
例6若集合 ,则有()
A. B. C. D.
例7若集合 , ,且 ,则 的值为()
A. B. C. 或 D. 或 或
例8已知 , ,则 等于()
A. B. C. D.
例9关于实数x的不等式 与x -3(a+1)x+2(3a+1)≤0(a∈R)的解集依次为A,B 求使 成立的实数a的取值范围
例10.已知集合A={x2x+2=0},集合B={xax4=0},且AB=A,求实数a的值.
3.设集合A={x|(x+2)(x-5)≤0},B={x|a+1≤x≤2a-1},若B A,则实数a的取值范围是________
4.已知 , ,则 .
5.已知 , , ,则 等于()
A. B. C. D.
6.设全集 , ,那么 等于_________.
7、已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是________.
10.空集 是一个特殊而又重要的集合,它不含任何元素, 是任何集合的, 是任何非空集合的,解题时不可忽视 .
四、集合的运算
1.交集:由的元素组成的集合,叫做集合A与B的交集,记作A∩B,即A∩B=.
2.并集:由的元素组成的集合,叫做集合A与B的并集,记作A∪B,即A∪B=.
3.补集:集合A是集合S的子集,由的元素组成的集合,叫做S中子集A的补集,记作 ,即 =.
解:(1) ,∴ ,解之得 .
(2) ,∴ .∴ 或 , 或
∴若 ,则 的取值范围是 ;若 ,则 的取值范围是 .
针对练习2:
1.已知集合A= B=
(1)当m=3时,求 ;
(2)若A B ,求实数m的值.
解:由 得 ∴-1<x≤5,∴A= .
(1)当m=3时,B= ,则 = ,
∴ = .
(2)∵A= ∴有42-2×4-m=0,解得m=8.
考点三:集合的综合应用
例1设集合M={x|x= ,k∈Z},N={x| x= k∈Z},则()
A.M=N B.M N C.M N D.M∩N=φ
例2满足 的集合M的个数是_______个.
例3已知集合A={0,2,3},B={x|x=a·b,a、b∈A},则集合B的真子集有()
A.7个B.8个C.15个D.16个
解:(1)a=0,S= , P成立a 0,S ,由S P,P={3,-1}
得3a+2=0,a=- 或-a+2=0,a=2;∴a值为0或- 或2.
(2)B= ,即m+1>2m-1,m<2∴ A成立.
B≠ ,由题意得 得2≤m≤3
∴m<2或2≤m≤3即m≤3为取值范围.
注:(1)特殊集合 作用,常易漏掉
得m=0或m≥ .
针对练习1:
1.若a,b R,集合 求b-a的值.
解:由 可知a≠0,则只能a+b=0,则有以下对应关系:
①或 ②
由①得 符合题意;②无解.所以b-a=2.
2:(1)P={x|x2-2x-3=0},S={x|ax+2=0},S P,求a取值?
(2)A={-2≤x≤5},B={x|m+1≤x≤2m-1},B A,求m。
五、集合的常用运算性质
1.A∩A=,A∩ =,A∩B=,B∩A,A∪A=,
A∪ =,A∪B=B∪A
2. =, =, .
3. ,
,
4.A∪B=A
A∩B=A
考点一:集合的概念
典型例题:
例1.已知集合 ,试求集合 的所有子集.
解:由题意可知 是 的正约数,所以 可以是 ;相应的 为
,即 .
∴ 的所有子集为 .
例11设 ,集合 , , .
若 中至少有一个不是空集,求实数 的取值范围.
课后作业:
1.满足条件M∪{1}={1,2,3}的集合M的个数为()
A.1 B.2 C.3 D.4
2如图所示,u是全集,M、P、S是U的三个子集,则阴影部分所表示的集合是()
A.(M∩P)∩S B.(M∩P)∪S C.(M∩P)∩( S) D.(M∩P)∪( S)
3.(1)已知A={a+2,(a+1)2,a2+3a+3}且1∈A,求实数a的值;
(2)已知M={2,a,b},N={2a,2,b2}且M=N,求a,b的值.
解:(1)由题意知:
a+2=1或(a+1)2=1或a2+3a+3=1,
∴a=-1或-2或0,根据元素的互异性排除-1,-2,∴a=0即为所求.
当a=-1时,B= 满足条件;
当a=-3时,B= 满足条件;
综上,a的值为-1或-3.
(2)对于集合B,
=4(a+1)2-4(a2-5)=8(a+3).
∵A B=A,∴B A,
①当 <0,即a<-3时,B= ,满足条件;
②当 =0,即a=-3时,B ,满足条件;
③当 >0,即a>-3时,B=A= 才能满足条件,
此时B= ,符合题意,故实数m的值为8.
2:设集合A= B
(1)若A B 求实数a的值;
(2)若A B=A,求实数a的取值范围;
(3)若U=R,A ( )=A.求实数a的取值范围.
解:由x2-3x+2=0得x=1或x=2,故集合A=
(1)∵A B ∴2 B,代入B中的方程,
得a2+4a+3=0,∴a=-1或a=-3;
例4设A={x|x= ,k∈N},B={x|x≤6,x≤Q},则A∩B等于()
A.{l,4} B.{1,6} C.{4,6} D.{1,4,6}
例5已知A={x|y=x,x∈R},B={y|y=x2,x∈R},则A∩B等于()
A.{x|x∈R} B.{y|y≥0} C.{(0,0),(1,1)} D.φ
三、集合与集合的关系
5.集合与集合的关系用符号表示.
6.子集:若集合A中都是集合B的元素,就说集合A包含于集合B(或集合B包含集合A),记作.
7.相等:若集合A中都是集合B的元素,同时集合B中都是集合A的元素,就说集合A等于集合B,记作.
8.真子集:如果就说集合A是集合B的真子集,记作.
Hale Waihona Puke 9.若集合A含有n个元素,则A的子集有个,真子集有个,非空真子集有个.
龙文教育学科教师辅导讲义
学员姓名:年级:新高一教师:
课题
集合运算的综合应用
教学目标
熟练掌握集合运算的方法与技巧,并能解决相关综合问题
重点、难点
集合运算的方法与技巧
考点及考试要求
熟练掌握集合运算的方法与技巧,并能解决相关综合问题
教学内容
知识框架:
一、集合
1.集合是一个不能定义的原始概念,描述性定义为:某些指定的对象就成为一个集合,简称.集合中的每一个对象叫做这个集合的.
