增长率问题
一元二次方程增长率问题公式

一元二次方程增长率问题公式
一元二次方程平均增长率问题公式:a(1+x)n=b。
(a为起始量,b 为终止量,n为增长的次数,x为平均增长率)
平均增长率中的数量关系:若增长的基数为a,平均增长率为x,则第一次增长后的数量为a(1+x);第二次增长是以a(1+x)为基数的,增长率也为x,故第二次增长后的数量为a(1+x)2。
同样的道理,平均降低率中的数量关系:若降低的基数为a,平均降低率为x,则第一次降低后的数量为a(1-x);第二次降低是以a(1-x)为基数的,降低率也为x,故第二次降低后的数量为a(1-x) 2。
在解决增长(降低)率的问题时,常用的方法技巧是:
通常是利用公式建立方程。
平均增长率公式:a(1+x)n=b。
(a为起始量,b为终止量,n为增长的次数,x为平均增长率);平均降低率公式:a(1-x) n =b。
(a为起始量,b为终止量,n为降低的次数,x为平均降低率)。
解析:本题中考察的是增长率的问题,(1)中设这两年该校植树
棵数的年平均增长率为x,根据第一年及第三年的植树棵数,即可得出关于x的一元二次方程,解之取其正值即可得出结论。
列出的方程为500(1+x)=720,得:x=0.2=20%,x=﹣2.2(不合题意,舍去);(2)中根据第四年植树的棵数=第三年植树的棵数×(1+增长率),即可求出结论。
720×(1+20%)=864(棵)。
严格套用增长率的公式求解即可,但是一定要明确n是多少,也就是一定要确定好年份之间的关系。
解题的关键和所有的方程解应用题是相同的:(1)找准等量关系,正确列出一元二次方程;(2)根据数量关系,列式计算。
资料分析--增长率问题

资料分析--增长率问题资料分析——增长率问题公务员行测考试的资料分析题目要想做的又快又准,首先要理解清楚题目问的什么,材料讲的又是什么。
说白了,就是能读懂题目和材料。
读懂题目和材料的前提是理解相关的统计概念,并熟练掌握相关统计概念的计算方法。
这里给大家介绍增长率、增长量两个概念。
当然提到增长率、增长量,就不能不提减少率、减少量,因为这是两个相对应的概念。
上一篇给大家了解了基期、末期,存有了基期、末期这两个量,就可以谋增长率、增长量或者增加率为、增加量,他们之间的关系如下:增长量(增量)、增加量(NaHCO)增长量=末期量-基期量(末期量>基期量)增加量=基期量-末期量(末期量增长率(增长幅度、增长速度、增幅、增速)增长率=增长量÷基期量×100%=(末期量-基期量)÷基期量×100%由此可知,增长量的另外一种算法为:增长量=基期量×增长率【讲解】真题中经常会问到增长最多、增长最快的量是哪一个?此时我们要注意增长最多是指的增长量谁最多,增长最快是指的增长率谁最大。
【基准】某校去年招生人数为2000人,今年招生人数为2400人,则今年的增幅为(2400-2000)/2000。
【注】解题时,我们不用乘上100%,自己知道就行了。
后面的讲解及其他真题解析,我们都省略掉了乘上100%,后面就不再解释。
减少率(减少幅度、减少速度)增加率为=增加量÷基期量×100%由此可知,减少量的另外一种算法为:增加量=基期量×增加率为【例】某校去年招生人数2400人,今年招生人数为1800人,则今年的减幅为(2400-1800)/2400。
【备注】很显著,“增加率为”本质上就是一种未拎负号的“增长率”。
如果发生增长率为-10%,就是指增加率仅10%。
【例1】(节选自2021年424联考材料二)2021年1~3月,法国货物贸易进出口总额为2734.4亿美元,同比快速增长13.4%。
LI一元一次方程应用题增长率问题

原计划:小麦x产量+玉1米8—产x量 =18吨
实际:小1.麦12产x量+玉1米.1(产18量—x) =20吨
1、某城市现有人口42万,计划一年后城镇人口 增加0.8%,农村人口增加1.1%,这样全市人 口将增加1%,求这个城市现有城镇人口数和 农村人口数。
分析:增长率:城镇12% 农村10%
解:设七月份节约煤x公斤。 则八月份节约煤(1+20%)x 公斤,
九月份节约煤(1+20%)(1+25%)x公斤
依题意得:x+ (1+20%)x +(1+20%)(1+25%)x=7400 x=2000
(1+20%) (1+25%)x=3000 答:该食堂九月份节约煤3000公斤.
4、 某商店为了促销G牌空调机,承诺 2004年元旦那天购买该机可分两期付款,
现在:城x镇 +农42村-x =42
一年后:1.城00镇8x +农1.村011(42-x) =42 ×(1+1%)
2、某工厂甲乙两个车间去年计划共完成利 税720万元,结果甲车间超过计划15%,乙车 间超过计划10%,两车间共完成利税812万元, 去年两车间各完成利税多少万元?
分析:增长率: 甲15% 乙10%
计划: 甲x + 7乙20-x =720
实际:(1+甲15%)x + (乙1+10%)(720-x) =812
X=400,则甲车间去年完成400×(1+15%) =460
乙车间去年完成320×(1+10%)=352
答:甲车间去年完成460万元,乙车间去年完成 352万元。
增长率问题

若设该校今明两年在实验器材投资上
的平均增长率是x,则可列方程 为 .
当 堂 训 练
4、某超市一月份营业额为200万元,一月、 二月、三月的营业额共 1000 万元,如果平 均月增长率为x,可得方程为 ( D )
A、200(1+x)2=1000
B、200+200×2×x=1000 C、200+200×3×x=1000
1210 斤。
7.某试验田去年亩产1000斤,今年比去年增产
了X%,今年亩产为 1000(1+X%) 斤,明年 再增产X%,明年产量为1000(1+X%) 斤。
2
课前热身
8.某厂一月份产钢50吨,二月份的增长率是
50(1+x) 吨。 x,则该厂二月分产钢____________
9.某厂一月份产钢50吨,二、三月份的增长
3.某产品,原来每件的成本价是200元,若
每件售价280元,则每件利润是
80元 。
每件利润率是 40% 。 利润=成本×利润率 4.康佳生产彩电,第一个月生产了5000台, 第二个月增产了50%,则第二个月比第一个
5000×50% 台,第二个月生产 了 5000(1+50%) 台。
月增加了
课前热身
5. 康佳生产彩电,第一个月生产了5000台,第 二个月增产到150%,则第二个月生产了
5000(1+50%) 台;第二个月比第一个月
增加了 5000×50% 台, 增长率是
50% 。
课前热身
6.某试验田去年亩产1000斤,今年比去年增产
1100 斤,计划明年再 10%,则今年亩产为______
增产10%,则明年的产量为
2.某厂今年一月总产量为500吨,三月总产量
初中数学 教案:增长率问题
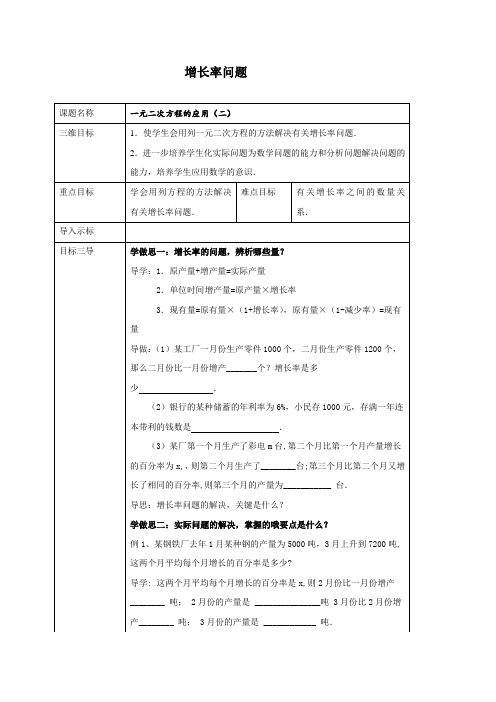
2.单位时间增产量=原产量×增长率
3.现有量=原有量×(1+增长率),原有量×(1-减少率)=现有量
导做:(1)某工厂一月份生产零件1000个,二月份生产零件1200个,那么二月份比一月份增产_______个?增长率是多少.
(2)银行的某种储蓄的年利率为6%,小民存1000元,存满一年连本带利的钱数是.
学做思三:课堂小结
(1)为计算简便、直接求得,可以直接设增长的百分率为x.
(2)认真审题,弄清基数,增长了,增长到、总共、季度总和等词语的关系.
(3)用直接开平方法做简单,不要将括号打开.
达标检测
1.2009年我市实现国民生产总值为1600亿元,计划全市国民生产总值以后三年都以相同的增长率一实现,并且2011年全市国民生产总值要达到1960亿元.
第二次降价后,每件为600(1-x)-600(1-x)·x=600(1-x)2(元).
导思:怎样更快的抓准题目中的量,建立方程?
例3 某人想把10000元钱存入银行,存两年.一年期定期年利率6%,两年期定期年利率为%.哪一种存款更划算?
导学:阅读,独立思考.
导做:独立完成,小组交流.
导思:解题的步骤是什么?
(1)求全市国民生产总值的年平均增第率;
(2)求2010年至2012年全市三年可实现国民生产总值多少亿元?(精确到1亿元)
2.某服装店花2000元进了批服装,按50%的利润定价,无人购买.决定打折出售,但仍无人购买,结果又一次打折后才售完.经结算,这批服装共盈利430元.如果两次打折相同,每次打了几折?
反思总结
课后作业
1.教材第42页练习第1题(只需设未知数后列出方程)
2.教材第42页习题第2题
应用题-增长率问题

一件商品的价格先增长25%,后想
恢复原价,应降百分之几?
一件商品的价格先降20%,欲恢复
原价,应增长百分之几?
甲、乙两家超市为了促销,
一价格相 同的商品, 甲超市连续两次降价了 10% ,乙超市一次降价20% ,在哪家 超市购买比较合算?
现对某商品降价20%促销,为了使
销售总金额不变,销售量比原来要 增加百分之几?
“丰收一号”油菜籽的平均每公顷产量为 2400kg,含油量40%。“丰收二号”油 菜籽比“丰收一号”的每公顷产量提高 了300kg,含油量提高了10个百分点。 某村去年种植“丰收一号”油菜,今年 改种“丰收二号”油菜,虽然种植面积 比去年减少3hm2,但是所产油菜籽的总产 油量 比去年提高3750kg,这个村去年 和今年种植油菜的面积各是多少?
某乡改种玉米优质杂粮后,今年农
民人均收入比去年提高20%,今年 人均收入去年的1.5倍少1200元, 这个乡今年和去年的农民人均收入 分别为多少?
思考:一件衣服原价100元,为了吸
引顾客,降低10%销售,后来货源 紧张,欲恢复原价,再增长10%可 以吗?算一算,由此你能得到什么 结论?
增长率问题
小明家去年收入为20000元,今年
比去年收入增加20%,今年的收入 则列式表示为_________.
小明家去年的支出为8000元,今
年的支出比去年减少了15%,则今 年的支出可列式表示为______.
学校今年购买图书600本,比去年的
购买数量增加了20%,则去年购买 数量为多少?
张强家去年总收入50000元,预计
今年水果收入比去年增加30%,玉 米收入比去年增加5%,这样今年的 总收入将比去年增加20%,求今年 的水果收入和玉米收入
增长率问题

增长率问题某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )A.500(1+2x)=720B.500(1+x)2=720C.500(1+x2)=720D.720(1+x)2=5002.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程为.一元二次方程中的有关增长率问题:增长率问题经常用公式,a为基数,b为增长或降低后的数,x为增长率,“n”表示n次增长或降低。
例3:雪融超市今年的营业额为280万元,计划后年的营业额为403.2万元,求平均每年增长的百分率?若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的数量关系可表示为其中增长取+,降低取-1、平均增长(降低)率公式2、注意:(1)1与x的位置不要调换(2)解这类问题列出的方程一般用直接开平方法一、平均增长率例1 (安徽省中考题)据报道,我省农作物秸秆的资源巨大,但合理利用量十分有限,2006年的利用率只有30%,大部分秸秆被直接焚烧了,假定我省每年产出的农作物秸秆总量不变,且合理利用量的增长率相同,要使2008年的利用率提高到60%,求每年的增长率.(取2≈1.41)解析设我省每年产出的农作物秸秆总量为a.,合理利用量的增长率为x,由题意得a·30%·(1+x)2=a·60%, 即(1+x)2=2.∴x1=≈0.41, x2≈-2.41(),所以我省每年秸秆合理利用量的增长率是41%.评注: 关于两次平均增长的问题,如果设平均增长率为x,前后两次的结果分别为a和b,则存在等量关系a(1+x)2=b,解方程的简便方法是直接开平方法.若x>0,表示增长;若x<0,表示降低.二、变化的增长率例2 (陕西省中考题)有一商场在第一季度内将某种家电商品连续降价,其中3月份的降幅比2月份的降幅要多2个百分点(一个百分点=1%),结果3月份的销售台数比1月份增加4倍,销售收入增加296%. 问2月份在1月份的基础上降价百分之几? bxa n=±)1(2(1)a x b±=分析: 若设2月份在1月份的基础上降价的百分数为x,则3月份在2月份的基础上降价的百分数为(x+2%);若把1月份的销售台数看作1,则3月份的销售台数为5;若把1月份的销售收入看作1,则3月份的销售收入为1×(1+296%).根据题意可列方程5(1-x)(1-x-2%)=1×(1+296%).解: 略点评:本题是一个变化的增长率问题.如果设增长前的值为a, 第一次增长率为x, 第二次增长率比第一次增长率多m, 那么第二次增长率为(x+m),增长后的结果为b,由题意列出方程的方法可以概括为公式a (1+x) (1+x+m)=b.当m =0时,变化的增长率问题就成为平均增长率问题三、相关的增长率例3 (南京市中考题)某农场种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜的种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60000,求南瓜亩产量的增长率.分析: 这是一道求两个相关量同时增长的问题,若设南瓜亩产量的增长率为x, 则新品种的亩产量为2000(1+x), 种植面积的增长率为2 x, 扩大后的种植面积为10(1+2 x)亩.由题意可列方程10(1+2 x)·2000(1+ x)=60000.我国年人均用纸量约为28公斤,每个初中毕业生离校时大约有10公斤废纸;用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树.(1)若我市2005年7万初中毕业生环保意识较强,他们都能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐?(2)宜昌市从2001年初开始实施天然林保护工程,到2003年初成效显著,森林面积大约由1374.094万亩增加到1500.545万亩.假设我市年用纸量的15%可以作为废纸回收利用,且森林面积年均增长率保持不变,请你按宜昌市总人口数约为415万计算:在从2005年初到2006年初这一年度内,我市新增加的森林面积与因废纸回收利用所能保护的森林面积之和最多可能达到多少亩.(精确到1亩)设2001年初到2003年初我市森林面积年均增长率为x,依题意可得1374.094×(1+x)2=1500.545 解得:x=0.045=4.5%∴2005年初到2006年初全市新增加的森林面积:1500.545×104×(1+4.5%)2×4.5%= 737385 亩又全市因回收废纸所能保护最多的森林面积: 415×104×28×15%÷1000×18÷50=6275 亩∴新增加的森林面积与保护的森林面积之和最多可能达到的亩数: 737385(亩)+6275(亩)= 743660(亩)练习:1.某石油进口国这个月的石油进口量比上个月减少了5%,由于国际油价上涨,这个月进口石油的费用反而比上个月增加了14%,求这个月的石油价格相对上个月的增长率?2.某市2007年9月招收区内初中班学生50名,并计划在2009年9月招生结束后,使区内初中班三年招生人数达到450名。
3 增长率问题

0.9x+(1+5%)(100-x)=100(1+2%)
例3.“种粮补贴”惠农政策的出台,大大激发了农民种粮的
积极性。某粮食生产专业户去年计划生产小麦和玉米共18 吨,实际生产了20吨,其中小麦超产12%,玉米超产10%, 该专业户去年实际生产小麦、玉米各多少吨。?
该专业户去年计划生产小麦x吨,去年计划生产玉米(18-x)吨,
去年实际生产小麦(1+12%)x吨,去年实际生产玉米(1+10%)(18-x) 吨。
(1+12%)x+(1+10%)(18-x)=20
例4.彩云家去年结余12000元,今年他家水果大丰收, 估计收入可比去年高15%,由于生活消费品价格略 有上涨,支出比去年高5%,今年可比去年多结余 6600元,求去年的收入和支出。
1×(1 + m%)=1×(1 – 5%)[ 1 +(m + 6)% ]
解得:
m = 14
例2.已知甲、乙两种商品原单价和为100元,因市 场变化,甲商品九折销售,乙商品提价5%,调价 后,甲、乙两种商品的单价和比原单价和提高了 2%,求甲、乙两种商品的原单价各是多少?
甲种商品的原单价是x元,则乙种商品的原单价是(100-x)元,
去年的总支出2x万元, 去年的总产值2(x+25)万元
今年的总支出2x(1-10%)万元, 去今年的总产值2(x+25)(1+15%)万元
2(x+25)(1+15%) =2x(1-10%)+95
例6:某企业向银行贷款,商定归还期为两 年,年利率为6%(不计复利),该企业立即用这 笔贷款购买一批货物,以高于本金37%的价格出 售,两年内售完,用所得收入还清代款本利后, 还余5万元.这笔贷款是多少元?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程
( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720
D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两
年在实验器材投资上的平均增长率是x,则可列方程
为 .
一元二次方程中的有关增长率问题:
增长率问题经常用公式 ,a为基数,b为增长或降低后的数,x为增长率,
“n”表示 n次增长或降低。
例3:雪融超市今年的营业额为280万元,计划后年的营业额为403.2万元,求平均每年增
长的百分率?
若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的
数量关系可表示为
其中增长取+,降低取-
1、平均增长(降低)率公式
2、注意:
(1)1与x的位置不要调换
(2)解这类问题列出的方程一般
用 直接开平方法
一、平均增长率
例1 (安徽省中考题)据报道,我省农作物秸秆的资源巨大,但合理利用量十分有限,
2006年的利用率只有30%,大部分秸秆被直接焚烧了,假定我省每年产出的农作物秸秆总
量不变,且合理利用量的增长率相同,要使2008年的利用率提高到60%,求每年的增长率.(取
2
≈1.41)
解析 设我省每年产出的农作物秸秆总量为a.,合理利用量的增长率为x,
由题意得a·30%·(1+x)2=a·60%, 即(1+x)2=2.
∴ x1=≈0.41, x2≈-2.41(),
所以我省每年秸秆合理利用量的增长率是41%.
评注: 关于两次平均增长的问题,如果设平均增长率为x,前后两次的结果分别为a和b,
则存在等量关系a(1+x)2=b,解方程的简便方法是直接开平方法.若x>0,表示增长;若x<0,
表示降低.
二、变化的增长率
例2 ( 陕西省中考题)有一商场在第一季度内将某种家电商品连续降价,其中3月份
的降幅比2月份的降幅要多2个百分点(一个百分点=1%),结果3月份的销售台数比1月
份增加4倍,销售收入增加296%. 问2月份在1月份的基础上降价百分之几?
bxan)1(
2
(1)axb
分析: 若设2月份在1月份的基础上降价的百分数为x,则3月份在2月份的基础上降价
的百分数为(x+2%);若把1月份的销售台数看作1,则3月份的销售台数为5;若把1月份的
销售收入看作1,则3月份的销售收入为1×(1+296%).根据题意可列方程5(1-x)( 1-x-2%)
=1×(1+296%).
解: 略
点评:本题是一个变化的增长率问题.如果设增长前的值为a, 第一次增长率为x, 第二次
增长率比第一次增长率多m, 那么第二次增长率为(x+m),增长后的结果为b,由题意列出方程
的方法可以概括为公式a (1+x) (1+x+m)=b.当m =0时,变化的增长率问题就成为平均增长率
问题
三、相关的增长率
例3 (南京市中考题)某农场种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,
今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜的种植面积的增长
率是亩产量的增长率的2倍,今年南瓜的总产量为60000,求南瓜亩产量的增长率.
分析: 这是一道求两个相关量同时增长的问题,若设南瓜亩产量的增长率为x, 则新品种
的亩产量为2000(1+x), 种植面积的增长率为2 x, 扩大后的种植面积为10(1+2 x)亩.由题意可
列方程10(1+2 x)·2000(1+ x)=60000.
我国年人均用纸量约为28公斤,每个初中毕业生离校时大约有10公斤废纸;用
1吨废纸造出的再生好纸,所
能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大
树.
(1) 若我市2005年7万初中毕业生环保意识较强,他们都能把自己离校时的全部
废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐?
(2) 宜昌市从2001年初开始实施天然林保护工程,到2003年初成效显著,森林面
积大约由1374.094万亩增加到1500.545万亩.假设我市年用纸量的15%可
以作为废纸回收利用,且森林面积年均增长率保持不变,请你按宜昌市总人
口数约为415万计算:在从2005年初到2006年初这一年度内,我市新增加
的森林面积与因废纸回收利用所能保护的森林面积之和最多可能达到多少
亩.(精确到1亩)
设2001年初到2003年初我市森林面积年均增长率为x,依题意可得 1374.094×(1+x)2
=1500.545 解得:x=0.045=4.5% ∴ 2005年初到2006年初全市新增加的森林面积:
1500.545×104×(1+4.5%)2×4.5% = 737385 亩又全市因回收废纸所能保护最多的森林面积:
415×104×28×15%÷1000×18÷50=6275 亩 ∴新增加的森林面积与保护的森林面积之和最多
可能达到的亩数: 737385(亩)+6275(亩)= 743660(亩)
练习:
1.某石油进口国这个月的石油进口量比上个月减少了5%,由于国际油价上涨,这个月进口
石油的费用反而比上个月增加了14%,求这个月的石油价格相对上个月的增长率?
2.某市2007年9月招收区内初中班学生50名,并计划在2009年9月招生结束后,使区内
初中班三年招生人数达到450名。若该市区内初中班招生人数平均每年的增长率相同,那
么增长率大约是多少(结果保留3个有效数字)?
3、某人2005年底买入一栋别墅,到2007年底其售价翻了一番,求去年平均增长率是多少?
(根号2≈1.414)
4、某果园今年栽种果树200棵,现计划扩大栽种面积,使今后两年的栽种量都比前一年增
长一个相同的百分数,这样三年(包括今年)的总栽种量为1400棵,求这个百分数。
5、某种汽车经过两次降价,每次降价幅度相同,加个降低了36%,求每次降价的百分率。
6、我国土地沙漠化日益严重,西部某市2003年有沙化土地100平方公里,
到2005年已增至144平方公里。请问:2003至2005年沙化土地的平均增长率
为多少?
7、机动车尾气是导致城市空气质量污染的重要原因。为了解决这一问题,某市试验将现有
部分汽车改装液化石油气燃料汽车(称为环保车)。按计划,该市今后两年内将使全市的这
种环保车由目前的325辆增加到637辆,求这种环保车平均每年增加的百分率。
8、某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明
两年在实验器材投资上的平均增长率是x,则可列方程为
9、某种药品两次降价后,每盒售价从原来6.4 元降到4.9元,平均每次降价的百分率是多
少?
10、哈尔滨市政府为了申办2010年冬奥会,决定改善城市容貌,绿化环境,计划用两年时
间,使绿地面积增加44%,这两年绿地平均每年增长百分率是多少?
11、某公司八月份出售电脑200台,十月份售出242台,这两个月平均增长的百分率是多少?
12.去年“十一”黄金周我市各旅游景点共接待游客334玩人,旅游总收入约9亿元,已知我
市2006年“十一”黄金周旅游总收入约6.25亿元,那么这两年同期旅游总收入的年平均增长
率约为百分之几?
13.国家实施惠农政策后,某镇农民人均收入经过两年提高44%,这两年该镇农民人均收入
平均年增长率是多少?
14.某市国民生产总值2006年为480亿元,2008年增加到591.6亿元,设平均每年的增长率
为x,则所列方程是_____
15.经过两年的连续治理,某城市的大气环境有了明显改善,其每年每平方公里的降尘量从
50t下降到40.5t,则平均每年下降的百分率是_____
16.张先生于2004年底在某小区购买了一套150平方米的住房,花了18万元,李先生于
2006年底在同一小区购买了一套100平方米的住房,花了20.28万元,该小区房价的年平
均增长率为___________18÷150=0.12万/平方米 20.28÷100=0.2028万/平方米
0.12(1+x)²=0.2028
17.某商场3月份的销售额为16万元,5月份的销售额为25万元,该商场这两个月的销售
额的平均增长率是________
18.某市全市一共有13233个自然村,2005年已建成生态文明村2315个,计划到2007年,
全是生态文明村数要达到自然村总数的24.4%,那么按这个计划,从2005年到2007年,
平均每年生态文明村的增长率约是多少?
19.某石油进口国这个月的石油进口量比上个月减少了5%,由于国际油价上涨,这个月进
口石油的费用反而比上个月增加了14%,求这个月的石油价格相对上个月的增长率?
20.某市2007年9月招收区内初中班学生50名,并计划在2009年9月招生结束后,使区
内初中班三年招生人数达到450名。若该市区内初中班招生人数平均每年的增长率相同,
那么增长率大约是多少(结果保留3个有效数字)?
