4.1 组合电路[兼容模式] [Repaired]
2. 组合逻辑电路的连接方式

2. 组合逻辑电路的连接方式1.引言1.1 概述概述部分是对整篇长文的一个简要介绍,它可以包括对组合逻辑电路以及不同的连接方式进行概括性的说明。
以下是一个可能的描述:引言部分将介绍组合逻辑电路的连接方式,其中包括串联连接方式、并联连接方式以及组合连接方式。
组合逻辑电路是现代电子系统中常见的一种电路类型,它由多个基本逻辑门和逻辑元件组成。
这些逻辑门和元件之间的连接方式决定了电路的功能和性能。
串联连接方式是一种将多个逻辑门按照顺序连接在一起的方式。
在串联连接中,一个逻辑门的输出作为下一个逻辑门的输入,以此类推。
这种连接方式常常用于构建复杂的逻辑功能,通过逐级传递信号来实现逻辑运算。
并联连接方式是一种将多个逻辑门同时连接在一起的方式。
在并联连接中,各个逻辑门的输入信号是相同的,它们的输出信号分别经过不同的逻辑运算后再进行组合。
这种连接方式可以实现多个逻辑功能并行执行,提高了电路的工作效率。
组合连接方式是一种将多个逻辑门按照一定规律进行连接的方式。
在组合连接中,逻辑门的输入和输出会根据一定的组合规则来进行连接,以实现特定的逻辑运算或逻辑控制。
这种连接方式常用于设计特定的逻辑功能电路,如加法器、减法器、多路选择器等。
在本文中,我们将详细介绍这三种组合逻辑电路的连接方式,并分析它们的特点、优势和适用范围。
通过深入了解这些连接方式,我们可以更好地理解组合逻辑电路的设计和实现原理,为后续电子系统的设计提供有益的指导和参考。
文章结构部分的内容应该是对整篇文章的框架进行介绍和概述,以便读者能够清晰地了解文章的组织结构和内容安排。
以下是对文章1.2 文章结构部分的内容的一个可能的描述:1.2 文章结构本文将围绕组合逻辑电路的连接方式展开讨论。
首先,在引言部分概述了本文的主题和目的,为接下来对组合逻辑电路连接方式的研究提供了背景和动机。
接着,在本章节中,我们将详细介绍三种常见的组合逻辑电路连接方式,包括串联连接方式、并联连接方式和组合连接方式。
组合电路的基本设计

2. 列真值表 3. 写输出表达式并化简 Y ABC ABC ABC ABC BC ABC ABC BC AC AB 最简与或式 最简与非-与非式
Y BC AC AB
BC AC AB
ABCY
000 0 001 0 010 0 011 1 100 0 101 1 110 1 111 1
第三章 组合逻辑电路
4. 画逻辑图 — 用与门和或门实现 Y BC AC AB — 用与非门实现 Y BC AC AB
A
& AB
B
& BC ≥&1 Y C
& AC
课后作业: 设计一个监视交通信号灯工作状态的逻辑 电路。正常情况下,红、黄、绿灯只有一个亮,否则 视为故障状态,发出报警信号,提醒有关人员修理。
组合电路的基本设计方法
一、 设计步骤
逻辑抽象
列真值表
写表达式 化简或变换
画逻辑图
逻辑抽象:
1. 根据因果关系确定输入、输出变量
2. 状态赋值 — 用 0 和 1 表示信号的不同状态
制数递增排列,也可按 循环码排列
根据所用元器件(分立元件 或 集成芯片)的情况将
函数式进行化简或变换。
二、 设计举例 [例 3. 1. 2] 设计一个表决电路,要求输出信号的电 平与三个输入信号中的多数电平一致。 [解] 1. 逻辑抽象
(1)设定变量: 输入 A、B、C , 输出 Y
(2)状态赋值:
A、B、C = 0 表示 输入信号为低电平 A、B、C = 1 表示 输入信号为高电平 Y = 0 表示 输入信号中多数为低电平 Y = 1 表示 输入信号中多数为高电平
组合电路设计报告总结分析

组合电路设计报告总结分析引言组合电路是由逻辑门和电子元件组成的,能够实现任意的逻辑运算和数据处理的电路。
本文将对组合电路设计的过程进行总结分析,并讨论其在实际应用中的意义。
设计过程确定需求在进行组合电路设计之前,首先需要明确设计目标和需求。
这包括了对输入输出的要求、电路的延时要求、功耗要求等。
只有明确了需求,才能有针对性地进行设计。
逻辑功能分析根据需求,进行逻辑功能分析。
这包括对输入输出的关系、逻辑关系的确定等。
通过逻辑功能分析,可以确定所需的逻辑门的类型和数量。
电路设计根据逻辑功能分析的结果,进行电路设计。
这包括了逻辑门的选择、布局设计、线路的布线等。
在电路设计过程中,需要考虑信号的传输延时、功耗等因素,以满足设计需求。
电路验证设计完成后,需要对电路进行验证,以确保其符合设计要求。
这可以通过电路仿真、实际测量等方法进行。
如果验证结果与设计需求相符,则可以进行后续步骤,否则需要进行相应的修改。
优化改进在验证过程中,可以发现电路中存在的问题和改进的空间。
通过优化和改进,可以提高电路的性能、减小功耗等。
优化改进是一个不断迭代的过程,可以通过多次验证和修改来实现。
实际应用意义组合电路设计在实际应用中具有重要意义。
首先,组合电路设计可以实现各种逻辑运算和数据处理,对于数字电路的设计和实现提供了基础。
在计算机、通信、控制等领域,组合电路的应用非常广泛。
其次,组合电路设计可以优化电路的性能和功耗。
通过合理的设计和优化改进,可以提高电路的响应速度、减小功耗,从而提高整体系统的性能。
此外,组合电路设计可以提高电路的可靠性和稳定性。
通过设计冗余电路、错误检测和纠正电路等,可以降低电路的故障率,提高系统的可靠性。
结论组合电路设计是一个复杂的过程,需要根据需求进行逻辑功能分析、电路设计、电路验证和优化改进。
组合电路设计在实际应用中具有广泛意义,可以实现各种逻辑运算和数据处理,优化电路的性能和功耗,提高电路的可靠性和稳定性。
数字电路第四版第4章组合逻辑电

03
利用多路复用器、编码 器等集成度更高的元件 代替多个小规模元件。
04
优化布线,减少不必要 的连线,降低元件间的 耦合。
提高电路速度
01
02
03
04
选择高速的逻辑门和元件,以 提高信号传输速度。
优化电路结构,减少信号传输 路径和延迟。
适当增加驱动强度,提高信号 的驱动能力。
避免信号在电路中产生反射和 振荡,减小信号延迟。
降低功耗
选择低功耗的逻辑门和元件,降低静 态功耗。
采用适当的电源管理技术,如电源关 断、时钟关断等,降低功耗。
优化电路结构,减少不必要的逻辑门 和元件,降低动态功耗。
优化布线,减小连线的电阻和电感, 降低信号传输过程中的功耗。
06 组合逻辑电路的实例分析
实例一:简单计算器电路
01
02
功能描述
实现基本的加、减、乘、除运 算功能。
的形式。
卡诺图法
利用卡诺图法将逻辑函 数表达式转换为易于实
现的形式。
卡诺图设计法
卡诺图法的基本原理
利用卡诺图法进行逻辑电路设 计的基本原理和方法。
卡诺图的构造
介绍如何构造卡诺图,以及卡 诺图中最小项和最大项的表示 方法。
卡诺图的简化
介绍如何利用卡诺图进行逻辑 函数的简化,以及如何利用卡 诺图进行逻辑电路的设计。
分析逻辑表达式时,需要注意表达式的化简,以减少所需的逻辑门数量,提高电路 的效率。
真值表分析
真值表是描述组合逻辑电路所有可能 输入情况下输出结果的表格。通过真 值表,可以全面了解电路的功能。
真值表可以帮助我们发现电路中可能 存在的冒险现象,如无关项引起的竞 争冒险。
真值表的列对应于输入变量的所有可能取值 ,行对应于输出变量的所有可能取值。在每 个格子中,填写对应输入取值下的输出取值 。
4组合接线图[1]长治组合开关
![4组合接线图[1]长治组合开关](https://img.taocdn.com/s3/m/cffc63f1700abb68a882fb09.png)
31-1 127-1 126-1 125-1 124-1 123-1 122-1 121-1 120-1
B A
HK7Z:13 HK7Z:8 HK7Z:7 HK7Z:6 HK7Z:5 HK7Z:4 HK7Z:3 HK7Z:2 HK7Z:1
TX:3 TX:8
QX3:9 QX3:8 QX3:7 QX3:6 QX3:5 QX3:4 QX3:3 QX3:2 QX3:1
QX2:7 QX2:6
0.5 0.35 0.35 0.35 0.35 0.35 0.35 0.35 0.35
0.5 0.5
蓝
所有的K3短接
蓝
蓝
蓝
蓝
蓝
蓝
蓝
蓝
屏蔽线
34-9
JXP1:14
QX2:1
0.5
33-6
JXP1:16
QX2:2
0.5
红 黄绿
207-1
JXP2:9
QX1:8
0.35
黄
206-1
JXP2:8
描
校
旧底图总号
HK3T
104-1
21
86-1
105-1 5 4 3 87-1
106-1 7 6 88-1
17-2 1
Ⅲ回路
3KM
52-1 2
技术要求 1、走线整齐、美观,不得有压线或绞线。 2、焊点之间连线牢固、可靠,不得有虚焊、
错焊、短路、断线等现象。
CA3T
8 17-2 34-3 1
3KM1
9
2
描
图
描
校
旧底图总号
底图总号
QBZ-4×315P
签
字
日
期
JXP2
组合逻辑器件dd4

逻辑图
6
2. 键盘输入 键盘输入8421BCD码编码器 码编码器
S0~S9 代表 十个按键,即对应十进制数 十个按键,即对应十进制数0~9输入 输入 为输出代码(A为最高位 鍵,ABCD为输出代码 为最高位 , 为输出代码 为最高位), GS为使能标志。 为使能标志。 为使能标志 该编码器为输入低电平有效。 该编码器为输入低电平有效。
4
1.
4线—2线编码器 线 线编码器
输入 I1 I2 0 0 1 0 0 1 0 0 输出 Y1 Y0 0 0 0 1 1 0 1 1
功能表
I0 1 0 0 0
I3 0 0 0 1
逻辑表达式
5
逻辑功能
中的某一个输入为1 当 I0~I3 中的某一个输入为 时 , 输 即为相对应的代码。 出Y1Y0即为相对应的代码。
(4)逻辑表达式
(5)引脚图 引脚图
14
复习
(1)逻辑图 ) (2编码器 线优先编码器74148
15
EI2=0,编码器工作。I15, EO2=EI1I150,I,片0Ⅱ , 编码器工作。 …I8任一为低电平, 如 I15…I8 不编码, 任一为低电平 …I 不编码 , 高位片的编码优先级别高于低位片, 最高, 任 高位片的编码优先级别高于低位片, =最高7,I0最 编码。 EI=EIⅠ编码器禁止编码。 一为低电平, 1=1, 。 编码。 编码。 编码。 EO2,片,编码器禁止编码。 一为低电平 2=1, 编码片Ⅰ不编码 , 低。 16
二进制译码器的一般原理图
X0
n个输入端 个输入端 2n个输出端 使能输入端EI 使能输入端
X1 Xn-1
二进制 译码器
Y0 Y1 Y2n-1
EI使能输入20
清华大学数电4组合课件
G1门是 非门, 强调低 电平有 效
YS ' ( I 0 ' I1 ' I 2 ' I 3 ' I 4 ' I 5 ' I 6 ' I 7 ' S )'
YEX ' (YS ' S )'
S’是“使能”信号 低电平有效 代表无输入信号 11
代表“有输入信号”
Y2' [( I 7 I 6 I 5 I 4 ) S ]'
一、编码器(Encodor)
编码: 用二值代码表示具体事物(变量)。 如:用0101表示十进制数5。 编码器分为普通编码器和 优先编码器。 (一)普通编码器 普通编码器任何时刻只允许 一个输入有效。 以3位二进制编码器的设计 为例:
注意这个名称
8
1.真 值表
2.函数式
' ' ' ' ' ' ' ' ' ' ' ' Y2 I 7 I 6 I 5 I 4 I 3 I 2 I1' I 0 I 7 I 6 I 5 I 4 I 3 I 2 I1' I 0
Z 3 m ( 2,3,5) ( m m m )
' 0 ' 2
' ' 5 ' 4 ' ' 7
Z 4 m (0,2,4,7 ) ( m m m m )
由于译码器输出 低电平有效,故 选用与非门
25
(四)显示译码器 1.七段字符显示器 这种显示器可用多种发光器件构 成。例如半导体发光二极管、液晶等。 这里以发光二极管为例进行说明。 半导体数码管BS201A的外形图、 等效电路: 驱动电路 共阴极接法 VCC T R 共阳极接法 VCC D
4-1 组合电路

HDL 範例 4-6
(2對 線多工器使用條件式運算子描述) (2對1線多工器使用條件式運算子描述)
//Dataflow description of 2-to-1-line multiplexer
module mux2x1_df (A,B,select,OUT); input A,B,select; output OUT; assign OUT = select ? A : B; endmodule
HDL 範例 4-2 (4位元加法器之底部向上層次化描述 位元加法器之底部向上層次化描述) (4位元加法器之底部向上層次化描述)
output [3:0] S; output C4; wire C1,C2,C3; //Intermediate carries //Instantiate the fulladder fulladder FA0 (S[0],C1,A[0],B[0],C0), FA1 (S[1],C2,A[1],B[1],C1), FA2 (S[2],C3,A[2],B[2],C2), FA3 (S[3],C4,A[3],B[3],C3); endmodule
HDL 範例 4-4 (4位元加法器之資料流程描述 位元加法器之資料流程描述) (4位元加法器之資料流程描述)
//Dataflow description of 4-bit adder module binary_adder (A,B,Cin,SUM,Cout); input [3:0] A,B; input Cin; output [3:0] SUM; output Cout; assign {Cout,SUM} = A + B + Cin; endmodule
HDL 範例 4-2 (4位元加法器之底部向上層次化描述 位元加法器之底部向上層次化描述) (4位元加法器之底部向上層次化描述)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020
第四章 组合逻辑电路
请设计一个逻辑电路满足要求:当输入代表的3位二进制 数取值在3和6之间(包含3和6)时输出为低电平。 1)构建真值表 ; 2) 写出最简与或表达式; 3) 只使用“与非”门设计实现该电路; 4)如果不限制使用门电路类型,最少可以用几个门电路实现?
第四章 组合逻辑电路
§4.1 小规模组合逻辑电路的分析与设计 §4.2 中规模组合逻辑器件的分析与应用
全加器、数值比较器、编码器、 译码器、 数据选择器 §4.3 组合逻辑电路的竞争与冒险
第四章
组合逻辑电路
本章的教学目标
1. 掌握组合电路的分析与设计; 2. 了解通用逻辑模块的设计原理和内部逻辑结构; 3. 掌握通用逻辑模块及其应用; 4. 理解组合逻辑电路的竞争与冒险。
2121
FFFABAABBADBABBBABCCC AADD
1515
第四章 组合逻辑电路
例 3 : 设 计 一 个 电 话 机 信 号 控 制 电 路 。 电 路 有 I0 ( 火 警 ) 、 I1 ( 盗 警 ) 和 I2 (日常业务)三种输入信号,通过排队电路分别从L0、L1、L2输出,在同 一时间只能有一个信号通过。如果同时有两个以上信号出现时,应首先 接通火警信号,其次为盗警信号,最后是日常业务信号。试按照上述轻 重缓急设计该信号控制电路。要求用集成门电路7400(每片含4个2输入 端与非门)实现。 解:(1)列真值表: (2)由真值表写出各输出 的逻辑表达式:
A
≧1
组成的逻辑电路为: B
≧1
≧1
F
C
≧1
1313
第四章 组合逻辑电路
定向化简: (1)化简为与非--与非式:
F的最简与或式 二次非,摩根定理与非--与非式
(2)化简为或非--或非式:
F的最简或与式 二次取反 或非--或非式
(3)化简为最简与或非式:
函数非的最简与或式 取非函数的最简与或非式
真值表
例1 用小规模集成器件设计一多数表 A B C
F
决电路(3输入1输出)。
000 0
解:
001
0
1. 根据题意,设A,B,C分别
010
0
代表三个输入,F为输出,列真值表
011
1
100
0
2 由真值表写出逻辑函数表达式: 1 0 1
1
F ABC ABC ABC ABC 1 1 0
1
111
公式法 图形法
描
简
述
化
真
电
函
值
路
数
表
功
式
能
55
例辑表达式
F AB BC AC
AB BC AC
(2)列真值表 (3)分析电路的逻辑功能
多数输入变量为1,输出F为1;
多数输入变量为0,输出 F为0
结论:电路为少数服从多数电 路, 称表决电路。
当A、B、C三个变量不一致时, 电路输出为“1”,所以这个电路 称为“不一致电路”。
88
第四章 组合逻辑电路
三、组 合 电 路 的 设 计
任务:根据要求设设计计步出骤实际逻辑电路
设列 计真 要值 求表
公式法 图形法
简 化 函 数 式
根据设计所用 芯片要求
表达式变换
画 逻 辑 图
99
第四章 组合逻辑电路
1616
第四章 组合逻辑电路
(3)根据要求,将上式转换为与非表达式: (4)画出逻辑图。
1717
第四章 组合逻辑电路
例4:设计一个将余3码变换成8421BCD码的组合逻辑 电路。
解:(1)根据题目要求,列出真值表:
1818
第四章 组合逻辑电路
(2)用卡诺图进行化简。(注意利用无关项)
1919
第四章 组合逻辑电路
AB
BC
AC
真值表 ABC F 000 0 001 0 010 0 011 1 100 0 101 1 110 1 111 1
第四章 组合逻辑电路
例2 :分析下列电路,指出逻辑功能
77
第四章 组合逻辑电路
解(1)由逻辑图逐级写出逻辑表达式。为了写表达式
方便,借助中间变量P。
(2)化简与变换:
(3)由表达式列出真值表。 (4)分析逻辑功能 :
根据上⑵式画出与非器件组成的逻辑电路。
A
&
B
&
C
&
&F
1212
第四章 组合逻辑电路
b若采用或非器器件,则对⑴式进行代数变换 ,先得到或与式,再对 或与式两次求反,变换成或非—或非表达式。
F =AB+BC+AC=A¨ £ B+C©£ +BC=¨ £ A+B£© £¨A+C©£ £¨B+C©£
=(A+B)(A+C)(B+C)=A+B + A+C + B+C ……⑶
22
第四章 组合逻辑电路
4.1 组合电路的分析和设计
组合电路概述 组合电路的分析 组合电路的设计
33
第四章 组合逻辑电路
4.1 组合电路的分析和设计
一、组 合 电 路 概 述
组合电路概念 输入: X1、X2、…、Xn
输出: F1、F2、…、Fm
逻辑关系:Fi = fi (X1、X2、…、Xn) i = (1、2、…、m)
1
1010
第四章 组合逻辑电路
3 利用卡诺图化简,得最简与—或表达式。
F AB AC BC
(1)
1111
第四章 组合逻辑电路
4 a 若 提供器件是与 - 非器件,则对上 ⑴式F 进行逻辑变换,使它
的表达式变成与非 - 与非表达式。 ( 两次取非)
F=AB+AC+BC=AB AC BC
⑵
1414
第四章 组合逻辑电路
例2 在只有原\变A量B 输入,没有反变量输入条件
下,
CD \ 00 01 11 10
用0与0非门实现函1数:1 1
01
F=(A,B,C,D)
111
11
=∑m1(4,5,16,7,8,9,
10 10,11,112,1 13,1 14)
解不:是用最两卡佳次诺(求图最反对简的函)得数结:进果行,化化简简。得
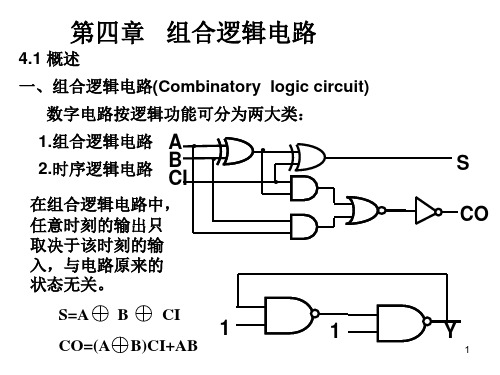
组合电路某一时刻的输出仅与该时刻的输入有关,而与 电路前一时刻的状态无关。
组合电路的特点
电路由逻辑门构成,不含记忆元件
输出与输入间无反馈延迟回路
输出与电路原来状态无关
44
第四章 组合逻辑电路
第一节 组合电路的分析和设计
二、组 合 电 路 的 分 析
任务:分析已知逻辑电路功能
分析步骤
已写 知输 组出 合函 电数 路式
