2008年新人教版八年级下数学期末试卷
2007-2008学年度八年级第二学期数学期末试题

2007-2008学年度八年级第二学期数学期末试题(时间120分钟,总分150分)班级 姓名 分数一、选择题(每小题3分,共30分) 1、计算:=-+xx x 11 ( )A xB 1C x 1D xx 1- 2、 在反比例函数xy 2=中,当4-=x 时,=y ( ) A 2- B 2 C 21- D 213 、把0.000043用科学记数法表示为 ( )A 、4.3×10-4B 、43×10-4C 、4.3×10-5D 、43×10-5 4、 菱形的两条对角线的长分别是cm 12和cm 16,则这个菱形的周长是 ( )A 72cmB 60cmC 48cmD 40cm5、 数据11.1,03.1,12.1,05.1,10.1,31.1的平均数是 ( )A 12.1 B 10.1 C 14.1 D 13.1 6、分式方程14143=-+--xx x 的解是( )A 2-=xB 2=xC 3-=xD 3=x 7 、若反比例函数x k y =的图像经过点()4,2-A ,则下列各点中,在xky =的图像上的是 ( )A ()8,1B ()8,1-C ()1,8D ()1,8--8 、平行四边形ABCD 中,有两个内角的比为2:1, ,则这个平行四边形较小的的内角是 ( )A ︒90B ︒60C ︒120D ︒45 9、 数据2,3,5,10,13的极差和中位数是 ( )A 10,6.6B 11,6.6C 10,5D 11,5 10、斜边长为17cm ,一条直角边为15cm 的直角三角形的面积为 ( )A 、30cm 2B 、60 cm 2C 、90cm 2D 、120 cm 2 二、填空题(每小题3分,共30分)11 、计算:()________________222=--a x a x 12、 若反比例函数xky =的图像经过点)2,1(-P ,则这个函数的解析式为_____________13 、如果一个三角形的一条直角边长为cm 9,另两条边是两个连续的自然数,则这个直角三角 形的周长为___________________以cm 。
2008学年度8年级下学期期末测试数学试题及其答案1.1(印刷版)

-1-2008学年第二学期八年级 数学科期末测试题(答案附后)一、选择题(本大题共10小题,每小题2分,满分20分.在每小题给出的四个选项中,只有一项是符合题目要求的,请选出来,填入下表中相对应的表格.) 1.如图1,在等腰梯形ABCD 中,AD BC ∥,70B ∠=, 则C =∠(※).(A )60 (B ) 68 (C )70 (D )1102. 某校8年级(2)班的10名同学某天的早餐费用分别为(单位:元):2 、5、3、3 、4、5 、3 、6 、5、3, 在这组数据的众数是(※).a (A )3 (B ) 3.5 (C )4 (D )6 3. 如图2是一个外轮廓为矩形的机器零件平面示意图, 根据图中的尺寸(单位:m m ),可以计算出两圆孔 中心A 和B 的距离为(※)m m .(A )120 (B ) 135 (C ) (D )150 4. 下列运算正确的是(※).(A )61233()b a b a -= (B )121231111R R R R ++==(C ) 51233()b a b a -= (D )1212112R R R R +=+5.如图3,已知□ABCD 的两条对角线AC 与BD 交于平面直角坐标系的原点,点A 的坐标为(-2,3),则点C 的坐标为(※).D(A )(-3,2) (B)(-2,-3) (C )(3,-2) (D )(2,-3)A D CB图1 图2图3-2-6. 下面命题中错误..的是(※). (A )梯形是轴对称图形(B )三角形的三条中线交于一点(C )菱形的四条边都相等 (D )有一个角是直角的菱形是正方形7.已知广州市的土地总面积约为7434 km 2,人均占有的土地面积S (单位:km 2/人)随全市人口n (单位:人)的变化而变化,则S 与n 的函数关系式为(※). B (A )7434S n = (B )7434S n=(C ) 7434n S = (D )7434nS =8.如图4,直线l 上有三个正方形A 、B 、C ,若A 、C 的面积分别为5和11,则正方形B 的面积为(※).C(A )4(B )6(C )16(D )559. 如图5,函数y x m =+与(0)my m x=≠在同一坐标 系内的图象可能是(※).b10. 矩形的面积为12cm 2,周长为14cm ,则它的对角线长为(※).(A )5cm (B )6cm (C(D)二、填空题(共6题,每题2分,共12分,直接把最简答案填写在题中的横线上)11.当_________x =时,分式11x x +-的值为0. 12.点(1,3)在反比例函数ky x=的图象上,则_________.k = 13.人体中成熟的红细胞的平均直径为0.00000077m ,用科学记数法表示0.00000077的结果为 .14.写出命题“直角三角形两直角边的平方和等于斜边的平方”的逆命题:. 15. 如图6,在菱形ABCD 中,对角线6AC cm =,5BC cm =,则菱形ABCD 的面积为 .xxxx 图5 (B )(A) (C) (D)图4-3-16. 如图7是甲、乙两地5月上旬的日平均气温统计图,则甲、乙两地这10天日平均气温的方差大小关系为:2S 甲 2S 乙.三、解答题(本大题共9小题,满分68分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分6分,每题3分)计算: (1)2324510m m n n ÷; (2)2235325953x x x x x ÷⨯--+.图71 2 3 4 5 6 7 8 9 10ODCBA 图6-4-如图8,是反比例函数5m y x-=(1) 图象的另一支位于哪个象限?常数m (2) 在这个函数图象的某一支上任取两点(,)A a b 若a c <,那么b 和d 有怎样的大小关系?19.(本小题满分7分)在“心系灾区”自愿捐款活动中,某班50名同学的捐款情况如下表: (1)问这个班级捐款总数是多少元? (2)求这50名同学捐款的平均数、中位数. (3)从表中你还能得到什么信息?(只写一条即可)图8-5-有一道试题:“先化简,再求值:22361()399x x x x x -+÷+--,其中“x =.小亮同学在做题时把“x =x =,但他的计算结果确也是正确,请你说明这是什么原因?21.(本小题满分8分)如图9,在梯形ABCD 中,AE BC ⊥于E ,DF BC ⊥于F ,且BE CF =. (1) 求证:梯形ABCD 为等腰梯形;(2) 若2AD AE ==,4BC =,求腰AB 的长.图9FEDCB A-6-22.(本小题满分8分)某中学八年级同学去距学校10千米远的工厂参加综合实践活动,一部分同学骑自行车先走,半小时后,其余同学再乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学的速度的2.5倍,求骑车同学和汽车的速度.23.(本小题满分8分)如图9,已知ABC ∆的两边AB 、AC 的中点分别为M 、N . (1) 线段MN 是ABC ∆的什么线? (2) 求证://MN BC ,且12MN BC =.图9B-7-如图10,已知(4,2)A -、(,4)B n -是一次函数y kx b =+的图象与反比例函数m y x=的图象的两个交点.(1) 求此反比例函数和一次函数的解析式; (2) 根据图象写出使一次函数的值小于反比 例函数的值的x 的取值范围.(3)过A 作AC y ⊥轴于点C ,过B 作BD y ⊥ 轴于点,D 连结AD 、BC ,试判断四边形ADBC 是否是平行四边形?并求出此四边形的面积。
2008 年八年级(下)数学期末试卷

2008 年八年级(下)数学期末试卷满分120分(人教版版用)一、选择题(每小题3分,共18分)下列各小题均有四个答案,其中只有一个是正确的,请将正确答案的代号字母填入题后括号内。
1.已知反比例函数1y x=-,则其图象在平面直角坐标系中可能是( )2. 以下列各组数据为边长,可以构成直角三角形的是(). A .3、5、6 B .2、3、4 C .6、7、9 D .1.5、2、2.53. 对角线互相垂直平分且相等的四边形一定是( ). A.正方形 B.菱形 C.矩形 D.等腰梯形4. 在某城市,80%的家庭年收入不少于2.5万元,下面一定不少于2.5万元的是( ) A .年收入的平均数 B .年收入的众数 C .年收入的中位数 D .年收入的平均数和众数5.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是A B C D6.长沙地区七、八月份天气较为炎热,小华对其中连续十天每天的最高气温进行统计,依次得到以下一组数据:34,35,36,34,36,37,37,36,37,37(单位℃).则这组数据的中位数和众数分别是( ) A.36,37 B.37,36 C.36.5,37 D.37,36.5二、填空题(每小题3分,共27分) 7.函数3y x=-的图象经过点(1)a -,,则a = .8. 如图,直角AOB ∠内的任意一点P 到这个角的两边的距离之和为6,则图中四边形的周中点 中点长为 .9.方程2101x x-=-的解是 .10.使分式13x x -+有意义的x 的取值范围是 .11.化简:333x x x+-- = .12.如图,在等腰梯形ABCD 中,AD BC ∥,AC 、BD 相交于点O ,有如下五个结论: ①AOD BOC △∽△; ②DAC DCA ∠=∠; ③梯形ABCD 是轴对称图形;④AOB AOD △≌△; ⑤AC BD =. 请把其中正确结论的序号填写在横线上 .13.如图,E 、F 是 ABCD 对角线BD 上的两点,请你添加一个适当的条件: ,使四边形AECF 是平行四边形.14.某学校举行理科(含数学、物理、化学、生物四科)综合能力比赛,四科的满分都为综合成绩按照数学、物理、化学、生物四科测试成绩的的比例计分,则综合成绩的第一名是 .D15. 如图,已知圆柱体底面圆的半径为2π,高为2,AB CD ,分别是两底面的直径,AD BC ,是母线.若一只小虫从A 点出发,从侧面爬行到C 点,则小虫爬行的最短路线的长度是 (结果保留根式).三、解答题(本题共8道小题,第16小题8分,第9 ~ 20小题各9分,第21、22小题各10分,第23题11分,共75分)16.(8分)已知:两个分式1111A x x =-+-,221B x =-,其中 1x ≠±.下面三个结论:①A B =,②A B ,互为倒数, ③A B ,互为相反数.请问这三个结论中哪一个结论正确?为什么? 17.(9分)在社会主义新农村建设中,某乡镇决定对一段公路进行改造.已知这项工程由甲工程队单独做需要40天完成;如果由乙工程队先单独做10天,那么剩下的工程还需要两队合做20天才能完成.(1)求乙工程队单独完成这项工程所需的天数; (2)求两队合做完成这项工程所需的天数.18.(9分)你吃过拉面吗?实际上做拉面的过程中就渗透着数学知识:一定..体积的面团做成拉面,面条总长度y (m )是面条的粗细(横截面积)s (mm 2)的反比例函数,其图象如图所示.(1)写出y 与s 的函数关系式;(2)求当面条粗1.6 mm 2时,面条的总长度...是多少米?2)19.(9分)如图,在两面墙之间有一个底端在A 点的梯子,当它靠在一侧墙上时,梯子的顶端在B 点;当它靠在另一侧墙上时,梯子的顶端在D 点.已知∠BAC =60°, ∠DAE =45°,点D 到地面的垂直距离DE =32m ,求点B 到地面的垂直距离BC .20.(9分)如图,在ABC △中,AB BC =,D、E、F分别是BC 、AC 、AB 边上的中点.(1) 求证:四边形BDEF 是菱形;(2) 若12AB =cm ,求菱形BDEF 的周长.21.(10分)为了调查七年级某班学生每天完成家庭作业所需的时间,在该班随机抽查了8名学生,他们每天完成作业所需时间(单位:分)分别为60,55,75,55,55,43,65,40.(I )求这组数据的众数、中位数;(II )求这8名学生每天完成家庭作业的平均时间;如果按照学校要求,学生每天完成家庭作业时间不能超过60分钟,问该班学生每天完成家庭作业的平均时间是否符合学校的要求?22.(10分)已知:如图,在梯形ABCD 中,AD BC ∥,90ABC ∠= ,45C ∠=,BE CD ⊥于点E ,1AD =,CD =求:BE 的长.23.(11分)一次期中考试中,A B C D E ,,,,五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)60 ︒ 45 ︒ AB C D EA B D C(1(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看,标准分大的考试成绩更好.请问A 同学在本次考试中,数学与英语哪个学科考得更好?友情提示:一组数据的标准差计算公式是S =,其中x 为n 个数据12n x x x ,,…,的平均数.八年级(下)期末试卷数学参考答案和评分标准(人教版)一、1.A 2.D 3.A 4.C 5.B 6.A二、7.3 8.12 9.1x =- 10.3x ≠- 11.1 12.①③⑤13.BE DF =等(只要符合条件即可 14.甲 15. 三、16.解:A B ,是互为相反数.2111(1)211(1)(1)1x x A x x x x x --+=-==-+-+--A B ∴=-.即A B ,是互为相反数. 17.解:(1)设乙工程队单独完成这项工程需要x 天,根据题意得:101120140x x ⎛⎫++⨯= ⎪⎝⎭解之得:60x = 经检验:60x =是原方程的解. 答:乙工程队单独完成这项工程所需的天数为60天.(2)设两队合做完成这项工程所需的天数为y 天,根据题意得: 1114060y ⎛⎫+=⎪⎝⎭解之得:24y = 答:两队合做完成这项工程所需的天数为24天.18.解:(1)设y 与s 的函数关系式为ky s=. 由图象可知,当4s =时,32y =,所以432128k =⨯=. 所以y 与s 的函数关系式为128y s=. (2)当 1.6s =时,128801.6y ==,所以面条的总长度是80m .19.解:在Rt △DAE 中,45DAE ∠=,DE =,s i n 45DEAD=∴.6AD =∴m . 在Rt △ACB 中,60BAC ∠=,6AB AD ==m ,s i n 60BCAB=∴.BC =∴.∴点B 到地面的垂直距离BC 为.20.解:(1)∵D 、E 、F 分别是BC 、AC 、AB 边上的中点,DE AB ∴∥ E FB C ∥ ∴四边形BDEF 是平行四边形.又12DE AB =,12EF BC =,且AB BC = DE EF =∴∴四边形BDEF 是菱形.另解: ∵D 、E 、F 分别是BC 、AC 、AB 边上的中点,12DE AB =∴,12EF BC =又AB BC =∵1122BD BF AB BC ===∴∴DE EF BF BD === ∴四边形BDEF 是菱形.(2)12AB =∵cm ,F 为AB 的中点, 6BF =∴cm ,∴菱形BDEF 的周长为:4624⨯=cm .21.解:(I )在这8个数据中,55出现了3次,出现的次数最多,即这组数据的众数是55; 将这8个数据按从小到大的顺序排列,其中最中间的两个数据都是55,即这组数据的中位数是55.(II ) 这8个数据的平均数是1(6055755555436540)568x =+++++++=(分).∴这8名学生完成家庭作业所需的平均时间为56分钟. 因为5660<,由此估计该班学生每天完成家庭作业的平均时间符合学校的要求.22.解:解:如图,过点D 作DF AB ∥交BC 于点F . 因为AD BC ∥,所以四边形ABFD 是平行四边形.所以1BF AD ==. 由DF AB ∥, 得90DFC ABC ∠=∠=.在Rt DFC △中,45C ∠=,CD =由cos CFC CD=, 求得2CF =.所以3BC BF FC =+=.在BEC △中,90BEC ∠=, sin BEC BC=.求得BE =.23.解:(1)数学考试成绩的平均分x 数学1(7172696870)705=++++=, 英语考试成绩的标准差S英语6=. (2)设A 同学数学考试成绩标准分为P 数学,英语考试成绩标准分为P英语,则P数学(7170)2=-=,P 英语1(8885)62=-÷=.P 数学>P 英语,∴从标准分来看,A 同学数学比英语考得更好.。
2008-2009八年级下册数学期末检测考试试卷及答案

第二届“思维四七九”八年级毕业考试数学卷姓名选择题 号案一、选择题: (每题3分,共30分)1、如果把223yx y-中的x 和y 都扩大5倍,那么分式的值( )A 、扩大5倍B 、不变C 、缩小5倍D 、扩大4倍2、如图,等腰梯形ABCD 中,AB ∥DC ,AD=BC=8,AB=10,CD=6,则梯形ABCD 的面积是 ( ) A 、1516 B 、516 C 、1532 D 、17163、若092=-x ,则62962-+-x x x 的值为( )A 、0B 、-3C 、0或-3D 、14、已知反比例函数的图象经过点P (-2,1),则这个函数图象位于( ) A 、 一、三象限 B 、二、三象限 C 、二、四象限 D 、三、四象限5、某反比例函数的图象经过点(-2,3),则此函数图象也经过点( ) A 、(2,-3) B 、(-3,-3) C 、(2,3) D 、(-4,6)6、◇ABCD 中,∠C=108°,BE 平分∠ABC ,则∠ABE 等于( )A 、18°B 、36°C 、72°D 、108° 7、如图是一段楼梯,BC=2m ,AB=4m.若在楼梯上铺地毯至少要() A 、4m B 、6m C 、8m D 、10m 8、如图,能判定四边形ABCD 是平行四边形的是( ) A 、AB//CD ,AD=BC B 、AB=CD ,AD=BC C 、∠A=∠B ,∠C= ∠D D 、AB=AD ,CB=CD9、如果等腰梯形ABCD 两底的差等于一腰的长,那么它的一个下底角为( ) A 、75° B 、60° C 、45° D 、30°10、为了判断甲乙两班成绩哪个班较整齐通常需要比较两个班成绩的( )A 、平均数B 、中位数C 、众数D 、方差 二、填空题:(每题3分,共24分)11、当x 时,分式15x -无意义;当m = 时,分式2(1)(3)32m m m m ---+的值为零 12、各分式222111,,121x x x x x x ---++的最简公分母是_________________ 13、已知双曲线xky =经过点(-1,3),如果A (11,b a ),B (22,b a )两点在该双曲线上,且1a <2a <0,那么1b 2b . 14、若23=b a ,则bba +的值为 ; 15、已知反比例函数图象经过(m ,2)和(-2,3),则m 的值为 ; 16、直角三角形三边长为6、8、10,则它斜边上的高为 ; 17、已知菱形两对角线长分别为6cm 和8cm ,则其面积为_ ______cm 2 ; 18、已知数据5,5,6,a ,7,7,8的平均数为6,则这组数据的中位数是___ _; 三、计算题:(41分)19、(本题满分分10) 已知实数a 满足a 2+2a -8=0,求22213211143a a a a a a a +-+-⨯+-++的值.20、(本题满分11分) 解方程 22416222-+=--+x x x x x -21、(本题满分10分) 计算:93629968122++•+-÷++-a a a a a a a22、(本题满分10分) 解方程:423532=-+-xx x四、应用题(55分)23、(本题满分10分) 已知,反比例函数图象经过点A (2,6) (1)求这个反比例函数的解析式; (2)这个函数的图象位于哪些象限; (3)y 随x 的增大如何变化;(4)点P (3,4)是否在这个函数图象上;24、(12分)E 是正方形ABCD 的对角线BD 上一点,EF ⊥BC ,EG ⊥CD ,垂足分别是F 、G.25、(本题满分15分) 甲乙两人分别从距目的地6千米和10千米的两地同时出发,甲乙的速度比是3:4,结果甲比乙提前20分钟到达目的地,求甲、乙两人的速度?26 (18分) 张老师为了从平时在班级里数学比较优秀的王军、张成两位同学中选拔一人参加“全国A D CB E G F初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测验,两位同学测验成绩记录如下表:利用表中提供的数据,解答下列问题: (1)填写完成下表:(2)张老师从测验成绩记录表中,求得王军10次测验成绩的方差2S 王=33.2,请你帮助张老师计算张成10次测验成绩的方差2S 张;(3)请根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由。
2008年人教八年级下期末测试题1
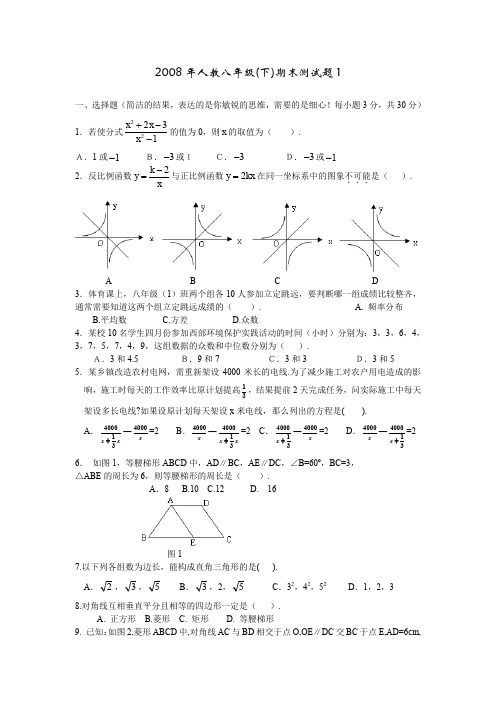
2008年人教八年级(下)期末测试题1一、选择题(简洁的结果,表达的是你敏锐的思维,需要的是细心!每小题3分,共30分)1.若使分式22231x x x +--的值为0,则x 的取值为( ). A.1或1-B.3-或1C.3-D.3-或1-2.反比例函数2k y x-=与正比例函数2y kx =在同一坐标系中的图象不可能...是( ).A B C D3.体育课上,八年级(1)班两个组各10人参加立定跳远,要判断哪一组成绩比较整齐,通常需要知道这两个组立定跳远成绩的( ). A. 频率分布 B.平均数 C.方差 D.众数4.某校10名学生四月份参加西部环境保护实践活动的时间(小时)分别为:3,3,6,4,3,7,5,7,4,9,这组数据的众数和中位数分别为( ).A.3和4.5 B.9和7 C.3和3 D.3和55.某乡镇改造农村电网,需重新架设4000米长的电线.为了减少施工对农户用电造成的影响,施工时每天的工作效率比原计划提高13,结果提前2天完成任务,问实际施工中每天架设多长电线?如果设原计划每天架设x 米电线,那么列出的方程是( ). A .400013x x+―4000x=2 B .4000x―400013x x+=2 C .400013x +―4000x=2 D .4000x―400013x +=26. 如图1,等腰梯形ABCD 中,AD ∥BC ,AE ∥DC ,∠B=60º,BC=3, △ABE 的周长为6,则等腰梯形的周长是( ).A .8 B.10 C.12 D. 16图17.以下列各组数为边长,能构成直角三角形的是( ).A .2,3,5B .3,2,5C .32,42,52D .1,2,3 8.对角线互相垂直平分且相等的四边形一定是( ). A. 正方形 B.菱形 C. 矩形 D. 等腰梯形 9. 已知:如图2,菱形ABCD 中,对角线AC 与BD 相交于点O,OE ∥DC 交BC 于点E,AD=6cm,则OE 的长为( ).A.6 cmB.4 cmC.3 cmD.2 cm图210.某学校有500名九年级学生,要知道他们在学业水平考试中成绩为A 等、B 等、C 等、D 等的人数是多少,需要做的工作是( ).A .求平均成绩 B.进行频数分布 C.求极差 D.计算方差 二、填空题(每小题4分,共40分)11.方程2332x x =--的解是 . 12.化简:22142a a a+=-- .13.若反比例函数my x=-的图象经过点(32)--,,则m = .14.在珠穆朗玛峰周围2千米的范围内,还有较著名的洛子峰(海拔8516米)、卓穷峰(海拔7589米)、马卡鲁峰(海拔8463米)、章子峰(海拔7543米)、努子峰(海拔7855米)、和普莫里峰(海拔7145米)六座山峰,则这六座山峰海拔高度的极差为 _______米.15.如图3,点P 是反比例函数2y x=-图象上的一点,PD 垂直于x 轴于点D ,则△POD 的面积为 .图316.在四边形ABCD 中,对角线AC 、BD 交于点O ,从(1)AB=CD ;(2)AB ∥CD ;(3)OA=OC ;(4)OB=OD ;(5)AC ⊥BD ;(6)AC 平分∠BAD 这六个条件中,选取三个推出四边形ABCD 是菱形.如(1)(2)(5)⇒ABCD 是菱形,再写出符合要求的两个:________⇒ABCD 是菱形;________⇒ABCD 是菱形.17.把图4的矩形纸片ABCD 折叠,B 、C 两点恰好重合落在AD 边上的点P 处如图5),已知∠MPN=90°,PM=3,PN=4,那么矩形纸片ABCD 的面积为_________.图4图518.下列命题:①对顶角相等;②等腰三角形的两个底角相等;③两直线平行,同位角相等.其中逆命题为真命题的有: (请填上所有符合题意的序号).19. 如图6,若将四根木条钉成的矩形木框变成平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的最小内角等于 .图620.10位学生分别购买如下尺码的鞋子:20,20,21,22,22,22,22,23,23,24(单位:cm)这组数据的平均数、中位数、众数三个指标中鞋店老板最不喜欢的是_______,最喜欢的是________. 三、解答题(共50分) 21.(6分)先将分式12)131(2-+÷-+x x x 进行化简,然后请你给x 选择一个合适的值,求原式的值22.(6分) 已知正比例函数x k y 1=与反比例函数xk y 2=的图象都经过点(2,1).求这两个函数关系式. 23.(6分)在4×4的正方形网格中,每个小方形的边长都是1.线段AB 、EA 分别是图7中1×3的两个长方形的对角线,请你证明AB ⊥EA.图7 24. 如图8,△ABC 中,∠ACB=90°,点D 、E 分别是AC 、AB 的中点,点F 在BC 的堰延长线上,且∠CDF=∠A ,求证:四边形DECF 是平行四边形.图825.如图9,在∠ABC中,AB = BC,D、E、F分别是BC、AC、AB边上的中点;(1)求证:四边形BDEF是菱形;12,求菱形BDEF的周长.(2)若AB = cm图9(2)若从中选一人参加市中学生运动会,你认为选谁去合适呢?请说明理由.27.如图10所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图11所示.已知展开图中每个正方形的边长为1.(1)求在该展开图中可画出最长线段的长度?这样的线段可画几条?(2)试比较立体图中∠BAC与平面展开图中∠B′A′C′的大小关系?图10 图1128.如图12,设四边形ABCD 是边长为1的正方形,以正方形ABCD 的对角线AC 为边作第二个正方形ACEF ,再以第二个正方形的对角线AE 为边作第三个正方形AEGH ,如此下去…….(1)记正方形ABCD 的边长为a 1=1,依上述方法所作的正方形的边长依次为a 2,a 3,a 4,……,a n ,求出a 2,a 3,a 4的值.(2)根据以上规律写出第n 个正方形的边长a n 的表达式.图12参考答案:一、1.C 2.D 3.C 4.A 5.B 6.A 7.A 8.A 9.C 10.B 二、11.x=5; 12.21+a ; 13.-6; 14.1371; 15.1 ;16. (1)(2)(6);(3)(4)(5)或(3)(4)(6)符合条件; 17.5144; 18.②③; 19.30°; 20.平均数,众数. 三、21. 解:原式=12)1)(1(12+=+-+⨯-+x x x x x x ,当x=0,原式=1. 22. 将x=2,y=1代入两个关系式,得k 1=21,k 2=2.所以正比例函数关系式为y=21x ,反比例函数关系式y=x2.23. 证明: 连接BE ,根据网格的特征,EF=AG=3,得∠F=∠G=∠BCE=90°,则在Rt △EFA 中,由勾股定理,得AE 2=EF 2+AF 2=10;在Rt △ABG 中,由勾股定理,得AB 2=AG 2+GB 2=10;在Rt △EBC 中,BE 2=BC 2+EC 2=20,所以AE 2+AB 2=10+10=20=BE 2,由勾股定理逆定理,得∠BAE=90°,所以AB ⊥EA. 24. 证明:因为点D 、E 分别是AC 、AB 的中点,所以DE//BC , 因为∠ACB=90°, 所以CE=21AB=AE ,所以∠A=∠ECA , 因为∠CDF=∠A ,所以∠CDF=∠ECA ,所以DF//CE ,所以四边形DECF 是平行四边形. 25. (1)因为D 、E 、F 分别是BC 、AC 、AB 的中点, 所以DE ∥AB ,EF ∥BC, 所以四边形BDEF 是平行四边形.又因为DE =21AB ,EF =21BC ,且AB = BC 所以DE = EF所以四边形BDEF 是菱形;(2)因为AB =cm 12,F 为AB 中点,所以BF = cm 6,所以菱形BDEF 的周长为cm 2446=⨯(2)两人的平均数相同,小兵成绩的众数和中位数都比小明高,且方差小,说明小兵的成绩较稳,但小明的成绩虽然波动很大,到从后几次的成绩来看,成绩都比小兵好,所以从发展的趋势来看应选小明参加. 27. 解析:(1)如图①中的A′C′,在Rt △A′C′D′中,C′D′=1,A′D′=3,由勾股定理得:A C ''∴=这样的线段可画4条(另三条用虚线标出).① ②(2)因为立体图中∠B′A′C′为平面等腰直角三角形的一锐角, 以∠B′A′C′=45°,在平面展开图中,连接线段B′C′,如图②, 由勾股定理可得:A′B′=5,B′C′=5. 又因为A′B′2+B′C′2=A′C′2,由勾股定理的逆定理可得△A′B′C′为直角三角形. 又因为A′B′=B′C′,△A′B′C′为等腰直角三角形. 所以∠BAC=45°,所以∠B′A′C′=∠BAC .28. 解:(1)在Rt △ABC 中,因为∠B=90°,所以AC 2=AB 2+BC 2=1+1=2,所以AC=2,同理AE=2,EH=22所以a 2=AC=2,a 3=AE=2,a 4=EH=22.(2)因为a 1=1=(2)0,a 2=(2)1,a 3=2=(2)2,a 4=(22)=(2)3,所以a n =(2)n-1 (n≥1,n 为整数).。
2008学年第二学期期末试卷(八年级)

2008学年第二学期期末试卷《八下数学》~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~1.下列计算正确的是( ▲ ) A .()13132-=- B .12223=- C .52553-=+- D .636±=2.八年级某班50位同学中,1月份出生的频率是0.20,那么这个班1月份生日的同学有( ▲ )A .10位B .11位C .12位D .13位3.如果等边三角形的边长为3,那么连结各边中点所成的三角形的周长为( ▲ ) A .9 B .6 C .3 D .29 4.方程()01=-x x 的根是( ▲ )A .0B .1C .0或1D .无解5.对于四边形ABCD ,下列条件中不能..判定为平行四边形的是( ▲ ) A .AB//DC 且AD//BC B .AB=DC 且AD=BC C .AB//DC 且AD=BC D .AB//DC 且AB=DC6.若平行四边形的一边长为5,则它的两条对角线长可以是( ▲ ) A .12和2 B .3和4 C .4和6 D .4和8 7.下列说法正确的是( ▲ )A .对角线相等的四边形是矩形B .有一组邻边相等的矩形是正方形C .菱形的四条边相等,四个角相等D .三角形一边上的中线等于这边的一半 8.用两个全等的直角三角形拼下列图形:①矩形;②菱形;③正方形;④平行四边形;⑤等腰三角形;⑥等腰梯形. 其中一定能拼成的图形是( ▲ ) A .①②③ B .①④⑤ C .①②⑤ D .②⑤⑥ 9.已知3是关于x 的方程03642=+-a x 的一个解,则a 6的值是( ▲ )A .42B .39C .36D .33 10.用反证法证明“a >b ”时,应假设( ▲ )A .a >bB .a <bC .a =bD .a ≤b 二.填空题(每小题4分,共40分) 11.计算16= .12.直角三角形的两条直角边分别是1,,则其斜边的长为 . 13.若方程02=-m x 有整数根,则m 的值可以是 (只填一个).14.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm ):2,-2,-1,1,0,则这组数据的极差为 cm .15.某食品店连续两次涨价10%后价格是a 元,那么原价是 . 16.将命题“同角的余角相等”改写成“如果……,那么……”的形式:.17.若一个多边形的内角和为1080°,则这个多边形的边数是 . 18.在平行四边形ABCD 中,若添加一个条件: ,则四边形ABCD 是矩形.19.如图,在平行四边形ABCD 中,∠A 的平分线交BC 于点E ,若AB=10cm ,AD=14cm ,则EC= .20.如图,在菱形ABCD 中,∠B=100°,EF 垂直平分AB ,交对角线AC 于点F ,E 为垂足,连接DF ,则∠CDF= 度. 三.解答题(每题10分,共70分) 21.计算:(1)12273+-; (2)21)22(2+-.22.解方程:(1)0822=-x x ; (2)03442=--x x .23.如图,在四边形ABCD 中,已知:AD ∥BC ,AD=BC .求证:△ABD ≌△CDB .24.为了解学生的身高情况,抽测了某校17岁的50名男生的身高,将数据分成7组,列出了相应的频数分布表(部分未列出)如下,请回答下列问题:(1)请将上述频数分布表填写完整; 某校50名17岁男生身高的频数分布表 (2)这所学校17岁男生中,身高不低于1.655m 且不高于1.715m 的学生所占的百分比大约是 ;(3)该校17岁男生中,身高在哪个范围内的频数最多? 如果该校17岁男生共有350名,那么在这个身高范围内的人数估计有多少人?25.如图,在正方形ABCD 中,AE ⊥BF ,垂足为P ,AE 与CD 交于点E ,•BF •与AD 交于点F ,求证:AE=BF .26.某工程队在老城区改造中承包了一项拆迁工程.原计划每天拆迁1250m 2,因为准备工作不足,第一天少拆迁了20%.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了1440m 2.(1)求该工程队第一天拆迁的面积;(2)若该工程队第二,三天每天的拆迁面积比前一天增长的百分数相同,求这个百分数.27.如图,已知梯形ABCD ,∠B=90°,AB=8cm ,AD=24cm ,BC=26cm ,点P 从A 出发,以1cm/s 的速度沿边AD 向D 运动,点Q 同时从C 出发,以3cm/s 的速度沿边CB 向B 运动,其中一动点达到端点时,另一动点随之停止运动。
初二数学试卷(2008、6、26)

初二数学·第 1页 共4页第9题图盐城市初级中学2007/2008学年度第二学期期末考试初二年级数学试题(考试时间:120分钟 卷面总分:150分)命题人:陶万红 审核人:韩俊元 亲爱的同学们:仔细审题,冷静作答.愿你们在答题中有一种快乐的心绪漾动,我们也期待着和你一起体验成功的喜悦!一.细心选择(本大题共10小题,每小题3分,计30分)1.计算3,所得结果为( )A .3B .9C .1 D.2.若如图所示的两个四边形相似,则∠α的度数是 ( ) A .870 B .600 C .750 D .12003.为了了解2008奥运会期间北京地区的气温分布状况,相关部门对往年8月8日至8月这组数据的极差为 (单位:℃) ( )A .8B .7C .6D .5 4.如果线段上一点P 把线段分割为两条线段P A 、PB ,当P A 2=PB ·AB ,即P A ≈0.618AB 时,则称点P 是线段AB 的黄金分割点,现已知线段AB =10,点P 是线段AB 的一个黄金分割点,如图所示,那么线段PB 的长约为 ( ) A .6.18 B .0.382 C .0.618 D .3.825.在梯形ABCD 中,AD//BC ,EF 是中位线.若AD =8,EF =12,则BC 长为( ) A .4 B .8 C .12 D .166.某地统计部门公布最近5年国民消费指数增长率分别为8.5%、9.2%、9.9%、10.2%、9.8%,业内人士评论说:“这五年消费指数增长率之间相当平稳”,从统计角度看,“增长率之间相当平稳”说明这组数据 比较小 ( ) A .平均数 B .方差 C .众数 D .中位数7.盐城市大纵湖旅游风景区中某两个景点之间的距离为75米,在一张比例尺为1:2000的导游图上,它们之间的距离大约相当于 ( ) A .一根火柴的长度 B .一支钢笔的长度 C .一支铅笔的长度 D .一根筷子的长度8.如图所示的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解: 甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形; 乙:只要指针连续转六次,一定会有一次停在6号扇形;丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大.你认为见解正确的是 ( ) A .甲B .乙C .丙D .丁9. 如图,四边形ABCD 是矩形,F 是AD 上一点,E 是CB 延长线上一点,且四边形AECF 是等腰梯形.下列结论中不一定...正确的是( )A .AE =FCB .AD =BCC .∠AEB =∠CFD D .BE =AF10.下列命题中:①有一个角相等的两个等腰三角形一定相似; ②6是同类二次根式,则a 的值只能是5; ③关于x 的一元二次方程ax 2 + bx + c=0( a≠0)若其中有一根是x =-ab2,则b 2-4ac=0; ④若(a + c )2-b 2=0,则关于x 的方程ax 2 + bx + c=0( a≠0)一定有实数根;其中,是真命题的有 ( ) A .1个 B .2个 C .3个 D .4个二.精心填空(本大题共8小题,每题3分,计24分) 11.一元二次方程(x -2)2=0的解是: . 12.使式子12-x 有意义的x 取值范围是 .13.如图,D 、E 两点分别在△ABC 的边AB 、AC 上,DE 与BC 不平行,当满足条件 (写出一个即可)时,△ADE ∽△ACB . 14.四川5·12大地震后,灾区急需药品.某企业急灾区所急,除加班加点生产外,还决定下调药品的价格,某种药品经过两次降价,由每盒72元调至52元.若每次平均降价的百分率为x ,由题意可列方程为_________________.15.如图,不等长的两条对角线AC 、BD 相交于点O ,且将四边形ABCD 分成甲、乙、丙、丁四个三角形.若21==ODBO OCAO ,则甲、乙、丙、丁这4个三角形中,一定相似的有 .6075α60138 第2题图ABP.. . 第4题图654123第8题图第13题图ABCDE 考场___________班级_____________ 姓名___________ 学号___________………………………………密…………封…………线…………内…………不…………得…………答…………题………………………………座位号:初二数学·第 2页 共4页16.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,北岸边每隔50米有一根电线杆.小丽站在离南岸边20米的点P 处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,且在这两棵树之间还有三棵树,则河宽为 米. 17.如图,ABCD 是矩形纸片,翻折∠B 、∠D ,使BC 、AD 恰好落在AC 上.设F 、H 分别是B 、D 落在AC 上的两点,E 、G 分别是折痕CE 、AG 与AB 、CD 的交点.若AB =4cm ,BC =3cm ,则线段EF 的长为 cm .18.△ABC 中,∠A =40°,若要△ABC 为等腰三角形 ,则∠B = .三.用心解答(本大题共6小题,计52分)19.(本题满分8分)用指定的方法解下列方程: (1)x 2- 2x = 3(因式分解法) (2)012212=-+x x (配方法) 20.(本题满分8分)计算下列各式: (1)23213138+-+ (2)(26-3)(22 + 1 )21.(本题满分8分)小亮同学想利用影长测量学校旗杆AB 的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD 处,另一部分在某一建筑的墙上CD 处,分别测得其长度为9.6米和2米,求旗杆AB 的高度.22.(本题满分 8 分)某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,要使月销售利润达到8000元,销售单价应定为多少?(月销售利润=月销售量×销售单价-月销售成本.) 23.(本题满分10分)有四张背面相同的纸牌A 、B 、C 、D 其正面分别画有四个不同的几何图形(如图),小明将这四张牌背面朝上洗匀后摸出一张,放回..洗匀后再摸一张. (1)用树状图(或列表法)表示两次摸牌的所有可能出现的结果(纸牌可用A 、B 、C 、D 表示).(2)求摸出两张牌面都是中心对称图形的纸牌的概率.A 第17题图BCDEFG H第16题图 A B C DO 甲 乙丙 丁 第15题图初二数学·第 3页 共4页③②①中点中点③②①24.(本题满分10分)如果关于x 的一元二次方程(m +5)x 2 – 2(m +2)x +m =0 没有..实数根. (1)求m 的取值范围;(2)试判别关于x 的方程(m -5)x 2 – 2(m -2)x +m =0根的情况.四.相信自己,挑战自我!(本大题共4小题,计44分)25.(本题满分10分)直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形,方法如下(方法不唯一):请你用上面图示方法,解答下列问题(不要求用尺.....规.作图,直接画出示意图即可............): (1)对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形...(2)对任意四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的矩形...26.(本题满分10分) 1、阅读理解:如图1,以原点O 为位似中心按比例尺OA ’:OA = 3:1在位似中心的同侧..将△OAB 放大..为△OA ’B ’,若A (1,2),B (3,1),则A ’、B ’两点的坐标分别为(3,6)和(9,3); 2、活动探索:(利用网格在下图中分别画出对应的图形)活动一:如图2,以点T (1,1)为位似中心按比例尺TE ’:TE = 3:1在位似中心的同.侧.将△TEF 放大..为△TE ’F ’,若E (2, 3),F (4,2),则E ’、F ’的坐标分别为_____________、_____________;活动二:如图3,以点W (2,3)为位似中心按比例尺WG ’:WG = 4:1在位似中心的同侧..将△WGH 放大..为△WG ’H ’,若G (3,5),H (5,4),则G ’、H ’的坐标分别为_____________、_____________; 3、归纳猜想:以第一象限内的点M (a ,b )为位似中心,按比例尺MP ’:MP =n :1在位似中心的同.侧.将图形放大,则点P (x ,y )的对应点P ’的横坐标为_________________,纵坐标为_________________.(用a 、b 、 n 、 x 、y 表示).考场___________ 班级_____________ 姓名___________ 学号___________………………………………密…………封…………线…………内…………不…………得…………答…………题………………………………座位号:初二数学·第 4页 共4页27.(本题满分12分)如图1,正方形ABCD 和正方形QMNP ,∠QMN =∠ABC ,M 是正方形ABCD 的对角线AC 、BD 的交点,MN 交AB 于F ,QM 交AD 于E .(1)线段ME 与线段 MF 的大小关系是:ME ______MF (填“<”、“=”、“>”)(不必说明理由).(2)如图2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME 与线段MF 的大小关系,并加以证明.(3)如图3,若将原题中的“正方形”改为“矩形”,且BC = 2AB ,其他条件不变,探索线段ME 与线段MF 的大小关系,并说明理由.(4)根据前面的探索和图4,若将原题中的“正方形”改为“平行四边形”,且BC = kAB (k 是常数,且k >1),其他条件不变,则ME 与MF 的大小关系又如何呢?请写出结论并加以说明.28、(本题满分12分)如图1,在平面直角坐标系中,点A (8,0)、B (6,23)、C (0,23)、D (-2,0),顺次连接AB 、BC 、CD 得四边形ABCD .点P 、Q 同时从A 点出发,分别作匀速运动,其中点P 以每秒2个单位的速度沿折线段AB →BC 向终点C 运动,到达终点停止运动;点Q 以每秒1个单位的速度沿AO 向终点O 运动,到达终点停止运动.设这两点从A 出发的运动时间为t 秒.(1)试判断四边形ABCD 的形状,并说明理由.(2)①四边形PQAB 能成为平行四边形吗?若有可能,请求出t 的值;若不可能,请说明理由.②四边形PQAB 能成为菱形吗?若有可能,请直接写出t 的值,不必说明理由. (3)四边形PQAB 有可能成为等腰梯形吗?若有可能,请求出..t 的值;若不可能,请修改点P 的运动速度(或范围),使得四边形PQAB 成为等腰梯形,同时直接写出此时对应的tB CA DE MPQ F N图4F AB CDMN P QE图3M AB C D EF N PQ 图1 AE DCB M NQ P F图2 x。
2008学年度第二学期期末练习卷

2008学年度第二学期期末练习卷 八年级数学(新教材) 洪山中学 2008.6(考试时间100分钟,满分100分)一、 填空题(本大题共14题,每题3分,满分42分)1. 必然事件的概率等于_______,不可能事件的概率等于_________.2. 从52扑克牌中任取一张,取到”A ”的概率为_____________3. 正五边形的外角和等于_________________.4. 一个多边形的内角和1008,这个多边形是___________边形.5. 如果梯形的上底长为5,中位线长为8,那么梯形的下底长为_____________. 6.平行四边形ABCD 中,若∠B =70°,AH ⊥CD 于H ,则∠DAH = 度. 7.菱形两条对角线长分别为4cm 和8cm ,则菱形的边长为 cm 8.梯形中位线长10cm,高8cm,则梯形面积______________ 9、对角线_____________________________四边形是正方形.10、 菱形的周长40,一条对角线长16,菱形的面积是_____ 11、正方形的对角线长10,则面积是______ 12、计算:_________=+++ 13、计算:________=+-14、在“石头、剪子、布”的游戏中,两人做出不同手势的概率是_____________二、选择题(本大题共4题,每题3分,满分12分)15、线段、正三角形、等腰三角形、菱形、矩形中既是轴对称,又是中心对称图形的个数是_________个 ( )A)2 B)3 C)4 D)516、平行四边形一条边长是10,下列各组数中可作为这个平行四边形的两条对角线的长是 ( )A )12,8B )13,6C )28,6D )20,6 17、顺次连结等腰梯形各边中点所得到的四边形是 ………………………… ( )A)正方形; B )菱形; C) 矩形; D )等腰梯形.18、下列命题中,真命题的是……………………………………………………( ) (A )对角线相等的四边形是矩形;(B )对角线互相垂直的四边形都是菱形; (C )对角线互相平分的四边形是平行四边形;(D )对角线互相垂直平分的四边形是正方形.三、(本大题共3题,每题6分,满分18分) 19.解方程:26x =.20. 解方程组:230,10.x y x y --=⎧⎨++=⎩21. 如图,点E 在平行四边形ABCD 的对角线BD 上.(1)填空:BC BA + =___ ;BC AE -= ; (2)求作:BC AE +.ACEBD四、(本大题共3题,每题6分,满分18分)22.如图,已知:在梯形ABCD 中,AD ∥BC ,AD +BC =CD ,M 是AB 的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009~~2010年度下学期八年级数学期末试卷
一、填空题(10×2'=20分)
1、如果反比例函数的图象过点(1、-2),则这个反比例函数的解析式为_______________。
2、若
53
=b a ,则b b a +__________________。
3、化简:b
a b a +--1
1 _______________。
4、如图1,在四边形ABCD 中AB//CD ,若加上AD//BC ,则四边形ABCD 为平行四边形。
现在请你
添加一个适当的条件:________________________,使得四边形AECF 为平行四边形。
( 图中不再添加点和线)。
E
F
D
C
B
A 1C
B A
图1 图2
图3
5、如图2,是根据四边形的不稳定性制作的边长为10cm 的可活动
菱形衣架,若墙上钉子间的距离AB =BC =10cm,则∠1=___________度。
6、如图3,正方形ABCD 中,AB=1,点P 是对角线AC 上一点,分别以AP,PC 为对角线作正方形,则两个小正方形的周长的和是_______________.
7、如图4,在梯形ABCD 中,AD //CD ,对角线AC ⊥BD ,且AC =5cm,BD=12cm,则该梯形的两底长之和等于_______________cm.
8、直线Y=2X-1与X 轴交于点A ,与Y 轴交于点B ,则AB 的长是____________。
图4
P 是反比例函数图象在第一象限的 点,且矩形PEOF 的面积为3,则反比例函数表达式为__________________
10、直线Y =2X -4与X 轴交于点A ,与Y 轴交于点B ,则AB 的长是
二.选择题(本大题共8小题,每小题3分,共24分。
第小题只有一个正确选项,把正确选项的代号填入题后括号内。
) 11、分式
3
1
-x 有意义,则x 的取值范围是( )
A 、X>3
B 、X<3
C 、X ≠3
D 、X ≠-3
12、天气预报报道宜春市今天最高气温34℃,最低气温20℃,则今天宜春市气温的极差是
( )
A 、54℃
B 、14℃
C 、-14℃
D 、-62℃
13、下列四个函数中,当X >0时,Y 随X 的增大而增大的是( ) A 、Y =
x 2 B 、Y =-x
2
C 、Y =-x
D 、Y =-2x -1 14、10名学生分虽购买如下尺码的鞋子:20,20,21,22,22,22,23,23,24.(单位:Cm),
这组数据中鞋店老板最关心的是( ) A 、平均数 B 、中位数 C 、众数 D 、方差
15、如图6,正比例函数Y =X 与反比例函数Y =x 1的图象相交于点A 、C ,AB ┴X 轴于B ,CD┴X
轴于D ,这四边形ABCD 的面积为( )
A 、1
B 、2
C 、
23 D 、2
5
A D
6 B E C 图7
16AD//BC ,AE//DC ,∠B =60°,BC =3,ΔABE 的周长为6,则等腰梯形ABCD 的周长是( ) A 、 8 B 、 10 C 、 12 D 、16 17、将一张矩形纸片ABCD 如图8那样折起,使顶点C 落在C'处,其中AB =4,若∠C'ED=30°,则折痕ED 的长为( ) A C' A 、4 B 、 C 、 D 、8 D
B
E
C 18、如图9,在同一直角坐标系中,正比例函数y =kx+3与反比例函数y=
x
k
的图象位置可能是( )
A B 三、(本大题共3小题,第19题,第20题各5分,第21题6分,共16分)
D C B A P
D
C B A
19、化简:
20、解方程:
21、先化简,再选择你喜欢的又使原式有意义的一个x 的值代
入求值。
四、(本大题共3小题,每小题7分,共21分)
22、宜丰县蔬菜大户老李有一块正方形菜地,他准备在菜地中间空出两条笔直的交叉的小路,把菜地平均分成面积相等的四部分进行特色种植。
请你在下图中添加两条相交线,帮助老李设计三种不同的分割方案,并简要说明作图方法。
方法一 方法二 方法三
23、如图10
,已知 ABCD 中,E 为AD 中点,CE 的延长线交BA 延长线于点F 。
求证:A 是
BF 的中点
C D E
B F
24、张老师要从班级里数学 成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学 联赛”。
(2)张老师从测验成绩表中,求得甲的方差S 甲 =33.2,请你计算乙10次测验成绩的方差。
(3)请你根据上面的信息,运用所学统计知识,帮张老师选拔出参加“全国数学联赛”的人选,并简要说明理由。
五.(本大题共两小题,第25题8分,第26题9分,共17分
2
1a b a b a b a ---+²²
÷²┼2ab ┼b
2
113224x x x =-+-┼11111x x x x x x +⎛⎫⎛⎫++ ⎪ ⎪---⎝⎭⎝⎭÷
25 .如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交边AB于F,∠ADC的平分线DG交边AB于G。
(1)求证:AF=GB;(2)请你在已知条件的基础上再添加一个条件,使得△EFG为等腰直角三角形,并说明理由.
26 .甲、乙两个工程队合做一项工程,需要16天完成,现在两队合做9天,甲队因有其他任务调走,乙队再做21天完成任务。
甲、乙两队独做各需几天才能完成任务?
五、(本大题共两小题,第25题10分,第26题12分,共22分)25、如图11,一次函数y=kx+b的图象与反比例函数y=
x
m
的图象交于A、B两点。
(1)利用图中条件,求反比例函数的解析式及n的值。
图11
(2)求一次函数的解析式。
(3)根据图象写出使一次函数的值大于反比例函数值的x的取值范围。
26、如图12,菱形ABCD的边CD在菱形ECGF的边CE上,且D是CE中点。
连接BE,DF。
(1)观察猜想BE与DF之间的大小关系,并证明你的结论。
(2)图中是否存在旋转能够互相重合的两个三角形?若存在,请说明旋转过程:若不存在,请说明理由。
E
F
G
C
B
A。
