高考数学第一轮复习章节练习题20-立体几何

合集下载

2023届高考数学总复习《立体几何》附答案解析

（2）若点 N 为 BC 的中点，求四面体 A'MNB 的体积．
【解答】证明：（1）连接 BD，设 BD∩EC＝F，连接 MF，
由题意可得四边形 BCDE 为正方形，则 F 为 BD 的中点，
∴MF 为△A′BD 的中位线，可得 MF∥A′B，
又 A′B⊄平面 EMC，MF⊂平面 EMC，
∴A'B∥平面 EMC；
2023 年高考：立体几何复习题及答案
1．如图，已知直角梯形 ABCD，BC∥AD，BC＝CD＝2，AD＝4，∠BCD＝90°，点 E 为 AD 的中点，现将三角形 ABE 沿 BE 折叠，得到四棱锥 A'﹣BCDE，其中∠A'ED＝120°，点 M 为 A'D 的中点．
（1）求证：A'B∥平面 EMC；
第2页共3页
∵BE⊂平面 BEF，∴平面 BEF⊥平面 AMD，结合题意分析知，点 F 在线段 AD 上，连接 MF，过 A 作 AH⊥MF，交 MF 的延长线于点 H，
则结合已知条件得
，解得 AH ，
设 Dt ，
第3页共3页
【解答】解：（1）证明：由题意知 PC2+AC2＝PA2，∴PC⊥AC，同理，PC⊥BC，又 AC∩BC＝C，∴PC⊥平面 ABC， ∵D，E 分别是 AC，PA 的中点，∴DE∥PC， ∴DE⊥平面 ABC，又 DE⊂平面 BDE，∴平面 BDE⊥平面 ABC．（2）在△BDE 中，DE⊥BD，BD＝2 ，DE＝2，∴BE＝4，如图，过 A 作 AM⊥BE 于 M，连接 MD，在△ABE 中，AB＝BE＝4，AE＝2 ，解得 AM ，ME＝1， ∵DM⊂平面 BDE，∴AC⊥DM，在 Rt△ADM 中，AM ，AD＝2，∴DM ， ∴DM2+EM2＝DE2，∴MD⊥BE， ∵AM∩MD＝M，∴BE⊥平面 AMD，

2015届高考数学一轮复习单元检测：立体几何(北师大版)

2015届高考数学一轮复习单元检测：立体几何（北师大版）(时间90分钟，满分120分)一、选择题(本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．(2013·东莞高一检测)如图1为某几何体的三视图，根据三视图可以判断这个几何体为()图1A．圆锥B．三棱锥C．三棱柱D．三棱台【解析】由三视图易知其图形为所以为三棱柱．【答案】 C2．(2014·湖北省八校联考)已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为V1，直径为4的球的体积为V2，则V1∶V2＝( )A．1∶2 B．2∶1C．1∶1 D．1∶4【解析】由三视图知，该几何体为圆柱内挖去一个底面相同的圆锥，因此V1＝8π－8π3＝16π3，V2＝4π3×23＝32π3，V1∶V2＝1∶2.【答案】A3．已知水平放置的△ABC是按“斜二测画法”得到如图2所示的直观图，其中B′O′＝C′O′＝1，A′O′＝32，那么原△ABC的面积是()图2 A. 3 B．2 2C.32D．34【解析】由题图可知原△ABC的高为AO＝3，∴S△ABC ＝12×BC×OA＝12×2×3＝3，故选A.【答案】 A4．l1，l2，l3是空间三条不同的直线，则下列命题正确的是()A．l1⊥l2，l2⊥l3⇒l1∥l3B．l1⊥l2，l2∥l3⇒l1⊥l3C．l1∥l2∥l3⇒l1，l2，l3共面D．l1，l2，l3共点⇒l1，l2，l3共面【解析】当l1⊥l2，l2⊥l3时，l1也可能与l3相交或异面，故A不正确；l1⊥l2，l2∥l3⇒l1⊥l3，B正确；当l1∥l2∥l3时，l1，l2，l3未必共面，如三棱柱的三条侧棱，故C不正确；l1，l2，l3共点时，l1，l2，l3未必共面，如正方体中从同一顶点出发的三条棱，故D不正确．故选B.【答案】 B5．如图3，在正方体ABCD—A1B1C1D1中，若E是A1C1的中点，则直线CE垂直于()图3A．AC B．BDC．A1D D．A1D1【解析】∵BD⊥AC，BD⊥AA1，∴BD⊥平面AA1C1C又CE平面AA1C1C，∴CE⊥BD.【答案】 B6．一个几何体的三视图如图4，该几何体的表面积为()图4A．280 B．292C．360 D．372【解析】由三视图可知该几何体是由下面一个长方体，上面一个长方体组合而成的几何体．下面长方体的表面积为8×10×2＋2×8×2＋10×2×2＝232，上面长方体的表面积为8×6×2＋6×2×2＋8×2×2＝152，又由于两个长方体的表面积重叠一部分，所以该几何体的表面积为232＋152－2×6×2＝360，应选C.【答案】 C7．(2013·哈师大附中检测)如图5是底面积为3，体积为3的正三棱锥的主视图(等腰三角形)和左视图(等边三角形)，此正三棱锥的侧视图的面积为()图5A.332B．3C. 3 D．3 2【解析】由题意知左视图是一个三角形，其底边长就是正三棱锥的底面正三角形的高，高就是正三棱锥的高．根据已知条件可得正三棱锥的底面边长是2，高为3，故侧视图的面积是12×3×3＝332.【答案】 A8．(2013·吉林高一检测)过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为()A.316B．916C.38D．932【解析】如图所示，设球的半径为R，由题意知OO′＝R2，OF＝R，∴r＝32R.∴S截面＝πr2＝π(32R)2＝3π4R2.又S球＝4πR2，∴S截面S球＝3π4R24πR2＝316.【答案】 A9．如图6是一建筑物的三视图(单位：米)，现需将其外壁用油漆刷一遍，若每平方米用漆a千克，则共需油漆的质量为()图6A．(48＋36π)a千克B．(39＋24π)a千克C．(36＋36π)a千克D．(36＋30π)a千克【解析】此建筑物是直四棱柱与圆锥的组合体，其外壁的面积S＝π×32－3×3＋π×3×5＋3×4×4＝39＋24π(平方米)，因此共需油漆的质量为(39＋24π)a千克．【答案】 B10．如图7(1)所示，已知正方体面对角线长为a，沿阴影面将它切割成两块，拼成如图7(2)所示的几何体，那么此几何体的表面积为()图7A．(1＋22)a2B．(2＋2)a2C．(3－22)a2D．(4＋2)a2【解析】由题意知新的几何体为平行六面体且共顶点的三条棱长分别为22a，22a和a，表面积为2×(22a)2＋2×(22a)2＋2×22a·a＝(2＋2)a2.【答案】 B二、填空题(本大题共4小题，每小题5分，共20分，将答案填在题中的横线上)11．如图8是一个四边形的直观图，则原图的面积为______．图8【解析】由四边形的直观图可知，原四边形是一个直角梯形，其上、下底边长分别为2、3，高为6，∴面积为2＋32×6＝15.【答案】1512．(2013·常熟高一检测)若圆锥的母线长为2 cm，底面圆的周长为2π cm，则圆锥的表面积为________．【解析】设圆锥的底面半径为r，则2πr＝2π，∴r＝1，∴圆锥的表面积S＝12×2π×2＋πr2＝3π.【答案】3π13．如图9，M是棱长为2 cm的正方体ABCD－A1B1C1D1的棱CC1的中点，沿正方体表面从点A到点M的最短路程是______cm.图9【解析】侧面展开，可得最短路程为(2＋2)2＋12＝17.【答案】1714．在直四棱柱ABCD—A1B1C1D1中，当底面四边形A1B1C1D1满足条件________时，有A1C⊥B1D1(注：填上你认为正确的一种情况即可) 【解析】由直四棱柱可知CC1⊥面A1B1C1D1，所以CC1⊥B1D1，要使B1D1⊥A1C，只要B1D1⊥平面A1CC1，所以只要B1D1⊥A1C1，还可以填写四边形A1B1C1D1是菱形，正方形等条件．【答案】B1D1⊥A1C1(答案不唯一)三、解答题(本大题共4小题，共50分．解答应写出文字说明，证明过程或演算步骤)15．(本小题12分)如图10是一个几何体的主视图和俯视图，(1)试判断这个几何体是什么几何体；图10(2)请画出它的左视图，并求该左视图的面积．【解】(1)由题图中的主视图和俯视图知该几何体是正六棱锥．(2)该几何体的左视图如图所示．其中两腰为斜高，底边长为3a，三角形的高即为正六棱锥的高，且长为3 a，所以该左视图的面积为123a·3a＝32a2.16．(本小题12分)如图11，正方形ABCD和四边形ACEF所在的平面互相垂直，EF∥AC，AB＝2，CE＝EF＝1.求证：图11(1)AF∥平面BDE；(2)CF⊥平面BDE.【证明】(1)设AC与BD交于点G.因为EF∥AG，且EF＝1，AG＝12AC＝1.所以四边形AGEF为平行四边形．所以AF∥EG.因为EG平面BDE.AF平面BDE，所以AF∥平面BDE.(2)连接FG，EG.因为EF∥CG，EF＝CG＝1，且CE＝1，所以四边形CEFG为菱形．所以CF⊥EG.因为四边形ABCD为正方形，所以BD⊥AC.又因为平面ACEF⊥平面ABCD，且平面ACEF∩平面ABCD＝AC.所以BD⊥平面ACEF.所以CF⊥BD.又BD∩EG＝G，所以CF⊥平面BDE.17．(本小题12分)如图12所示是某几何体的三视图，请你指出这个几何体的结构特征，并求出它的表面积与体积．图12【解】此几何体是一个组合体(如图)，下半部分是直四棱柱，上半部分是半圆柱，其轴截面的大小与四棱柱的上底面大小一致．表面积S＝8×6×2＋6×4×2＋8×4＋π×22＋π×2×8＝176＋20π(cm2)则体积V＝8×6×4＋12×π×22×8＝192＋16π(cm3)．所以几何体的表面积为(176＋20π)cm2，体积为(192＋16π)cm3.18．(本小题14分)如图13，四棱锥S—ABCD中，底面ABCD是菱形，其对角线的交点为O，且SA＝SC，SA⊥BD.图13(1)求证：SO⊥平面ABCD；(2)设∠BAD＝60°，AB＝SD＝2，P是侧棱SD上的一点，且SB∥平面APC，求三棱锥A—PCD的体积．【解】(1)证明：∵底面ABCD是菱形，∴AC⊥BD.又∵BD⊥SA，SA∩AC＝A，∴BD⊥平面SAC.又∵SO平面SAC.∴BD⊥SO.∵SA ＝SC ，AO ＝OC ，∴SO ⊥AC . 又∵AC ∩BD ＝O ， ∴SO ⊥平面ABCD . (2)连接OP ，∵SB ∥平面APC ，SB 平面SBD ，平面SBD ∩平面APC ＝OP ，∴SB ∥OP . 又∵O 是BD 的中点，∴P 是SD 的中点．由题意知△ABD 为正三角形．∴OD ＝1. 由(1)知SO ⊥平面ABCD ，∴SO ⊥OD . 又∵SD ＝2，∴在Rt △SOD 中，SO ＝ 3. ∴P 到面ABCD 的距离为32，∴V A —PCD ＝V P —ACD ＝13×(12×2×2sin 120°)×32＝12.。

高考数学第一轮复习立体几何专题题库19.doc

241. 已知点P 是正方形ABCD 所在的平面外一点，PD ⊥面AC ，PD=AD=l ，设点C 到面PAB 的距离为d 1，点B 到平面PAC 的距离为d 2，则（）（A ）l <d 1 <d 2（B ）d 1< d 2<l （C ）d 1<l < d 2（D ）d 2<d 1<l解析：l d 221=，l d 332=，故d 2<d 1<l ，选D 。

242.如图，正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。

点M 在AC 上移动，点N 在BF 上移动，若CM=BN=a ).20(<<a （1）求MN 的长；（2）当a 为何值时，MN 的长最小；（3）当MN 长最小时，求面MNA 与面MNB 所成的二面角α的大小。

解析：（1）作MP ∥AB 交BC 于点P ，NQ ∥AB 交BE 于点Q ，连接PQ ，依题意可得MP ∥NQ ，且MP=NQ ，即MNQP 是平行四边形。

∴MN=PQ,由已知，CM=BN=a,CB=AB=BE=1,∴2==BF AC ,21,21a BQ a CP ==, 即2aBQ CP ==, ∴=+-==22)1(BQ CP PQ MN )20(21)22()2()21(222<<+-=+-a a a a（2）由（1）知: 2222==MN a 时，当，的中点时，分别移动到即BF AC N M ,, 22的长最小，最小值为MN (3)取MN 的中点G ，连接AG 、BG ，∵AM=AN,BM=BN ，∴AG ⊥MN,BG ⊥MN ，∴∠AGB 即为二面角α的平面角。

又46==BG AG ，所以由余弦定理有 ADE31464621)46()46(cos 22-=∙∙-+=α。

故所求二面角)31arccos(-=α。

243. 如图，边长均为a 的正方形ABCD 、ABEF 所在的平面所成的角为)20(πθθ<<。

2023年高考数学----立体几何解答题常考全归类专项练习题(含答案解析)

2023年高考数学----立体几何解答题常考全归类专项练习题（含答案解析）1．（2022·重庆沙坪坝·重庆八中校考模拟预测）如图，在三棱柱111ABC A B C -中，1BC CC =，1AC AB =.(1)证明：平面1ABC ⊥平面11BCC B ；(2)若BC ，1AB B C =，160CBB ∠=︒，求直线1BA 与平面111A B C 所成角的正弦值.【解析】（1）证明：设11BC B C O =,连接AO ,如图所示：则O 为11,BC B C 的中点，因为1BC CC =，所以1CO BC ⊥，即11B C BC ⊥，又因为1AC AB =，所以1AO B C ⊥，又因为1AO BC O ⋂=，所以1B C ⊥平面1ABC ，又因为1B C ⊂平面11BCC B ，所以平面1ABC ⊥平面11BCC B ；（2）因为160CBB ∠=︒，所以1CBB 为正三角形，四边形11BCC B 为菱形，因为BC ，1AB B C =，设1AC =，则11AB =，BC =所以1ACB 为等腰直角三角形，所以OA 又因为四边形11BCC B 为菱形，所以1CO OB =BO ，又因为1AB B C = 所以22226244OA OB AB +=+==，所以1OA BC ⊥，即11,,OA BC B C 两两垂直，以O 为坐标原点，1,,OB OB OA 所在的直线分别为x 轴，y 轴，z 轴，建立如图所示的坐标系：所以B ，1B ，(0,C ，A ，1(C ，设1000(,,)A x y z ，由11CA C A =uu r uuu u r 可得000(,)x y z =，所以00022x y z ===，所以1(A ，所以1(BA =uuu r，11(B C =uuu u r，11(B A =uuu u r ，设平面111A B C 的法向量为(,,)n x y z =，所以111100B C n B A n ⎧⋅=⎪⎨⋅=⎪⎩，即有00x y x z ⎧=⎪⎪⎨⎪+=⎪⎩，令z =1,x y ==所以(1,3,n =−，设直线1BA 与平面111A B C 所成角为θ，则有1sin |cos ,|BA n θ=<>==. 所以直线1BA 与平面111A B C2．（2022·四川达州·统考一模）如图，三棱柱111ABC A B C −中，底面ABC 为等腰直角三角形，112AB AC BB ===，，160ABB ∠=.(1)证明: 1AB B C ⊥；(2)若12B C =，求1AC 与平面1BCB 所成角的正弦值.【解析】（1）证明: 连接1AB ，在1ABB 中，111260AB BB ABB ==∠=，，，由余弦定理得，22211111214223cos 2AB AB BB AB BB ABB ⋅=+−⋅∠=+−⨯⨯=，1AB ∴22211BB AB AB ∴=+，1AB AB ∴⊥.又ABC 为等腰直角三角形，且AB AC =，AC AB ∴⊥，1AC AB A =，1,AC AB ⊂平面1AB C ，AB ∴⊥平面1AB C .∵1B C ⊂平面1AB C ，∴1AB B C ⊥（2）11312AB AB AC B C ====，，22211B C AB AC ∴=+，1AB AC ∴⊥，如图，以 A 为原点， 1,,AB AC AB 的方向分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系，则()(()()10,0,0,,1,0,0,0,1,0A B B C ，()()11,0,3,1,1,0.BB BC ∴=−=− 设平面1BCB 的一个法向量为(),,n x y z =，由100BB n BC n ⎧⋅=⎪⎨⋅=⎪⎩，得00x x y ⎧−=⎪⎨−+=⎪⎩，令1z =，得x y == ∴平面1BCB 的一个法向量为()331n=，，. ()((1110,1,0AC AC CC AC BB =+=+=+−=−，设1AC 与平面1BCB 所成角的大小为θ，(1111,1,sin cos 11AC nAC n AC n θ−∴=====+⋅⋅， 1AC ∴与平面1BCB. 3．（2022·陕西宝鸡·统考一模）如图在四棱锥P ABCD −中，PA ⊥底面ABCD ，且底面ABCD是平行四边形.已知2,1,PA AB AD AC E ===是PB 中点.(1)求证：平面PBC ⊥平面ACE ；(2)求平面PAD 与平面ACE 所成锐二面角的余弦值.【解析】（1）PA ⊥面ABCD ，且2,1PA AC ==，PC BC ∴==.∵E 是PB 中点,所以PB CE ⊥.同理可证：PB AE ⊥.又AE ⊂面ACE ，CE ⊂面ACE ，AE CE E =I ,PB ∴⊥平面ACE .∵PB ⊂面PBC ，∴平面PBC ⊥平面ACE .（2）222BC AB AC =+， ∴AB AC ⊥. 以A 为原点，,,AC AB AP 分别为x ，y ，z 轴正方向建系，如图：则()()()()()0,0,0,0,2,0,1,2,0,0,0,2,0,1,1A B D P E −.设平面PAD 的法向量(),,,n x y z =则00n AP n AD ⎧⋅=⎪⎨⋅=⎪⎩，得2020z x y =⎧⎨−=⎩，不妨取1y =，则()2,1,0n =. 由（1）得()0,2,2PB =−是平面ACE 的一个法向量，所以cos ,5n PBn PB n PB ⋅==⨯，所以平面PAD 与平面ACE 4．（2022·广东广州·统考一模）如图，已知四棱锥P ABCD −的底面ABCD 是菱形，平面PBC ⊥平面ABCD ，30,ACD E ∠=为AD 的中点，点F 在PA 上，3AP AF =.(1)证明：PC //平面BEF ；(2)若PDC PDB ∠∠=，且PD 与平面ABCD 所成的角为45，求平面AEF 与平面BEF 夹角的余弦值.【解析】（1）设,AC BE 的交点为O ，连接FO ，已知O 为ABD △的重心，所以12AO AC =，12AF AP =，所以在APC △中，12AO AF AC AP ==，所以//FO PC ，所以FO ⊂平面BEF ，PC ⊄平面BEF ，则PC //平面BEF .（2）因为30,ACD ∠=所以30,ACB ∠=所以DCB △为等边三角形，所以DC DB =，又因为PDC PDB ∠∠=，所以PDB PDC ≅，所以PB PC =，取BC 的中点为H ，连接PH ，则PH BC ⊥，平面PBC ⊥平面ABCD ，平面PBC ⋂平面ABCD BC =，则PH ⊥平面ABCD ，以H 为坐标原点，,,HD HB HP 为,,x y z 轴，建立如图所示的空间直角坐标系，因为PD 与平面ABCD 所成的角为45PDH ∠=︒，所以=PH DH ，设菱形的边长为2，所以PH DH ==(()))),0,1,0,,,P B A D E ，因为3AP AF =，所以43F ⎝⎭， ()()313,,,0,1,0,3,0,0333EF AE BE ⎛⎫=−=−=⎪ ⎪⎝⎭，设(),,n x y z =⊥平面AEF ，001003y n AE y z n EF −=⎧⎧⋅=⎪⎪⇒⎨⎨+=⋅=⎪⎪⎩⎩，令1,0,1x y z ===，所以()1,0,1n =，设()222,,m x y z =⊥平面BEF ，2222001003m BEm EF y =⎧⋅=⎪⇒⎨⎨⋅=+=⎪⎪⎩⎩，令2220,1y x z ===−，所以()0,3,1m =−，则2cos ,4m n m n m n ⋅==−，所以平面AEF 与平面BEF5．（2022·上海奉贤·统考一模）如图，在四面体ABCD 中，已知BA BD CA CD ===.点E 是AD 中点.(1)求证：AD ⊥平面BEC ；(2)已知95,arccos,625AB BDC AD ∠===，作出二面角D BC E −−的平面角，并求它的正弦值.【解析】（1）,AB BD E =是AD 中点，BE AD ∴⊥ 又,AC CD E =是AD 中点，CE AD ∴⊥,BE CE E BE CE =⊂，Q I 面BEC所以AD ⊥面BEC（2）由题知，5BA BD CA CD ====，9arccos,625BDC AD ∠==，取BC 的中点F ，连接,EF DF ， ,DB DC DF BC =∴⊥,根据三角形全等证明方法,可以证明,BDE CDE EB EC ≅∴=,EF BC ∴⊥,所以DFE ∠是二面角D BC E −−的平面角，利用勾股定理计算出4,BE =, 由余弦定理得225259cos 25525BC BDC +−∠==⨯⨯，解得BC =所以DF =EF === 所以222EF DE DF +=，所以Rt DEF △中，sinDE DFE DF ∠===6．（2022·上海浦东新·统考一模）如图，三棱锥−P ABC 中，侧面PAB 垂直于底面ABC ，PA PB =，底面ABC 是斜边为AB 的直角三角形，且30ABC ∠=︒，记O 为AB 的中点，E 为OC 的中点.(1)求证：PC AE ⊥；(2)若2AB =，直线PC 与底面ABC 所成角的大小为60°，求四面体PAOC 的体积.【解析】（1）连接PO ，因为PA PB =，所以PO AB ⊥，侧面PAB 垂直于底面ABC ，PO ⊂平面PAB ，平面PAB ⋂平面ABC AB =，所以PO ⊥底面ABC ，AE ⊂底面ABC ，所以PO AE ⊥， ABC 是斜边为AB 的直角三角形，且30ABC ∠=，所以12AC AB =，又因为O 为AB 的中点，所以12CO AO AB ==,所以AOC 为等边三角形，又E 为OC 的中点，所以AE OC ⊥，因为PO AE ⊥，AE OC ⊥，PO OC O =，,PO OC ⊂POC ，所以⊥AE 平面POC ，又PC ⊂平面POC ，所以PC AE ⊥；（2）由（1）知PO ⊥底面ABC ，所以直线PC 与底面ABC 所成角为PCO ∠，因为直线PC 与底面ABC 所成角的大小为60，60PCO ∠=，因为2AB =，所以1OC =，在Rt POC △中，tan60PO =︒=111sin602AOC S =⨯⨯︒=，所以1134PAOC V ==. 7．（2022·四川成都·石室中学校考模拟预测）如图，在四棱锥P ABCD −中，AB BD BP ==PA PD ==90APD ∠=︒，E 是棱PA 的中点，且BE 平面PCD(1)证明：CD ⊥平面PAD ；(2)若1CD =，求二面角A PB C −−的正弦值.【解析】（1）取AD 中点Q ，连接QE ，QB ，PQ ，EQ PD ∥，EQ ⊄面PCD ，PD ⊂面PCD ，故EQ 面PCD ，//BE 面PCD ，BE EQ E ⋂=，面//BEQ 面PCD ，平面ABCD ⋂平面PBQ BQ =，平面ABCD ⋂平面PCD CD =，故BQ CD ∥.2AD =，1PQ =，2BQ ，222BQ PQ BP +=，故PQ BQ ⊥，AB BD =，Q 是AD 中点，故AD BQ ⊥，PQ AD Q =，,PQ AD ⊂平面ADP ，故BQ ⊥面ADP ，//BQ CD ，故CD ⊥面PAD .（2）如图所示以,,QB QD QP 为,,x y z 轴建立空间直角坐标系，(0,0,0)Q ，(0,1,0)A −，(0,0,1)P ，(2,0,0)B ，(1,1,0)C ，，设平面APB 法向量为(),,n x y z =r ，200n PB x z n AP y z ⎧⋅=−=⎪⎨⋅=+=⎪⎩ ，取=1x −，(1,2,2)n =−−，设平面PBC 法向量为(),,m a b c =，200m PB a c m PC a b c ⎧⋅=−=⎪⎨⋅=+−=⎪⎩，取1a =，()1,1,2m =，12cos ,||||9m n m n m n ⋅−+<>===⋅ 设二面角A PB C −−的平面角为θ，630sin ,m n θ>=8．（2022春·江苏徐州·高三期末）如图，四棱锥P ABCD −中，PA ⊥底面ABCD ，AD ∥BC ，N 为PB 的中点.(1)若点M 在AD 上，2AM MD =，34AD BC =，证明：MN 平面PCD ； (2)若3PA AB AC AD ====，4BC =，求二面角D AC N −−的余弦值.【解析】（1）证明：如图所示：取PC 中点F ，连接,NF DF ，因为2MD AM =，所以23MD AD =，又因为34AD BC =，所以12MD BC =，又因为AD ∥BC ，所以MD ∥BC ，又因为N 为PB 的中点，所以NF ∥BC 且12NF BC =，即有NF ∥MD 且NF MD =，所以四边形NFDM 是平行四边形，所以MN ∥DF ，又因为MN ⊄平面PCD ，DF ⊂平面PCD ，所以MN 平面PCD ；（2）连接NC ，因为3AB AC ==，所以ABC 为等腰三角形，取BC 中点Q ，连接AQ ，则有AQ BC ⊥，又因为AD ∥BC ，所以AQ AD ⊥，又因为PA ⊥底面ABCD ，所以建立如以AQ 为x 轴，AD 为y 轴，AP 为z 轴的空间坐标系，如图所示：因为3PA AB AC AD ====，4BC =，则有(0,0,0)A ，(0,3,0)D ，C ，31,)2N −，所以53(,1,),(5,2,0)22AN AC =−=，设平面ACN 的法向量为(,,)n x y z =，则有30220y z y −+=+=，所以,y x z x ==，令6x =，则(6,3n =−−，因为PA ⊥底面ABCD ，取平面ACD 的法向量(0,0,1)m =，设二面角D AC N −−的大小为θ(θ为钝角)，则有4cos cos ,||||161m n m n m n θ⋅−=<>===⋅9．（2022·陕西汉中·统考一模）如图，多面体ABCDEF 中，四边形ABCD 为菱形，60,ABC FA ∠=⊥平面,ABCD ED FA ∥，且22AB FA ED ===.(1)求证：BD FC ⊥；(2)求二面角F AC E −−的大小.【解析】（1）证明：由于四边形ABCD 为菱形，则AC BD ⊥FA⊥平面,ABCD BD ⊂平面ABCDFA BD ∴⊥又,FA AC A FA ⋂=⊂平面,FAC AC ⊂平面FACBD ∴⊥平面FAC ，又FC ⊂平面FACBD FC ∴⊥（2）如下图，取BC 的中点G ，连接,60,AG ABC AB BC ∠==，ABC ∴为等边三角形，AG BC ∴⊥，以A 为原点，AG 为x 轴，AD 为y 轴，AF 为z 轴建立空间直角坐标系，则由题意得()0,0,2,1,1F BG AG DE ===，又DE FA ∥，则()))()()0,0,0,,1,0,0,2,0,0,2,1A CB D E −， ()()()3,1,0,3,3,0,0,2,1AC DB AE ==−=，由（1）知BD ⊥平面FAC ，则可取DB 为平面FAC 的法向量设平面AEC 的法向量为(),,n x y z =r ，则00n AC n AE ⎧⋅=⎪⎨⋅=⎪⎩，020y y z +=∴+=⎪⎩，令6z =得()3,3,6n =−，设二面角F AC E −−的平面角为θ，则121cos 223||DB n DB n θ⋅===⨯⋅，由题知二面角F AC E −−的锐二面角，所以二面角F AC E −−大小为60. 10．（2022·陕西汉中·统考一模）如图，多面体ABCDEF 中，四边形ABCD 为菱形，60,ABC FA ∠=⊥平面,ABCD FA ED ∥，且22AB FA ED ===.(1)求证：BD FC ⊥；(2)求点A 到平面FBD 的距离.【解析】（1）证明：FA ⊥平面ABCD ，BD ⊂平面ABCDFA BD ∴⊥，四边形ABCD 为菱形，AC BD ∴⊥，又FA AC A =，FA ⊂平面,FAC AC ⊂平面FAC ，BD ∴⊥平面FACBD FC ∴⊥（2）11122sin1202332ABD F ABD V S FA −⎛⎫=⋅⋅=⨯⨯⨯⨯= ⎪⎝⎭三棱锥 FA ⊥平面ABCD ，,FA AB FA AD ∴⊥⊥FB FD ∴==由四边形ABCD 为菱形，60ABC ∠=，可得BD =FBD S ∴=设点A 到平面FBD 的距离为h ，则13FBD A FBD V S h −=三棱锥，由A FBD F ABD V V −−=三棱维三棱倠=解得h =∴点A 到平面FBD .11．（2022·四川广安·广安二中校考模拟预测）APD △是等腰直角三角形，AP PD ⊥且AD =ABCD 是直角梯形，AB BC ⊥，DC BC ⊥，且222AB BC CD ===，平面APD ⊥平面ABCD .(1)求证：AP ⊥平面BPD ；(2)若点E 是线段PB 上的一个动点，问点E 在何位置时三棱锥D APE −【解析】（1）证明：直角梯形ABCD 中，AB BC ⊥，DC BC ⊥，且222AB BC CD ===，则2222BD BC CD =+=，由222AD BD AB +=得AD BD ⊥，∵平面APD ⊥平面ABCD ，平面APD 平面ABCD AD =，BD ⊂平面APD ，∴BD ⊥平面APD ，∵AP ⊂平面APD ，∴BD AP ⊥，又AP PD ⊥，,PD BD D PD BD =⊂、平面BPD ，∴AP ⊥平面BPD ；（2）设PE PB λ=，∵BD ⊥平面APD ，则E 到平面PAD 的距离d 有：d PE d BD PBλ==⇒，等腰直角三角形APD △，AP PD ⊥且AD 1PA PD ==，∴1111113322P PA D E D D AP E A V V S d λ−−⎛⎫==⋅=⨯⨯⨯== ⎪⎝⎭.故点E 在PB 中点时三棱锥D APE −. 12．（2022·四川南充·统考一模）在平面五边形ABCDE 中（如图1），ABCD 是梯形，//AD BC ，2AD BC ==AB =90ABC ∠=︒，ADE V 是等边三角形．现将ADE V 沿AD 折起，连接EB ，EC 得四棱锥E ABCD −（如图2）且CE =(1)求证：平面EAD ⊥平面ABCD ；(2)在棱EB 上有点F ，满足13EF EB =，求二面角E AD F −−的余弦值．【解析】（1）依题意，ABCD 是梯形，//AD BC ，2AD BC ==AB90ABC ∠=︒，ADE V 是等边三角形．设O 是AD 的中点，则,,C O E 三点共线，且OE AD ⊥，OC AB OE =折叠后，OE AD ⊥，222CE OC OE =+，即OE OC ⊥，由于,,OC AD O OC AD =⊂平面ABCD ，所以OE ⊥平面ABCD ，由于OE ⊂平面EAD ，所以平面EAD ⊥平面ABCD .（2）由（1）可知,,OC OA OE 两两相互垂直，以O 为原点建立空间直角坐标系如图所示，平面EAD 的法向量为()1,0,0m =， )(()(),,,0,B E A D ，13EF EB =，(1133OF OE EF OE EB =+=+=+=⎝⎭,()0,AD =−，设平面FAD 的法向量为(),,n x y z =，则20320n OF y z n AD ⎧⋅==⎪⎨⎪⋅=−=⎩，故可设()23,0,1n =−，设二面角E ADF −−为θ，由图可知θ为锐角，所以23cos 13m nm n θ⋅===⋅13．（2022·贵州贵阳·贵阳六中校考一模）如图，在四棱锥P ABCD−中，DA AB ⊥，PD PC ⊥，PB PC ⊥，1AB AD PD PB ====，4cos 5DCB ∠=.(1)求证：BD ⊥平面PAC .(2)设E 为BC 的中点，求PE 与平面ABCD 所成角的正弦值.【解析】（1）∵PD PC ⊥，PB PC ⊥，PB =PD ，∴Rt △PDC ≌Rt △PBC ，∴BC =DC ，又PB ∩PD =P ，∴PC ⊥平面PBD ，∵BD ⊂平面PBD ，∴PC ⊥BD ，∵AB =AD ，BC =CD ，∴易知AC ⊥BD ，又∵AC ∩PC =C ，AC,PC 含于面PAC ∴BD ⊥平面PAC ；（2）如图，设AC 交BD 于O ，则O 是BD 的中点，连接OP ，过P 作PF AC ⊥，连接EF ，由（1）得，BD ⊥平面PAC ，PF ⊂面PAC ，故BD PF ⊥，又BD AC O ⋂=，所以，PF ⊥面ABCD ，故PEF ∠为PE 与平面ABCD 所成角，设PEF θ=∠，因为E 为BC 中点，且PC PB ⊥，故在Rt PBC △中，12PE BC =，又由BC =CD ，且BD 4cos 5DCB ∠=， ∴在△BCD 中，由余弦定理得：2222cos BD BC DC BC DC DCB ∠=+−⋅⋅，即2242225BC BC =−⋅，解得BC =12PE BC =，∴OC OA OP =2PC ==，∵PC ⊥平面PBD ，∴PC OP ⊥，所以，在Rt PCO △中，利用等面积法，得到PC PO CO PF ⋅=⋅，故223PC PO PF CO ⋅===23，所以，在Rt PEF △中， sin PF PEθ==223==14．（2022春·广东广州·高三校考期中）如图所示，在四棱锥P ABCD −中，PC ⊥底面ABCD ，四边形ABCD 是直角梯形，AB AD ⊥，//,222AB CD PC AB AD CD ====，点E 在侧棱PB 上.(1)求证：平面EAC ⊥平面PBC ；(2)若平面PAC 与平面ACE，求PE BE 的值. 【解析】（1）证明：∵PC ⊥平面ABCD ，AC ⊂平面ABCD ，∴AC PC ⊥.∵四边形ABCD 是直角梯形，AB AD ⊥，//AB CD ，1AD CD ==，∴AC ==取AB 中点为F ,连接CF ，∵四边形ABCD 是直角梯形，AB AD ⊥，//AB CD ，222AB AD CD ===，∴//AF DC ，AF DC =，1AF BF ==，1CF AD ==，∴四边形ADCF 为矩形，BC =∴222AC BC AB +=.∴AC ⊥BC ，又BC PC C ⋂=，,BC PC ⊂平面PBC ，∴AC ⊥平面PBC .∵AC ⊂平面EAC ，∴平面EAC ⊥平面PBC .（2）方法一：由（1）知AC ⊥平面PBC ，又∵CE ⊂平面PBC ，∴AC ⊥CE ，由（1）知AC PC ⊥，所以PCE ∠是二面角P AC E −−的平面角.由图知平面PAC 与平面ACE 的夹角即为二面角P AC E −−，∵平面PAC 与平面ACE ，∴cos PCE ∠= ∵PC ⊥平面ABCD ，BC ⊂平面ABCD ，∴BC PC ⊥.在Rt PCB 中，由2PC =，BC =PB∴cosCPB ∠==， ∴CPB PCE ∠=∠，CE PE =，∵∠CPB 与∠CBP 互余，∠PCE 与∠ECB 互余，∴CBP ECB ∠=∠，CE EB =， ∴1PE BE=；方法二：如图，以C 为原点，CB ，CA ，CP 所在直线分别为x 轴、y 轴、z 轴，建立空间直角坐标系.则()0,0,0C，()A，)B ，()002P ,,，显然平面PAC 的一个法向量为CB ，则()2,0,0CB =，设(),,E x y z ，()01PE PB λλ=≤≤，则(),,2PE x y z =−，()2,0,2PB =−∴()),,22x y z λ−=−， ∴),0,22E λ−，当1λ=时，,E B 重合，此时平面PAC 与平面ACE 的夹角为90°，此时余弦值为1，不合要求，当[)0,1λ∈时，设()111,,x n y z=为平面EAC 的法向量，()CA =，()2,0,22CE λ=− 则0n CA n CE⋅=⋅=，即()1110220x z λ=+−=，得10y =，取11x =得1z=， ∴1,0,2n λ⎛= ⎝⎭，设平面1ABC 与平面11AC P 的夹角为θ，()2,0,0CB =，则cos cos ,2CB n CB n CB n θ⋅=== 解得：12λ=.∴12PE PB =， ∴1PE BE=.。

2020届高考数学(理)大一轮复习：专题突破练(5) 立体几何的综合问题

专题突破练(5)立体几何的综合问题2.如图，三棱柱ABC－A1B1C1中，AA1⊥平面ABC，A1A＝AB＝2，BC＝1，AC＝5，若规定正视方向垂直平面ACC1A1，则此三棱柱的侧视图的面积为()45C.5 D．6答案C折成四面体A′－BCD，使平面A′BD⊥平面BCD，则下列结论正确的是()A．A′C⊥BDB.∠BA′C＝90°5.[2018·河南豫东、豫北十校测试]鲁班锁是中国传统的智力玩具，起源于古代汉族建筑中首创的榫卯结构，这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合，十分巧妙，原为木质结构，外观看是严丝合缝的十字立方体，其上下、左右、前后完全对称．从外表上看，六根等长的正四棱柱体分成三组，经90度榫卯起来，若正四棱柱体的高为4，底面正方形的边长为1，则该鲁班锁的表面积为 ( )A.48 B ．60 C ．72 D ．846．如图所示，已知在多面体ABC －DEFG 中，AB ，AC ，AD 两两垂直，平面ABC ∥平面DEFG ，平面BEF ∥平面ADGC ，AB ＝AD ＝DG ＝2，AC ＝EF ＝1，则该多面体的体积为( )A.2 B ．4 C ．6 D ．8答案 B解析如图所示，将多面体补成棱长为2的正方体，那么显然所求的多面体的体积即为该正方体体积的一半，于是所求几何体的体积为V ＝12×23＝4.选B.7.[2017·湖北黄冈中学二模]一个几何体的三视图如图所示，其中正视图是边长为2的等边三角答案 B解析由三视图可知，该几何体是半圆锥，其展开图如图所示，则依题意，点A ，M 的最短距离，即为线段AM .∵P A ＝PB ＝2，半圆锥的底面半圆的弧长为π，∴展开图中的∠BPM ＝πPB＝π2， π5π5π答案 B解析如图所示，为组合体的轴截面，记BO 1的长度为x ，由相似三角形的比例关系，得PO 13R＝x R，则PO 1＝3x ，圆柱的高为3R －3x ，所以圆柱的表面积为S ＝2πx 2＋2πx ·(3R －3x )＝－4πx 2＋6πRx ，则当x ＝34R 时，S 取最大值，S max ＝94πR 2.选B.9．在正方体ABCD －A 1B 1C 1D 1中，P 为正方形A 1B 1C 1D 1四边上的动点，O 为底面正方形ABCD的中心，M ，N 分别为AB ，BC 边的中点，点Q 为平面ABCD 内一点，线段D 1Q 与OP 互相平分，则满足MQ →＝λMN →的实数λ的值有( )A.0个 B ．1个 C ．2个 D ．3个10. [2017·东北三省三校二模]已知三棱柱ABC －A 1B 1C 1，侧棱BB 1⊥平面ABC ，AB ＝2，AC ＝3，AA 1＝14，AC ⊥BC ，将其放入一个水平放置的水槽中，使AA 1在水槽底面内，平面ABB 1A 1与水槽底面垂直，且水面恰好经过棱BB 1，现水槽底面出现一个小洞，水位下降，则在水位下降过程中，几何体露出水面部分的面积S 关于水位下降的高度h 的函数图象大致为( )答案 A1x 时，正四棱锥的体积最大，则x 为 ( )A ．0.5B ．0.8C ．0.2D ．1答案 C二、填空题13．如图，在正方体ABCD－A1B1C1D1中，P为棱DC的中点，则D1P与BC1所在直线所成角的余弦值等于________.10514.如图，已知球O的面上有四点A，B，C，D，DA⊥平面ABC，AB⊥BC，DA＝AB＝BC＝2，则球O的体积等于________.答案6π解析如图，以DA，AB，BC为棱长构造正方体，设正方体的外接球球O的半径为R，则正方体的体对角线长即为球O的直径，所以64πR315．如图，用一个边长为2的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个巢，将半径为1的球体放入其中，则球心与巢底面的距离为__________.3＋12解析由题意知，折起后原正方形顶点间最远的距离为1，如图中的DC ；折起后原正方形顶点到底面的距离为12，如图中的BC .由图知球心与巢底面的距离OF ＝1－122＋12＝3＋12. 16.[2017·安徽黄山第二次质检]如图所示，正方体ABCD －A ′B ′C ′D ′的棱长为1，E ，F 分别是棱AA ′，CC ′的中点，过直线EF 的平面分别与棱BB ′，DD ′交于点M ，N ，设BM＝x ，x ∈[0,1]．给出以下五个命题：①当且仅当x ＝0时，四边形MENF 的周长最大；17．[2017·河南洛阳月考]如图，在直三棱柱ABC－A1B1C1中，∠ACB＝90°，AA1＝BC＝2AC＝4.(1)若点P为AA的中点，求证：平面B CP⊥平面B C P；值；若不存在，说明理由.解(1)证明：如图，以C为原点，CA，CB，CC1所在直线分别为x轴，y轴，z轴建立空间直角坐标系，则C(0,0,0)，A(2,0,0)，B1(0,4,4)，C1(0,0,4)，P(2，0,2)，B(0,4,0)，→→118.719.[2018·广东韶关调研]已知四棱锥P－ABCD中，P A⊥平面ABCD，底面ABCD为菱形，∠ABC(2)由(1)得AE，AD，AP两两垂直，连接AM，以AE，AD，AP所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系.520.[2017·湖北黄冈期末]如图，在各棱长均为2的三棱柱ABC－A1B1C1中，侧面A1ACC1⊥底面ABC，∠A1AC＝60°.(1)求侧棱AA与平面AB C所成角的正弦值的大小；1故以O为坐标原点，建立如图所示的空间直角坐标系Oxyz，。

2020年(江苏)高考数学(理)大一轮复习检测：专题十七立体几何

专题十七立体几何一、填空题考向一立体几何中的计算问题1.(2017·苏州、无锡、常州、镇江二模)已知正四棱锥的底面边长是2,侧棱长是,则该正四棱锥的体积为.2.(2018·南通、泰州一模)如图,铜质六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的,已知正六棱柱的底面边长、高都为4 cm,圆柱的底面积为9 cm2.若将该螺帽熔化后铸成一个高为6 cm 的正三棱柱零件,则该正三棱柱的底面边长为cm.(不计损耗)(第2题)(第3题)3.(2018·苏州期初)如图,正四棱锥P-ABCD的底面一边AB的长为2 cm,侧面积为8 cm2,则它的体积为cm3.4.(2017·江苏大联考)已知正四面体P-ABC的棱长为2,若M,N分别是PA,BC的中点,则三棱锥P-BMN 的体积为.(第5题)5.(2018·苏州一模)鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱体分成三组,经90°榫卯起来.若正四棱柱的高为5,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为.(容器壁的厚度忽略不计,结果保留π)6.(2018·无锡一模)在直三棱柱ABC-A1B1C1中,已知AB⊥BC,AB=3,BC=4,AA1=5,若三棱柱的所有顶点都在同一球面上,则该球的表面积为.考向二立体几何中的命题真假的判定问题7.(2017·丹阳高级中学期初)设α,β为两个不重合的平面,m,n为两条不同的直线,给出下列四个命题:①若m⊥n,m⊥α,则n∥α;②若n⊂α,m⊂β,α与β相交且不垂直,则n与m不垂直;③若α⊥β,α∩β=m,n⊂α,n⊥m,则n⊥β;④若m∥n,n⊥α,α∥β,则m⊥β.其中正确的命题是.(填序号)8.(2016·南京三模)已知α,β是两个不重合的平面,l,m是两条不同的直线,l⊥α,m⊂β.给出下列四个命题:①α∥β⇒l⊥m;②α⊥β⇒l∥m;③m∥α⇒l⊥β;④l⊥β⇒m∥α.其中正确的命题是.(填序号)9.(2016·镇江期末)已知b,c表示两条不同的直线,α,β表示两个不重合的平面,给出下列四个命题:①若b⊂α,c∥α,则b∥c;②若b⊂α,b∥c,则c∥α;③若c∥α,α⊥β,则c⊥β;④若c∥α,c⊥β,则α⊥β.其中正确的命题是.(填序号)10.(2017·南京、盐城、连云港二模)已知α,β是两个互不重合的平面,m,n是两条不同的直线,下列命题中正确的是.(填序号)①若α∥β,m⊂α,则m∥β;②若m∥α,n⊂α,则m∥n;③若α⊥β,α∩β=n,m⊥n,则m⊥β;④若n⊥α,n⊥β,m⊥α,则m⊥β.11.(2017·广州模拟)已知α,β是两个不重合的平面,m,n是两条不同的直线,则下列说法中正确的是.(填序号)①若m∥α,α∩β=n,则m∥n;②若m⊥α,n⊥m,则n∥α;③若m⊥α,n⊥β,α⊥β,则m⊥n;④若α⊥β,α∩β=n,m⊥n,则m⊥β.(第12题)12.(2017·咸阳模拟)如图,在棱长均相等的正四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,有下列结论:①PC∥平面OMN;②平面OMN⊥平面PAB;③OM⊥PA;④平面PCD∥平面OMN.其中正确的结论是.(填序号)考向三立体几何中的综合问题(第13题)13.(2016·无锡期末)如图,在圆锥VO中,O为底面圆的圆心,点A,B在圆O上,且OA⊥OB.若OA=VO=1,则点O到平面VAB的距离为.14.(2016·南通、扬州、淮安、宿迁、泰州二调)在体积为的四面体ABCD中,若AB⊥平面BCD,AB=1,BC=2,BD=3,则CD长度的所有值为.二、解答题15.(2017·常州一模)如图,在三棱柱ABC-A1B1C1中,所有棱长都相等,且∠ABB1=60°,D为AC的中点.(1)求证:B1C∥平面A1BD;(2)求证:AB⊥B1C.(第15题)16.(2017·苏州、无锡、常州、镇江二模)如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1∩A1C=O,E是棱AB上一点,且OE∥平面BCC1B1.(1)求证:E是AB中点;(2)若AC1⊥A1B,求证:AC1⊥BC.(第16题)17.(2017·扬州一模)如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F分别是棱PC和PD的中点.(1)求证:EF∥平面PAB;(2)若AP=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.(第17题)18.(2018·苏州一模)如图,在正方体ABCD-A1B1C1D1中,已知E,F,G,H分别是A1D1,B1C1,D1D,C1C的中点.(1)求证:EF∥平面ABHG;(2)求证:平面ABHG⊥平面CFED.(第18题)19.(2018·苏州期初)如图,在三棱锥P-ABC中,已知平面PBC⊥平面ABC.(1)若AB⊥BC,CP⊥PB,求证:CP⊥PA;(2)若过点A作直线l⊥平面ABC,求证:l∥平面PBC.(第19题)20.(2018·常州一模)如图,四棱锥P-ABCD的底面ABCD是平行四边形,PC⊥平面ABCD,PB=PD,点Q 是棱PC上异于P,C的一点.(1)求证:BD⊥AC;(2)过点Q和AD的平面截四棱锥得到截面ADQF(点F在棱PB上),求证:QF∥BC.(第20题)专题十七立体几何(第1题)1.【解析】如图,在正四棱锥P-ABCD中,PA=,AB=2,故AO=AB=,所以PO==1,所以V=Sh=×22×1=.2. 2【解析】由题知,铜质六角螺帽毛坯的体积V=6××42×sin60°-9×4=60(cm3).设正三棱柱的底面边长为a cm,则×a2×sin60°×6=60,解得a=2,所以正三棱柱的底面边长为2 cm.3. 4【解析】设正四棱锥P-ABCD的高为H,斜高为h,由题意得×2×4h=8,解得h=2,所以H==1,所以该四棱锥的体积V=S·H=×(2)2×1=4(cm3).4.【解析】如图,连接AN,作MD⊥PN,垂足为D.因为正四面体P-ABC的棱长为2,M,N分别是PA,BC 的中点,所以AN⊥BC,PN⊥BC,由此可得MN⊥AP,且AN=PN=.因为AN∩PN=N,AN⊂平面PAN,PN⊂平面PAN,所以BC⊥平面PAN.因为MD⊂平面PNA,所以MD⊥BC.因为MD⊥PN,BC∩PN=N,BC⊂平面PBN,PN⊂平面PBN,所以MD⊥平面PBN.又由题知MN==,因为PN·MD=PM·MN,所以MD===,所以三棱锥P-BMN 的体积==×S△PBN×MD=××1××=.(第4题)5. 30π【解析】由题图知,该鲁班锁外接球的直径与长、宽、高分别为2,1,5的长方体的外接球直径相同.设该球形容器的半径为R,则2R≥,即R≥,所以S=4πR2≥4π×=30π.6. 50π【解析】在直三棱柱ABC-A1B1C1中,因为AB⊥BC,所以可以将该直三棱柱补形成长、宽、高分别为3,4,5的长方体,该长方体的体对角线长即为该直三棱柱的直径,且2R==5,所以S=4πR2=50π.7.③④【解析】因为m⊥α,m⊥n,所以n∥α或n⊂α,故①错误;对于②,当m平行α与β的交线,n垂直于α与β的交线时,m⊥n,故②错误;由面面垂直的性质定理知③正确;因为n⊥α,α∥β,所以n⊥β,又m∥n,所以m⊥β,故④正确.8.①④【解析】对于①,因为l⊥α且α∥β,所以l⊥β,又m⊂β,所以l⊥m,故①正确;对于②,由l⊥α,α⊥β,可知l∥β或l⊂β,则l与m的位置关系不确定,故②不正确;对于③,由m∥α且m⊂β,可知α与β平行或相交,若α与β相交,则l与β不垂直,故③不正确;对于④,由l⊥α且l⊥β,可知α∥β,又m⊂β,所以m∥α,故④正确.9.④【解析】对于①,b与c的位置关系不确定;对于②,可能c⊂α;对于③,c与β的位置关系不确定;只有④是正确的.10.①④【解析】①是面面平行的性质,故①正确;②m,n可能异面,故②错误;③当m⊄α时,m⊥β不成立,故③错误;④由m⊥α,n⊥α,得m∥n,又n⊥β,所以m⊥β,故④正确.(第11题)11.③【解析】对于①,如图,m∥α,α∩β=n,此时m,n异面,故①错误;对于②,若m⊥α,m⊥n,则n∥α或n⊂α,故②错误;对于③,若n⊥β,α⊥β,则n∥α或n⊂α,又m⊥α,所以m⊥n,故③正确;对于④,若α⊥β,α∩β=n,m⊥n,则m也可能与β相交、平行或在β内,故④错误.12.①③④【解析】如图,其中E,F分别为AD,BC的中点,G为OE的中点,平面OMN即平面MNFE.因为PC∥OM,所以PC∥平面OMN,同理PD∥ON,又OM∩ON=O,所以平面PCD∥平面OMN,故①④正确;由于四棱锥的棱长均相等,所以PA2+PC2=AB2+BC2=AC2,所以PC⊥PA,又PC∥OM,所以OM⊥PA,故③正确;因为OM=PC=PD=ME,所以MG⊥OE,又MN∥OE,所以GM⊥MN,假设平面OMN⊥平面PAB,则GM⊥平面PAB,则MG⊥PA,设四棱锥的棱长为4,则MA=2,AG=,MG=,三边长度不满足勾股定理,所以MG不垂直PA,与假设矛盾,故②不正确.(第12题)13.【解析】方法一:设点O到平面VAB的距离为h.由题意知=,所以××1×1×1=××h,解得h=.方法二:取AB的中点M,连接OM,VM.在Rt△VOM中,点O到VM的距离即为点O到平面VAB的距离.因为VO=1,OM=,VM=,所以点O到VM的距离d==,故点O到平面VAB的距离为.14.,【解析】因为四面体ABCD的体积V=××2×3×sin∠CBD×1=,所以sin∠CBD=,所以∠CBD=60°或120°.当∠CBD=60°时,CD2=22+32-2×2×3×cos 60°=7,所以CD=;当∠CBD=120°时,CD2=22+32-2×2×3×cos 120°=19,所以CD=.综上,CD长度的所有值为,.15.(1)连接AB1交A1B于点E,连接DE.因为D,E分别为AC,AB1的中点,所以DE∥B1C.因为DE⊂平面A1BD,B1C⊄平面A1BD,所以B1C∥平面A1BD.(2)取AB的中点O,连接OC,OB1.因为BA=BB1,且∠ABB1=60°,所以△ABB1为正三角形.而O为AB的中点,所以OB1⊥AB.在正三角形ABC中,O为AB的中点,所以OC⊥AB.因为OB1∩OC=O,且OB1⊂平面OB1C,OC⊂平面OB1C,所以AB⊥平面OB1C.又因为B1C⊂平面OB1C,所以AB⊥B1C.16.(1)如图,连接BC1,因为OE∥平面BCC1B1,OE⊂平面ABC1,平面BCC1B1∩平面ABC1=BC1,所以OE∥BC1.因为侧面AA1C1C是菱形,AC1∩A1C=O,所以O是AC1的中点.所以==1,即E是AB的中点.(2)因为侧面AA1C1C是菱形,所以AC1⊥A1C.因为AC1⊥A1B,A1C∩A1B=A1,A1C⊂平面A1BC,A1B⊂平面A1BC,所以AC1⊥平面A1BC.因为BC⊂平面A1BC,所以AC1⊥BC.(第16题)17.(1)因为点E,F分别是棱PC和PD的中点,所以EF∥CD.又在矩形ABCD中,AB∥CD,所以EF∥AB.又AB⊂平面PAB,EF⊄平面PAB,所以EF∥平面PAB.(2)在矩形ABCD中,AD⊥CD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,所以CD⊥平面PAD.又AF⊂平面PAD,所以CD⊥AF.因为PA=AD且F是PD的中点,所以AF⊥PD.因为PD⊂平面PCD,CD⊂平面PCD,PD∩CD=D,所以AF⊥平面PCD.18.(1)因为E,F分别是A1D1,B1C1的中点,所以EF∥A1B1.在正方体ABCD-A1B1C1D1中,A1B1∥AB,所以EF∥AB.又EF⊄平面ABHG,AB⊂平面ABHG,所以EF∥平面ABHG.(2)在正方体ABCD-A1B1C1D1中,CD⊥平面BB1C1C.又BH⊂平面BB1C1C,所以BH⊥CD.①如图,设BH∩CF=P,△BCH≌△CC1F,所以∠HBC=∠FCC1.因为∠HBC+∠PHC=90°,所以∠FCC1+∠PHC=90°,所以∠HPC=90°,即BH⊥CF.②由①②,又DC∩CF=C,CF,CD⊂平面CFED,所以BH⊥平面CFED.又因为BH⊂平面ABHG,所以平面ABHG⊥平面CFED.(第18题)(第19题)19.(1)因为平面PBC⊥平面ABC,平面PBC∩平面ABC=BC,AB⊂平面ABC,AB⊥BC,所以AB⊥平面PBC.因为CP⊂平面PBC,所以CP⊥AB.又因为CP⊥PB,且PB∩AB=B,AB,PB⊂平面PAB,所以CP⊥平面PAB,因为PA⊂平面PAB,所以CP⊥PA.(2)如图,在平面PBC内过点P作PD⊥BC,垂足为D.因为平面PBC⊥平面ABC,平面PBC∩平面ABC=BC,PD⊂平面PBC,所以PD⊥平面ABC.又l⊥平面ABC,所以l∥PD.又l⊄平面PBC,PD⊂平面PBC,所以l∥平面PBC.20.(1)因为PC⊥平面ABCD,BD⊂平面ABCD,所以BD⊥PC.如图,记AC,BD的交点为O,连接OP.平行四边形对角线互相平分,则O为BD的中点,又在△PBD中,PB=PD,所以BD⊥OP.又PC∩OP=P,PC,OP⊂平面PAC,所以BD⊥平面PAC.又AC⊂平面PAC,所以BD⊥AC.(2)因为四边形ABCD是平行四边形,所以AD∥BC.又AD⊄平面PBC,BC⊂平面PBC,所以AD∥平面PBC.又AD⊂平面ADQF,平面ADQF∩平面PBC=QF,所以AD∥QF.又AD∥BC,所以QF∥BC.(第20题)。

专题8.9 《空间向量与立体几何》单元测试卷-2021年新高考数学一轮复习学与练(原卷版)

专题8.9 《空间向量与立体几何》单元测试卷一、单选题1．（2021·湖南湘潭·月考（理））已知正四棱锥P ABCD -2AB =，则正四棱锥P ABCD -的侧面积为（）A ．B ．4C ．D ．2．（2020·北京高三二模）某四棱锥的三视图如图所示，则该四棱锥的最长侧棱的长为（）A ．2B ．C ．D ．43．（2020·四川武侯·成都七中月考）某几何体的三视图如图所示，则该几何体的体积为（）A ．32B ．1C ．13D ．124．（2019·陕西西安·高新一中高二期末（理））如图，在四面体O ABC -中，1G 是ABC 的重心，G 是1OG 上的一点，且12OG GG =，若OG xOA yOB zOC =++，则(,,)x y z 为（）A ．111(, , )222B ．222(,, )333 C ．111(, , )333 D ．222(, , )999 5．（2020·云南高三月考（理））如图所示，在正方体1111ABCD A BC D -中，点E 为线段AB 的中点，点F 在线段AD 上移动，异面直线1BC 与EF 所成角最小时，其余弦值为（）A ．0B ．12CD ．11166．（2020·河北正定中学高三月考）已知平面α，β，γ和直线l ，下列命题中错误的是（） A ．若αβ⊥，//βγ，则αγ⊥B ．若αβ⊥，则存在l α⊂，使得//l βC ．若a γ⊥，βγ⊥，l αβ=，则l γ⊥D ．若αβ⊥，//l α，则l β⊥7．（2020·山东济宁·高二月考）在正方体1111ABCD A BC D -中，棱AB ，11A D 的中点分别为E ，F ，则直线EF 与平面11AA D D 所成角的正弦值为（）A B C D 8．（2020·山东济宁·高二月考）如图，在棱长为2的正方体1111ABCD A BC D -中，E 为BC 的中点，点P 在底面ABCD 上（包括边界．．．．）移动，且满足11B P D E ⊥，则线段1B P 的长度的最大值为（）A．B．C．D．359．（2020·福建省泉州第一中学月考）如图，已知正方体ABCD-A1B1C1D1棱长为8，点H在棱AA1上，且HA1＝2，在侧面BCC1B1内作边长为2的正方形EFGC1，P是侧面BCC1B1内一动点，且点P到平面CDD1C1HP的最小值是（）距离等于线段PF的长，则当点P在侧面BCC1B1运动时，2A．87B．88C．89D．9010．（2020·广西柳州·二模（理））如图所示，在直角梯形BCEF中，∠CBF=∠BCE=90°，A，D分别是BF，CE上的点，AD∥BC，且AB=DE=2BC=2AF（如图1），将四边形ADEF沿AD折起，连结BE、BF、CE（如图2）．在折起的过程中，下列说法中正确的个数（）①AC∥平面BEF；②B、C、E、F四点可能共面；③若EF⊥CF，则平面ADEF⊥平面ABCD；④平面BCE与平面BEF可能垂直A．0B．1C．2D．3二、多选题11．（2020·山东曲阜一中）在正方体1111ABCD A BC D -中，若E 为11AC 的中点，则与直线CE 不垂直的有（）A ．ACB ．BDC ．1AD D ．1A A12．（2020·山东曲阜一中）如图，已知E 是棱长为2的正方体1111ABCD A BC D -的棱BC 的中点，F 是棱1BB 的中点，设点D 到面1AED 的距离为d ，直线DE 与面1AED 所成的角为θ，面1AED 与面AED 的夹角为α，则（）A ．DF ⊥面1AEDB ．43d =C ．45sin 15θ=D ．2cos 3α= 13．（2020·历下·山东师范大学附中高二月考）下列命题中不正确的是（）A ．a b a b -=+是,a b 共线的充要条件B ．若,C ABD 共线，则//AB CDC ．,,A B C 三点不共线，对空间任意一点O ，若311488OP OA OB OC =++，则,,,P A B C 四点共面 D ．若,,,P A B C 为空间四点，且有PA PB PC λμ=+(,PB PC 不共线)，则1λμ+=是,,A B C 三点共线的充分不必要条件14．（2020·南京市第十四中学高二月考）如图，在直三棱柱111ABC A B C -中，12AC BC AA ===，90ACB ∠=︒，D ，E ，F 分别为AC ，1AA ，AB 的中点．则下列结论正确的是（）A ．1AC 与EF 相交B ．11//BC 平面DEFC ．EF 与1AC 所成的角为90︒D ．点1B 到平面DEF 的距离为2三、填空题 15．（2020·山东曲阜一中）已知向量1e ，2e ，3e 是三个不共面的非零向量，且1232a e e e =-+，12342b e e e =-+-，123115c e e e λ=++，若向量a ，b ，c 共面，则λ=________.16．（2020·扬州大学附属中学东部分校高三月考）在长方体1111ABCD A BC D -中，11,AB BC AA ===则异面直线1AD 与1DB 所成角的余弦值为__________.17．（2020·江苏省梅村高级中学高三开学考试）二面角的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于AB .已知4AB =，6AC =，8BD =，CD =，则该二面角的大小为________．18．（2020·全国高二课时练习）已知()3211a λ=-，，，()102b μμ=+，，．若a b ⊥，则μ＝_____；若//a b ，则λ+μ＝_____．19．（2020·福建省泉州第一中学月考）在长方体ABCD -A ’B ’C ’D ’中，AB ＝AA ’＝2AD ＝2，以D 为原点，DA ，DC ，'DD 方向分别为x 轴，y 轴，z 轴正方向建立空间直角坐标系，则'AC =_______，若点P 为线段AB 的中点，则P 到平面A ’BC ’距离为___________20．（2020·福建省泰宁第一中学月考）如图，在正四棱1111ABCD A BC D -中，底面边长为2，1CC =4，直线1A B 与1AD 所成角的余弦值为______.直线1CC 与平面1ACD 所成角的正弦值为 ______.21．（2020·山东潍坊·高三月考）正方体1111ABCD A BC D -的棱长为1，E ，F 分别为BC ，1CC 的中点．则平面AEF 截正方体所得的截面面积为______；以点E 11ACC A 的交线长为______．四、解答题22．（2020·历下·山东师范大学附中高二月考）如图，已知1111ABCD A BC D -是四棱柱，底面ABCD 是正方形，132AA AB ==，，且1160C CB C CD ︒∠=∠=，设1,,CD C a b B CC c ===.（1）试用,,a b c 表示1AC ；（2）已知O 为对角线1AC 的中点，求CO 的长.23．（2020·历下·山东师范大学附中高二月考）如图，在直三棱柱111ABC A B C -中，2ABC π∠=，D 是棱AC 的中点，且11AB BC BB ===.（1）求证： 1//AB 平面1BC D ；（2）求直线1AB 到平面1BC D 的距离.24．（2020·江苏鼓楼·南京师大附中高三月考）如图所示，在多面体ABCDFE 中，四边形ABEF 为正方形，平面ABEF ⊥平面,CDFE CD ∥,90,22EF CDF DFE EF CD ∠=∠=︒==.（1）若1DF =，证明：平面ACF ⊥平面BCE ；（2）若二面角A BC E --的余弦值为，求DF 的长. 25．（2020·宁夏高三其他（理））如图，在四棱柱1111ABCD A BC D -中，1AA ⊥平面ABCD ，底面ABCD满足AD ∥BC ，且12AB AD AA BD DC =====，(Ⅰ)求证:AB ⊥平面11ADD A ;(Ⅱ)求直线AB 与平面11B CD 所成角的正弦值.26．（2020·河南高三其他（理））如图，在三棱锥P ABC -中，底面是正三角形，24AB PA ==，PA ⊥底面ABC ，点E ，F 分别为AC ，PC 的中点.（1）求证：平面BEF ⊥平面P AC ；（2）在线段PB （不含端点）上是否存在点G ，使得平面EFG 与平面PBC 若存在，确定点G 的位置；若不存在，请说明理由.27．（2020·历下·山东师范大学附中高二月考）如图（1）所示，在Rt ABC 中，90︒∠=C ，3,6BC AC ==，,D E 分别是,AC AB 上的点，且//,2DE BC DE =，将ADE 沿DE 折起到1A DE △的位置，使1AC CD ⊥，如图（2）所示.（1）求证：1AC ⊥平面BCDE ；（2）若M 是1A D 的中点，求CM 与平面1A BE 所成角的大小；（3）线段BC （不包括端点）上是否存在点P ，使平面1A DP 与平面1A BE 垂直？说明理由.。

专题20 立体几何解答题

(2)若，求四棱锥的体积．
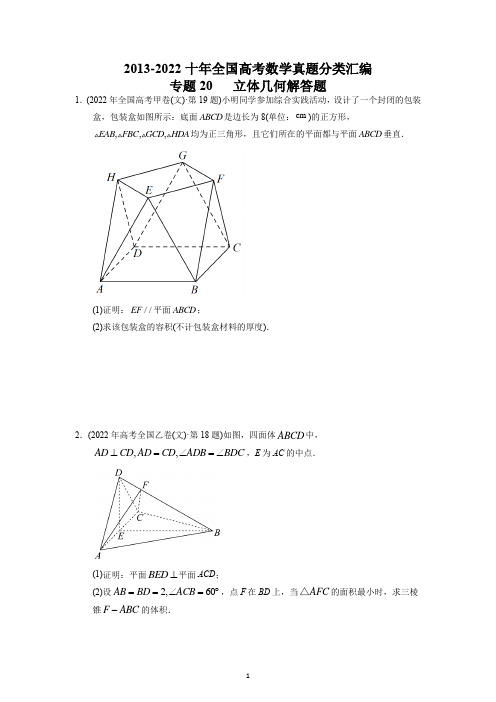
11．(2020年高考数学课标Ⅰ卷文科·第19题)如图，为圆锥的顶点，是圆锥底面的圆心，是底面的内接正三角形，为上一点，∠APC=90°．
(1)证明：平面PAB⊥平面PAC；
(2)设DO= ，圆锥侧面积为，求三棱锥P−ABC的体积．
12．(2020年高考数学课标Ⅱ卷文科·第20题)如图，已知三棱柱ABC–A1B1C1 底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点．过B1C1和P的平面交AB于E，交AC于F．
(Ⅱ)求平面把该长方体分成的两部分体积的比值．
27．(2015年高考数学课标Ⅰ卷文科·第18题)(本小题满分12分)如图四边形ABCD 为菱形，为与交点，，
( )证明：平面平面；
( )若，三棱锥的体积为，求该三棱锥的侧面积．
28．(2014年高考数学课标Ⅱ卷文科·第18题)如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．
( )证明G是AB的中点；
( )在图中作出点E在平面PAC内的正投影F(说明作法及理由)，并求四面体PDEF的体积．
26．(2015年高考数学课标Ⅱ卷文科·第19题)(本小题满分12分)如图,长方体中，点分别在上, 过点的平面与此长方体的面相交,交线围成一个正方形．
(Ⅰ)在图中画出这个正方形(不必说明画法与理由)；
(1)证明：平面；
(2)求点到平面的距离．
17．(2018年高考数学课标Ⅲ卷文科·第19题)(12分)如图，矩形所在平面与半圆弧所在平面垂直，是上异于，的点．
(1)证明：平面平面；
(2)在线段上是否存在点，使得平面？说明理由．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高三数学章节训练题37《立体几何》
时量：60分钟满分：80分班级：姓名：计分：
个人目标：□优秀（70’~80’） □良好（60’～69’） □合格（50’～59’）
一、选择题：本大题共5小题，每小题5分，满分25分．

1. 下列四个命题中，正确的一个是（）
A.空间的三个点确定一个平面 B.四边形一定是平面图形
C.梯形一定是平面图形 D.六边形一定是平面图形
2. 已知一几何体的三视图如图所示，则该几何体的体积为（）

A.193403 B. 133403

C. 193403 D. 133403
3. 一个圆锥的母线长为20cm，母线与轴的夹角为30，则圆锥的高为（）
A.103cm B.203cm C.20cm D.10cm
4. 平面，直线b，m，且bm，则b与（）.
A.b B.b与斜交 C.//b D.位置关系不确定
5. 过三棱柱 ABC－A1B1C1 的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有
（）条.
A.2 B.4 C.6 D.8
二、填空题：本大题共3小题，每小题5分，满分15分.
6. 如图所示，PA⊥平面ABC，∠ACB＝90°，且PA＝AC＝BC＝2，则：①二面角P―BC―
A的大小为；② PB与底面ABC所成的角的正切值等于 .
7. 有以下四个命题○1a//，bab；○2,//abba○
3
//,abba ○4,//abba
. 其中正确的命题是： .

8. 柱体的体积计算公式为“底面积高＝V柱”，将一块84的矩形折成一个四棱柱的
侧面，则卷成的棱柱的体积是；如折成的是正三棱柱的侧面，则体积是 .
三、解答题：本大题共3小题，满分40分，第9、10小题各12分，第11小题16分. 解答须
写出文字说明、证明过程或演算步骤．
9. 粉碎机的下料斗是无底、无盖的正四棱台形，它的上、下底面边长分别为40cm、50cm，
高是52cm, 计算制造这样一个下料斗所需铁板的面积.（结果保留到12cm）

P
A
B
C
10. 在正四棱锥ABCDP中，2PA，直线PA与平面ABCD所成的角为60，求
正四棱锥ABCDP的体积V．

11. 如图所示，在棱长为2的正方体1111ABCDABCD中，E、F分别为1DD、DB的中
点．
（1）求证：EF//平面11ABCD；
（2）求证：1EFBC；
（3）求三棱锥EFCBV1的体积．

C
D
B
F

D
1
C

B
1

A
A
1

P
B
C
A
D
P

B
C
A
D

高三数学章节训练题
1～5 CAADC

6. 1个或3个 7. ○1和○3 8. 16或8；32364399或
9. 解：根据题意，只需求出这个下料斗的侧面积即可.
如图，1140,50,52BCBCEF.

1
202,252ECFC
，110CC.

即侧面梯形的上底为40，下底为50，腰为10，故侧面梯形的高
为53.

2
1
4(4050)5390031559()2Scm
.

所以，制造这样一个下料斗所需铁板的面积约为21559cm.
10. 解：作PO平面ABCD，垂足为O．连接AO，O是

正方形ABCD的中心，PAO是直线PA与平面ABCD所成的角．
PAO＝60，2PA
． 3PO．

1AO，2AB，
112332333ABCDVPOS．
11. 解：（1）连结1BD，在BDD1中，E、F分别为1DD，DB的中点，则
1
11111
11

////EFDB
DBABCDEFABCDEFABCD平面平面
平面

2）1111111,BCABBCBCABBCABCDABBCB平面111111BCABCDBDABCD平面平面111//BCBDEFBD1EFBC

（3）11CFBDDB平面1CFEFB平面且 2CFBF
1
1
32EFBD
，222211(2)26BFBFBB

2222
1111
1(22)3BEBDDE

，∴22211EFBFBE，即190EFB

111
13BEFCCBEFBEFVVSCF=11132EFBFCF=11
362132