四年级奥数 第4讲 解决问题(1)
小学四年级奥数举一反三第1讲至第40讲全

小学四年级奥数举一反三第1讲至第40讲全目录第1讲找规律(一)第2讲找规律(二)第3讲简单推理第4讲应用题(一)第5讲算式谜(一)第6讲算式谜(二)第7讲最优化问题第8讲巧妙求和(一)第9讲变化规律(一)第10讲变化规律第11讲错中求解第12讲简单列举第13讲和倍问题第14讲植树问题第15讲图形问题第16讲巧妙求和第17讲数数图形第18讲数数图形第19讲应用题第20讲速算与巧算第二十一周速算与巧算(二)第二十二周平均数问题第二十三周定义新运算第二十四周差倍问题第二十五周和差问题第二十六周巧算年龄第二十七周较复杂的和差倍问题第二十八周周期问题第二十九周行程问题(一)第三十周用假设法解题第三十一周还原问题第三十二周逻辑推理第三十三周速算与巧算(三)第三十四周行程问题(二)第三十五周容斥原理第三十六周二进制第三十七周应用题(三)第三十八周应用题(四)第三十九周盈亏问题第四十周数学开放题第1讲找规律(一)一、知识要点观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
二、精讲精练【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19【思路导航】在这列数中,相邻的两个数的差都是3,即每一个数加上3都等于后面的数。
根据这一规律,括号里应填的数为:10+3=13或16-3=13。
像上面按照一定的顺序排列的一串数叫做数列。
练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)19,3,17,3,15,3,(),(),11,3..【例题2】先找出下列数排列的规律,然后在括号里填上适当的数。
四年级奥数:积商错中求解问题的解题方法

错中求解,顾名思义我们便可以知道,是通过错误的算式求正确的结果,错中求解知识涉及加、减、乘、除四则运算中的各种类型,上一次我们已经讲过了关于和差中的错中求解问题,本次我们重点分析计算乘除法出错的问题,解答这类题目必须掌握以下几点:
纠正乘法中的错算题时,先要认真分析因数与积相对应的变化,再根据乘除法的关系,用积变化前后的差除以其中一个因数变化前后的差,求出另一个因数,因为一个因数增加或减少几,积增加或者减少的就是另一个因数的几倍。
纠正除法中的错算题时,主要是围绕被除数、除数与商和余数之间的关系求解。
当除数错误,求正确的商时,用错误的除数乘错误的商求出正确的被除数,再用被除数除以正确的除数就等于正确的商。
当被除数错误,除数不变时,在没有余数或余数相同的除法算式中,商增加或减少几,被除数就增加或减少除数的几倍。
若余数不相同,则先通过增加或减少被除数使余数变成相同。
例题1
例题2
在乘法算式中,一个因数增加或减少几,积就增加或减少另一个因数的几倍。
例题3
在除法九三中除数看错,计算过程没有出错时,根据现在的商与看错的除数可以求出
正确的被除数,然后再用被除数除以正确的除数求出正确的商。
例题4
在除法算式中,把被除数看错,计算没有出错时,根据“被除数=除数×商+余数”求出被
除数,然后再用被除数除以正确的除数求出正确的商和余数。
例题5
例题6
通过上面的例题,我们发现:
(1)在除法算式中,被除数看错,除数和余数不变时,商增加几,被除数就增加除数的几倍;
(2)在除法算式中,被减数看错,余数改变时,如果余数比原来增加或减少多少,那么被除数就减少或增加多少,这样就把余数变成相同,然后再求出除数。
四年级下册数学奥数试题-培优拓展训练--第4讲:等积变形(学生版)

第4讲 等积变形(不用添加内容,任课老师根据学生情况自行添加)(不用添加内容,也不做修改)1、三角形的面积=21底边长 高;所以,两个面积相等的三角形,当底边相等时,高也相等;反之亦然。
2、当两个三角形高相等时,面积之比等于底边长之比。
3、当两个三角形的底边长相等时,面积之比等于高之比。
4、在等底等高的情况下,三角形面积是平行四边形面积的一半;5、底边之和等于平行四边形的一边,且高相等的所有三角形,面积之和是平行四边形面积的一半;6、高之和等于平行四边形的高,且分别以这条高的两边为底的所有三角形,面积之和是平行四边形面积的一半。
1、灵活运用三角形和四边形的面积公式2、掌握三角形的等积变形技巧(不用添加内容,任课老师根据学生情况自行添加)例1:如图,三角形ABC的面积为1,其中AE=3AB,BD=2BC,三角形BDE的面积是多少?A B EC例2:正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中三角形BDF面积为多少平方厘米?GFHEC例3:图中三角形AOB的面积为15平方厘米,线段OB的长度为OD的3倍,求梯形ABCD的面积。
A DO例4:如下图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若三角形ADE 的面积为1,求三角形BEF的面积。
例5:如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?ADEB C例6:B C如图所示,长方形ABCD的长是12厘米,宽是8厘米,三角形CEF的面积是32平方厘米,则OG是多少厘米?1、如图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:△AOB与△COD 面积相等.2、如图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE的面积为1平方厘米.求三角形ABC的面积.3、如下图,在△ABC中,BD=2AD,AG=2CG,BE=EF=FC=4、如右图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米.求三角形CDF的面积.5、如右图,四边形ABCD 面积为1,且AB=AE ,BC=BF ,DC=CG ,AD=DH .求四边形EFGH 的面积.6、如右图,在平行四边形ABCD 中,直线CF 交AB 于E ,交DA 延长线于F ,若S △ADE=1,求△BEF 的面积.1、如右图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC ∆的面积是 平方厘米.DA2、图中三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.那么三角形AEF 的面积是多少平方厘米?CB3、如图,在长方形ABCD 中,Y 是BD 的中点,Z 是DY 的中点,如果24AB =厘米,8BC =厘米,求三角形ZCY 的面积.ABC DZ Y4、如图,三角形ABC 的面积是24,D 、E 和F 分别是BC 、AC 和AD 的中点.求三角形DEF 的面积.FE DCBA5、图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是多少平方厘米.6、右图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC 的面积.G4ABCDEF(不用添加内容,也不做修改)1、如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是 平方厘米.2、如下图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD ,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是 .F E DCBA3、图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是 .E D GCBA4、在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.5、如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。
北京华罗庚学校四年级奥数补习教案 第四讲 等差数列及其应用

第四讲等差数列及其应用许多同学都知道这样一个故事:大数学家高斯在很小的时候,就利用巧妙的算法迅速计算出从1到100这100个自然数的总和.大家在佩服赞叹之余,有没有仔细想一想,高斯为什么算得快呢?当然,小高斯的聪明和善于观察是不必说了,往深处想,最基本的原因却是这100个数及其排列的方法本身具有极强的规律性——每项都比它前面的一项大1,即它们构成了差相等的数列,而这种数列有极简便的求和方法.通过这一讲的学习,我们将不仅掌握有关这种数列求和的方法,而且学会利用这种数列来解决许多有趣的问题.一、等差数列什么叫等差数列呢?我们先来看几个例子:①l,2,3,4,5,6,7,8,9,…②1,3,5,7,9,11,13.③ 2,4,6,8,10,12,14…④ 3,6,9,12,15,18,21.⑤100,95,90,85,80,75,70.⑥20,18,16,14,12,10,8.这六个数列有一个共同的特点,即相邻两项的差是一个固定的数,像这样的数列就称为等差数列.其中这个固定的数就称为公差,一般用字母d表示,如:数列①中,d=2-1=3-2=4-3= (1)数列②中,d=3-1=5-3=…=13-11=2;数列⑤中,d=100-95=95-90=…=75-70=5;数列⑥中,d=20-18=18-16=…=10-8=2.例1下面的数列中,哪些是等差数列?若是,请指明公差,若不是,则说明理由.①6,10,14,18,22, (98)②1,2,1,2,3,4,5,6;③ 1,2,4,8,16,32,64;④ 9,8,7,6,5,4,3,2;⑤3,3,3,3,3,3,3,3;⑥1,0,1,0,l,0,1,0;解:①是,公差d=4.②不是,因为数列的第3项减去第2项不等于数列的第2项减去第1项.③不是,因为4-2≠2-1.④是,公差d=l.⑤是,公差d=0.⑥不是,因为第1项减去第2项不等于第2项减去第3项.一般地说,如果一个数列是等差数列,那么这个数列的每一项或者都不小于前面的项,或者每一项都大于前面的项,上述例1的数列⑥中,第1项大于第2项,第2项却又小于第3项,所以,显然不符合等差数列的定义.为了叙述和书写的方便,通常,我们把数列的第1项记为a1,第2项记为a2,…,第n项记为an,an。
四年级下册数学试题-奥数专题训练:第4讲 和差问题(解析版)全国通用

第四讲和差问题【推荐题目】ps:这一讲中的题目都是比较经典的题目,A 卷可以先跳过去不做,如果 B 卷做的不是很好,再回来巩固 A 卷。
【B 卷的第 12 题】张强用 270 元买了一件外衣、一顶帽子和一双鞋,外衣比鞋贵 140 元,买外衣和鞋比买帽子多花了 210 元,问张强买外衣。
帽子和鞋分别花了多少钱?【解析】:外衣+鞋+帽子=270 元——和外衣+鞋-帽子=210 元——差帽子=(270-210)÷2=30 元外衣+鞋=270-30=240 元又外衣-鞋=140 元鞋=(240-140)÷2=50 元【点评】:这道题目丌是难题,属于和差问题中的一种捆绑思想,我们把两个戒者更多的东西捆绑成一个整体做和差,比如在这道题目中就是把外衣和鞋捆绑成一个整体来做。
戒者这道题用等量代换的思想直接解。
外衣+鞋+帽子=270 元外衣+鞋-帽子=210 元外衣-鞋=140 元接下来就是方程思想。
【C 卷的第 10 题】甲箱里叧有五元的纸币,乙箱里叧有两元的纸币,甲箱里的钱比乙箱里的钱多 13 元,乙箱里的纸币比甲箱里的纸币多 19 张,共有()张纸币。
【解析】:(19×2+13)÷(5-2)=17(张)——5 元17+19=36(张)——2 元共有纸币 17+36=53(张)【点评】:有的小朋友木有看明白这个式子的意思,那问一句,这道题目是什么类型呢,像丌像鸡兔同笼呢?有一种奇怪的兔子 5 条腿,普通的鸡 2 条腿,兔子比鸡多了 13 条腿,但是鸡比兔子多 19 叧,鸡兔共几叧?怎么样,这样是丌是看起来就顺眼了许多。
那接下来我们就来解一道头差脚差的鸡兔同笼,先砍掉鸡 19 叧,则鸡将少了 38 条腿,所以此时兔子比鸡多了 38+13=51 条腿。
而这时候鸡的数量和兔子的数量是一样多,之所腿上会有差,是因为每叧兔子比鸡多 3 条腿,因此兔子有51÷3=17 叧,鸡有17+19=36 叧。
奥数四年级--容斥问题(一)
经 例2、有62名学生,其中会弹钢琴的有11人,会吹竖笛的有56人,
典 两样都不会的有4人,两样都会的有多少人?
题 依题意,画圈框图。
总人数62人
型 依图可知,会弹钢琴+会竖笛
=11+56=67人, 67 > 总人数62人
会弹钢琴的 会两样 会吹竖笛
有11人
?人
既不是5的倍数,也不是7的倍数??。
(3)求既是5的倍数又是7的倍数的数量: 1000÷35 = 28...20
总1--1000的自然数
(4)根据容斥原理: 是5或7的倍数的数有: 200+142-28=314
(5)既不是5,也不是7的倍数的: 1000-314=686
5的倍数 有200
5和7的 公倍数
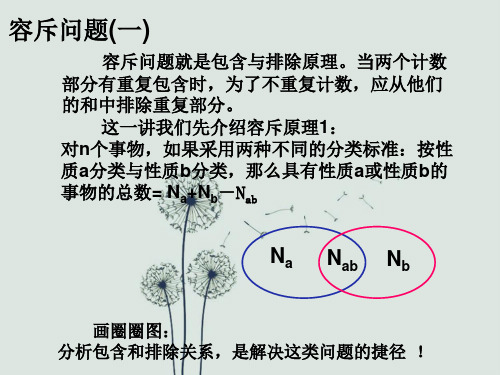
容斥问题(一)
容斥问题就是包含与排除原理。当两个计数 部分有重复包含时,为了不重复计数,应从他们 的和中排除重复部分。
这一讲我们先介绍容斥原理1: 对n个事物,如果采用两种不同的分类标准:按性 质a分类与性质b分类,那么具有性质a或性质b的 事物的总数= Na+Nb-Nab
Na Nab Nb
画圈圈图: 分析包含和排除关系,是解决这类问题的捷径 !
48名
练 9、有一根36cm长的绳子,从一端开始每隔3 习 厘米做一个记号,每隔4厘米也做一个记号,
然后把标有记号的地方剪断。绳子共被剪成 了多少段?
18段
练 10、科技节那天,学校的科技室里展出了每 习 个年级学生的科技作品,其中有114件不是
一年级的,有96件不是二年级的,一、二年 级参展的作品共32件。其他年级参展的作品 共有多少件?
分析搞清数量关系,是解决数学问题的不二法门。
小学四年级奥数竞赛班作业第4讲:加法原理和乘法原理
加法原理和乘法原理练习题一.夯实基础1.有不同的语文书6本,数学书4本,英语书3本,科学书2本,从中任取一本,共有多少种取法?2.阳光小学四年级有3个班,各班分别有男生18人、20人、16人.从中任意选一人当升旗手,有多少种选法?3.由3、6、9这3个数字可以组成多少个没有重复数字的三位数?4.邮递员投递邮件由A村去B村的道路有3条,由B村去C村的道路有2条,那么邮递员从A村经B村去C村,共有多少种不同的走法?5.从全班20人中选出3名学生排队,一共有多少种排法?6..在右图中,一只甲虫要从A点沿着线段爬到B点,要求任何点不得重复经过.问:这只甲虫最多有几种不同走法?ACB二.拓展提高:7.“数学”这个词的英文单词是“MATH”.用红、黄、蓝、绿、紫五种颜色去分别给字母染色,每个字母染的颜色都不一样.这些颜色一共可以染出多少种不同搭配方式?8.小明到图书馆借书时,图书馆有不同的外语书15本,不同的科技书20本,不同的小说10本,那么,小明要选两本不同类的书有多少种选法?9.从四年级六个班中评选出学习、体育、卫生先进集体,如果要求同一个班级只能得到一个先进集体,那么一共有多少种评选方法?10.由数字1,2,3 可以组成多少个没有重复数字的数?11.由0,2,5,6,7,8组成无重复数字的数.四位奇数有多少个?12.有6种不同颜色的笔,来写“学习改变命运”这六个字,要求相邻字的颜色不能相同,有多少种不同的方法?13.甲、乙、丙三个工厂共订300份报纸,每个工厂至少订了99份,至多101份,问:一共有多少种不同的订法?三.超常挑战:14.北京到广州之间有10个站,其中只有两个站是大站(不包括北京、广州,广州和北京是大站),从大站出发的车辆可以配卧铺,那么铁路局要准备多少种不同的卧铺车票?四.杯赛演练:15.(北京“数学解题能力展示”读者评选活动)袋中有3个红球,4个黄球和5个白球,小明从中任意拿出6个球,他拿出球的情况共有多少种可能?16.(希望杯)如图5所示的电子钟可显示从00:00:00到23:59:59的时间,在一昼夜内(24小时)钟表上显示的时间恰由数字1、2、3、4、5、6组成的共有种。
小学奥数举一反三(四年级)
第1讲找规律(一)一、知识要点观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
二、精讲精练【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19【思路导航】在这列数中,相邻的两个数的差都是3,即每一个数加上3都等于后面的数。
根据这一规律,括号里应填的数为:10+3=13或16-3=13。
像上面按照一定的顺序排列的一串数叫做数列。
练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)19,3,17,3,15,3,(),(),11,3..【例题2】先找出下列数排列的规律,然后在括号里填上适当的数。
1,2,4,7,(),16,22【思路导航】在这列数中,前4个数每相邻的两个数的差依次是1,2,3。
由此可以推算7比括号里的数少4,括号里应填:7+4=11。
经验证,所填的数是正确的。
应填的数为:7+4=11或16-5=11。
练习2:先找出下列数排列的规律,然后在括号里填上适当的数。
(1)10,11,13,16,20,(),31(2)1,4,9,16,25,(),49,64(3)3,2,5,2,7,2,(),(),11,2(4)53,44,36,29,(),18,(),11,9,8(5)81,64,49,36,(),16,(),4,1,0(6)28,1,26,1,24,1,(),(),20,1(7)30,2,26,2,22,2,(),(),14,2(8)1,6,4,8,7,10,(),(),13,14【例题3】先找出规律,然后在括号里填上适当的数。
小学四年级奥数(40讲)
小学四年级奥数1—40讲第1讲找规律(一)第2讲找规律(二)第3讲简单推理第4讲应用题(一)第5讲算式谜(一)第6讲算式谜(二)第7讲最优化问题第8讲巧妙求和(一)第9讲变化规律(一)第10讲变化规律第11讲错中求解第12讲简单列举第13讲和倍问题第14讲植树问题第15讲图形问题第16讲巧妙求和第17讲数数图形第18讲数数图形第19讲应用题第20讲速算与巧算第二十一周速算与巧算(二)第二十二周平均数问题第二十三周定义新运算第二十四周差倍问题第二十五周和差问题第二十六周巧算年龄第二十七周较复杂的和差倍问题第二十八周周期问题第二十九周行程问题(一)第三十周用假设法解题第三十一周还原问题第三十二周逻辑推理第三十三周速算与巧算(三)第三十四周行程问题(二)第三十五周容斥原理第三十六周二进制第三十七周应用题(三)第三十八周应用题(四)第三十九周盈亏问题第四十周数学开放题第1讲找规律(一)一、知识要点观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
二、精讲精练【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19【思路导航】在这列数中,相邻的两个数的差都是3,即每一个数加上3都等于后面的数。
根据这一规律,括号里应填的数为:10+3=13或16-3=13。
像上面按照一定的顺序排列的一串数叫做数列。
练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)19,3,17,3,15,3,(),(),11,3..【例题2】先找出下列数排列的规律,然后在括号里填上适当的数。
小学奥数举一反三(四年级)全
(4)61-16
(5)95-59
2.找规律计算。
(1) 62+26=
(2) 87+78=
(3) 54+45=
【例题5】计算(1)26×11(2)38×11
【思路导航】一个两位数与11相乘,只要把这个两位数的两个数字的和插入这两个数字中间,就是所求的积。(1) 26×11=2(2+6)6=286(2) 38×11=3(3+8)8=418
二、精讲精练
【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19
【思路导航】在这列数中,相邻的两个数的差都是3,即每一个数加上3都等于后面的数。根据这一规律,括号里应填的数为:10+3=13或16-3=13。
像上面按照一定的顺序排列的一串数叫做数列。
练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(6)(64,62)(48,46)(29,27)(15,□)
(7)(100,50)(86,43)(64,32)(□,21)
(8)(8,6)(16,3)(24,2)(12,□)
第2讲找规律(二)
一、知识要点
对于较复杂的按规律填数的问题,我们可以从以下几个方面来思考:
1.对于几列数组成的一组数变化规律的分析,需要我们灵活地思考,没有一成不变的方法,有时需要综合运用其他知识,一种方法不行,就要及时调整思路,换一种方法再分析;
【例题2】一头象的重量等于4头牛的重量,一头牛的重量等于3匹小马的重量,一匹小马的重量等于3头小猪的重量。一头象的重量等于几头小猪的重量?
【思路导航】根据“一头象的重量等于4头牛的重量”与“一头牛的重量等于3匹小马的重量”可推出:“一头象的重量等于12匹小马的重量”,而“一匹小马的重量等于3头小猪的重量”,因此,一头象的重量等于36头小猪的重量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4周解决问题(一)
专题简析:
解答应用题时,必须认真审题,理解题意,深入细致地分析题目中数量间的关系。
通过对条件进行比较、转化、重新组合等多种途径,找到解题的突破口,从而使问题顺利地得到解决。
例题1:某玩具厂把630件玩具装在5个塑料箱和6个纸箱里,1个塑料箱与3个纸箱装的玩具同样多,每个塑料箱和纸箱各装多少件玩具?
练习一1、:百货商店运来300双球鞋,装在2个木箱和6个纸箱里。
如果2个纸箱同1个木箱装的球鞋同样多,每个木箱和每个纸箱各装多少双球鞋?
2、新华小学买了2张桌子和5把椅子,共付款195元。
已知每张桌子的价钱是每把椅子的4倍,问每张桌子多少元?
3、王叔叔买了3千克荔枝和4千克桂圆,共付156元。
已知5千克荔枝的价钱等于2千克桂圆的价钱,问每千克荔枝和每千克桂圆各多少元?
例题2:一桶油连桶重180千克,用去一半油后,连桶还有100千克。
问原来油和桶各多少千克?
练习二:1、一筐梨连筐重38千克,卖掉一半后,连筐还有20千克。
问原来梨和筐各多少千克?
2、一筐苹果连筐重35千克,先拿一半送给幼儿园小朋友们,再拿剩下的一半送给一年级小朋友,余下的苹果连筐共11千克。
问这筐苹果原来重多少千克?
3、一只油桶里有一些油,如果把油加到原来的2倍,桶连油重38千克;如果把油加到原来的4倍,这时油和桶重46千克。
问原来油桶里有油多少千克?
例题3:有5盒一样的茶叶,如果从每盒中取出200克,那么5盒茶叶中剩下的茶叶和原来4盒茶叶的质量相等。
原来每盒茶叶有多少克?
练习三:1、有6筐梨,每筐梨的个数相等。
如果从每筐中拿出40个,6 筐梨剩下的个数的总和正好和原来两筐梨的个数相等。
原来每筐有多少个梨?
2、在5个木箱中放着同样多的橘子。
如果从每个木箱中拿出60个橘子,那么5个木箱中剩下的橘子个数的总和等于原来2个木箱里橘子个数的总和。
原来每个木箱中有多少个橘子?
3、某食品店有5箱饼干,如果从每个箱子里取出20千克,那么5个箱子里剩下的饼干正好等于原来3饼干的质量。
原来每个箱子里装有多少千克饼干?
例4:一个木器厂要生产一批课桌。
原计划每天生产60张,实际每天比原计划多生产4张,结果提前一天完成任务。
原计划要生产多少张课桌?
练习四:1、电视机厂接到一生产任务,计划每天生产90台电视机,可以按期完成。
实际每天多生产5台,结果提前一天完成任务。
那么这批电视机共有多少台?
2、小明看一本故事书,计划每天看12页,实际每天多看8页,结果提前两天看完。
这本故事书有
多少页?
3、修一条公路,计划每天修60米,实际每天比计划多修15米,结果提前4天修完。
一共修了多
少米?
例5:有两盒图钉,甲盒有72只,乙盒有48只,从甲盒中拿出多少只放入乙盒,才能使两盒中的图钉数相等?
练习五:1、有两袋面粉,第一袋面粉重24千克,第二袋面粉重18千克。
从第一袋中取出几千克放入第二袋,才能使两袋中的面粉质量相等?
2、有两盒图钉,甲盒有72只,乙盒有48只。
每次从甲盒中拿4只放入乙盒,拿几次后才能使两盒图钉数目相等?
4、有两袋糖,一袋有68粒,另一袋有20粒。
每次从多的一袋中拿出6粒放入少的一袋里,拿几
次才能使两袋糖数目同样多?
课后练习
1、菜市场运来1520千克蔬菜,分别装在24个大筐和40个小筐中,已知两个大筐装的蔬菜和3个小筐装的蔬菜一样多。
每个大筐和每个小筐分别能装多少千克?
2、一瓶油,连瓶重46千克,把油加到原来的3倍,连瓶重86千克。
原来瓶中有油多少千克?瓶重多少千克?
3、一筐鲜鱼,连筐共120千克,先卖出鲜鱼的一半,再卖出剩下的一半,剩下的鱼连筐共39千克。
原来筐里有鱼多少千克?
4、有8盒糖果,如果从每盒中取出200克,那么8盒剩下的糖果质量正好等于原来4盒的质量。
原来每盒糖果多少克?
5、某超市有5筐大米,如果从每个筐中取出60千克,那么5个筐里剩下的大米正好是原来的3筐。
原来每个筐里装多少千克大米?
6、有6筐梨,每筐梨的个数相等。
如果从每筐中取出30个,那么6管梨剩下的个数的总和比原来2筐梨多24个,原来每筐有梨多个?
提优练习
1、做一批玩具,原计划每天生产80个,实际每天比原计划多生产20个,结果提前1天完成任务。
原计划要生产多少个玩具?
2、丽丽写毛笔字,计划每天写15个,实际每天多写5个,结果提前2天完成任务。
丽丽共要写多少个毛笔字?
3、甲、乙两个修路队共同修一条路。
甲队每天修18米,乙队每天比甲队少修6米,结果甲队修完路的一半后8天乙队才修完另一半。
这条路共长多少米?
4、有两袋大米,第一袋有100千克,第二袋有76千克。
从第一袋中取出几千克放入第二袋,才能使两袋大米的质量相等?
5、兄弟俩各有书若干本,哥哥有60本,弟弟有36本,每天哥哥送给弟弟2本书,多少天后兄弟俩的书就一样多了?
6、小红、军军、小桦分别有44、16、51块巧克力,小红和小桦分别给军军多少块巧克力,他们三人的巧克力才一样多?。
