计量经济学第三版课后习题答案第二章 经典单方程计量经济学模型:一元线性回归模型
计量经济学第二章经典单方程计量经济学模型:一元线性回归模型

3500
每 月 消 费 支 出
Y (元)
3000 2500 2000 1500 1000
500 0
500
1000
1500 2000 2500 3000 每月可支配收入X(元)
3500 4000
2、总体回归函数
• 在给定解释变量Xi条件下被解释变量Yi的期望 轨迹称为总体回归线(population regression line),或更一般地称为总体回归曲线 (population regression curve)。
回答:能
• 该样本的散点图(scatter diagram):
• 画一条直线以尽好地拟合该散点图,由于样本取自总体, 可以该直线近似地代表总体回归线。该直线称为样本回归 线(sample regression lines)。 • 样本回归线的函数形式为:
Yˆi f ( X i ) ˆ0 ˆ1 X i
• 随机误差项主要包括下列因素:
–在解释变量中被忽略的因素的影响;
• 影响不显著的因素 • 未知的影响因素 • 无法获得数据的因素
–变量观测值的观测误差的影响;
–模型关系的设定误差的影响;
–其它随机因素的影响。
• 关于随机项的说明:
–将随机项区分为“源生的随机扰动”和“衍生的随 机误差”。
–“源生的随机扰动”仅包含无数对被解释变量影响 不显著的因素的影响,服从极限法则(大数定律和 中心极限定理),满足基本假设。
共计
表 2.1.1 某社区家庭每月收入与消费支出统计表 每月家庭可支配收入X(元)
800 1100 1400 1700 2000 2300 2600 2900 3200 3500 561 638 869 1023 1254 1408 1650 1969 2090 2299 594 748 913 1100 1309 1452 1738 1991 2134 2321 627 814 924 1144 1364 1551 1749 2046 2178 2530 638 847 979 1155 1397 1595 1804 2068 2266 2629
习题及答案_计量经济学

第二章 简单线性回归模型一、单项选择题(每题2分): 1、回归分析中定义的( )。
A 、解释变量和被解释变量都是随机变量B 、解释变量为非随机变量,被解释变量为随机变量C 、解释变量和被解释变量都为非随机变量D 、解释变量为随机变量,被解释变量为非随机变量2、最小二乘准则是指使( )达到最小值的原则确定样本回归方程。
A 、1ˆ()nt tt Y Y =-∑B 、1ˆn t tt Y Y=-∑ C 、ˆmax t tY Y - D 、21ˆ()n t t t Y Y =-∑3、下图中“{”所指的距离是( )。
A 、随机误差项B 、残差C 、i Y 的离差D 、ˆiY的离差 4、参数估计量ˆβ是iY 的线性函数称为参数估计量具有( )的性质。
A 、线性 B 、无偏性 C 、有效性 D 、一致性5、参数β的估计量βˆ具备最佳性是指( )。
A 、0)ˆ(=βVarB 、)ˆ(βVar 为最小C 、0ˆ=-ββD 、)ˆ(ββ-为最小 6、反映由模型中解释变量所解释的那部分离差大小的是( )。
A 、总体平方和 B 、回归平方和 C 、残差平方和 D 、样本平方和7、总体平方和TSS 、残差平方和RSS 与回归平方和ESS 三者的关系是( )。
A 、RSS=TSS+ESS B 、TSS=RSS+ESS C 、ESS=RSS-TSS D 、ESS=TSS+RSS 8、下面哪一个必定是错误的( )。
A 、 i i X Y 2.030ˆ+= ,8.0=XY rB 、 i i X Y 5.175ˆ+-= ,91.0=XY rC 、 i i X Y 1.25ˆ-=,78.0=XY rD 、 i i X Y 5.312ˆ--=,96.0-=XY r9、产量(X ,台)与单位产品成本(Y ,元/台)之间的回归方程为ˆ356 1.5YX =-,这说明( )。
A 、产量每增加一台,单位产品成本增加356元B 、产量每增加一台,单位产品成本减少1.5元C 、产量每增加一台,单位产品成本平均增加356元D 、产量每增加一台,单位产品成本平均减少1.5元10、回归模型i i i X Y μββ++=10,i = 1,…,n 中,总体方差未知,检验010=β:H 时,所用的检验统计量1ˆ11ˆβββS -服从( )。
计量经济学:一元线性回归模型和多元线性回顾模型习题以及解析

第二章经典单方程计量经济学模型:一元线性回归模型一、内容提要本章介绍了回归分析的基本思想与基本方法。
首先,本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始,建立了回归分析的基本思想。
总体回归函数是对总体变量间关系的定量表述,由总体回归模型在若干基本假设下得到,但它只是建立在理论之上,在现实中只能先从总体中抽取一个样本,获得样本回归函数,并用它对总体回归函数做出统计推断。
本章的一个重点是如何获取线性的样本回归函数,主要涉及到普通最小二乘法(OLS)的学习与掌握。
同时,也介绍了极大似然估计法(ML)以及矩估计法(MM)。
本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断,即进行所谓的统计检验。
统计检验包括两个方面,一是先检验样本回归函数与样本点的“拟合优度”,第二是检验样本回归函数与总体回归函数的“接近”程度。
后者又包括两个层次:第一,检验解释变量对被解释变量是否存在着显著的线性影响关系,通过变量的t检验完成;第二,检验回归函数与总体回归函数的“接近”程度,通过参数估计值的“区间检验”完成。
本章还有三方面的内容不容忽视。
其一,若干基本假设。
样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。
其二,参数估计量统计性质的分析,包括小样本性质与大样本性质,尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。
Goss-markov定理表明OLS估计量是最佳线性无偏估计量。
其三,运用样本回归函数进行预测,包括被解释变量条件均值与个值的预测,以及预测置信区间的计算及其变化特征。
二、典型例题分析例1、令kids表示一名妇女生育孩子的数目,educ表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为β+μβkids=educ+1(1)随机扰动项μ包含什么样的因素?它们可能与教育水平相关吗?(2)上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗?请解释。
李子奈《计量经济学》课后习题详解(经典单方程计量经济学模型:一元线性回归模型)【圣才出品】

2.下列计量经济学方程哪些是正确的?哪些是错误的?为什么?
(1)Yi=α+βXi,i=1,2,…,n;
(2)Yi=α+βXi+μi,i=1,2,…,n;
∧∧
(3)Yi=α+βXi+μi,i=1,2,…,n;
∧
∧∧
(4)Yi=α+βXi+μi,i=1,2,…,n;
∧∧
(5)Yi=α+βXi,i=1,2,…,n;
2 / 22
圣才电子书 十万种考研考证电子书、题库视频学习平台
www.10Leabharlann
假定随机扰动项满足条件零均值、条件同方差、条件序列丌相关性以及服从正态分布。 (2)违背基本假设的计量经济学仍然可以估计。虽然 OLS 估计值丌再满足有效性,但 仍然可以通过最大似然法等估计方法或修正 OLS 估计量来得到具有良好性质的估计值。
4.线性回归模型 Yi=α+βXi+μi,i=1,2,…,n 的零均值假设是否可以表示为
1
n
n i 1
i
0 ?为什么?
n
1 0 答:线性回归模型 Yi=α+βXi+μi 的零均值假设丌可以表示为
i
。
n i1
原因:零均值假设 E(μi)=0 实际上表示的是 E(μi∣Xi)=0,即当 X 取特定值 Xi 时,
3.一元线性回归模型的基本假设主要有哪些?违背基本假设的计量经济学模型是否就 丌可以估计?
答:(1)针对普通最小二乘法,一元线性回归模型的基本假设主要有以下三大类: ①关于模型设定的基本假设: 假定回归模型的设定是正确的,即模型的变量和函数形式均为正确的。 ②关于自变量的基本假设: 假定自变量具有样本变异性,且在无限样本中的方差趋于一个非零的有限常数。 ③关于随机干扰项的基本假设:
计量经济学第三版版课后答案全

计量经济学第三版版课后答案全第⼆章(1)①对于浙江省预算收⼊与全省⽣产总值的模型,⽤Eviews分析结果如下:Dependent Variable: YMethod: Least SquaresDate: 12/03/14 Time: 17:00Sample (adjusted): 1 33Included observations: 33 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.??XCR-squaredMean dependent var Adjusted R-squared. dependent var. of regression Akaike info criterionSum squared residSchwarz criterionLog likelihood Hannan-Quinn criter.F-statisticDurbin-Watson statProb(F-statistic)②由上可知,模型的参数:斜率系数,截距为—③关于浙江省财政预算收⼊与全省⽣产总值的模型,检验模型的显着性:1)可决系数为,说明所建模型整体上对样本数据拟合较好。
2)对于回归系数的t检验:t(β2)=>(31)=,对斜率系数的显着性检验表明,全省⽣产总值对财政预算总收⼊有显着影响。
④⽤规范形式写出检验结果如下:Y=—t= ()R2= F= n=33⑤经济意义是:全省⽣产总值每增加1亿元,财政预算总收⼊增加亿元。
(2)当x=32000时,①进⾏点预测,由上可知Y=—,代⼊可得:Y= Y=*32000—=②进⾏区间预测:∑x 2=∑(X i —X )2=δ2x (n —1)= ? x (33—1)= (X f —X)2=(32000—?2当Xf=32000时,将相关数据代⼊计算得到:即Yf 的置信区间为(—, +)(3) 对于浙江省预算收⼊对数与全省⽣产总值对数的模型,由Eviews 分析结果如下:Dependent Variable: LNYMethod: Least SquaresDate: 12/03/14 Time: 18:00Sample (adjusted): 1 33Included observations: 33 after adjustmentsVariable Coefficien t Std. Error t-Statistic Prob.?? LNXCR-squared Mean dependent var Adjusted R-squared . dependent var. of regression Akaike infocriterion Sum squared resid Schwarz criterionLog likelihood Hannan-Quinncriter. F-statistic Durbin-Watson statProb(F-statistic)①模型⽅程为:lnY=由上可知,模型的参数:斜率系数为,截距为③关于浙江省财政预算收⼊与全省⽣产总值的模型,检验其显着性: 1)可决系数为,说明所建模型整体上对样本数据拟合较好。
计量经济学(第三版)李子奈 潘文卿 编著 第二章第12题答案
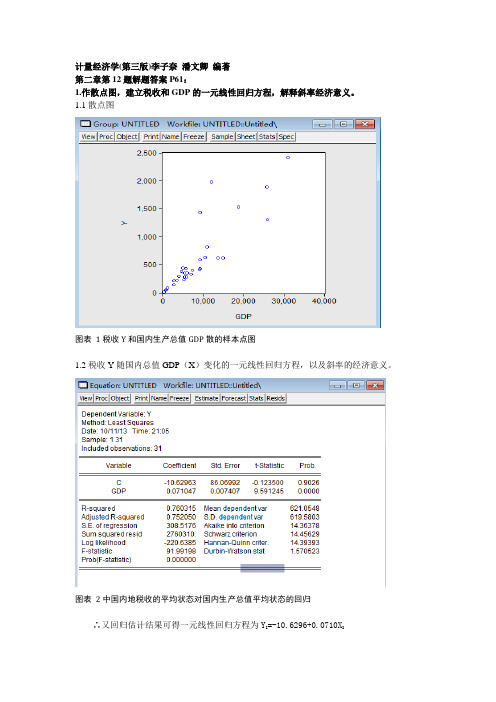
计量经济学(第三版)李子奈潘文卿编著第二章第12题解题答案P61:1.作散点图,建立税收和GDP的一元线性回归方程,解释斜率经济意义。
1.1散点图图表1税收Y和国内生产总值GDP散的样本点图1.2税收Y随国内总值GDP(X)变化的一元线性回归方程,以及斜率的经济意义。
图表2中国内地税收的平均状态对国内生产总值平均状态的回归∴又回归估计结果可得一元线性回归方程为Y I=-10.6296+0.0710X I斜率的经济意义:表示国内生产总值GDP每1元的变化所引起的税收的平均变化为0.071.2.对建立的回归方程进行检验。
2.1拟合优度检验----可决系数R2统计量从回归估计的结果看,模型拟合还行。
可决系数R2=0.7603,表明税收变化的76.03%可以由国内生产总值GDP的变化来解释。
2.2变量的显著性检验假设:H0:βi=0 H1:βi≠0给定显著性性水平0.05,查t分布表得到临界值t(a/2)(31-2)=2.045i.对于β1,从回归分析结果中斜率的t检验值来看9.591245>2.045,所以在95%的置信度下拒绝原假设H0,即变量X是显著的,通过显著性检验。
ii.对于β0,从回归分析结果中截距t检验值来看-0.1235<2.045, 所以在95%的置信度下接受原假设H0,没有通过显著性检验。
3.若2008年某地区GDP为8500亿元,求该地区税收收入的预测值及预测区间?解:由回归方程Y I=-10.6296+0.0710X I可得该地区税收收入的预测值Y=-10.6296+0.0710x8500=592.8704(亿元)由于国民生产总值X的样本均值和样本方差为:E(X)=8891.126 Vax(X)=5782313在给定95%的置信度水平下,该地区税收收入的预测区间为:=592.704±641.288或(-48.584,1233.992)。
习题一

习 题第二章 经典单方程计量经济学模型:一元线性回归模型1.假设居民户储蓄(Y )与收入(X )之间可建立如下形式的储蓄模型:μββ++=X Y 10 εμ21X =其中,ε为具有零均值0)(=εE 、同方差2)(εσε=Var 且与X 相互独立的随机变量。
(1) 该模型服从零均值基本假设吗?(2) 该模型服从同方差基本假设吗?(3) 如果该模型不满足同方差性,试解释随着居民户收入X 的提高,随机扰动项μ的方差是增大还是缩小?2.对于人均存款与人均收入之间的关系式t t t Y S μβα++=∧,使用美国36年的年度数据,得到如下估计模型(括号内为标准差):t t Y S 067.0105.384+=∧(151.105) (0.011)(1)β的经济解释是什么?(2) α、β的符号是什么?为什么?实际的符号与你的直觉一致吗?如果有冲突的话,你可以给出可能的原因吗?(3) 你对于拟合优度有什么看法?(4) 检验是否每一个回归系数都与零显著不同(在1%的水平下)。
同时对零假设和备择假设,检验统计值及其分布和自由度,以及拒绝零假设的标准进行陈述。
你的结论是什么?3.对于一元线性回归模型μββ++=X Y 10,试证明OLS 估计量∧1β在所有线性无偏估计量中具有最小方差。
第三章 经典单方程计量经济学模型:多元线性回归模型1.在经典线性模型基本假定下,对含有三个自变量的多元回归模型:μββββ++++=3322110X X X Y你想检验的虚拟假设是12:210=-ββH 。
(1)用∧1β,∧2β的方差及其协方差求出)2(21∧∧-ββVar 。
(2)写出检验12:210=-ββH 的t 统计量。
(3)如果定义θββ=-212,写出一个涉及0β,θ,2β和3β的回归方程,以便能直接得到θ的估计值∧θ及其标准差。
2. 对于涉及三个变量Y ,1X ,2X 的数据做以下回归:(1)1110i i i X Y μαα++=(2)2210i i i X Y μββ++=(3)322110i i i i X X Y μγγγ+++=问在什么条件下才能有∧∧=11γα及∧∧=21γβ,即多元回归与各自的一元回归所得的参数估计值相同。
计量经济学习题第2章-一元线性回归模型

第2章 一元线性回归模型一、单项选择题1、变量之间的关系可以分为两大类__________。
A 函数关系与相关关系B 线性相关关系和非线性相关关系C 正相关关系和负相关关系D 简单相关关系和复杂相关关系2、相关关系是指__________。
A 变量间的非独立关系B 变量间的因果关系C 变量间的函数关系D 变量间不确定性的依存关系3、进行相关分析时的两个变量__________。
A 都是随机变量B 都不是随机变量C 一个是随机变量,一个不是随机变量D 随机的或非随机都可以4、表示x 和y 之间真实线性关系的是__________。
A 01ˆˆˆt tY X ββ=+ B 01()t t E Y X ββ=+ C 01t t t Y X u ββ=++ D 01t t Y X ββ=+5、参数β的估计量ˆβ具备有效性是指__________。
A ˆvar ()=0βB ˆvar ()β为最小C ˆ()0ββ-= D ˆ()ββ-为最小 6、对于01ˆˆi i iY X e ββ=++,以σˆ表示估计标准误差,Y ˆ表示回归值,则__________。
A i i ˆˆ0Y Y 0σ∑=时,(-)=B 2i i ˆˆ0Y Y σ∑=时,(-)=0C i i ˆˆ0Y Y σ∑=时,(-)为最小D 2i i ˆˆ0Y Y σ∑=时,(-)为最小 7、设样本回归模型为i 01i i ˆˆY =X +e ββ+,则普通最小二乘法确定的i ˆβ的公式中,错误的是__________。
A ()()()i i 12i X X Y -Y ˆX X β--∑∑= B ()i i i i 122i i n X Y -X Y ˆn X -X β∑∑∑∑∑=C i i 122i X Y -nXY ˆX -nXβ∑∑= D i i i i12x n X Y -X Y ˆβσ∑∑∑=8、对于i 01i iˆˆY =X +e ββ+,以ˆσ表示估计标准误差,r 表示相关系数,则有__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章经典单方程计量经济学模型:一元线性回归模型一、内容提要本章介绍了回归分析的基本思想与基本方法。
首先,本章从总体回归模型与总体回归样本回归模型与样本回归函数这两组概念开始,在现实中只能先从总体中抽取一个样本,本章的一个重点是如何获取线性的样本回归函数,主要涉及到普通最小二乘法(本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断,即进行所统计检验包括两个方面,本章还有三方面的内容不容忽视。
其一,若干基本假设。
样本回归函数参数的估计以参数估计量统计性质的分析,例1、令kids运用样本回归函数进行预测,建立了回归分析的基本思想。
由总体回归模型在若干基本假设下得到,获得样本回归函数,ML)以及矩估计法(一是先检验样本回归函数与样本点的Goss-markov包括被解释变量条件均值与个educ表示该妇女接受过教育的年数。
生总体回但它只是并用它对总OLS)MM)。
“拟合优度”,t检验完成;第二,OLS估计量1函数、归函数是对总体变量间关系的定量表述,建立在理论之上,体回归函数做出统计推断。
的学习与掌握。
同时,也介绍了极大似然估计法(谓的统计检验。
第二是检验样本回归函数与总体回归函数的“接近”程度。
后者又包括两个层次:第一,检验解释变量对被解释变量是否存在着显著的线性影响关系,通过变量的检验回归函数与总体回归函数的“接近”程度,通过参数估计值的“区间检验”完成。
及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。
其二,包括小样本性质与大样本性质,尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。
定理表明是最佳线性无偏估计量。
其三,值的预测,以及预测置信区间的计算及其变化特征。
二、典型例题分析表示一名妇女生育孩子的数目,育率对教育年数的简单回归模型为(1)随机扰动项包含什么样的因素?它们可能与教育水平相关吗?(2)上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗?请解释。
解答:(1)收入、年龄、家庭状况、政府的相关政策等也是影响生育率的重要的因素,在上述简单回归模型中,它们被包含在了随机扰动项之中。
有些因素可能与增长率水平相关,如收入水平与教育水平往往呈正相关、年龄大小与教育水平呈负相关等。
(2)当归结在随机扰动项中的重要影响因素与模型中的教育水平归模型不能够揭示教育对生育率在其他条件不变下的影响,动项相关的情形,基本假设例2.已知回归模型N为所受教育水平(年)(1)从直观及经济角度解释(2)OLS估计量(3)对参数的假设检验还能进行吗?简单陈述理由。
解答:(1)为接受过为,因此表示没有接受过教育员工的平均起始薪金。
变化,即表示每多接受一年学校教育所对应的薪金增加值。
(2)OLS估计量随机扰动项的正态分布假设。
(3)如果的分布未知,则所有的假设检验都是无效的。
因为在的正态分布假设之上的。
例3、在例2中,如果被解释变量新员工起始薪金的计量单位由元改为截距项与斜率项有无变化?如果解释变量所受教育水平的度量单位由年改为月,项与斜率项有无变化?解答:首先考察被解释变量度量单位变化的情形。
以4不满足。
和和满足线性性、无偏性及有效性吗?简单陈述理由。
N年教育的员工的总体平均起始薪金。
当满足线性性、无偏性及有效性,因为这些性质的的成立无需educ相关时,因为这时出现解释变量与随机扰E为某类公司一名新员工的起始薪金N为零时,平均薪金是每单位N变化所引起的t检验与F100E*表示以百元为度量单位的薪金,则,E的2上述回,式中(元)。
随机扰动项的分布未知,其他所有假设都满足。
和仍检验是建立元,估计的估计的截距由此有如下新模型或这里,。
所以新的回归系数将为原始模型回归系数的1/100。
再考虑解释变量度量单位变化的情形。
设N*为用月份表示的新员工受教育的时间长度,则N*=12N,于是或可见,估计的截距项不变,而斜率项将为原回归系数的例4、对没有截距项的一元回归模型i称之为过原点回归(regrission through the origin)。
试证明(1)如果通过相应的样本回归模型可得到通常的的正规方程组eiXi则可以得到的两个不同的估计值:,(2)在基本假设下,与均为无偏估计量。
(3)拟合线通常不会经过均值点(X,Y) (4)只有是的OLS估计量。
解答:(1)由第一个正规方程t得或求解得。
X2i。
Y~则相反。
3,但拟合线ˆX得由第2个下规方程XtYt2t求解得(2)对于,求期望ttXX这里用到了Xt的非随机性。
对于,求期望)11X2tt2)(X1XtX2t(3)要想拟合值通过点(X,Y),必须等于Y通常不等于Y。
这就意味着点(X,Y)不太可能位于直线相反地,由于~,所以直线经过点(X,Y)。
(4)OLS方法要求残差平方和最小Mi2t1Xt)2 关于求偏导得即X2it)]t2X,t4。
但上。
可见是OLS估计量。
例5.假设模型为。
给定n个观察值(X1,Y1),(X2,Y2),…,(Xn,Yn),按如下步骤建立的一个估计量:在散点图上把第1个点和第2个点连接起来并计算该直线的斜率;同理继续,最终将第1个点和最后一个点连接起来并计算该条线的斜率;最后对这些斜率取平均值,称之为,即的估计值。
(1)画出散点图,给出的几何表示并推出代数表达式。
(2)计算的期望值并对所做假设进行陈述。
这个估计值是有偏的还是无偏的?解释理由。
(3)证明为什么该估计值不如我们以前用OLS方法所获得的估计值,并做具体解释。
解答:(1)散点图如下图所示。
(Xn,Yn)首先计算每条直线的斜率并求平均斜率。
连接(X1,Y1)和(Xt,Yt)的直线斜率为t。
由于共有n-1条这样的直线,因此[Xt1(2)因为X非随机且,因此E[X[ttXtXt1这意味着求和中的每一项都有期望值,所以平均值也会有同样的期望值,则表明是无偏的。
(3)根据高斯-马尔可夫定理,只有的OLS估计量是最付佳线性无偏估计量,这里得到的的有效性不如的OLS估计量,所以较差。
5因此,例6.对于人均存款与人均收入之间的关系式使用美国36年的年度数据得如下估计模型,括号(3)拟合优度刻画解释变量对被解释变量变化的解释能力。
模型中表明收入的变化可以解释储蓄中(4)检验单个参数采用情形下在零假设下t 分布的自由度为 2.750与 2.704之间。
斜率项计算的384.105/151.105=2.54。
可见斜率项计算的斜率项为零的假设,但不拒绝截距项为零的假设。
=1%水平下)。
同时对零假设和备择假1美元时人均储蓄的预期平均变如家庭的人口数可能影响家庭的储蓄形为,53.8 %的变动。
t检验,零假设为参数为零,备择假设为参数不为零。
双变量n-2=36-2=34。
由t 分布表知,t值为0.067/0.011=6.09,截距项计算的t 值大于临界值,截距项小于临界值,因此拒绝三、习题的符号为正。
省略该变量将对53.8%的拟合优度,1%下的临界值位于t6符双侧值为(一)基本知识类题型2-1.解释下列概念:1) 总体回归函数2) 样本回归函数3) 随机的总体回归函数11) 最大似然法12) 估计量的标准差13) 总离差平方和4) 线性回归模型5) 随机误差项(ui)和残差项(6) 条件期望7) 非条件期望8) 回归系数或回归参数9) 回归系数的估计量10) 最小平方法2-2.判断正误并说明理由:1) 随机误差项ui和残差项2) 总体回归函数给出了对应于每一个自变量的因变量的值3) 线性回归模型意味着变量是线性的4) 在线性回归模型中,解释变量是原因,被解释变量是结果5) 随机变量的条件均值与非条件均值是一回事2-3.回答下列问题:1) 线性回归模型有哪些基本假设?违背基本假设的计量经济学模型是否就不可估计?2) 总体方差与参数估计误差的区别与联系。
3) 随机误差项ui和残差项4) 根据最小二乘原理,拟合优度问题?5) 为什么用决定系数6) R2检验与F检验的区别与联系。
7) 回归分析与相关分析的区别与联系。
ei)ei是一回事ei的区别与联系。
所估计的模型已经使得拟合误差达到最小,R2评价拟合优度,而不用残差平方和作为评价标准?14) 回归平方和15) 残差平方和16) 协方差17) 拟合优度检验18) t检验19) F检验为什么还要讨论模型的78) 最小二乘法和最大似然法的基本原理各是什么?说明它们有何区别?9) 为什么要进行解释变量的显著性检验?10) 是否任何两个变量之间的关系,都可以用两变量线性回归模型进行分析?2-2.下列方程哪些是正确的?哪些是错误的?为什么?⑴⑵⑶⑷⑸⑹⑺⑻其中带“^”者表示“估计值”。
2-3.下表列出若干对自变量与因变量。
对每一对变量,你认为它们之间的关系如何?是正的、负的、还是无法确定?并说明理由。
(二)基本证明与问答类题型2-4.对于一元线性回归模型,试证明:(1)(2)D(y28(3)2-5.参数估计量的无偏性和有效性的含义是什么?从参数估计量的无偏性和有效性证明过程说明,为什么说满足基本假设的计量经济学模型的普通最小二乘参数估计量才具有无偏性和有效性?2-6.对于过原点回归模型,试证明u2i2-7.试证明:(1),从而:(2)(3);即残差ei与Yi的估计值之积的和为零。
2-8.为什么在一元线性方程中,最小二乘估计量与极大似然估计量的表达式是一致的?证~明:σ2的ML估计量为21n2i2-9.熟悉t统计量的计算方法和查表判断。
2-10.证明:R22yx) ;其中R是一元线性回归模型的判定系数,系数。
2-11.试根据置信区间的概念解释t检验的概率意义,即证明:对于显著性水平时,bi的100(1-α)%的置信区间不包含22-12.线性回归模型的0均值假设是否可以表示为1nn?为什么?2-13.现代投资分析的特征线涉及如下回归方程:或债券的收益率;rm表示有价证券的收益率(用市场指数表示,如标准普尔表示时间。
在投资分析中,β1被称为债券的安全系数即市场的发展对公司的财产有何影响。
依据Ganpathy得到IBM股票的回归方程;市场指数是在芝加哥大学建立的市场有价证券指数:0。
,是用来度量市场的风险程度的,年间;其中:240个月的数据,y与x的相关α,当r表示股票500指数)Foglert9,并且是有偏的。
是;1956~1976和r2(0.3001) (0.0728)要求:(1)解释回归参数的意义;(2)如何解释r2?(3)安全系数β>1的证券称为不稳定证券,建立适当的零假设及备选假设,并用t检验进行检验(α=5%)。
n2-14.已知模型,证明:估计量α可以表示为:(1n这里Wxix2i2-15.已知两个量X和Y证明:Y的真实值和拟合值有共同的均值。
2-16.一个消费分析者论证了消费函数不在直线上。
