2019考研数学二线性代数复习内容
数学专业考研复习资料线性代数重点知识点整理

数学专业考研复习资料线性代数重点知识点整理数学专业考研复习资料:线性代数重点知识点整理一、向量与矩阵1. 向量的定义和性质- 向量的表示与运算- 单位向量和零向量- 向量的线性相关性2. 矩阵的定义和性质- 矩阵的基本运算- 矩阵的转置和逆矩阵- 矩阵的秩和行列式二、线性方程组1. 线性方程组的概念- 线性方程组的解和解的存在唯一性- 齐次线性方程组和非齐次线性方程组2. 线性方程组的解法- 列主元消元法- 矩阵的初等变换和阶梯形矩阵 - 高斯消元法和高斯约当法三、线性空间和子空间1. 线性空间的定义和性质- 线性空间的子空间和直和- 基和维数的概念- 线性空间的同构与等价2. 子空间的性质与判定- 线性子空间的交与和- 维数公式和秩-零化定理- 子空间的降维与升维四、线性变换和特征值1. 线性变换的定义和性质- 线性变换的表示和运算- 线性变换的核与像- 线性变换的矩阵表示和判定2. 特征值和特征向量- 特征方程和特征值的求解 - 特征空间和特征子空间- 相似矩阵和对角化矩阵五、内积空间和正交变换1. 内积的定义和性质- 内积的基本性质和判定- 正交向量和正交子空间- 构造内积空间2. 正交变换和正交矩阵- 正交变换的性质和表示- 正交矩阵的特点和运算- 正交矩阵的对角化和特征值六、二次型和正定矩阵1. 二次型的定义和性质- 二次型的标准形和规范形 - 二次型的正定性和负定性- 二次型的规约和降维2. 正定矩阵的定义和性质- 正定矩阵的判定和运算- 正定矩阵的特征值和特征向量- 正定矩阵及其应用总结:线性代数是数学专业考研中的重要内容之一。
通过对向量与矩阵、线性方程组、线性空间和子空间、线性变换和特征值、内积空间和正交变换、二次型和正定矩阵等知识点的学习和掌握,能够为考研复习提供有力的理论基础和解题方法。
在复习过程中,需要注重概念的理解、性质的掌握以及应用题的练习,同时注意归纳总结和思维方法的培养。
线性代数复习提纲

线性代数复习提纲线性代数是数学中的一个基础课程,涵盖了向量空间、线性变换、矩阵理论等内容。
它在计算机科学、物理学、经济学和工程学等领域都有广泛的应用。
下面是线性代数的复习提纲,帮助你回顾相关的知识点。
一、向量空间1.向量的定义和性质2.向量空间的定义和性质3.子空间的定义和判断条件4.向量的线性相关性与线性无关性5.基和维数的概念二、线性变换1.线性变换的定义和性质2.线性变换的矩阵表示3.线性变换的核与像空间4.线性变换的维数公式5.线性变换的复合与逆变换三、矩阵理论1.矩阵的定义和性质2.矩阵的运算:加法、数乘、乘法3.矩阵的逆与转置运算4.矩阵的秩和行列式5.矩阵的特征值与特征向量四、特殊矩阵和特征值问题1.对称矩阵的性质和对角化2.可逆矩阵与相似矩阵3.正交矩阵与正交对角化4.特征值问题的求解方法五、解线性方程组1.线性方程组的矩阵表示2.高斯消元法与矩阵的初等变换3.初等矩阵的性质与应用4.齐次线性方程组和非齐次线性方程组的解的结构六、向量空间的基变换1.基变换的定义和性质2.过渡矩阵的求解3.变换矩阵的求解与应用4.基变换下的坐标表示和坐标变换公式七、内积空间和正交性1.内积的定义和性质2.内积空间的定义和性质3.正交基和正交投影4.标准正交基和正交矩阵的定义和性质八、二次型与正定性1.二次型的定义和性质2.二次型的矩阵表示和标准化3.正定二次型和半正定二次型的定义和性质4.二次型的规范形和合同变换以上是线性代数的复习提纲,可以通过对每个知识点的回顾、理解和练习来复习线性代数。
在复习过程中,可以结合教材、习题和课堂笔记,通过解题和思考来巩固知识点的掌握。
另外,可以参考相关的教学视频或在线课程来帮助理解和学习线性代数的概念和方法。
最重要的是多做习题,加深对知识点的理解和应用。
2019考研数学备考:线性代数必看考点目录

【导语】愿你像那⼩⼩的溪流,将那⾼⾼的⼭峰作为⽣命的起点,⼀路跳跃,⼀路奔腾,勇敢地、勇敢地奔向⽣活的⼤海。
⽆忧考整理考研数学线性代数部分各章必看考点⽬录,⼤家复习的时候注意结合课后练习和真题来掌握:
第⼀章⾏列式
1、⾏列式的定义
2、⾏列式的性质
3、特殊⾏列式的值
4、⾏列式展开定理
5、抽象⾏列式的计算
第⼆章矩阵
1、矩阵的定义及线性运算
2、乘法
3、矩阵⽅幂
4、转置
5、逆矩阵的概念和性质
6、伴随矩阵
7、分块矩阵及其运算
8、矩阵的初等变换与初等矩阵
9、矩阵的等价
10、矩阵的秩
第三章向量
1、向量的概念及其运算
2、向量的线性组合与线性表出
3、等价向量组
4、向量组的线性相关与线性⽆关
5、极⼤线性⽆关组与向量组的秩
6、内积与施密特正交化
7、n维向量空间(数学⼀)
第四章线性⽅程组
1、线性⽅程组的克莱姆法则
2、齐次线性⽅程组有⾮零解的判定条件
3、⾮齐次线性⽅程组有解的判定条件
4、线性⽅程组解的结构
第五章矩阵的特征值和特征向量
1、矩阵的特征值和特征向量的概念和性质
2、相似矩阵的概念及性质
3、矩阵的相似对⾓化
4、实对称矩阵的特征值、特征向量及其相似对⾓矩阵 第六章⼆次型
1、⼆次型及其矩阵表⽰
2、合同变换与合同矩阵
3、⼆次型的秩
4、⼆次型的标准型和规范型
5、惯性定理
6、⽤正交变换和配⽅法化⼆次型为标准型
7、正定⼆次型及其判定。
考研数学线性代数的知识点怎么复习范本三份

考研数学线性代数的知识点怎么复习范本三份知识点一:矩阵1.矩阵的定义:矩阵是一个由数域中的元素排列成的矩形阵列。
2.矩阵的运算:包括矩阵的加法、减法、数乘、乘法等。
3.矩阵的类型:包括列矩阵、行矩阵、方阵、行满秩矩阵、列满秩矩阵等。
4.矩阵的转置:行变为列,列变为行。
5.矩阵的逆:满足矩阵乘法交换律的方阵,存在逆矩阵。
6.矩阵的秩:线性无关行(列)向量的最大个数。
知识点二:行列式1.行列式的概念:一个由n*n个元素构成的方阵,与其他方阵不同的一个特殊数。
2.行列式的性质:包括行互换、列互换、其中一行(列)乘以一个非零常数、其中一行(列)加上另外一行(列)的k倍等运算。
3.行列式的计算:包括按定义计算、按行(列)展开、按行列式的性质计算等方法。
4.行列式的性质与结论:含有零行(列)的行列式为零、对调两行(列)行列式变号、行列式与其转置行列式相等等。
知识点三:向量空间1.向量空间的定义:满足一定条件的集合,其中的元素可以进行向量运算。
2.向量空间的性质:包括封闭性、线性组合、线性无关、向量子空间等性质。
3.线性相关与线性无关:一组向量之间的线性组合关系。
4.基、维数与坐标:向量空间的基、维数与坐标之间的关系。
5.线性映射:保持向量空间的线性性质的映射。
6.矩阵的秩与线性方程组的解:矩阵的秩与方程组解的个数及解的性质之间的关系。
知识点四:特征值与特征向量1.特征值与特征向量的定义:对于一个n*n矩阵A,如果存在常数λ和非零向量x,使得Ax=λx,则称λ为矩阵A的特征值,x为矩阵A的特征向量。
2.特征值与特征向量的计算:包括求解特征方程、求解特征向量的过程。
3.特征值与特征向量的性质:特征值的和等于矩阵的迹,特征向量对应不同特征值的特征向量线性无关等。
知识点五:二次型1.二次型的定义:一个含有二次项和线性项的多项式。
2.二次型的矩阵表示:用矩阵表示二次型。
3.二次型的规范化:将二次型化为标准形,即去除二次项的干涉项。
线性代数考研知识点总结

线性代数考研知识点总结线性代数是数学的一个重要分支,它研究向量空间及其上的线性变换。
在计算机科学、物理学、工程学等领域中,线性代数都有着广泛的应用。
在考研中,线性代数是一个必考的科目,以下是线性代数考研的一些重要知识点总结。
1. 向量空间:向量空间是线性代数的基础概念,它包括一组向量和一些满足特定条件的运算规则。
向量空间中的向量可以进行加法和数乘运算,满足交换律、结合律和分配律。
2. 向量的线性相关性和线性无关性:如果向量可以通过线性组合表示为另一组向量的形式,那么这组向量就是线性相关的;如果向量不满足线性相关的条件,那么它们就是线性无关的。
3. 矩阵:矩阵是线性代数中的另一个重要概念,它是一个由数字排列成的矩形阵列。
矩阵可以用于表示线性变换、解线性方程组等。
常见的矩阵类型有方阵、对称矩阵、对角矩阵、单位矩阵等。
4. 行列式:行列式是一个用于刻画矩阵性质的重要工具。
行列式可以用来计算线性变换的缩放因子,判断矩阵是否可逆,以及计算矩阵的逆等。
5. 矩阵的相似和对角化:两个矩阵A和B,如果存在一个非奇异矩阵P,使得PAP^(-1)=B,那么矩阵A和B就是相似的。
相似的矩阵有着相同的特征值和特征向量。
对角化是指将一个矩阵通过相似变换变成对角矩阵的过程。
6. 线性变换:线性变换是指一个向量空间到另一个向量空间的映射,它满足线性性质。
线性变换可以用矩阵表示,相应的矩阵称为线性变换的矩阵表示。
线性变换可以进行合成、求逆等操作。
7. 内积空间:内积空间是一个带有内积运算的向量空间。
内积运算满足对称性、线性性、正定性等性质。
内积空间可以用来定义向量的长度、夹角、正交性等概念。
8. 特征值和特征向量:对于一个线性变换,如果存在一个非零向量使得线性变换作用在该向量上等于该向量的某个常数倍,那么这个常数就是该线性变换的特征值,而对应的非零向量就是特征向量。
特征值和特征向量可以用来分析矩阵的性质,求解线性方程组等。
9. 奇异值分解:奇异值分解是矩阵分解的一种常用方法,它将一个矩阵分解为三个矩阵的乘积,其中一个矩阵是正交矩阵,另两个矩阵是对角矩阵。
考研数学《线性代数》考点知识点总结
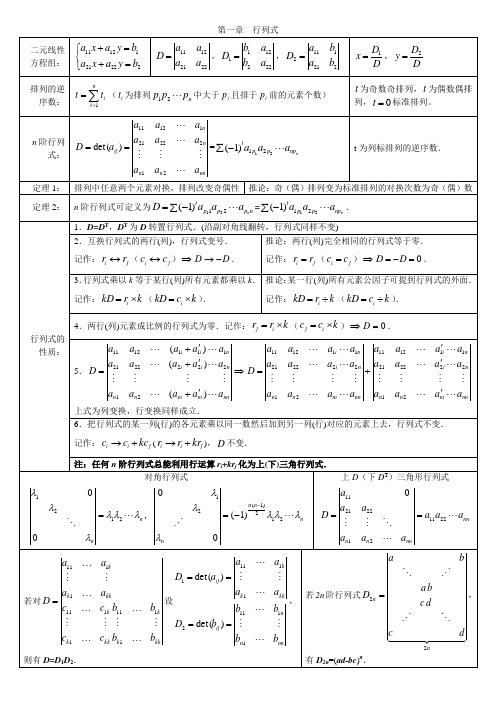
记作: ri rj ( ci cj ) D D 0 .
3.行列式乘以 k 等于某行(列)所有元素都乘以 k. 推论:某一行(列)所有元素公因子可提到行列式的外面.
记作: kD ri k ( kD ci k ).
记作: kD ri k ( kD ci k ).
行列式的 性质:
a2i a2n
a21
a22
a2i a2n
an1 an2 (ani ani ) ann
an1 an2 ani ann an1 an2 ani ann
上式为列变换,行变换同样成立.
6.把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变.
记作: ci ci kcj ( ri ri krj ), D 不变.
n
aki Akj
k 1
Dij
D, 0,
当i 当i
j, n
j;
或
k 1
aik
Ajk
Dij
D, 0,
当i 当i
j, j; 其中ij
1, 0,
当i j, 当i j.
1 1 11
范德蒙德 行列式:
x1 Dn x12
x2 x22
x3 xn
x32 xn2 = (xi x j ) .证明用数学归纳法.
定理 2:
n 阶行列式可定义为 D (1)ta a p11 p2 2 apnn = (1)ta1p1a2 p2 anpn .
1.D=DT,DT 为 D 转置行列式.(沿副对角线翻转,行列式同样不变)
2.互换行列式的两行(列),行列式变号.
推论:两行(列)完全相同的行列式等于零.
记作: ri rj ( ci c j ) D D .
考研数学公式定理背诵手册(数学二):线性代数

性质 3 行列式的某一行(列)中所有的元素都乘以同一数 k ,等于用数 k 乘此行列式.
推论 行列式中某一(列)的所有元素的公因子可以提到行列式符号的外面.
性质 4 行列式中如果有两行(列)元素成比例,则此行列式等于零.
性质 5 若行列式的某一列(行)的元素都是两数之和,如第 i 列的元素都是两数之和:
(2)若 A 可逆,则 A−1 亦可逆,且 ( A−1)−1 = A . (3)若 A 可逆,数 λ ≠ 0 ,则 λ A 可逆,且 (λ A)−1 = 1 A−1 .
λ (4)若 A, B 为同阶矩阵且均可逆,则 AB 亦可逆,且 ( AB)−1 = B−1A−1 .
(5)若 A 可逆,则 AΤ 亦可逆,且 ( AΤ )−1 = ( A−1)Τ .
A = O 或 B = O ;A2 = O
A=O;
109
AB = AC
B = C . 但 是 A, B 为 方 阵 , 则 有 | AB |=| BA |=| A || B | ;
| AB |= 0 ⇔| A |= 0 或| B |= 0 .
2.逆矩阵的性质
(1)若矩阵 A 是可逆的,则 A−1 是唯一的.
定理 设非齐次线性方程组 Ax = b ,其系数矩阵的秩 r( A) = r(r > 0) ,增广矩阵的秩
第二部分 线性代数
一、行 列 式
1. 行列式的重要定理及公式
定理 对换改变 n 元排列的奇偶性. 定理 任一 n 元排列与排列1 2 3 n 可以经过一系列对换互变,并且所作对换的次数 与这个 n 元排列有相同的奇偶性.
2.行列式的基本性质 性质 1 行列式与它的转置行列式相等. 性质 2 互换行列式的两行(列),行列式变号. 推论 如果行列式有两行(列)完全相同,则此行列式等于零.
考研数学二知识点总结

考研数学二知识点总结数学二是考研数学的一部分,该科目主要考察线性代数和概率统计的知识。
以下是数学二考研知识点的总结:一、线性代数1. 行列式:行列式的定义、性质和计算方法,如代数余子式、拉普拉斯展开等。
2. 线性方程组:线性方程组的解的判定、求解和应用,如高斯消元法、矩阵法等。
3. 矩阵与向量:矩阵的运算、性质和逆矩阵的求解,向量的线性相关性、内积、外积等。
4. 线性空间与线性变换:线性空间的定义、性质和子空间的判定,线性变换的定义、性质和矩阵表示等。
5. 特征值与特征向量:特征值与特征向量的定义、性质和计算方法,对角化与相似矩阵等。
6. 数量积空间与内积空间:数量积空间的定义、性质和正交性质,内积空间的定义、性质和正交投影等。
7. 线性映射与线性规范:线性映射的定义、性质和矩阵表示,线性规范的定义、性质和单位正交基等。
8. 奇异值与奇异值分解:奇异值与奇异向量的定义、性质和计算方法,奇异值分解的定义和计算等。
二、概率统计1. 随机事件与概率:随机事件的定义、性质和基本运算规则,概率的定义、性质和计算方法等。
2. 随机变量:随机变量的定义、分布函数、密度函数和分布列,离散随机变量和连续随机变量的特点和计算方法等。
3. 二维随机变量:二维随机变量的定义、边缘分布、条件分布和独立性,相关系数和协方差等。
4. 多维随机变量:多维随机变量的定义、分布函数和密度函数,边缘分布、条件分布和独立性等。
5. 随机变量的数字特征:随机变量的数学期望、方差、协方差等,大数定律和中心极限定理等。
6. 统计量与抽样分布:统计量的定义、性质和抽样分布,样本均值、样本方差和样本均数的分布等。
7. 参数估计:点估计的方法和性质,最大似然估计和矩估计等。
8. 假设检验:假设检验的基本原理和步骤,显著性水平和拒绝域的确定等。
9. 方差分析与回归分析:单因素方差分析和双因素方差分析,一元线性回归和多元线性回归等。
10. 随机过程与时间序列分析:随机过程的定义、性质和分类,平稳时间序列的分析和估计等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019考研数学二线性代数复习内容
来源:智阅网
线性代数是考研数学二中,很重要的一部分。
所以,一本考研数学二的相关复习图书,是否适合学生使用,就通过看这本书对于线性代数基础内容的讲解了。
这里就来熟悉一下线性代数的基础内容。
线代概念很多,重要的有代数余子式、伴随矩阵、逆矩阵、初等变换与初等矩阵、正交变换与正交矩阵、秩(矩阵、向量组、二次型)、等价(矩阵、向量组)、线性组合与线性表出、线性相关与线性无关、极大线性无关组、基础解系与通解、解的结构与解空间、特征值与特征向量、相似与相似对角化、二次型的标准形与规范形、正定、合同变换与合同矩阵。
而运算法则也有很多必须掌握:行列式(数字型、字母型)的计算、求逆矩阵、求矩阵的秩、求方阵的幂、求向量组的秩与极大线性无关组、线性相关的判定或求参数、求基础解系、求非齐次线性方程组的通解、求特征值与特征向量(定义法,特征多项式基础解系法)、判断与求相似对角矩阵、用正交变换化实对称矩阵为对角矩阵(亦即用正交变换化二次型为标准形)。
汤老师的2019《考研数学接力题典1800》(数学二),对相关线性代数的基础和重要知识点都有详尽的讲解,介绍了不少解题方法,对咱们提高考研数学二复习效果,有很大帮助。
