数据分析spss作业
第4章 SPSS基本统计分析(课后练习参考)

第4章 SPSS基本统计分析(课后练习参考)1、利用习题二第6题数据,采用SPSS数据筛选功能将数据分成两份文件。
其中,第一份数据文件存储常住地是“沿海或中心繁华城市”且本次存款金额在1000至5000之间的调查数据;第二份数据文件是按照简单随机抽样所选取的70%的样本数据。
第一份文件:选取数据数据——选择个案——如果条件满足——存款>=1000&存款<5000&常住地=沿海或中心繁华城市。
第二份文件:选取数据数据——选择个案——随机个案样本——输入70。
2、利用习题二第6题数据,将其按常住地(升序)、收入水平(升序)、存款金额(降序)进行多重排序。
排序数据——排序个案——把常住地、收入水平、存款金额作为排序依据分别设置排列顺序。
3、利用习题二第4题的完整数据,对每个学生计算得优课程数和得良课程数,并按得优课程数的降序排序。
计算转换——对个案内的值计数输入目标变量及目标标签,把所有课程选取到数字变量,定义值——设分数的区间,之后再排序。
4、利用习题二第4题的完整数据,计算每个学生课程的平均分以及标准差。
同时,计算男生和女生各科成绩的平均分。
方法一:利用描述性统计,数据——转置学号放在名称变量,全部课程放在变量框中,确定后,完成转置。
分析——描述统计——描述,将所有学生变量全选到变量框中,点击选项——勾选均值、标准差。
先拆分数据——拆分文件按性别拆分,分析——描述统计——描述,全部课程放在变量框中,选项——均值。
方法二:利用变量计算,转换——计算变量分别输入目标变量名称及标签——均值用函数mean完成平均分的计算,标准差用函数SD完成标准差的计算。
数据——分类汇总——性别作为分组变量、全部课程作为变量摘要、(创建只包含汇总变量的新数据集并命名)——确定5、利用习题二第6题数据,大致浏览存款金额的数据分布状况,并选择恰当的组限和组距进行组距分组。
根据存款金额排序,观察其最大值与最小值,算出组数和组距。
SPSS操作实验作业1(附答案)

SPSS操作实验 (作业1)作为华夏儿女都曾为有着五千年的文化历史而骄傲过,作为时代青年都曾为中国所饱受的欺压而愤慨过,因为我们多是炎黄子孙。
然而,当代大学生对华夏文明究竟知道多少呢某研究机构对大学电气、管理、电信、外语、人文几个学院的同学进行了调查,各个学院发放问卷数参照各个学院的人数比例,总共发放问卷250余份,回收有效问卷228份。
调查问卷设置了调查大学生对传统文化了解程度的题目,如“佛教的来源是什么”、“儒家的思想核心是什么”、“《清明上河图》的作者是谁”等。
调查问卷给出了每位调查者对传统文化了解程度的总得分,同时也列出了被调查者的性别、专业、年级等数据信息。
请利用这些资料,分析以下问题。
问题一:分析大学生对中国传统文化的了解程度得分,并按了解程度对得分进行合理的分类。
问题二:研究获得文化来源对大学生了解传统文化的程度是否存在影响。
要求:直接导出查看器文件为.doc后打印(导出后不得修改)对分析结果进行说明,另附(手写、打印均可)。
于作业布置后,1周内上交本次作业计入期末成绩答案问题一操作过程1.打开数据文件作业。
同时单击数据浏览窗口的【变量视图】按钮,检查各个变量的数据结构定义是否合理,是否需要修改调整。
2.选择菜单栏中的【分析】→【描述统计】→【频率】命令,弹出【频率】对话框。
在此对话框左侧的候选变量列表框中选择“X9”变量,将其添加至【变量】列表框中,表示它是进行频数分析的变量。
3.单击【统计量】按钮,在弹出的对话框的【割点相等组】文本框中键入数字“5”,输出第20%、40%、60%和80%百分位数,即将数据按照题目要求分为等间隔的五类。
接着,勾选【标准差】、【均值】等选项,表示输出了解程度得分的描述性统计量。
再单击【继续】按钮,返回【频率】对话框。
4.单击【图表】按钮,勾选【直方图】和【显示正态曲线】复选框,即直方图中附带正态曲线。
再单击【继续】按钮,返回【频率】对话框。
最后,单击【确定】按钮,操作完成。
SPSS数据统计与分析考试习题集(附答案淮师)

SPSS数据统计与分析考试习题集(附答案淮师)第三章统计假设检验二、计算题1.桃树枝条的常规含氮量为2.40%,现对一桃树新品种枝条的含氮量进行了10次测定,其结果为2.38%、2.38%、2.41%、2.50%、2.47%、2.41%、2.38%、2.26%、2.32%、2.41%,试问该测定结果与常规枝条含氮量有无差别。
单个样本显著值0.349>0.052.随机抽测了10只兔的直肠温度,其数据为:38.7、39.0、38.9、39.6、39.1、39.8、38.5、39.7、39.2、38.4(℃),已知该品种兔直肠温度的总体平均数为39.5(℃),试检验该样本平均温度与该品种兔直肠温度的总体平均数是否存在显著差异?单个样本显著值0.027<0.053.假说:“北方动物比南方动物具有较短的附肢。
”为验证这一假说,调查了如下鸟类翅长(mm)资料。
试检验这一假说。
双个样本成组这个说法不正确,差异不明显。
显著值0.581>0.05北方(1)120 113 125 118 116 114 119 /南方(2)116 117 121 114 116 118 123120234.11只60日龄的雄鼠在x射线照射前后之体重数据见下表(单位:g):检验雄鼠在照射x射线前后体重差异是否显著?双个样本成对编号123456789111照射前25.724.421.125.226.423.821.522.923.125.129.5照射222222222224后2.53.2 0.6 3.4 5.4 0.4 0.6 1.9 2.6 3.54.35. 用中草药青木香治疗高血压,记录了13个病例,所测定的舒张压数据如下:试检验该药是否具有降低血压的作用。
双个样本 成对序 号 1 2 3 4 5 6 7 8 9 10 11 12 13 治疗前 110 115 133 133 126 108 110 110 140 104 160 120 120 治疗后90116101103110889210412686114881126.为测定A、B两种病毒对烟草的致病力,取8株烟草,每一株皆半叶接种A病毒,另半叶接种B病毒(每一株的哪半边接种哪一种病毒由抽签随机决定),以叶面出现枯斑病的多少作为致病力强弱的指标,得结果如下表。
SPSS简单的练习作业

在上图中,分别显示了两两广告形式下销售额均值检验的结果。在SPSS中全部采用了LSD方法中的分布标准误,因此各种方法的前两列计算结果完全相同。表中第三列是检验统计量观测值在不同分布中概率值p,可以发现各种方法在检验敏感度上市存在差异的。以报纸广告与其他三种广告形式的两两检验结果为例,如果显著性水平α=0.05,在LSD方法中,报纸广告和广播广告的效果没有显著性差异,p值为0.412,与宣传品和体验均有显著性差异,概率p值分别是0.00,接近和0.021;但是在其他三种方法中,报纸广告只与宣传品广告存在显著性差异,而与体验无显著性差异。表中第一列星号的含义是,在显著性水平α=0.05的情况下,相应两总体的均值存在显著性差异,与第三列的结果相对应。
实验一SPSS的方差分析、相关分析与线性回归分析………………………17
1.单因素方差分析的基本操作……………………………………………17
2.单因素方差分析进一步分析的操作……………………………………18
作业一SPSS数据文件的建立和管理、数据的预处理
实验一SPSS数据文件的建立和管理、数据的预处理
【实验目的】
【实验结果与分析】
以上结果是广告形式对销售额的单因素方差的分析结果。可以看到,观测变量销售额的总离差平方和为26169.306;如果仅考虑“广告形式”单个因素的影响,则销售额总变差中,广告形式可解释的变差为5866.083,抽样误差引起的变差为20303.222,它们的方差(平均变差)分别为1955.361和145.023,相除所得的F统计量的观测值为13.483,对应的概率p值近似为0。如果显著性水平α为0.05,由于概率p值小于显著性水平α,则应拒绝零假设,认为不同广告形式对销售产生显著影响,它对销售额的影响效应不全为0。
数据分析spss作业..

数据分析方法及软件应用(作业)题目:4、8、13、16题指导教师:学院:交通运输学院姓名:学号:4、在某化工生产中为了提高收率,选了三种不同浓度,四种不同温度做试验。
在同一浓度与温度组合下各做两次试验,其收率数据如下面计算表所列。
试在α=0.05显著性水平下分析(1)给出SPSS数据集的格式(列举前3个样本即可);(2)分析浓度对收率有无显著影响;(3)分析浓度、温度以及它们间的交互作用对收率有无显著影响。
解答:(1)分别定义分组变量浓度、温度、收率,在变量视图与数据视图中输入表格数据,具体如下图。
(2)思路:本问是研究一个控制变量即浓度的不同水平是否对观测变量收率产生了显著影响,因而应用单因素方差分析。
假设:浓度对收率无显著影响。
步骤:【分析-比较均值-单因素】,将收率选入到因变量列表中,将浓度选入到因子框中,确定。
输出:變異數分析收率平方和df 平均值平方 F 顯著性群組之間39.083 2 19.542 5.074 .016在群組內80.875 21 3.851總計119.958 23显著性水平α为0.05,由于概率p值小于显著性水平α,则应拒绝原假设,认为浓度对收率有显著影响。
(3)思路:本问首先是研究两个控制变量浓度及温度的不同水平对观测变量收率的独立影响,然后分析两个这控制变量的交互作用能否对收率产生显著影响,因而应该采用多因素方差分析。
假设,H01:浓度对收率无显著影响;H02:温度对收率无显著影响;H03:浓度与温度的交互作用对收率无显著影响。
步骤:【分析-一般线性模型-单变量】,把收率制定到因变量中,把浓度与温度制定到固定因子框中,确定。
输出:主旨間效果檢定因變數: 收率來源第 III 類平方和df 平均值平方 F 顯著性修正的模型70.458a11 6.405 1.553 .230截距2667.042 1 2667.042 646.556 .000浓度39.083 2 19.542 4.737 .030温度13.792 3 4.597 1.114 .382浓度 * 温度17.583 6 2.931 .710 .648錯誤49.500 12 4.125總計2787.000 24校正後總數119.958 23a. R 平方 = .587(調整的 R 平方 = .209)第一列是对观测变量总变差分解的说明;第二列是观测变量变差分解的结果;第三列是自由度;第四列是均方;第五列是F检验统计量的观测值;第六列是检验统计量的概率p值。
用SPSS对数据进行分析
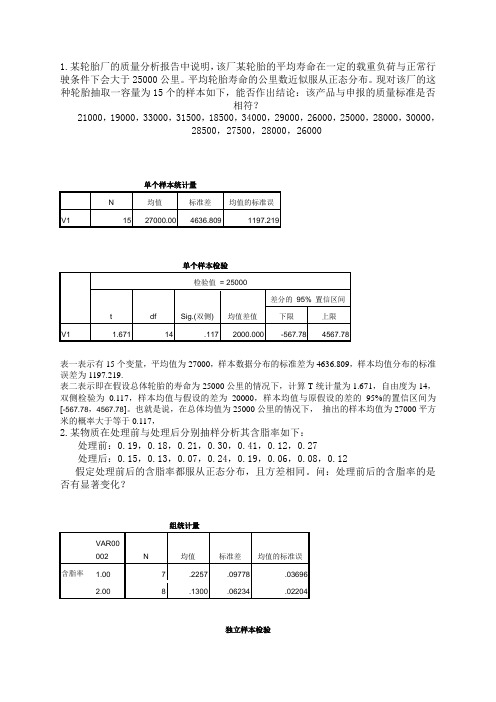
1.某轮胎厂的质量分析报告中说明,该厂某轮胎的平均寿命在一定的载重负荷与正常行驶条件下会大于25000公里。
平均轮胎寿命的公里数近似服从正态分布。
现对该厂的这种轮胎抽取一容量为15个的样本如下,能否作出结论:该产品与申报的质量标准是否相符?21000,19000,33000,31500,18500,34000,29000,26000,25000,28000,30000,28500,27500,28000,26000表一表示有15个变量,平均值为27000,样本数据分布的标准差为4636.809,样本均值分布的标准误差为1197.219.表二表示即在假设总体轮胎的寿命为25000公里的情况下,计算T统计量为1.671,自由度为14,双侧检验为0.117,样本均值与假设的差为20000,样本均值与原假设的差的95%的置信区间为[-567.78,4567.78]。
也就是说,在总体均值为25000公里的情况下,抽出的样本均值为27000平方米的概率大于等于0.117,2.某物质在处理前与处理后分别抽样分析其含脂率如下:处理前:0.19,0.18,0.21,0.30,0.41,0.12,0.27处理后:0.15,0.13,0.07,0.24,0.19,0.06,0.08,0.12假定处理前后的含脂率都服从正态分布,且方差相同。
问:处理前后的含脂率的是否有显著变化?组统计量VAR00002 N 均值标准差均值的标准误含脂率 1.00 7 .2257 .09778 .036962.00 8 .1300 .06234 .02204表1是分1,2进行的描述统计。
其内容的解释与单个样本描述统计的解释完全相同表2是两组平均数差异的T检验结果。
下面对表中各项的内容解释如下:①等方差假定。
也就是检验的原假设为两总体分布的方差相等。
②方差齐性检验。
采用T检验的方法对两个总体的均值差进行检验的前提条件是两个总体分布的方差必须相等。
SPSS数据分析与应用(微课版)-实训案例参考答案 第1-8章

SPSS数据分析与应用(微课版)-实训案例参考答案参考实训案例1数据分析案例:未来一周某电商平台手机的销量分析。
(1)在这个问题中,手机的销量就是不确定性因素,在未来一周,有的手机可以畅销、也可能滞销,具体销量会是多少,都是不确定性。
(2)为了分析未来一周手机的销量,可以通过网络爬虫获取该平台手机的相关信息,比如,手机的品牌、型号、主屏幕尺寸、重量、颜色、商家、价格、评论数、好评率、销量等。
参考实训案例2(1)利用SPSS分别导入数据集“个人信息.xlsx”“支出数据.xlsx”。
图1 数据导入(2)在菜单栏中选择【数据(D)】→【合并文件(G)】→【添加变量(V)】。
图2 合并文件菜单(3)在弹出的对话框中,将另一个打开数据集选中,点击继续。
图3 变量添加对话框(4)选择合并方法为“基于键值一对一合并(N)”,点击确定。
图4 合并方法(5)查看合并后的数据集,包括了5列。
图5 合并后数据样例(6)在菜单栏中选择【文件(F)】→【另存为(A)】,在弹出的对话框中选择存储的路径,并命名文件名为“学生消费信息”后保存。
图6 数据另存对话框参考实训案例3本案例通过2020条数据来探究信用卡是否按期还款问题。
数据集见“信用卡还款.csv”。
案例因变量为是否按期还款,是定性变量,共分为按期与逾期两个水平,分别用 1 和 0 表示。
案例自变量性别,是定性变量,分为男女两类,分别用 1 和 0 表示;已婚_未婚,是定 性变量,已婚用 1 表示,未婚用 0 表示;已育_未育,是定性变量,已育用 1 表示,未育用 0 表示;收入,是连续变量,取值范围为[426,120940];教育水平,是定性变量,共分为高中及以下、大专、本科、研究生及以上四个水平,分别用 1、2、3、4 来表示;英语水平,是定性变量,共分为三级及以下、四级、六级、八级及以上四个水平,分别用 1、2、3、4 来表示;微博好友数,是连续变量,取值范围为[6,114];消费理念,是连续变量,取值范围为[0,1]。
spss数据分析题目

一、单选题1.F值越大,组间方差中()所占比例就越大。
A.试验误差B. 互作效应C.主效应D.处理效应2.中心极限定理表明,不管原总体的分布形态如何,其样本容量()的抽样分布呈正态分布。
A. B. C. D.3.显著性水平由研究者事先确定,常用的 值有0.01、0.05、0.10,分别代表()、()、()水平。
A.显著、建议显著、极显著B.显著、极显著、建议显著C.极显著、显著、建议显著4.在自然和社会现象中存在最多的关系是()。
A..函数关系B.相关关系C.线性关系5.统计推断的基本问题可以分为两大类:一类是参数估计;另一类是()。
A.方差分析B.t检验C.假设检验D.实验验证二、多选题1.原假设为待检验的假设,又称“()。
A.有效假设B.无效假设C.0假设D.研究假设2.秩和检验不受总体分布限制,适用面广,()型数据皆可。
A.数值B.顺序C.分类3.试验设计中必须遵循的重要基本原则是()。
A.重复B.循环C.局部控制D.随机4.逐步引入-剔除法(Stepwise)亦称()。
A.向前引入法B.向后剔除法C.逐步法D.步进法5.影响置信区间宽窄的因素有()。
A.样本容量B.置信水平 (1- a)值C.总体数据的离散程度三、判断题1.定量计算样本容量,最关键的是确定边际误差。
A.正确B.错误2.χ2分布是F分布的基础。
A.正确B.错误3.显著差异就是指有大的差异。
A.正确B.错误4.不考虑是否有用,得到一高置信水平的区间估计很容易。
A.正确B.错误5.用什么统计量进行假设检验,由研究者随意选择。
A.正确B.错误四、问答题1.多重比较有哪些常用方法?2.为什么统计推断的结论有可能发生错误?3.进行多重比较的充分必要条件是什么?A B C DⅠⅡ鲜叶处理工艺流程肥料用量配合比例1111178.978.1 212227777 3133377.578.9 4212380.180.9 5223177.678.4 623127879 7313276.776.3 8321381.382.7度重复0.97 0.91 0.86 0.83 0.80 0.80 0.44 0.96 0.90 0.85 0.82 0.80 0.79 0.45A电极 5.78 5.74 5.84 5.80 5.80 5.79 5.82 5.81 5.85 5.78 B电极 5.82 5.87 5.96 5.89 5.90 5.81 5.83 5.86 5.90 5.80。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据分析方法及软件应用(作业)题目:4、8、13、16题指导教师:学院:交通运输学院姓名:学号:4、在某化工生产中为了提高收率,选了三种不同浓度,四种不同温度做试验。
在同一浓度与温度组合下各做两次试验,其收率数据如下面计算表所列。
试在α=0.05显著性水平下分析(1)给出SPSS数据集的格式(列举前3个样本即可);(2)分析浓度对收率有无显著影响;(3)分析浓度、温度以及它们间的交互作用对收率有无显著影响。
解答:(1)分别定义分组变量浓度、温度、收率,在变量视图与数据视图中输入表格数据,具体如下图。
(2)思路:本问是研究一个控制变量即浓度的不同水平是否对观测变量收率产生了显著影响,因而应用单因素方差分析。
假设:浓度对收率无显著影响。
步骤:【分析-比较均值-单因素】,将收率选入到因变量列表中,将浓度选入到因子框中,确定。
输出:變異數分析收率平方和df 平均值平方 F 顯著性群組之間39.083 2 19.542 5.074 .016在群組內80.875 21 3.851總計119.958 23显著性水平α为0.05,由于概率p值小于显著性水平α,则应拒绝原假设,认为浓度对收率有显著影响。
(3)思路:本问首先是研究两个控制变量浓度及温度的不同水平对观测变量收率的独立影响,然后分析两个这控制变量的交互作用能否对收率产生显著影响,因而应该采用多因素方差分析。
假设,H01:浓度对收率无显著影响;H02:温度对收率无显著影响;H03:浓度与温度的交互作用对收率无显著影响。
步骤:【分析-一般线性模型-单变量】,把收率制定到因变量中,把浓度与温度制定到固定因子框中,确定。
输出:主旨間效果檢定因變數: 收率來源第 III 類平方和df 平均值平方 F 顯著性修正的模型70.458a11 6.405 1.553 .230截距2667.042 1 2667.042 646.556 .000浓度39.083 2 19.542 4.737 .030温度13.792 3 4.597 1.114 .382浓度 * 温度17.583 6 2.931 .710 .648錯誤49.500 12 4.125總計2787.000 24校正後總數119.958 23a. R 平方 = .587(調整的 R 平方 = .209)第一列是对观测变量总变差分解的说明;第二列是观测变量变差分解的结果;第三列是自由度;第四列是均方;第五列是F检验统计量的观测值;第六列是检验统计量的概率p值。
可以看到观测变量收率的总变差为119.958,由浓度不同引起的变差是39.083,由温度不同引起的变差为13.792,由浓度和温度的交互作用引起的变差为17.583,由随机因素引起的变差为49.500。
浓度,温度和浓度*温度的概率p值分别为0.030,0.382和0.648。
浓度:显著性<0.05说明拒绝原假设(浓度对收率无显著影响),证明浓度对收率有显著影响;温度:显著性>0.05说明不拒绝原假设(温度对收率无显著影响),证明温度对收率无显著影响;浓度与温度: 显著性>0.05说明不拒绝原假设(浓度与温度的交互作用对收率无显著影响),证明温浓度与温度的交互作用对收率无显著影响。
8、以高校科研研究数据为例:以课题总数X5为被解释变量,解释变量为投入人年数X2、投入科研事业费X4、专著数X6、获奖数X8;建立多元线性回归模型,分析它们之间的关系。
解释变量采用逐步筛选策略,并做多重共线性、方差齐性和残差的自相关性检验。
解答:思路:根据要求采用逐步筛选的解释变量筛选策略,利用回归分析方法建立多元线性回归模型,分析它们之间的关系,并且要求做多重共线性、方差齐性和残差的自相关性检验。
(1)步骤:【分析-回归-线性】,X5选入因变量,X2、X4、X6、X8选入自变量,方法选择【逐步】。
【统计量】勾选【估计】、【模型拟合度】、【共线性诊断】与【Durbin-Waston(U)】。
【绘制(T)按钮】,将*ZRESID添加到Y(Y)框中,将*ZPRED 添加到X2(X)框中,勾选【正态概率图】,【保存(S)】按钮。
在预测值与残差中勾选【标准化】选项。
选择菜单【分析→相关→双变量】将标准化预测值和标准化残差选入【变量】框,在相关系数中选择Spearman,各项完成后点击【确定】。
输出:變數已輸入/已移除a模型變數已輸入變數已移除方法1投入人年数. 逐步(準則:F-to-enter 的機率 <= .050,F-to-remove 的機率 >= .100)。
a. 應變數: 课题总数模型摘要b模型R R 平方調整後 R 平方標準偏斜度錯誤Durbin-Watson1 .959a.919 .917 241.9582 1.747a. 預測值:(常數),投入人年数b. 應變數: 课题总数表中变量为投入人年数,参考调整的判定系数,由于调整的判定系数(0.917)较接近于1,因此认为拟合优度较高,被解释变量可以被模型解释的部分较多,未能被解释的部分较少。
方程DW检验值为1.747,残差存在一定的正自相关。
變異數分析a模型平方和df 平均值平方 F 顯著性1 迴歸19379040.047 1 19379040.047 331.018 .000b殘差1697769.953 29 58543.791總計21076810.000 30a. 應變數: 课题总数b. 預測值:(常數),投入人年数被解释变量的总离差平方和为21076810.00,回归平方和及均方分别为19379040.047 和19379040.047,剩余平方和及均方分别为1697769.953和58543.791,检验统计量的观测值为331.018,对应的概率值近似为0。
依据该表可进行回归方程的显著性检验。
如果显著性水平为0.05,由于概率值小于显著性水平,应拒绝回归方程显著性检验的零假设,认为回归系数不为0,被解释变量与解释变量的线性关系是显著的,可建立线性模型。
係數a模型非標準化係數標準化係數T 顯著性共線性統計資料B 標準錯誤Beta 允差VIF1 (常數)-94.524 72.442 -1.305 .202投入人年数.492 .027 .959 18.194 .000 1.000 1.000 a. 應變數\: 课题总数依据该表可以进行回归系数显著性检验,写出回归方程和检测多重共线性。
可以看到,如果显著性水平为0.05,投入人年数变量的回归系数显著性t检验的概率p值小于显著性水平,因此拒绝零假设,认为其偏回归系数与0有显著差异,与被解释变量与解释变量的线性关系是显著的,应保留在方程中。
同时从容忍度和方差膨胀因子看,解释变量与投入人年数多重共线性很弱,可以建立模型。
最终回归方程为,课题总数= -94.524+0.492投入人年数。
排除的變數a模型Beta 入T 顯著性偏相關共線性統計資料允差VIF允差下限1 投入科研事业费(百元).152b 1.528 .138 .278 .267 3.748 .267专著数.023b.182 .857 .034 .188 5.308 .188 获奖数.030b.411 .684 .077 .542 1.846 .542a. 應變數: 课题总数b. 模型中的預測值:(常數),投入人年数该表展示回归方程的剔除变量,可以看到,如果显著性水平为0.05,表中三个变量的回归系数显著性t检验的概率p值大于显著性水平,因此不拒绝零假设,认为其偏回归系数与0无显著差异,与被解释变量与解释变量的线性关系是不显著的,不应保留在方程中。
同时从容忍度和方差膨胀因子看,解释变量与三个解释变量多重共线性严重,在建立模型的时候应当被剔除。
共線性診斷a模型維度特徵值條件指數變異數比例(常數)投入人年数1 1 1.800 1.000 .10 .102 .200 3.001 .90 .90a. 應變數: 课题总数依据该表可进行多重共线性检测,从方差比例上看第二个变量可解释常量的90%,也可解释投入人年数的90%,一次认为这些变量存在多重共线性。
条件指数都小于10,说明存在共线性较弱,低个变量特征值小于0.7,说明线性相关关系较弱。
殘差統計資料a最小值最大值平均數標準偏差N預測值-57.642 3246.986 960.000 803.7213 31殘差-466.2850 509.6787 .0000 237.8914 31標準預測值-1.266 2.845 .000 1.000 31標準殘差-1.927 2.106 .000 .983 31a. 應變數: 课题总数数据点围绕基准线还存在一定的规律性,但标准化残差的非参数检验结果表明标准化残差与标准正态分布不存在显著差异,可以认为残差满足了线性模型的前提要求。
随着标准化预测值的变化,残差点在0线周围随机分布,但残差的等方差性并不完全满足,方差似乎有增大的趋势。
但计算残差与预测值的Spearman 等级相关系数为-0.176,且检验并不显著,因此认为异方差现象并不明显。
相關Standardized PredictedValueStandardized ResidualSpearman 的 rhoStandardized Predicted Value相關係數 1.000-.176 顯著性 (雙尾) . .344 N31 31 Standardized Residual相關係數 -.176 1.000顯著性 (雙尾) .344 . N3131依据该表可以对标准化残差和标准化预测值的Spearman 等级进行分析,可以看到,计算残差与预测值的相关性弱,认为异方差现象不明显。
13、利用1950年~1990年的天津食品消费数据,分析这段时间内的人均生活费用年收入的变化情况。
要求:数据进行对数变换后,运用Holt 线性趋势平滑模型分析。
(1)输出均方根误差和参数估计结果;(2)输出ACF 和PACF 图形并对其特征进行分析,是否满足白噪声序列的条件; (3)给出1991-1992的预测值,并输出拟合图。
解答:思路:根据题意,先不进行序列图和自相关、偏自相关的观察和检验阶段处理。
直接利用指数平滑模型中的Holt 线性趋势模型对数据进行分析,同时输出均方根误差和参数估计误差,ACF 和PACF 图像判断是否满足白噪音序列的条件;最后然后对数据进行1991年、1992年做出预测,并用模型进行拟合。
步骤:【分析-预测-创建模型】,将人均生活费年收入选入【因变量】中,将【方法】选为【指数平滑法】;点击【条件】,在【因变量转换】中选【自然对数】,在【模型类型】中【Holt线性趋势】,【继续】。
【统计量】,在【拟合度量】中选择【平稳的R方、均方根误差】,在【个别模型的统计量】中选中【参数估计】,在【比较模型的统计量】中选中【拟合优度】,选中【显示预测值】,【确定】【图表】,在【单个模型图】中选择【序列、残差自相关函数、残差部分自相关函数】,在【每张图显示的内容】中现则【观察值、预测值、拟合值】。
