流体力学 第五章 习题new1
工程流体力学(水力学)闻德第五章-实际流体动力学基础课后答案

⼯程流体⼒学(⽔⼒学)闻德第五章-实际流体动⼒学基础课后答案⼯程流体⼒学闻德课后习题答案第五章实际流体动⼒学基础5—1设在流场中的速度分布为u x =2ax ,u y =-2ay ,a 为实数,且a >0。
试求切应⼒τxy 、τyx 和附加压应⼒p ′x 、p ′y 以及压应⼒p x 、p y 。
解:0y x xy yx u u x y ττµ==+=24xxu p a xµµ?'=-=-?,24y y u p a y µµ?'=-=?, 4x x p p p p a µ'=+=-,4y y p p p p a µ'=+=+5-2 设例5-1中的下平板固定不动,上平板以速度v 沿x 轴⽅向作等速运动(如图所⽰),由于上平板运动⽽引起的这种流动,称柯埃梯(Couette )流动。
试求在这种流动情况下,两平板间的速度分布。
(请将d 0d px=时的这⼀流动与在第⼀章中讨论流体粘性时的流动相⽐较)解:将坐标系ox 轴移⾄下平板,则边界条件为 y =0,0X u u ==;y h =,u v =。
由例5-1中的(11)式可得2d (1)2d h y p y yu v h x h h µ=-- (1)当d 0d p x =时,y u v h=,速度u为直线分布,这种特殊情况的流动称简单柯埃梯流动或简单剪切流动。
它只是由于平板运动,由于流体的粘滞性带动流体发⽣的流动。
当d 0d px≠时,即为⼀般的柯埃梯流动,它是由简单柯埃梯流动和泊萧叶流动叠加⽽成,速度分布为(1)u y y yp v h h h=-- (2)式中2d ()2d h pp v xµ=- (3)当p >0时,沿着流动⽅向压强减⼩,速度在整个断⾯上的分布均为正值;当p <0时,沿流动⽅向压强增加,则可能在静⽌壁⾯附近产⽣倒流,这主要发⽣p <-1的情况.5-3 设明渠⼆维均匀(层流)流动,如图所⽰。
流体力学 建工 课后作业答案 第五版

管进口到闸门总损失为1m,求管中平均流速v。
体
解:阀关时,由静力学方程
力 学
z1
p1
g
z2
p2
g
5mH2O
阀开时,由伯努利方程
1
1
2
z1
p1
g
v12 2g
z2
p2
g
v22 2g
hl
2
5 0 0.1 v2 1
2g
v 8.74m/s
50
3.28 管末端喷嘴d =10cm,D =40cm,Q=0.4m3/s,12 流
v3
2g
Q
Q/
4
v2 d32
4
d 2 67.2l/s 15.22m/s
v4
v2
Δh
2 d2 p 3
对3-3,4-4列能量方程
3d3
p4 v32 v42
g 2g
p4
(v32 v42 )
2
79.2kPa
H v32 11.82m
2g
49
3-18 阀关压力表读数时 p=49kPa,阀开时p=0.98kPa, 流
l=10m,d=50mm,λ=0.03。若AB两断面测压管水头 差Δh=0.629m,经2分钟流入水箱的水量为0.329m3。
流 体 力
解: Q 0.329 / 60 2 2.74103m3/s 学
v Q / d 2 1.4m/s
Δh
4
A
hf
l
d
v2 2g
0.03 10 1.42 0.6m
1
2 v1 2.572m/s, v2 =4.287m/s
列动量方程
F P1 P2 Q(2v2 1v1)
《流体力学》徐正坦主编课后答案第五章

第五章习题简答5-1有一薄壁圆形孔口,直径d= 10mm ,水头H 为2m 。
现测得射流收缩断面的直径d c 为8m m,在32.8s 时间内,经孔口流出的水量为0.01m3,试求该孔口的收缩系数ε,流量系数μ,流速系数φ及孔口局部损失系数ζ。
解: 64.010822=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==d d A A c c εs m d Q v /06.6008.08.32/01.04422=⨯⨯==ππ 62.097.064.006.0197.011197.028.9206.62222=⨯===-=-==⨯⨯==⇒=εϕμϕζϕϕgHvgH v5-2薄壁孔口出流,直径d=2cm,水箱水位恒定H =2m,试求:(1)孔口流量Q ;(2)此孔口外接圆柱形管嘴的流量Qn ;(3)管嘴收缩断面的真空高度。
题5-2图解:(1)孔口出流流量为s L s m gH A Q /219.1/10219.128.9202.0462.02332=⨯=⨯⨯⨯⨯⨯==πϕ(2)s L gH A Q n /612.128.9202.0482.022=⨯⨯⨯⨯⨯==πμ(3)真空高度:m H gpg p C Cv 48.1274.074.0=⨯==-=ρρ 5-3 水箱用隔板分为A 、B 两室,隔板上开一孔口,其直径d1=4cm ,在B 室底部装有圆柱形外管嘴,其直径d 2=3cm 。
已知H=3m ,h3=0.5m 试求:(1)h 1,h 2;(2)流出水箱的流量Q 。
题5-3图解:隔板孔口的流量 112gh A Q μ=圆柱形外管嘴的流量()()132222h H g A h h g A Q -=+=μμ由题意可得Q 1=Q 2,则()()1212122212111211303.082.004.062.022h h h H d h d h H g A gh A -⨯⨯=⨯⨯-=-=μμμμ解得m h 07.11=sL s m gh A Q mh h H h /56.3/1056.307.18.9204.0462.0243.15.007.1333211312=⨯=⨯⨯⨯⨯⨯==∴=--=--=∴-πμ5-4 有一平底空船,其船底面积Ω为8m 2,船舷高h为0.5m ,船自重G 为9.8kN 。
《流体力学》所有做过的习题答案
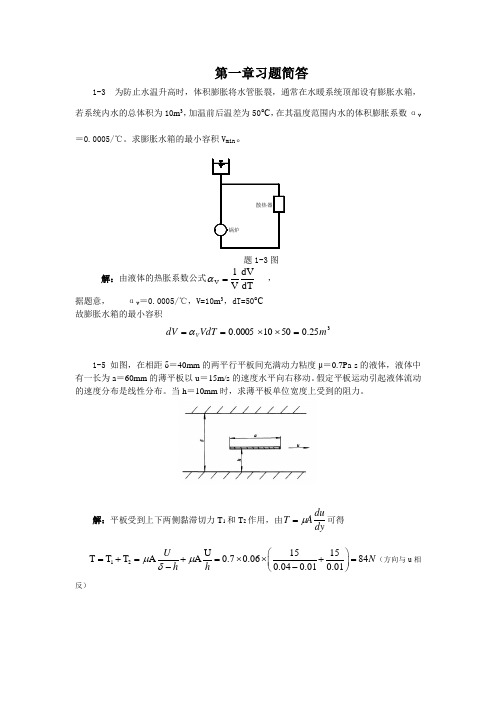
第一章习题简答1-3 为防止水温升高时,体积膨胀将水管胀裂,通常在水暖系统顶部设有膨胀水箱,若系统内水的总体积为10m 3,加温前后温差为50°С,在其温度范围内水的体积膨胀系数αv=0.0005/℃。
求膨胀水箱的最小容积V min 。
题1-3图解:由液体的热胀系数公式dTdVV 1V =α , 据题意, αv =0.0005/℃,V=10m 3,dT=50°С 故膨胀水箱的最小容积325.050100005.0m VdT dV V =⨯⨯==α1-5 如图,在相距δ=40mm 的两平行平板间充满动力粘度μ=0.7Pa·s 的液体,液体中有一长为a =60mm 的薄平板以u =15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h =10mm 时,求薄平板单位宽度上受到的阻力。
解:平板受到上下两侧黏滞切力T 1和T 2作用,由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭(方向与u 相反)1-7 温度为20°С的空气,在直径为2.5cm 的管中流动,距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的黏滞切力为多少?解:温度为20°С的空气的黏度为18.3×10-6 Pa·s 如图建立坐标系,且设u=ay 2+c 由题意可得方程组⎪⎩⎪⎨⎧+-=+=ca ca 22)001.00125.0(03.00125.00 解得a = -1250,c =0.195 则 u=-1250y 2+0.195则y dy y d dy du 2500)195.01250(2-=+-= Pa dyduAT 561048.4)0125.02500(1025.0103.18--⨯-=⨯-⨯⨯⨯⨯⨯==∴πμ (与课本后的答案不一样。
流体力学第五章作业题

5.1 管道直径d =100mm ,输送水的流量为10kg/s ,如水温为50C ,试确定管内水流的流态。
如用这管道输送同样质量的石油,已知石油的密度ρ=850kg/m 3,运动粘性系数ν=1.14cm 2/s ,试确定石油的流态。
解:50C 时,水的运动粘性系数ν=1.52×10-6m 2/s ,24Q u d ρπ= 水的雷诺数Re 为:4Re ud Q v v dρπ== -623410kg/s 84000138001.5210m /s 1000kg/m 3.140.1m⨯==>⨯⨯⨯⨯,紊流 石油:-423410kg/s Re 1314.623201.1410m /s 850kg/m 3.140.1m ud v ⨯===<⨯⨯⨯⨯,层流 5.2 有一梯形断面的排水沟,底宽b =70cm ,断面的边坡为1:1.5,当水深h =40cm ,断面平均流速u =5.0cm/s ,水温100C ,试判别此时的水流形态。
如果水深和水温都保持不变,问断面平均流速减到多少才是层流?题5.2图解:100C 时,水的运动粘性系数ν=1.31×10-6m 2/s水力直径为424.27cm A d χ=== -620.05m/s 0.2427m Re 9263.31.3110m /sud v ⨯===⨯,2320Re 13800<<,层流和紊流都可能存在 水流为层流时Re 2320ud v ≤=,故6Re 2320 1.3110 1.2522cm/s 0.2427v u d -⨯⨯≤== 5.4 在长度l =10000m ,直径d =300mm 的管路中输送重度为9.31kN/m 3的重油,其重量流量Q =2371.6kN/h ,运动粘性系数ν=25cm 2/s ,判断其流态并求其沿程阻力损失。
解:雷诺数Re ud v =,流速241m/s Q u d γπ==, 所以343442371.610/3600Re 120232025109.3110 3.140.3ud Q v v d γπ-⨯⨯====<⨯⨯⨯⨯⨯,层流沿程阻力损失为:276761000011077.1m Re 21200.329.8L L u h d g ==⋅⋅=⨯ 5.5 润滑油在圆管中作层流运动,已知管径d =1cm ,管长l =5m ,流量Q =80cm 3/s ,沿程损失h L =30m(油柱),试求油的运动粘度ν。
流体力学第五章题库

名词解释1.黏性流体单位中立形式的伯努利方程:w a a h gv g pz g v g p +++=++22z 22222111αραρ2.方程适用条件1.流动为定常流动2流体为黏性不可压缩的重力流体3列方程的两过流断面必须是缓变流截面,而不必顾忌两截面间是否有急变流。
3.动能修正系数α的大小取决于过流断面上流速分布的均匀程度,以及断面的形状和大小,流速分布越均匀,其数值越接近于一,流速分布越不均匀,其数值就越大,。
4.流体在其流动过程中要克服黏性摩擦力,总流的机械能沿流程不断减小,总水头线不断降低。
5.相似准则:在几何相似的条件下,两种物理现象保证相似的条件或准则。
6.牛顿数:作用力与惯性力的比值。
Ne=F/ρl ²v ²7.弗劳德数:物理意义为惯性力与重力的比值。
Fr=v/(gl )½ 8.雷诺数:物理意义为惯性力与黏性力的比值。
Re=vl/υ 9.欧拉数:物理意义为总压力与惯性力的比值。
Eu=Δp/ρv ² 10.柯西数:物理意义为惯性力与弹性力的比值。
Ca=ρv ²/K 11.马赫数:(流场中流体为气体)物理意义为惯性力与弹性力的比值。
Ma=v/c 12.韦伯数:物理意义为惯性力与表面张力的比值。
We=ρv ²l/σ13.斯特劳哈尔数:物理意义为当地惯性力与迁移惯性力的比值。
Sr=l/vt14.层流:着色流体和周围的流体互不掺混,流线为直线,流体质点只有沿圆管轴向的运动,而没有径向运动,这种流动状态称为层流或片流。
15.紊流:流体质点不仅有轴向运动,也具有径向运动,处于一种无序的紊乱状态,这种流动状态称为紊流或湍流。
16.边界层:黏性流体流经固体壁面时,在固体壁面法线方向上存在一速度急剧变化的薄层,称为边界层。
17.管道进口段:边界层相交以前的管段称为管道进口段(或称起始段),其长度以L*表示。
18.准定常流动/时均定常流:流场中的时均参数不随时间改变的紊流流动称为准定常流动或时均定常流。
第五流体力学习题答案
第五章习题简答5-1有一薄壁圆形孔口,直径d= 10mm ,水头H 为2m 。
现测得射流收缩断面的直径d c为8mm ,在32.8s 时间内,经孔口流出的水量为0.01m 3,试求该孔口的收缩系数ε,流量系数μ,流速系数φ及孔口局部损失系数ζ。
解: 64.010822=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==d d A A c c εs m d Q v /06.6008.08.32/01.04422=⨯⨯==ππ 62.097.064.006.0197.011197.028.9206.62222=⨯===-=-==⨯⨯==⇒=εϕμϕζϕϕgHvgH v5-2薄壁孔口出流,直径d=2cm ,水箱水位恒定H=2m ,试求:(1)孔口流量Q ;(2)此孔口外接圆柱形管嘴的流量Q n ;(3)管嘴收缩断面的真空高度。
题5-2图解:(1)孔口出流流量为s L s m gH A Q /219.1/10219.128.9202.0462.02332=⨯=⨯⨯⨯⨯⨯==πϕ(2)s L gH A Q n /612.128.9202.0482.022=⨯⨯⨯⨯⨯==πμ(3)真空高度:m H gpg p C Cv 48.1274.074.0=⨯==-=ρρ 5-3 水箱用隔板分为A 、B 两室,隔板上开一孔口,其直径d 1=4cm ,在B 室底部装有圆柱形外管嘴,其直径d 2=3cm 。
已知H=3m ,h 3=0.5m 试求:(1)h 1,h 2;(2)流出水箱的流量Q 。
题5-3图解:隔板孔口的流量 112gh A Q μ=圆柱形外管嘴的流量 ()()132222h H g A h h g A Q +=+=μμ由题意可得Q1=Q2,则()()1212122212111211303.082.004.062.022h h h H d h d h H g A gh A -⨯⨯=⨯⨯+=+=μμμμ解得m h 07.11=sL s m gh A Q mh h H h /56.3/1056.307.18.9204.0462.0243.15.007.1333211312=⨯=⨯⨯⨯⨯⨯==∴=--=--=∴-πμ5-4 有一平底空船,其船底面积Ω为8m 2,船舷高h 为0.5m ,船自重G 为9.8kN。
流体力学B5-new

M0 L 0 T0 = ( M L –3) a ( L T–2 ) b L c ( L3 T –1 )
p ( ,V , d , , , l )
2.选择基本量:ρ、V、d 3.列П表达式求解П数 ① П1=ρa V bd cΔp M 0 L 0 T 0 = (M L – 3 ) a (L T – 1 )b L c (M L –1 T – 2 )
[例B5.2.2]
粗糙管中粘性流动的压降:量纲分析一般步骤
密度,重度 力,力矩
dim Q L3T 1
dim ML3
dim F MLT 2
dim L ML2T 2
压强,压力,弹性模量
粘度系数 其他量 角速度,角加速度 应变率
dim p dim dim K ML1T 2
dim ML1T 1
dim v L2T 1
解得 a1 = -1 , b1 = -2 , c1= -2
Π1 FD
V d
2
2
CD
0
(CD 称为阻力系数)
-3 a 2 -1 b2 c2
2 a2 V b2 d c2
M L T = (ML ) (LT ) L (ML -1T -1 )
0 0
B5
量纲分析与П定理
B5.2.2
量纲分析法
M:a2 1 0 L: 3a2 b2 c2 1 0 T : b 1 0 2
解得: a 2 = -1, b 2 = -1, c 2 = -1
2
Vd
1 Re
(Re为雷诺数)
第5步、用П数组成新的方程。 П1 = f (П2 )
CD FD
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5-19
水从封闭水箱上部直径d1=30mm 的孔口流至下部,然后经 d2=20mm的圆柱行管嘴排向大气
c
c
中,流动恒定后,水深h1=2m, h2=3m,水箱上的压力计读数为 4.9MPa,求流量Q和下水箱水面 上的压强p2,设为定常流。已知:
1 0.6 2 0.82
5-19
解:经过孔口的流量 = 经过管嘴的流量
h f 1 L1 16 30 8 2 3 2 Q 0.04 (4.46 10 ) 6.32m 1 5 2 5 2 d1 2 g 0.05 9.8 3.14
5-8.
CD管由A、B联合供水,Q0=100L/s,求Q1,Q2,d2。
解:分支管路,串联,先求h fCD
20m A B 19m
4 3 4
5-13
Q 103 m3 / s, h1 2m, l 44m, 104 m2 / s, 900kg / m3
2) hV=5.4m水柱,对1-1,3-3列能量方程 1/2l,d
3 3
A
1/2l,d
1
1h
h1
v2 0 hmax hf 2g pA
θ
h
( D1 D2 ) D D2 h D2 h h0
T
d D2
1
d 2 2g
1
2
h0
0
( D2 h)2 dh h
4 2 5/2 h0 3/2 D2 h h ]0 3 5
T
d
2g
[2 D h
2 1/2 2
T
1 4 2 5/2 5/2 5/2 [2 0.1 0.1 0.1 ] 172.04s 2 3 5 0.62 0.005 19.6
Q 103 m3 / s, h1 2m, l 44m, 104 m2 / s, 900kg / m3
保证层流,d 应为多少?l/2处A断面上的极限真空为hV=5.4m
水柱,输油管在贮油池油面以上的最大允许高度hmax=?
1/2l,d h
A
1/2l,d
h1
5-13
Q 103 m3 / s, h1 2m, l 44m, 104 m2 / s, 900kg / m3
d D2
1 2 [2 D 2 ( h0 h0 / 2) 2 d 4 2 3 3 5 5 D2 ( h0 h0 / 8) ( h0 h0 / 32)] 3 5
104 0.0056 81.61s 2 0.62 0.5 19.6
Th0 /2
2
2
hmax
v 2 h1 2g 2 pA
4Q 4 103 v 0.42m / s 2 2 d 3.14 0.055 hmax 5.4 0.422 1 4.99m 0.9 19.6
5-16 d=0.03m,圆柱形外管嘴。管嘴内的真空度1.5m,求Q。
Q1=1
c c
d12
4
d1 p1 p 2 2g h 1 2 p2 2g h2
Q2= 2
d 22
4
p2 4.34 10 4 Pa
Q Q2= 2
d 22
4
p2 3 3 2g h 3 . 11 10 m /s 2
T
0
Qdt
0
D2
4
2 gh
h0
dh
d D2
Q
T
d2
4
T dt
0
1
d 2 2g
h0
0
D2 dh h
5-20
D1 20cm, D2 10cm, h0 10cm, d 0.5cm, 0.62
D1 D
dh h0
T
1
d 2 2g
h0
0
D2 dh h
2
2 0.024
3 0.025
Q Q1 Q2 1.805Q2 0.1m3 / s Q2 0.055m3 / s, Q1 0.045m3 / s h f 1 4.29m
5-7
图中一根管长L1=30m,直径d1=50mm,另一根管长L2 =50m ,直径d2=100mm,阀门的局部阻力系数ζ=3,假设沿程阻力 3 Q 25 103 m /s 系数λ1=0.04和λ2=0.03。试求流量 在两并联 管路中是如何分配的?并联管路中水头损失又为多少?
1 0.025
D2 200mm
2 0.026
q 25L / s
Q 25L / s
5-5
L1 v12 103 1.0192 h f 1 1 0.025 D1 2 g 0.25 19.6 5.30m
L1 1000m D1 250mm
L2 500m
5-5
求图示串联管路按长管计算所需的水头H=?
解: Q1 Q q
L1 1000m D1 250mm
L2 500m
H
4Q 4 25 103 v2 0.796m / s 2 2 D2 3.14 0.2 4(Q q) 4 50 103 v1 1.019m / s 2 2 D1 3.14 0.25
h f CD
L0 16Q02 0 5 d 0 2 g 2
500 16 0.12 0.025 10.6m 5 2 0.25 19.6 3.14 z A z D h fAC h fCD
5m
C D
h fAC
L1 16Q12 15 10.6 1 5 d1 2 g 2
5-20
圆台形容器如图所示,液体经过容器底部直径d的小孔口流 出,求容器排空及排出液体深度的1/2时所需的时间。
D1 20cm, D2 10cm, h0 10cm, d 0.5cm, 0.62
D1 dh h h0
解:流出的体积=容器减少的体积。 设dt时间液面下降dh,液面直径 为D,容器排空时间为T。
可见流速水头很小,可以忽略
5-6. Q=100L/s,确定Q1,Q2及AB间的水头损失
解:
L1 1000m D1 250mm
1 0.025
Q
Q2
L2 900m D2 300mm
Q1
L3 300m D3 250mm
2 16 Q Q L2 1 h f 2 2 hf 1 hf 2 hf 3 2 D2 2 g 2 L3 16 Q Q1 h f 3 3 D3 2 g 2 L1 16Q12 h f 1 1 D1 2 g 2 2.56Q12 1.66 Q Q1 Q1 0.805Q2
L2, d2
解:并联管2需考虑局部水头损失:
Q Q1 Q2
2 v2 hf 1 hf 2 2g
2 L1 v12 L2 v2 1 (2 ) d1 2 g d2 2g
Q
L1 , d1
5-7
L2, d2
Q 25 103 m3 /s
1
L1 4Q1 2 L 4Q 2 ( 2 ) (2 2 )( 2 ) 2 d1 d1 d2 d2
h1 h2
Q1 1
d12
A
d1
B
d2
C H h d3
4 d22 Q2 2 2 gh2 4 d32 Q3 3 2 g ( H h) 4 Q3 1.135 104 m3 / s h2 0.16m, h1 0.27 m h1 h2 0.11m
2 gh1
解:hv 1.5m 0.75H H 2m
H
Q
hv
d2
4
2 gH 0.00363m3 / s
5-17
已知x=4.8m,y=2m,H=3m 求:孔口的流速系数
解:
p0
x vct 1 2 y gt 2
H
g 9.8 vc x 4.8 7.513m / s 2y 2 2
Q
L1 , d1
2 Q2 30 50 2 0.04 Q1 (0.03 3) 4 5 0.05 0.1 0.1 24 0.14 2 2 Q2 Q1 4 18 0.05 Q2 4.61Q1
Q1 25 103 / 5.61
Q1 4.46 103 m3 /s Q2 20.54 103 m3 /s
5-20
D1 20cm, D2 10cm, h0 10cm, d 0.5cm, 0.62
D1 D
dh h0
T 172.04s
Th0 /2
1
θ
h
d
2
2g
[2 D h
2 1/2 2
4 2 5/2 h0 3/2 D2 h h ]h0 /2 3 5
Th0 /2
H
1 0.025
D2 200mm
hf 2
2 0.026
2 L2 v2 500 0.7962 2 0.026 D2 2 g 0.2 19.6
q 25L / s
Q 25L / s
2.10m
H h f 1 h f 2 7.4m
2 v2 ( 0.03m) 2g
解:1)按层流计算,对两池液面1-1,2-2列能量方程 1/2l,d
A
1/2l,d
l v2 h1 h f d 2g
2 2
1
1h
h1
64 l 42 Q 2 h1 Re d 2 d 4 2 g
Q l h1 4.1 44 2 0.055m
