九年级数学竞赛卷

合集下载

九年级数学竞赛综合训练题(1)(含解答)-

九年级数学竞赛综合训练题(1)（满分120分，考试时间120分）学校班级姓名一、选择题:（每小题5分，共30分）1．过点P （-1，3）作直线，使它与两坐标轴围成的三角形面积为5，这样的直线可以作（）条（A ）4 （B ）3 （C ）2 （D ）1 2．方程13++x x －y=0的整数解有（）组（A ）1 （B ）2 （C ）3 （D ）4 3．如图，若将图（a ）的正方形剪成四块，恰能拼成图(b)的矩形，设a=1，则这个正方形的面积为（）（A ）2537+ （B ）253+（C ）251+ （D ）21(+)24．关于x 的不等式组255332x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩只有5个整数解，则a 的取值范围是（）（A ）－6＜a ＜－211 （B ）－6≤a ＜－211 （C ）－6＜a ≤－211 （D ）－6≤a ≤－2115．已知四边形ABCD ，从下列条件：（1）AB ∥CD （2）BC ∥AD （3）AB ＝CD （4）BC ＝AD （5）∠A ＝∠C （6）∠B ＝∠D中任取其中两个，可以得出“四边形ABCD 是平行四边形”这一结论的情况有（）种（A ）4 （B ）9 （C ）13 （D ）15 6．已知x 、y 、z 都是实数，且x 2+y 2+z 2=1，则m=xy+yz+zx （）(A)只有最大值（B ）只有最小值（C ）既有最大值又有最小值（D ）既无最大值又无最小值二、填空题:（每小题5分，共30分）jab a b ⅠⅡⅢⅣⅣⅢⅡⅠ(b)(a)ba7．已知x=1313+-，y=1313-+, 则x 4+y 4等于 .8．甲、乙两商店某种铅笔标价都是1元，一天，让学生小王欲购这种铅笔，发现甲、乙两商店都让利优惠：甲店实行每买5枝送1枝（不足5枝不送）；乙店实行买4枝或4枝以上打8.5折，小王买了13枝这种铅笔，最少需要花元.9．若1≤p ≤20， 1≤q ≤10，且方程4x 2－px+q=0的两根均为奇数，则此方程的根为 . 10．在1、2、……，2003中有些正整数n ，使得x 2+x －n 能分解为两个整系数一次式的乘积，则这样的n 共有个.11．已知如图所示，∠MON=40°，P 为∠MON 内一点，A 为OM 上一点，B 为ON 上一点，则当△PAB 的周长取最小值时，∠APB 的度数为 .12．若关于x 的方程rx 2－(2r+7)x+r+7=0的根是正整数，则整数r 的值可以是 .三、解答题:（每小题15分，共60分）13．已知a 、b 、c满足方程组2848a b ab c +=⎧⎪⎨-+=⎪⎩, 试求方程bx 2+cx-a=0的根.PNMBOA14．已知两个二次函数y1 和y2，当x=a（a＞0）时，y1取得最大值5，且y2=25. 又y2的最小值为-2，y1+y2=x2+16x+13. 求a的值及二次函数y1、y2的解析式.15．如图所示，正方形ABCD的边长为1，点M、N分别在BC、CD上，使得△CMN的周长为2.求：（1）∠MAN的大小;（2）△MAN面积的最小值.ND CMAB16．如图所示，四边形ABCD 是矩形，甲、乙两人分别从A 、B 同时出发，沿矩形按逆时针方向前进，即按A →B →C →D →……顺序前进，已知甲的速度为每分钟65米，乙的速度为每分钟74米，问乙至少在跑第几圈时才有可能第一次追上甲？又乙至多在跑第几圈时一定能追上甲？请说明理由。

甘肃省天水市甘谷县第五中学2021-2022学年上学期九年级数学竞赛试卷+

2021-2022学年甘肃省天水市甘谷五中九年级（上）竞赛数学试卷一.选择题（本大题共5小题，每小题5分，共25分）1．（5分）最简二次根式可以合并，那么m＝（）A．2B．﹣2C．3D．﹣32．（5分）如图，在△ABC中，D，E分别是AB，AC边上的点，DE∥BC，若AD＝2，AB ＝3，DE＝4，则BC等于（）A．5B．6C．7D．83．（5分）已知实数a、b满足，则a+b等于（）A．﹣1B．2C．3D．54．（5分）已知因变量y是自变量x的函数，且因变量y的值随自变量x的增大而减小，对于任意两个自变量x1、x2，x1对应的函数值为y1，x2对应的函数值为y2．若x1＜x2，则（）A．y1＜y2B．y1＝y2C．y1＞y2D．不能确定5．（5分）定义符号函数则|x|＝（）A．Sgn|x|B．xSgnx C．D．二．填空题（本大题共5小题，每题5分，共25分）6．（5分）如图，在平行四边形ABCD中，AF交DC于E，交BC的延长线于F，若＝，AD＝4厘米，则CF＝厘米．7．（5分）写一个一元二次方程，使它的两个根x1＝1，x2＝2．．8．（5分）已知互不相等的实数a，b满足a2﹣﹣1009＝0，b2﹣b﹣1009＝0，则a2+b2的值为．9．（5分）已知P是等边△ABC内的任意一点，PE⊥AB，PF⊥AC，PG⊥BC，若等边三角形的边长为4，则PE+PF+PG的值为．10．（5分）已知函数y＝的值随x的增大而增大，则a的取值范围为．三.解答题（本大题共5小题，每小题10分，共50分）11．（10分）（1）解方程：（x﹣2）（2x+1）＝1+2x．（2）先化简，再求值：，其中a＝．12．（10分）如图，在△ABC中，AB＝AC，AD为BC边上的中线，DE⊥AB于点E．（1）求证：△BDE∽△CAD．（2）若AB＝13，BC＝10，求线段DE的长．13．（10分）计算：+．14．（10分）在△ABC中，已知AD是△ABC的角平分线，求证：＝．15．（10分）如图所示，已知在四边形ABCD中，AB∥CD且AB＜CD，E为AC的中点，F为BD的中点，求证：EF＝（AB﹣CD）．2021-2022学年甘肃省天水市甘谷五中九年级（上）竞赛数学试卷参考答案与试题解析一.选择题（本大题共5小题，每小题5分，共25分）1．（5分）最简二次根式可以合并，那么m＝（）A．2B．﹣2C．3D．﹣3【分析】根据能合并同类二次根式得出4m﹣1＝2m+3，再求出方程的解即可．【解答】解：∵最简二次根式可以合并，∴4m﹣1＝2m+3，解得：m＝2，故选：A．2．（5分）如图，在△ABC中，D，E分别是AB，AC边上的点，DE∥BC，若AD＝2，AB ＝3，DE＝4，则BC等于（）A．5B．6C．7D．8【分析】由平行线得出△ADE∽△ABC，得出对应边成比例＝，即可得出结果．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∴＝，即＝，解得：BC＝6，故选：B．3．（5分）已知实数a、b满足，则a+b等于（）A．﹣1B．2C．3D．5【分析】根据二次根式有意义的条件得到a≤1，根据非负数的性质分别求出a、b，根据有理数的加法法则计算，得到答案．【解答】解：由题意得，1﹣a≥0，解得，a≤1，则﹣a+3+|b+2|+＝3﹣a，整理得|b+2|+＝0，则b+2＝0，1﹣a＝0，解得，b＝﹣2，a＝1，则a+b＝﹣1，故选：A．4．（5分）已知因变量y是自变量x的函数，且因变量y的值随自变量x的增大而减小，对于任意两个自变量x1、x2，x1对应的函数值为y1，x2对应的函数值为y2．若x1＜x2，则（）A．y1＜y2B．y1＝y2C．y1＞y2D．不能确定【分析】由因变量y的值随自变量x的增大而减小，再结合x1＜x2，即可求解．【解答】解：∵因变量y的值随自变量x的增大而减小，x1＜x2，∴y1＞y2，故选：C．5．（5分）定义符号函数则|x|＝（）A．Sgn|x|B．xSgnx C．D．【分析】根据绝对值的性质即可解答．【解答】解：因为|x|＝，Sgnx＝，所以|x|＝xSgnx．故选：B．二．填空题（本大题共5小题，每题5分，共25分）6．（5分）如图，在平行四边形ABCD中，AF交DC于E，交BC的延长线于F，若＝，AD＝4厘米，则CF＝2厘米．【分析】由平行四边形中CD∥AB，则∠FEC＝∠FAB，∠FCE＝∠FBA，可知△FEC∽△FAB，从而得到相似比FE：AE＝1：2，又由AD∥BC，所以∠EAD＝∠ECF，∠EDA ＝∠ECF，可知△ADE∽△FCE，从而得到CF：AD＝FE：EA，所以可以得到CF＝2．【解答】解：∵平行四边形ABCD∴CD∥AB∴∠FEC＝∠FAB，∠FCE＝∠FBA∴△FEC∽△FAB∴EC：AB＝FE：AF＝1：3∵AF＝EF+AE∴FE：AE＝1：2∵AD∥BC∴∠EAD＝∠ECF，∠EDA＝∠ECF∴△ADE∽△FCE∴CF：AD＝FE：EA∵AD＝4∴CF＝27．（5分）写一个一元二次方程，使它的两个根x1＝1，x2＝2．x2﹣3x+2＝0（答案不唯一）．【分析】此题是一道开放型的题目，答案不唯一，根据所给两根的值，求出x1+x2和x1•x2的值，可令a＝1，进而可求b、c的值．【解答】解：∵x1＝1，x2＝2，∴x1+x2＝3，x1•x2＝2，∴满足要求的方程可以是x2﹣3x+2＝0，故答案为：x2﹣3x+2＝0（答案不唯一）．8．（5分）已知互不相等的实数a，b满足a2﹣﹣1009＝0，b2﹣b﹣1009＝0，则a2+b2的值为2021．【分析】根据根与系数的关系即可求出答案．【解答】解：由题意可知：a、b是方程x2﹣x﹣1009＝0的两根，∴a+b＝，ab＝﹣1009，∴a2+b2＝（a+b）2﹣2ab＝（）2﹣2×（﹣1009）＝2021，故答案为：2021．9．（5分）已知P是等边△ABC内的任意一点，PE⊥AB，PF⊥AC，PG⊥BC，若等边三角形的边长为4，则PE+PF+PG的值为2．【分析】过A作AM垂直于BC，由三角形ABC为等边三角形，利用三线合一得到M为BC的中点，由等边三角形的边长求出BM的长，在直角三角形ABM中，利用勾股定理求出AM的长，进而求出三角形ABC的面积，而三角形ABC的面积＝三角形ABP的面积+三角形ACP的面积+三角形BCP的面积，列出关系式，整理后即可求出所求式子的值．【解答】解：过A作AM⊥BC于M，连接AP，BP，CP，由△ABC为等边三角形，得到M为BC的中点，∵等边三角形的边长为4，∴AB＝AC＝BC＝4，BM＝2，在Rt△ABM中，利用勾股定理得：AM＝，∵S△ABC＝S△ABP+S△ACP+S△BCP，∴BC•AM＝AB•PE+AC•PF+BC•PG，即，则PE+PF+PD＝2．故答案为：2．10．（5分）已知函数y＝的值随x的增大而增大，则a的取值范围为1＜a≤．【分析】根据y的值随x的增大而增大，得，解得即可求出a的取值范围．【解答】解：由已知得，解得：1＜a≤．故答案为：1＜a≤．三.解答题（本大题共5小题，每小题10分，共50分）11．（10分）（1）解方程：（x﹣2）（2x+1）＝1+2x．（2）先化简，再求值：，其中a＝．【分析】（1）先移项得到（x﹣2）（2x+1）﹣（2x+1）＝0，然后利用因式分解法解方程；（2）先把括号内通分，再把除法运算化为乘法运算，则约分得到原式＝，然后把a ＝+1代入计算即可．【解答】解：（1）（x﹣2）（2x+1）＝1+2x，（x﹣2）（2x+1）﹣（2x+1）＝0，（2x+1）（x﹣2﹣1）＝0，2x+1＝0或x﹣2﹣1＝0，所以x1＝﹣，x2＝3；（2）原式＝•＝•＝，当a＝+1时，原式＝＝＝．12．（10分）如图，在△ABC中，AB＝AC，AD为BC边上的中线，DE⊥AB于点E．（1）求证：△BDE∽△CAD．（2）若AB＝13，BC＝10，求线段DE的长．【分析】（1）想办法证明∠B＝∠C，∠DEB＝∠ADC＝90°即可解决问题；（2）利用面积法：•AD•BD＝•AB•DE求解即可；【解答】解：（1）∵AB＝AC，BD＝CD，∴AD⊥BC，∠B＝∠C，∵DE⊥AB，∴∠DEB＝∠ADC，∴△BDE∽△CAD．（2）∵AB＝AC，BD＝CD，∴AD⊥BC，在Rt△ADB中，AD＝＝＝12，∵•AD•BD＝•AB•DE，∴DE＝．13．（10分）计算：+．【分析】首先求得式子的平方，然后求算术平方根即可求解．【解答】解：（+）2＝2++2﹣+2＝6，则原式＝．14．（10分）在△ABC中，已知AD是△ABC的角平分线，求证：＝．【分析】先作辅助线CE∥AD，交BA的延长线于点E，然后根据平行线的性质和平行线分线段成比例，可以证明结论成立．【解答】证明：作CE∥AD，交BA的延长线于点E，如图所示，∵AD∥EC，∴∠1＝∠4，∠2＝∠3，∵AD平分BAC，∴∠1＝∠2，∴∠3＝∠4，∴AE＝AC，∵AD∥EC，∴，∴，∴＝．15．（10分）如图所示，已知在四边形ABCD中，AB∥CD且AB＜CD，E为AC的中点，F为BD的中点，求证：EF＝（AB﹣CD）．【分析】延长CF交AB于H，根据相似三角形的判断定理证明△DFC∽△BFH，得到CF＝FH，CD＝BH，根据三角形中位线定理得到EF＝AH，证明结论．【解答】证明：延长CF交AB于H，∵AB∥CD，∴△DFC∽△BFH，又F是BD的中点，∴CF＝FH，CD＝BH，∴AH＝AB﹣CD，∵E是AC的中点，F是CH的中点，∴EF＝AH，∴EF＝（AB﹣CD）．。

人教版九年级上册数学竞赛专题：平行线分线段成比例(含答案)

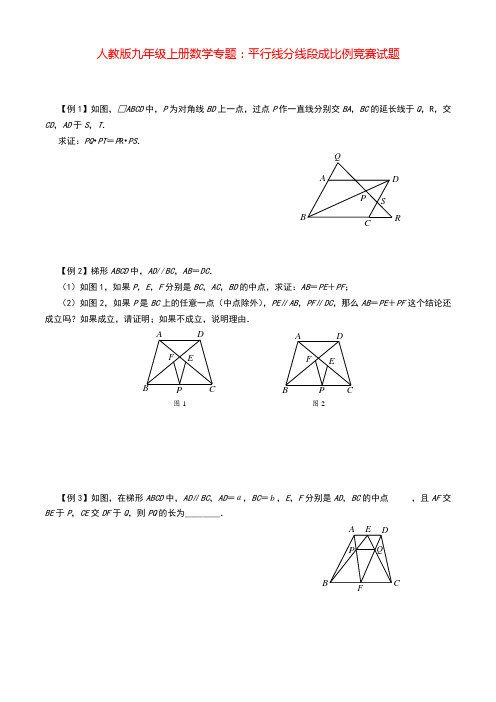
人教版九年级上册数学专题：平行线分线段成比例竞赛试题【例1】如图，□ABCD 中，P 为对角线BD 上一点，过点P 作一直线分别交BA ，BC 的延长线于Q ，R ，交CD ，AD 于S ，T ．求证：PQ •PT ＝P R •PS ．【例2】梯形ABCD 中，AD //BC ，AB ＝DC ．（1）如图1，如果P ，E ，F 分别是BC ，AC ，BD 的中点，求证：AB ＝PE ＋PF ；（2）如图2，如果P 是BC 上的任意一点（中点除外），PE ∥AB ，PF ∥DC ，那么AB ＝PE ＋PF 这个结论还成立吗？如果成立，请证明；如果不成立，说明理由．【例3】如图，在梯形ABCD 中，AD ∥BC ，AD ＝a ，BC ＝b ，E ，F 分别是AD ，BC 的中点，且AF 交BE 于P ，CE 交DF 于Q ，则PQ 的长为＿＿＿＿．QA BCDEFPA BCD EF P图2A BCD EF P图1QARBCD SP【例4】如图，在△ABC中，D，E是BC的三等分点，M是AC的中点，BM交AD，AE于G，H，则BG︰GH：HM等于（）A．3︰2︰1 B．4︰2︰1 C．5︰4︰3 D．5︰3︰2【例5】如图，已知AB∥CD，AD∥CE，F，G分别是AC和FD的中点，过G的直线依次交AB，AD，CD，CE于点M，N，P，Q．求证：MN＋PQ＝2PN．【例6】已知：△ABC是任意三角形．（1）如图1，点M，P，N分别是边AB，BC，CA的中点，求证：∠MPN＝∠A；（2）如图2，点M，N分别在边AB，AC上，且AMAB＝13，ANAC＝13，点P1，P2是边BC的三等分点，你认为∠MP1N＋∠MP2N＝∠A是否正确？请说明你的理由；能力训练AB CM NP图1AB CM N1P2P图2AM NB C1P2P2009P图3QA BC DEFGMNPAB CD EG HMA 卷1．如图，工地上竖立着两根电线杆AB ，CD ，它们相距15cm ，分别自两杆上高出地面4m ，6m 的A ，C 处，向两侧地面上的E ，D 和B ，F 点处，用钢丝绳拉紧，以固定电线杆，那么钢丝绳AD 与BC 的交点P 离地面的高度为＿＿＿＿m ．2．如图，□ABCD 的对角线交于O 点，过O 任作一直线与CD ，BC 的延长线分别交于F ，E 点．设BC ＝a ，CD ＝b ，CF ＝c ，则CE ＝＿＿＿＿．3．如图，D ，F 分别是△ABC 边AB ，AC 上的点，且AD ︰DB ＝CF ︰FA ＝2︰3，连结DF 交BC 边的延长线于点E ，那么EF ︰FD ＝＿＿＿＿．4．如图，设AF ＝10，FB ＝12，BD ＝14，DC ＝6，CE ＝9，EA ＝7，且KL ∥DF ，LM ∥FE ，MN ∥ED ，则EF ︰FD ＝＿＿＿＿．5．如图，AB ∥EF ∥CD ，已知AB ＝20，CD ＝80，那么EF 的值是（） A ．10B ．12C ．16D ．186．如图，CE ，CF 分别平分∠ACB ，∠ACD ，AE ∥CF ，AF ∥CE ，直线EF 分别交AB ，AC 于点M ，N ．若BC ＝a ，AC ＝b ，AB ＝c ，且c ＞a ＞b ，则EM 的长为（）A ．2c a- B ．2a b- C ．2c b- D ．2a b c+- 7．如图，在□ABCD 的边AD 延长线上取一点F ，BF 分别交AC 与CD 于E ，G ．若EF ＝32，GF ＝24，则BE 等于（）A ．4B ．8C ．10D ．12E ．168．如图，在梯形ABCD 中，AB ∥CD ，AB ＝3CD ，E 是对角线AC 的中点，直线BE 交AD 于点F ，则AF ︰FD 的值是（）A ．2B ．53C ．32D ．1ABCD EFG第7题 ABCDEF第8题 ABCD E F M NP第9题A BCDE F第5题 ABC D E F L K MN第4题ABDEFM 第6题 ABCDEF O第2题ABCD EF 第3题QABCD EF 第1题9．如图，P是梯形ABCD的中位线MN所在直线上的任意一点，直线AP，BP分别交直线CD于E，F．求证：MNNP＝1()2AE BFEP FP+．10．如图，在四边形ABCD中，AC与BD相交于O，直线l平行于BD且与AB，DC，BC，AD及AC的延长线分别交于点M，N，R，S和P．求证：PM·PN＝P R·PS．11．如图，AB⊥BC，CD⊥BC，B，D是垂足，AD和BC交于E，EF⊥BD于F．我们可以证明：11 AB CD+＝1EF成立（不要求证出）．以下请回答：若将图中垂直改为AB∥CD∥EF，那么，（1）11AB CD+＝1EF还成立吗？如果成立，请给出证明；如果不成立，请说明理由．（2）请找出S△ABD，S△BED和S△BDC的关系式，并给出证明．12．在Rt△ABC中，∠BAC＝90°，AD平分∠BAC，过D点的直线PQ交边AC于点P，交边AB的延长线于点Q．（1）如图1，当PQ⊥AC时，求证：11AQ AP+；（2）如图2，当PQ不与AD垂直时，（1）的结论还成立吗？证明你的结论；（3）如图3，若∠BAC＝60°，其它条件不变，且11AQ AP+＝nAD，则n＝＿＿＿＿（直接写出结果）AQ B CDP图1AQB CDP图2AQB CDP图3ABCDEF第11题SARBCDM NOPl第10题B 卷1．设K ＝a b c c +-＝a b c b -+＝a b ca-++，则K ＝＿＿＿＿． 2．如图，AD ∥EF ∥BC ，AD ＝15，BC ＝21，2AE ＝EB ，则EF ＝＿＿＿＿．3．如图，在△ABC 中，AM 与BN 相交于D ，BM ＝3MC ，AD ＝DM ，则BD ︰DN ＝＿＿＿＿．4．如图，ABCD 是正方形，E ，F 是AB ，BC 的中点，连结EC 交DB ，交DF 于G ，H ，则EG ︰GH ︰HC ＝＿＿＿＿．5．如图，在正△ABC 的边BC ，CA 上分别有点E ，F ，且满足BE ＝CF ＝a ，EC ＝FA ＝b （a ＞b ），当BF 平分AE 时，则ab 的值为（） ABCD6．如图，△ABC 中，AD 是BC 边上的中线，F 是AD 上的一点，且AF ︰FD ＝1︰5，连结CF 并延长交AB 于E ，则AE ︰EB 等于（）A ．1︰10B ．1︰9C ．1︰8D ．1︰77．如图，PQ ∥AB ，PQ ＝6，BP ＝4，AB ＝8，则PC 等于（） A ．4B ．8C ．12D ．168．如图，EF ∥BC ，FD ∥AB ，BD ＝35BC ，则BE ︰EA 等于（）A ．3︰5B ．2︰5C ．2︰3D ．3︰29．（1）阅读下列材料，补全证明过程．已知，如图，矩形ABCD 中，AC ，BD 相交于点O ，OE ⊥BC 于E ，连结DE 交OC 于点F ，作FG ⊥BC 于G ．求证：点G 是线段BC 的一个三等分点．（2）请你依照上面的画法，在原图上画出BC 的一个四等分点．（要求：保留画图痕迹，不写画法及证明过程）ABCDE F第6题QABCP第7题AB CDEF 第8题A BCD E F 第2题ABD M N第3题ABCDEFGH第4题A BCEFG第5题10．如图，已知在□ABCD 中，E 为AB 边的中点，AF ＝12FD ，FE 与AC 相交于G ．求证：AG ＝15AC ．11．如图，梯形ABCD 中，AD ∥BC ，EF 经过梯形对角线的交点O ，且EF ∥AD ．（1）求证：OE ＝OF ；（2）求OE AD ＋OEBC的值；（3）求证：1AD ＋1BC ＝2EF．12．如图，四边形ABCD 是梯形，点E 是上底边AD 上的一点，CE 的延长线与BC 的延长线交于点F ，过点E 作BA 的平行线交CD 的延长线于点M ，MB 与AD 交于点N ．求证：∠AFN ＝∠DME ．QABCDEF M NP ABCDE FGO第9题ABCDEG第10题ABCD EFO第11题参考答案例1 提示：PQ PB PRPS PD PT==例2 （1）略（2）结论仍然成立提示：,PF BP PE CPCD BC AB BC==. 例3aba b+ 提示：由AP DQ a PF QF b ==,推得PQ ∥AD 。

全国各地初中(九年级)数学竞赛《不等式》真题大全 (附答案)

全国初中（九年级））数学竞赛专题大全竞赛专题5 不等式一、单选题1．（2021·全国·九年级竞赛）若满足不等式871513n n k <<+的整数k 只有一个，则正整数n 的最大值为（）． A ．100B ．112C ．120D ．1502．（2021·全国·九年级竞赛）27234x x x ----有意义，则x 的取值范围是（）A ．4x >B ．7x ≥5x ≠C ．4x >且5x ≠D ．45x <<3．（2021·全国·九年级竞赛）某校初一运动队为了备战校运动会需要购置一批运动鞋．已知该运动队有20名同学，统计表如下表，由于不小心弄脏了统计表，下表中阴影部分的两个数据看不到．鞋码 38 394041 42 人数 532下列说法正确的是（）．A ．这组鞋码数据中的中位数是40，众数是39 B ．这组鞋码数据中的中位数与众数一定相等 C ．这组鞋码数据中的平均数p 满足3940p ≤≤ D ．以上说法都不对4．（2021·全国·九年级竞赛）如果不等式组9080x a x b -≥⎧⎨-<⎩的整数解仅为1，2，3，那么适合这个不等式组的有序对(),a b 共有（）． A ．17个B ．64个C ．72个D ．81个5．（2021·全国·九年级竞赛）若不等式054ax ≤+≤的整数解是1，2，3，4，则a 的取值范围是（）． A ．54a -B ．1a <-C ．514a -≤<-D ．54a -6．（2021·全国·九年级竞赛）2009x y 且0x y <<，则满足此等式的不同整数对(,)x y 有（）对． A ．1B ．2C ．3D ．47．（2021·全国·九年级竞赛）有两个四位数，它们的差是534，它们平方数的末四位数相同．则较大的四位数有（）种可能．A ．1B ．2C ．3D ．48．（2021·全国·九年级竞赛）一个正方形纸片，用剪刀沿一条不过顶点的直线将其剪成两部分，拿出其中一部分，再沿一条不过任何顶点的直线将其剪成两部分，又从得到的3部分中拿出其中之一，还是沿一条不过任何顶点的直线将其剪成两部分，……，如此下去，最后得到34个六十二边形和一些多边形纸片，则至少要剪的刀数是（）． A ．2004B ．2005C ．2006D ．20079．（2021·全国·九年级竞赛）若正数a ，b ，c 满足不等式1126352351124c a b c a b c a b a c b ⎧<+<⎪⎪⎪<+<⎨⎪⎪<+<⎪⎩则a ，b ，c 的大小关系是（）A ．a b c <<B ．b c a <<C ．c a b <<D ．不确定10．（2021·全国·九年级竞赛）设114,,11(1)r a b c r r r r r r r ≥=-==++++的是（）． A ．a b c >> B ．b c a >> C ．c a b >> D ．c b a >>二、填空题11．（2021·全国·九年级竞赛）设a ，b 为正整数，且2537a b <<则b 取最小值时a b +=_____ 12．（2021·全国·九年级竞赛）已知实数x ，y 满足234x y -=且0,1x y ≥≤，则x y -的最大值是______，最小值是_______．13．（2021·全国·九年级竞赛）已知01a ≤≤，且满足122918303030a a a ⎡⎤⎡⎤⎡⎤++++++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ （[]x 表示不超过x 的最大整数），则[]10a 的值等于_______．14．（2021·全国·九年级竞赛）若化简2269x x x --+25x -，则满足条件是x 的取值围是_________．15．（2021·全国·九年级竞赛）[]x 表示不超过x 的最大整数（例如[]3.23=）．已知正整数n 小于2006，且362n n n⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦，则这样的n 有___________个． 16．（2021·全国·九年级竞赛）不等式2242x ax a +<的解是___________．17．（2021·全国·九年级竞赛）已知正整数m 和n 有大于1的最大公约数，并且满足3371m n +=，则mn =________．18．（2021·全国·九年级竞赛）长沙市某中学100名学生向某“希望学校”捐书1000本，其中任意10人捐书总数不超过190本，那么捐书最多的某同学最多能捐书_________本．19．（2021·全国·九年级竞赛）已知由小到大的10个正整数1210,,,a a a 的和是2000，那么5a 的最大值是_________，这时10a 的值应是_________．三、解答题20．（2021·全国·九年级竞赛）某宾馆底楼客房比二楼客房少5间，某旅游团有48人．若全部安排底楼，每间房间住4人，房间不够；每间住5人，则有房间没有住满5人．又若全部安排住2楼，每间住3人，房间不够；每间住4人，则有房间没有住满4人．问该宾馆底楼有多少间客房？21．（2021·全国·九年级竞赛）一座大楼有4部电梯，如果每部电梯可停靠三层（不一定连续三层，也不一定停最低层），对大楼中的任意两层，至少有一部电梯可在这两层停靠．问：这座大楼最多有几层22．（2021·全国·九年级竞赛）解方程22424x x x x ⎡⎤+-=⎢⎥⎣⎦．23．（2021·全国·九年级竞赛）证明：对任意实数x 及任意正整数n 有[][]121n x x x x nx n n n -⎡⎤⎡⎤⎡⎤+++++++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦．24．（2021·全国·九年级竞赛）已知01,01,01a b c <<<<<<，证明： ()()()1,1,1a b b c c a ---中至少有一个不大于14． 25．（2021·全国·九年级竞赛）设正数a ，b ，c ，x ，y ，x 满足a x b y c z k +=+=+=，证明；2ay bz cx k ++<． 26．（2021·全国·九年级竞赛）已知实数a ，b ，c 满足0,10a b c ac ++==，证明1110a b c++<．27．（2021·全国·九年级竞赛）下图是某单位职工年龄（取正整数）的频率分布图（每组可含最低年龄但不含最高值），根据图中提供的信息回答下列问题：（1）该厂共有多少职工?（2）年龄不小于38但小于44岁的职工人数占职工总人数的百分比是多少? （3）如果42岁的职工有4人，那么42岁以上的职工有多少人?（4）有人估计该单位职工的平均年龄在39岁与42岁之间，问这个估计正确吗?28．（2021·全国·九年级竞赛）某人到花店买花，他只有24元，打算买6支玫瑰和3支百合，但发现钱不够，只买了4支玫瑰和5支百合，这样还剩下2元多钱．请你算一算：2支玫瑰和3支百合哪个价格高？29．（2021·全国·九年级竞赛）1132x x -+ 30．（2021·全国·九年级竞赛）解不等式：2243414143x x x x x x x x +-->-++-- 31．（2021·全国·九年级竞赛）求满足下列条件的最小正整数n ，使得对这样的n ，有唯一的正整数k ，满足871513n n k <<+． 32．（2021·全国·九年级竞赛）解不等式： 2256154x x x x -+≤++．33．（2021·全国·九年级竞赛）解不等式21311x x x x -+>-+． 34．（2021·全国·九年级竞赛）如果二次不等式：28210ax ax ++<的解是71x -≤<-，求a 的值． 35．（2021·全国·九年级竞赛）某校参加全国数，理，化，计算机比赛的人数分别是20，16，x ，20人．已知这组数据的中位数和平均数相等，求这组数据的中位数．36．（2021·全国·九年级竞赛）某个学生参加军训，进行打靶训练，必须射击10次，在第6次、第7次，第8次，第9次射击中，分别得到9.0环、8.4环、8.1环、9.3环，他的前9次射击所得平均环数高于前5次射击所得平均环数，如果要使10次射击的平均环数超过8.8环，那么他第10次射击至少要得多少环?（每次射击环数精确到0.1环）37．（2021·全国·九年级竞赛）今有浓度为5%,8%,9%的甲、乙、丙三种盐水分别为60g,60g,47g ，现要配制成浓度为7%的盐水100g ．间甲盐水最多可用多少克?最少可用多少克?38．（2021·全国·九年级竞赛）求证：对任意的实数x ，y ，[2][2][][][]x y x x y y ++++．39．（2021·全国·九年级竞赛）某个学生参加军训，进行打靶训练，必须射击10次，在第6、第7、第8、第9次射击中，分别得了9.0环，8.4环，8.1环，9.3环，他的前9次射击所得环数的平均值高于前5次射击所得的平均环数．如果他要使10次射击的平均环数超过8.8环，那么他在第10次射击中最少要得多少环？（每次射击所得环数都精确到0.1环）40．（2021·全国·九年级竞赛）已知x ，y ，z 都是正数，证明：32()()()()()()x y x z y z y x z x z y +≤++++++．41．（2021·全国·九年级竞赛）某饮料厂生产A 、B 两种矿泉水，每天生产B 种矿泉水比A 种矿泉水多10吨，A 种矿泉水比B 种矿泉水每天多获利润2000元，其中A 种矿泉水每吨可获利润200元，B 种矿泉水每吨可获利润100元．（1）问：该厂每天生产A 种，B 种矿泉水各多少吨？（2）由于江水受到污染，市政府要求该厂每天必须多生产10吨矿泉水，该厂决定响应市政府的号召，在每天的利润不超过原利润的情况下不少于8000元，该厂每天生产A 种矿泉水最多多少吨？42．（2021·全国·九年级竞赛）要使不等式2320x x -+≤①与不等式2(1)(3)20m x m x -+--<②无公共解，求m 的取值范围．43．（2021·全国·九年级竞赛）已知三个非负数a ，b ，c ，满足325a b c ++=和231a b c +-=．若37m a b c =+-，求m 的最大值和最小值．44．（2021·全国·九年级竞赛）某班学生到公园进行活动，划船的有22人，乘电动车的有20人，乘过山车的有19人，既划船又乘电动车的有9人，既乘电动车又乘过山车的有6人，既划船又乘过山车的有8人，并且有4人没有参加上述3项活动中任何一项活动，问这个班学生人数的可能值是多少？竞赛专题5 不等式答案解析（竞赛真题强化训练）一、单选题1．（2021·全国·九年级竞赛）若满足不等式871513n n k <<+的整数k 只有一个，则正整数n 的最大值为（）． A ．100 B ．112C ．120D ．150【答案】B 【解析】【分析】【详解】由已知不等式得13156767,,787878n k k n nk n n +<<<<<<．因由已知条件，67n 与78n 之间只有唯一一个整数k ，所以76287n n-≤解得112n ≤．当112n =时，9698k ≤≤，存在唯一97k =，所以n 的最大值为112．故应选B ．2．（2021·全国·九年级竞赛）27234x x x ----有意义，则x 的取值范围是（）A ．4x >B ．7x ≥5x ≠C ．4x >且5x ≠D ．45x <<【答案】C 【解析】【分析】【详解】依题意得27077321544x x x x x x x x ⎧⎧-≥≤≥⎪⎪-≠⇒≠≠⎨⎨⎪⎪>>⎩⎩或且，4x ⇒>且5x ≠．故选C ．3．（2021·全国·九年级竞赛）某校初一运动队为了备战校运动会需要购置一批运动鞋．已知该运动队有20名同学，统计表如下表，由于不小心弄脏了统计表，下表中阴影部分的两个数据看不到．鞋码 38 39 40 41 42 人数 532下列说法正确的是（）．A ．这组鞋码数据中的中位数是40，众数是39 B ．这组鞋码数据中的中位数与众数一定相等 C ．这组鞋码数据中的平均数p 满足3940p ≤≤ D ．以上说法都不对【答案】C 【解析】【分析】【详解】设穿39码和40码的学生分别有x 人和y 人，则()2052310x y +=-++=．（1）若y x ≥，即穿40码的人数最多时，中位数和众数都等于40，故选A 错；（2）若5x y ==，则中位数1(3940)39.52=+=，众数为39和40，中位数不等于众数，故选B 错；（3）平均数[]13853940(10)41342239.75220xp x x =⨯++⨯-+⨯+⨯=-，且010x ≤≤，于是39.2539.75p <≤，满足3940p ≤≤，故选C 正确．所以应选C ．4．（2021·全国·九年级竞赛）如果不等式组9080x a x b -≥⎧⎨-<⎩的整数解仅为1，2，3，那么适合这个不等式组的有序对(),a b 共有（）． A ．17个 B ．64个 C ．72个 D ．81个【答案】C 【解析】【分析】【详解】解因98ax b x ⎧≥⎪⎪⎨⎪<⎪⎩中x 的整数值仅为1，2，3，所以01,34,98a b <≤<≤即9a <≤， 2432b <≤，故a 可取1，2，…，9这9个值，b 可取25，26，…．32这8个值，所以有序对(),a b 有8972⨯=个．故选C ．5．（2021·全国·九年级竞赛）若不等式054ax ≤+≤的整数解是1，2，3，4，则a 的取值范围是（）． A ．54a -B ．1a <-C ．514a -≤<-D ．54a -【答案】C 【解析】【分析】【详解】解由054ax ≤+≤得51ax -≤≤-，且已知0x >，所以0a <，15ax a ≤-≤-．又不等式054ax ≤+≤的整数解是1，2，3，4，所以101a <-≤，且545a≤-<解得 1a ≤-且5114a -<-≤，故514a -≤<-，所以选C ．6．（2021·全国·九年级竞赛）2009x y 且0x y <<，则满足此等式的不同整数对(,)x y 有（）对． A ．1 B ．2 C ．3 D ．4【答案】C 【解析】【分析】【详解】选C ．理由：由20094941=⨯，得200941= 又0x y <<2009200941641241541341441===20094114761641025369656===因此，满足条件的整数对(,)x y 为(41,1476),(164,1025),(369,656)．共有3对．7．（2021·全国·九年级竞赛）有两个四位数，它们的差是534，它们平方数的末四位数相同．则较大的四位数有（）种可能． A ．1 B ．2C ．3D ．4【答案】C 【解析】【分析】【详解】理由：设较大的四位数为x ，较小的四位数为y ，则534x y -=， ① 且22x y -能被10000整除．而22()()x y x y x y -=+-2672()x y =⨯+，则x y +能被5000整除．令()5000x y k k ++=∈N ． ②由式①②解得2500267,2500267.x k y k =+⎧⎨=-⎩ 考虑到x ，y 均为四位数，于是，100025002679999,100025002679999,k k ≤+≤⎧⎨≤-≤⎩解得126755832500625k ≤≤． k 可取1，2或3．从而，x 可取的值有3个：2767，5267，7767．8．（2021·全国·九年级竞赛）一个正方形纸片，用剪刀沿一条不过顶点的直线将其剪成两部分，拿出其中一部分，再沿一条不过任何顶点的直线将其剪成两部分，又从得到的3部分中拿出其中之一，还是沿一条不过任何顶点的直线将其剪成两部分，……，如此下去，最后得到34个六十二边形和一些多边形纸片，则至少要剪的刀数是（）． A ．2004 B ．2005C ．2006D ．2007【答案】B 【解析】【分析】【详解】解（算两次方法）依题意，用剪刀沿不过顶点的直线剪成两部分时，所得各张多边形（包括三角形）的纸片的内角和增加了2180360⨯︒=︒，剪过k 刀后，可得(1)+k 个多边形，这些多边形的内角总和为360360(1)360k k ︒+⨯︒=+⨯︒．另一方面，因为这1k +个多边形中有34个为六十二边形，它们的内角总和为34(622)1802040180⨯-⨯=⨯︒︒，余下的多边形（包括三角形）有13433k k +-=-个，其内角总和至少为(33)180k -⨯︒，于是(1)3602040180(33)180k k +⨯︒≥⨯︒+-⨯︒，解得2005k ≥．其次，我们按如下方式剪2005刀时，可得到符合条件的结论．先从正方形剪下1个三角形和1个五边形，再将五边形剪成1个三角形和1个六边形，…，如此下去，剪了58刀后，得到1个六十二边形和58个三角形，取出其中33个三角形，每个各剪一刀，又可得到33个四边形和33个三角形，对这33个四边形，按上述方法各剪58刀，便得到33个六十二边形和3358⨯个三角形，于是共剪了583333582005++⨯=（刀），故选B ．9．（2021·全国·九年级竞赛）若正数a ，b ，c 满足不等式1126352351124c a b c a b c a b a c b ⎧<+<⎪⎪⎪<+<⎨⎪⎪<+<⎪⎩则a ，b ，c 的大小关系是（）A ．a b c <<B ．b c a <<C ．c a b <<D ．不确定【答案】B 【解析】【分析】【详解】解由已知条件及加法的单调性得1126352251124c c a b c c c a a a b c a a b b a b c b b ⎧+<++<+⎪⎪⎪+<++<+⎨⎪⎪+<++<+⎪⎩，即1736582371524c a b c c a a b c a b a b c b ⎧<++<⎪⎪⎪<++<⎨⎪⎪<++<⎪⎩①②③由①，②得17816176366c a b c a a a <++<=< （传递性），所以a c >．由①，③得7673222b a bc c c c <++<=< （传递性），所以b c <．可见，a ，b ，c 的大小关系是a c b >>，故选B ． 10．（2021·全国·九年级竞赛）设114,,11(1)r a b c r r r r r r r ≥=-==++++的是（）． A ．a b c >> B ．b c a >>C ．c a b >>D ．c b a >>【答案】D 【解析】【分析】【详解】解：因111221r r r ≥<+=+，故 ()(111a b r r r r r r =+<=+++， 1111r r r r c b r r r x +-+->=+⋅+．所以c b a >>．故选：D ．二、填空题11．（2021·全国·九年级竞赛）设a ，b 为正整数，且2537a b <<则b 取最小值时a b +=_____ 【答案】17 【解析】【分析】【详解】由已知条件得32,57a b b a >>．令32,57A a b B b a =-=-，则A ，B 均为正整数，解出52,737310a A B b A B =+=+≥+=．当1,1A B ==时等号成立，故b 的最小值为10，这时527a =+=，17a b +=．故应填17．12．（2021·全国·九年级竞赛）已知实数x ，y 满足234x y -=且0,1x y ≥≤，则x y -的最大值是______，最小值是_______．【答案】 4352【解析】【分析】【详解】 434370222y x ++≤=≤=．又243x y -=所以24433x x x y x -+-=-=．故当0x =时，x y -取最小值43；当72x =时，x y -取最大值175(4)322+=所以应填45,32．13．（2021·全国·九年级竞赛）已知01a ≤≤，且满足122918303030a a a ⎡⎤⎡⎤⎡⎤++++++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ （[]x 表示不超过x 的最大整数），则[]10a 的值等于_______．【答案】6 【解析】【分析】【详解】因122902303030a a a <+<+<<+<，所以1229,,,303030a a a ⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦每一个等于0或1．由题设知其中恰有18个等于1，所以12111213290,1303030303030a a a a a a ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=+==+=+=+==+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦于是111201,123030a a <+<≤+<，解得1183019,61063a a ≤<≤<所以[]106a =．故应填6． 14．（2021·全国·九年级竞赛）若化简2269x x x --+25x -，则满足条件是x 的取值围是_________．【答案】23x ≤≤ 【解析】【分析】【详解】由()2226923232(3)25x x x x x x x x x x --+=--=---=---=-，得2030x x -≥⎧⎨-≤⎩即23x ≤≤．故填23x ≤≤．15．（2021·全国·九年级竞赛）[]x 表示不超过x 的最大整数（例如[]3.23=）．已知正整数n 小于2006，且362n n n⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦，则这样的n 有___________个．【答案】334 【解析】【分析】【详解】解设[]6n m =则(01)6na a m =≤+<从而66n m a =+．当102a ≤<时， 22(021)3n m a a =+≤<，故23n m ⎡⎤=⎢⎥⎣⎦．于是由362n n n⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦得662332m a m m m a ++==+，从而0a =．此时(6204)06133n m m =<≤≤．当112a ≤<，223n m a =+由212222m m a m +≤+<+得213n m ⎡⎤=+⎢⎥⎣⎦代入 362n n n ⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦得2133m m m a ++=+，得13a =，与112a ≤<矛盾，舍去．故所有的n 共有334个．16．（2021·全国·九年级竞赛）不等式2242x ax a +<的解是___________．【答案】67a a x -<<（当0a >时）；76a ax <<-（当0a <时）；无解（当0a =时）．【解析】【分析】【详解】解原不等式化为()()670x a x a +-<，方程()()670x a x a +-=的两根为6a -和7a．若0a >，则67a a -<不等式的解为67a ax -<<；若0a <，则76a a <-不等式的解为76a a x <<-；若0a =，则67a a-=，不等式无解．故应填：67a a x -<< （当0a >时）; 76a ax <<-（当0a <时）;无解（当0a =时）． 17．（2021·全国·九年级竞赛）已知正整数m 和n 有大于1的最大公约数，并且满足3371m n +=，则mn =________．【答案】196 【解析】【分析】【详解】理由：设k 是m ，n 的最大公约数，则m 和n 可以表示为,m ka n kb ==（1k >，a ，b 均为正整数）．于是，()3323()371753m n ka kb k k a b +=+=+==⨯．因为1k >且7与53都是质数，23232k a b k a k k +>≥>，所以7k =且2353k a b +=，即34953a b ⨯+=．由a ，b 是正整数，得1,4a b ==．所以7,28m n ==．故728196mn =⨯=．18．（2021·全国·九年级竞赛）长沙市某中学100名学生向某“希望学校”捐书1000本，其中任意10人捐书总数不超过190本，那么捐书最多的某同学最多能捐书_________本．【答案】109 【解析】【分析】【详解】设100名学生捐书数分别是12100,,,a a a ，不妨设其中100a 为最大，于是100101000a +=()129100a a a a +++++()101118100a a a a ++++()192027100a a a a +++++(91a +++)9299100a a a +++190190190≤+++111902090=⨯=，所以100109a ≤．另一方面，当12999a a a ====，100109a =时，满足题目要求，故捐书最多的人最多能捐书109本．19．（2021·全国·九年级竞赛）已知由小到大的10个正整数1210,,,a a a 的和是2000，那么5a 的最大值是_________，这时10a 的值应是_________．【答案】 329 335或334 【解析】【分析】【详解】要使10a 最大，必须1a ，2a ，3a ，4a 及6a ，7a ，8a ，9a ，10a 尽量小．又因为1210a a a <<<，且1a ，2a ，3a ，4a 的最小可能值依次为1，2，3，4，于是有2000123≥+++56104a a a ++++，即56101990a a a +++≤．又651a a ≥+，752a a ≥+，853a a ≥+，954a a ≥+，1055a a ≥+，故51990615a ≥+，51975132966a ≤=．又5a 为正整数，所以5329a ≤，于是6710a a a +++=199********-=．又761a a ≥+，862a a ≥+，963a a ≥+，1064a a ≥+，故65101661a +≤，616515a ≤=13305，且6a 为正整数，所以6330a ≤，而651330a a ≥+=，所以6330a =，要7a ，8a ，9a 最小得7331a =，8332a =，9333a =，这时101661a =-()6789335a a a a +++=．但如果取1a ，2a ，3a ，4a 依次为1，2，3，5，那么同样可得569,,,a a a 取上述值，这时10334a =．故应填5a 的最大值是329，这时10a 的值应是335或334．三、解答题20．（2021·全国·九年级竞赛）某宾馆底楼客房比二楼客房少5间，某旅游团有48人．若全部安排底楼，每间房间住4人，房间不够；每间住5人，则有房间没有住满5人．又若全部安排住2楼，每间住3人，房间不够；每间住4人，则有房间没有住满4人．问该宾馆底楼有多少间客房？【答案】宾馆的底楼有客房10间【解析】【分析】【详解】设底楼有x 间客房，则2楼有()5+x 间客房．简4485483(5)484(5)48x x x x <⎧⎪>⎪⎨+<⎪⎪+>⎩依题意可得不等式组解不等式组得9.611x <<．又x 为正整数，所以10x =．答：宾馆的底楼有客房10间．21．（2021·全国·九年级竞赛）一座大楼有4部电梯，如果每部电梯可停靠三层（不一定连续三层，也不一定停最低层），对大楼中的任意两层，至少有一部电梯可在这两层停靠．问：这座大楼最多有几层? 【答案】这座大楼最多有5层【解析】【分析】【详解】设大楼有n 层，则楼层对的个数为(1)2n n -每架电梯停3层，有3232⨯=个楼层对，所以(1)43,(1)242n n n n -⨯≥-≤，且n 为正整数，所以5n ≤．设置4部电梯使它们停靠的楼层分别为 ()()()()1,4,5,2,4,5,3,4,5,1,2,3满足题目要求，故这座大楼最多有5层．22．（2021·全国·九年级竞赛）解方程22424x x x x ⎡⎤+-=⎢⎥⎣⎦．【答案】4x =-或45【解析】【分析】【详解】原方程中显然0x ≠，故原方程可化为2241()2x x ⎡⎤+-=⎢⎥⎣⎦．又2222221()21()2()1x x x ⎡⎤⎡⎤⎡⎤+-=+-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，故原方程可化为224[()]1x x=+，所以4x 为整数，设4n x =（n 为整数），原方程又化为2[]14n n =+．于是2124n n n +≤<+，即222(12)2(12)440,2(13)2(12)4802(13)2(13)n n n n n n n n ⎧≤≥+⎧--≥⎪⇒≤≤⎨⎨--<<<⎩⎪⎩或或．2(12)2(13n <<）．又n 为整数，所以1n =-或5n =，故4x =-或4523．（2021·全国·九年级竞赛）证明：对任意实数x 及任意正整数n 有[][]121n x x x x nx n n n -⎡⎤⎡⎤⎡⎤+++++++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦．【答案】见解析【解析】【分析】【详解】设[]x x α=-，则01a ≤≤，于是存在小于n 的正整数r ，使1r rn nα-≤<故[][]1r rx x x n n-+<<+，故当0k n r ≤≤-时，[][][][]11r k r n rx x x x x n n n n--≤+≤+<++=-，故[](0)k x x k n r n ⎡⎤+=≤≤-⎢⎥⎣⎦当11n r k n -+≤≤-时，[][][][][]1111111r n r k r n r x x x x x x n n n n n n--+--+=++≤+<++=++<+，故[]1(11)k x x n r k n n ⎡⎤+=+-+≤≤-⎢⎥⎣⎦，于是[]1111[]()(n n r n r x x x x x x x n n n n n ---+⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=++++++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦[][]21)(1)(1)(1)[]1n r n x x n r x r x n x r n n -+-⎡⎤⎡⎤++++=-++-+=+-⎢⎥⎢⎥⎣⎦⎣⎦①．又因为[][]1n x r nx n x r +-≤≤+，所以[][]1nx n x r =+-②．由①及②便知要证等式成立．24．（2021·全国·九年级竞赛）已知01,01,01a b c <<<<<<，证明： ()()()1,1,1a b b c c a ---中至少有一个不大于14．【答案】见解析【解析】【分析】【详解】 (1)1(1)22a a a a +--≤=11(1)(1)22b bc c --≤三式平方后相乘得 31(1)(1)(1)()4a b b c c a -⋅-⋅-≤故()()()1,1,1a b b c c a ---中至少有一个不大于14．25．（2021·全国·九年级竞赛）设正数a ，b ，c ，x ，y ，x 满足a x b y c z k +=+=+=，证明； 2ay bz cx k ++<．【答案】见解析【解析】【分析】【详解】因3()()()()()()k a x b y c z abc xyz ay c z bz a x cx b y =+++=+++++++()()abc xyz k ay bz cx k ay bx cx =++++>++．又0k >，所以2ay bz cx k ++<．26．（2021·全国·九年级竞赛）已知实数a ，b ，c 满足0,10a b c ac ++==，证明1110a b c++<．【答案】见解析【解析】【分析】【详解】因10abc =，故a ，b ，c 都不为零．又2222()2()0a b c a b c ab bc ca ++=+++++=且2220a b c ++>，所以0ab bc ca ++<，于是1110bc ca ab a b c abc++++=<． 27．（2021·全国·九年级竞赛）下图是某单位职工年龄（取正整数）的频率分布图（每组可含最低年龄但不含最高值），根据图中提供的信息回答下列问题：（1）该厂共有多少职工?（2）年龄不小于38但小于44岁的职工人数占职工总人数的百分比是多少? （3）如果42岁的职工有4人，那么42岁以上的职工有多少人?（4）有人估计该单位职工的平均年龄在39岁与42岁之间，问这个估计正确吗? 【答案】（1）50；（2）60%；（3）15人；（4）正确【解析】【分析】【详解】（1）职工人数47911106350=++++++=；（2）年龄不小于38但小于44岁职工人数占职工总数的百分比为91110100%60%50++⨯=；（3）年龄在42岁以上职工人数()1063415=++-=（人）；（4）设该厂职工的年龄平均值为n ，则11(34436738940114210446463)199239.84395050n ≥⨯+⨯+⨯+⨯+⨯+⨯+⨯=⨯=>且11(36438740942114410466483)209241.84425050n <⨯+⨯+⨯+⨯+⨯+⨯+⨯=⨯=<，故所作的估计是正确的．28．（2021·全国·九年级竞赛）某人到花店买花，他只有24元，打算买6支玫瑰和3支百合，但发现钱不够，只买了4支玫瑰和5支百合，这样还剩下2元多钱．请你算一算：2支玫瑰和3支百合哪个价格高？【答案】2支玫瑰的价格高于3支百合的价格．【解析】【分析】【详解】解设玫瑰每支x 元，百合每支y 元，依题意得632445242x y x y +>⎧⎨+=-⎩①② 32⨯-⨯②①得918y <，故2y <． 53⨯-⨯①②得1854x >，故3x >．答：2支玫瑰的价格高于3支百合的价格．29．（2021·全国·九年级竞赛）1132x x -+ 【答案】8313x ---≤≤【解析】【分析】【详解】解首先，由1030x x -≥⎧⎨+≥⎩得31x -≤≤．1132x x -≥+① 数上式两边均非负（当31x -≤≤时），两边平方后，整理得 9843x x --≥+②于是980x --≥，即98x ≤-结合31x -≤≤得938x -≤≤-．并且②式两边平方，得2(98)16(3)x x ≥--+，整理得264128330x x ++≥．③因方程264128330x x ++=的两根为1,2831x -±= 所以③的解为831x --≤或831x -+≥结合938x -≤≤-得原不等式的解为8313x ---≤≤30．（2021·全国·九年级竞赛）解不等式：2243414143x x x x x x x x +-->-++-- 【答案】1144x -<<或364x -<<634x <【解析】【分析】【详解】解不等式两边乘以4，化简为5115(1)(1)(1)(1)43414143x x x x +-->+--++-- 移项、整理得22151169161x x ->--，移项、通分得2224(646)0(169)(161)x x x -<--，可化为222(646)(169)(161)0x x x ---<，即222139()()()0163216x x x ---<．如右图得2116x <或2393216x <<，解得1144x -<<或364x -<<634x <<31．（2021·全国·九年级竞赛）求满足下列条件的最小正整数n ，使得对这样的n ，有唯一的正整数k ，满足871513n n k <<+．【答案】15 【解析】【分析】【详解】因n ，k 为正整数，所以0,0n n k >+>．由题中不等式得151387n k n +>>，即1513187k n >+>所以7687k n >>，故76,87k n k n ><．令760,780A k n B n k =-≥=-≥，可解出87,76n A B k A B =+=+．又因为A ，B 均为正整数，1,1A B ≥≥，所以8715n ≥+=．当且仅当1,1A B ==时n 取最小值15，这时k 有唯一值716113⨯+⨯=．故所求n 的最小值为15．32．（2021·全国·九年级竞赛）解不等式： 2256154x x x x -+≤++．【答案】41x -≤<-或4x <-或15x ≥．【解析】【分析】【详解】解移项，通分整理得1020(1)(4)x x x -+≤++故得（Ⅰ） 1020(1)(4)0x x x -+≥⎧⎨++<⎩，或（Ⅱ）1020(1)(4)0x x x -+≤⎧⎨++>⎩．解（I ） 1541x x ⎧≤⎪⎨⎪-<<-⎩，∴41x -≤<-．解（Ⅰ）1541x x x ⎧≥⎪⎨⎪--⎩或∴4x <-或15x ≥．综上所述得，原不等式的解为41x -≤<-或4x <-或15x ≥．33．（2021·全国·九年级竞赛）解不等式21311x x x x -+>-+．【答案】1x <-或1x > 【解析】【分析】【详解】解移项通分得(21)(1)(3)(1)0(1)(1)x x x x x x -+-+->-+，即220(1)(1)x x x x -+>-+．因22172()024xx x，故上述不等式化为()()110,1x x x -+>∴<-或1x >. 34．（2021·全国·九年级竞赛）如果二次不等式：28210ax ax ++<的解是71x -≤<-，求a 的值．【答案】3a =【解析】【分析】【详解】解依题意，1,7--是方程28210ax ax ++=的两个根，且0a >，由韦达定理得 2(1)(7)a-⨯-=，所以3a =． 35．（2021·全国·九年级竞赛）某校参加全国数，理，化，计算机比赛的人数分别是20，16，x ，20人．已知这组数据的中位数和平均数相等，求这组数据的中位数．【答案】18或20．【解析】【分析】【详解】（1）当16x ≤时，平均数为564x x +=，中位数为2016182+=．由56184x+=，解得16x =，满足16x ≤；（2）当1620x ≤≤时，平均数564x x +=，中位数为202x +．由562042x x++=，解得16x =，不符合1620x <<；当20x ≥时，平均数为564x x +=，中位数为2020202+=．由56204x+=，解得24x =，符合20x ≥．因此，所求中位数为18或20．36．（2021·全国·九年级竞赛）某个学生参加军训，进行打靶训练，必须射击10次，在第6次、第7次，第8次，第9次射击中，分别得到9.0环、8.4环、8.1环、9.3环，他的前9次射击所得平均环数高于前5次射击所得平均环数，如果要使10次射击的平均环数超过8.8环，那么他第10次射击至少要得多少环?（每次射击环数精确到0.1环）【答案】第10次至少要射9.9环【解析】【分析】【详解】设前9次射击共得x 环，依题意得1(9.08.48.19.3)95x x -+++>，解得78.3x <，故78.30.178.2x ≤-=．依题目要求，第10次射击至少要达到的环数为()8.8100.178.29.9⨯+-=（环）．答：第10次至少要射9.9环37．（2021·全国·九年级竞赛）今有浓度为5%,8%,9%的甲、乙、丙三种盐水分别为60g,60g,47g ，现要配制成浓度为7%的盐水100g ．间甲盐水最多可用多少克?最少可用多少克? 【答案】甲种盐水最多可用49g ，最少可用35g 【解析】【分析】【详解】设3种盐水应分别取,,xg yg zg ，1005%8%9%1007%060060047x y z x y z x y z ++=⎧⎪++=⨯⎪⎪≤≤⎨⎪≤≤⎪≤≤⎪⎩，解得20043100y x z x =-⎧⎨=-⎩所以02004600310047x x ≤-≤⎧⎨≤-≤⎩，解得3549x ≤≤．答：甲种盐水最多可用40g ，最少可用35g ．38．（2021·全国·九年级竞赛）求证：对任意的实数x ，y ，[2][2][][][]x y x x y y ++++．【答案】见解析．【解析】【分析】【详解】设[],[]x x y y n αββ=+=+=+，其中0,1αβ≤<，m ，n 为整数．（1）若110,022αβ≤<≤<，则021,021,01αβαβ≤<≤<≤+<．这时有 [2][2][22][22]22x y m m m n αβ+=+++=+，[][][]x x y y +++[][()()][]m a m n n αββ=+++++++()22m m n n m n =+++=+，所以[2][2][][][]x y x x y y +=+++．（2）若111,122αβ≤<≤<，则122,122,12αβαβ≤<≤<≤+<．这时有 [2][2][22][22]2121x y m n m n αβ+=+++=+++222m n =++，[][][][][()()][]x x y y m m n n ααββ+++=+++++++()1221m m n n m n =++++=++．所以[2][2][][][]x y x x y y +>+++．（3）若110,122αβ≤<≤<（111,022αβ≤<≤<的情况类似），这时有021α≤<，13122,22βαβ≤<≤+<，这时有[2][2][22][22]221x y m a n m n β+=+++=++，[][][][()()]221x x y y m m n a n m n β+++=+++++++．综上所述，不论何种情况，都有[2][2][][][]x y x x y y +≤+++．39．（2021·全国·九年级竞赛）某个学生参加军训，进行打靶训练，必须射击10次，在第6、第7、第8、第9次射击中，分别得了9.0环，8.4环，8.1环，9.3环，他的前9次射击所得环数的平均值高于前5次射击所得的平均环数．如果他要使10次射击的平均环数超过8.8环，那么他在第10次射击中最少要得多少环？（每次射击所得环数都精确到0.1环）【答案】第10次最少要得9.9环．【解析】【分析】【详解】9．设前5次射击所得平均环数为a ，第10次击中x 环，依题意59.08.48.19.39a a ++++<， ① 59.08.48.19.38.810a x +++++<． ② 由①得8.7a <，从而558.70.143.4a ≤⨯-=．由②得8834.8553.243.49.8x a >--≥-=，所以9.9x ≥，即第10次最少要得9.9环．40．（2021·全国·九年级竞赛）已知x ，y ，z 都是正数，证明：32()()()()()()x y x z y z y x z x z y +≤++++++．【答案】见解析【解析】【分析】【详解】 (0,0)2a b ab a b +≥≥得 []()()()()11()2()()2()()x x y x z x x y x z x x x y x z x y x z x y x z +++++=⋅=+++++++①． 1()2()()y y y x y zy x y z ≤+++++②． 1()2()()z z z x z yz x z y ≤+++++③由①+②+③即得要证不等式． 41．（2021·全国·九年级竞赛）某饮料厂生产A 、B 两种矿泉水，每天生产B 种矿泉水比A 种矿泉水多10吨，A 种矿泉水比B 种矿泉水每天多获利润2000元，其中A 种矿泉水每吨可获利润200元，B 种矿泉水每吨可获利润100元．（1）问：该厂每天生产A 种，B 种矿泉水各多少吨？（2）由于江水受到污染，市政府要求该厂每天必须多生产10吨矿泉水，该厂决定响应市政府的号召，在每天的利润不超过原利润的情况下不少于8000元，该厂每天生产A 种矿泉水最多多少吨？【答案】（1）该厂每天生产A 种矿泉水30吨，B 种矿泉水40吨．（2）该厂每天最多生产A 种矿泉水20吨．【解析】【分析】【详解】解（1）设该厂每天生产A 种矿泉水x 吨，则该厂每天生产B 种矿泉水10x +吨，依题意得()200100102000x x -+=，解得30,1040x x =+=．（2）设该厂每天生产A 吨矿泉水y 吨，依题意得该厂每天共生产30401080++=吨矿泉水且()10000200100808000y y ≥+-≥，其中100002003010040=⨯+⨯为该厂原来每天获得的利润，解上述不等式得020y ≤≤．答：（1）该厂每天生产A 种矿泉水30吨，B 种矿泉水40吨．（2）该厂每天最多生产A 种矿泉水20吨．42．（2021·全国·九年级竞赛）要使不等式2320x x -+≤①与不等式2(1)(3)20m x m x -+--<②无公共解，求m 的取值范围．【答案】0m ≥【解析】【分析】【详解】解 ①化为()()120x x --<，故①的解为12x <<．②化为()()1210m x x ⎡⎤⎣⎦-+-<．③（1）当1m =，③为()210x -<，即1x <，符合题意．（2）当10m ->，即1m 时，③的解为211x m -<<-符合题意．（3）当10m -<，即1m <时，又分两种情形讨论：若211m <-，即1m <-时，③的解为21x m <-或1x >，不符合题意; 若211m >-，即1m >-时，③的解为1x <或21x m>-．要使①与②无公共解，必须221m ≥-即0m ≥，结合1m <得01m ≤<．综上所述，得到要使①与②无公共解，m 的取值范围是0m ≥．43．（2021·全国·九年级竞赛）已知三个非负数a ，b ，c ，满足325a b c ++=和231a b c +-=．若37m a b c =+-，求m 的最大值和最小值．【答案】m 的最大值为111-；m 的最小值为57- 【解析】【分析】【详解】解由325,231a b c a b c ++=+-=可解出73,711a c b c =-=-，于是()()37373711732m a b c c c c c =+-=-+--=-．由0,0,0a b c ≥≥≥得73071100c c c -≥⎧⎪-≥⎨⎪≥⎩解得37711c ≤≤．所以m 的最大值为71321111m =⨯-=-，m 的最小值为353277m =⨯-=-． 44．（2021·全国·九年级竞赛）某班学生到公园进行活动，划船的有22人，乘电动车的有20人，乘过山车的有19人，既划船又乘电动车的有9人，既乘电动车又乘过山车的有6人，既划船又乘过山车的有8人，并且有4人没有参加上述3项活动中任何一项活动，问这个班学生人数的可能值是多少？【答案】这个班的学生人数可能是42,43,44,45,46,47,48．【解析】【分析】【详解】解设3项活动都参加了的学生有n 人，于是由容斥原理I 知至少参加了一项活动人数为222019(968)38n n ++-+++=+．所以，这个班的学生人数为38442n n ++=+．另一方面参加了两项活动的学生人数分别是9,6,8，所以06n ≤≤，故424248n ≤+≤．综上所述，这个班的学生人数可能是42,43,44,45,46,47,48．。

湖南师大附中教育集团第十一届攀登杯学科知识竞赛九年级数学试题

湖南师大附中教育集团第十一届攀登杯学科知识竞赛九年级数学试题卷总分：150分时量：120分钟第一试（满分100分）一、填空题：（满分50分）1.若从长度分别为6、10、12、18的四条线段中任取三条，则能组成三角形的概率为.2.计算：383341121+-+=．3.因式分解：22-+-y x xy =.4.化简)121(1212+-÷++-a a a a 的结果是.5.已知c b a 、、均为整数，且1)()(20182018=-+-c b b a ，则||||||a c c b b a -+-+-=.6.如果单项式13a xy +-与212b y x 是同类项，那么)()(a b b a -+=.7.ABC △中，C ∠=90°，A ∠=60°，A ∠的平分线交BC 于D ，过D 作AD 的垂线交AB 于E .则ACBE的值为.8.已知n 个数的平均数为17，将61放入后，这1+n 个数的平均数为19，再放入一个数a ，这2+n 个数的平均数变为21.则a =.9.如图，H G F E 、、、分别是正方形ABCD 四边中点，则图中全等三角形共有对.10.小区有一三角形公园，记三个顶点为C B A 、、，已知BC AB =，某天甲、乙两人同时出发匀速散步前行，甲从A 地出发，依次经C B 、两地再回到A 地；乙从B 地出发依次经C A 、两地回到B 地.出发10分钟后，甲、乙两人第一次相遇，再过40分钟，甲回到了A 地，乙恰好到达C 地.则乙还需分钟可回到B 地.二、解答题：（共50分）11.本题满分10分不等式组⎪⎩⎪⎨⎧->++≤+x x ax x 321234859恰有3个整数解.求实数a 的取值范围.12.本题满分10分平面直角坐标系中，矩形OABC 的顶点O 是坐标原点，边OC OA 、分别在y x 、轴上，B 点坐标为)2,3(，反比例函数图像分别交线段AB BC 、于E D 、两点，且BDE △的面积是矩形OABC 的面积的181.求此反比例函数的解析式.13.本题满分15分某商场试销B A 、两种商品，第一天售出A 商品x 件，B 商品y 件，销售额为15000元；第二天两种商品均涨价10元，A 商品销量减少5件，B 商品销量未变，销售额为15635元；第三天较第二天A 商品再涨价5元，销量又减少5件，B 商品价格和销量均未变，销售额为15290元.(Ⅰ)求y x 、的关系式；(Ⅱ)若3天B A 、两种商品销量共计大于375件，小于380件.求B A 、商品第一天的销售价.14.本题满分15分平面直角坐标系中，在x 轴的上方作半径为1的圆Γ，与x 轴相切于坐标原点O .平行于x 轴的直线1l 与y 轴交点的纵坐标为1-，),(y x A 是圆Γ外一动点，A 与圆Γ上的点的最小距离比A 到1l 的距离小1.(Ⅰ)求y 与x 的函数关系式;(Ⅱ)设2l 是圆Γ平行于x 轴的切线，试探究在y 轴上是否存在一定点B ，使得以AB 为直径的圆截直线2l 所得的弦长不变.第二试（满分50分）一、填空：（每题5分，共20分）1.ABC △中，AC AB =，BD 是AC 边上的高，且AD CD 2=，若62=BC ，则ABC △的面积为.2.记[]x 为不大于实数x 的最大整数，{}[]x x x -=，若7122=+x x ，则{}=⎭⎬⎫⎩⎨⎧+x x 1.3.已知ABC △的三边长分别为c b a 、、，且c b a 、、均为有理数，满足)2)(2()22(2++=+c b a .则acc b b a ++=.4.如图，四边形ABCD 是边长为4的菱形，︒=∠60A ，四个小圆均与菱形的两条邻边相切且都与菱形内切圆外切.则以这四个小圆的圆心为顶点的四边形的面积是.二、解答题：（每题15分，共30分）5.已知实数y x 、满足：⎩⎨⎧=+++=+++10)1()1(52)2()14(22x y y x x y y y x 求yx 11+的值.6.已知四边形ABCD 是平行四边形，直线BD 交)(ABC ⊙于P B 、两点，E 是)(ABC ⊙上一点，满足AC BE ∥，PE 交AC 于Q .求证：DQC PQA ∠=∠.。

九年级数学竞赛题

九年级数学竞赛题一、代数部分1. 一元二次方程竞赛题题目：已知关于公式的一元二次方程公式有两个实数根公式和公式。

（1）求实数公式的取值范围；（2）当公式时，求公式的值。

解析：（1）对于一元二次方程公式，判别式公式。

在方程公式中，公式，公式，公式，因为方程有两个实数根，所以公式。

展开公式得公式，即公式，解得公式。

（2）由公式可得公式。

根据韦达定理，在一元二次方程公式中，公式，公式。

对于方程公式，公式，公式。

当公式时，即公式，解得公式，但公式不满足公式（由（1）得），舍去。

当公式时，即公式，那么公式，由（1）中公式，解得公式。

2. 二次函数竞赛题题目：二次函数公式的图象经过点公式，且与公式轴交点的横坐标分别为公式、公式，其中公式，公式，求公式的取值范围。

解析：因为二次函数公式的图象经过点公式，所以公式，则公式。

二次函数与公式轴交点的横坐标是方程公式的根，由韦达定理公式，公式。

设公式，因为公式，公式，当公式时，公式；当公式时，公式；当公式时，公式。

将公式代入公式，公式中：由公式得公式，化简得公式，即公式。

由公式得公式，化简得公式，即公式，公式。

所以公式，则公式，解得公式。

二、几何部分1. 圆的竞赛题题目：在公式中，弦公式与弦公式相交于点公式，公式、公式分别是弦公式、公式的中点，连接公式、公式，若公式，公式的半径为公式。

（1）求证：公式是等边三角形；（2）求公式的长（用公式表示）。

解析：（1）连接公式、公式。

因为公式、公式分别是弦公式、公式的中点，根据垂径定理，公式，公式。

在四边形公式中，公式，公式，根据四边形内角和为公式，可得公式。

又因为公式（半径），公式、公式分别是弦公式、公式的中点，所以公式，公式。

在公式中，公式，公式（同圆中，弦心距相等则弦相等的一半也相等），所以公式是等边三角形。

（2）设公式与公式交于点公式，公式与公式交于点公式。

在公式中，公式，公式，公式，则公式。

同理，在公式中，公式。

因为公式是等边三角形，公式，在公式中，公式，公式，则公式，所以公式。

九年级初中竞赛数学试卷

一、选择题（每题5分，共50分）1. 下列各数中，绝对值最小的是（）A. -2B. 0C. 2D. -1/22. 若m和n是方程x^2 - 3x + 2 = 0的两个根，则m+n的值是（）A. 3B. 2C. 1D. 03. 在直角坐标系中，点A（2，3）关于y轴的对称点是（）A. （-2，3）B. （2，-3）C. （-2，-3）D. （2，3）4. 下列函数中，是反比例函数的是（）A. y = 2x + 1B. y = x^2C. y = 1/xD. y = 3x - 55. 若a、b、c是等差数列的连续三项，且a+b+c=21，则b的值为（）A. 7B. 14C. 21D. 286. 在等腰三角形ABC中，AB=AC，且∠BAC=60°，则∠B的度数是（）A. 30°B. 45°C. 60°D. 90°7. 若a^2 + b^2 = 1，且a+b=0，则ab的值为（）A. 0B. 1C. -1D. 28. 下列方程中，有唯一解的是（）A. x^2 - 4x + 4 = 0B. x^2 - 4x + 5 = 0C. x^2 - 4x + 6 = 0D. x^2 - 4x + 8 = 09. 若函数y = ax^2 + bx + c的图像开口向上，且顶点坐标为（1，-2），则a的值是（）A. 1B. -1C. 2D. -210. 在梯形ABCD中，AD∥BC，AB=CD，AD=8cm，BC=12cm，则梯形的高是（）A. 6cmB. 8cmC. 10cmD. 12cm二、填空题（每题5分，共50分）11. 已知等差数列{an}的第一项为2，公差为3，则第10项an=__________。

12. 若函数y = kx + b的图像过点（2，-1），则k+b=__________。

13. 在直角坐标系中，点P（-3，4）到原点O的距离是__________。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B
初三数学竞赛《小题狂做》（共60题，每题2分，总分120分）
1.已知关于x 的方程2x 3x m 0-+=的一个根是1，则m = .
2.若⊙O 的半径为4cm ，点A 到圆心O 的距离为3cm ，那么点A 与⊙O 的位置关系是
3、已知一个布袋里装有2个红球，3个白球和a 个黄球，这些球除颜色外其余都相同．若从该布袋里任意摸出1个球，是红球的概率为31
，则a 等于_________
4．如果方程2（x-3）2=72，那么，这个一元二次方程的两根是________．
5.代数式222
1x x x ---的值为0，则x 的值为________．
6.二次函数y ＝ax 2＋bx －1(a ≠0)的图象经过点(1，1)．则代数式1－a －b 的值为________
7．在平面直角坐标系中，将二次函数22x y =的图象向上平移2个单位，所得图象的解析式为________
8.已知x （x+3）=1，则代数式2x 2+6x ﹣5的值为．
9..若关于x 的一元二次方程2x x m 0++=有两个相等的实数根，则m=
10.已知⊙O 的半径为5,弦AB 的弦心距为3,则AB 的长是
11.如图1，有一圆弧开桥拱，拱的跨度AB ＝16cm ，拱高CD ＝4cm ，那么拱形的半径是＿m
12.已知直角三角形的两直角边长分别为5和12，则它的外接圆半径R =______，内切圆半径r =______．
13.如图2，⊙O 中，弦AB ⊥弦CD 于E ，OF ⊥AB 于F ，OG ⊥CD 于G ，若AE=8cm ，EB=4cm ，则OG= ______cm 。

图1 图2 图3
14.如图3，四边形ABCD 内接于⊙O ，若它的一个外角∠DCE ＝70°，则∠BOD 等于＿＿。

15.由一已知点P 到圆上各点的最大距离为5，最小距离为1，则圆的半径为______。

16 .⊙O 的半径为6，⊙O 的一条弦AB 为63，以3为半径的同心圆与直线AB 的位置关系是．
17.已知圆锥的母线长为5厘米，底面半径为3厘米，则它的侧面积为
18．如果抛物线y ＝－2x 2＋mx －3的顶点在x 轴负半轴上，则m ＝_______．
19、若一组数据1,0,2,4,x -的极差为7，则x 的值是 .
20．己知三角形两边长分别为2和9，第三边的长为二次方程x 2－14x ＋48＝0的一根，则这个三角形的周长为___________
21.两个相似三角形周长之比为2:3，面积之差为10cm 2，则它们的面积之和为________cm 2。

22、y=x 2-3x-4与x 轴的交点坐标是__________,与y 轴交点坐标是____________
图4 图5 图6
23、如图4，AB 是⊙O 的直径，点D 在AB 的延长线上，过点D 作⊙O 的切线，切点为C ，若∠A=35°，则∠D= _________ ．
24.如图5，△ABC 与△A ′B ′C ′是位似图形，点O 是位似中心，若OA=2A A ′,S △ABC =8，则S △A ′B ′C ′ ′=________．
25、如图6是一个古代车轮的碎片，小明为求其外圆半径，连结外圆上的两点A 、B ，并使AB 与车轮内圆相切于点D ，做CD ⊥AB 交外圆于点C ．测得CD=10cm ，AB=60cm ，则这个车轮的外圆半径为 cm ．
26.矩形周长为16cm, 它的一边长为xcm ，面积为ycm 2，则y 与x 之间函数关系为______。

27.三角形的三条边长分别为5cm ，9cm ，12cm ，则连结各边中点所成三角形的周长为____cm 。

28.已知AB 是⊙O 的弦，且AB=OA ，则∠AOB ＝度。

29.扇形的圆心角是300，半径是2cm ，则扇形的面积是 cm 2 .
30、已知实数a 、b 满足（a 2+b 2）2﹣2（a 2+b 2）=8，则a 2+b 2的值为__________
31.一组数据4，7，10，13，16的方差是 _______
32、已知6
53z y x ==，且623+=z y ，则__________,==y x 。

33、小明的身高是1.6m ，影长为2m ，同一时刻教学楼的影长为24m ，则教学楼的高是；
34.已知AD 为Rt △ABC 斜边BC 上的高，且AB=15cm ，BD=9cm ，则AD= ，CD= 。

35.二次函数2365y x x =--+的图象的顶点坐标是________
36.二次函数2)1(2+-=x y 的最小值是________
37.关于x 的方程kx 2+3x-1=0有实数根，则k 的取值范围是 .
38若x 1、x 2是方程07x 5x 2
=--的两根，那么.________)x (x 221=-
39.把二次函数34
12+--=x x y 用配方法化成()k h x a y +-=2的形式________ 40.将函数2y x x =+的图象向右平移a (0)a >个单位，得到函数232y x x =-+的图象，则a 的值为________
41．如图7，在矩形ABCD 中，AD=4，DC=3，将△ADC 绕点A 按逆时针方向旋转到△AEF （点A 、B 、E 在同一直线上），则AC 在运动过程中所扫过的面积为 _________ ．
图7
42.图8（1）是一个横断面为抛物线形状的拱桥，当水面在l 时，拱顶（拱桥洞的最高点）离水面2m ，水面宽4m ．如图8（2）建立平面直角坐标系，则抛物线的关系式是________
43．抛物线2y x bx c =-++的图象如图9所示，则此抛物线的解析式为．
图10
44.二次函数c bx ax y ++=2的图象如图10，则直线bc ax y +=的图象不经过第象限.
45.函数 y ＝12
(x －1)2＋3，当 x____________时，函数值 y 随 x 的增大而增大. 46.已知抛物线的顶点坐标为()2,1，且抛物线过点()3,0，则抛物线的关系式是
图8（1）图8（2
）
图9
47..函数x x y +-=22有最____值，最值为_______；
48.二次函数122--=x x y 的图象在x 轴上截得的线段长为________
49.若x 是3和6的比例中项，则x 的值为
50.设α、β是方程02012x x 2=-+的两个实数根，则βαα++22
的值为 51.关于x 的方程03)3(12=+---x x
m m 是一元二次方程，则=m ；
52.圆锥的轴截面的顶角为600，这个圆锥的母线长为8cm ，则这个圆锥的高为 _________ 53.若数据a 1, a 2,a 3┈a n 的平均数为3，方差为
21，则数据4 a 1-3，4 a 2-3,4 a 3-3 ┈4 a n -3的平均数为方差为
54.等边三角形的中线与中位线长的比值是_______
55.已知二次函数2(0)y ax bx c a =++≠的图象如图11所示，则下列结论：0ac >①；②方程2
0ax bx c ++=的两根之和大于0；y ③随x 的增大而增大；④0a b c -+<，其中正确的是________
图11 图12 图13
56.如图12，在△ABC 中，点D 在线段BC 上，∠BAC=∠ADC ，AC=8，BC=16，那么CD=______.
57．如图13，已知在△ABC 中，点D 、E 、F 分别是边AB 、AC 、BC 上的点，DE ∥BC ，EF ∥AB ，且AD ：DB=3：5，那么CF ：CB 等于_______
58..抛物线(1)(3)(0)y a x x a =+-≠的对称轴是直线________
59.若方程02
=++c bx ax 的两个根是－3和1，那么二次函数c bx ax y ++=2的图象的对称轴是直线________
60．如果抛物线y ＝x 2－6x ＋c －2的顶点到x 轴的距离是3，那么c 的值为_________。