北师大版高中数学必修一第三章指数函数与对数函数测试题

合集下载

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(有答案解析)(1)

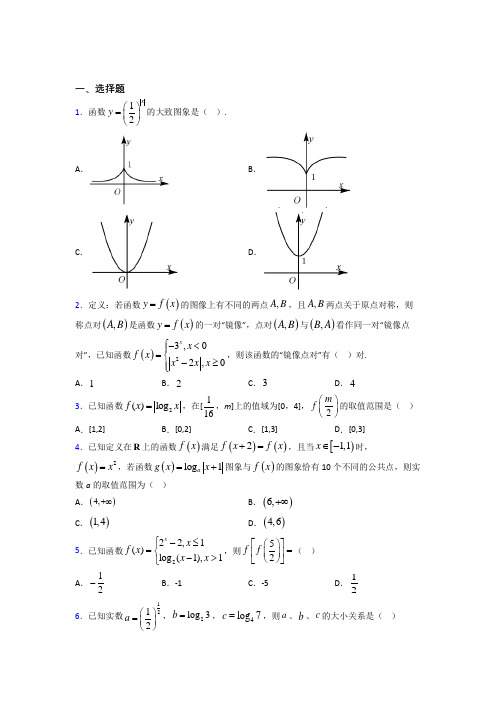
一、选择题1．函数12xy ⎛⎫= ⎪⎝⎭的大致图象是（）. A ． B ．C ．D ．2．定义：若函数()y f x =的图像上有不同的两点,A B ，且,A B 两点关于原点对称，则称点对(),A B 是函数()y f x =的一对“镜像”，点对(),A B 与(),B A 看作同一对“镜像点对”，已知函数()23,02,0x x f x x x x ⎧-<⎪=⎨-≥⎪⎩，则该函数的“镜像点对”有（）对.A ．1B ．2C ．3D ．43．已知函数2()log x f x =，在[116，m ]上的值域为[0，4]，2m f ⎛⎫⎪⎝⎭的取值范围是（） A ．[1,2]B ．[0,2]C ．[1,3]D ．[0,3]4．已知定义在R 上的函数()f x 满足()()2f x f x +=，且当[)1,1x ∈-时，()2f x x =，若函数()log 1a g x x =+图象与()f x 的图象恰有10个不同的公共点，则实数a 的取值范围为（） A ．()4,+∞ B ．()6,+∞ C ．()1,4D ．()4,65．已知函数222,1()log (1),1x x f x x x ⎧-≤=⎨->⎩，则52f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦（） A ．12-B ．-1C ．-5D ．126．已知实数1212a ⎛⎫= ⎪⎝⎭，2log 3b =，4log 7c =，则a 、b 、c 的大小关系是（）A ．c b a <<B ．c a b <<C ．b a c <<D ．a c b <<7．设函数()ln |31|ln |31|f x x x =+--，则()f x （） A ．是偶函数，且在11(,)33-单调递增 B ．是偶函数，且在1(,)3-∞-单调递增 C ．是奇函数，且在11(,)33-单调递减 D ．是奇函数，且在1(,)3-∞-单调递减8．如图是指数函数①y =x a ；②y =x b ；③y =c x ；④y =d x 的图象，则a ，b ，c ，d 与1的大小关系是（）A ．a 且1a ≠）在[]0,3上为增函数，则实数a 的取值范围是（） A ．2,13⎛⎫⎪⎝⎭B ．(0,1)C ．20,3⎛⎫ ⎪⎝⎭D ．[)3,+∞ 11．已知()243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩满足对任意12x x ≠，都有()()12120f x f x x x -<-成立，那么a 的取值范围是（）A ．10,2⎛⎤ ⎥⎝⎦B ．1,12⎡⎫⎪⎢⎣⎭C ．12,23⎡⎤⎢⎥⎣⎦D ．2,13⎡⎫⎪⎢⎣⎭12．若函数()()212log 45f x x x =-++在区间()32,2m m -+内单调递增，则实数m 的取值范围为（） A ．4,33⎡⎤⎢⎥⎣⎦B ．4,23⎡⎤⎢⎥⎣⎦C ．4,23⎡⎫⎪⎢⎣⎭D ．4,3⎡⎫+∞⎪⎢⎣⎭二、填空题13．现有下列四个结论：①若25a b m ==且a b =时，则1m =； ②若236log log log a b c ==，则c ab =；③对函数()3xf x =定义域内任意的1x ，都存在唯一的2x ，使得()()121f x f x ⋅=成立；④存在实数a ，使得函数()()2ln g x x ax a =++的定义域和值域均为R .其中所有正确结论的序号是_________. 14．已知()(3),1log ,1aa x a x f x x x --<⎧=⎨≥⎩的值域为R ，那么实数a 的取值范围是_________．15．已知函数()212log y x ax a =-+在()3,+∞上是减函数，则a 的取值范围是______.16．函数()()12log 13y x x =-+的递增区间为______．17．已知函数log (3)a y ax =-在(1,2)上单调递减，则实数a 的取值范围为___________. 18．若幂函数()2()57m f x m m x =-+在R上为增函数则1log 2log 2lg5lg4mm m+-=_____．19．已知函数()f x 满足()()1f x f x =-+，当()0,1x ∈时，函数()3xf x =，则13log 19f ⎛⎫= ⎪⎝⎭______. 20．已知2336m n ==，则11m n+=______．三、解答题21．计算下列各式的值：（1）1100.753270.064()160.258---++;（2）53log 425log lg lg 4522++-.22．已知函数()22x x f x k -=+. （1）若()f x 为偶函数，求实数k 的值；（2）若()4f x 在2[log x m ∈，2log (2)](m m +为大于0的常数)上恒成立，求实数k 的最小值.23．分别计算下列数值：（1）1lg3lg94lg81lg 27+--；（2）已知()1401x xx -+=<<，求221122x x x x---+.24．（1）若223a a -+=，求1a a --和33a a --的值；（2）计算33(lg 2)3lg 2lg 5(lg 5)+⋅+的值.25．（1）160.25371.586-⨯-+-⎫⎛ ⎪⎝⎭（2）1324lg lg82493-+26．设函数()log (1)a f x ax =-，其中01a << (1)证明()f x 是1(,)a-∞上的增函数； (2)解不等式()1f x >.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】去绝对值符号后根据指数函数的图象与性质判断．【详解】由函数解析式可得：1,022,0xx x y x ⎧⎛⎫≥⎪ ⎪=⎨⎝⎭⎪<⎩可得值域为：01y <≤，由指数函数的性质知：在(),0-∞上单调递增；在()0,∞+上单调递减. 故选：A. 【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.2．C解析：C 【分析】由新定义可知探究y 轴左侧部分图像关于原点中心对称的图像与y 轴右侧部分图像的交点个数即得结果. 【详解】由题意可知，函数()y f x =的图像上有不同的两点,A B ，且,A B 两点关于原点对称，则称点对(),A B 是函数()y f x =的一对“镜像”，因为()23,02,0xx f x x x x ⎧-<⎪=⎨-≥⎪⎩，由y 轴左侧部分()3,0xy x =-<图像关于原点中心对称的图像3x y --=-，即3xy -=，()0x >，作函数3xy -=，()0x >和()22,0y x x x =-≥的图象如下：由图像可知两图象有三个公共点，即该函数有3对“镜像点对”. 故选：C. 【点睛】本题解题关键是理解新定义，寻找对称点对，探究y 轴左侧部分图像关于原点中心对称的图像与y 轴右侧部分图像的交点个数，通过数形结合，即突破难点.3．D解析：D 【分析】由对数函数的单调性可得[]1,16m ∈，再结合对数函数的性质即可得解. 【详解】由题意，函数2()log x f x =在(]0,1上单调递减，在[)1,+∞上单调递增，且()116416f f ⎛⎫==⎪⎝⎭，()10f =，结合该函数在1,16m ⎡⎤⎢⎥⎣⎦上的值域为[0,4]可得[]1,16m ∈，所以1,8 22m⎡⎤∈⎢⎥⎣⎦，[]2lo2g0,32m mf⎛⎫=⎪⎝∈⎭.故选：D.【点睛】关键点点睛：解决本题的关键是由对数函数的图象变换及单调性确定[]1,16m∈，即可得解.4．D解析：D【分析】转化条件为函数()f x是周期为2的周期函数，且函数()g x、()f x的图象均关于1x=-对称，由函数的对称性可得两图象在1x=-右侧有5个交点，画出图象后，数形结合即可得解.【详解】因为函数()f x满足()()2f x f x+=，所以函数()f x是周期为2的周期函数，又函数()log1ag x x=+的图象可由函数logay x=的图象向左平移一个单位可得，所以函数()log1ag x x=+的图象的对称轴为1x=-，当[)1,1x∈-时，()2f x x=，所以函数()f x的图象也关于1x=-对称，在平面直角坐标系中作出函数()y f x=与()y g x=在1x=-右侧的图象，数形结合可得，若函数()log1ag x x=+图象与()f x的图象恰有10个不同的公共点，则由函数图象的对称性可得两图象在1x=-右侧有5个交点，则()()13log415log61aaagg⎧>⎪=<⎨⎪=>⎩，解得()4,6a∈.故选：D.【点睛】关键点点睛：解决本题的关键是函数的周期性、对称性及数形结合思想的应用.5．A解析：A 【分析】根据分段函数解析式，依次计算255log 122f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭，23log 2f ⎛⎫ ⎪⎝⎭，即可得选项.【详解】因为函数222,1()log (1),1x x f x x x ⎧-≤=⎨->⎩，所以2253log log 2122f ⎛⎫=<= ⎪⎝⎭，23log 2531222222f f⎡⎤⎛⎫∴=-=-=- ⎪⎢⎥⎝⎭⎣⎦. 故选：A. 【点睛】本题考查根据分段函数求解函数值，关键在于根据解析式分段求解，由内到外，准确认清自变量的所在的范围和适用的解析式.6．D解析：D 【分析】本题首先可根据2log 3b =以及2log c =得出b c >，然后根据1a <以及1c >得出c a >，即可得出结果.【详解】因为2log 3b =，42log 7log 7c ，函数2log y x =在()0,∞+上是增函数，所以b c >，因为01211122a <⎛⎫⎛⎫= ⎪ ⎪⎝⎝⎭=⎭，44log 7log 41c ，所以c a >，综上所述，a c b <<，故选：D. 【点睛】指数、对数的大小比较，可通过寻找合适的单调函数来构建大小关系，不同类型的数比较大小，应找一个中间数，通过它实现大小关系的传递，考查计算能力，是中档题.7．D解析：D 【分析】根据奇偶性定义判断奇偶性，然后判断单调性，排除错误选项得正确结论．【详解】函数定义域是1{|}3x x ≠±，()ln 31ln 31ln 31ln 31()f x x x x x f x -=-+---=--+=-，()f x 是奇函数，排除AB ，312()lnln 13131x f x x x +==+--，11,33x ⎛⎫∈- ⎪⎝⎭时，2310x -<-<，2231x <--，即21031x +<-，而131u x =-是减函数，∴2131v x =+-是增函数，∴()f x 在11,33⎛⎫- ⎪⎝⎭上是增函数，排除C ．只有D 可选．故选：D ．【点睛】结论点睛：本题考查函数的单调性与奇偶性，判断函数的奇偶性与单调性后用排除法确定正确选项，掌握复合函数的单调性是解题关键．()y f x =与()y f x =-的单调性相反，在()f x 恒为正或恒为负时，()y f x =与1()y f x =的单调性相反，若()0f x <，则()y f x =与()y f x =的单调性相反．0a >时，()y af x =与()y f x =的单调性相同．8．B解析：B 【分析】根据指数函数的图象与性质可求解. 【详解】根据函数图象可知函数①y =x a ；②y =x b 为减函数，且1x =时，②y =1b <①y =1a ，所以1b a <<，根据函数图象可知函数③y =c x ；④y =d x 为增函数，且1x =时，③y =c 1>④y =d 1，所以1c d >> 故选：B 【点睛】本题主要考查了指数函数的单调性，指数函数的图象，数形结合的思想，属于中档题.9．C解析：C 【解析】要使函数有意义，需使210{340x x x +>--+>，即1{41x x >--<<，所以1 1.x -<< 故选C10．C解析：C 【分析】根据对数函数性质与复合函数的单调性求解．【详解】因为0a >且1a ≠，令2t ax =-，所以函数2t ax =-在[]0,3上为减函数，所以函数log a y t =应是减函数，()f x 才可能是增函数， ∴01a <<，因为函数()f x 在[]0,3上为增函数，由对数函数性质知230a ->，即23<a ，综上023a <<．故选：C ．【点睛】本题考查复合函数的单调性，掌握对数函数性质是解题关键，考查逻辑思维能力和计算能力，属于常考题．11．C解析：C 【分析】判断函数的单调性．利用分段函数解析式，结合单调性列出不等式组求解即可．【详解】解：243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩（）满足对任意12x x ≠，都有()()12120f x f x x x --＜成立，所以分段函数是减函数，所以：0121442a a a a<<⎧⎪≥⎨⎪-≥⎩，解得12,23a ⎡⎤∈⎢⎥⎣⎦．故选C ．【点睛】本题考查分段函数的单调性的应用，函数的单调性的定义的理解，考查转化思想以及计算能力．12．C解析：C 【分析】求得函数()y f x =的定义域，利用复合函数法求得函数()y f x =的单调递增区间，根据题意可得出区间的包含关系，由此可求得实数m 的取值范围. 【详解】解不等式2450x x -++>，即2450x x --<，解得15x -<<，内层函数245u x x =-++在区间()1,2-上单调递增，在区间()2,5上单调递减，而外层函数12log y u =在定义域上为减函数，由复合函数法可知，函数()()212log 45f x x x =-++的单调递增区间为()2,5，由于函数()()212log 45f x x x =-++在区间()32,2m m -+上单调递增，所以，32232225m m m m -≥⎧⎪-<+⎨⎪+≤⎩，解得423m ≤<. 因此，实数m 的取值范围是4,23⎡⎫⎪⎢⎣⎭.故选：C. 【点睛】本题考查利用对数型复合函数在区间上的单调性求参数，考查计算能力，属于中等题.二、填空题13．①②③【分析】利用换底公式结合求得的值可判断①的正误；设利用对数与指数的互化以及指数的运算性质可判断②的正误；由求得可判断③的正误；求出函数的定义域值域分别为时对应的实数的取值范围可判断④的正误【详解析：①②③ 【分析】利用换底公式结合a b =，求得m 的值，可判断①的正误；设236log log log a b c t ===，利用对数与指数的互化以及指数的运算性质可判断②的正误；由()()121f x f x ⋅=求得21x x =-，可判断③的正误；求出函数()g x 的定义域、值域分别为R 时，对应的实数a 的取值范围，可判断④的正误. 【详解】对于①，由于250abm ==>，可得2lg log lg 2m a m ==，5lg log lg 5mb m ==，由于a b =可得lg lg lg 2lg 5m m=，则lg 0m =，解得1m =，①正确；对于②，设236log log log a b c t ===，可得2t a =，3t b =，6t c =，则236t t t ab c =⋅==，②正确；对于③，对任意的1x R ∈，则()()1212123331xxx x f x f x +⋅=⋅==，120x x ∴+=，可得21x x =-，③正确；对于④，若函数()()2ln g x x ax a =++的定义域为R ，对于函数2y x ax a =++，240a a ∆=-<，解得01a <<；若函数()()2ln g x x ax a =++的值域为R ，则函数2y x ax a =++的值域包含()0,∞+，则240a a ∆=-≥，解得0a ≤或1a ≥.所以，不存在实数a ，使得函数()()2ln g x x ax a =++的定义域和值域均为R ，④错误.故答案为：①②③. 【点睛】关键点点睛：解本题第④问的关键点在于找到函数()()2ln g x x ax a =++的定义域为R的等价条件∆<0；函数()()2ln g x x ax a =++的值域为R 的等价条件0∆≥.14．【分析】分类讨论和结合已知和对数函数及一次函数的单调性得a 的不等式组求解即可【详解】解：若当时当时此时的值域不为R 不符合题意；若当时当时要使函数的值域为R 需使解得综上所述故答案为：【点睛】本题考查分解析：31,2⎛⎤⎥⎝⎦【分析】分类讨论01a <<和1a >，结合已知和对数函数及一次函数的单调性，得a 的不等式组求解即可．【详解】解：若01a <<，当1≥x 时，log 0a x ≤，当1x <时，()3332a x a a a a --<--=-，此时f x （）的值域不为R ，不符合题意；若1a >，当1≥x 时，log 0a x ≥，当1x <时，要使函数f x （）的值域为R ，需使30log 13a a a a ->⎧⎨≤--⎩，解得332a a <⎧⎪⎨≤⎪⎩，312a ∴<≤，综上所述，312a <≤，故答案为：31,2⎛⎤ ⎥⎝⎦．【点睛】本题考查分段函数的值域及对数函数的性质，考查分类讨论思想与数学运算能力，是中档题.15．【分析】函数为复合函数且原函数为减函数根据题意需要满足一元二次函数在上是增函数且在上恒大于或等于零然后求解关于a 的不等式即可得到结果【详解】令则原函数化为此函数为定义域内的减函数要使函数在上是减函数解析：9,2⎛⎤-∞ ⎥⎝⎦ 【分析】函数为复合函数,且原函数为减函数,根据题意需要满足一元二次函数2x ax a -+在()3,+∞上是增函数,且在()3,+∞上恒大于或等于零,然后求解关于a 的不等式即可得到结果. 【详解】令2t x ax a =-+,则原函数化为12()log g t t =,此函数为定义域内的减函数,要使函数()212log y x ax a =-+在()3,+∞上是减函数,则函数2t x ax a =-+在()3,+∞上是增函数,且在()3,+∞上恒大于或等于零,即有232330aa a ⎧≤⎪⎨⎪-+≥⎩,解得92a ≤. 故答案为:9,2⎛⎤-∞ ⎥⎝⎦【点睛】本题考查了复合函数的单调性,需要掌握复合函数的同增异减,本题还要注意对数函数的定义域是求解的前提,这里容易漏掉,需要掌握此类题目的解题方法.16．【分析】首先求出函数的定义域再根据复合函数的单调性计算可得【详解】解：则解得即函数的定义域为令则因为在上单调递增在上单调递减；在定义域上单调递减根据复合函数的单调性同增异减可知函数在上单调递增故答案解析：()1,1-【分析】首先求出函数的定义域，再根据复合函数的单调性计算可得. 【详解】解：()()12log 13y x x =-+则()()130x x -+>解得31x -<<即函数的定义域为()3,1- 令()()()()21314t x x x x =-+=-++，()3,1x ∈-，则12logy t =因为()t x 在()3,1--上单调递增，在()1,1-上单调递减；12log y t =在定义域上单调递减根据复合函数的单调性“同增异减”可知函数()()12log 13y x x =-+在()1,1-上单调递增故答案为：()1,1- 【点睛】本题考查复合函数的单调区间的计算，属于基础题.17．【分析】由复合函数的单调性：同增异减由于递减因此必须递增即有还要考虑函数定义域即在时恒成立【详解】∵∴是减函数又在上是减函数所以且∴故答案为：【点睛】本题考查对数型复合函数的单调性掌握复合函数单调性解析：3(1,]2【分析】由复合函数的单调性：同增异减，由于3u ax =-递减，因此log a y u =必须递增，即有1a >，还要考虑函数定义域，即在(1,2)x ∈时，30ax ->恒成立．【详解】∵0a >，∴3u ax =-是减函数，又log (3)a y ax =-在(1,2)上是减函数，所以1a >，且320a -≥，∴312a <≤．故答案为：3(1,]2．【点睛】本题考查对数型复合函数的单调性，掌握复合函数单调性是解题关键，同时要考虑函数的定义域．18．3【分析】利用幂函数的定义与性质求得将代入利用对数的运算法则化简得解【详解】在上为增函数解得(舍去）故答案为：3【点睛】正确理解幂函数的定义求得的值和熟练运用对数恒等式是关键解析：3 【分析】利用幂函数的定义与性质求得3m =，将3m =代入，利用对数的运算法则化简得解. 【详解】()()257m f x m m x =-+在R 上为增函数，25710m m m ⎧-+=∴⎨>⎩，解得3,2m m ==(舍去）， 1log2log 2lg 5lg 4mm m∴+-=31log 23l l og 3g1003+=故答案为：3. 【点睛】正确理解幂函数的定义求得m 的值和熟练运用对数恒等式是关键.19．【分析】由满足得到函数是以2为周期的周期函数结合对数的运算性质即可求解【详解】由题意函数满足化简可得所以函数是以2为周期的周期函数又由时函数且则故答案为：【点睛】函数的周期性有关问题的求解策略：求解解析：2719-【分析】由()f x 满足()()1f x f x =-+，得到函数()f x 是以2为周期的周期函数，结合对数的运算性质，即可求解. 【详解】由题意，函数()f x 满足()()1f x f x =-+，化简可得()()2f x f x =+，所以函数()f x 是以2为周期的周期函数，又由()0,1x ∈时，函数()3xf x =，且()()1f x f x =-+，则133339(log 19)(log 19)(log 192)(log )19f f f f =-=-+= 327log 193392727(log 1)(log )3191919f f =-+=-=-=-.故答案为：2719- 【点睛】函数的周期性有关问题的求解策略：求解与函数的周期性有关问题，应根据题目特征及周期定义，求出函数的周期；解决函数周期性、奇偶性和单调性结合问题，通常先利用周期性中为自变量所在区间，再利用奇偶性和单调性求解.20．【分析】根据对数的定义和运算法则即可求解【详解】由可得所以所以故答案为：【点睛】本题主要考查对数的运算法则的应用考查了学生的计算能力属于中档题解析：12【分析】根据对数的定义和运算法则即可求解．【详解】由2336m n ==可得23log 36,log 36m n == 所以361log 2m =，361log 3n=，所以363636111log 2log 3log 62m n +=+==，故答案为：12【点睛】本题主要考查对数的运算法则的应用，考查了学生的计算能力，属于中档题．三、解答题21．（1）10 （2）0 【分析】（1）利用指数幂的运算性质求解即可；（2）利用对数的运算性质求解即可. 【详解】解:（1）1100.753270.064()160.258---++()11333244211254-⎡⎤⎛⎫⎛⎫=-++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦51182210=（2）53log 425log lg lg 4522++-34223log 2log 2lg 5lg 22lg 24=-+-+- ()331lg5lg 244=-++- 331144=-+- 0=【点睛】本题考查指数幂的运算,考查对数的运算.22．（1）1k =；（2）当02m <<时，k 的最小值为4，当2m 时，k 的最小值为24m m -+. 【分析】（1）根据函数是偶函数，利用偶函数的定义求解. （2）将()4f x ，转化为2(2)42x x k-+⨯，令2[x t m =∈，2]m +，构造函数2()4g t t t =-+，利用二次函数的性质求得其最大值即可..【详解】（1）()f x 为偶函数，()()f x f x ∴=-， 2?22?2x x x x k k --∴+=+，即(1)(22)0x x k ---=，对任意的x 恒成立，1k ∴=.（2）由()4f x ，可得2?24x x k -+，即2(2)42x x k -+⨯，令2[xt m =∈，2]m +，2()4g t t t ∴=-+，当02m <<时，对称轴2[t m =∈，2]m +，则()max g t g =（2）4244=-+⨯=，当2m 时，对称轴2t m =，则2()()4max g t g m m m ==-+，故当02m <<时，k 的最小值为4，当2m 时，k 的最小值为24m m -+. 【点睛】本题主要考查函数的奇偶性的和不等式恒成立的问题，还考查了分类讨论的思想和运算求解的能力，属于中档题. 23．（1）32；（2）-. 【分析】（1）利用对数的运算性质化简可求得所求代数式的值；（2）由已知条件可求得1x x --的值，可求得22x x -+，并求得1122x x -+的值，代入计算可求得所求代数式的值. 【详解】（1）原式11lg3lg3lg3111lg3322lg5lg 2lg1081222lg32lg 27+-=++=+=；（2）因为()()()221114x x x x x x x x -----=+-=-，所以()()2211412x xx x ---=+-=，因为01x <<，则1x x -<，所以1x x --=-22x x --=-，又因为21112226x x x x --⎛⎫+=++= ⎪⎝⎭，所以1122x x -+=所以221122x x x x---=-+【点睛】本题考查指数式与对数式的计算，考查了平方关系以及对数运算性质的应用，考查计算能力，属于基础题.24．（1）1,4±±；（2）1.【分析】（1）利用完全平方公式和立方差公式计算．（2）由对数的运算法则计算．【详解】（1）1222()2321a a a a ---=-+=-=，所以11a a --=±，33122()(1)1(31)4a a a a a a ----=-++=±⨯+=±；（2）lg 2lg5lg(25)1+=⨯=．3322(lg 2)3lg 2lg5(lg5)(lg 2lg5)(lg 2lg 2lg5lg 5)3lg 2lg5+⋅+=+-++ 2222lg 2lg 2lg5lg 53lg 2lg5lg 22lg 2lg5lg 5=-++=++2(lg 2lg 5)1=+=．【点睛】本题考查幂的运算法则和对数的运算法则，掌握幂与对数运算法则是解题基础． 25．（1）110；（2）13lg5lg 222- 【分析】（1）利用指数幂的运算法则即得解；（2）利用对数的运算法则即得解. 【详解】（1）原式1111323334422()12223()33⨯=⨯+⨯+⨯-2108110=+=（2）原式153222124lg lg 2lg(57)273=-+⨯11(5lg 22lg 7)4lg 2(lg5+2lg7)22=--+ 11(5lg 22lg 7)4lg 2(lg5+2lg7)22=--+ 31lg 2lg522=-+【点睛】本题考查了指数与对数运算，考查了学生概念理解，数学运算能力，属于基础题. 26．（1）见解析；（2）11{|}a x x a a-<< 【分析】(1)根据函数单调性的定义及对数函数的性质，即可证出结果；(2)根据函数()f x 的单调性，可将不等式()1f x >转化为一元一次不等式，即可得到原不等式的解集．【详解】(1)由10ax ->，01a <<得1x a<，所以()f x 的定义域为1(,)a -∞，设1x ，2x 为区间1(,)a -∞的任意两个值，且211x x a<<，则 211ax ax ->->-，所以21110ax ax ->->，又01a <<，所以21log (1)log (1)a a ax ax -<-，即21()()f x f x <，所以()f x 是1(,)a-∞上的增函数．(2)由()1f x >得log (1)1log a a ax a ->=，又01a <<，所以01ax a <-<，所以11ax a -<-<-，所以11a x a a-<<，所以不等式()1f x >的解集为11{|}a x x a a-<<．【点睛】本题主要考查对数型复合函数单调性的证明及对数不等式的解法，属于中档题．。

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》测试(包含答案解析)(4)

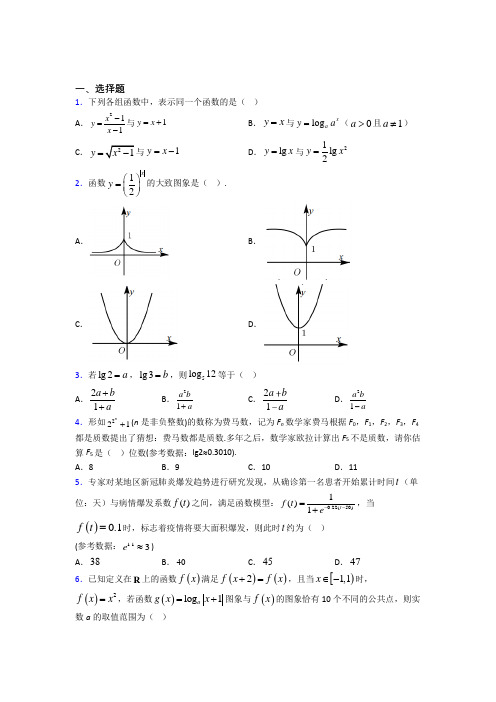
一、选择题1．下列各组函数中，表示同一个函数的是（）A ．211x y x -=-与1y x =+B ．y x =与log xa y a =（0a >且1a ≠）C ．21y x =-与1y x =-D ．lg y x =与21lg 2y x =2．函数12xy ⎛⎫= ⎪⎝⎭的大致图象是（）. A ． B ．C ．D ．3．若lg 2a =，lg3b =，则5log 12等于（）A ．21a b a++B ．21a b a+C ．21a b aD ．21a b a-4．形如221n+(n 是非负整数)的数称为费马数，记为F n 数学家费马根据F 0，F 1，F 2，F 3，F 4都是质数提出了猜想：费马数都是质数.多年之后，数学家欧拉计算出F 5不是质数，请你估算F 5是（）位数(参考数据：lg2≈0.3010). A ．8B ．9C ．10D ．115．专家对某地区新冠肺炎爆发趋势进行研究发现，从确诊第一名患者开始累计时间t （单位：天）与病情爆发系数()f t 之间，满足函数模型：0.22(50)11()t f t e --=+，当()0.1f t =时，标志着疫情将要大面积爆发，则此时t 约为（）(参考数据： 1.13e ≈) A ．38B ．40C ．45D ．476．已知定义在R 上的函数()f x 满足()()2f x f x +=，且当[)1,1x ∈-时，()2f x x =，若函数()log 1a g x x =+图象与()f x 的图象恰有10个不同的公共点，则实数a 的取值范围为（）A ．()4,+∞B ．()6,+∞C ．()1,4D ．()4,67．已知函数3()22x f x =+，则111357(1)432234f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭（） A ．212B ．214C ．7D ．1528．若13log 2a =，131()2b =，2log 3c =，则,,a b c 的大小关系是（） A ．b a c << B ．b c a << C ．a b c << D ．c b a <<9．在数学史上，一般认为对数的发明者是苏格兰数学家——纳皮尔（Napier ，1550-1617年）．在纳皮尔所处的年代，哥白尼的“太阳中心说”刚刚开始流行，这导致天文学成为当时的热门学科．可是由于当时常量数学的局限性，天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”，因此浪费了若干年甚至毕生的宝贵时间．纳皮尔也是当时的一位天文爱好者，为了简化计算，他多年潜心研究大数字的计算技术，终于独立发明了对数．在那个时代，计算多位数之间的乘积，还是十分复杂的运算，因此纳皮尔首先发明了一种计算特殊多位数之间乘积的方法．让我们来看看下面这个例子：这两行数字之间的关系是极为明确的：第一行表示2的指数，第二行表示2的对应幂．如果我们要计算第二行中两个数的乘积，可以通过第一行对应数字的和来实现．比如，计算64×256的值，就可以先查第一行的对应数字:64对应6，256对应8，然后再把第一行中的对应数字加和起来：6＋8＝14；第一行中的14，对应第二行中的16384，所以有：64×256＝16384,按照这样的方法计算：16384×32768=（） A ．134217728B ．268435356C ．536870912D ．51376580210．若函数()()212log 45f x x x =-++在区间()32,2m m -+内单调递增，则实数m 的取值范围为（） A ．4,33⎡⎤⎢⎥⎣⎦B ．4,23⎡⎤⎢⎥⎣⎦C ．4,23⎡⎫⎪⎢⎣⎭D ．4,3⎡⎫+∞⎪⎢⎣⎭11．已知1()44x f x x -=+-e ，若正实数a 满足3(log )14a f <，则a 的取值范围为（）A ．34a >B ．304a <<或43a >C ．304a <<或1a > D ．1a >12．设()lg (21)f xx a =-+是奇函数，则使f(x)<0的x 的取值范围是( )． A ．(－1,0) B ．(0, 1)C ．(－∞，0)D ．(－∞，0)∪(1，＋∞)二、填空题13．下列命题中所有正确的序号是_____________.①函数1()3x f x a -=+(0a >且1)a ≠的图像一定过定点(1,4)P ； ②函数(1)f x -的定义域是(1,3)，则函数()f x 的定义域为(2,4)；③若1log 12a >，则a 的取值范围是112⎛⎫⎪⎝⎭，； ④若22ln ln()x y x y -->-- (0x >,0y <)，则0x y +<. 14．已知0a >，函数()y f x =，其中21()log f x a x ⎛⎫=+⎪⎝⎭，若对任意1,12t ⎡⎤∈⎢⎥⎣⎦，函数()y f x =在区间[,1]t t +上的最大值与最小值的差不超过1，则a 的取值范围为_______．15．定义{},,max ,,x x y x y y x y≥⎧=⎨<⎩，设{}()max ,log xa f x a a x=--(),1x R a +∈>.则不等式()2f x ≥的解集是_____________.16．函数()()cos1log sin f x x =的单调递增区间是____________. 17．方程()()22log 972log 31xx+=++的解为______. 18．有以下结论：①将函数xy e =的图象向右平移1个单位得到1x y e -=的图象； ②函数()x f x e =与()g x lnx =的图象关于直线y =x 对称③对于函数()xf x a =(a >0,且1a ≠)，一定有()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭④函数()22log (2)f x x x =-+的图象恒在x 轴上方.其中正确结论的序号为_________.19．已知奇函数()()y f x x R =∈满足：对一切x ∈R ，()()11f x f x +=-且[]0,1x ∈时，()1xf x e =-，则()2019f f =⎡⎤⎣⎦__________.20．如果()231log 2log 9log 64x x x f x =-+-，则使()0f x <的x 的取值范围是______.三、解答题21．已知函数()23x x f x a b =⋅+⋅，其中常数,a b 满足0ab ≠.（1）若0ab >，判断函数()f x 的单调性；（2）若0ab <，求(1)()f x f x +>时x 的取值范围.22．计算11213321(4()40.1()ab a b ----⋅（其中0a >，0b >）23．已知函数()12,012,0m x x x f x x n x x ⎧⎛⎫+-> ⎪⎪⎪⎝⎭=⎨⎛⎫⎪++< ⎪⎪⎝⎭⎩是奇函数.（1）求实数m ，n 的值；（2）若对任意实数x ，都有()()420xxf f λ+≥成立.求实数λ的取值范围.24．设函数()log (0,1)a f x x a a =>≠. （1）解不等式(26)(5)f a f a +；（2）已知对任意的实数()23,14m f m m f ⎛⎫++ ⎪⎝⎭恒成立，是否存在实数k ，使得对任意的[1,0]x ∈-，不等式()()142240x x xf f k ++--⋅>恒成立，若存在，求出k 的范围；若不存在，请说明理由.25．已知222log ()log log x y x y +=+，则x y +的取值范围是__________. 26．已知函数11()ln 12f x x x ⎛⎫=+ ⎪-⎝⎭. （1）先求1(2)2f f ⎛⎫-⎪⎝⎭的值，再求[]1111(11)(12)(29)(66)11122966f f f f f f f f ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++-+++⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦的值；（2）求()f x 的定义域，并证明()f x 在定义域上恒正.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】分析各个选项中每组函数的定义域和对应关系，若定义域和对应关系均相同则为同一个函数，由此判断出正确选项.【详解】A ．211x y x -=-的定义域为{}1x x ≠，1y x =+的定义域为R ，所以不是同一个函数；B ．y x =与log xa y a =的定义域均为R ，且log xa y a =即为y x =，所以是同一个函数； C．y =(][),11,-∞-+∞，1y x =-的定义域为R ，所以不是同一个函数；D ．lg y x =的定义域为()0,∞+，21lg 2y x =的定义域为{}0x x ≠，所以不是同一个函数，故选：B. 【点睛】思路点睛：同一函数的判断步骤：（1）先判断函数定义域，若定义域不相同，则不是同一函数；若定义域相同，再判断对应关系；（2）若对应关系不相同，则不是同一函数；若对应关系相同，则是同一函数.2．A解析：A 【分析】去绝对值符号后根据指数函数的图象与性质判断．【详解】由函数解析式可得：1,022,0xx x y x ⎧⎛⎫≥⎪ ⎪=⎨⎝⎭⎪<⎩可得值域为：01y <≤，由指数函数的性质知：在(),0-∞上单调递增；在()0,∞+上单调递减. 故选：A. 【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.3．C解析：C 【分析】利用对数的换底公式可将5log 12用a 、b 表示. 【详解】根据对数的换底公式得，5lg12lg3lg 4lg32lg 22log 12lg5lg10lg 21lg 21a ba+++====---，故选：C ．【点睛】关键点点睛：该题考查的是有关对数的运算，解答本题的关键是熟记换底公式以及对数的运算性质，利用运算性质化简、运算，其中lg5lg10lg 2=-是题目的一个难点和易错点.4．C解析：C 【分析】根据所给定义表示出9.632951010F =⨯，进而即可判断出其位数．【详解】根据题意，53223232lg232lg2320.30109.6320.6329521212101010101010F ⨯=+=+≈==≈==⨯，因为0.63211010<<，所以5F 的位数是10．故选：C 【点睛】关键点睛：解答本题的关键是转化成对数运算，即3232lg 2210=.5．B解析：B 【分析】根据()0.1f t =列式求解即可得答案.【详解】解：因为()0.1f t =，0.22(50)11()t f t e --=+，所以0.22(50)()0.111t f t e--==+，即0.22(50)011t e --=+，所以0.22(50)9t e --=，由于 1.13e ≈，故()21.12.29e e =≈，所以0.222().250t e e --=，所以()0.2250 2.2t --=，解得40t =. 故选：B. 【点睛】本题解题的关键在于根据题意得0.22(50)9t e --=，再结合已知 1.13e ≈得()21.12.29e e =≈，进而根据0.222().250t e e --=解方程即可得答案，是基础题.6．D解析：D【分析】转化条件为函数()f x 是周期为2的周期函数，且函数()g x 、()f x 的图象均关于1x =-对称，由函数的对称性可得两图象在1x =-右侧有5个交点，画出图象后，数形结合即可得解. 【详解】因为函数()f x 满足()()2f x f x +=，所以函数()f x 是周期为2的周期函数，又函数()log 1a g x x=+的图象可由函数log a y x =的图象向左平移一个单位可得，所以函数()log 1a g x x =+的图象的对称轴为1x =-，当[)1,1x ∈-时，()2f x x =，所以函数()f x 的图象也关于1x =-对称，在平面直角坐标系中作出函数()y f x =与()y g x =在1x =-右侧的图象，数形结合可得，若函数()log 1a g x x =+图象与()f x 的图象恰有10个不同的公共点，则由函数图象的对称性可得两图象在1x =-右侧有5个交点，则()()13log 415log 61a a a g g ⎧>⎪=<⎨⎪=>⎩，解得()4,6a ∈. 故选：D. 【点睛】关键点点睛：解决本题的关键是函数的周期性、对称性及数形结合思想的应用.7．B解析：B 【分析】先利用解析式计算3()(2)2f x f x +-=，再计算和式即可得到结果. 【详解】因为3()22xf x =+，所以2332(2)22224xx x f x -⋅-==+⋅+，()3323()(2)222222x x x f x f x ⋅+-=+=++. 故1113573321(1)34322342224f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++=⨯+=⎪ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭. 故选：B. 【点睛】本题解题关键是通过指数式运算计算3()(2)2f x f x +-=，再配对求和即解决问题. 8．C解析：C 【分析】由题容易看出，0a <， 01b <<，2log 31c =>，便得出,,a b c 的大小关系. 【详解】1133log 2log 10a =<=，310110122b ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭，22log 3log 21c =>=，因此a b c <<. 故选：C. 【点睛】本题考查指数函数和对数函数的比较大小，常与中间值0-1,1，来比较，再结合函数的单调性即可求解，属于中档题.9．C解析：C 【分析】先找到16384与32768在第一行中的对应数字，进行相加运算，再找和对应第二行中的数字即可. 【详解】由已知可知，要计算16384×32768，先查第一行的对应数字: 16384对应14，32768对应15，然后再把第一行中的对应数字加起来：14＋15＝29，对应第二行中的536870912，所以有：16384×32768＝536870912, 故选C. 【点睛】本题考查了指数运算的另外一种算法，关键是认真审题，理解题意，属于简单题.10．C解析：C 【分析】求得函数()y f x =的定义域，利用复合函数法求得函数()y f x =的单调递增区间，根据题意可得出区间的包含关系，由此可求得实数m 的取值范围.【详解】解不等式2450x x -++>，即2450x x --<，解得15x -<<，内层函数245u x x =-++在区间()1,2-上单调递增，在区间()2,5上单调递减，而外层函数12log y u =在定义域上为减函数，由复合函数法可知，函数()()212log 45f x x x =-++的单调递增区间为()2,5，由于函数()()212log 45f x x x =-++在区间()32,2m m -+上单调递增，所以，32232225m m m m -≥⎧⎪-<+⎨⎪+≤⎩，解得423m ≤<. 因此，实数m 的取值范围是4,23⎡⎫⎪⎢⎣⎭. 故选：C. 【点睛】本题考查利用对数型复合函数在区间上的单调性求参数，考查计算能力，属于中等题.11．C解析：C 【分析】先判断1()44x f x x -=+-e 是R 上的增函数，原不等式等价于3log 14a <，分类讨论，利用对数函数的单调性求解即可. 【详解】因为1x y e -=与44y x =-都是R 上的增函数，所以1()44x f x x -=+-e 是R 上的增函数，又因为11(1)441f e -=+-=所以()3(log )114af f <=等价于3log 14a <，由1log a a =，知3log log 4a a a <,当01a <<时，log a y x =在()0,∞+上单调递减，故34a <，从而304a <<；当1a >时，log ay x =在()0,∞+上单调递增，故34a >，从而1a >，综上所述， a 的取值范围是304a <<或1a >，故选C. 【点睛】解决抽象不等式()()f a f b <时，切勿将自变量代入函数解析式进行求解，首先应该注意考查函数()f x 的单调性．若函数()f x 为增函数，则a b <；若函数()f x 为减函数，则a b >．12．A解析：A 【解析】试题分析：由()lg (21)fxx a =-+为奇函数，则()()f xf x -=-，可得1a =-，即()lg11f xxx =+-，又()0f x <，即lg110xx+-<，可变为0111x x <+-<，解得10x -<<．考点：函数的奇偶性，对数函数性质，分式不等式．二、填空题13．①③④【分析】由指数函数的图象函数的定义域对数函数的性质判断各命题①令代入判断②利用函数的定义求出的定义域判断③由对数函数的单调性判断④引入新函数由它的单调性判断【详解】①令则即图象过点①正确；②则解析：①③④ 【分析】由指数函数的图象，函数的定义域，对数函数的性质判断各命题．①，令1x =代入判断，②利用函数的定义求出()f x 的定义域判断，③由对数函数的单调性判断，④引入新函数1()ln 2ln 2xxg x x x -⎛⎫=-=- ⎪⎝⎭，由它的单调性判断．【详解】①令1x =，则(1)4f =，即()f x 图象过点(1,4)，①正确； ②13x <<，则012x <-<，∴()f x 的定义域是(0,2)，②错；③1log 1log 2a a a ，∴0112a a <<⎧⎪⎨>⎪⎩，∴112a <<．③正确； ④由22ln ln()x y x y -->-- (0x >,0y <)，得ln 2ln()2x y x y --<--，又1()ln 2ln 2xx g x x x -⎛⎫=-=- ⎪⎝⎭是(0,)+∞上的增函数， ∴由ln 2ln()2x y x y --<--，得x y <-，即0x y +<，④正确．故答案为：①③④【点睛】关键点点睛：本题考查指数函数的图象，对数函数的单调性，函数的定义域问题，定点问题：（1）指数函数(0x y a a =>且1)a ≠的图象恒过定点(0,1)；（2）对数函数log (0a y x a =>且1)a ≠的图象恒过定点(1,0)，解题时注意整体思想的应用．14．【分析】由函数单调性可得在区间上的最大值最小值则可得对任意恒成立利用二次函数的性质即可求出【详解】因为在区间内单调递减所以函数在区间上的最大值与最小值分别为则得整理得对任意恒成立令则的图象是开口向上解析：23⎡⎫+∞⎪⎢⎣⎭，【分析】由函数单调性可得()f x 在区间[1]t t ，+上的最大值()f t ，最小值(1)f t +，则可得2(1)10at a t ++-≥对任意1,12t ⎡⎤∈⎢⎥⎣⎦恒成立，利用二次函数的性质即可求出. 【详解】因为()f x 在区间[1]t t ，+内单调递减，所以函数()f x 在区间[1]t t ，+上的最大值与最小值分别为()f t ，(1)f t +，则2211()(1)log log 11f t f t a a t t ⎛⎫⎛⎫-+=+-+≤ ⎪⎪+⎝⎭⎝⎭，得1121a a t t ⎛⎫+≤+ ⎪+⎝⎭，整理得2(1)10at a t ++-≥对任意1,12t ⎡⎤∈⎢⎥⎣⎦恒成立．令2()(1)1h t at a t =++-，则()h t 的图象是开口向上，对称轴为11022t a=--<的抛物线，所以()h t 在1,12t ⎡⎤∈⎢⎥⎣⎦上是增函数，2(1)10at a t ++-≥等价于102h ⎛⎫≥ ⎪⎝⎭，即211(1)1022a a ⎛⎫⨯++⨯-≥ ⎪⎝⎭，解得23a ≥，所以a 的取值范围为23⎡⎫+∞⎪⎢⎣⎭，．故答案为：23⎡⎫+∞⎪⎢⎣⎭，.关键点睛：由单调性判断出最大值和最小值，从而转化为2(1)10at a t ++-≥对任意1,12t ⎡⎤∈⎢⎥⎣⎦恒成立，根据二次函数性质求解. 15．【分析】利用分段函数列出不等式求解即可【详解】解：在上为单调递增函数又当时当时不等式或解得或故答案为：【点睛】本题考查分段函数的应用函数值的求法考查转化思想以及计算能力解析：21(0,][log (2),)a a a++∞ 【分析】利用分段函数列出不等式求解即可.【详解】解：()log log x xa a a a x a a x ---=-+， 1a >，()log x a g x a a x =-+在()0,∞+上为单调递增函数，又1(1)log 10a g a a =-+=，当()0,1x ∈时，log 0x a a a x -+<，当()1,x ∈+∞时，log 0xa a a x -+>， ,1()log ,01x a a a x f x x x ⎧->∴=⎨-<<⎩不等式()2f x ≥，21x a a x ⎧-≥∴⎨>⎩或log 201a x x -≥⎧⎨<<⎩，解得log (2)a x a ≥+或210x a <≤，故答案为：21(0,][log (2),)a a a++∞. 【点睛】本题考查分段函数的应用，函数值的求法，考查转化思想以及计算能力. 16．【分析】根据对数型复合函数单调性列不等式再根据正弦函数性质得结果【详解】单调递增区间为单调递减区间且所以故答案为：【点睛】本题考查对数型复合函数单调性以及正弦函数性质考查基本分析求解能力属基础题解析：[2,2),()2k k k Z ππππ++∈ 【分析】根据对数型复合函数单调性列不等式，再根据正弦函数性质得结果.()()cos1cos1(0,1)log sin f x x ∈∴=单调递增区间为sin y x =单调递减区间且sin 0x >，所以22,()2k x k k Z ππππ+≤<+∈，故答案为：[2,2),()2k k k Z ππππ++∈【点睛】本题考查对数型复合函数单调性以及正弦函数性质，考查基本分析求解能力，属基础题. 17．或【分析】由对数的运算性质化对数方程为关于的一元二次方程求得的值进一步求得值得答案【详解】由得即化为解得：或或故答案为：或【点睛】本题主要考查的是对数方程的求解将对数方程转化为指数方程是解决本题的关解析：0x =或1x =.【分析】由对数的运算性质化对数方程为关于3x 的一元二次方程，求得3x 的值，进一步求得x 值得答案.【详解】由()()22log 972log 31x x +=++，得 ()()22log 97log 431x x +=+，即()97431x x +=+，化为()234330x x -⋅+=，解得：31x =或33x =，0x ∴=或1x =.故答案为：0x =或1x =.【点睛】本题主要考查的是对数方程的求解，将对数方程转化为指数方程是解决本题的关键，考查学生的计算能力，是基础题.18．②③④【分析】①根据图象的平移规律直接判断选项；②根据指对函数的对称性直接判断；③根据指数函数的图象特点判断选项；④先求的范围再和0比较大小【详解】①根据平移规律可知的图象向右平移1个单位得到的图象解析：②③④【分析】①根据图象的平移规律，直接判断选项；②根据指对函数的对称性，直接判断；③根据指数函数的图象特点，判断选项；④先求22x x -+的范围，再和0比较大小.①根据平移规律可知x y e =的图象向右平移1个单位得到1x y e -=的图象，所以①不正确；②根据两个函数的对称性可知函数()x f x e =与()g x lnx =的图象关于直线y =x 对称，正确；③如下图，设1a >，122x x f +⎛⎫⎪⎝⎭对应的是曲线上横坐标为122x x +的点C 的纵坐标，()()122f x f x +是线段AB 的中点D 的纵坐标，由图象可知()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭，同理，当01a <<时，结论一样，故③正确；④2217721244x x x ⎛⎫-+=-+≥> ⎪⎝⎭ 根据函数的单调性可知()222log 2log 10x x -+>=，所以函数()22log (2)f x x x =-+的图象恒在x 轴上方，故④正确.故答案为：②③④【点睛】思路点睛：1.图象平移规律是“左＋右－”，相对于自变量x 来说，2.本题不易判断的就是③，首先理解122x x f +⎛⎫ ⎪⎝⎭和()()122f x f x +的意义，再结合图象判断正误. 19．【分析】根据题意求得的周期性则可求再结合函数解析式求得函数值即可【详解】由题可知：因为对一切故关于对称；又因为是奇函数则可得故可得故函数是周期为的函数则又当故则故答案为：【点睛】本题考查利用函数周期解析：31e e --【分析】根据题意，求得()f x 的周期性，则()2019f 可求，再结合函数解析式，求得函数值即可.【详解】由题可知：因为对一切x R ∈，()()11f x f x +=-，故()f x 关于1x =对称；又因为()f x 是奇函数，则可得()()()()()21111f x f x f x f x f x +=++=--=-=-，故可得()()()()4222f x f x f x f x +=++=-+=，故函数()f x 是周期为4的函数.则()()()201911f f f =-=-，又当[]0,1x ∈，()1x f x e =-，故()()201911f f e =-=-，则()()()()()320191131e f f f e f e f e e -=-=--=--=-.故答案为：31e e --.【点睛】本题考查利用函数周期性求函数值，属综合中档题；难点在于求得函数的周期. 20．【分析】可结合对数化简式将化简为再解对数不等式即可【详解】由由得即当时故；当时无解综上所述故答案为：【点睛】本题考查对数化简公式的应用分类讨论求解对数型不等式属于中档题解析：81,3⎛⎫ ⎪⎝⎭【分析】可结合对数化简式将()f x 化简为()1log 2log 3log 4x x x f x =-+-，再解对数不等式即可【详解】由()2323231log 2log 9log 641log 2log 3log 4x x x x x x f x =-+-=-+- 31log 2log 3log 41log 8x x x x =-+-=+，由()0f x <得81log 03x -<，即8log log 3x x x >，当1x >时，83x <，故81,3x ⎛⎫∈ ⎪⎝⎭；当()0,1x ∈时，83x >，无解综上所述，81,3x ⎛⎫∈ ⎪⎝⎭ 故答案为：81,3⎛⎫ ⎪⎝⎭【点睛】本题考查对数化简公式的应用，分类讨论求解对数型不等式，属于中档题三、解答题21．（1）当0,0a b >>时，函数()f x 在R 上是增函数,当0,0a b <<时，函数()f x 在R 上是减函数；（2）当0,0a b <>时，则 1.5log ()2a x b>-；当0,0a b ><时，则1.5log ()2a x b<-. 【详解】（1）当0,0a b >>时，任意1212,,x x R x x ∈<，则121212()()(22)(33)x x x x f x f x a b -=-+- ∵121222,0(22)0x x x x a a ⇒-<，121233,0(33)0x x x xb b ⇒-<，∴12())0(f x f x -<，函数()f x 在R 上是增函数,当0,0a b <<时，同理，函数()f x 在R 上是减函数；（2）(1)()2230x x f x f x a b +-=⋅+⋅> 当0,0a b <>时，3()22x a b >-，则 1.5log ()2a x b >-；当0,0a b ><时，3()22x a b <-，则 1.5log ()2a x b<-. 22．85【分析】将小数转化为分数，根式转化为分数幂的形式，利用指数幂的运算性质化简求值.【详解】1113132211133133221(4)1(4)()=()4410.1()()()10ab ab a b a b --------⋅⋅ 原式131********()()(4)()410ab a b ----= 原式33333002222211848555a b a b a b --=⨯⨯=⨯⨯= 【点睛】本题考查指数幂的运算，要熟练掌握基本的运算法则和运算性质，小数转化为分数，根式转化为分数幂的形式，更有利于运算.23．（1）22m n =⎧⎨=⎩；（2）1λ≥-. 【分析】（1）根据()f x 是奇函数，即()()f x f x -=-即可求解实数m ，n 的值；（2）利用换元法，转化为二次函数的问题讨论最值恒成立即可求解实数λ的取值范围.【详解】（1）当0x >时，()()()12f x x n x ⎡⎤-=-++⎢⎥-⎣⎦，因为()f x 为奇函数，()()f x f x ∴-=-，()()()1122f x x n m x x x ⎡⎤⎡⎤⎛⎫∴-=-++=-+-⎢⎥ ⎪⎢⎥-⎝⎭⎣⎦⎣⎦，即()()1220m x n x ⎛⎫-++-= ⎪⎝⎭总成立. 2020m n -=⎧∴⎨-=⎩，22m n =⎧∴⎨=⎩，又当0x <时，同理可得22m n =⎧⎨=⎩，综上：22m n =⎧∴⎨=⎩. （2）40x >，20x >，原不等式化为11242222042x x x x λλ⎛⎫⎛⎫+-++-≥ ⎪ ⎪⎝⎭⎝⎭，令122x xt =+，则2t ≥，原不等式进一步化为230t t λλ+--≥在2t ≥上恒成立. 记()23g t t t λλ=+--，[)2,t ∈+∞ ①当22λ-≤时，即4λ≥-时，()()min 210g t g λ==+≥， 1λ∴≥-合理；②当22λ->时，即4<-λ时，()n 2mi 3024g t g λλλ⎛⎫-=---≥ ⎪⎝⎭=，显然不成立. 综上实数λ的取值范围为：1λ≥-.【点睛】本题考查的知识点是分段函数的应用，指数函数的单调性，奇函数的性质，是函数图象和性质的综合应用，难度中档.24．（1）(0,1)[2,)a ∈⋃+∞（2）实数k 不存在，详见解析【分析】（1）分类讨论，利用对数函数的单调性，将不等式具体化，解不等式即可；（2）判断函数()f x 为增函数，将不等式具体化，再分离参数求最值，即可得出结论.【详解】解：（1）当01a <<时，有2650a a +>，解得02a <≤，即(0,1)∈a ；当1a >时，有0265a a <+，解得2a ，即[2,)a ∈+∞.综上可知，(0,1)[2,)a ∈⋃+∞.（2）由于221331244m m m ⎛⎫++=++ ⎪⎝⎭，且()2314f m m f ⎛⎫++ ⎪⎝⎭，可知()f x 为增函数. ()()142240x x x f f k ++--⋅>，即()()14224x x x f f k ++>-⋅，则有14224x x x k ++>-⋅在[1,0]-上恒成立，即1342x x k +<⋅+在[1,0]-上恒成立，令12,12x t ⎡⎤=∈⎢⎥⎣⎦，设2()32,()g t t t g t =+在1,12⎡⎤⎢⎥⎣⎦上单调递增，则min 17()24g t g ⎛⎫== ⎪⎝⎭，即74k <. 又由于[1,0]x ∈-时，240x k -⋅>恒成立，解得2k >，故符合题意的实数k 不存在.【点睛】本题考查对数函数的单调性、恒成立问题的转化分析、指数函数与二次函数的复合函数的最值问题.25．[4,)+∞【分析】利用对数式的运算性质把给出的等式变形，去掉对数符号后利用基本不等式转化为关于(x +y )的二次不等式，求解后即可得到x +y 的取值范围.【详解】222log ()log log x y x y +=+，x y xy ∴+=，0,0x y >>，2()2x y x y xy +∴+=≤，当且仅当2x y ==时，等号成立。

北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(答案解析)(1)

一、选择题1．若关于x 的不等式34log 2xa x -≤在10,2x ⎛⎤∈ ⎥⎝⎦恒成立，则实数a 的取值范围是（） A ．1,14⎡⎫⎪⎢⎣⎭B ．10,4⎛⎤ ⎥⎝⎦C ．3,14⎡⎫⎪⎢⎣⎭D ．30,4⎛⎤ ⎥⎝⎦2．已知函数()()2log 2xf x m =+，则满足函数()f x 的定义域和值域都是实数集R 的实数m 构成的集合为（） A ．{}|0m m =B ．{}0|m m ≤C ．{}|0m m ≥D ．{}|1m m =3．若()()22ln 1f x x x e =+≤≤(e 为自然对数的底数)，则函数()()22y f x f x =+⎡⎤⎣⎦的最大值为（） A ．6B ．13C ．22D ．334．已知函数()()2log 23a f x x x =--+，若()00f <，则此函数的单调递增区间是（） A ．(],1-∞-B ．[)1,-+∞C ．[)1,1-D ．(]3,1--5．已知函数)()lnf x x =，则120212020a f ⎛⎫= ⎪⎝⎭，20201log 2021b f ⎛⎫= ⎪⎝⎭，()2021log 2020c f =的大小关系为（）A ．a b c >>B ．a c b >>C ．b a c >>D ．b c a >>6．已知函数22()lg[(1)(1)1]f x a x a x =-+++的值域为R ．则实数a 的取值范围是（） A ．5[1,]3B ．5(1,]3C ．(]5,1(,)3-∞-⋃+∞ D ．()5,1[1,)3-∞-7．已知函数3()22x f x =+，则111357(1)432234f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭（） A ．212 B ．214C ．7D ．1528．5G 技术的数学原理之一便是著名的香农公式：2log 1S C W N ⎛⎫=+⎪⎝⎭，它表示：在受高斯白噪声干扰的信道中，最大信息传递速率C 取决于信道带宽W 、信道内所传信号的平均功率S 、信道内部的高斯噪声功率N 的大小，其中SN叫做信噪比.按照香农公式，在不改变W 的情况下，将信噪比SN从1999提升至λ，使得C 大约增加了20%，则λ的值约为（参考数据：lg 20.3≈， 3.96109120≈）（） A ．7596B ．9119C ．11584D ．144699．已知()lg(10)lg(10)f x x x =++-，则()f x 是（） A ．偶函数，且在(0,10)是增函数 B ．奇函数，且在(0,10)是增函数 C ．偶函数，且在(0,10)是减函数 D ．奇函数，且在(0,10)是减函数10．函数()22x xxf x -=+的大致图象为（） A ． B ．C ．D ．11．若1a b >>，lg lg P a b ⋅，1(lg lg )2Q a b =+，lg()2a b R +=，则（） A ．R P Q < 在R 上是增函数；②函数(1)f x -的定义域是(1,3)，则函数()f x 的定义域为(2,4)； ③已知()f x =538x ax bx ++-，且()28f -=，则(2)8f =-； ④11()122x f x =--为奇函数．14．若函数()22log 3y x ax a =-+在[2,)+∞上是单调增函数，则a 的取值范围是____________．15．设函数2()ln(1)fx x x =++，若()23(21)0f a f a +-<，则实数a 的取值范围为_____. 16．若3log 14a>（0a >且1a ≠），则实数a 的取值范围为________ 17．已知函数()4sin 22xx f x π=++，则122019101010101010f f f ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭______.18．如图，在面积为2的平行四边形OABC 中，AC CO ⊥，AC 与BO 交于点E .若指数函数()01xy aa a =>≠,经过点E ，B ，则函数()af x x x=-在区间[]1,2上的最小值为________.19．设log c a ､log c b 是方程2530x x +-=的两个实根，则log b ac =______.20．下列结论正确的是____________①1()2(0,1)x f x a a a -=+>≠的图像经过定点(1,3)； ②已知28log 3,43yx ==，则2x y +的值为3； ③若3()6f x x ax =+-，且(2)6f -=，则(2)18f =； ④11()()122xf x x =--为偶函数； ⑤已知集合{}{}1,1,|1A B x mx =-==；且B A ⊆，则m 的值为1或-1.三、解答题21．设131()log 1axf x x -=-为奇函数，a 为常数．（1）求a 的值．（2）若[2,4]x ∀∈，不等式1()3xf x x m ⎛⎫+>+ ⎪⎝⎭恒成立，求实数m 的取值范围．22．已知函数()13xf x ⎛⎫= ⎪⎝⎭，函数()13log g x x =.（1）若函数()22y g mx mx =++的定义域为R ，求实数m 的取值范围；（2）是否存在非负实数,m n ，使得函数()2y g f x ⎡⎤=⎣⎦的定义域为[],m n ，值域为[]2,2m n ，若存在，求出,m n 的值；若不存在，则说明理由；（3）当[]1,1x ∈-时，求函数()()223y f x af x =-+⎡⎤⎣⎦的最小值()h a . 23．已知函数()ln(32)f x x =+，()ln(32)g x x =-.设函数()()()F x f x g x =-. （1）求函数()F x 的定义域；（2）判断()F x 奇偶性并证明；（3）若()0F x >成立，求x 的取值范围.24．已知函数()12,012,0m x x x f x x n x x ⎧⎛⎫+-> ⎪⎪⎪⎝⎭=⎨⎛⎫⎪++< ⎪⎪⎝⎭⎩是奇函数.（1）求实数m ，n 的值；（2）若对任意实数x ，都有()()420xxf f λ+≥成立.求实数λ的取值范围. 25．已知集合(){}2log 33A x x =+≤，{}213B x m x m =-<≤+.（1）若2m =-，求A B ；（2）若A B A ⋃=，求实数m 的取值范围.26．化简计算：（1）160.25361.587-⎛⎫⨯-+ ⎪⎝⎭（2）lg5lg 20lg 2lg50lg 25⋅-⋅-.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】转化为当10,2x ⎛⎤∈ ⎥⎝⎦时，函数342xy =-的图象不在log a y x =的图象的上方，根据图象列式可解得结果.【详解】由题意知关于x的不等式34log2xax-≤在10,2x⎛⎤∈ ⎥⎝⎦恒成立，所以当10,2x⎛⎤∈ ⎥⎝⎦时，函数342xy=-的图象不在log ay x=的图象的上方，由图可知0111log22aa<<⎧⎪⎨≥⎪⎩，解得114a≤<.故选：A【点睛】关键点点睛：利用函数342xy=-的图象与函数log ay x=的图象求解是解题关键. 2．A解析：A【分析】若定义域为实数集R，则20x m+>对于x∈R恒成立，可得0m≥，若值域为实数集R，令2xt m=+，则2logy t=此时需满足2xt m=+的值域包括()0,∞+，可得0m≤，再求交集即可.【详解】若()()2log2xf x m=+定义域为实数集R，则20x m+>对于x∈R恒成立，即2xm>-对于x∈R恒成立，因为20x>，所以20x-<，所以0m≥，令2xt m=+，则2logy t=若()()2log2xf x m=+值域为实数集R，则2xt m=+的值域包括()0,∞+，因为t m>，所以0m≤，所以0m=，故选：A【点睛】关键点点睛：本题的关键点是要找到定义域为R 的等价条件即20x m +>对于x ∈R 恒成立，分离参数m 求其范围，值域为R 的等价条件即2x t m =+可以取遍所有大于0的数，由t m >，所以0m ≤，再求交集.3．B解析：B 【分析】先依题意求函数定义域，再化简函数，进行换元后求二次函数在区间上的最大值即可. 【详解】由21x e ≤≤及()2f x知221x e ≤≤，故定义域为[]1,e ，又()()()()()222222ln 2ln ln 6ln 61y f x f x x x x x x e =+=+++=++≤≤⎡⎤⎣⎦令[]ln 0,1t x =∈，则266y t t =++，易见y 在[]0,1t ∈上单调递增，故当1t =时，即x e =时，max 16613y =++=. 故选：B. 【点睛】易错点睛：利用换元法求函数最值时，要注意函数的定义域，否则求得的易出错.4．C解析：C 【分析】由()00f <求得01a <<，求出函数()f x 的定义域，利用复合函数法可求得函数()f x 的单调递增区间. 【详解】由题意可得()0log 30log 1a a f =<=，01a ∴<<.对于函数()()2log 23a f x x x =--+，2230x x --+>，可得2230x x +-<，解得31x -<<.所以，函数()f x 的定义域为()3,1-.由于内层函数223u x x =--+在区间(]3,1--单调递增，在区间[)1,1-单调递减. 外层函数log a y u =单调递减，由复合函数法可知，函数()f x 的单调递增区间为[)1,1-. 故选：C. 【点睛】方法点睛：函数单调性的判定方法与策略：（1）定义法：一般步骤：设元→作差→变形→判断符号→得出结论；（2）图象法：如果函数()f x 是以图象的形式给出或者函数()f x 的图象易作出，结合图象可得出函数的单调区间；（3）导数法：先求出函数的导数，利用导数值的正负确定函数的单调区间；（4）复合函数法：先将函数()y f g x ⎡⎤=⎣⎦分解为内层函数()u g x =和外层函数()y f u =，再讨论这两个函数的单调性，然后根据复合函数法“同增异减”的规则进行判定. 5．D解析：D 【分析】先判断出()f x 在R 上单调递减，再利用指数对数函数的单调性求出120212020，20201log 2021， 2021log 2020的范围，即可根据单调性比较大小.【详解】210x x +->恒成立，()f x ∴定义域为R ，))()lnlnf x x x ===-，其中y x 单调递增，则()f x 单调递减，102021202020120>=，202020201log log 102021<=，2021202120210log 1log 2020log 20211=<<=，b c a ∴>>. 故选：D. 【点睛】关键点睛：本题考查利用函数的单调性比较大小，解题的关键是判断出)()ln f x x =在R 上单调递减，进而可利用单调性比较.6．A解析：A 【分析】当函数的值域为R 时，命题等价于函数()()22111y a x a x =-+++的值域必须包含区间()0+∞，得解【详解】22()lg[(1)(1)1]f x a x a x =-+++的值域为R令()()22111y a x a x =-+++，则()()22111y a x a x =-+++的值域必须包含区间()0+∞，当210a -=时，则1a =± 当1a =时，21y x =+符合题意；当1a =-时，1y =不符合题意；当1a ≠±时，()()222101410a a a ⎧->⎪⎨∆=+--≥⎪⎩，解得513a <≤ 513a ∴≤≤，即实数a 的取值范围是5[1,]3故选：A 【点睛】转化命题的等价命题是解题关键.7．B解析：B 【分析】先利用解析式计算3()(2)2f x f x +-=，再计算和式即可得到结果. 【详解】因为3()22x f x =+，所以2332(2)22224xx x f x -⋅-==+⋅+，()3323()(2)222222xx x f x f x ⋅+-=+=++. 故1113573321(1)34322342224f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++=⨯+=⎪ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭. 故选：B. 【点睛】本题解题关键是通过指数式运算计算3()(2)2f x f x +-=，再配对求和即解决问题. 8．B解析：B 【分析】根据题设条件列出方程，计算即可. 【详解】由题可知 ()()()22log 119991+20%log 1W W λ+⨯=+，即()221.2log 2000log 1λ⨯=+，所以()lg 1lg 20001.2lg 2lg 2λ+⨯=，即()()lg 1 1.2lg2000 1.23lg2 3.96λ+=⨯=⨯+≈，所以 3.961109120λ+≈≈，所以9119λ≈.故选：B 【点睛】本题主要考查对属于对数函数，考查学生的运算能力.9．C解析：C 【分析】先判断函数的定义域关于原点对称，再由奇偶性的定义判断奇偶性，根据复合函数的单调判断其单调性，从而可得结论. 【详解】由100100x x +>⎧⎨->⎩，得(10,10)x ∈-，故函数()f x 的定义域为()10,10-，关于原点对称，又()()lg 10lg(10)()f x x x f x -=-++=，故函数()f x 为偶函数，而()()2lg(10)lg(10)lg 100f x x x x=++-=-，因为函数2100y x =-在()0,10上单调递减，lg y x =在()0,∞+上单调递增，故函数()f x 在()0,10上单调递减，故选C. 【点睛】本题主要考查函数的奇偶性与单调性，属于中档题. 判断函数的奇偶性首先要看函数的定义域是否关于原点对称，如果不对称，既不是奇函数又不是偶函数，如果对称常见方法有：（1）直接法， ()()f x f x -=±(正为偶函数，负为减函数)；（2）和差法，()()0f x f x -±=（和为零奇函数，差为零偶函数）；（3）作商法，()()1f x f x -=±（1 为偶函数，1- 为奇函数） .10．B解析：B 【分析】根据函数为奇函数排除C ，取特殊值排除AD 得到答案. 【详解】当()22x xx f x -=+，()()22x x xf x f x ---==-+，函数为奇函数，排除C ； 2221(2)22242f -=<=+，排除A ；3324(3)22536f -==+，4464(4)224257f -==+，故()()34f f >，排除D.故选：B. 【点睛】本题考查了函数图象的识别，意在考查学生的计算能力和识图能力，取特殊值排除是解题的关键.11．B解析：B 【分析】利用对数函数lg y x =，结合基本不等式即可确定P 、Q 、R 的大小关系【详解】由于函数lg y x =在(0,)+∞上是增函数1a b >>，则lg lg 0a b >>由基本不等式可得11(lg lg )lg()lg 222a bP a b ab R +=<+==<=因此，P Q R <<故选：B 【点睛】本题考查了利用对数函数的单调性比较大小，应用函数思想构造对数函数，并利用其单调性和基本不等式比较大小12．B解析：B 【分析】根据指数式与对数的互化公式，求得11lg2,lg5a b==，再结合对数的运算公式，即可求解. 【详解】因为2510a b ==，可得25log 10,log 10a b ==，所以11lg2,lg5a b==，则11lg 2lg5lg101a b +=+==. 故选：B. 【点睛】本题主要考查指数式与对数的互化，以及对数的运算公式的化简、求值，其中解答中熟记指数式与对数的互化公式，以及对数的运算公式，准确运算是解答的关键，着重考查运算与求解能力.二、填空题13．①④【分析】根据指数的运算性质且恒成立求出函数图象所过的定点可判断①；根据抽象函数的定义域的求法可判断②；根据奇函数的图象和性质求出可判断③；根据奇函数的定义及判定方法可判断④【详解】解：当时且恒成解析：①④ 【分析】根据指数的运算性质01(0a a =>且1)a ≠恒成立，求出函数图象所过的定点，可判断①；根据抽象函数的定义域的求法，可判断②；根据奇函数的图象和性质，求出()2f ，可判断③；根据奇函数的定义及判定方法，可判断④ 【详解】解：当1x =时，101(0x a a a -==>且1)a ≠恒成立，故f （1）4=恒成立，故函数1()3(0x f x a a -=+>且1)a ≠的图象一定过定点(1,4)P ，故①正确；函数(1)f x -的定义域是(1,3)，则函数()f x 的定义域为(0,2)，故②错误；已知53()8f x x ax bx =++-，且(2)8f -=，则()224f =-，故③错误；11()122x f x =--的定义域为{|0}x x ≠，且112111()()122212212x x x xf x f x ---=-=-=-=----，故()f x 为奇函数，故④正确；故答案为：①④ 【点睛】本题以命题的真假判断为载体，考查了指数函数的图象和性质，函数的定义域，函数的奇偶性，是函数图象和性质的综合应用，难度不大，属于基础题．14．【分析】利用复合函数单调性的判断方法分内层和外层分别判断解出的取值范围【详解】由题意得设根据对数函数及复合函数单调性可知：在上是单调增函数且所以所以故答案为:【点睛】本题考查复合函数单调性的应用考查解析：(4,4]-【分析】利用复合函数单调性的判断方法,分内层和外层分别判断,解出a 的取值范围. 【详解】由题意得，设2()3g x x ax a =-+，根据对数函数及复合函数单调性可知：()g x 在[)2,+∞上是单调增函数，且(2)0g >，所以2240aa ⎧≤⎪⎨⎪+>⎩，所以44a -<≤．故答案为: (4,4]- 【点睛】本题考查复合函数单调性的应用,考查对数函数的性质,考查学生运算求解能力,属于中档题.15．【分析】根据已知可得为奇函数且在上单调递增不等式化为转化为关于自变量的不等式即可求解【详解】的定义域为是奇函数设为增函数在为增函数在为增函数在处连续的所以在上单调递增化为等价于即所以实数的取值范围为解析：1(1,)3-【分析】根据已知可得()f x 为奇函数且在R 上单调递增，不等式化为()23(12)f a f a <-，转化为关于自变量的不等式，即可求解. 【详解】()f x 的定义域为R ，()()))ln10f x f x x x +-=+==，()f x ∴是奇函数，设,[0,)()x u x x =∈+∞为增函数，()f x 在[0,)+∞为增函数，()f x 在(,0)-∞为增函数， ()f x 在0x =处连续的，所以()f x 在R 上单调递增，()23(21)0f a f a +-<，化为()23(12)f a f a <-，等价于2312a a <-，即213210,13a a a +-<-<<，所以实数a 的取值范围为1(1,)3-. 故答案为: 1(1,)3- 【点睛】本题考查利用函数的单调性和奇偶性解不等式，熟练掌握函数的性质是解题的关键，属于中档题.16．【分析】讨论和两种情况利用函数单调性解不等式得到答案【详解】当时满足不成立；当时综上所述：故答案为：【点睛】本题考查了利用函数单调性解不等式分类讨论是解题的关键解析：3,14⎛⎫⎪⎝⎭【分析】讨论1a >和01a <<两种情况，利用函数单调性解不等式得到答案. 【详解】3log 1log 4aa a >=，当1a >时，满足34a >，不成立；当01a <<时，34a >. 综上所述：3,14a ⎛⎫∈⎪⎝⎭. 故答案为：3,14⎛⎫⎪⎝⎭.【点睛】本题考查了利用函数单调性解不等式，分类讨论是解题的关键.17．2019【分析】观察的特点探究得再利用倒序相加法求解【详解】因为所以故答案为：2019【点睛】本题主要考查了函数求值中的倒序相加法还考查了抽象概括的能力属于中档题解析：2019 【分析】观察122019101010101010⎛⎫⎛⎫⎛⎫+++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭f f f 的特点，探究得()(2)2+-=f x f x ，再利用倒序相加法求解. 【详解】因为()()()2442sin sin 222222x x f x f x x x πππ-+-=+++-=++ 所以1220192[]101010101010⎛⎫⎛⎫⎛⎫+++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭f f f12019120191010101010101010f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭22019=⨯1220192019101010101010f f f ⎛⎫⎛⎫⎛⎫∴+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故答案为：2019.【点睛】本题主要考查了函数求值中的倒序相加法，还考查了抽象概括的能力，属于中档题.18．【分析】设点则点B 的坐标为由题意得则再根据平行四边形的面积求得由此得得函数的解析式从而得函数的的单调性与最值【详解】解：设点则点B 的坐标为∵∴∵平行四边形OABC 的面积又平行四边形OABC 的面积为2 解析：3-【分析】设点(),tE t a ，则点B 的坐标为()2,2tt a ，由题意得22tt aa =，则2t a =，再根据平行四边形的面积求得12t =，由此得4a =，得函数()f x 的解析式，从而得函数()f x 的的单调性与最值．【详解】解：设点(),tE t a ，则点B 的坐标为()2,2tt a ，∵22t t a a =，∴2t a =，∵平行四边形OABC 的面积24t S OC AC a t t =⨯⨯==，又平行四边形OABC 的面积为2，∴42t =，12t =，所以122a =，4a =， ∴()4f x x x=-在[]1,2为增函数，∴函数()f x 的最小值为()4111f =-=3-，故答案为：3-．【点睛】本题主要考查指数函数的图象和性质，考查利用函数的单调性求最值，属于中档题．19．【分析】根据题意由韦达定理得进而得再结合换底公式得【详解】解：因为､是方程的两个实根所以由韦达定理得所以所以所以故答案为：【点睛】本题解题的关键在于根据韦达定理与换底公式进行计算其中两个公式的转化是解析：37±【分析】根据题意由韦达定理得log log 5c c a b +=-，log log 3c c a b ⋅=-，进而得()2log log 37c c a b -=，再结合换底公式得1log log b acc b a==【详解】解：因为log c a ､log c b 是方程2530x x +-=的两个实根，所以由韦达定理得log log 5c c a b +=-，log log 3c c a b ⋅=-，所以()()22log log log log 4log log 37c c c c c c a b a b a b -=+-⋅=，所以log log c c b a -=所以11log log log 37log b c c acc b b a a===±-.故答案为：37± 【点睛】本题解题的关键在于根据韦达定理与换底公式进行计算，其中()()22log log log log 4log log c c c c c c a b a b a b -=+-⋅，1log log b acc b a=两个公式的转化是核心，考查运算求解能力，是中档题.20．①②④【分析】①根据指数函数的性质进行判断②根据对数的运算法则进行判断③根据函数的运算性质进行运算④根据偶函数的定义进行判断⑤根据集合关系利用排除法进行判断【详解】①当时（1）则函数的图象经过定点；解析：①②④ 【分析】①根据指数函数的性质进行判断，②根据对数的运算法则进行判断，③根据函数的运算性质进行运算，④根据偶函数的定义进行判断，⑤根据集合关系，利用排除法进行判断．【详解】①当1x =时，f （1）02123a =+=+=，则函数的图象经过定点(1,3)；故①正确， ②已知2log 3x =，843y=，则2823y=，282log 3y =，则2222882log 3log log (3)log 8333x y +=+=⨯==；故②正确， ③若3()6f x x ax =+-，且(2)6f -=，则32266a ---=，即10a =-，则f （2）32210618=-⨯-=-，故③错误；④函数的定义域为{|0}x x ≠，关于原点对称，1112()()?1222(12)xx x f x x x +=-=--，则122112()?··()2(12)2(21)2(12)x x xx x x f x x x x f x --+++-=-=-==---，即()f x 为偶函数，故④正确，⑤已知集合{1A =-，1}，{|1}B x mx ==，且B A ⊆，当0m =时，B =∅，也满足条件，故⑤错误，故正确的是①②④，故答案为：①②④ 【点睛】本题主要考查命题的真假判断，涉及指数函数的性质，函数奇偶性的判断，以及对数的运算法则，综合性较强，涉及的知识点较多．三、解答题21．（1）1a =-；（2）89m <. 【分析】（1）由奇函数的性质()()0f x f x ，代入运算后可得1a =±，代入验证即可得解；（2）转化条件为131log 113xx x m x +<⎛⎫- ⎝+⎪⎭-对于[2,4]x ∀∈恒成立，令()[]131log ,2,4113xx g x x x x ⎛⎫-+=+⎝⎭∈- ⎪，结合函数的单调性求得()min g x 即可得解.【详解】（1）因为131()log 1axf x x -=-为奇函数，则1113331111()()log log log 1111ax ax ax ax f x f x x x x x +-⎡+-⎤⎛⎫⎛⎫-+=+= ⎪⎪⎢⎥------⎝⎭⎝⎭⎣⎦ ()21231log 01ax x-==-，则()22111ax x -=-，所以21a =即1a =±，当1a =时，()11331()log log 11xf x x -==--，不合题意；当1a =-时，131()log 1x f x x +=-，由101xx +>-可得1x >或1x <-，满足题意；故1a =-；（2）由1()3xf x x m ⎛⎫+>+ ⎪⎝⎭可得131log 113xx x m x ⎛⎫>+ +⎪⎭+⎝-，则131log 113xx x m x +<⎛⎫- ⎝+⎪⎭-对于[2,4]x ∀∈恒成立，令()[]131log ,2,4113xx g x x x x ⎛⎫-+=+⎝⎭∈- ⎪，因为函数12111x y x x +==+--在[2,4]上单调递减，所以函数131log 1xy x +=-在[2,4]上单调递增，所以()g x 在[2,4]上单调递增，所以()()1min32log 182993g x g -===+，所以89m <. 【点睛】关键点点睛：解决本题的关键是将恒成立问题转化为求函数的最值.22．（1）08m ≤<；（2）存在，0,2m n ==；（3）答案不唯一，见解析. 【分析】（1）根据函数定义域为R ，转化为220mx mx ++>恒成立，分类讨论求解；（2）根据二次函数单调性可得2222m mn n ⎧=⎨=⎩，求解即可；（3）换元，令11,333xt ⎛⎫⎡⎤=∈ ⎪⎢⎥⎝⎭⎣⎦，分类讨论求二次函数的最小值即可. 【详解】（1）∵定义域为R ，即220mx mx ++>恒成立 ∴0m =，或00m >⎧⎨∆<⎩得08m << 综上得08m ≤< （2）2yx 的定义域为[],m n ，值域为[]2,2m n∴222(0)2m mm n n n ⎧=≤<⎨=⎩ ，解得0,2m n ==. （3）令11,333xt ⎛⎫⎡⎤=∈ ⎪⎢⎥⎝⎭⎣⎦，则223y t at =-+ 若13a ≤，则228()39a h a =-+；若133a <<，则2()3h a a =-；若3a ≥，则()612h a a =-+；【点睛】关键点点睛：涉及指数型复合函数的单调性最值问题，多采用换元法，能够使问题简捷，突出问题本质，大多转化为二次函数，利用二次函数的图象和性质，体现转化思想，属于中档题. 23．（1）33,22⎛⎫- ⎪⎝⎭；（2）奇函数，证明见解析；（3）302x <<【分析】（1）由320320x x +>⎧⎨->⎩可解得结果；（2）()F x 是奇函数，根据奇函数的定义可证结论正确；（3）根据对数函数的单调性可解得结果. 【详解】（1）由320320x x +>⎧⎨->⎩，解得3322x -<<，所以函数()F x 的定义域为33(,)22-.（2）()F x 是奇函数. 证明如下：x ∀∈33(,)22-，都有x -∈33(,)22-，因为 ()ln(32)ln(32)()F x x x F x -=--+=-， ∴()F x 是奇函数.（3）由()0F x >可得()()0f x g x ->，得ln(32)ln(32)0x x +-->，即ln(32)ln(32)x x +>-，由对数函数的单调性得32320x x ，解得302x <<.【点睛】易错点点睛：利用对数函数的单调性解对数不等式时，容易忽视函数的定义域. 24．（1）22m n =⎧⎨=⎩；（2）1λ≥-. 【分析】（1）根据()f x 是奇函数，即()()f x f x -=-即可求解实数m ，n 的值；（2）利用换元法，转化为二次函数的问题讨论最值恒成立即可求解实数λ的取值范围. 【详解】（1）当0x >时，()()()12f x x n x ⎡⎤-=-++⎢⎥-⎣⎦，因为()f x 为奇函数，()()f x f x ∴-=-，()()()1122f x x n m x x x ⎡⎤⎡⎤⎛⎫∴-=-++=-+-⎢⎥ ⎪⎢⎥-⎝⎭⎣⎦⎣⎦，即()()1220m x n x ⎛⎫-++-= ⎪⎝⎭总成立. 2020m n -=⎧∴⎨-=⎩，22m n =⎧∴⎨=⎩，又当0x <时，同理可得22m n =⎧⎨=⎩，综上：22m n =⎧∴⎨=⎩. （2）40x >，20x >，原不等式化为11242222042xx xxλλ⎛⎫⎛⎫+-++-≥ ⎪ ⎪⎝⎭⎝⎭，令122xxt =+，则2t ≥，原不等式进一步化为230t t λλ+--≥在2t ≥上恒成立. 记()23g t t t λλ=+--，[)2,t ∈+∞①当22λ-≤时，即4λ≥-时，()()min 210g t g λ==+≥，1λ∴≥-合理；②当22λ->时，即4<-λ时，()n2mi 3024g t g λλλ⎛⎫-=---≥ ⎪⎝⎭=，显然不成立.综上实数λ的取值范围为：1λ≥-. 【点睛】本题考查的知识点是分段函数的应用，指数函数的单调性，奇函数的性质，是函数图象和性质的综合应用，难度中档.25．（1）{}31A B x x ⋂=-<≤；（2）[][)1,24,m ∈-+∞【分析】（1）计算{}35A x x =-<≤，{}51B x x =-<≤，再计算交集得到答案. （2）A B A ⋃=，故B A ⊆，讨论B =∅和B ≠∅，计算得到答案. 【详解】（1）(){}{}2log 3335A x x x x =+≤=-<≤，{}51B x x =-<≤，故{}31A B x x ⋂=-<≤.（2）{}35A x x =-<≤，A B A ⋃=，故B A ⊆，当B =∅时，213m m -≥+，解得4m ≥；当B ≠∅时，4m <，故21335m m -≥-⎧⎨+≤⎩，解得12m -≤≤.综上所述：[][)1,24,m ∈-+∞.【点睛】本题考查交集运算，根据集合的包含关系求参数，意在考查学生的计算能力和综合应用能力.26．（1）110；（2）-1 【分析】（1）原式化简为分数指数幂，计算结果；（2）根据对数运算公式化简求值. 【详解】（1）原式113133234432222323-⎛⎫⎛⎫=+⨯+⨯- ⎪ ⎪⎝⎭⎝⎭113322210833⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭110=（2）原式()()22lg5lg 25lg 2lg 510lg5=⨯⨯-⋅⨯-()()lg52lg2lg5lg2lg512lg5=⨯+-⋅+-()22lg 2lg5lg5lg 2lg5lg 22lg5=⋅+-⋅--()()2lg 2lg5lg5lg 2lg5lg5=⋅+-+-()lg5lg2lg51lg5=⋅+--lg51lg51=--=-【点睛】本题考查指数幂和对数运算，重点考查计算能力，转化与变形，属于基础题型.。

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(含答案解析)(3)

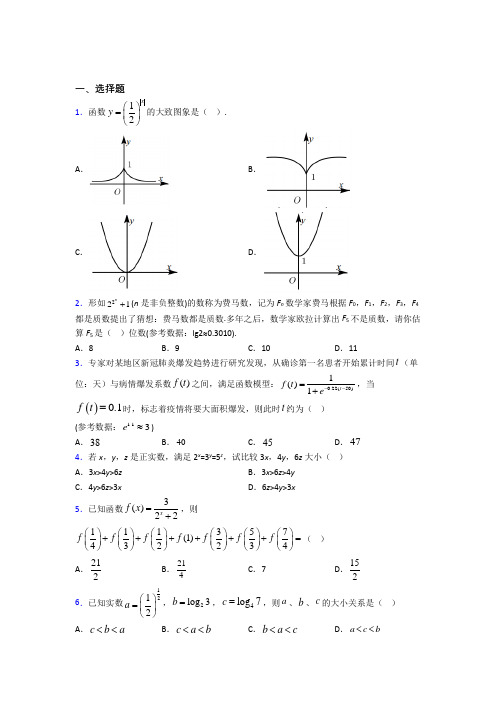
一、选择题1．函数12xy ⎛⎫= ⎪⎝⎭的大致图象是（）. A ． B ．C ．D ．2．形如221n+(n 是非负整数)的数称为费马数，记为F n 数学家费马根据F 0，F 1，F 2，F 3，F 4都是质数提出了猜想：费马数都是质数.多年之后，数学家欧拉计算出F 5不是质数，请你估算F 5是（）位数(参考数据：lg2≈0.3010). A ．8B ．9C ．10D ．113．专家对某地区新冠肺炎爆发趋势进行研究发现，从确诊第一名患者开始累计时间t （单位：天）与病情爆发系数()f t 之间，满足函数模型：0.22(50)11()t f t e --=+，当()0.1f t =时，标志着疫情将要大面积爆发，则此时t 约为（）(参考数据： 1.13e ≈) A ．38 B ．40C ．45D ．474．若x ，y ，z 是正实数，满足2x =3y =5z ，试比较3x ，4y ，6z 大小（）A ．3x >4y >6zB ．3x >6z >4yC ．4y >6z >3xD ．6z >4y >3x5．已知函数3()22x f x =+，则111357(1)432234f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭（） A ．212B ．214C ．7D ．1526．已知实数1212a ⎛⎫= ⎪⎝⎭，2log 3b =，4log 7c =，则a 、b 、c 的大小关系是（）A ．c b a <<B ．c a b <<C ．b a c <<D ．a c b <<7．函数1()1x f x a +=-恒过定点（）A ．(1,1)B ．(1,1)-C ．(1,0)-D ．(1,1)--8．已知3log 2a =，那么33log 82log 6-用a 表示是( ) A ．52a -B ．2a -C ．23(1)a a -+D ．231a a --9．已知()lg(10)lg(10)f x x x =++-，则()f x 是（） A ．偶函数，且在(0,10)是增函数 B ．奇函数，且在(0,10)是增函数 C ．偶函数，且在(0,10)是减函数D ．奇函数，且在(0,10)是减函数10．若函数112xy m -⎛⎫=+ ⎪⎝⎭的图象与x 轴有公共点，则m 的取值范围是（）A ．1m ≤-B ．10m -≤<C ．m 1≥D ．01m <≤11．设()lg (21)fx x a =-+是奇函数，则使f(x)<0的x 的取值范围是( )．A ．(－1,0)B ．(0, 1)C ．(－∞，0)D ．(－∞，0)∪(1，＋∞)12．函数()log (3)a f x ax =-在[]13，上单调递增，则a 的取值范围是（） A ．()1+∞， B ．()01，C ．103⎛⎫ ⎪⎝⎭，D ．()3+∞，二、填空题13．已知函数()2log f x x =，正实数m ，n 满足m n <，且()()f m f n =，若()f x 在区间2,m n ⎡⎤⎣⎦上的最大值为2，则m n +=________.14．若函数()22log 3y x ax a =-+在[2,)+∞上是单调增函数，则a 的取值范围是____________．15．若()2lg 2lg lg x y x y -=+，则2x y=______．16．已知1122x x-+=22165x x x x --+-=+-______.17．关于x 的不等式()()222log 1log 2x x ->-的解集为______.18．设函数()f x =，则()()()()()()543456f f f f f f -+-+-++++=_____.19．已知2336m n ==，则11m n+=______． 20．已知函数()()log 21101a y x a a =-+>≠,的图象过定点A ，若点A 也在函数()2x f x b =+的图象上，则()2log 3f =________. 三、解答题21．已知函数21()log 1x f x x +=-. （1）求函数()f x 的定义域并证明该函数是奇函数；（2）若当(1,)x ∈+∞时，2()()log (1)g x f x x =+-，求函数()g x 的值域. 22．计算：（1）1ln 224()9e-+；（2）()223lg 2lg5lg 20log 3log 4+⋅+⋅.23．已知函数()log (1)a f x x =+，()log (1)(0a g x x a =->，且1)a ≠. （1）求函数()()f x g x -的定义域；（2）判断函数()()f x g x -的奇偶性，并说明理由；（3）当2a =时，判断函数()()f x g x -的单调性，并给出证明.24．已知函数()12xf x ⎛⎫= ⎪⎝⎭，函数()2log g x x =. （1）若()22g mx x m ++的定义域为R ，求实数m 的取值范围；（2）当[]1,1x ∈-时，函数()()223y f x af x =-+⎡⎤⎣⎦的最小值为1，求实数a 的值. 25．已知函数()21log 1x f x x +=-，（1）求函数()y f x =的定义域；（2）证明：()y f x =是奇函数；（3）设()()()14h x f x f x =+，求函数()y h x =在[]3,7内的值域； 26．已知函数()f x 是定义在R 上的奇函数，当0x 时，()121xaf x =++. （1）求实数a 的值及()f x 的解析式；（2）求方程4|(1)|5f x -=的解.【参考答案】***试卷处理标记，请不要删除一、选择题1．A 解析：A 【分析】去绝对值符号后根据指数函数的图象与性质判断．【详解】由函数解析式可得：1,022,0xx x y x ⎧⎛⎫≥⎪ ⎪=⎨⎝⎭⎪<⎩可得值域为：01y <≤，由指数函数的性质知：在(),0-∞上单调递增；在()0,∞+上单调递减. 故选：A. 【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.2．C解析：C 【分析】根据所给定义表示出9.632951010F =⨯，进而即可判断出其位数．【详解】根据题意，53223232lg232lg2320.30109.6320.6329521212101010101010F ⨯=+=+≈==≈==⨯，因为0.63211010<<，所以5F 的位数是10．故选：C 【点睛】关键点睛：解答本题的关键是转化成对数运算，即3232lg 2210=.3．B解析：B 【分析】根据()0.1f t =列式求解即可得答案.【详解】解：因为()0.1f t =，0.22(50)11()t f t e --=+，所以0.22(50)()0.111t f t e--==+，即0.22(50)011t e --=+，所以0.22(50)9t e --=，由于 1.13e ≈，故()21.12.29e e =≈，所以0.222().250t e e --=，所以()0.2250 2.2t --=，解得40t =. 故选：B. 【点睛】本题解题的关键在于根据题意得0.22(50)9t e --=，再结合已知 1.13e ≈得()21.12.29e e =≈，进而根据0.222().250t e e --=解方程即可得答案，是基础题.4．B解析：B 【分析】令235x y z t ===，则1t >，lg lg 2t x =，lg lg 3t y =，lg lg 5tz =，利用作差法能求出结果. 【详解】∵x 、y 、z 均为正数，且235x y z ==，令235x y z t ===，则1t >，故2lg log lg 2t x t ==，3lg log lg 3t y t ==，5lg log lg 5tz t ==， ∴()3lg lg5lg 4lg 2lg 3630lg 2lg5lg 2lg5t t t x z -⎛⎫-=-=>⎪⋅⎝⎭，即36x z >； ()2lg lg 27lg 253lg 2lg 6420lg5lg3lg3lg5t t t z y -⎛⎫-=-=> ⎪⋅⎝⎭，即64z y >，即364x z y >>成立，故选：B. 【点睛】关键点点睛：（1）将指数式转化为对数式；（2）利用作差法比较大小.5．B解析：B 【分析】先利用解析式计算3()(2)2f x f x +-=，再计算和式即可得到结果. 【详解】因为3()22x f x =+，所以2332(2)22224xx x f x -⋅-==+⋅+，()3323()(2)222222x x x f x f x ⋅+-=+=++.故1113573321(1)34322342224f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++=⨯+=⎪ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭. 故选：B. 【点睛】本题解题关键是通过指数式运算计算3()(2)2f x f x +-=，再配对求和即解决问题. 6．D解析：D 【分析】本题首先可根据2log 3b =以及2log c =得出b c >，然后根据1a <以及1c >得出c a >，即可得出结果.【详解】因为2log 3b =，42log 7log 7c ，函数2log y x =在()0,∞+上是增函数，所以b c >，因为01211122a <⎛⎫⎛⎫= ⎪ ⎪⎝⎝⎭=⎭，44log 7log 41c ，所以c a >，综上所述，a c b <<，故选：D. 【点睛】指数、对数的大小比较，可通过寻找合适的单调函数来构建大小关系，不同类型的数比较大小，应找一个中间数，通过它实现大小关系的传递，考查计算能力，是中档题.7．C解析：C 【分析】根据指数函数性质求定点. 【详解】因为01a =,所以()011f a -=-=0,因此过定点()1,0-,选C.【点睛】本题考查指数函数性质以及定点问题，考查基本分析求解能力，属于基础题.8．B解析：B 【解析】试题分析：33333333log 82log 6log 22log 233log 22(log 2log 3)-=-⨯=-+3log 222a =-=-,所以答案选B .考点：指数对数的计算9．C解析：C 【分析】先判断函数的定义域关于原点对称，再由奇偶性的定义判断奇偶性，根据复合函数的单调判断其单调性，从而可得结论. 【详解】由100100x x +>⎧⎨->⎩，得(10,10)x ∈-，故函数()f x 的定义域为()10,10-，关于原点对称，又()()lg 10lg(10)()f x x x f x -=-++=，故函数()f x 为偶函数，而()()2lg(10)lg(10)lg 100f x x x x=++-=-，因为函数2100y x =-在()0,10上单调递减，lg y x =在()0,∞+上单调递增，故函数()f x 在()0,10上单调递减，故选C. 【点睛】本题主要考查函数的奇偶性与单调性，属于中档题. 判断函数的奇偶性首先要看函数的定义域是否关于原点对称，如果不对称，既不是奇函数又不是偶函数，如果对称常见方法有：（1）直接法， ()()f x f x -=±(正为偶函数，负为减函数)；（2）和差法，()()0f x f x -±=（和为零奇函数，差为零偶函数）；（3）作商法，()()1f x f x -=±（1 为偶函数，1- 为奇函数） .10．B解析：B 【分析】11()+2x y m -=与x 有公共点，转化为11()2xy -=与y m =-有公共点，结合函数图象，可得结果. 【详解】11()+2x y m -=与x 有公共点，即11()2x y -=与y m =-有公共点，11()2xy -=图象如图可知0110m m <-≤⇒-≤< 故选：B 【点睛】本题考查了函数的交点问题，考查了运算求解能力和数形结合思想，属于基础题目.11．A解析：A 【解析】试题分析：由()lg (21)fxx a =-+为奇函数，则()()f xf x -=-，可得1a =-，即()lg 11f x xx =+-，又()0f x<，即lg110xx+-<，可变为0111x x <+-<，解得10x -<<．考点：函数的奇偶性，对数函数性质，分式不等式．12．D解析：D 【分析】由题意可得可得1a >，且30a ->，由此求得a 的范围．【详解】解：函数()log (3)a f x ax =-在[]13，上单调递增，而函数()3t x ax =-在[]13，上单调递增，根据复合函数的单调性可得1a >，且30a ->，解得3a >，即()3a ∈+∞，故选：D ．【点睛】本题主要考查对数函数的定义域、单调性，复合函数的单调性，属于基础题．二、填空题13．【分析】先画出函数图像并判断再根据范围和函数单调性判断时取最大值最后计算得到答案【详解】如图所示：根据函数的图象得所以结合函数图象易知当时在上取得最大值所以又所以再结合可得所以故答案为：【点睛】本题解析：52【分析】先画出函数图像并判断01m n <<<，再根据范围和函数单调性判断2x=m 时取最大值，最后计算得到答案. 【详解】如图所示：根据函数2()log x f x =的图象得01m n <<<，所以201m m <<<．结合函数图象，易知当2x=m 时()f x 在2,m n ⎡⎤⎣⎦上取得最大值，所以()222log2f m m== 又01m <<，所以12m =，再结合()()f m f n =，可得2n =，所以21522m n +=+=. 故答案为：52【点睛】本题考查对数型函数的图像和性质、函数的单调性的应用和最值的求法，是中档题.14．【分析】利用复合函数单调性的判断方法分内层和外层分别判断解出的取值范围【详解】由题意得设根据对数函数及复合函数单调性可知：在上是单调增函数且所以所以故答案为:【点睛】本题考查复合函数单调性的应用考查解析：(4,4]-【分析】利用复合函数单调性的判断方法,分内层和外层分别判断,解出a 的取值范围. 【详解】由题意得，设2()3g x x ax a =-+，根据对数函数及复合函数单调性可知：()g x 在[)2,+∞上是单调增函数，且(2)0g >，所以2240aa ⎧≤⎪⎨⎪+>⎩，所以44a -<≤．故答案为: (4,4]-【点睛】本题考查复合函数单调性的应用,考查对数函数的性质,考查学生运算求解能力,属于中档题.15．16【分析】由通过对数运算得出由此再求的值要注意定义域【详解】∵∴解得∴故答案为：16【点睛】本题主要考查对数的运算还考查了运算求解能力属于基础题解析：16 【分析】由()2lg 2lg lg x y x y -=+，通过对数运算得出4x y =，由此再求2x y的值．要注意定义域. 【详解】∵()2lg 2lg lg x y x y -=+，∴2(2)2000x y xy x y x y ⎧-=⎪->⎪⎨>⎪⎪>⎩，解得4x y =，∴42216x y==．故答案为：16 【点睛】本题主要考查对数的运算，还考查了运算求解能力，属于基础题．16．【分析】对平方可得再平方可得即可求解【详解】两边同时平方得：所以对两边同时平方得：则故答案为：【点睛】此题考查指数式的化简求值进行整体变形处理利用平方关系得出等量关系解析：12-【分析】对1122x x -+=13x x -+=，再平方可得227x x -+=，即可求解. 【详解】1122x x-+=125x x -++=，所以13x x -+=对13x x -+=两边同时平方得：2229x x -++=，227x x -+=则22167615352x x x x --+--==-+--. 故答案为：12- 【点睛】此题考查指数式的化简求值，进行整体变形处理，利用平方关系得出等量关系.17．【分析】由对数函数的性质化对数不等式为一元二次不等式组求解【详解】由得解得∴不等式的解集为故答案为：【点睛】本题考查对数不等式的解法考查了对数函数的性质是基础题解析：(,1-∞-. 【分析】由对数函数的性质化对数不等式为一元二次不等式组求解. 【详解】由()()222log 1log 2x x ->-，得21220x xx ⎧->-⎨->⎩，解得1x <--∴不等式()()222log 1log 2x x ->-的解集为(,1-∞-.故答案为：(,1-∞-. 【点睛】本题考查对数不等式的解法，考查了对数函数的性质，是基础题.18．【分析】根据指数的运算律计算出的值由此可计算出所求代数式的值【详解】因此故答案为【点睛】本题考查指数幂的化简计算解题的关键在于观察代数式结构并计算出为定值考查计算能力属于中等题解析：【分析】根据指数的运算律计算出()()1f x f x +-=的值，由此可计算出所求代数式的值. 【详解】()f x =()1122xx f x ∴-====， ()()12x x x f x f x ∴+-=+===，因此，()()()()()()54345662f f f f f f -+-+-++++=⨯=.故答案为【点睛】本题考查指数幂的化简计算，解题的关键在于观察代数式结构并计算出()()1f x f x +-为定值，考查计算能力，属于中等题.19．【分析】根据对数的定义和运算法则即可求解【详解】由可得所以所以故答案为：【点睛】本题主要考查对数的运算法则的应用考查了学生的计算能力属于中档题解析：12【分析】根据对数的定义和运算法则即可求解．【详解】由2336m n ==可得23log 36,log 36m n == 所以361log 2m =，361log 3n=，所以363636111log 2log 3log 62m n +=+==，故答案为：12【点睛】本题主要考查对数的运算法则的应用，考查了学生的计算能力，属于中档题．20．2【分析】先利用函数的解析式得出其图象必过哪一个定点再将该定点的坐标代入函数中求出最后即可求出相应的函数值得到结果【详解】因为函数的图象恒过定点将代入得所以所以则故答案为：【点睛】该题考查的是有关函解析：2 【分析】先利用函数log (21)1(0,1)a y x a a =-+>≠的解析式得出其图象必过哪一个定点，再将该定点的坐标代入函数()2xf x b =+中求出b ，最后即可求出相应的函数值2(log 3)f ，得到结果. 【详解】因为函数log (21)1(0,1)a y x a a =-+>≠的图象恒过定点(1,1)，将1,1x y ==代入()2xf x b =+，得121b +=，所以1b =-，所以()21xf x =-，则2log 32(log 3)21312f =-=-=，故答案为：2. 【点睛】该题考查的是有关函数值的求解问题，涉及到的知识点有对数型函数图象过定点问题，点在函数图象上的条件，已知函数解析式求函数值，属于简单题目.三、解答题21．（1）{1x x <-或}1x >，证明见解析；（2）()1,+∞. 【分析】（1）本题首先可通过求解101xx +>-得出函数()f x 的定义域，然后通过()()f x f x -=-证得函数()f x 是奇函数；（2）本题可根据题意将函数转化为2()log (1)g x x =+，然后通过当1x >时2log (1)1x +>即可求出函数()g x 的值域.【详解】（1）因为函数21()log 1x f x x +=-，所以101xx +>-，解得1x <-或1x >，则函数的定义域为{1x x <-或}1x >，且定义域关于原点对称，因为222111()log log log ()111x x x f x f x x x x --+-===-=---+-，所以函数()f x 为奇函数.（2）22221l ()()log (1)log (1)log (1)og 1g x x x f x x x x +=+-==-+-+，当1x >时，22log (1)log 21x +>=，函数2()log (1)g x x =+是增函数，故当(1,)x ∈+∞时，()1g x >，函数()g x 的值域为()1,+∞. 【点睛】方法点睛：判断或证明函数奇偶性，首先要判断函数的定义域是否关于原点对称，然后通过()()f x f x -=-判断函数是奇函数或者通过()()f x f x -=判断函数是偶函数. 22．（1）32；（2）3. 【分析】（1）利用指对数运算对数恒等式直接得解（2）利用对数运算及换底公式得解. 【详解】（1）1ln 22433()22922e -++=+-=，（2）223(lg 2)lg 5lg 20log 3log 4+⋅+⋅.22(lg 2)lg 5(1lg 2)log 4(lg 2)(lg 2lg 5)lg 52=+⋅++=+++lg 2lg523=++=【点睛】解决对数运算问题的常用方法(1)将真数化为底数的指数幂的形式进行化简． (2)将同底对数的和、差、倍合并．(3)利用换底公式将不同底的对数式转化成同底的对数式，要注意换底公式的正用、逆用及变形应用．(4)利用常用对数中的lg 2lg51+=23．（1）(1,1)-；（2）是奇函数，理由见解析；（3）单调递增，证明见解析. 【分析】（1）由对数有意义的条件列出不等式组1010x x +>⎧⎨->⎩，解之即可；（2）由（1）知，函数()()f x g x -的定义域关于原点对称，再根据函数奇偶性的概念进行判断即可；（3）当2a =时，函数()()f x g x -单调递增.根据用定义证明函数单调性的“五步法”：任取､作差､变形､定号､下结论，即可得证. 【详解】（1）10x +>，10x ->，11x ∴-<<，∴函数()()f x g x -的定义域为(1,1)-.（2）由（1）知，函数()()f x g x -的定义域关于原点对称，()()log (1)log (1)log (1)log (1)[()()]a a a a f x g x x x x x f x g x ---=-+-+=--+=--，∴函数()()f x g x -是奇函数.（3）当2a =时，函数()()f x g x -单调递增.理由如下：当(1,1)x ∈-时，1()()log 1a x f x g x x+-=-，设1211x x -<<<，则2121211222112121211211111[()()][()()]log log log (?)log 11111aa a ax x x x x x x x f x g x f x g x x x x x x x x x +++-+-----=-==---+-+-，1211x x -<<<，2121x x x x ∴->-+，21122112110x x x x x x x x ∴+-->-+->， ∴21122112111x x x x x x x x +-->-+-，即211221121log 01ax x x x x x x x +-->-+-， 2211()()()()f x g x f x g x ∴->-，故当2a =时，函数()()f x g x -单调递增. 【点睛】本题考查函数的单调性与奇偶性的判断､对数的运算法则，熟练掌握用定义证明函数单调性和奇偶性的方法是解题的关键，考查学生的逻辑推理能力和运算求解能力，属于中档题. 24．（1）()1,+∞；（2）a =【分析】（1）由220mx x m ++>恒成立，得关于m 的不等式组，求解得答案；（2）令12xt ⎛⎫= ⎪⎝⎭，1,22t ⎡⎤∈⎢⎥⎣⎦，可得()223y t a a =-+-，1,22t ⎡⎤∈⎢⎥⎣⎦，根据二次函数的定义域和对称轴的关系分类讨论求最小值，进一步求得实数a 的值. 【详解】（1）()()2222log 2g mx x m mx x m ++=++， ∵()22g mx x m ++的定义域为R ，∴220mx x m ++>恒成立，当0m =时，不符合，当0m ≠时，满足2440m m >⎧⎨∆=-<⎩，解得1m ， ∴实数m 的取值范围为()1,+∞；（2）令12xt ⎛⎫= ⎪⎝⎭，当[]1,1x ∈-时，1,22t ⎡⎤∈⎢⎥⎣⎦，则函数()()223y f x af x =-+⎡⎤⎣⎦化为()222233y t at t a a =-+=-+-，1,22t ⎡⎤∈⎢⎥⎣⎦. ①当2a >时，可得当2t =时y 取最小值，且min 741y a =-=，解得32a =（舍去）； ②当122a ≤≤时，可得当t a =时y 取最小值，且2min 31y a =-=，解得a =a =③12a <时，可得当12t =时y 取最小值，且min 1314y a =-=，解得94a =（舍去），综上，a =【点睛】本题考查对数函数的定义域，考查不等式的恒成立问题，考查二次函数的最值，属于中档题.25．（1）见解析；（2）见解析；（3）[]4,5 【分析】（1）由不等式101x x +>-即可求出()f x 的定义域；（2）证明()()f x f x -=-可得()f x 为奇函数；（3）先求出()f x 在[]3,7上的值域，令()t f x =，求()14h t t t=+的值域.【详解】（1）由101x x +>-得：1x >或1x <-， ()f x ∴的定义域为()(),11,-∞-+∞；（2）()()222111log log log 111x x x f x f x x x x -+-+-===-=---+-， ()f x ∴为奇函数；（3）()22log 11f x x ⎛⎫=+ ⎪-⎝⎭在[]3,7上单调递减，令()t f x =，则24log ,13t ⎡⎤∈⎢⎥⎣⎦，而()14h t t t =+在10,2⎛⎤ ⎥⎝⎦单调递减，在1,12⎡⎤⎢⎥⎣⎦上单调递增，又()2411log 15,4342h h h h ⎛⎫⎛⎫⎛⎫<=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ∴函数()h x 在[]3,7内的值域为[]4,5.【点睛】本题主要考查了对数型函数的定义域，奇偶性，考查了复合函数的单调性，值域求解，属于中档题.26．(1) 2a =-,()2121x x f x -=+;(2) 212log 3x =+或212log 3x =-【分析】(1)根据奇函数(0)0f =求解a ,再根据奇函数的性质求解()f x 的解析式即可.(2)根据(1)可得()2121x x f x -=+为奇函数,可先求解4|()|5f t =的根,再求解4|(1)|5f x -=即可.【详解】(1)因为()f x 是定义在R 上的奇函数,且当0x ≥时,()121xaf x =++,故0(0)1021a f =+=+,即102a +=,解得2a =-.故当0x ≥时,()22112121xx x f x -=-=++. 所以当0x < 时, ()()211221211221x x x x x x f x f x -----=--=-=-=+++. 故()2121x x f x -=+(2) 先求解4|()|5f t =,此时()214215t t f t -==±+.当()()214421521215t t t t -=⇒+=-+,即29t =解得22log 92log 3t ==.因为()2121x x f x -=+为奇函数,故当214215t t -=-+时, 22log 3t =-.故4|(1)|5f x -=的解为212log 3x -=或212log 3x -=-, 解得212log 3x =+或212log 3x =- 【点睛】本题主要考查了根据奇函数求解参数的值以及解析式的方法,同时也考查了根据函数性质求解绝对值方程的问题,属于中档题.。

北师大版高中数学必修一第三单元《指数函数和对数函数》测试(包含答案解析)

一、选择题1．已知函数()()2log 2xf x m =+，则满足函数()f x 的定义域和值域都是实数集R 的实数m 构成的集合为（） A ．{}|0m m =B ．{}0|m m ≤C ．{}|0m m ≥D ．{}|1m m =2．若函数()()23log 5f x x ax a =+++，()f x 在区间(),1-∞上是递减函数，则实数a的取值范围为（） A ．[]3,2-- B ．[)3,2--C ．(],2-∞-D ．(),2-∞-3．函数()f x =的定义域是（） A ．(0,2)B ．[2,)+∞C ．(0,)+∞D ．(,2)-∞4．设()|lg |f x x =，且0a b c <<<时，有()()()f a f c f b >>，则（） A ．(1)(1)0a c --> B ．1ac >C ．1ac =D ．01ac <<5．函数()213log 23y x x =-++的单调递增区间是（）A ．(]1,1-B ．(1)∞－，C ．[) 1,3D ．(1)∞，＋ 6．一种放射性元素最初的质量为500g ，按每年10%衰减．则这种放射性元素的半衰期为（）年.（注：剩余质量为最初质量的一半，所需的时间叫做半衰期），（结果精确到0.1，已知lg 20.3010=，lg30.4771=）A ．5.2B ．6.6C ．7.1D ．8.37．设52a -=，5log 2b =，8log 5c =，则（） A ．a b c <<B ．b c a <<C ．c b a <<D ．c a b <<8．已知函数()f x 满足()()11f x f x -=+，当(],1-∞时，函数()f x 单调递减，设()41331=log ,log 3,92a f b f c f log ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，则,,a b c 的大小关系是（）A ．a b c <且1a ≠）在[]0,3上为增函数，则实数a 的取值范围是（） A ．2,13⎛⎫⎪⎝⎭B ．(0,1)C ．20,3⎛⎫ ⎪⎝⎭D ．[)3,+∞11．若函数()()212log 45f x x x =-++在区间()32,2m m -+内单调递增，则实数m 的取值范围为（） A ．4,33⎡⎤⎢⎥⎣⎦B ．4,23⎡⎤⎢⎥⎣⎦C ．4,23⎡⎫⎪⎢⎣⎭D ．4,3⎡⎫+∞⎪⎢⎣⎭12．已知0.22a =，0.20.4b =，0.60.4c =，则（）A ．a b c >>B ．a c b >>C ．c a b >>D ．b c a >>二、填空题13．已知()(3),1log ,1aa x a x f x x x --<⎧=⎨≥⎩的值域为R ，那么实数a 的取值范围是_________．14．函数()f x =的定义域为______.15．函数()22log 617y x x =-+的值域是__．16．已知函数()f x 满足()()1f x f x =-+，当()0,1x ∈时，函数()3xf x =，则13log 19f ⎛⎫= ⎪⎝⎭______. 17．已知函数2()log x f x =，实数,a b 满足0a b <<，且()()f a f b =，若()f x 在2,a b ⎡⎤⎣⎦上的最大值为2，则1b a+=________. 18．32a b-=________（其中0a >，0b >）19．设函数122,1()1log ,1x x f x x x -⎧≤=⎨->⎩，则满足()2f x ≤的x 的取值范围是_______________.20．已知函数()()log 21101a y x a a =-+>≠,的图象过定点A ，若点A 也在函数()2x f x b =+的图象上，则()2log 3f =________. 三、解答题21．已知函数()1,02,0x x x f x x +≤⎧=⎨>⎩（Ⅰ）求()()()1ff f -的值；（Ⅱ）画出函数()f x 的图象，根据图象写出函数()f x 的单调区间；（Ⅲ）若()112f x f x ⎛⎫+-> ⎪⎝⎭，求x 的取值范围．22．化简下列各式：（1）22.53105330.06438π-⎡⎤⎛⎫⎢⎥ ⎪⎢⎥⎝⎭⎣⎦；（2）2lg 2lg3111lg 0.36lg1624++⋅+ 23．定义在D 上的函数()f x ，如果满足：对任意x D ∈，存在常数0M >，都有()f x M ≤成立，则称()f x 是D 上的“有上界函数”，其中M 称为函数()f x 的上界．已知函数11()139x xf x a ⎛⎫⎛⎫=+⋅+ ⎪ ⎪⎝⎭⎝⎭．（1）当12a =-时，求函数()f x 在(,0)-∞上的值域，并判断函数()f x 在(,0)-∞上是否为“有上界函数”，请说明理由；（2）若函数()f x 在[0,)+∞上是以4为上界的“有上界函数”，求实数a 的取值范围．24．（1）求函数()22log 32y x x =-+的定义域；（2）求函数221y x x =-+-，[]2,2x ∈-的值域；（3）求函数223y x x =--的单调递增区间.25．已知函数()log (1)a f x x =+，()log (1)(0a g x x a =->，且1)a ≠. （1）求函数()()f x g x -的定义域；（2）判断函数()()f x g x -的奇偶性，并说明理由；（3）当2a =时，判断函数()()f x g x -的单调性，并给出证明.26．已知函数()12xf x ⎛⎫= ⎪⎝⎭，函数()2log g x x =. （1）若()22g mx x m ++的定义域为R ，求实数m 的取值范围；（2）当[]1,1x ∈-时，函数()()223y f x af x =-+⎡⎤⎣⎦的最小值为1，求实数a 的值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】若定义域为实数集R ，则20x m +>对于x ∈R 恒成立，可得0m ≥，若值域为实数集R ，令2x t m =+，则2log y t = 此时需满足2x t m =+的值域包括()0,∞+，可得0m ≤，再求交集即可. 【详解】若()()2log 2xf x m =+定义域为实数集R ，则20x m +>对于x ∈R 恒成立，即2x m >-对于x ∈R 恒成立，因为20x >，所以20x -<，所以0m ≥，令2x t m =+，则2log y t =若()()2log 2xf x m =+值域为实数集R ，则2x t m =+的值域包括()0,∞+，因为t m >，所以0m ≤，所以0m =，故选：A 【点睛】关键点点睛：本题的关键点是要找到定义域为R 的等价条件即20x m +>对于x ∈R 恒成立，分离参数m 求其范围，值域为R 的等价条件即2x t m =+可以取遍所有大于0的数，由t m >，所以0m ≤，再求交集.2．A解析：A 【分析】判断复合函数的单调性，首先要分清楚内外层函数，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求即可. 【详解】由题意知，()f x 在区间(),1-∞上是递减函数，由()()23log 5f x x ax a =+++可知，此复合函数外层函数为：()3log f x x =，在定义域上为增函数，内层函数为()25h x x ax a =+++，要使()f x 在区间(),1-∞上是递减函数，根据复合函数“同增异减”原则，内层函数为()h x 在区间(),1-∞上必须是递减函数，同时须保证最大值()10h ≥，所以()1210a h ⎧-≥⎪⎨⎪≥⎩，解得32a --≤≤. 故选：A. 【点睛】易错点睛：判断复合函数的单调性，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求.3．A解析：A 【分析】根据函数的形式，直接列解析式有意义的不等式，求出函数的定义域. 【详解】由题意得，函数的定义域需满足02>0x x >⎧⎨-⎩，解得：02x <<所以函数的定义域是()0,2. 故选：A . 【点睛】方法点睛：常见的具体函数求定义域：(1)偶次根号下的被开方数大于等于0；(2)分母不为0；(3)对数函数中真数大于0.4．D解析：D 【分析】作出()f x 的图象，利用数形结合即可得到结论．【详解】∵函数()|lg |f x x =，作出()f x 的图象如图所示，∵0a b c <<<时，有()()()f a f c f b >>，∴0＜a ＜1，c ＞1，即f （a ）＝|lga |＝﹣lga ，f （c ）＝|lgc |＝lgc ，∵f （a ）＞f （c ）， ∴﹣lga ＞lgc ，则lga +lgc ＝lgac ＜0，则01ac <<. 故选：D ．【点睛】关键点点睛：利用对数函数的图象和性质，根据条件确定a ，c 的取值范围.5．C解析：C 【分析】由不等式2230x x -++>，求得函数的定义域()1,3-，令()223g x x x =-++，得到()g x 在区间(]1,1-上单调递增，在区间[1,3)上单调递减，结合复数函数的单调性的判定方法，即可求解. 【详解】由题意，函数213()log 23y x x =-++有意义，则满足2230x x -++>，即223(3)(1)0x x x x --=-+<，解得13x，即函数的定义域为()1,3-，令()223g x x x =-++，则函数()g x 表示开口向下，对称轴方程为1x =的抛物线，所以函数()g x 在区间(]1,1-上单调递增，在区间[1,3)上单调递减，又由函数13log y x =在定义上是递减函数，结合复数函数的单调性的判定方法，可得函数213()log 23y x x =-++的递增区间为[1,3). 故选：C. 【点睛】函数单调性的判定方法与策略：定义法：一般步骤：设元→作差→变形→判断符号→得出结论；图象法：如果函数()f x 是以图象形式给出或函数()f x 的图象易作出，结合图象可求得函数的单调区间；导数法：先求出函数的导数，利用导数值的正负确定函数的单调区间；复合函数法：先将函数(())y f g x =分解为()y f t =和()t g x =，再讨论这两个函数的单调性，最后根据复合函数“同增异减”的规则进行判定.6．B解析：B 【分析】先根据题意列出关于时间的方程，然后利用指对互化以及对数换底公式并结合所给数据可计算出半衰期. 【详解】设放射性元素的半衰期为x 年，所以()500110%250x-=，所以()1110%2x-=，所以0.91log 2x =，所以109log 2x =，所以lg 2lg10lg9x =-，所以lg 212lg 3x =-，所以0.3010120.4771x =-⨯，所以 6.6x ≈，故选：B. 【点睛】思路点睛：求解和对数有关的实际问题的思路：（1）根据题设条件列出符合的关于待求量的等式；（2）利用指对互化、对数运算法则以及对数运算性质、对数换底公式求解出待求量的值.7．A解析：A 【分析】由551112,2332log -<<<，8152log >，即可得出a ，b ，c 的大小关系. 【详解】52112243--<=<，11325551152532log log log =<<=，12881582log log >=，a b c ∴<<.故选：A 【点睛】本题主要考查了指数函数、对数函数的单调性，对数的运算性质，还考查了转化求解问题的能力，属于中档题.8．B解析：B 【分析】由()()11f x f x -=+可得函数()f x 关于直线1x =对称，根据对数的运算法则，结合函数的对称性，变形41log 2、13log 3、39log 到区间[)1,+∞内，由函数()f x 在[)1,+∞上单调递增，即可得结果. 【详解】根据题意，函数()f x 满足()()11f x f x -=+，则函数()f x 关于直线1x =对称，又由当(],1-∞时，函数()f x 单调递减，则函数在[)1,+∞上单调递增，又由()44115log log 2222a f f f f ⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ()()13log 313b f f f ⎛⎫==-= ⎪⎝⎭，()()3log 92c f f ==，则有c a b <<，故选B.【点睛】在比较()1f x ，()2f x ，，()n f x 的大小时，首先应该根据函数()f x 的奇偶性（对称性）与周期性将()1f x ，()2f x ，，()n f x 通过等值变形将自变量置于同一个单调区间，然后根据单调性比较大小．9．A解析：A 【解析】x y z ，，为正实数，且235log log log 0x y z ==<，111235235k k k x y z ---∴===，，，可得：1112352131,51k k k x y z---=>=>=>，．即10k -> 因为函数1kf x x -=（）单调递增，∴235x y z<<. 故选A.10．C解析：C 【分析】根据对数函数性质与复合函数的单调性求解．【详解】因为0a >且1a ≠，令2t ax =-，所以函数2t ax =-在[]0,3上为减函数，所以函数log a y t =应是减函数，()f x 才可能是增函数， ∴01a <<，因为函数()f x 在[]0,3上为增函数，由对数函数性质知230a ->，即23<a ，综上023a <<．故选：C ．【点睛】本题考查复合函数的单调性，掌握对数函数性质是解题关键，考查逻辑思维能力和计算能力，属于常考题．11．C解析：C 【分析】求得函数()y f x =的定义域，利用复合函数法求得函数()y f x =的单调递增区间，根据题意可得出区间的包含关系，由此可求得实数m 的取值范围. 【详解】解不等式2450x x -++>，即2450x x --<，解得15x -<<，内层函数245u x x =-++在区间()1,2-上单调递增，在区间()2,5上单调递减，而外层函数12log y u =在定义域上为减函数，由复合函数法可知，函数()()212log 45f x x x =-++的单调递增区间为()2,5，由于函数()()212log 45f x x x =-++在区间()32,2m m -+上单调递增，所以，32232225m m m m -≥⎧⎪-<+⎨⎪+≤⎩，解得423m ≤<.因此，实数m 的取值范围是4,23⎡⎫⎪⎢⎣⎭. 故选：C. 【点睛】本题考查利用对数型复合函数在区间上的单调性求参数，考查计算能力，属于中等题.12．A解析：A 【解析】分析：0.20.4b =， 0.60.4c =的底数相同，故可用函数()0.4xf x =在R 上为减函数，可得0.60.200.40.40.41<<=．用指数函数的性质可得0.20221a =>=，进而可得0.20.20.620.40.4>>．详解：因为函数()0.4xf x =在R 上为减函数，且0.2<0.4所以0.60.200.40.40.41<<= 因为0.20221a =>=．所以0.20.20.620.40.4>>．故选A ．点睛：本题考查指数大小的比较，意在考查学生的转化能力．比较指数式的大小，同底数的可利用指数函数的单调性判断大小，底数不同的找中间量1，比较和1的大小．二、填空题13．【分析】分类讨论和结合已知和对数函数及一次函数的单调性得a 的不等式组求解即可【详解】解：若当时当时此时的值域不为R 不符合题意；若当时当时要使函数的值域为R 需使解得综上所述故答案为：【点睛】本题考查分解析：31,2⎛⎤⎥⎝⎦【分析】分类讨论01a <<和1a >，结合已知和对数函数及一次函数的单调性，得a 的不等式组求解即可．【详解】解：若01a <<，当1≥x 时，log 0a x ≤，当1x <时，()3332a x a a a a --<--=-，此时f x （）的值域不为R ，不符合题意；若1a >，当1≥x 时，log 0a x ≥，当1x <时，要使函数f x （）的值域为R ，需使30log 13a a a a ->⎧⎨≤--⎩，解得332a a <⎧⎪⎨≤⎪⎩，312a ∴<≤，综上所述，312a <≤，故答案为：31,2⎛⎤⎥⎝⎦．【点睛】本题考查分段函数的值域及对数函数的性质，考查分类讨论思想与数学运算能力，是中档题.14．【分析】根据二次根式和对数式有意义的条件得到不等式组求解函数的定义域即可得结果【详解】根据题意可得：解得所以函数的定义域为故答案为：【点睛】该题考查的是有关求函数的问题涉及到的知识点有求给定函数的定解析：(2,3]【分析】根据二次根式和对数式有意义的条件，得到不等式组求解函数的定义域即可得结果. 【详解】根据题意可得：1220log (2)0x x ->⎧⎪⎨-≥⎪⎩，解得23x <≤，所以函数()f x =(2,3]，故答案为：(2,3]. 【点睛】该题考查的是有关求函数的问题，涉及到的知识点有求给定函数的定义域，在解题的过程中，注意二次根式和对数式需要满足的条件即可得结果.15．【分析】设转化为函数根据在上单调递增可求解【详解】设函数则函数∵在上单调递增∴当时最小值为故答案为：【点睛】本题考察了二次函数对数函数性质综合解决问题解析：[)3,+∞【分析】设()2261738t x x x =-+=-+，转化为函数2log y t =，[)8,t ∈+∞，根据2log y t =在[)8,t ∈+∞上单调递增，可求解．【详解】设()2261738t x x x =-+=-+函数()22log 617y x x =-+，则函数2log y t =，[)8,t ∈+∞， ∵2log y t =，在[)8,t ∈+∞上单调递增， ∴当8t =时，最小值为2log 83=，故答案为：[)3,+∞. 【点睛】本题考察了二次函数，对数函数性质，综合解决问题．16．【分析】由满足得到函数是以2为周期的周期函数结合对数的运算性质即可求解【详解】由题意函数满足化简可得所以函数是以2为周期的周期函数又由时函数且则故答案为：【点睛】函数的周期性有关问题的求解策略：求解解析：2719-【分析】由()fx 满足()()1f x f x =-+，得到函数()f x 是以2为周期的周期函数，结合对数的运算性质，即可求解. 【详解】由题意，函数()f x 满足()()1f x f x =-+，化简可得()()2f x f x =+，所以函数()f x 是以2为周期的周期函数，又由()0,1x ∈时，函数()3xf x =，且()()1f x f x =-+，则133339(log 19)(log 19)(log 192)(log )19f f f f =-=-+= 327log 193392727(log 1)(log )3191919f f =-+=-=-=-.故答案为：2719- 【点睛】函数的周期性有关问题的求解策略：求解与函数的周期性有关问题，应根据题目特征及周期定义，求出函数的周期；解决函数周期性、奇偶性和单调性结合问题，通常先利用周期性中为自变量所在区间，再利用奇偶性和单调性求解.17．4【分析】先画出函数图像并判断再根据范围和函数单调性判断时取最大值最后计算得到答案【详解】如图所示：根据函数的图象得所以结合函数图象易知当时在上取得最大值所以又所以再结合可得所以故答案为：4【点睛】解析：4 【分析】先画出函数图像并判断01a b <<<，再根据范围和函数单调性判断2x a =时取最大值，最后计算得到答案. 【详解】如图所示：根据函数2()log x f x =的图象得01a b <<<，所以201a a <<<．结合函数图象，易知当2=x a 时()f x 在2,a b ⎡⎤⎣⎦上取得最大值，所以()222log2f aa ==又01a <<，所以12a =，再结合()()f a f b =，可得2b =，所以2241b a+=+=. 故答案为：4 【点睛】关键点睛：解题关键在于，作出对数函数2()log x f x =的图象，得到01a b <<<，进而求解，属于中档题18．【分析】根据指数幂的运算法则即可求解【详解】根据指数幂的运算法则可得故答案为：【点睛】指数幂运算的一般原则：（1）由括号的先算括号里的无括号的弦做指数运算；（2）弦乘除后加减负指数幂化为正指数幂的倒解析：a【分析】根据指数幂的运算法则，即可求解. 【详解】212132()33113322a b aa a ba b----⨯===.故答案为：a . 【点睛】指数幂运算的一般原则：（1）由括号的先算括号里的，无括号的弦做指数运算；（2）弦乘除后加减，负指数幂化为正指数幂的倒数；（3）底数是负数，先确定符号，底数是小数，先化成分数，底数是带分数的，先化成假分数；（4）若是根式，应化为分数指数幂，尽可能用幂的形式表示，运用指数幂的运算性质来求解.19．【分析】根据分段函数分段解不等式最后求并集【详解】当时因为解得：∴当时解得：所以综上原不等式的解集为故答案为：【点睛】本题主要考查了解分段函数不等式涉及指数与对数运算属于基础题解析：[0,)+∞【分析】根据分段函数，分段解不等式，最后求并集. 【详解】当1x ≤时，1()2xf x -=，因为11x -≤，解得：0x ≥，∴01x ≤≤ ，当1x >时，2()1log 2f x x =-≤，2log 1x ≥-，解得：12x ≥，所以1x >，综上，原不等式的解集为[)0,+∞. 故答案为：[)0,+∞. 【点睛】本题主要考查了解分段函数不等式，涉及指数与对数运算，属于基础题.20．2【分析】先利用函数的解析式得出其图象必过哪一个定点再将该定点的坐标代入函数中求出最后即可求出相应的函数值得到结果【详解】因为函数的图象恒过定点将代入得所以所以则故答案为：【点睛】该题考查的是有关函解析：2 【分析】先利用函数log (21)1(0,1)a y x a a =-+>≠的解析式得出其图象必过哪一个定点，再将该定点的坐标代入函数()2xf x b =+中求出b ，最后即可求出相应的函数值2(log 3)f ，得到结果. 【详解】因为函数log (21)1(0,1)a y x a a =-+>≠的图象恒过定点(1,1)，将1,1x y ==代入()2xf x b =+，得121b +=，所以1b =-，所以()21xf x =-，则2log 32(log 3)21312f =-=-=，故答案为：2. 【点睛】该题考查的是有关函数值的求解问题，涉及到的知识点有对数型函数图象过定点问题，点在函数图象上的条件，已知函数解析式求函数值，属于简单题目.三、解答题21．（Ⅰ）2；（Ⅱ）图象见解析，单调递增区间为(),-∞+∞；（Ⅲ）14x >-．【分析】（Ⅰ）依次求出()1f -，()()1ff -，()()()1f f f -即可（Ⅱ）根据函数解析式即可画出图象，根据图象即可得出单调区间；（Ⅲ）分段讨论可解出不等式. 【详解】解：（Ⅰ）()1110f -=-+=，所以()()1011ff -=+=，所以()()()1122f f f -==；（Ⅱ）函数图象如下：由图可知，()f x 的单调递增区间为(),-∞+∞，无单调递减区间；（Ⅲ）①当0x ≤时，102x -≤，所以()1f x x =+，1111222f x x x ⎛⎫⎛⎫-=-+=+ ⎪ ⎪⎝⎭⎝⎭ 所以()132122f x f x x ⎛⎫+-=+> ⎪⎝⎭，解得14x >-，所以014x -<≤； ②当102x <≤时，102x -<，所以()2xf x =，1111222f x x x ⎛⎫⎛⎫-=-+=+ ⎪ ⎪⎝⎭⎝⎭，所以()112122xf x f x x ⎛⎫+-=++> ⎪⎝⎭显然成立，所以102x <≤符合题意； ③当12x >时，102x ->，所以()2xf x =，12122x f x ⎛⎫- ⎪⎝⎭⎛⎫-= ⎪⎝⎭，所以()1212212x xf x f x ⎛⎫- ⎪⎝⎭⎛⎫+-=+> ⎪⎝⎭显然成立，所以12x >符合题意，综上所述：x 的取值范围为1,4⎛⎫-+∞ ⎪⎝⎭. 【点睛】关键点睛：本题考查函数不等式的求解，解题的关键是分段讨论x 的取值范围，根据不同范围函数的解析式求解. 22．（1）0；（2）1. 【分析】（1）根据指数幂的运算性质，准确运算，即可求解；（2）根据对数的运算性质，准确运算，即可求解. 【详解】（1）根据指数幂的运算性质，可得原式22.5311536427110008-⎧⎫⎡⎤⎪⎪⎛⎫⎛⎫⎢⎥=--⎨⎬ ⎪⎪⎢⎥⎝⎭⎝⎭⎪⎪⎣⎦⎩⎭ 1521335233431102⎛⎫⨯- ⎪⎝⎭⨯⎡⎤⎡⎤⎛⎫⎛⎫=--⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦531022=--=. （2）由对数的运算性质，可得原式242lg 2lg32lg 2lg311231lg 0.6lg 21lg lg 22410++==⨯++++ 2lg 2lg 32lg 2lg 311lg 2lg 3lg10lg 22lg 2lg 3++===++-++. 【点睛】本题主要考查了指数幂和对数的运算性质的化简、求值，其中解答中熟记指数幂与对数的运算性质，准确运算是解答的关键，着重考查运算与求解能力. 23．（1）值域为3,2⎛⎫+∞ ⎪⎝⎭，不是“有上界函数”；理由见解析；（2）(,2]-∞ 【分析】（1）把12a =-代入函数的表达式，令13xt ⎛⎫= ⎪⎝⎭，可得1t >，可求出2112y t t =-+的值域，即为()f x 在(,0)-∞的值域，结合“有上界函数”的定义进行判断即可；（2）由题意知，()4f x ≤对[0,)x ∈+∞恒成立，令13xt ⎛⎫= ⎪⎝⎭，可得(0,1]t ∈，整理得3a t t ⎛⎫≤- ⎪⎝⎭对(0,1]t ∈恒成立，只需min 3a t t ⎛⎫≤- ⎪⎝⎭即可.【详解】（1）当12a =-时，111()1239x xf x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭，令13xt ⎛⎫= ⎪⎝⎭，0x <，1t ∴>，2112y t t =-+， 2112y t t =-+在(1,)+∞上单调递增，111232y -∴>+=，即()f x 在(,0)-∞的值域为3,2⎛⎫+∞⎪⎝⎭，故不存在常数0M >，使()f x M ≤成立． ∴函数()f x 在(,0)-∞上不是“有上界函数” （2）由题意知，()4f x ≤对[0,)x ∈+∞恒成立，令13xt ⎛⎫= ⎪⎝⎭，0x ≥，(0,1]t ∴∈，214at t ∴++≤对(0,1]t ∈恒成立，即3a t t ⎛⎫≤-⎪⎝⎭对(0,1]t ∈恒成立，设3()g t t t=-，易知()g t 在(0,1]t ∈上递减， ()g t ∴在(0,1]t ∈上的最小值为(1)2g =．∴min ()2a g t ≤=，∴实数a 的取值范围为(,2]-∞ 【点睛】本题考查新定义，考查函数的值域与最值，考查学生的推理能力与计算求解能力，属于中档题.24．（1）()(),12,-∞⋃+∞；（2）[]9,0-；（3）[]1,1-，[)3,+∞. 【分析】（1）解不等式2320x x -+>可求得函数()22log 32y x x =-+的定义域；（2）利用二次函数的基本性质可求得函数221y x x =-+-，[]2,2x ∈-的值域；（3）将函数223y x x =--的解析式表示为分段函数，利用二次函数的基本性质可求得原函数的单调递增区间. 【详解】（1）对于函数()22log 32y x x =-+，有2320x x -+>，解得1x <或2x >. 因此，函数()22log 32y x x =-+的定义域为()(),12,-∞⋃+∞；（2）当[]2,2x ∈-时，()[]222119,0y x x x =-+-=--∈-，因此，函数221y x x =-+-，[]2,2x ∈-的值域为[]9,0-；（3）解不等式2230x x -->，解得1x <-或3x >，所以，222223,12323,1323,3x x x y x x x x x x x x ⎧--<-⎪=--=-++-≤≤⎨⎪-->⎩.二次函数223y x x =--的图象开口向上，对称轴为直线1x =. 当1x <-时，函数223y x x =--单调递减；当13x -≤≤时，函数2y x 2x 3=-++在区间[]1,1-上单调递增，在区间[]1,3上单调递减；当3x >时，函数223y x x =--单调递增.综上所述，函数223y x x =--的单调递增区间为[]1,1-，[)3,+∞.【点睛】本题考查与二次函数相关问题的求解，考查了对数型复合函数的定义域、二次函数的值域以及含绝对值的二次函数单调区间的求解，考查计算能力，属于中等题. 25．（1）(1,1)-；（2）是奇函数，理由见解析；（3）单调递增，证明见解析. 【分析】（1）由对数有意义的条件列出不等式组1010x x +>⎧⎨->⎩，解之即可；（2）由（1）知，函数()()f x g x -的定义域关于原点对称，再根据函数奇偶性的概念进行判断即可；（3）当2a =时，函数()()f x g x -单调递增.根据用定义证明函数单调性的“五步法”：任取､作差､变形､定号､下结论，即可得证. 【详解】（1）10x +>，10x ->，11x ∴-<<，∴函数()()f x g x -的定义域为(1,1)-.（2）由（1）知，函数()()f x g x -的定义域关于原点对称，()()log (1)log (1)log (1)log (1)[()()]a a a a f x g x x x x x f x g x ---=-+-+=--+=--，∴函数()()f x g x -是奇函数.（3）当2a =时，函数()()f x g x -单调递增.理由如下：当(1,1)x ∈-时，1()()log 1a x f x g x x+-=-，设1211x x -<<<，则2121211222112121211211111[()()][()()]log log log (?)log 11111aa a ax x x x x x x x f x g x f x g x x x x x x x x x +++-+-----=-==---+-+-，1211x x -<<<，2121x x x x ∴->-+，21122112110x x x x x x x x ∴+-->-+->，∴21122112111x x x x x x x x +-->-+-，即211221121log 01ax x x x x x x x +-->-+-， 2211()()()()f x g x f x g x ∴->-，故当2a =时，函数()()f x g x -单调递增. 【点睛】本题考查函数的单调性与奇偶性的判断､对数的运算法则，熟练掌握用定义证明函数单调性和奇偶性的方法是解题的关键，考查学生的逻辑推理能力和运算求解能力，属于中档题. 26．（1）()1,+∞；（2）a =【分析】（1）由220mx x m ++>恒成立，得关于m 的不等式组，求解得答案；（2）令12xt ⎛⎫= ⎪⎝⎭，1,22t ⎡⎤∈⎢⎥⎣⎦，可得()223y t a a =-+-，1,22t ⎡⎤∈⎢⎥⎣⎦，根据二次函数的定义域和对称轴的关系分类讨论求最小值，进一步求得实数a 的值. 【详解】（1）()()2222log 2g mx x m mx x m ++=++， ∵()22g mx x m ++的定义域为R ，∴220mx x m ++>恒成立，当0m =时，不符合，当0m ≠时，满足2440m m >⎧⎨∆=-<⎩，解得1m ， ∴实数m 的取值范围为()1,+∞；（2）令12xt ⎛⎫= ⎪⎝⎭，当[]1,1x ∈-时，1,22t ⎡⎤∈⎢⎥⎣⎦，则函数()()223y f x af x =-+⎡⎤⎣⎦化为()222233y t at t a a =-+=-+-，1,22t ⎡⎤∈⎢⎥⎣⎦. ①当2a >时，可得当2t =时y 取最小值，且min 741y a =-=，解得32a =（舍去）； ②当122a ≤≤时，可得当t a =时y 取最小值，且2min 31y a =-=，解得a =a =③12a <时，可得当12t=时y取最小值，且min1314y a=-=，解得94a=（舍去），综上，a=【点睛】本题考查对数函数的定义域，考查不等式的恒成立问题，考查二次函数的最值，属于中档题.。

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(含答案解析)

一、选择题1．设a ，b ，c 为正数，且3a =4b =6c ，则有（） A ．111c a b=+ B ．221c a b=+ C ．122c a b=+ D ．212c a b=+ 2．若关于x 的不等式34log 2xa x -≤在10,2x ⎛⎤∈ ⎥⎝⎦恒成立，则实数a 的取值范围是（） A ．1,14⎡⎫⎪⎢⎣⎭B ．10,4⎛⎤ ⎥⎝⎦C ．3,14⎡⎫⎪⎢⎣⎭D ．30,4⎛⎤ ⎥⎝⎦3．已知0.20.33log 0.2,3,0.2a b c ===，则（）A ．a b c <的零点分别为,,a b c ，则,,a b c 的大小顺序为（）A ．a b c >>B ．c a b >>C ．b c a >>D ．b a c >>5．5G 技术的数学原理之一便是著名的香农公式：2log 1S C W N ⎛⎫=+⎪⎝⎭，它表示：在受高斯白噪声干扰的信道中，最大信息传递速率C 取决于信道带宽W 、信道内所传信号的平均功率S 、信道内部的高斯噪声功率N 的大小，其中SN叫做信噪比.按照香农公式，在不改变W 的情况下，将信噪比SN从1999提升至λ，使得C 大约增加了20%，则λ的值约为（参考数据：lg 20.3≈， 3.96109120≈）（） A ．7596B ．9119C ．11584D ．144696．若13log 2a =，131()2b =，2log 3c =，则,,a b c 的大小关系是（） A ．b a c << B ．b c a << C ．a b c << D ．c b a <<7．已知函数 ()lg 2x xe ef x --=，则f (x )是（）A ．非奇非偶函数，且在(0，+∞)上单调递增B ．奇函数，且在R 上单调递增C ．非奇非偶函数，且在(0，+∞)上单调递减D ．偶函数，且在R 上单调递减 8．已知函数()f x 满足()()11f x f x -=+，当(],1-∞时，函数()f x 单调递减，设()41331=log ,log 3,92a f b f c f log ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，则,,a b c 的大小关系是（）A ．a b c <<B ．c a b <<C ．a c b <<D ．c b a <<9．函数2y 34x x =--+的定义域为（）A ．(41)--，B ．(41)-，C ．(11)-，D ．(11]-， 10．已知函数()a f x x 满足(2)4f =，则函数()log (1)a g x x =+的图象大致为（）A ．B ．C ．D ．11．已知函数222,0()2,0x x x f x x x x ⎧+≥=⎨-<⎩，212(log )(log )2(1)f a f f a ≤+，则实数a 的取值范围是（） A ．1,22⎡⎤⎢⎥⎣⎦B ．102⎛⎤ ⎥⎝⎦，C ．[]1,2D ．(]0,2 12．物理学规定音量大小的单位是分贝（dB ），对于一个强度为I 的声波，其音量的大小η可由如下公式计算：010lgII η=(其中0I 是人耳能听到声音的最低声波强度).我们人类生活在一个充满声音的世界中，人们通过声音交换信息、交流情感，人正常谈话的音量介于40dB 与60dB 之间，则60dB 声音的声波强度1I 是40dB 声音的声波强度2I 的（） A ．32倍 B ．3210倍C ．100倍D ．3lg2倍二、填空题13．函数12()log (2)f x x =-的定义域为______.14．已知21()1,()log 2xf xg x x m ⎛⎫=+=+ ⎪⎝⎭，若()()1212[1,3],[1,3],x x f x g x ∀∈∃∈≥，则实数m 的取值范围是_______.15．设函数2()ln(1)f x x x =+，若()23(21)0f a f a +-<，则实数a 的取值范围为_____. 16．72log 2338log272lg 5lg 47-+++=______.17．定义在(,0)(0,)-∞+∞上的函数1,0(),0x x e x f x e m x -⎧->=⎨+<⎩是奇函数，则实数m 的值为______．18．若幂函数()2()57m f x m m x =-+在R 上为增函数则1log2log 2lg5lg4mm m+-=_____．19．函数()()212log 56f x x x =-+的单调递增区．．．间是__________． 20．7log 31lg 25lg 272++=________. 三、解答题21．已知指数函数()f x 的图象经过点()1,3-，()()2()23x g x f a x f =-+在区间[]1,1-上的最小值是()h a . （1）求函数()f x 的解析式；（2）若3a ≥时，求函数()g x 的最小值()h a 的表达式；（3）是否存在m 、n ∈R 同时满足以下条件：①3m n >>；②当()h a 的定义域为[],n m 时，值域为22,n m ⎡⎤⎣⎦；若存在，求出m 、n 的值；若不存在，说明理由.22．已知函数()2log f x x =，()241g x ax x =-+.（1）若函数()()y f g x =的值域为R ，求实数a 的取值范围；（2）函数22()()()h x f x f x =-，若对于任意的1,22x ⎡∈⎤⎢⎥⎣⎦，都存在[]1,1t ∈-使得不等式()22th x k >⋅-成立，求实数k 的取值范围. 23．化简与求值：（1）2ln 43(0.125)e-++；（2）若1122x x -+=1x x --的值. 24．（1）已知函数()()()2110x g x a a -=++>的图像恒过定点A ，且点A 又在函数()()f x x a =+的图像上，求不等式()3g x >的解集；（2）已知121log 1x -≤≤，求函数1114242x xy -⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭的最大值和最小值. 25．已知函数()2log 11a f x x ⎛⎫=-⎪+⎝⎭（0a >且1a ≠）.（1）判断函数()f x 的奇偶性并说明理由；（2）当01a <<时，判断函数()f x 在()1,+∞上的单调性，并利用单调性的定义证明；（3）是否存在实数a ，使得当()f x 的定义域为[],m n 时，值域为[]1log ,1log a a n m ++？若存在，求出实数a 的取值范围；若不存在，请说明理由.26．求函数()log 23=-2-3y x x 的定义域、值域和单调区间.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】首先根据指对互化求出,,a b c ，再根据换底公式表示111,,a b c，最后根据对数运算法则化简. 【详解】设3a =4b =6c =k ，则a =log 3k ， b =log 4k ， c =log 6k ， ∴311log 3log k a k ==，同理1log 4k b =，1log 6k c=，而11log 2,log 3log 22k k k b c ==+， ∴1112c a b =+，即221c a b =+．故选：B 【点睛】本题考查指对数运算，换底公式，以及对数运算的性质，关键是灵活应用对数运算公式，公式1log log a b b a=是关键. 2．A解析：A 【分析】转化为当10,2x ⎛⎤∈ ⎥⎝⎦时，函数342xy =-的图象不在log a y x =的图象的上方，根据图象列式可解得结果. 【详解】由题意知关于x 的不等式34log 2xa x -≤在10,2x ⎛⎤∈ ⎥⎝⎦恒成立，所以当1 0,2x⎛⎤∈ ⎥⎝⎦时，函数342xy=-的图象不在log ay x=的图象的上方，由图可知0111log22aa<<⎧⎪⎨≥⎪⎩，解得114a≤<.故选：A【点睛】关键点点睛：利用函数342xy=-的图象与函数log ay x=的图象求解是解题关键.3．B解析：B【分析】根据指数函数的单调性以及对数函数的单调性分别判断出,,a b c的取值范围，从而可得结果【详解】因为33log0.2log10<=，0.20331>=，...030002021<<=，a c b∴<<．故选：B．【点睛】比较大小问题，常见思路有两个：一是利用中间变量；二是利用函数的单调性直接解答4．B解析：B【分析】将函数3131()(),()log,()(0)2xf x xg x x xh x x x x=-=-=->的零点，转化为函数y x=的图象分别与函数3131(),log,(0)2xy y x y x x===>的图象交点的横坐标，利用数形结合法求解.【详解】函数3131()(),()log ,()(0)2x f x x g x x x h x x x x =-=-=->的零点，即为函数y x =的图象分别与函数3131(),log ,(0)2x y y x y x x ===>的图象交点的横坐标，如图所示：由图象可得：c a b >>，故选：B 【点睛】本题主要考查函数的零点以及指数函数，对数函数和幂函数的图象的应用，还考查了数形结合的思想方法，属于中档题.5．B解析：B 【分析】根据题设条件列出方程，计算即可. 【详解】由题可知 ()()()22log 119991+20%log 1W W λ+⨯=+，即()221.2log 2000log 1λ⨯=+，所以()lg 1lg 20001.2lg 2lg 2λ+⨯=，即()()lg 1 1.2lg2000 1.23lg2 3.96λ+=⨯=⨯+≈，所以 3.961109120λ+≈≈，所以9119λ≈. 故选：B 【点睛】本题主要考查对属于对数函数，考查学生的运算能力.6．C解析：C 【分析】由题容易看出，0a <， 01b <<，2log 31c =>，便得出,,a b c 的大小关系. 【详解】1133log 2log 10a =<=，310110122b ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭，22log 3log 21c =>=，因此a b c <<.故选：C. 【点睛】本题考查指数函数和对数函数的比较大小，常与中间值0-1,1，来比较，再结合函数的单调性即可求解，属于中档题.7．A解析：A 【分析】本题考查函数的奇偶性和和单调性的概念及简单复合函数单调性的判定. 【详解】要使函数有意义，需使0,2x x e e -->即21,1,x xx e e e >∴>解得0;x >所以函数()f x 的为(0,);+∞定义域不关于原点对称，所以函数()f x 是非奇非偶函数；因为1,xxx y e y ee-==-=-是增函数，所以2x xe e y --=是增函数，又lg y x =是增函数，所以函数()lg 2x xe ef x --=在定义域(0,)+∞上单调递增.故选：A 【点睛】本题考查对数型复合函数的奇偶性和单调性，属于中档题.8．B解析：B 【分析】由()()11f x f x -=+可得函数()f x 关于直线1x =对称，根据对数的运算法则，结合函数的对称性，变形41log 2、13log 3、39log 到区间[)1,+∞内，由函数()f x 在[)1,+∞上单调递增，即可得结果. 【详解】根据题意，函数()f x 满足()()11f x f x -=+，则函数()f x 关于直线1x =对称，又由当(],1-∞时，函数()f x 单调递减，则函数在[)1,+∞上单调递增，又由()44115log log 2222a f f f f ⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ()()13log 313b f f f ⎛⎫==-= ⎪⎝⎭，()()3log 92c f f ==，则有c a b <<，故选B.【点睛】在比较()1f x ，()2f x ，，()n f x 的大小时，首先应该根据函数()f x 的奇偶性（对称性）与周期性将()1f x ，()2f x ，，()n f x 通过等值变形将自变量置于同一个单调区间，然后根据单调性比较大小．9．C解析：C 【解析】要使函数有意义，需使210{340x x x +>--+>，即1{41x x >--<<，所以1 1.x -<< 故选C10．C解析：C 【分析】由已知求出a ，得()g x 表达式，化简函数式后根据定义域和单调性可得正确选项．【详解】由恬24a=，2a =，222log (1),10()log (1)log (1),0x x g x x x x -+-<<⎧=+=⎨+≥⎩，函数定义域是(1,)-+∞，在(1,0)-上递减，在(0,)+∞上递增．故选：C ．【点睛】本题考查对数型复合函数的图象问题，解题方法是化简函数后，由定义域，单调性等判断．11．A解析：A 【分析】根据条件判断()f x 的奇偶性和单调性，把不等式212(log )(log )2(1)f a f f a ≤+转化为2log 1a ≤进行求解即可.【详解】当0x <时，0x ->，则2()2()f x x x f x -=-=，当0x >时，0x -<，则2()2()-=+=f x x x f x ， ∴函数()f x 为偶函数，∴222122(log )(log )(log )(log )2(log )f a f a f a f a f a +=+-=.又当0x ≥时，函数()f x 单调递增，∴22(log )2(1)f a f ≤可转化为2((log 1))f a f ≤，则2log 1a ≤， ∴21log 1a -≤≤，解得122a ≤≤. 故选：A. 【点睛】本题考查了分段函数的性质，考查函数的单调性与奇偶性，考查学生的推理能力与计算求解能力，属于中档题.12．C解析：C 【分析】先根据010lg II η=得10010I I η=，再将60dB 和40dB 代入得计算12I I 即可得答案.【详解】解：因为音量大小与强度为I 的声波的关系为010lg II η=，所以10010I I η=，所以606101001010I I I ==，404102001010I I I ==，所以6014201010010I I I I ==，故选：C. 【点睛】本题以物理知识为背景，考查指对数的互化，运算等，是中档题.二、填空题13．【分析】根据二次根式和对数式有意义的条件得到不等式组求解函数的定义域即可得结果【详解】根据题意可得：解得所以函数的定义域为故答案为：【点睛】该题考查的是有关求函数的问题涉及到的知识点有求给定函数的定解析：(2,3]【分析】根据二次根式和对数式有意义的条件，得到不等式组求解函数的定义域即可得结果.【详解】根据题意可得：1220log (2)0x x ->⎧⎪⎨-≥⎪⎩，解得23x <≤，所以函数()f x =(2,3]，故答案为：(2,3]. 【点睛】该题考查的是有关求函数的问题，涉及到的知识点有求给定函数的定义域，在解题的过程中，注意二次根式和对数式需要满足的条件即可得结果.14．【分析】求出函数在上的最值最后根据题意列出不等式进行求解即可【详解】当时因此；当时因此因为所以有即故答案为：【点睛】本题考查了求指数型函数和对数型函数的最小值考查了存在性和任意性的概念的理解考查了数解析：9,8⎛⎤-∞ ⎥⎝⎦【分析】求出函数(),()f x g x 在[1,3]x ∈上的最值，最后根据题意列出不等式进行求解即可. 【详解】当[1,3]x ∈时，11[,1]28x⎛⎫∈ ⎪⎝⎭，因此9()[,2]8f x ∈；当[1,3]x ∈时，22(log )[0,log 3]x ∈，因此2()[,log 3]g x m m ∈+，因为()()1212[1,3],[1,3],x x f x g x ∀∈∃∈≥，所以有min min ()()f x g x ≥，即9988m m ≥⇒≤. 故答案为：9,8⎛⎤-∞ ⎥⎝⎦【点睛】本题考查了求指数型函数和对数型函数的最小值，考查了存在性和任意性的概念的理解，考查了数学运算能力.15．【分析】根据已知可得为奇函数且在上单调递增不等式化为转化为关于自变量的不等式即可求解【详解】的定义域为是奇函数设为增函数在为增函数在为增函数在处连续的所以在上单调递增化为等价于即所以实数的取值范围为解析：1(1,)3-【分析】根据已知可得()f x 为奇函数且在R 上单调递增，不等式化为()23(12)f a f a <-，转化为关于自变量的不等式，即可求解. 【详解】()f x 的定义域为R ，()()))ln10f x f x x x +-=+==，()f x ∴是奇函数，设,[0,)()x u x x =∈+∞为增函数，()f x 在[0,)+∞为增函数，()f x 在(,0)-∞为增函数， ()f x 在0x =处连续的，所以()f x 在R 上单调递增，()23(21)0f a f a +-<，化为()23(12)f a f a <-，等价于2312a a <-，即213210,13a a a +-<-<<，所以实数a 的取值范围为1(1,)3-. 故答案为: 1(1,)3- 【点睛】本题考查利用函数的单调性和奇偶性解不等式，熟练掌握函数的性质是解题的关键，属于中档题.16．【分析】根据指数幂运算法则和对数运算法则化简可得【详解】故答案为：【点睛】此题考查指数对数的综合运算关键在于熟练掌握运算法则和相关公式准确化简求值解析：32【分析】根据指数幂运算法则和对数运算法则化简可得. 【详解】72log 2338log 2lg 5lg 47-+++()732log 232332log 32lg52lg 27=-++++34222=-+++32= 故答案为：32【点睛】此题考查指数对数的综合运算，关键在于熟练掌握运算法则和相关公式，准确化简求值.17．【分析】由奇函数定义求解【详解】设则∴此时时为奇函数故答案为：【点睛】方法点睛：本题考查函数的奇偶性对于分段函数一般需要分类求解象这种由奇函数求参数可设求得参数值然后再验证这个参数值对也适用即可本题解析：1-．【分析】由奇函数定义求解．【详解】设0x >，则()1x f x e -=-，()xf x em --=+，∴10x x e m e --++-=，1m =-．此时，0x <时，()1,x f x e =-()1()xf x e f x -=-=-，()f x 为奇函数．故答案为：1-．【点睛】方法点睛：本题考查函数的奇偶性，对于分段函数，一般需要分类求解．象这种由奇函数求参数，可设0x >，求得参数值，然后再验证这个参数值对0x <也适用即可．本题也可以由特殊值如(1)(1)f f -=-求出参数，然后检验即可．18．3【分析】利用幂函数的定义与性质求得将代入利用对数的运算法则化简得解【详解】在上为增函数解得(舍去）故答案为：3【点睛】正确理解幂函数的定义求得的值和熟练运用对数恒等式是关键解析：3 【分析】利用幂函数的定义与性质求得3m =，将3m =代入，利用对数的运算法则化简得解. 【详解】()()257m f x m m x =-+在R 上为增函数，25710m m m ⎧-+=∴⎨>⎩，解得3,2m m ==(舍去）， 1log2log 2lg 5lg 4mm m∴+-=31log 23l l og 3g1003+=故答案为：3. 【点睛】正确理解幂函数的定义求得m 的值和熟练运用对数恒等式是关键.19．【分析】求出函数的定义域利用复合函数法可求得函数的单调递增区间【详解】对于函数有解得或所以函数的定义域为内层函数在区间上单调递减在区间上单调递增外层函数为减函数所以函数的单调递增区间为故答案为：【点解析：(),2-∞【分析】求出函数()f x 的定义域，利用复合函数法可求得函数()()212log 56f x x x =-+的单调递增区间. 【详解】对于函数()()212log 56f x x x =-+，有2560x x -+>，解得2x <或3x >. 所以，函数()()212log 56f x x x =-+的定义域为()(),23,-∞+∞，内层函数256u x x =-+在区间(),2-∞上单调递减，在区间()3,+∞上单调递增，外层函数12log y u =为减函数，所以，函数()f x 的单调递增区间为(),2-∞.故答案为：(),2-∞. 【点睛】复合函数()y f g x ⎡⎤=⎣⎦的单调性规律是“同则增，异则减”，即()y f u =与()u g x =.若具有相同的单调性，则()y f g x ⎡⎤=⎣⎦为增函数，若具有不同的单调性，则()y f g x ⎡⎤=⎣⎦必为减函数．20．4【分析】结合对数的基本运算化简求值即可【详解】解：故答案为：4【点睛】本题主要考查对数的基本运算性质熟记公式熟练运用对数的化简对数恒等式是最基本的要求属于基础题型解析：4 【分析】结合对数的基本运算化简求值即可. 【详解】解：7log 3211lg 25lg 27lg5lg 23lg5lg 23lg103422++=++=++=+=. 故答案为：4. 【点睛】本题主要考查对数的基本运算性质，熟记公式，熟练运用对数的化简、对数恒等式是最基本的要求，属于基础题型.三、解答题21．（1）1()3xf x ⎛⎫= ⎪⎝⎭；（2）()126h a a =-；（3）不存在，理由见解析. 【分析】（1）设()xf x c =（0c >且1c ≠），由题意可得()13f -=，可求得c 的值，进而可求得函数()f x 的解析式；（2）令11,333xt ⎛⎫⎡⎤=∈ ⎪⎢⎥⎝⎭⎣⎦，设()223k t t at =-+，分析当3a ≥时，函数()k t 的单调性，进而可得出()()min h a k t =，即可得解；（3）分析出函数()h a 在区间[],n m 上单调递减，可得出22126126n m m n⎧-=⎨-=⎩，将两个等式作差可得出6m n +=，结合3m n >>判断可得出结论. 【详解】（1）设()xf x c =（0c >且1c ≠），因为指数函数()f x 的图象经过点()1,3-，()113f c-∴-==，即13c =，因此，()13xf x ⎛⎫= ⎪⎝⎭；（2）令()13xt f x ⎛⎫== ⎪⎝⎭，[]1,1x ∈-，1,33t ⎡⎤∴∈⎢⎥⎣⎦，所以，设()223k t t at =-+，对称轴为t a =.3a ≥，可知()k t 在1,33⎡⎤⎢⎥⎣⎦上单调递减，当3t =时，()k t 取最小值，即()g x 取最小值()()3126h a k a ==-；（3）由（2）知3m n >>时，()126h a a =-在[],n m 上单调递减，若此时()h a 的值域为22,n m ⎡⎤⎣⎦，则22126126n m m n ⎧-=⎨-=⎩，即()()()6m n m n m n -=-+，m n ≠，则0m n -≠，6m n ∴+=，又3m n >>，则6m n +>，故不存在满足条件的m 、n 的值. 【点睛】方法点睛：（1）二次函数在闭区间上的最值主要有三种类型：轴定区间定、轴动区间定、轴动区间定，不论哪种类型，解决的关键就是考查对称轴于区间的位置关系，当含有参数时，要依据对称轴与区间的位置关系进行分类讨论；（2）二次函数的单调性主要依据二次函数图象的对称轴进行分析讨论求解. 22．（1）[]0,4a ∈；（2）2k <. 【分析】（1）由()2log f x x =，()()y f g x =的值域为R ，知()g x 值域应为小于等于0的数直至正无穷，分类讨论参数a 的正负，再结合二次函数值域与判别式的关系即可求解；（2）对恒成立问题与存在性问题转化得()22tmin k h x ⋅<+在[]1,1t ∈-有解，求得()min h x ，再结合函数单调性即可求解【详解】（1）0a <时，内函数有最大值，故函数值不可能取到全体正数，不符合题意；当0a =时，内函数是一次函数，内层函数值可以取遍全体正数，值域是R ，符合题意；当0a >时，要使内函数的函数值可以取遍全体正数，只需要函数最小值小于等于0，故只需0≥，解得(]0,4a ∈.综上得[]0,4a ∈；2（）由题意可得2222()222t k h x log x log x ⋅<+=-+在1,22x ⎡∈⎤⎢⎥⎣⎦恒成立，则()221tmin k h x ⋅<+=在[]1,1t ∈-有解，即1<2tk 在[]1,1t ∈-有解， 122t maxk ⎛⎫∴<= ⎪⎝⎭，综上，实数k 的取值范围2k <.【点睛】关键点睛：本题考查由对数型复合函数的值域求解参数取值范围，由恒成立与存在性问题建立的不等式求解参数取值范围，解题关在在于：（1）()()()log a f x g x =值域为R ，()g x 值域范围的判断；（2）全称命题与存在性命题逻辑关系的理解与正确转化.23．（1）14；（2）【分析】（1）利用幂的运算法则和对数的运算法则计算；（2）利用完全平方公式求得1x x -+，再求得22x x -+，然后可求得1x x --．【详解】(1)原式=236342464⎛⎫-⨯- ⎪⎝⎭++=++＝14;-(2)由1122x x -+=1+25x x -+=，所以13x x -+=所以2222+29=7x x x x --+=+，则1222()2=5x x x x ---=-+所以1=x x -- 【点睛】幂的运算法则从整数范围推广到有理数范围，实数范围后，乘法公式也随之推广过来，即公式222()2a b a ab b +=++，222()2a b a ab b -=-+，22()()a b a b a b +-=-中,a b 是是分数指数幂时，公式也适用，解题时要注意体会．24．（1）()3,+∞；（2）min 1y =，max 54y =. 【分析】（1）结合指数函数性质首先求a 的值，再解指数不等式；（2）通过换元，设12xt ⎛⎫= ⎪⎝⎭，并且求变量的取值范围，转化为二次函数在定义域内的最大值和最小值. 【详解】（1）由题意知定点A 的坐标为()2,2， ∴)22a =+解得1a =.∴()221x g x -=+.∴由()3g x >得，2213x -+>. ∴222x ->. ∴21x ->. ∴3x >.∴不等式()3g x >的解集为()3,+∞.（2）由121log 1x -≤≤得122x ≤≤令12xt ⎛⎫= ⎪⎝⎭，则14t ≤≤， 221442412y t t t ⎛⎫=-+=-+ ⎪⎝⎭.∴当12t =，即1122x⎛⎫= ⎪⎝⎭，1x =时，min 1y =，当14t =，即1124x⎛⎫= ⎪⎝⎭，2x =时，max 54y =. 【点睛】本题考查指数函数与对数函数的图象与性质，考查求对数型函数的值域，求值域的方法是用换元法把函数转化为二次函数，然后求解．25．（1）奇函数，理由见详解；（2）单调递减，过程见详解；（3）存在(0,3∈-a .【分析】（1）先由函数解析式求出定义域，再由()f x ，求出()f x -，根据函数奇偶性的概念，即可得出结果；（2）先令2()11=-+g x x ，用单调性的定义，即可判断2()11=-+g x x 的单调性，再由复合函数单调性的判定原则，即可得出结果；（3）先假设存在满足条件的实数a ，由题意得出01a <<，()1log ()1log a a f n nf m m =+⎧⎨=+⎩，推出,m n 是方程2log 11log 1⎛⎫-=+ ⎪+⎝⎭a a x x 的两根，进而得到2(1)10ax a x +-+=在()1,+∞上有两个不同解，根据一元二次方程根的分布情况，列出不等式组，即可求出结果. 【详解】（1）由2101->+x 解得1x >或1x <-，即函数()f x 的定义域为(,1)(1,)-∞-+∞；又()21log 1log 11-⎛⎫=-= ⎪++⎝⎭a a x f x x x ，所以()22121log 1log 1log log 1111-+-+⎛⎫⎛⎫-=-=-== ⎪ ⎪-+-+-+-⎝⎭⎝⎭a a a a x x f x x x x x ，因此()()log 10+-==a f x f x ，所以()()f x f x -=-，所以函数()f x 为奇函数；（2）令2()11=-+g x x ，任取121x x <<，则12121221212222()()111111(1)(1)⎛⎫⎛⎫--=---=-= ⎪ ⎪++++++⎝⎭⎝⎭x x g x g x x x x x x x ，因为120x x -<，110x +>，210x +>，所以121221()()0(1)(1)--=<++x x g x g x x x ，即函数2()11=-+g x x 在()1,+∞上单调递增；又01a <<，所以log ay x =单调递减，根据同增异减的原则，可得：()2log 11a f x x ⎛⎫=- ⎪+⎝⎭在()1,+∞上单调递减；（3）假设存在实数a ，使得当()f x 的定义域为[],m n 时，值域为[]1log ,1log a a n m ++，由m n <，1log 1log +<+a a n m 可得01a <<；所以()1log ()1log a a f n n f m m =+⎧⎨=+⎩，因此,m n 是方程2log 11log 1⎛⎫-=+ ⎪+⎝⎭a a x x 的两根，即2(1)10ax a x +-+=在()1,+∞上有两个不同解，设2()(1)1=+-+h x ax a x ，则(1)01120h a a >⎧⎪-⎪->⎨⎪∆>⎪⎩，解得03a <<-.所以存在(0,3∈-a ，使得当()f x 的定义域为[],m n 时，值域为[]1log ,1log a a n m ++.【点睛】本题主要考查函数奇偶性的判定，单调性的判定，以及由函数定义域与值域求参数的问题，熟记函数单调性与奇偶性的定义即可，属于常考题型. 26．定义域为(,1)(3,)-∞-+∞，函数值域为R ，减区间是(,1)-∞-，增区间是(3,)+∞．【分析】结合对数函数性质求解．【详解】由2230x x -->得1x <-或3x >，∴定义域为(,1)(3,)-∞-+∞．由2230x x -->得y R ∈，函数值域为R ，223y x x =--在(,1)-∞-上递减，在(3,)+∞上递增，∴()log 23=-2-3y x x 的减区间是(,1)-∞-，增区间是(3,)+∞．【点睛】本题考查对数型复合函数的性质，掌握对数函数的性质是解题关键．。

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测卷(包含答案解析)

一、选择题1．设a ，b ，c 为正数，且3a =4b =6c ，则有（） A ．111c a b=+ B ．221c a b=+ C ．122c a b=+ D ．212c a b=+ 2．下列等式成立的是（） A ．222log (35)log 3log 5+=+ B ．2221log 3log 32-=C ．222log 3log 5log (35)⋅=+D ．231log 3log 2=3．专家对某地区新冠肺炎爆发趋势进行研究发现，从确诊第一名患者开始累计时间t （单位：天）与病情爆发系数()f t 之间，满足函数模型：0.22(50)11()t f t e --=+，当()0.1f t =时，标志着疫情将要大面积爆发，则此时t 约为（）(参考数据： 1.13e ≈) A ．38 B ．40C ．45D ．474．若x ，y ，z 是正实数，满足2x =3y =5z ，试比较3x ，4y ，6z 大小（）A ．3x >4y >6zB ．3x >6z >4yC ．4y >6z >3xD ．6z >4y >3x5．已知()()514,1log ,1a a x a x f x x x ⎧-+<=⎨≥⎩是(),-∞+∞上的减函数，那么a 的取值范围是（）.A ．()0,1B ．10,5⎛⎫ ⎪⎝⎭C ．11,95⎡⎫⎪⎢⎣⎭D ．1,19⎡⎫⎪⎢⎣⎭6．我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微：数形结合百般好，隔离分家万事休”．在数学学习中和研究中，常用函数的图象来研究函数的性质，页常用函数的解析式来琢磨函数图象的特征，如函数()22xy xx R =-∈的大致图象是（）A ．B ．C ．D ．7．已知()f x ，()g x 分别为定义在R 上的偶函数和奇函数，且满足()()2xf xg x +=，若对于任意的[]1,2x ∈，都有()()20f x a g x a -⋅-≤⎡⎤⎡⎤⎣⎦⎣⎦恒成立，则实数a 的取值范围是（） A ．317,44⎡⎤⎢⎥⎣⎦B ．155,82⎡⎤⎢⎥⎣⎦ C ．15,28⎡⎤⎢⎥⎣⎦D ．172,4⎡⎤⎢⎥⎣⎦8．设0.34()5a =，0.254b ⎛⎫= ⎪⎝⎭，125log 4c =，则a ，b ，c 的大小关系为（） A ．b a c >> B ．c a b >> C ．c b a >> D ．b c a >>9．函数2()ln(43)f x x x =+-的单调递减区间是（） A ．32⎛⎤-∞ ⎥⎝⎦，B ．3,42⎡⎫⎪⎢⎣⎭C ．3,2⎡⎫+∞⎪⎢⎣⎭D ．31,2⎛⎤- ⎥⎝⎦10．若a ＞b ＞0，0＜c ＜1，则 A ．log a c ＜log b cB ．log c a ＜log c bC ．a c ＜b cD ．c a ＞c b11．函数213()log 4f x x =-的单调减区间是（）A ．(]()2,02,-+∞B ．(]2,0-和(2,)+∞ C ．(),20,2[)-∞-D ．(,2)-∞-和[0,2)12．物理学规定音量大小的单位是分贝（dB ），对于一个强度为I 的声波，其音量的大小η可由如下公式计算：010lgII η=(其中0I 是人耳能听到声音的最低声波强度).我们人类生活在一个充满声音的世界中，人们通过声音交换信息、交流情感，人正常谈话的音量介于40dB 与60dB 之间，则60dB 声音的声波强度1I 是40dB 声音的声波强度2I 的（）A ．32倍B ．3210倍C ．100倍D ．3lg2倍二、填空题13．若函数()2log 12a a f x x x ⎛⎫=-+ ⎪⎝⎭，()0,1a a >≠没有最小值，则实数a 的取值范围是______.14．给出下列四个命题：①函数f （x ）＝log a （2x ﹣1）﹣1的图象过定点（1，0）；②已知函数f （x ）是定义在R 上的偶函数，当x ≤0时，f （x ）＝x （x +1），则f （x ）的解析式为f （x ）＝x 2﹣|x |；③若log a12＜1，则a 的取值范围是（0，12）∪（2，+∞）；④若2﹣x ﹣2y ＞ln x ﹣ln （﹣y ）（x ＞0，y ＜0），则x +y ＜0.其中所有正确命题的序号是_____. 15．已知12512.51000x y ==，则11x y＝_____.16．已知1a b >>，若10log log 3a b b a +=，b a a b =，则ab =___________. 17．已知函数f （x ）＝[log a （x +2）]+3的图象恒过定点（m ，n ），且函数g （x ）＝mx 2﹣2bx +n 在[1，+∞）上单调递减，则实数b 的取值范围是________.18．设正数,x y 满足222log (3)log log x y x y ++=+，则x y +的取值范围是_____. 19．7log 31lg 25lg 272++=________. 20．设函数()f x 满足()22221x f x ax a =-+-，且()f x 在21222,2a aa --+⎡⎤⎣⎦上的值域为[]1,0-，则实数a 的取值范围为______.三、解答题21．已知函数2()46f x ax x =-+．（1）若函数2log ()y f x =的值域为R ，求实数a 的取值范围；（2）若函数log ()a y f x =在区间(1,3)上单调递增，求实数a 的取值范围． 22．设函数()()1xxf x a k a -=--，(0a >且1a ≠)是定义域为R 的奇函数，且()312f =. （1）求k ，a 的值；（2）求函数()f x 在[)1,+∞上的值域；（3）设()()222xx g x a a m f x -=+-⋅，若()g x 在[)1,+∞上的最小值为2-，求m 的值；（4）对于（3）中函数()g x ，如果()0g x >在[)1,+∞上恒成立，求m 的取值范围. 23．设()log (1)log (3)(0,1)a a f x x x a a =++->≠，且(1)2f =. （1）求a 的值及()f x 的定义域；（2）求()f x 在区间302⎡⎤⎢⎥⎣⎦，上的最大值.24．已知12324xA x ⎧⎫=≤≤⎨⎬⎩⎭，121log ,264B y y x x ⎧⎫==≤≤⎨⎬⎩⎭．（1）求AB ；（2）若{}11C x m x m =-≤≤+，若C A ⊆，求m 的取值范围．25．已知函数1()log a f x a x ⎛⎫=-⎪⎝⎭，其中实数0a >且1a ≠. （1）当3a =时，求不等式()0f x >的解集；（2）若()f x 在区间[1,3]上单调递增，求a 的取值范围；26．已知函数214()log (238)f x mx x m =-+. （Ⅰ）当1m =时，求函数()f x 在1[,2]2上的值域；（Ⅱ）若函数()f x 在(4,)+∞上单调递减，求实数m 的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】首先根据指对互化求出,,a b c ，再根据换底公式表示111,,a b c，最后根据对数运算法则化简. 【详解】设3a =4b =6c =k ，则a =log 3k ， b =log 4k ， c =log 6k ， ∴311log 3log k a k ==，同理1log 4k b =，1log 6k c=，而11log 2,log 3log 22k k k b c ==+， ∴1112c a b =+，即221c a b=+．故选：B 【点睛】本题考查指对数运算，换底公式，以及对数运算的性质，关键是灵活应用对数运算公式，公式1log log a b b a=是关键. 2．D解析：D 【分析】根据对数的运算法则和换底公式判断．【详解】22222log 3log 5log (35)log 15log (35)+=⨯=≠+，A 错误；22221log 32log 3log 32-=-≠，B 错误； 222log 3log 5log (35)⋅≠+，C 错误；3233log 31log 3log 2log 2==，D 正确．故选：D ．【点睛】关键点点睛：本题考查对数的运算法则．log log log ()a a a M N MN +=，log log n a a b n b =，一般log ()log log a a a M N M N +≠+．log ()log log a a a MN M N ≠⋅， 1log log n a a b b n≠． 3．B解析：B 【分析】根据()0.1f t =列式求解即可得答案.【详解】解：因为()0.1f t =，0.22(50)11()t f t e --=+，所以0.22(50)()0.111t f t e--==+，即0.22(50)011t e --=+，所以0.22(50)9t e --=，由于 1.13e ≈，故()21.12.29e e =≈，所以0.222().250t e e --=，所以()0.2250 2.2t --=，解得40t =. 故选：B. 【点睛】本题解题的关键在于根据题意得0.22(50)9t e --=，再结合已知 1.13e ≈得()21.12.29e e =≈，进而根据0.222().250t e e --=解方程即可得答案，是基础题.4．B解析：B 【分析】令235x y z t ===，则1t >，lg lg 2t x =，lg lg3t y =，lg lg5tz =，利用作差法能求出结果. 【详解】∵x 、y 、z 均为正数，且235x y z ==，令235x y z t ===，则1t >，故2lg log lg 2t x t ==，3lg log lg 3t y t ==，5lg log lg 5tz t ==， ∴()3lg lg5lg 4lg 2lg 3630lg 2lg5lg 2lg5t t t x z -⎛⎫-=-=> ⎪⋅⎝⎭，即36x z >； ()2lg lg 27lg 253lg 2lg 6420lg5lg3lg3lg5t t t z y -⎛⎫-=-=> ⎪⋅⎝⎭，即64z y >，即364x z y >>成立，故选：B. 【点睛】关键点点睛：（1）将指数式转化为对数式；（2）利用作差法比较大小.5．C解析：C 【分析】由51001514log 1a a a a a -<⎧⎪<<⎨⎪-+≥⎩解得结果即可得解. 【详解】因为()()514,1log ,1a a x a x f x x x ⎧-+<=⎨≥⎩是(),-∞+∞上的减函数，所以51001514log 1a a a a a -<⎧⎪<<⎨⎪-+≥⎩，解得1195a ≤<.故选：C 【点睛】易错点点睛：容易忽视两段交界点处函数值的大小关系.6．A解析：A 【分析】分析函数()()22xf x xx R =-∈的奇偶性，结合()01f =可得出合适的选项.【详解】令()22=-xf x x ，该函数的定义域为R ，()()()2222xxf x x x f x --=--=-=，函数()22=-xf x x 为偶函数，排除B 、D 选项；又()010f =>，排除C 选项.故选：A. 【点睛】函数图象的辨识可从以下方面入手：（1）从函数的定义域，判断图象的左右位置；（2）从函数的值域，判断图象的上下位置．（3）从函数的单调性，判断图象的变化趋势；（4）从函数的奇偶性，判断图象的对称性；（5）从函数的特征点，排除不合要求的图象.7．B解析：B 【分析】利用奇偶性求出()222x x f x -+=，()222x x g x --=，讨论()22x xh x -=+和()g x 的单调性求最值可得()()h x g x >恒成立，则不等式恒成立等价于()()max min g x a h x ≤≤. 【详解】()()2x f x g x +=，()()2x f x g x --+-=∴，()f x 是偶函数，()g x 分是奇函数，()()2x f x g x -=∴-，可得()222x xf x -+=，()222x xg x --=，则不等式为()()1222202x xx x a a --⎡⎤+-⋅--≤⎢⎥⎣⎦，令()22xxh x -=+，令2x t =，由对勾函数的性质可得1y t t=+在[]2,4单调递增，则()22xxh x -=+在[]1,2单调递增，则()()()()min max 5171,224h x h h x h ====，对于()222x xg x --=，因为2x y =单调递增，2x y -=-单调递增，()g x ∴在[]1,2单调递增，()()()()min max 3151,248g x g g x g ∴====， ()()h x g x ∴>恒成立，则不等式()()0h x a g x a --≤⎡⎤⎡⎤⎣⎦⎣⎦，解得()()g x a h x ≤≤，()()max min g x a h x ∴≤≤，即15582a ≤≤. 故选：B. 【点睛】关键点睛：本题考查不等式的恒成立问题，解题的关键是利用奇偶性求出函数解析式，根据函数的单调性求出最值将不等式等价为()()max min g x a h x ≤≤即可求解.8．A解析：A 【分析】根据指数函数、对数函数的性质结合中间值0和1比较．【详解】由指数函数性质得0.34015⎛⎫<< ⎪⎝⎭，0.2514⎛⎫> ⎪⎝⎭，由对数函数性质得125log 04<， ∴b a c >>．故选：A ．【点睛】本题考查比较幂与对数的，掌握指数函数与对数函数的性质是解题关键．解题方法是借助中间值比较大小．9．B解析：B 【分析】先求函数的定义域，再利用复合函数的单调性同增异减，即可求解. 【详解】由2430x x +->得2340x x --<，解得：14x -<<，2()ln(43)f x x x =+-由ln y t =和234t x x =-++复合而成，ln y t =在定义域内单调递增，234t x x =-++对称轴为32x =，开口向下，所以 234t x x =-++在31,2⎛⎫- ⎪⎝⎭ 单调递增，在3,42⎡⎫⎪⎢⎣⎭单调递减，所以2()ln(43)f x x x =+-的单调减区间为3,42⎡⎫⎪⎢⎣⎭，故选：B 【点睛】本题主要考查了利用同增异减求复合函数的单调区间，注意先求定义域，属于中档题10．B解析：B 【解析】试题分析：对于选项A ，a b 1gc 1gclog c ,log c lg a lg b==，01c <<，10gc ∴<，而0a b >>，所以lg lg a b >，但不能确定lg lg a b 、的正负，所以它们的大小不能确定;对于选项B ，c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >，两边同乘以一个负数1lg c改变不等号方向，所以选项B 正确;对于选项C ，利用c y x =在第一象限内是增函数即可得到c c a b >，所以C 错误;对于选项D ，利用x y c =在R 上为减函数易得a b c c <，所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较；若底数不同,可考虑利用中间量进行比较.11．B解析：B 【分析】先分析函数的定义域，然后根据定义域以及复合函数的单调性判断方法确定出()f x 的单调递减区间. 【详解】因为240x ->，所以定义域为()()(),22,22,-∞--+∞，令()24u x x =-，13log y u =在()0,∞+上单调递减，当(),2x ∈-∞-时，()u x 单调递减，所以()f x 单调递增；当(]2,0x ∈-时，()u x 单调递增，所以()f x 单调递减；当()0,2x ∈时，()u x 单调递减，所以()f x 单调递增；当()2,x ∈+∞时，()u x 单调递增，所以()f x 单调递减；综上可知：()f x 的单调递减区间为(]2,0-和()2,+∞. 故选：B. 【点睛】本题考查对数型复合函数的单调区间的求解，难度一般.分析复合函数的单调性，注意利用判断的口诀“同增异减”，当内外层函数单调性相同时，整个函数为增函数，当内外层函数单调性相反时，整个函数为减函数.12．C解析：C 【分析】先根据010lg II η=得10010I I η=，再将60dB 和40dB 代入得计算12I I 即可得答案.【详解】解：因为音量大小与强度为I 的声波的关系为010lgII η=，所以10010I I η=，所以606101001010I I I ==，404102001010I I I ==，所以6014201010010I I I I ==，故选：C. 【点睛】本题以物理知识为背景，考查指对数的互化，运算等，是中档题.二、填空题13．【分析】讨论和两种情况结合对数函数的单调性可判断求解【详解】当时在单调递减没有最大值没有最小值符合题意；当时在单调递增则可得当有解时没有最小值解得综上的取值范围为故答案为：【点睛】关键点睛：结合对数解析：(0,1)[4,)∞⋃+【分析】讨论01a <<和1a >两种情况结合对数函数的单调性可判断求解. 【详解】当01a <<时，log ay x =在(0,)+∞单调递减，212a y x x =-+没有最大值，()2log 12a a f x x x ⎛⎫∴=-+ ⎪⎝⎭没有最小值，符合题意；当1a >时，log ay x =在(0,)+∞单调递增，则可得当2102ax x -+≤有解时，()2log 12a a f x x x ⎛⎫=-+ ⎪⎝⎭没有最小值，2402a ⎛⎫∴∆=--≥ ⎪⎝⎭，解得4a ≥，综上，a 的取值范围为(0,1)[4,)∞⋃+.故答案为：(0,1)[4,)∞⋃+. 【点睛】关键点睛：结合对数函数的单调性进行讨论求解，将题目转化为2102ax x -+≤有解进行求解.14．②④【分析】根据对数函数的图像与性质以及函数的单调性和奇偶性逐个分析判断即可得解【详解】对于①由2x ﹣1＝1得x ＝1∴函数f （x ）＝loga （2x ﹣1）﹣1的图象过定点（1﹣1）故①错误；对于②函数解析：②④ 【分析】根据对数函数的图像与性质，以及函数的单调性和奇偶性，逐个分析判断即可得解. 【详解】对于①，由2x ﹣1＝1，得x ＝1，∴函数f （x ）＝log a （2x ﹣1）﹣1的图象过定点（1，﹣1），故①错误；对于②，函数f （x ）是定义在R 上的偶函数，当x ≤0时，f （x ）＝x （x +1），设x ＞0，则﹣x ＜0， ∴f （x ）＝f （﹣x ）＝﹣x （﹣x +1）＝x （x ﹣1），则f （x ）的解析式为f （x ）＝x 2﹣|x |，故②正确；对于③，由log a12＜1，得log a 12＜log a a ，当a ＞1时，不等式成立，当0＜a ＜1时，解得012a <<. 则a 的取值范围是（0，12）∪（1，+∞），故③错误；对于④，由2﹣x ﹣2y ＞ln x ﹣ln （﹣y ）（x ＞0，y ＜0），得2﹣x ﹣lnx ＞2y ﹣ln （﹣y ），∵函数f （x ）＝2﹣x ﹣ln x 为定义域内的减函数， ∴x ＜﹣y ，即x +y ＜0，故④正确. 故答案为：②④. 【点睛】本题考查了对数函数的运算以及对数函数的性质，考查了函数奇偶性和单调性的应用，考查了转化思想，属于中档题.本题涉及的方法有一下几个：（1）根据奇偶性求解析式，注意范围的设定；（2）构造函数，利用函数的单调性，确定大小关系.15．【分析】根据指数与对数之间的关系求出利用对数的换底公式即可求得答案【详解】∵∴∴∴故答案为：【点睛】本题考查了指数与对数之间的关系掌握对数换底公式:是解本题的关键属于基础题解析：13【分析】根据指数与对数之间的关系,求出,x y ,利用对数的换底公式,即可求得答案. 【详解】∵12512.51000x y ==， ∴12512.51000100011log 1000,log 1000log 125log 12.5x y ====，∴1000100011log 125,log 12.5x y==，∴1000111log 103x y -==. 故答案为：13. 【点睛】本题考查了指数与对数之间的关系.掌握对数换底公式:log log log c a c bb a=是解本题的关键.属于基础题.16．9【分析】由对数的运算性质解并整理得由可求出的值【详解】解：整理得解得或因为所以则即因为所以所以解得或因为所以所以所以故答案为：9【点睛】关键点睛：本题主要考查对数运算和指数运算解题的关键是由得出再解析：9 【分析】由对数的运算性质解10log log 3a b b a +=并整理得3a b =，由b a a b =可求出,a b 的值. 【详解】解：110log log log log 3a b b b b a a a +=+=，整理得()23log 10log 30b b a a -+=，解得log 3b a =或13，因为1a b >>，所以log 1b a >，则log 3b a =，即3a b =，因为b a a b =，所以33b b b b =，所以33b b =，解得b =0，因为1b >，所以b =所以3a ==，所以9ab ==. 故答案为：9. 【点睛】关键点睛：本题主要考查对数运算和指数运算，解题的关键是由10log log 3a b b a +=得出3a b =，再根据指数运算求解.17．【分析】先求出m=-1n=3再利用二次函数的图像和性质分析得解【详解】因为函数f （x ）＝loga （x+2）+3的图象恒过定点所以m=-1n=3所以g （x ）＝-x2﹣2bx+3因为g （x ）＝-x2﹣2 解析：[)1,-+∞【分析】先求出m =-1,n =3.再利用二次函数的图像和性质分析得解. 【详解】因为函数f （x ）＝[log a （x +2）]+3的图象恒过定点(1,3)-，所以m =-1,n =3，所以g （x ）＝-x 2﹣2bx +3，因为g （x ）＝-x 2﹣2bx +3在[1，+∞）上单调递减，所以对称轴1x b =-≤，解得1b ≥-，故答案为：[)1,-+∞ 【点睛】关键点点睛：本题考查了对数型函数过定点，可求出,m n 的值，利用了二次函数的单调性与对称轴的关系求出b 的范围.18．【分析】由题设知再由得到所以设由此可求出的取值范围【详解】解：正数满足又所以左右加上得到所以由得到设即解得或即或根据定义域均大于零所以取值范围是故答案为：【点睛】本题考查对数的运算法则基本不等式的应解析：[)6,+∞【分析】由题设知3x y xy ++=，再由2220x xy y -+，得到2224x xy y xy ++，所以2()4x y xy+，设x y a +=，由此可求出x y +的取值范围．【详解】解：正数x ，y 满足222log (3)log log x y x y ++=+，22log (3)log x y xy ∴++=，3x y xy ∴++=，又2220x xy y -+，所以左右加上4xy 得到2224x xy y xy ++，所以2()4x y xy +，由3x y xy ++=得到2()34x y x y +++，设x y a +=即2412a a +，解得6a ≥或2a ≤-即(],2a ∈-∞-或[)6,+∞．根据定义域x ，y 均大于零，所以x y +取值范围是[)6,+∞．故答案为：[)6,+∞．【点睛】本题考查对数的运算法则，基本不等式的应用，解题时要认真审题，仔细解答，注意公式的灵活运用，属于中档题．19．4【分析】结合对数的基本运算化简求值即可【详解】解：故答案为：4【点睛】本题主要考查对数的基本运算性质熟记公式熟练运用对数的化简对数恒等式是最基本的要求属于基础题型解析：4 【分析】结合对数的基本运算化简求值即可. 【详解】解：7log 3211lg 25lg 27lg 5lg 23lg 5lg 23lg103422++=++=++=+=. 故答案为：4. 【点睛】本题主要考查对数的基本运算性质，熟记公式，熟练运用对数的化简、对数恒等式是最基本的要求，属于基础题型.20．【分析】利用换元法可得然后采用等价转换的方法可得在的值域为最后根据二次函数的性质可得结果【详解】由令所以则令由在上的值域为等价为在的值域为的对称轴为且所以可得或所以故答案为：【点睛】本题主要考查函数解析：⎤⎡⋃⎥⎢⎣⎦⎣⎦【分析】利用换元法，可得()2221g x x ax a =-+-，然后采用等价转换的方法，可得()g x 在21,22a a a ⎡⎤--+⎣⎦的值域为[]1,0-，最后根据二次函数的性质，可得结果.【详解】由()22221x f x ax a =-+-令22,log xt x t ==，所以()()2222log 2log 1f t t a t a =-+-则令()2221g x x ax a =-+-由()f x 在21222,2a aa --+⎡⎤⎣⎦上的值域为[]1,0- 等价为()g x 在21,22a a a ⎡⎤--+⎣⎦的值域为[]1,0-()g x 的对称轴为x a =，且()()1,10g a g a =--= 所以()()22122222a a a a a a -+-+≤≤-+1a ≤≤或2a ≤≤所以a ⎤⎡∈⋃⎥⎢⎣⎦⎣⎦故答案为：⎤⎡⋃⎥⎢⎣⎦⎣⎦【点睛】本题主要考查函数值域的应用，难点在于使用等价转换思想，使问题化繁为简，属中档题.三、解答题21．（1）20,3⎡⎤⎢⎥⎣⎦；（2）[)2,+∞. 【分析】（1）根据条件分析出2()46f x ax x =-+的值域包含()0,∞+，由此根据a 与0的关系分类讨论，求解出结果；（2）根据1,01a a ><<两种情况结合复合函数单调性的判断方法进行分类讨论，然后求解出a 的取值范围. 【详解】（1）因为()22log 46y ax x =-+的值域为R ，所以246y ax x =-+的值域包含()0,∞+，当0a =时，246y ax x =-+即46y x =-+，此时46y x =-+的值域为R ，满足；当0a ≠时，则有016240a a >⎧⎨∆=-≥⎩，所以203a <≤，综上可知：20,3a ⎡⎤∈⎢⎥⎣⎦；（2）当1a >时，log a y x =在()0+∞，上单调递增，所以2()46f x ax x =-+在()1,3上递增，所以()2110a f ⎧≤⎪⎨⎪>⎩，所以2a ≥，当01a <<时，log a y x =在()0+∞，上单调递减，所以2()46f x ax x =-+在()1,3上递减，所以()2330a f ⎧≥⎪⎨⎪>⎩，此时a 无解，综上可知：[)2,a ∈+∞.【点睛】思路点睛：形如()()()2lg 0f x ax bx ca =++≠的函数，若函数的定义域为R ，则有00a >⎧⎨∆<⎩；若函数的值域为R ，则有00a >⎧⎨∆≥⎩. 22．（1）2a =，2k =；（2）3,2⎡⎫+∞⎪⎢⎣⎭；（3）2m =；（4）17,12⎛⎫-∞ ⎪⎝⎭. 【分析】（1）由奇函数性质求得k ，由3(1)2f =可求得a ；（2）利用函数的单调性得值域；（3）换元，设22x x t -=-，则3,2t ⎡⎫∈+∞⎪⎢⎣⎭，()g x 转化为()222k t t mt =-+，3,2t ⎡⎫∈+∞⎪⎢⎣⎭，由二次函数的性质求得最小值，再由最小值为2-可得m ，（4）在（3）基础上，由()k t 的最小值大于0可得m 的取值范围．【详解】解：（1）∵函数()()1xxf x a k a -=--，(0a >且1a ≠)是定义域为R 的奇函数，∴()00f =，即()110k --=，2k =， ∵()312f =.∴132a a -=，2a =， ∴2a =，2k =，（2）1()2222x x xx f x -=-=-是增函数，∴1≥x 时，13()222f x ≥-=，即值域中3,2⎡⎫+∞⎪⎢⎣⎭；（3）()()2222222xx x x g x m --=+--，设22x x t -=-，[)1,x ∈+∞，3,2t ⎡⎫∈+∞⎪⎢⎣⎭，∴()222k t t mt =-+，3,2t ⎡⎫∈+∞⎪⎢⎣⎭， ∵若()g x 在[)1,+∞上的最小值为2-，∴()222k t t mt =-+，3,2t ⎡⎫∈+∞⎪⎢⎣⎭的最小值为2-，∴23222m m ⎧≥⎪⎨⎪-+=-⎩或3293224m m ⎧<⎪⎪⎨⎪-+=-⎪⎩ 即2m =，或2512m =(舍去)，故2m =；（4）()222k t t mt =-+，3,2t ⎡⎫∈+∞⎪⎢⎣⎭，∵()0g x >在[)1,+∞上恒成立，∴()0k t >在3,2t ⎡⎫∈+∞⎪⎢⎣⎭上恒成立， ∴23220m m ⎧≥⎪⎨⎪-+>⎩或3293204m m ⎧<⎪⎪⎨⎪-+>⎪⎩，解不等式得出x ∈∅或1712m <， ∴m 的取值范围为17,12⎛⎫-∞ ⎪⎝⎭. 【点睛】方法点睛：本题考查指数函数的性质，考查奇偶性，由奇偶性同函数解析式，由单调性是函数的值域，在求函数()g x 的最值问题，不等式恒成立问题时，解题方法是换元法，即设22x x t -=-，把指数函数转化为二次函数，然后利用二次函数性质求解． 23．（1）2a =；(1,3)-；（2）2.【分析】（1）由函数值求得a ，由对数的真数大于0可得定义域；（2）函数式变形为22()log (1)4f x x ⎡⎤=--+⎣⎦，由复合函数的单调性得出单调区间后可得最大值．【详解】解：（1）(1)2f =，log (11)log (31)log 42a a a ∴++-==，解得2(0,1)a a a =>≠，由1030x x +>⎧⎨->⎩，得(1,3)x ∈-.∴函数()f x 的定义域为()13-，.（2）22222()log (1)log (3)log (1)(3)log (1)4f x x x x x x ⎡⎤=++-=+-=--+⎣⎦∴当[0,1]x ∈时，()f x 是增函数；当3[1,]2x ∈时，()f x 是减函数.所以函数()f x 在3[0,]2上的最大值是2(1)log 42f ==. 【点睛】本题考查对数函数的性质，掌握复合函数的单调性解题关键：（前提条件：在函数定义域内）24．（1）[1,5]A B ⋂=-；（2）(],3-∞. 【分析】（1）根据指数运算解不等式求出集合A ，利用对数的运算求出集合B ，由此能求出A B ；（2）由{}11C x m x m =-≤≤+和C A ⊆，对C 是否为空集分类讨论，列出不等式组，由此能求出m 的取值范围．【详解】解：（1）1{|232}{|25}4xA x x x ==-， 12{|log B y y x==，12}{|16}64x x x =-， [1,5]A B ∴=-.（2）{}11C x m x m =-≤≤+且C A ⊆，若,11,0C m m m =∅->+<若C ≠∅，则111512m m m m -≤+⎧⎪+⎨⎪--⎩，解得03m ≤≤，m ∴的取值范围是(],3-∞.【点睛】本题考查交集的运算以及根据集合间的包含关系求参数的取值范围，还涉及指对数的运算，属于基础题．25．(1) 10,4⎛⎫ ⎪⎝⎭;(2) 103a << 【分析】(1)代入3a =,根据对数函数的单调性求解即可.(2)先根据区间[1,3]结合定义域可求得a 的大致范围,从而确定log a y x =的单调性,再根据复合函数的单调性确定a 的取值范围即可. 【详解】(1) 当3a =时, 31()log 3f x x ⎛⎫=-⎪⎝⎭,故()0f x >即31log 30x ⎛⎫-> ⎪⎝⎭,即131x ->,14x >,解得104x <<.故()0f x >解集为10,4⎛⎫⎪⎝⎭.(2)由定义域可知,10a x->,即1a x >在区间[1,3]上恒成立,故103a <<,所以log a y x =为减函数.又1y a x =-在区间[1,3]上为减函数,故1()log a f x a x ⎛⎫=- ⎪⎝⎭在区间[1,3]上为增函数.满足题意.故103a << 【点睛】本题主要考查了对数函数的不等式求解以及对数型复合函数的单调性求解参数的问题.属于中档题.26．（Ⅰ）114455log 10,log 8⎡⎤⎢⎥⎣⎦（Ⅱ）3,10⎡⎫+∞⎪⎢⎣⎭【分析】（Ⅰ）把1m =代入，可得()122()log 238f x x x =-+，令2238y x x =-+，求出其在1[,2]2上的值域，利用对数函数的单调性即可求解. （Ⅱ）根据对数函数的单调性可得2()238g x mx x m =-+在(4,)+∞上单调递增，再利用二次函数的图像与性质可得0,34,4(4)0,m m g >⎧⎪⎪≤⎨⎪≥⎪⎩解不等式组即可求解. 【详解】（Ⅰ）当1m =时，()122()log 238f x x x =-+，此时函数()f x 的定义域为1,22⎡⎤⎢⎥⎣⎦.因为函数2238y x x =-+的最小值为242835588⨯⨯-=. 最大值为22232810⨯-⨯+=，故函数()f x 在1,22⎡⎤⎢⎥⎣⎦上的值域为114455log 10,log 8⎡⎤⎢⎥⎣⎦；（Ⅱ）因为函数14log y x =在(0,)+∞上单调递减，故2()238g x mx x m =-+在(4,)+∞上单调递增，则0,34,4(4)0,m m g >⎧⎪⎪≤⎨⎪≥⎪⎩ 解得310m ≥，综上所述，实数m 的取值范围3,10⎡⎫+∞⎪⎢⎣⎭. 【点睛】本题主要考查了利用对数函数的单调性求值域、利用对数型函数的单调区间求参数的取值范围以及二次函数的图像与性质，属于中档题.。

北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(答案解析)

一、选择题1．若函数()()23log 5f x x ax a =+++，()f x 在区间(),1-∞上是递减函数，则实数a的取值范围为（） A ．[]3,2--B ．[)3,2--C ．(],2-∞-D ．(),2-∞-2．若实数a ，b ，c 满足232log log ab c k ===，其中()1,2k ∈，则下列结论正确的是（） A ．b c a b > B ．log log a b b c >C ．log b a c >D ．b a c b >3．已知()()514,1log ,1a a x a x f x x x ⎧-+<=⎨≥⎩是(),-∞+∞上的减函数，那么a 的取值范围是（）. A ．()0,1B ．10,5⎛⎫ ⎪⎝⎭C ．11,95⎡⎫⎪⎢⎣⎭D ．1,19⎡⎫⎪⎢⎣⎭4．我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微：数形结合百般好，隔离分家万事休”．在数学学习中和研究中，常用函数的图象来研究函数的性质，页常用函数的解析式来琢磨函数图象的特征，如函数()22xy xx R =-∈的大致图象是（）A ．B ．C ．D ．5．已知函数3131()(),()log ,()(0)2x f x x g x x x h x x x x =-=-=->的零点分别为,,a b c ，则,,a b c 的大小顺序为（）A ．a b c >>B ．c a b >>C ．b c a >>D ．b a c >>6．已知函数()f x 满足()()11f x f x -=+，当(],1-∞时，函数()f x 单调递减，设()41331=log ,log 3,92a f b f c f log ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，则,,a b c 的大小关系是（）A ．a b c <<B ．c a b <<C ．a c b <<D ．c b a <<7．已知235log log log 0x y z ==<，则2x 、3y 、5z的大小排序为 A ．235x y z <<B ．325y x z <<C ．523z x y <<D ．532z y x<<8．在数学史上，一般认为对数的发明者是苏格兰数学家——纳皮尔（Napier ，1550-1617年）．在纳皮尔所处的年代，哥白尼的“太阳中心说”刚刚开始流行，这导致天文学成为当时的热门学科．可是由于当时常量数学的局限性，天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”，因此浪费了若干年甚至毕生的宝贵时间．纳皮尔也是当时的一位天文爱好者，为了简化计算，他多年潜心研究大数字的计算技术，终于独立发明了对数．在那个时代，计算多位数之间的乘积，还是十分复杂的运算，因此纳皮尔首先发明了一种计算特殊多位数之间乘积的方法．让我们来看看下面这个例子：这两行数字之间的关系是极为明确的：第一行表示2的指数，第二行表示2的对应幂．如果我们要计算第二行中两个数的乘积，可以通过第一行对应数字的和来实现．比如，计算64×256的值，就可以先查第一行的对应数字:64对应6，256对应8，然后再把第一行中的对应数字加和起来：6＋8＝14；第一行中的14，对应第二行中的16384，所以有：64×256＝16384,按照这样的方法计算：16384×32768=（） A ．134217728B ．268435356C ．536870912D ．5137658029．已知函数()sin 2f x x x =-，且()0.3231ln ,log ,223a f b f c f ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，则以下结论正确的是 A ．c a b >>B ．a c b >>C ．a b c >>D ．b a c >>10．设()21,xf x c b a =-，且()()()f a f c f b >>，则下列说法正确的是（） A ．0,0,0a b c <<且1)a ≠与二次函数()21y a x x =--在同一坐标系内的图象可能是（）A ．B ．C ．D ．二、填空题13．已知函数()1122,121,1x x x f x x x --⎧-≤⎪=⎨-->⎪⎩，则关于x 的不等式()()10f x f x -+≤的解集为___________________．14．已知(5)3,1()log ,1a a x a x f x x x --<⎧=⎨≥⎩是(),-∞+∞上的增函数，则a 的取值范围为_________15．测量地震级别的里氏震级M 的计算公式为:0lg lg M A A =-，其中A 是测震仪记录的地震曲线的最大振幅，常数A 0是相应的标准地震的振幅.假设在一次地震中，测震仪记录的最大振幅是1000，而此次地震的里氏震级恰好为6级，那么里氏9级地震的最大的振幅是里氏5级地震最大振幅的______倍.16．已知21()1,()log 2xf xg x x m ⎛⎫=+=+ ⎪⎝⎭，若()()1212[1,3],[1,3],x x f x g x ∀∈∃∈≥，则实数m 的取值范围是_______.17．已知43==m n k ，且20+=≠m n mn ，则k =______.18．如图，在面积为2的平行四边形OABC 中，AC CO ⊥，AC 与BO 交于点E .若指数函数()01xy aa a =>≠,经过点E ，B ，则函数()af x x x=-在区间[]1,2上的最小值为________.19．设实数x 满足01x <<，且2log 4log 1x x -=，则x =______.20．设函数122,1()1log ,1x x f x x x -⎧≤=⎨->⎩，则满足()2f x ≤的x 的取值范围是_______________.三、解答题21．已知函数()21log 1xf x x-=+. （1）求函数()f x 的定义域；（2）讨论函数()f x 的奇偶性；（3）证明：函数()f x 在定义域上单调递减. 22．求下列各式的值.（1）74log 2327log lg 25lg 47++. （2）()146230.25341622322428201249-⎛⎫⨯+-⨯+- ⎪⎝⎭.23．已知函数()22x x f x k -=+. （1）若()f x 为偶函数，求实数k 的值；（2）若()4f x 在2[log x m ∈，2log (2)](m m +为大于0的常数)上恒成立，求实数k 的最小值.24．分别计算下列数值：（1）1lg3lg93452lg81lg 27+--；（2）已知()1401x xx -+=<<，求221122x x x x---+.25．（1）求值:)()141231()105220538500---+⨯-（2）已知14,x x -+=3322x x -+.26．已知函数1()log a f x a x ⎛⎫=-⎪⎝⎭，其中实数0a >且1a ≠.（1）当3a =时，求不等式()0f x >的解集；（2）若()f x 在区间[1,3]上单调递增，求a 的取值范围；【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】判断复合函数的单调性，首先要分清楚内外层函数，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求即可. 【详解】由题意知，()f x 在区间(),1-∞上是递减函数，由()()23log 5f x x ax a =+++可知，此复合函数外层函数为：()3log f x x =，在定义域上为增函数，内层函数为()25h x x ax a =+++，要使()f x 在区间(),1-∞上是递减函数，根据复合函数“同增异减”原则，内层函数为()h x 在区间(),1-∞上必须是递减函数，同时须保证最大值()10h ≥，所以()1210a h ⎧-≥⎪⎨⎪≥⎩，解得32a --≤≤. 故选：A. 【点睛】易错点睛：判断复合函数的单调性，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求.2．D解析：D 【分析】首先确定a ，b ，c 的取值范围，再根据指对互化得到2k b =，3k c =，再代入选项，比较大小. 【详解】由题意可知a ∈(0，1)，b ∈(2，4)，c ∈(3，9)，且23k k b c ==，，对于A 选项，01b a <<，1c b >可得到b c a b <，故选项A 错误；对于B 选项，log log 2log 20k a a a b k ==<，log log 3log 30k b b b c k ==>，所以log log a b b c <，故B 选项错误；对于C 选项，22log log 3log 31k kb c a ==>>，故C 选项错误；对于D 选项，1a b b b <=，1b c c c >=，而c >b ，所以b a c b >，故D 选项正确. 故选：D . 【点睛】关键点点睛：本题考查指对数比较大小，本题的关键是首先确定,,a b c 的大小，并结合指对数运算化简选项中的对数式，再和中间值0或1比较大小，本题属于中档题型.3．C解析：C 【分析】由51001514log 1a a a a a -<⎧⎪<<⎨⎪-+≥⎩解得结果即可得解. 【详解】因为()()514,1log ,1a a x a x f x x x ⎧-+<=⎨≥⎩是(),-∞+∞上的减函数，所以51001514log 1a a a a a -<⎧⎪<<⎨⎪-+≥⎩，解得1195a ≤<.故选：C 【点睛】易错点点睛：容易忽视两段交界点处函数值的大小关系.4．A解析：A 【分析】分析函数()()22xf x xx R =-∈的奇偶性，结合()01f =可得出合适的选项.【详解】令()22=-xf x x ，该函数的定义域为R ，()()()2222xxf x x x f x --=--=-=，函数()22=-xf x x 为偶函数，排除B 、D 选项；又()010f =>，排除C 选项. 故选：A. 【点睛】函数图象的辨识可从以下方面入手：（1）从函数的定义域，判断图象的左右位置；（2）从函数的值域，判断图象的上下位置．（3）从函数的单调性，判断图象的变化趋势；（4）从函数的奇偶性，判断图象的对称性；（5）从函数的特征点，排除不合要求的图象.5．B解析：B 【分析】将函数3131()(),()log ,()(0)2x f x x g x x x h x x x x =-=-=->的零点，转化为函数y x=的图象分别与函数3131(),log ,(0)2xy y x y x x ===>的图象交点的横坐标，利用数形结合法求解. 【详解】函数3131()(),()log ,()(0)2xf x xg x x xh x x x x =-=-=->的零点，即为函数y x =的图象分别与函数3131(),log ,(0)2x y y x y x x ===>的图象交点的横坐标，如图所示：由图象可得：c a b >>，故选：B 【点睛】本题主要考查函数的零点以及指数函数，对数函数和幂函数的图象的应用，还考查了数形结合的思想方法，属于中档题.6．B解析：B 【分析】由()()11f x f x -=+可得函数()f x 关于直线1x =对称，根据对数的运算法则，结合函数的对称性，变形41log 2、13log 3、39log 到区间[)1,+∞内，由函数()f x 在[)1,+∞上单调递增，即可得结果. 【详解】根据题意，函数()f x 满足()()11f x f x -=+，则函数()f x 关于直线1x =对称，又由当(],1-∞时，函数()f x 单调递减，则函数在[)1,+∞上单调递增，又由()44115log log 2222a f f f f ⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ()()13log 313b f f f ⎛⎫==-= ⎪⎝⎭，()()3log 92c f f ==，则有c a b <<，故选B.【点睛】在比较()1f x ，()2f x ，，()n f x 的大小时，首先应该根据函数()f x 的奇偶性（对称性）与周期性将()1f x ，()2f x ，，()n f x 通过等值变形将自变量置于同一个单调区间，然后根据单调性比较大小．7．A解析：A 【解析】x y z ，，为正实数，且235log log log 0x y z ==<，111235235k k k x y z ---∴===，，，可得：1112352131,51k k k x y z---=>=>=>，．即10k -> 因为函数1kf x x -=（）单调递增，∴235x y z<<.故选A.8．C解析：C 【分析】先找到16384与32768在第一行中的对应数字，进行相加运算，再找和对应第二行中的数字即可. 【详解】由已知可知，要计算16384×32768，先查第一行的对应数字: 16384对应14，32768对应15，然后再把第一行中的对应数字加起来：14＋15＝29，对应第二行中的536870912，所以有：16384×32768＝536870912, 故选C. 【点睛】本题考查了指数运算的另外一种算法，关键是认真审题，理解题意，属于简单题.9．D解析：D 【解析】因为()cos 20f x x '=-<，所以函数()sin 2f x x x =-的单调递减函数，又因为0.3213log 0,ln ln 1,12232e <<=<<，即0.3213log ln 232<<，所以由函数的单调性可得：0.3213(log )(ln )(2)32f f f >>，应选答案D ．10．D解析：D 【详解】分析：先画出函数()21xf x =-的图像，根据c b a >>且()()()f a f c f b >>得到a ＜0，b ＞0，c ＞0,再找正确的选项. 详解：作出函数()21xf x =-的图像，因为c b a >>且()()()f a f c f b >>，所以a ＜0， c ＞0,因为()()f a f c >，所以2121,1221,222acacac->-∴->-∴+<.故答案为D.点睛：（1）本题主要考查图像的作法，考查函数的图像和性质，意在考查学生对这些知识的掌握水平和数形结合思想方法.(2)解答本题的关键是通过图像分析出a ＜0，b ＞0，c ＞0.11．C解析：C 【分析】根据对数的运算性质，换底公式以及其推论即可求出．【详解】原式＝23443232448log 2log 3log 2log 3233⋅=⋅=．故选：C ．【点睛】本题主要考查对数的运算性质，换底公式以及其推论的应用，属于基础题．12．A解析：A 【分析】由对数函数，对a 分类，01a <<和1a >，在对数函数图象确定的情况下，研究二次函数的图象是否相符．方法是排除法．【详解】由题意，若01a <<，则log a y x =在()0+∞，上单调递减，又由函数()21y a x x =--开口向下，其图象的对称轴()121x a =-在y 轴左侧，排除C ，D.若1a >，则log a y x =在()0+∞，上是增函数，函数()21y a x x =--图象开口向上，且对称轴()121x a =-在y 轴右侧，因此B 项不正确，只有选项A 满足. 故选：A ．【点睛】本题考查由解析式先把函数图象，解题方法是排除法，可按照其中一个函数的图象分类确定另一个函数图象，排除错误选项即可得．二、填空题13．【分析】对自变量分情况讨论即然后对各种情况分别解不等式最后取并集；【详解】当时所以由此时不等式恒成立；当时则由则此时不等式恒成立；当时符合题意；当时解得∴综上可得不等式的解集为故答案为：【点睛】关键解析：7,2⎛⎤-∞ ⎥⎝⎦【分析】对自变量分情况讨论，即1x ≤，12x <≤，23x <<，3x ≥，然后对各种情况分别解不等式，最后取并集；【详解】当1x ≤时，10x -≤，121x -≤，121x -≥，所以()11220x x f x --=-≤由2122x -≤，222x -≥，()221220x xf x ---=-<，此时不等式()()10f x f x +-≤恒成立；当12x <≤时，()212110f x x x x =--=--=-<，011x <-≤，则()22122x xf x ---=-，由221x -≤，221x -≥，则()10f x -≤此时不等式()()10f x f x +-≤恒成立；当23x <<时，()()12131f x f x x x +-=--+--213110x x =--+--=-<，符合题意；当3x ≥时，()()12131270f x f x x x x +-=--+--=-≤，解得72x ≤， ∴732x ≤<．综上可得，不等式()()10f x f x +-<的解集为7,2⎛⎤-∞ ⎥⎝⎦．故答案为：7,2⎛⎤-∞ ⎥⎝⎦【点睛】关键点睛：本题考查分别函数解不等式的问题，涉及分类讨论思想的应用，解答本题的关键是对自变量x 的范围进行分类，即1x ≤，12x <≤，23x <<，3x ≥，从而得出()f x 和()1f x -的表达式，从而求解不等式，属于中档题.14．【分析】根据在上单调递增列出不等式组求解即可【详解】解：在上单调递增即解得：即故答案为：【点睛】易错点点睛：在解决分段函数的单调性问题时要注意上下段端点值的问题解析：5,54⎡⎫⎪⎢⎣⎭【分析】根据()f x 在R 上单调递增，列出不等式组，求解即可. 【详解】解：(5)3,1()log ,1aa x a x f x x x --<⎧=⎨≥⎩在R 上单调递增，即50153log 1a a a a a ->⎧⎪>⎨⎪--≤⎩，解得：554a ≤<，即5,54a ⎡⎫∈⎪⎢⎣⎭，故答案为：5,54⎡⎫⎪⎢⎣⎭. 【点睛】易错点点睛：在解决分段函数的单调性问题时，要注意上下段端点值的问题.15．10000【分析】根据条件先计算出的值然后分别计算出里氏9级地震的最大的振幅和里氏5级地震最大振幅由此可求解出最终结果【详解】由条件可知：所以设里氏9级地震的最大的振幅为里氏5级地震最大振幅为所以所解析：10000 【分析】根据条件先计算出0A 的值，然后分别计算出里氏9级地震的最大的振幅和里氏5级地震最大振幅，由此可求解出最终结果. 【详解】由条件可知：06lg1000lg A =-，所以3010A -=，设里氏9级地震的最大的振幅为1A ，里氏5级地震最大振幅为2A ，所以31329lg lg105lg lg10A A --⎧=-⎨=-⎩，所以621210,10A A ==，所以1210000A A =，故答案为：10000. 【点睛】关键点点睛：解答本题的关键在于理解公式0lg lg M A A =-中各个量的含义并先求解出0A 的值，由此继续分析.16．【分析】求出函数在上的最值最后根据题意列出不等式进行求解即可【详解】当时因此；当时因此因为所以有即故答案为：【点睛】本题考查了求指数型函数和对数型函数的最小值考查了存在性和任意性的概念的理解考查了数解析：9,8⎛⎤-∞ ⎥⎝⎦【分析】求出函数(),()f x g x 在[1,3]x ∈上的最值，最后根据题意列出不等式进行求解即可. 【详解】当[1,3]x ∈时，11[,1]28x⎛⎫∈ ⎪⎝⎭，因此9()[,2]8f x ∈；当[1,3]x ∈时，22(log )[0,log 3]x ∈，因此2()[,log 3]g x m m ∈+，因为()()1212[1,3],[1,3],x x f x g x ∀∈∃∈≥，所以有min min ()()f x g x ≥，即9988m m ≥⇒≤. 故答案为：9,8⎛⎤-∞ ⎥⎝⎦【点睛】本题考查了求指数型函数和对数型函数的最小值，考查了存在性和任意性的概念的理解，考查了数学运算能力.17．【分析】根据对数和指数的关系将指数式化成对数式再根据对数的运算计算可得【详解】解：故答案为：【点睛】本题考查对数和指数的关系对数的运算属于基础题解析：36【分析】根据对数和指数的关系，将指数式化成对数式，再根据对数的运算计算可得. 【详解】解：43m n k ==4log m k ∴=，3log =n k20m n mn +=≠ 211n m ∴+=，1log 4k m =，1log 3k n= 2log 3log 41k k ∴+= 2log 3log 41k k ∴+=()log 941k ∴⨯=36k ∴=故答案为：36 【点睛】本题考查对数和指数的关系，对数的运算，属于基础题.18．【分析】设点则点B 的坐标为由题意得则再根据平行四边形的面积求得由此得得函数的解析式从而得函数的的单调性与最值【详解】解：设点则点B 的坐标为∵∴∵平行四边形OABC 的面积又平行四边形OABC 的面积为2 解析：3-【分析】设点(),tE t a ，则点B 的坐标为()2,2tt a ，由题意得22tt aa =，则2t a =，再根据平行四边形的面积求得12t =，由此得4a =，得函数()f x 的解析式，从而得函数()f x 的的单调性与最值．【详解】解：设点(),tE t a ，则点B 的坐标为()2,2tt a ，∵22t t a a =，∴2t a =，∵平行四边形OABC 的面积24t S OC AC a t t =⨯⨯==，又平行四边形OABC 的面积为2，∴42t =，12t =，所以122a =，4a =， ∴()4f x x x=-在[]1,2为增函数，∴函数()f x 的最小值为()4111f =-=3-，故答案为：3-．【点睛】本题主要考查指数函数的图象和性质，考查利用函数的单调性求最值，属于中档题．19．【分析】利用换底公式和对数运算法则可将方程转化为解方程求得或进而结合的范围求得结果【详解】即解得：或或故答案为：【点睛】本题考查对数方程的求解问题涉及到对数运算法则和换底公式的应用；考查基础公式的应解析：14【分析】利用换底公式和对数运算法则可将方程转化为222log 1log x x-=，解方程求得2log 2x =-或2log 1x =，进而结合x 的范围求得结果.【详解】22log 42log 2log x x x ==2222log 4log log 1log x x x x∴-=-= 即()222log log 20x x +-=，解得：2log 2x =-或2log 1x = 14x ∴=或2x = 01x << 14x ∴=故答案为：14【点睛】本题考查对数方程的求解问题，涉及到对数运算法则和换底公式的应用；考查基础公式的应用能力.20．【分析】根据分段函数分段解不等式最后求并集【详解】当时因为解得：∴当时解得：所以综上原不等式的解集为故答案为：【点睛】本题主要考查了解分段函数不等式涉及指数与对数运算属于基础题解析：[0,)+∞【分析】根据分段函数，分段解不等式，最后求并集. 【详解】当1x ≤时，1()2xf x -=，因为11x -≤，解得：0x ≥，∴01x ≤≤ ，当1x >时，2()1log 2f x x =-≤，2log 1x ≥-，解得：12x ≥，所以1x >，综上，原不等式的解集为[)0,+∞. 故答案为：[)0,+∞. 【点睛】本题主要考查了解分段函数不等式，涉及指数与对数运算，属于基础题.三、解答题21．(1) (1,1)- (2) 函数()f x 为奇函数 (3)证明见解析. 【分析】(1)由()f x 的定义域满足101xx->+可得答案. (2)直接判断()f x 与()f x -的关系可得答案. (3) 设1211x x -<<<，先作差判断出212111011--<<++x x x x ，再由对数函数2log y x =在(0,)+∞上单调递增有，21222111log log 11x x x x --<++，即可得出结论. 【详解】解：（1）令101xx->+，可得()()110x x -+>，即()()110x x -+<，解得11x -<< 函数()f x 的定义域为(1,1)-（2）由（1）知函数()f x 的定义域关于原点对称由2211()log log ()11x xf x f x x x+--==-=--+，可得函数()f x 为奇函数（3）设1211x x -<<<设()()()()()()()()()122112212112121111211111111+--+-----==++++++x x x x x x x x x x x x x x∵1211x x -<<<∴121210,10,0x x x x +>+>-< ∴212111011--<<++x x x x 利用对数函数2log y x =在(0,)+∞上单调递增有，21222111log log 11x x x x --<++ 即()()21f x f x <故函数()f x 在(1,1)-上单调递减．【点睛】关键点睛：本题考查函数的定义域、奇偶性的判断和用定义法证明单调性，解答本题的关键是先得出2211x x -+与1111x x -+的大小关系，再由函数2log y x =在(0,)+∞上单调递增得到21222111log log 11x x x x --<++，即()()21f x f x <，属于中档题. 22．（1）154；（2）210 【分析】（1）根据对数的运算法则运算求值即可（2）根据指数的运算法则化简求值. 【详解】（1）7log 23log lg 25lg 473+++ 143log 3lg1002-=++1224=-++154= （2）()146230.2516248201249-⎛⎫⨯+-⨯+- ⎪⎝⎭43132334447223(2)42214=⨯⨯+-⨯-⨯+2162721=+--+210=【点睛】本题主要考查了对数的运算，指数的运算，属于中档题.23．（1）1k =；（2）当02m <<时，k 的最小值为4，当2m 时，k 的最小值为24m m -+. 【分析】（1）根据函数是偶函数，利用偶函数的定义求解. （2）将()4f x ，转化为2(2)42x x k-+⨯，令2[x t m =∈，2]m +，构造函数2()4g t t t =-+，利用二次函数的性质求得其最大值即可..【详解】（1）()f x 为偶函数，()()f x f x ∴=-， 2?22?2x x x x k k --∴+=+，即(1)(22)0xxk ---=，对任意的x 恒成立，1k ∴=.（2）由()4f x ，可得2?24x x k -+，即2(2)42x x k -+⨯，令2[xt m =∈，2]m +，2()4g t t t ∴=-+，当02m <<时，对称轴2[t m =∈，2]m +，则()max g t g =（2）4244=-+⨯=，当2m 时，对称轴2t m =，则2()()4max g t g m m m ==-+，故当02m <<时，k 的最小值为4，当2m 时，k 的最小值为24m m -+. 【点睛】本题主要考查函数的奇偶性的和不等式恒成立的问题，还考查了分类讨论的思想和运算求解的能力，属于中档题. 24．（1）32；（2）-. 【分析】（1）利用对数的运算性质化简可求得所求代数式的值；（2）由已知条件可求得1x x --的值，可求得22x x -+，并求得1122x x -+的值，代入计算可求得所求代数式的值. 【详解】（1）原式11lg3lg3lg3111lg3322lg5lg 2lg1081222lg32lg 27+-=++=+=；（2）因为()()()221114x xx x x x x x -----=+-=-，所以()()2211412x x x x ---=+-=，因为01x <<，则1x x -<，所以1x x --=-22x x --=-，又因为21112226x x x x --⎛⎫+=++= ⎪⎝⎭，所以1122x x -+=所以221122x x x x---=-+【点睛】本题考查指数式与对数式的计算，考查了平方关系以及对数运算性质的应用，考查计算能力，属于基础题.25．（1）16-；（2）【分析】（1）由指数幂的运算法则直接计算即可；（2）由2111222x x x x --⎛⎫+=++ ⎪⎝⎭可求出1122x x -+，再利用()3311122221x xx x x x ---⎛⎫+=++- ⎪⎝⎭即可求出. 【详解】（1）原式412500102012=-⨯-)10201126=+-20201616=+-=-；（2）14x x -+=，2111222426x x x x --⎛⎫∴+=++=+= ⎪⎝⎭，又11220x x ->+，1122x x -∴=+())112233122141x x x x x x ---⎛⎫+=+-=-= ⎪⎝⎭+【点睛】本题考查指数幂的运算，考查完全平方公式和立方和公式的应用，属于基础题. 26．(1) 10,4⎛⎫ ⎪⎝⎭;(2) 103a << 【分析】(1)代入3a =,根据对数函数的单调性求解即可.(2)先根据区间[1,3]结合定义域可求得a 的大致范围,从而确定log a y x =的单调性,再根据复合函数的单调性确定a 的取值范围即可. 【详解】(1) 当3a =时, 31()log 3f x x ⎛⎫=-⎪⎝⎭,故()0f x >即31log 30x ⎛⎫-> ⎪⎝⎭,即131x ->,14x >,解得104x <<.故()0f x >解集为10,4⎛⎫⎪⎝⎭.(2)由定义域可知,10a x->,即1a x >在区间[1,3]上恒成立,故103a <<,所以log a y x =为减函数.又1y a x =-在区间[1,3]上为减函数,故1()log a f x a x ⎛⎫=- ⎪⎝⎭在区间[1,3]上为增函数.满足题意.故103a << 【点睛】本题主要考查了对数函数的不等式求解以及对数型复合函数的单调性求解参数的问题.属于中档题.。

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(答案解析)(3)

一、选择题1．若()()22ln 1f x x x e =+≤≤(e 为自然对数的底数)，则函数()()22y f x f x =+⎡⎤⎣⎦的最大值为（） A ．6B ．13C ．22D ．332．已知函数()()3,<1log ,1a a x a x f x x x ⎧--=⎨≥⎩的值域．．是R ，那么实数a 的取值范围是（） A ．31,2⎛⎤ ⎥⎝⎦B ．()1,+∞C ．()()0,11,3D ．3,32⎡⎫⎪⎢⎣⎭3．已知函数22()lg[(1)(1)1]f x a x a x =-+++的值域为R ．则实数a 的取值范围是（） A ．5[1,]3B ．5(1,]3C ．(]5,1(,)3-∞-⋃+∞D ．()5,1[1,)3-∞-4．已知1311531log ,log ,363a b c π-===，则,,a b c 的大小关系是（）A ．b a c <<B ．a c b <<C ．c b a <<D ．b c a <<5．一种放射性元素最初的质量为500g ，按每年10%衰减．则这种放射性元素的半衰期为（）年.（注：剩余质量为最初质量的一半，所需的时间叫做半衰期），（结果精确到0.1，已知lg 20.3010=，lg30.4771=）A ．5.2B ．6.6C ．7.1D ．8.36．已知函数222,1()log (1),1x x f x x x ⎧-≤=⎨->⎩，则52f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦（） A ．12-B ．-1C ．-5D ．127．设函数()ln |31|ln |31|f x x x =+--，则()f x （） A ．是偶函数，且在11(,)33-单调递增 B ．是偶函数，且在1(,)3-∞-单调递增 C ．是奇函数，且在11(,)33-单调递减 D ．是奇函数，且在1(,)3-∞-单调递减8．若函数y ＝x aa - (a >0，a ≠1)的定义域和值域都是[0，1]，则log a 56＋log a 485＝( ) A ．1B ．2C ．3D ．49．如图是指数函数①y =x a ；②y =x b ；③y =c x ；④y =d x 的图象，则a ，b ，c ，d 与1的大小关系是（）A ．a <b <1<c <dB ．b <a <1<d <cC ．1<a <b <c <dD ．a <b <1<d <c10．已知3log 2a =，那么33log 82log 6-用a 表示是( ) A ．52a -B ．2a -C ．23(1)a a -+D ．231a a --11．已知()243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩满足对任意12x x ≠，都有()()12120f x f x x x -<-成立，那么a 的取值范围是（）A ．10,2⎛⎤ ⎥⎝⎦B ．1,12⎡⎫⎪⎢⎣⎭C ．12,23⎡⎤⎢⎥⎣⎦D ．2,13⎡⎫⎪⎢⎣⎭12．已知1()44x f x x -=+-e ，若正实数a 满足3(log )14a f <，则a 的取值范围为（）A ．34a >B ．304a <<或43a >C ．304a <<或1a > D ．1a >二、填空题13．若3763,a b ==则21a b+的值为_______ 14．函数f （x ）=lg （x 2-3x -10）的单调递增区间是______．15．设函数123910()lg 10x x x x x af x +++++=,其中a 为实数,如果当(,1]x ∈-∞时()f x 有意义,则a 的取值范围是________.16．已知函数log (3)a y ax =-在(1,2)上单调递减，则实数a 的取值范围为___________. 17．设log c a ､log c b 是方程2530x x +-=的两个实根，则log b ac =______.18．给出下列四个命题：（1）函数()log (21)1a f x x =--的图象过定点(1,0)；（2）函数2log y x =与函数2x y =互为反函数；（3）若1log 12a>，则a 的取值范围是1,12⎛⎫⎪⎝⎭或(2,)+∞；（4）函数log (5)a y ax =-在区间[1-，3)上单调递减，则a 的范围是5(1,]3；其中所有正确命题的序号是___________.19．函数y ＝x 2与函数y ＝x ln x 在区间(0，＋∞)上增长较快的一个是________ .20．设函数()122,12log ,1x x f x x x +⎧≤=⎨->⎩，若()()04f f x =则0x ______.三、解答题21．已知指数函数()f x 的图象经过点()1,3-，()()2()23x g x f a x f =-+在区间[]1,1-上的最小值是()h a . （1）求函数()f x 的解析式；（2）若3a ≥时，求函数()g x 的最小值()h a 的表达式；（3）是否存在m 、n ∈R 同时满足以下条件：①3m n >>；②当()h a 的定义域为[],n m 时，值域为22,n m ⎡⎤⎣⎦；若存在，求出m 、n 的值；若不存在，说明理由.22．已知二次函数()f x 满足(0)(2)1f f ==-且(1)4f =-. （1）求函数()f x 的解析式；（2）若()(0xy f a a =>且1)a ≠在[]1,1x ∈-上的最大值为8，求实数a 的值.23．设()log (1)log (3)(0,1)a a f x x x a a =++->≠，且(1)2f =. （1）求a 的值及()f x 的定义域；（2）求()f x 在区间302⎡⎤⎢⎥⎣⎦，上的最大值.24．已知函数210(),22,01xx ax a x f x a a x ⎧+--≤<=⎨-≤≤⎩，其中a >0且a ≠1. （1）当12a =时，求f (x )的值域；（2）函数y =f (x )能否成为定义域上的单调函数，如果能，则求出实数a 的范围；如果不能，则给出理由；（3）()2f x -在其定义域上恒成立，求实数a 的取值范围. 25．已知函数()f x 是定义在R 上的奇函数，当0x 时，()121xaf x =++. （1）求实数a 的值及()f x 的解析式；（2）求方程4|(1)|5f x -=的解.26．（1）0160.25371.586-⨯-+-⎫⎛ ⎪⎝⎭（2）1324lg lg82493-+【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】先依题意求函数定义域，再化简函数，进行换元后求二次函数在区间上的最大值即可. 【详解】由21x e ≤≤及()2f x知221x e ≤≤，故定义域为[]1,e ，又()()()()()222222ln 2ln ln 6ln 61y f x f x x x x x x e =+=+++=++≤≤⎡⎤⎣⎦令[]ln 0,1t x =∈，则266y t t =++，易见y 在[]0,1t ∈上单调递增，故当1t =时，即x e =时，max 16613y =++=. 故选：B. 【点睛】易错点睛：利用换元法求函数最值时，要注意函数的定义域，否则求得的易出错.2．A解析：A 【分析】当0＜a ＜1时，当1≥x 时，log 0a y x =≤，则当1x <时，()3y a x a =--的值域必须要包含()0,+∞，，当1a >时，当1≥x 时，[)log 0a y x =∈+∞，，则当1x <时，()3y a x a =--的值域必须要包含()0-∞，,从而可得答案. 【详解】由题意，()f x 的值域为R ，当0＜a ＜1时，当1≥x 时，log 0a y x =≤，所以当1x <时，()3y a x a =--的值域必须要包含()0,+∞，当1x <时，()3y a x a =--单调递增，()332y a x a a =--<- 所以不满足()f x 的值域为R .当1a >时，当1≥x 时，[)log 0a y x =∈+∞，，所以当1x <时，()3y a x a =--的值域必须要包含()0-∞，, 若3a =时，当1x <时，3y a =-=-，不满足()f x 的值域为R .若3a >时，当1x <时，()3y a x a =--单调递减，()332y a x a a =-->- 所以不满足()f x 的值域为R .若13a <<时，当1x <时，()3y a x a =--单调递增，()332y a x a a =--<- 要使得()f x 的值域为R ，则320a -≥，即32a ≤ 所以满足条件的a 的取值范围是：312a <≤，故选：A ．【点睛】关键点睛：本题考查根据函数的值域求参数的范围，解答本题的关键是当0＜a ＜1时，当1≥x 时，log 0a y x =≤，则当1x <时，()3y a x a =--的值域必须要包含()0,+∞，，当1a >时，当1≥x 时，[)log 0a y x =∈+∞，，则当1x <时，()3y a x a =--的值域必须要包含()0-∞，，属于中档题. 3．A解析：A 【分析】当函数的值域为R 时，命题等价于函数()()22111y a x a x =-+++的值域必须包含区间()0+∞，得解【详解】22()lg[(1)(1)1]f x a x a x =-+++的值域为R令()()22111y a x a x =-+++，则()()22111y a x a x =-+++的值域必须包含区间()0+∞，当210a -=时，则1a =± 当1a =时，21y x =+符合题意；当1a =-时，1y =不符合题意；当1a ≠±时，()()222101410a a a ⎧->⎪⎨∆=+--≥⎪⎩，解得513a <≤513a ∴≤≤，即实数a 的取值范围是5[1,]3故选：A 【点睛】转化命题的等价命题是解题关键.4．D解析：D 【分析】根据指数函数和对数函数性质，借助0和1进行比较．【详解】由对数函数性质知151log 16>，13log 03π<，由指数函数性质知13031-<<，∴b c a <<．故选：D ．【点睛】方法点睛：本题考查指数式、对数式的大小比较，比较指数式大小时，常常化为同底数的幂，利用指数函数性质比较，或化为同指数的幂，利用幂函数性质比较，比较对数式大小，常常化为同底数的对数，利用对数函数性质比较，如果不能化为同底数或同指数，或不同类型的数常常借助中间值如0或1比较大小．5．B解析：B 【分析】先根据题意列出关于时间的方程，然后利用指对互化以及对数换底公式并结合所给数据可计算出半衰期. 【详解】设放射性元素的半衰期为x 年，所以()500110%250x-=，所以()1110%2x-=，所以0.91log 2x =，所以109log 2x =，所以lg 2lg10lg9x =-，所以lg 212lg 3x =-，所以0.3010120.4771x =-⨯，所以 6.6x ≈，故选：B. 【点睛】思路点睛：求解和对数有关的实际问题的思路：（1）根据题设条件列出符合的关于待求量的等式；（2）利用指对互化、对数运算法则以及对数运算性质、对数换底公式求解出待求量的值.6．A解析：A 【分析】根据分段函数解析式，依次计算255log 122f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭，23log 2f ⎛⎫ ⎪⎝⎭，即可得选项.【详解】因为函数222,1()log (1),1x x f x x x ⎧-≤=⎨->⎩，所以2253log log 2122f ⎛⎫=<= ⎪⎝⎭，23log 2531222222f f⎡⎤⎛⎫∴=-=-=- ⎪⎢⎥⎝⎭⎣⎦. 故选：A. 【点睛】本题考查根据分段函数求解函数值，关键在于根据解析式分段求解，由内到外，准确认清自变量的所在的范围和适用的解析式.7．D解析：D 【分析】根据奇偶性定义判断奇偶性，然后判断单调性，排除错误选项得正确结论．【详解】函数定义域是1{|}3x x ≠±，()ln 31ln 31ln 31ln 31()f x x x x x f x -=-+---=--+=-，()f x 是奇函数，排除AB ，312()lnln 13131x f x x x +==+--，11,33x ⎛⎫∈- ⎪⎝⎭时，2310x -<-<，2231x <--，即21031x +<-，而131u x =-是减函数，∴2131v x =+-是增函数，∴()f x 在11,33⎛⎫- ⎪⎝⎭上是增函数，排除C ．只有D 可选．故选：D ．【点睛】结论点睛：本题考查函数的单调性与奇偶性，判断函数的奇偶性与单调性后用排除法确定正确选项，掌握复合函数的单调性是解题关键．()y f x =与()y f x =-的单调性相反，在()f x 恒为正或恒为负时，()y f x =与1()y f x =的单调性相反，若()0f x <，则()y f x =与()y f x =的单调性相反．0a >时，()y af x =与()y f x =的单调性相同．8．C解析：C 【分析】先分析得到a ＞1，再求出a =2,再利用对数的运算求值得解. 【详解】由题意可得a －a x ≥0，a x ≤a ，定义域为[0，1]，所以a >1，y[0，1]上单调递减，值域是[0，1]，所以f (0)1，f (1)＝0，所以a ＝2，所log a 56＋log a 485＝log 256＋log 2485＝log 28＝3. 故选C 【点睛】本题主要考查指数和对数的运算，考查函数的单调性的应用，意在考查学生对这些知识的理解掌握水平，属于基础题.9．B解析：B 【分析】根据指数函数的图象与性质可求解. 【详解】根据函数图象可知函数①y =x a ；②y =x b 为减函数，且1x =时，②y =1b <①y =1a ，所以1b a <<，根据函数图象可知函数③y =c x ；④y =d x 为增函数，且1x =时，③y =c 1>④y =d 1，所以1c d >> 故选：B 【点睛】本题主要考查了指数函数的单调性，指数函数的图象，数形结合的思想，属于中档题.10．B解析：B 【解析】试题分析：33333333log 82log 6log 22log 233log 22(log 2log 3)-=-⨯=-+3log 222a =-=-,所以答案选B .考点：指数对数的计算11．C解析：C 【分析】判断函数的单调性．利用分段函数解析式，结合单调性列出不等式组求解即可．【详解】解：243,1log 2,1a x ax x f x x a x ⎧-+<=⎨+≥⎩（）满足对任意12x x ≠，都有()()12120f x f x x x --＜成立，所以分段函数是减函数，所以：0121442a a a a<<⎧⎪≥⎨⎪-≥⎩，解得12,23a ⎡⎤∈⎢⎥⎣⎦．故选C ．【点睛】本题考查分段函数的单调性的应用，函数的单调性的定义的理解，考查转化思想以及计算能力．12．C解析：C 【分析】先判断1()44x f x x -=+-e 是R 上的增函数，原不等式等价于3log 14a <，分类讨论，利用对数函数的单调性求解即可. 【详解】因为1x y e -=与44y x =-都是R 上的增函数，所以1()44x f x x -=+-e 是R 上的增函数，又因为11(1)441f e -=+-=所以()3(log )114af f <=等价于3log 14a <，由1log a a =，知3log log 4a a a <,当01a <<时，log a y x =在()0,∞+上单调递减，故34a <，从而304a <<；当1a >时，log ay x =在()0,∞+上单调递增，故34a >，从而1a >，综上所述， a 的取值范围是304a <<或1a >，故选C. 【点睛】解决抽象不等式()()f a f b <时，切勿将自变量代入函数解析式进行求解，首先应该注意考查函数()f x 的单调性．若函数()f x 为增函数，则a b <；若函数()f x 为减函数，则a b >．二、填空题13．1【分析】将指数式化为对数式得代入可得根据换底公式可求值【详解】由题意可得∵故答案为：1【点睛】本题主要考查对数与指数的互化对数的换底公式的应用考查基本运算求解能力解析：1【分析】将指数式化为对数式得3log 63a =，7log 63b =，代入可得，372121log 63log 63a b +=+，根据换底公式可求值. 【详解】由题意可得，3log 63a =，7log 63b =， ∵6363363721212log 3log 7log 631log 63log 63a b +=+=+== 故答案为：1 【点睛】本题主要考查对数与指数的互化，对数的换底公式的应用，考查基本运算求解能力.14．（5+∞）【分析】确定函数的定义域考虑复合函数的单调性即可得出结论【详解】由x2-3x-10＞0可得x ＜-2或x ＞5∵u=x2-3x-10在（5+∞）单调递增而y=lgu 是增函数由复合函数的同增异减解析：（5，+∞）【分析】确定函数的定义域，考虑复合函数的单调性，即可得出结论．【详解】由x 2-3x-10＞0可得x ＜-2或x ＞5，∵u=x 2-3x-10在（5，+∞）单调递增，而y=lgu 是增函数由复合函数的同增异减的法则可得，函数f （x ）=lg （x 2-3x-10）的单调递增区间是（5，+∞）故答案为（5，+∞）．【点睛】本题考查对数函数的单调性和应用，考查学生的计算能力，属于中档题15．【分析】由题意可得对任意的恒成立分离变量后利用函数的单调性求得在上的范围即可得解【详解】根据题意对任意的恒成立即恒成立则因为函数在上为增函数所以故答案为：【点睛】本题考查对数函数的定义域指数函数的单解析：[ 4.5,)-+∞【分析】由题意可得对任意的(,1]x ∈-∞，10210x x a ⋅+⋯++>恒成立，分离变量a 后利用函数的单调性求得981()101010x x xg x ⎛⎫⎛⎫⎛⎫=---⋯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭在(,1]x ∈-∞上的范围，即可得解. 【详解】根据题意对任意的(,1]x ∈-∞，123910010x x x x x a+++++>恒成立，即10210xxa ⋅+⋯++>恒成立，则981101010x x xa ⎛⎫⎛⎫⎛⎫>---⋯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，因为函数981()101010x x xg x ⎛⎫⎛⎫⎛⎫=---⋯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭在(,1]x ∈-∞上为增函数，所以111981 4.5101010a ⎛⎫⎛⎫⎛⎫---=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故答案为：[ 4.5,)-+∞【点睛】本题考查对数函数的定义域，指数函数的单调性，不等式恒成立问题，属于基础题.16．【分析】由复合函数的单调性：同增异减由于递减因此必须递增即有还要考虑函数定义域即在时恒成立【详解】∵∴是减函数又在上是减函数所以且∴故答案为：【点睛】本题考查对数型复合函数的单调性掌握复合函数单调性解析：3(1,]2【分析】由复合函数的单调性：同增异减，由于3u ax =-递减，因此log a y u =必须递增，即有1a >，还要考虑函数定义域，即在(1,2)x ∈时，30ax ->恒成立．【详解】∵0a >，∴3u ax =-是减函数，又log (3)a y ax =-在(1,2)上是减函数，所以1a >，且320a -≥，∴312a <≤．故答案为：3(1,]2．【点睛】本题考查对数型复合函数的单调性，掌握复合函数单调性是解题关键，同时要考虑函数的定义域．17．【分析】根据题意由韦达定理得进而得再结合换底公式得【详解】解：因为､是方程的两个实根所以由韦达定理得所以所以所以故答案为：【点睛】本题解题的关键在于根据韦达定理与换底公式进行计算其中两个公式的转化是解析：37±【分析】根据题意由韦达定理得log log 5c c a b +=-，loglog 3c c a b ⋅=-，进而得()2log log 37c c a b -=，再结合换底公式得1log log b acc b a==【详解】解：因为log c a ､log c b 是方程2530x x +-=的两个实根，所以由韦达定理得log log 5c c a b +=-，log log 3c c a b ⋅=-，所以()()22log log log log 4log log 37c c c c c c a b a b a b -=+-⋅=，所以log log c c b a -=所以11log log log log b c c acc b b a a===-故答案为：【点睛】本题解题的关键在于根据韦达定理与换底公式进行计算，其中()()22log log log log 4log log c c c c c c a b a b a b -=+-⋅，1log log b acc b a=两个公式的转化是核心，考查运算求解能力，是中档题.18．（2）（4）【分析】（1）函数的图象过定点所以该命题错误；（2）函数与函数互为反函数所以该命题正确；（3）若所以的取值范围是所以该命题错误；（4）由题得解得的范围是所以该命题正确【详解】（1）当时（解析：（2）（4）【分析】（1）函数()log (21)1a f x x =--的图象过定点(1,1)-，所以该命题错误；（2）函数2log y x =与函数2x y =互为反函数，所以该命题正确；（3）若1log 12a>，所以a 的取值范围是1(,1)2，所以该命题错误；（4）由题得1530a a >⎧⎨-⎩，解得a 的范围是5(1,]3，所以该命题正确. 【详解】（1）当1x =时，f （1）1=-恒成立，故函数()log (21)1a f x x =--的图象过定点(1,1)-，所以该命题错误；（2）函数2log y x =与函数2xy =互为反函数，所以该命题正确；（3）若1log 12a >，所以112a a >⎧⎪⎨>⎪⎩或0112a a <<⎧⎪⎨<⎪⎩，则a 的取值范围是1(,1)2，所以该命题错误；（4）函数log (5)a y ax =-在区间[1-，3)上单调递减，则1530a a >⎧⎨-⎩，解得a 的范围是5(1,]3，所以该命题正确. 故答案为：（2）（4）【点睛】本题主要考查对数函数的定点问题和反函数，考查对数函数的单调性和解对数不等式，意在考查学生对这些知识的理解掌握水平.19．【解析】由于对数函数y=lnx 在区间(0＋∞)上的增长速度慢于一次函数y=x 所以函数y ＝x2比函数y ＝xlnx 在区间(0＋∞)上增长较快填解析：2yx【解析】由于对数函数y=lnx 在区间(0，＋∞)上的增长速度慢于一次函数y=x ，所以函数y ＝x 2比函数y ＝x ln x 在区间(0，＋∞)上增长较快，填2y x =.20．或2【分析】已知复合函数值求自变量从外层求出里层设求出对应的的值再由求出即可【详解】令则当若若当（舍去）故答案为：或【点睛】本题考查由函数值求自变量涉及到简单指数和对数方程考查分类讨论思想和数学计算解析：1-或2 【分析】已知复合函数值求自变量，从外层求出里层，设0()t f x =，求出()4f t =对应的t 的值，再由0()t f x =求出0x 即可. 【详解】令0()t f x =，则()4f t =，当11,24,1tt t +≤==，若010001,()21,1x x f x x +≤===-，若00202001,()2log 1,log 1,2x f x x x x >=-===，当2211,()2log 4,log 2,4t f t t t t >=-==-=（舍去）故答案为：1-或2. 【点睛】本题考查由函数值求自变量，涉及到简单指数和对数方程，考查分类讨论思想和数学计算能力，属于中档题.三、解答题21．（1）1()3xf x ⎛⎫= ⎪⎝⎭；（2）()126h a a =-；（3）不存在，理由见解析. 【分析】（1）设()xf x c =（0c >且1c ≠），由题意可得()13f -=，可求得c 的值，进而可求得函数()f x 的解析式；（2）令11,333xt ⎛⎫⎡⎤=∈ ⎪⎢⎥⎝⎭⎣⎦，设()223k t t at =-+，分析当3a ≥时，函数()k t 的单调性，进而可得出()()min h a k t =，即可得解；（3）分析出函数()h a 在区间[],n m 上单调递减，可得出22126126n m m n ⎧-=⎨-=⎩，将两个等式作差可得出6m n +=，结合3m n >>判断可得出结论. 【详解】（1）设()xf x c =（0c >且1c ≠），因为指数函数()f x 的图象经过点()1,3-，()113f c-∴-==，即13c =，因此，()13xf x ⎛⎫= ⎪⎝⎭；（2）令()13xt f x ⎛⎫== ⎪⎝⎭，[]1,1x ∈-，1,33t ⎡⎤∴∈⎢⎥⎣⎦，所以，设()223k t t at =-+，对称轴为t a =.3a ≥，可知()k t 在1,33⎡⎤⎢⎥⎣⎦上单调递减，当3t =时，()k t 取最小值，即()g x 取最小值()()3126h a k a ==-；（3）由（2）知3m n >>时，()126h a a =-在[],n m 上单调递减，若此时()h a 的值域为22,n m ⎡⎤⎣⎦，则22126126n m m n ⎧-=⎨-=⎩，即()()()6m n m n m n -=-+，m n ≠，则0m n -≠，6m n ∴+=，又3m n >>，则6m n +>，故不存在满足条件的m 、n 的值. 【点睛】方法点睛：（1）二次函数在闭区间上的最值主要有三种类型：轴定区间定、轴动区间定、轴动区间定，不论哪种类型，解决的关键就是考查对称轴于区间的位置关系，当含有参数时，要依据对称轴与区间的位置关系进行分类讨论；（2）二次函数的单调性主要依据二次函数图象的对称轴进行分析讨论求解. 22．（1）2()361f x x x =--；（2）3a =或13a = 【分析】（1）由(0)(2)f f =，可知()f x 关于1x =对称，结合(1)4f =-、(0)1f =-，可求出函数()f x 的解析式；（2）分1a >和01a <<两种情况，分别讨论函数()x y f a =的最大值，令最大值等于8，可求出实数a 的值. 【详解】（1）∵(0)(2)1f f ==-，∴函数()f x 关于1x =对称，又(1)4f =-，故设2()(1)4f x b x =--，0b ≠，而(0)1f =-，41b ∴-=-，解得3b =，2()3(1)4f x x ∴=--，即2()361f x x x =--.（2）①当1a >时，101a <<，由11x -≤≤，则1x a a a≤≤，由二次函数的性质可知，()xf a 的最大值为1(),()f f a a中的较大者，若211()3(1)48f a a=--=，解得13a =或1a =-，都不符合题意，舍去；若()23(1)48f a a =--=，解得3a =或1a =-，只有3a =符合题意. ②当01a <<时，11a >，由11x -≤≤，则1x a a a≤≤，由二次函数的性质可知，()xf a 的最大值为1(),()f f a a中的较大者，若211()3(1)48f a a=--=，解得13a =或1a =-，只有13a =符合题意；若()23(1)48f a a =--=，解得3a =或1a =-，都不符合题意. 综上所述，实数a 的值为3a =或13a =. 【点睛】易错点睛：本题主要考查二次函数相关知识，属于中档题.解决该问题应该注意的事项：（1）要注意二次函数的开口方向、对称轴、顶点；（2）开口向上的二次函数，图象上的点离对称轴越远，函数值越大；离对称轴越近，函数值越小；（3）开口向下的二次函数，图象上的点离对称轴越远，函数值越小；离对称轴越近，函数值越大.23．（1）2a =；(1,3)-；（2）2. 【分析】（1）由函数值求得a ，由对数的真数大于0可得定义域；（2）函数式变形为22()log (1)4f x x ⎡⎤=--+⎣⎦，由复合函数的单调性得出单调区间后可得最大值．【详解】解：（1）(1)2f =，log (11)log (31)log 42a a a ∴++-==，解得2(0,1)a a a =>≠，由1030x x +>⎧⎨->⎩，得(1,3)x ∈-.∴函数()f x 的定义域为()13-，.（2）22222()log (1)log (3)log (1)(3)log (1)4f x x x x x x ⎡⎤=++-=+-=--+⎣⎦∴当[0,1]x ∈时，()f x 是增函数；当3[1,]2x ∈时，()f x 是减函数.所以函数()f x 在3[0,]2上的最大值是2(1)log 42f ==. 【点睛】本题考查对数函数的性质，掌握复合函数的单调性解题关键：（前提条件：在函数定义域内）24．（1）()f x 的值域为9[16-，1]；（2）能，a 的取值集合为{2}；（3）232a -. 【分析】（1）由二次函数和指数函数的值域求法，可得()f x 的值域；（2）讨论1a >，01a <<，结合指数函数的单调性和二次函数的单调性，即可得到所求范围；（3）讨论x 的范围和a 的范围，结合参数分离和对勾函数的单调性、指数函数的单调性，计算可得所求范围．【详解】（1）当10x -<时，21122y x x =+-，对称轴为1[14x =-∈-，0)，可得y 的最小值为916-，y 的最大值为0；当01x 时，12?()1[02xy =-∈，1]；综上()f x 的值域为9[16-，1]；（2）当1a >时，函数22xy a a =-在[0，1]递增，故二次函数2y x ax a =+-在[1-，0]也要递增，1222aa a⎧--⎪⎨⎪--⎩，故只有2a =符合要求；当01a <<时，函数22x y a a =-在[0，1]递减，故二次函数2y x ax a =+-在[1-，0]也要递减，0222aa a⎧-⎪⎨⎪--⎩，无解．综上，a 的取值集合为{2}；（3）①当[1x ∈-，0]时，22x ax a +--恒成立，即有2(1)2a x x ---，即221x a x+-，由221x y x+=-，令1t x =-，[1t ∈，2]，可得32232y t t=+--，当且仅当t =时，取得等号，可得232a -；②当[0x ∈，1]时，①当1a >时，22x y a a =-，222x a a --，即有222a -，求得2a ，故12a <； ②当01a <<时，成立，综上可得a 的范围为232a -．【点睛】本题考查分段函数的值域和单调性的判断和运用，考查分类讨论思想方法和化简运算能力，以及不等式恒成立问题解法，属于中档题．25．(1) 2a =-,()2121x x f x -=+;(2) 212log 3x =+或212log 3x =-【分析】(1)根据奇函数(0)0f =求解a ,再根据奇函数的性质求解()f x 的解析式即可.(2)根据(1)可得()2121x x f x -=+为奇函数,可先求解4|()|5f t =的根,再求解4|(1)|5f x -=即可.【详解】(1)因为()f x 是定义在R 上的奇函数,且当0x ≥时,()121xaf x =++,故0(0)1021a f =+=+,即102a +=,解得2a =-.故当0x ≥时,()22112121xx x f x -=-=++. 所以当0x < 时, ()()211221211221x x x x xxf x f x -----=--=-=-=+++. 故()2121x x f x -=+(2) 先求解4|()|5f t =,此时()214215t t f t -==±+.当()()214421521215t t t t -=⇒+=-+,即29t =解得22log 92log 3t ==. 因为()2121x x f x -=+为奇函数,故当214215t t -=-+时, 22log 3t =-.故4|(1)|5f x -=的解为212log 3x -=或212log 3x -=-, 解得212log 3x =+或212log 3x =- 【点睛】本题主要考查了根据奇函数求解参数的值以及解析式的方法,同时也考查了根据函数性质求解绝对值方程的问题,属于中档题. 26．（1）110；（2）13lg5lg 222- 【分析】（1）利用指数幂的运算法则即得解；（2）利用对数的运算法则即得解. 【详解】（1）原式1111323334422()12223()33⨯=⨯+⨯+⨯-2108110=+=（2）原式153222124lg lg 2lg(57)273=-+⨯11(5lg 22lg 7)4lg 2(lg5+2lg7)22=--+ 11(5lg 22lg 7)4lg 2(lg5+2lg7)22=--+ 31lg 2lg522=-+【点睛】本题考查了指数与对数运算，考查了学生概念理解，数学运算能力，属于基础题.。

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(包含答案解析)(4)

一、选择题1．函数12xy ⎛⎫= ⎪⎝⎭的大致图象是（）. A ． B ．C ．D ．2．形如221n+(n 是非负整数)的数称为费马数，记为F n 数学家费马根据F 0，F 1，F 2，F 3，F 4都是质数提出了猜想：费马数都是质数.多年之后，数学家欧拉计算出F 5不是质数，请你估算F 5是（）位数(参考数据：lg2≈0.3010). A ．8B ．9C ．10D ．11 3．设0.60.6a =， 1.20.6b =，0.61.2c =中，则a ，b ，c 的大小关系是（）A ． a b c <<B ．a c b <<C ．b a c <<D ．b c a <<4．若函数()()23log 5f x x ax a =+++，()f x 在区间(),1-∞上是递减函数，则实数a的取值范围为（） A ．[]3,2--B ．[)3,2--C ．(],2-∞-D ．(),2-∞-5．已知函数2()log x f x =，在[116，m ]上的值域为[0，4]，2m f ⎛⎫⎪⎝⎭的取值范围是（） A ．[1,2]B ．[0,2]C ．[1,3]D ．[0,3]6．若()()22ln 1f x x x e =+≤≤(e 为自然对数的底数)，则函数()()22y f x f x =+⎡⎤⎣⎦的最大值为（） A ．6B ．13C ．22D ．337．集合{}1002,x x x x R =∈的真子集的个数为（）A ．2B ．4C ．6D ．78．已知函数()f x 是定义在R 上的单调递增的函数，且满足对任意的实数x 都有[()3]4x f f x -=，则()()f x f x +-的最小值等于（）.A ．2B ．4C ．8D ．129．已知函数()a f x x 满足(2)4f =，则函数()log (1)a g x x =+的图象大致为（）A ．B ．C ．D ．10．已知函数()y f x =与x y e =互为反函数，函数()y g x =的图象与()y f x =的图象关于x 轴对称，若()1g a =，则实数a 的值为 A ．e -B ．1e-C ．eD ．1e11．已知0.22a =，0.20.4b =，0.60.4c =，则（）A ．a b c >>B ．a c b >>C ．c a b >>D ．b c a >>12．若1a b >>，lg lg P a b ⋅，1(lg lg )2Q a b =+，lg()2a b R +=，则（） A ．R P Q <<B ．P Q R <<C ．Q P R <<D ．P R Q <<二、填空题13．现有下列四个结论：①若25a b m ==且a b =时，则1m =； ②若236log log log a b c ==，则c ab =；③对函数()3xf x =定义域内任意的1x ，都存在唯一的2x ，使得()()121f x f x ⋅=成立；④存在实数a ，使得函数()()2ln g x x ax a =++的定义域和值域均为R .其中所有正确结论的序号是_________.14．已知函数log (3)a y ax =-在(1,2)上单调递减，则实数a 的取值范围为___________. 15．已知函数()4sin 22xx f x π=++，则122019101010101010f f f ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭______.16．函数()()()212log 24f x ax x a R =-+∈，若()f x 的值域为(],1-∞，则a 的值为______.17．设log c a ､log c b 是方程2530x x +-=的两个实根，则log b ac =______.18．已知1a b >>，若10log log 3a b b a +=，b a a b =，则ab =___________. 19．设函数122,1()1log ,1x x f x x x -⎧≤=⎨->⎩，则满足()2f x ≤的x 的取值范围是_______________.20．7log 31lg 25lg 272++=________. 三、解答题21．已知函数1()log 1a mxf x x -=-（0a >且1a ≠）是奇函数．（1）求实数m 的值；（2）若关于x 的方程2()6(1)50f x kx x a -+--=对(1,)x ∈+∞恒有解，求k 的取值范围．22．已知函数()log (1)log (1)a a f x x x =+--，（0a >且1a ≠）（1）求()f x 的定义域；（2）判断()f x 的奇偶性，并予以证明；（3）求使()0f x >的x 取值范围. 23．已知函数2()46f x ax x =-+．（1）若函数2log ()y f x =的值域为R ，求实数a 的取值范围；（2）若函数log ()a y f x =在区间(1,3)上单调递增，求实数a 的取值范围．24．已知函数210(),22,01xx ax a x f x a a x ⎧+--≤<=⎨-≤≤⎩，其中a >0且a ≠1. （1）当12a =时，求f (x )的值域；（2）函数y =f (x )能否成为定义域上的单调函数，如果能，则求出实数a 的范围；如果不能，则给出理由；（3）()2f x -在其定义域上恒成立，求实数a 的取值范围.25．已知集合{|123}A x m x m =-≤≤+，函数()2()lg 28f x x x =-++的定义域为B ．（1）当2m =时，求A B 、()R A B ⋂；（2）若AB A =，求实数m 的取值范围．26．已知函数()12xf x ⎛⎫= ⎪⎝⎭，函数()2log g x x =. （1）若()22g mx x m ++的定义域为R ，求实数m 的取值范围；（2）当[]1,1x ∈-时，函数()()223y f x af x =-+⎡⎤⎣⎦的最小值为1，求实数a 的值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】去绝对值符号后根据指数函数的图象与性质判断．【详解】由函数解析式可得：1,022,0xx x y x ⎧⎛⎫≥⎪ ⎪=⎨⎝⎭⎪<⎩可得值域为：01y <≤，由指数函数的性质知：在(),0-∞上单调递增；在()0,∞+上单调递减. 故选：A. 【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.2．C解析：C 【分析】根据所给定义表示出9.632951010F =⨯，进而即可判断出其位数．【详解】根据题意，53223232lg232lg2320.30109.6320.6329521212101010101010F ⨯=+=+≈==≈==⨯，因为0.63211010<<，所以5F 的位数是10．故选：C 【点睛】关键点睛：解答本题的关键是转化成对数运算，即3232lg 2210=.3．C解析：C 【分析】根据指数函数，幂函数的单调性即可判断．【详解】因为指数函数0.6x y =是单调减函数，0.6 1.2<，所以0.6 1.20.60.6>，即a b >；因为幂函数0.6y x=在()0,∞+上是增函数，0.6 1.2<，所以0.60.61.20.6>，即c a >．综上，b a c <<．故选：C ．【点睛】熟练掌握指数函数，幂函数的单调性是解题关键．4．A解析：A 【分析】判断复合函数的单调性，首先要分清楚内外层函数，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求即可. 【详解】由题意知，()f x 在区间(),1-∞上是递减函数，由()()23log 5f x x ax a =+++可知，此复合函数外层函数为：()3log f x x =，在定义域上为增函数，内层函数为()25h x x ax a =+++，要使()f x 在区间(),1-∞上是递减函数，根据复合函数“同增异减”原则，内层函数为()h x 在区间(),1-∞上必须是递减函数，同时须保证最大值()10h ≥，所以()1210a h ⎧-≥⎪⎨⎪≥⎩，解得32a --≤≤. 故选：A. 【点睛】易错点睛：判断复合函数的单调性，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求.5．D解析：D 【分析】由对数函数的单调性可得[]1,16m ∈，再结合对数函数的性质即可得解. 【详解】由题意，函数2()log x f x =在(]0,1上单调递减，在[)1,+∞上单调递增，且()116416f f ⎛⎫==⎪⎝⎭，()10f =，结合该函数在1,16m ⎡⎤⎢⎥⎣⎦上的值域为[0,4]可得[]1,16m ∈，所以1,822m ⎡⎤∈⎢⎥⎣⎦，[]2lo 2g 0,32m m f ⎛⎫= ⎪⎝∈⎭.故选：D. 【点睛】关键点点睛：解决本题的关键是由对数函数的图象变换及单调性确定[]1,16m ∈，即可得解.6．B解析：B 【分析】先依题意求函数定义域，再化简函数，进行换元后求二次函数在区间上的最大值即可. 【详解】由21x e ≤≤及()2f x知221x e ≤≤，故定义域为[]1,e ，又()()()()()222222ln 2ln ln 6ln 61y f x f x x x x x x e =+=+++=++≤≤⎡⎤⎣⎦令[]ln 0,1t x =∈，则266y t t =++，易见y 在[]0,1t ∈上单调递增，故当1t =时，即x e =时，max 16613y =++=. 故选：B. 【点睛】易错点睛：利用换元法求函数最值时，要注意函数的定义域，否则求得的易出错.7．D解析：D 【分析】分析指数函数2xy =与幂函数100y x=的图像增长趋势，当0x <时，有1个交点；当0x >时，有2个交点；即集合{}1002,x x x x R =∈有3个元素，所以真子集个数为3217-=【详解】分析指数函数2xy =与幂函数100y x =的图像增长趋势，当0x <时，显然有一个交点；当0x >时，当1x =时，110021>；当2x =时，210022<；故()1,2x ∈时，有一个交点；分析数据发现，当x 较小时，100y x=比2xy =增长的快；当x 较大时，2xy =比100y x =增长的快，即2x y =是爆炸式增长，所以还有一个交点.即2x y =与100y x =的图像有三个交点，即集合{}1002,x x x x R =∈有3个元素，所以真子集个数为3217-= 故选：D. 【点睛】结论点睛：本题考查集合的子集个数，集合A 中含有n 个元素，则集合A 的子集有2n 个，真子集有()21n-个，非空真子集有()22n-个.8．B解析：B 【分析】根据()3x f x -为定值，可假设()3xf x m =+，然后计算()()f x f x +-，并计算m 的值，然后使用基本不等式，可得结果. 【详解】由题可知：()3xf x -为定值故设()3xf x m -=，即()3xf x m =+又[()3]4xf f x -=，所以()341mf m m m =+=⇒= 则()31xf x =+()()3131x x f x f x -+-=+++则1()()32243x x f x f x +-=++≥= 当且仅当133xx =时，取等号所以()()f x f x +-的最小值为：4故选：B 【点睛】本题考查基本不等式的应用，还考查镶嵌函数的应用，难点在于()3xf x -为定值，审清题意，细心计算，属中档题.9．C解析：C 【分析】由已知求出a ，得()g x 表达式，化简函数式后根据定义域和单调性可得正确选项．【详解】由恬24a=，2a =，222log (1),10()log (1)log (1),0x x g x x x x -+-<<⎧=+=⎨+≥⎩，函数定义域是(1,)-+∞，在(1,0)-上递减，在(0,)+∞上递增．故选：C ．【点睛】本题考查对数型复合函数的图象问题，解题方法是化简函数后，由定义域，单调性等判断．10．D解析：D 【分析】根据指数函数与对数函数的关系，以及函数()y g x =的图象与()y f x =的图象关于x 轴对称，求得()ln g x x =-，再由()1g a =，即可求解. 【详解】由题意，函数()y f x =与xy e =互为反函数，所以()ln f x x =，函数()y g x =的图象与()y f x =的图象关于x 轴对称，所以()ln g x x =-，又由()1g a =，即ln 1a -=，解得 1a e= 故选D. 【点睛】本题主要考查了指数函数与对数函数的关系，其中熟记指数函数与对数函数的关系，以及函数的对称性求得函数()g x 的解析式是解答的关键，着重考查了推理与运算能力，属于基础题.11．A解析：A 【解析】分析：0.20.4b =， 0.60.4c =的底数相同，故可用函数()0.4xf x =在R 上为减函数，可得0.60.200.40.40.41<<=．用指数函数的性质可得0.20221a =>=，进而可得0.20.20.620.40.4>>．详解：因为函数()0.4xf x =在R 上为减函数，且0.2<0.4 所以0.60.200.40.40.41<<= 因为0.20221a =>=．所以0.20.20.620.40.4>>．故选A ．点睛：本题考查指数大小的比较，意在考查学生的转化能力．比较指数式的大小，同底数的可利用指数函数的单调性判断大小，底数不同的找中间量1，比较和1的大小．12．B解析：B 【分析】利用对数函数lg y x =，结合基本不等式即可确定P 、Q 、R 的大小关系【详解】由于函数lg y x =在(0,)+∞上是增函数1a b >>，则lg lg 0a b >>由基本不等式可得11(lg lg )lg()lg 222a bP a b ab R +=<+==<=因此，P Q R <<故选：B 【点睛】本题考查了利用对数函数的单调性比较大小，应用函数思想构造对数函数，并利用其单调性和基本不等式比较大小二、填空题13．①②③【分析】利用换底公式结合求得的值可判断①的正误；设利用对数与指数的互化以及指数的运算性质可判断②的正误；由求得可判断③的正误；求出函数的定义域值域分别为时对应的实数的取值范围可判断④的正误【详解析：①②③ 【分析】利用换底公式结合a b =，求得m 的值，可判断①的正误；设236log log log a b c t ===，利用对数与指数的互化以及指数的运算性质可判断②的正误；由()()121f x f x ⋅=求得21x x =-，可判断③的正误；求出函数()g x 的定义域、值域分别为R 时，对应的实数a 的取值范围，可判断④的正误. 【详解】对于①，由于250a b m ==>，可得2lg log lg 2m a m ==，5lg log lg 5mb m ==，由于a b =可得lg lg lg 2lg 5m m=，则lg 0m =，解得1m =，①正确；对于②，设236log log log a b c t ===，可得2t a =，3t b =，6t c =，则236t t t ab c =⋅==，②正确；对于③，对任意的1x R ∈，则()()1212123331xxx x f x f x +⋅=⋅==，120x x ∴+=，可得21x x =-，③正确；对于④，若函数()()2ln g x x ax a =++的定义域为R ，对于函数2y x ax a =++，240a a ∆=-<，解得01a <<；若函数()()2ln g x x ax a =++的值域为R ，则函数2y x ax a =++的值域包含()0,∞+，则240a a ∆=-≥，解得0a ≤或1a ≥.所以，不存在实数a ，使得函数()()2ln g x x ax a =++的定义域和值域均为R ，④错误.故答案为：①②③. 【点睛】关键点点睛：解本题第④问的关键点在于找到函数()()2ln g x x ax a =++的定义域为R的等价条件∆<0；函数()()2ln g x x ax a =++的值域为R 的等价条件0∆≥.14．【分析】由复合函数的单调性：同增异减由于递减因此必须递增即有还要考虑函数定义域即在时恒成立【详解】∵∴是减函数又在上是减函数所以且∴故答案为：【点睛】本题考查对数型复合函数的单调性掌握复合函数单调性解析：3(1,]2【分析】由复合函数的单调性：同增异减，由于3u ax =-递减，因此log a y u =必须递增，即有1a >，还要考虑函数定义域，即在(1,2)x ∈时，30ax ->恒成立．【详解】∵0a >，∴3u ax =-是减函数，又log (3)a y ax =-在(1,2)上是减函数，所以1a >，且320a -≥，∴312a <≤．故答案为：3(1,]2．【点睛】本题考查对数型复合函数的单调性，掌握复合函数单调性是解题关键，同时要考虑函数的定义域．15．2019【分析】观察的特点探究得再利用倒序相加法求解【详解】因为所以故答案为：2019【点睛】本题主要考查了函数求值中的倒序相加法还考查了抽象概括的能力属于中档题解析：2019 【分析】观察122019101010101010⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭f f f 的特点，探究得()(2)2+-=f x f x ，再利用倒序相加法求解.【详解】因为()()()2442sin sin 222222x xf x f x x x πππ-+-=+++-=++所以1220192[]101010101010⎛⎫⎛⎫⎛⎫+++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭f f f12019120191010101010101010f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭22019=⨯1220192019101010101010f f f ⎛⎫⎛⎫⎛⎫∴+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故答案为：2019.【点睛】本题主要考查了函数求值中的倒序相加法，还考查了抽象概括的能力，属于中档题.16．【分析】根据对数的性质可知且最小值为即可求得的值【详解】因为的值域为所以函数的最小值为即解得故答案为：【点睛】本题考查对数函数的值域考查对数的性质合理转化是解题的关键考查了运算能力属于中档题解析：27【分析】根据对数的性质可知2240y ax x =-+>，且最小值为1，即可求得a 的值.【详解】因为()()()212log 24f x ax x a R =-+∈的值域为(],1-∞，所以2240ax x -+>，函数224y ax x =-+的最小值为12，即()20442142a a a >⎧⎪⎨⨯--=⎪⎩，解得27a =，故答案为：27【点睛】本题考查对数函数的值域，考查对数的性质，合理转化是解题的关键，考查了运算能力，属于中档题.17．【分析】根据题意由韦达定理得进而得再结合换底公式得【详解】解：因为､是方程的两个实根所以由韦达定理得所以所以所以故答案为：【点睛】本题解题的关键在于根据韦达定理与换底公式进行计算其中两个公式的转化是解析：【分析】根据题意由韦达定理得log log 5c c a b +=-，log log 3c c a b ⋅=-，进而得()2log log 37c c a b -=，再结合换底公式得1log 37log b acc b a==±【详解】解：因为log c a ､log c b 是方程2530x x +-=的两个实根，所以由韦达定理得log log 5c c a b +=-，log log 3c c a b ⋅=-，所以()()22log log log log 4log log 37c c c c c c a b a b a b -=+-⋅=，所以log log c c b a -=所以11log log log log b c c acc b b a a===-故答案为：【点睛】本题解题的关键在于根据韦达定理与换底公式进行计算，其中()()22log log log log 4log log c c c c c c a b a b a b -=+-⋅，1log log b acc b a=两个公式的转化是核心，考查运算求解能力，是中档题.18．9【分析】由对数的运算性质解并整理得由可求出的值【详解】解：整理得解得或因为所以则即因为所以所以解得或因为所以所以所以故答案为：9【点睛】关键点睛：本题主要考查对数运算和指数运算解题的关键是由得出再解析：9 【分析】由对数的运算性质解10log log 3a b b a +=并整理得3a b =，由b a a b =可求出,a b 的值. 【详解】解：110log log log log 3a b b b b a a a +=+=，整理得()23log 10log 30b b a a -+=，解得log 3b a =或13，因为1a b >>，所以log 1b a >，则log 3b a =，即3a b =，因为b a a b =，所以33b b b b =，所以33b b =，解得b =0，因为1b >，所以b =所以3a ==，所以9ab ==. 故答案为：9.【点睛】关键点睛：本题主要考查对数运算和指数运算，解题的关键是由10log log 3a b b a +=得出3a b =，再根据指数运算求解.19．【分析】根据分段函数分段解不等式最后求并集【详解】当时因为解得：∴当时解得：所以综上原不等式的解集为故答案为：【点睛】本题主要考查了解分段函数不等式涉及指数与对数运算属于基础题解析：[0,)+∞【分析】根据分段函数，分段解不等式，最后求并集. 【详解】当1x ≤时，1()2xf x -=，因为11x -≤，解得：0x ≥，∴01x ≤≤ ，当1x >时，2()1log 2f x x =-≤，2log 1x ≥-，解得：12x ≥，所以1x >，综上，原不等式的解集为[)0,+∞. 故答案为：[)0,+∞. 【点睛】本题主要考查了解分段函数不等式，涉及指数与对数运算，属于基础题.20．4【分析】结合对数的基本运算化简求值即可【详解】解：故答案为：4【点睛】本题主要考查对数的基本运算性质熟记公式熟练运用对数的化简对数恒等式是最基本的要求属于基础题型解析：4 【分析】结合对数的基本运算化简求值即可. 【详解】解：7log 3211lg 25lg 27lg5lg 23lg5lg 23lg103422++=++=++=+=. 故答案为：4. 【点睛】本题主要考查对数的基本运算性质，熟记公式，熟练运用对数的化简、对数恒等式是最基本的要求，属于基础题型.三、解答题21．（1）1m =-；（2）(0,7)．【分析】（1）由函数()f x 为奇函数，则()()f x f x -=-，可得()2210m x -=，从而求出m 的值.(2)由（1）即将原问题化为2610kx x --=对(1,)x ∈+∞恒有解，即216k x x=+，令1t x =，则26k t t =+，(0,1)t ∈有解，从而得出答案. 【详解】解：（1）因为函数()f x 为奇函数，则()()f x f x -=-，即11log log 11a a mx mxx x +-=---- 化简得()2210m x-=，所以1m =±，当1m =时1101mx x +=-<--不成立，当1m =-时1111mx x x x +-=--+，经验证成立所以1m =-．（2）由（1）知函数1()log 1ax f x x +=-，则方程可化为： 216(1)501x kx x x +-+--=-，即2610kx x --=对(1,)x ∈+∞恒有解所以分离参数得216k x x=+，令1t x =，则26k t t =+，(0,1)t ∈有解而2067t t <+<，故k 的取值范围为(0,7)．【点睛】关键点睛：本题考查根据函数为奇函数求参数和不等式有解求参数的范围，解答本题的关键是将问题转化为2610kx x --=对(1,)x ∈+∞恒有解，分离参数即216k x x=+在(1,)x ∈+∞恒有解，属于中档题.22．（1）{|11}x x -<<；（2）函数()f x 是奇函数，证明见解析；（3）当1a >时，01x <<；当01a <<时，10x -<<【分析】（1）根据对数的真数为正数列式可解得结果；（2）函数()f x 是奇函数，根据奇函数的定义证明即可；（3）不等式化为log (1)log (1)a a x x +>-后，分类讨论底数a ，根据对数函数的单调性可解得结果. 【详解】（1）要使函数数()f x 有意义，则必有1010x x +>⎧⎨->⎩，解得11x -<<，所以函数()f x 的定义域是{|11}x x -<< . （2）函数()f x 是奇函数，证明如下： ∵(1,1)x ∈-，(1,1)x -∈-，()log (1)log (1)a a f x x x -=--+[]log (1)log (1)a a x x =-+-- ()f x =-，∴函数()f x 是奇函数（3）使()0f x >，即log (1)log (1)a a x x +>-当1a >时，有111010x x x x +>-⎧⎪->⎨⎪+>⎩，解得01x <<，当01a <<时，有111010x x x x +<-⎧⎪->⎨⎪+>⎩，解得10x -<<.综上所述：当1a >时，01x <<；当01a <<时，10x -<<. 【点睛】方法点睛：已知函数解析式，求函数定义域的方法：有分式时：分母不为0；有根号时：开奇次方，根号下为任意实数，开偶次方，根号下大于或等于0；有指数时：当指数为0时，底数一定不能为0；有根号与分式结合时，根号开偶次方在分母上时：根号下大于0；有指数函数形式时：底数和指数都含有x ，指数底数大于0且不等于1；有对数函数形式时，自变量只出现在真数上时，只需满足真数上所有式子大于0，自变量同时出现在底数和真数上时，要同时满足真数大于0，底数要大0且不等于1. 23．（1）20,3⎡⎤⎢⎥⎣⎦；（2）[)2,+∞.【分析】（1）根据条件分析出2()46f x ax x =-+的值域包含()0,∞+，由此根据a 与0的关系分类讨论，求解出结果；（2）根据1,01a a ><<两种情况结合复合函数单调性的判断方法进行分类讨论，然后求解出a 的取值范围. 【详解】（1）因为()22log 46y ax x =-+的值域为R ，所以246y ax x =-+的值域包含()0,∞+，当0a =时，246y ax x =-+即46y x =-+，此时46y x =-+的值域为R ，满足；当0a ≠时，则有016240a a >⎧⎨∆=-≥⎩，所以203a <≤，综上可知：20,3a ⎡⎤∈⎢⎥⎣⎦；（2）当1a >时，log a y x =在()0+∞，上单调递增，所以2()46f x ax x =-+在()1,3上递增，所以()2110a f ⎧≤⎪⎨⎪>⎩，所以2a ≥，当01a <<时，log a y x =在()0+∞，上单调递减，所以2()46f x ax x =-+在()1,3上递减，所以()2330a f ⎧≥⎪⎨⎪>⎩，此时a 无解，综上可知：[)2,a ∈+∞. 【点睛】思路点睛：形如()()()2lg 0f x ax bx ca =++≠的函数，若函数的定义域为R ，则有00a >⎧⎨∆<⎩；若函数的值域为R ，则有00a >⎧⎨∆≥⎩. 24．（1）()f x 的值域为9[16-，1]；（2）能，a 的取值集合为{2}；（3）232a -.【分析】（1）由二次函数和指数函数的值域求法，可得()f x 的值域；（2）讨论1a >，01a <<，结合指数函数的单调性和二次函数的单调性，即可得到所求范围；（3）讨论x 的范围和a 的范围，结合参数分离和对勾函数的单调性、指数函数的单调性，计算可得所求范围．【详解】（1）当10x -<时，21122y x x =+-，对称轴为1[14x =-∈-，0)，可得y 的最小值为916-，y 的最大值为0；当01x 时，12?()1[02xy =-∈，1]；综上()f x 的值域为9[16-，1]；（2）当1a >时，函数22xy a a =-在[0，1]递增，故二次函数2y x ax a =+-在[1-，0]也要递增，1222aa a⎧--⎪⎨⎪--⎩，故只有2a =符合要求；当01a <<时，函数22xy a a =-在[0，1]递减，故二次函数2y x ax a =+-在[1-，0]也要递减，0222aa a⎧-⎪⎨⎪--⎩，无解．综上，a 的取值集合为{2}；（3）①当[1x ∈-，0]时，22x ax a +--恒成立，即有2(1)2a x x ---，即221x a x+-，由221x y x+=-，令1t x =-，[1t ∈，2]，可得32232y t t=+--，当且仅当t =时，取得等号，可得232a -；②当[0x ∈，1]时，①当1a >时，22x y a a =-，222x a a --，即有222a -，求得2a ，故12a <； ②当01a <<时，成立，综上可得a 的范围为232a -．【点睛】本题考查分段函数的值域和单调性的判断和运用，考查分类讨论思想方法和化简运算能力，以及不等式恒成立问题解法，属于中档题． 25．(1) {|27}B x x A -<≤⋃=，(){|21}RA B x x =-<<；(2)()1,41,2⎛⎫-∞-⋃- ⎪⎝⎭．【分析】（1）根据题意，由2m =可得{|17}x A x =≤≤，由并集定义可得A B 的值，由补集定义可得{|1RA x x =<或7}x >，进而由交集的定义计算可得()R AB ⋂，即可得答案；（2）根据题意，分析可得A B ⊆，进而分2种情况讨论：①、当A =∅时，有123m m ->+，②当A ≠∅时，有12312234m m m m -≤+⎧⎪->-⎨⎪+<⎩，分别求出m 的取值范围，进而对其求并集可得答案．【详解】根据题意，当2m =时，{|17}x A x =≤≤，()2()lg 28f x x x =-++有意义，则2280x x -++>，得{|24}B x x =-<<，则{|27}B x x A -<≤⋃=，又{|1RA x x =<或7}x >，则(){|21}R AB x x =-<<；（2）根据题意，若A B A =，则A B ⊆，分2种情况讨论：①当A =∅时，有123m m ->+，解可得4m <-， ②当A ≠∅时，若有A B ⊆，必有12312234m m m m -≤+⎧⎪->-⎨⎪+<⎩，解可得112m -<<，综上可得：m 的取值范围是：()1,41,2⎛⎫-∞-⋃- ⎪⎝⎭．【点睛】本题考查集合间关系的判定，涉及集合间的混合运算，考查了学生的计算能力，培养了学生分析问题与解决问题的能力. 26．（1）()1,+∞；（2）a =【分析】（1）由220mx x m ++>恒成立，得关于m 的不等式组，求解得答案；（2）令12xt ⎛⎫= ⎪⎝⎭，1,22t ⎡⎤∈⎢⎥⎣⎦，可得()223y t a a =-+-，1,22t ⎡⎤∈⎢⎥⎣⎦，根据二次函数的定义域和对称轴的关系分类讨论求最小值，进一步求得实数a 的值. 【详解】（1）()()2222log 2g mx x m mx x m ++=++， ∵()22g mx x m ++的定义域为R ，∴220mx x m ++>恒成立，当0m =时，不符合，当0m ≠时，满足2440m m >⎧⎨∆=-<⎩，解得1m ， ∴实数m 的取值范围为()1,+∞；（2）令12xt ⎛⎫= ⎪⎝⎭，当[]1,1x ∈-时，1,22t ⎡⎤∈⎢⎥⎣⎦，则函数()()223y f x af x =-+⎡⎤⎣⎦化为()222233y t at t a a =-+=-+-，1,22t ⎡⎤∈⎢⎥⎣⎦. ①当2a >时，可得当2t =时y 取最小值，且min 741y a =-=，解得32a =（舍去）； ②当122a ≤≤时，可得当t a =时y 取最小值，且2min 31y a =-=，解得a =a =③12a <时，可得当12t =时y 取最小值，且min 1314y a =-=，解得94a =（舍去），综上，a =【点睛】本题考查对数函数的定义域，考查不等式的恒成立问题，考查二次函数的最值，属于中档题.。

新北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(包含答案解析)

一、选择题1．已知函数()()2log 2xf x m =+，则满足函数()f x 的定义域和值域都是实数集R 的实数m 构成的集合为（） A ．{}|0m m =B ．{}0|m m ≤C ．{}|0m m ≥D ．{}|1m m =2．已知函数)()lnf x x =，则120212020a f ⎛⎫= ⎪⎝⎭，20201log 2021b f ⎛⎫= ⎪⎝⎭，()2021log 2020c f =的大小关系为（）A ．a b c >>B ．a c b >>C ．b a c >>D ．b c a >>3．已知()f x ，()g x 分别为定义在R 上的偶函数和奇函数，且满足()()2xf xg x +=，若对于任意的[]1,2x ∈，都有()()20f x a g x a -⋅-≤⎡⎤⎡⎤⎣⎦⎣⎦恒成立，则实数a 的取值范围是（） A ．317,44⎡⎤⎢⎥⎣⎦B ．155,82⎡⎤⎢⎥⎣⎦ C ．15,28⎡⎤⎢⎥⎣⎦D ．172,4⎡⎤⎢⎥⎣⎦4．已知定义在R 上的函数()f x 满足(3)()f x f x +=，且当(1x ∈，3]时，4()log f x x =，则(2021)f =（）A ．12B ．0C ．4log 3D ．15．已知函数222,1()log (1),1x x f x x x ⎧-≤=⎨->⎩，则52f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦（） A ．12-B ．-1C ．-5D ．126．若函数ya >0，a ≠1)的定义域和值域都是[0，1]，则log a 56＋log a 485＝( ) A ．1 B ．2 C ．3D ．47．函数y =）A ．(41)--，B ．(41)-，C ．(11)-，D ．(11]-， 8．已知奇函数()f x 与偶函数()g x 满足()()2x x f x g x a a -+=-+，且()g b a =，则()2f 的值为（）A ．2aB ．2C ．154D ．1749．若函数()()212log 45f x x x =-++在区间()32,2m m -+内单调递增，则实数m 的取值范围为（）A ．4,33⎡⎤⎢⎥⎣⎦B ．4,23⎡⎤⎢⎥⎣⎦C ．4,23⎡⎫⎪⎢⎣⎭D ．4,3⎡⎫+∞⎪⎢⎣⎭10．设()lg (21)fx x a =-+是奇函数，则使f(x)<0的x 的取值范围是( )．A ．(－1,0)B ．(0, 1)C ．(－∞，0)D ．(－∞，0)∪(1，＋∞)11．函数()log (3)a f x ax =-在[]13，上单调递增，则a 的取值范围是（） A ．()1+∞， B ．()01，C ．103⎛⎫ ⎪⎝⎭，D ．()3+∞， 12．函数()log 1a f x x =+（且）．当(1,0)x ∈-时，恒有()0f x >，有（）．A ．()f x 在(,0)-∞+上是减函数B ．()f x 在(,1)-∞-上是减函数C ．()f x 在(0,)+∞上是增函数D ．()f x 在(,1)-∞-上是增函数二、填空题13．下列命题中所有正确的序号是___________． ①函数()13x f x a-=+()1a > 在R 上是增函数；②函数(1)f x -的定义域是(1,3)，则函数()f x 的定义域为(2,4)； ③已知()f x =538x ax bx ++-，且()28f -=，则(2)8f =-；④11()122x f x =--为奇函数． 14．已知()f x 是定义在[0,)+∞的函数，满足(1)()f x f x +=-，当[0,1)x ∈时，()3x f x =，则3(log 30)f =________.15．函数12()log (2)f x x =-的定义域为______.16．已知()f x 是定义在R 上的奇函数，且当0x 时，2log (1),01,()31,1,x x f x x x +<⎧=⎨--⎩则方程1()2f x =的所有实根之和为________. 17．方程()()22log 972log 31xx+=++的解为______. 18．方程()()122log 44log 23xx x ++=+-的解为____；19．若函数11x y a+=+()0,1a a >≠恒过点(,)P m n ，则函数()11142x xf x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭在[],m n 上的最小值是_____.20．已知函数(12)3,1()ln ,1a x a x f x x x -+<⎧=⎨≥⎩的值域为R ，则实数a 的取值范围是________．三、解答题21．已知函数()2()log 41xf x kx =++是偶函数. （1）求k 的值；（2）若函数()y f x =的图像与直线y x a =+没有交点，求实数a 的取值范围；（3）设函数()()221f x xx g x m +=+⋅-，[]20,log 3x ∈，是否存在实数m ，使得()g x 的最小值为0？若存在，求出m 的值；否则，说明理由.22．已知函数()2221log 2m x f x x-=-（0m >且1m ≠）（1）求()f x 的解析式；（2）判断函数()f x 的奇偶性，并说明理由；（3）若关于x 的方程()1log m f x x =+有解，求m 的取值范围. 23．已知函数()log (1)log (1)a a f x x x =+--，（0a >且1a ≠）（1）求()f x 的定义域；（2）判断()f x 的奇偶性，并予以证明；（3）求使()0f x >的x 取值范围.24．已知函数22()log (23).f x x x =-++（1）求函数()f x 的定义域和值域；（2）写出函数()f x 的单调增区间和减区间（不要求证明）. 25．计算下列各式的值：（1）1100.753270.064()160.258---++;（2）53log 425log lg lg 4522++-.26．设函数()log (0,1)a f x x a a =>≠. （1）解不等式(26)(5)f a f a +；（2）已知对任意的实数()23,14m f m m f ⎛⎫++ ⎪⎝⎭恒成立，是否存在实数k ，使得对任意的[1,0]x ∈-，不等式()()142240x x xf f k ++--⋅>恒成立，若存在，求出k 的范围；若不存在，请说明理由.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】若定义域为实数集R ，则20x m +>对于x ∈R 恒成立，可得0m ≥，若值域为实数集R ，令2x t m =+，则2log y t = 此时需满足2x t m =+的值域包括()0,∞+，可得0m ≤，再求交集即可. 【详解】若()()2log 2xf x m =+定义域为实数集R ，则20x m +>对于x ∈R 恒成立，即2x m >-对于x ∈R 恒成立，因为20x >，所以20x -<，所以0m ≥，令2x t m =+，则2log y t =若()()2log 2xf x m =+值域为实数集R ，则2x t m =+的值域包括()0,∞+，因为t m >，所以0m ≤，所以0m =，故选：A 【点睛】关键点点睛：本题的关键点是要找到定义域为R 的等价条件即20x m +>对于x ∈R 恒成立，分离参数m 求其范围，值域为R 的等价条件即2x t m =+可以取遍所有大于0的数，由t m >，所以0m ≤，再求交集.2．D解析：D 【分析】先判断出()f x 在R 上单调递减，再利用指数对数函数的单调性求出120212020，20201log 2021， 2021log 2020的范围，即可根据单调性比较大小.【详解】210x x +->恒成立，()f x ∴定义域为R ，))()lnlnf x x x ===-，其中y x 单调递增，则()f x 单调递减，102021202020120>=，202020201log log 102021<=，2021202120210log 1log 2020log 20211=<<=，b c a ∴>>. 故选：D. 【点睛】关键点睛：本题考查利用函数的单调性比较大小，解题的关键是判断出)()ln f x x =在R 上单调递减，进而可利用单调性比较.3．B解析：B 【分析】利用奇偶性求出()222x x f x -+=，()222x x g x --=，讨论()22x xh x -=+和()g x 的单调性求最值可得()()h x g x >恒成立，则不等式恒成立等价于()()max min g x a h x ≤≤. 【详解】()()2x f x g x +=，()()2x f x g x --+-=∴，()f x 是偶函数，()g x 分是奇函数，()()2x f x g x -=∴-，可得()222x xf x -+=，()222x xg x --=，则不等式为()()1222202x xx x a a --⎡⎤+-⋅--≤⎢⎥⎣⎦，令()22xxh x -=+，令2x t =，由对勾函数的性质可得1y t t=+在[]2,4单调递增，则()22x xh x -=+在[]1,2单调递增，则()()()()min max 5171,224h x h h x h ====，对于()222x x g x --=，因为2xy =单调递增，2x y -=-单调递增，()g x ∴在[]1,2单调递增，()()()()min max 3151,248g x g g x g ∴====， ()()h x g x ∴>恒成立，则不等式()()0h x a g x a --≤⎡⎤⎡⎤⎣⎦⎣⎦，解得()()g x a h x ≤≤，()()max min g x a h x ∴≤≤，即15582a ≤≤. 故选：B. 【点睛】关键点睛：本题考查不等式的恒成立问题，解题的关键是利用奇偶性求出函数解析式，根据函数的单调性求出最值将不等式等价为()()max min g x a h x ≤≤即可求解.4．A解析：A 【分析】根据题意，由(3)()f x f x +=可得()f x 是周期为3的周期函数，则有(2021)f f =（2），结合函数的解析式计算可得答案. 【详解】根据题意，定义在R 上的函数()f x 满足(3)()f x f x +=，则()f x 是周期为3的周期函数，则(2021)(23673)(2)f f f =+⨯=，又由当(1x ∈，3]时，4()log f x x =，则f （2）41log 22==，故1(2021)2f =，故选：A. 【点睛】关键点点睛：根据函数的周期性将(2021)f 化为(2)f ，再利用函数解析式求值是解题关键.5．A解析：A 【分析】根据分段函数解析式，依次计算255log 122f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭，23log 2f ⎛⎫ ⎪⎝⎭，即可得选项.【详解】因为函数222,1()log (1),1x x f x x x ⎧-≤=⎨->⎩，所以2253log log 2122f ⎛⎫=<= ⎪⎝⎭，23log 2531222222f f⎡⎤⎛⎫∴=-=-=- ⎪⎢⎥⎝⎭⎣⎦. 故选：A. 【点睛】本题考查根据分段函数求解函数值，关键在于根据解析式分段求解，由内到外，准确认清自变量的所在的范围和适用的解析式.6．C解析：C 【分析】先分析得到a ＞1，再求出a =2,再利用对数的运算求值得解. 【详解】由题意可得a －a x ≥0，a x ≤a ，定义域为[0，1]，所以a >1，y [0，1]上单调递减，值域是[0，1]，所以f (0)1，f (1)＝0，所以a ＝2，所log a 56＋log a 485＝log 256＋log 2485＝log 28＝3. 故选C 【点睛】本题主要考查指数和对数的运算，考查函数的单调性的应用，意在考查学生对这些知识的理解掌握水平，属于基础题.7．C解析：C 【解析】要使函数有意义，需使210{340x x x +>--+>，即1{41x x >--<<，所以1 1.x -<<故选C8．C解析：C 【分析】根据奇函数()f x 与偶函数()g x ，由()()2x xf xg x a a -+=-+得到()()2﹣﹣﹣=+xx g x f x a a ，两式相加、相减并结合()g b a =求得()f x 即可.【详解】∵奇函数()f x 与偶函数()g x ，()()()(),-∴=-=f x f x g x g x .又()()2﹣+=+-x x f x g x a a ，①()()2﹣---∴+=+x x f x g x a a ，()()2﹣∴=--+x x g x f x a a .② +①②，得()24g x =，()2g x ∴=.(),2g b a a =∴=. ()22﹣-∴=x x f x . 22115(2)22444f -∴=-=-=. 故选：C. 【点睛】本题主要考查函数奇偶性的综合应用，还考查了运算求解的能力，属于中档题.9．C解析：C 【分析】求得函数()y f x =的定义域，利用复合函数法求得函数()y f x =的单调递增区间，根据题意可得出区间的包含关系，由此可求得实数m 的取值范围. 【详解】解不等式2450x x -++>，即2450x x --<，解得15x -<<，内层函数245u x x =-++在区间()1,2-上单调递增，在区间()2,5上单调递减，而外层函数12log y u =在定义域上为减函数，由复合函数法可知，函数()()212log 45f x x x =-++的单调递增区间为()2,5，由于函数()()212log 45f x x x =-++在区间()32,2m m -+上单调递增，所以，32232225m m m m -≥⎧⎪-<+⎨⎪+≤⎩，解得423m ≤<.因此，实数m 的取值范围是4,23⎡⎫⎪⎢⎣⎭. 故选：C. 【点睛】本题考查利用对数型复合函数在区间上的单调性求参数，考查计算能力，属于中等题.10．A解析：A 【解析】试题分析：由()lg (21)fxx a=-+为奇函数，则()()f xf x -=-，可得1a =-，即()lg11f xxx=+-，又()0f x <，即lg 110x x +-<，可变为0111x x <+-<，解得10x -<<．考点：函数的奇偶性，对数函数性质，分式不等式．11．D解析：D 【分析】由题意可得可得1a >，且30a ->，由此求得a 的范围．【详解】解：函数()log (3)a f x ax =-在[]13，上单调递增，而函数()3t x ax =-在[]13，上单调递增，根据复合函数的单调性可得1a >，且30a ->，解得3a >，即()3a ∈+∞，故选：D ．【点睛】本题主要考查对数函数的定义域、单调性，复合函数的单调性，属于基础题．12．D解析：D 【解析】试题分析：根据题意，当(1,0)x ∈-时，1(0,1)x +∈，而此时log 10a x +>，所以有01a <<，从而能够确定函数在(,1)-∞-上是增函数，在区间(1,)-+∞上是减函数，故选D ．考点：函数的单调性．二、填空题13．①④【分析】根据指数的运算性质且恒成立求出函数图象所过的定点可判断①；根据抽象函数的定义域的求法可判断②；根据奇函数的图象和性质求出可判断③；根据奇函数的定义及判定方法可判断④【详解】解：当时且恒成解析：①④ 【分析】根据指数的运算性质01(0a a =>且1)a ≠恒成立，求出函数图象所过的定点，可判断①；根据抽象函数的定义域的求法，可判断②；根据奇函数的图象和性质，求出()2f ，可判断③；根据奇函数的定义及判定方法，可判断④ 【详解】解：当1x =时，101(0x a a a -==>且1)a ≠恒成立，故f （1）4=恒成立，故函数1()3(0x f x a a -=+>且1)a ≠的图象一定过定点(1,4)P ，故①正确；函数(1)f x -的定义域是(1,3)，则函数()f x 的定义域为(0,2)，故②错误；已知53()8f x x ax bx =++-，且(2)8f -=，则()224f =-，故③错误；11()122xf x =--的定义域为{|0}x x ≠，且112111()()122212212x x x xf x f x ---=-=-=-=----，故()f x 为奇函数，故④正确；故答案为：①④ 【点睛】本题以命题的真假判断为载体，考查了指数函数的图象和性质，函数的定义域，函数的奇偶性，是函数图象和性质的综合应用，难度不大，属于基础题．14．【分析】利用对数的运算性质得出结合周期性即可得出的值【详解】且则则函数的周期为2故答案为：【点睛】本题主要考查了由抽象函数的周期求函数值涉及了对数的运算属于中档题解析：109-【分析】利用对数的运算性质得出3310log 303log 9=+，结合周期性，即可得出3(log 30)f 的值. 【详解】33333101010log 30log 27log 27log 3log 999⎛⎫=⨯=+=+ ⎪⎝⎭，且333100log log log 9131=<<= (1)()f x f x +=-，(11)(1)()f x f x f x ∴++=-+=，则(2)()f x f x +=，则函数()f x 的周期为2310log 3333310101010(log 30)21log 1log log 39999f f f f⎛⎫⎛⎫⎛⎫∴=++=+=-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故答案为：109- 【点睛】本题主要考查了由抽象函数的周期求函数值，涉及了对数的运算，属于中档题.15．【分析】根据二次根式和对数式有意义的条件得到不等式组求解函数的定义域即可得结果【详解】根据题意可得：解得所以函数的定义域为故答案为：【点睛】该题考查的是有关求函数的问题涉及到的知识点有求给定函数的定解析：(2,3]【分析】根据二次根式和对数式有意义的条件，得到不等式组求解函数的定义域即可得结果.【详解】根据题意可得：1220log (2)0x x ->⎧⎪⎨-≥⎪⎩，解得23x <≤，所以函数12()log (2)f x x =-的定义域为(2,3]，故答案为：(2,3].【点睛】该题考查的是有关求函数的问题，涉及到的知识点有求给定函数的定义域，在解题的过程中，注意二次根式和对数式需要满足的条件即可得结果.16．【分析】画出分段函数的图像根据图像结合解析式进行求解【详解】根据分段函数的解析式以及函数为奇函数作图如下：由图容易知因为在区间上关于对称且在区间上关于对称故其与直线的所有交点的横坐标之和为0故所有根解析：21-【分析】画出分段函数的图像，根据图像，结合解析式，进行求解.【详解】根据分段函数的解析式，以及函数为奇函数，作图如下：由图容易知，因为31y x =--在区间[)1,+∞上，关于3x =对称，且31y x =---+在区间(],1-∞上，关于3x =-对称，故其与直线12y =的所有交点的横坐标之和为0. 故1()2f x =所有根之和，即为当()0,1x ∈时的根，此时()21log 12x +=，解得21x =. 21.【点睛】本题考查函数图像的交点，涉及函数图像的绘制，函数奇偶性的应用，属函数综合题.17．或【分析】由对数的运算性质化对数方程为关于的一元二次方程求得的值进一步求得值得答案【详解】由得即化为解得：或或故答案为：或【点睛】本题主要考查的是对数方程的求解将对数方程转化为指数方程是解决本题的关解析：0x =或1x =.【分析】由对数的运算性质化对数方程为关于3x 的一元二次方程，求得3x 的值，进一步求得x 值得答案.【详解】由()()22log 972log 31x x +=++，得 ()()22log 97log 431x x +=+，即()97431x x +=+，化为()234330x x -⋅+=，解得：31x =或33x =，0x ∴=或1x =.故答案为：0x =或1x =.【点睛】本题主要考查的是对数方程的求解，将对数方程转化为指数方程是解决本题的关键，考查学生的计算能力，是基础题.18．【分析】直接利用对数的运算法则化简求解即可【详解】解：可得即：解得（舍去）可得经检验是方程的解故答案为：【点睛】本题考查方程的解的求法对数的运算法则的应用考查计算能力解析：2【分析】直接利用对数的运算法则化简求解即可．【详解】解：()()122log 44log 23x x x ++=+-()()1222log 44log log 232x x x +∴+=+-可得()()122log 44log 232x x x ++=-⎡⎤⎣⎦，即：()144232x x x ++=-， ()223240x x -⋅-=，解得21x =-（舍去）24x =，可得2x =．经检验2x =是方程的解．故答案为：2．【点睛】本题考查方程的解的求法，对数的运算法则的应用，考查计算能力．19．【分析】先利用指数型函数恒过定点问题求定点得到换元令利用二次函数的单调性即可求解【详解】函数恒过点则区间变为由函数令则利用二次函数的单调性当时则函数在上的最小值是故答案为：【点睛】关键点睛：把指数型解析：34【分析】先利用指数型函数恒过定点问题求定点，得到1,2m n =-=，换元，令11,224x t t ⎛⎫=≤≤ ⎪⎝⎭，利用二次函数的单调性，即可求解. 【详解】函数11x y a +=+()0,1a a >≠恒过点()1,2-，则1,2m n =-=，区间[],x m n ∈变为[]1,2x ∈-，由函数()11142x xf x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭，令11,224x t t ⎛⎫=≤≤ ⎪⎝⎭，则()2213124f t t t t ⎛⎫=-+=-+ ⎪⎝⎭，利用二次函数的单调性，当12t =时，()min 34f t =，则函数()11142x x f x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭在[],m n 上的最小值是34. 故答案为：34. 【点睛】关键点睛：把指数型复合函数求最值问题转化为二次函数求最值问题是解决本题的关键. 20．【分析】根据的值域为可知需在单调递增且即可【详解】由题意知的值域为故要使的值域为则必有为增函数且所以且解得故答案为：【点睛】本题主要考查了已知分段函数值域求参数范围属于中档题解析：112⎡⎫-⎪⎢⎣⎭，【分析】根据()ln (1)f x x x =≥的值域为[0,)+∞，可知()(12)3(1)f x a x a x =-+<需在(,1)-∞单调递增且(1)0f ≥即可.【详解】由题意知()ln (1)f x x x =≥的值域为[0,)+∞，故要使()f x 的值域为R ，则必有()(12)3f x a x a =-+为增函数，且1230a a -+≥，所以120a ->，且1a ≥-，解得112a -≤<. 故答案为：112⎡⎫-⎪⎢⎣⎭，【点睛】本题主要考查了已知分段函数值域求参数范围，属于中档题.三、解答题21．（1）1-；（2）0a ≤；（3）存在，1m =-.【分析】（1）由(1)(1)f f -=得1k =-，再验证此时()f x 为偶函数；（2）化简()g x ，换元，令2x t =化为关于t 的二次函数，分类讨论对称轴，求出最小值，结合已知最小值可解得结果.【详解】（1）因为函数()2()log 41xf x kx =++是偶函数，所以(1)(1)f f -=，即()()122log 41log 41k k -+-=++，即2252log log 54k =-2=-，解得1k =-；当1k =-时，()2()log 41x f x x =+-，()2()log 41x f x x --=++， ()()22()()log 41log 412x x f x f x x ---=+-+-241log 241x x x -+=-+2log 42x x =-220x x =-=，所以()()f x f x -=，所以()f x 为偶函数，所以1k =-符合题题.（2）因为函数()y f x =的图像与直线y x a =+没有交点，所以()2241()()log 412log 4x xx f x x a x a a ⎛⎫+-+=+--=- ⎪⎝⎭21log 104x a ⎛⎫=+-= ⎪⎝⎭无解，而21log 104x ⎛⎫+> ⎪⎝⎭，故0a ≤. （3）()()221f x x x g x m +=+⋅-2log (41)221x x x x m +-+=+⋅-()241214222x x x x x x m m m =++⋅-=+⋅=+⋅22(2)24xm m =+-，令2x t =，因为[]20,log 3x ∈，所以[1,3]t ∈，令22()24m m y t =+-，[1,3]t ∈，当12m -≤，即2m ≥-时，22()24m m y t =+-单调递增，所以y 的最小值为10m +=，解得1m =-；当32m -≥，即6m ≤-时，22()24m m y t =+-单调递减，所以y 的最小值为2330m +=，解得3m =-（舍）；当132m <-<，即62m -<<-时，y 的最小值为204m -=，解得0m =（舍）. 综上所述：1m =-.【点睛】关键点点睛：化简()g x ，换元，令2x t =化为关于t 的二次函数，利用二次函数知识求解是解题关键.22．（1）()1log 1mx f x x +=-；（2）()f x 为奇函数，理由见解析；（3）3m ≥+. 【分析】（1）令21t x =-，采用换元法求解函数解析式；（2）先确定函数的定义域，再由函数奇偶性的定义判断即可；（3）由条件可转化为()11x m x x +=-在()0,1x ∈上有解问题即可. 【详解】（1）令21t x =-，则21x t =+，则()()11log log 211mm t t f t t t ++==-+-，所以()1log 1mx f x x +=-；（2）由101x x+>-得11x -<<，又()()()11log log 11m m x x f x f x x x---===---+，所以()f x 为定义域上的奇函数；（3）由110x x -<<⎧⎨>⎩得01x <<，又1log 1log log 1m m m x x mx x +=+=-，11x mx x+=-在()0,1x ∈上有解，()11x m x x +=-，令()11,2u x =+∈，2132323t m u u u u ==≥=+-+-⎛⎫-++ ⎪⎝⎭，当且仅当u =,所以3m ≥+.【点睛】易错点睛：（1）判断函数的奇偶性一定不要忘记先判断定义域是否关于原点对称；（2）利用基本不等式求解范围，一定要注意满足“一正二定三相等”的条件.23．（1）{|11}x x -<<；（2）函数()f x 是奇函数，证明见解析；（3）当1a >时，01x <<；当01a <<时，10x -<<【分析】（1）根据对数的真数为正数列式可解得结果；（2）函数()f x 是奇函数，根据奇函数的定义证明即可；（3）不等式化为log (1)log (1)a a x x +>-后，分类讨论底数a ，根据对数函数的单调性可解得结果.【详解】（1）要使函数数()f x 有意义，则必有1010x x +>⎧⎨->⎩，解得11x -<<，所以函数()f x 的定义域是{|11}x x -<< .（2）函数()f x 是奇函数，证明如下：∵(1,1)x ∈-，(1,1)x -∈-，()log (1)log (1)a a f x x x -=--+[]log (1)log (1)a a x x =-+--()f x =-，∴函数()f x 是奇函数（3）使()0f x >，即log (1)log (1)a a x x +>-当1a >时，有111010x x x x +>-⎧⎪->⎨⎪+>⎩，解得01x <<，当01a <<时，有111010x x x x +<-⎧⎪->⎨⎪+>⎩，解得10x -<<.综上所述：当1a >时，01x <<；当01a <<时，10x -<<.【点睛】方法点睛：已知函数解析式，求函数定义域的方法：有分式时：分母不为0；有根号时：开奇次方，根号下为任意实数，开偶次方，根号下大于或等于0；有指数时：当指数为0时，底数一定不能为0；有根号与分式结合时，根号开偶次方在分母上时：根号下大于0；有指数函数形式时：底数和指数都含有x ，指数底数大于0且不等于1；有对数函数形式时，自变量只出现在真数上时，只需满足真数上所有式子大于0，自变量同时出现在底数和真数上时，要同时满足真数大于0，底数要大0且不等于1. 24．（1）定义域为(1,3)-,值域为(,2]-∞（2）递增区间为(1,1)-，递减区间为[1,3)【分析】（1）由2230x x -++>解得结果可得定义域，根据二次函数知识求出真数的值域，根据对数函数的单调性可求得()f x 的值域；（2）在定义域内求出真数的单调区间，根据底数大于1可得函数()f x 的单调区间.【详解】（1）由函数有意义可得2230x x -++>，即2230x x --<，解得13x，所以函数()f x 的定义域为(1,3)-，因为13x ，所以2223(1)4x x x -++=--+(0,4]∈，所以()(,2]f x ∈-∞，即函数()f x 的值域为(,2]-∞.（2）因为函数()f x 的定义域为(1,3)-，且函数2y x 2x 3=-++在(1,1)-上递增，在(1,3)上递减，又对数函数的底数为21>，所以函数()f x 的递增区间为(1,1)-，递减区间为[1,3).【点睛】方法点睛：已知函数解析式，求函数定义域的方法：有分式时：分母不为0；有根号时：开奇次方，根号下为任意实数，开偶次方，根号下大于或等于0；有指数时：当指数为0时，底数一定不能为0；有根号与分式结合时，根号开偶次方在分母上时：根号下大于0；有指数函数形式时：底数和指数都含有x ，指数底数大于0且不等于1；有对数函数形式时，自变量只出现在真数上时，只需满足真数上所有式子大于0，自变量同时出现在底数和真数上时，要同时满足真数大于0，底数要大0且不等于1. 25．（1）10 （2）0【分析】（1）利用指数幂的运算性质求解即可；（2）利用对数的运算性质求解即可.【详解】解:（1）1100.753270.064()160.258---++()11333244211254-⎡⎤⎛⎫⎛⎫=-++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦ 51182210=（2）53log 425log lg lg 4522++- 34223log 2log 2lg 5lg 22lg 24=-+-+-()331lg5lg 244=-++- 331144=-+- 0=【点睛】本题考查指数幂的运算,考查对数的运算.26．（1）(0,1)[2,)a ∈⋃+∞（2）实数k 不存在，详见解析【分析】（1）分类讨论，利用对数函数的单调性，将不等式具体化，解不等式即可；（2）判断函数()f x 为增函数，将不等式具体化，再分离参数求最值，即可得出结论.【详解】解：（1）当01a <<时，有2650a a +>，解得02a <≤，即(0,1)∈a ；当1a >时，有0265a a <+，解得2a ，即[2,)a ∈+∞.综上可知，(0,1)[2,)a ∈⋃+∞.（2）由于221331244m m m ⎛⎫++=++ ⎪⎝⎭，且()2314f m m f ⎛⎫++ ⎪⎝⎭，可知()f x 为增函数. ()()142240x x x f f k ++--⋅>，即()()14224x x x f f k ++>-⋅，则有14224x x x k ++>-⋅在[1,0]-上恒成立，即1342x x k +<⋅+在[1,0]-上恒成立，令12,12x t ⎡⎤=∈⎢⎥⎣⎦，设2()32,()g t t t g t =+在1,12⎡⎤⎢⎥⎣⎦上单调递增，则min 17()24g t g ⎛⎫== ⎪⎝⎭，即74k <. 又由于[1,0]x ∈-时，240x k -⋅>恒成立，解得2k >，故符合题意的实数k 不存在.【点睛】本题考查对数函数的单调性、恒成立问题的转化分析、指数函数与二次函数的复合函数的最值问题.。

北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(包含答案解析)

一、选择题1．设a ，b ，c 为正数，且3a =4b =6c ，则有（）A ．111c a b =+ B ．221c a b=+ C ．122c a b=+ D ．212c a b=+ 2．下列各组函数中，表示同一个函数的是（）A ．211x y x -=-与1y x =+B ．y x =与log xa y a =（0a >且1a ≠）C．y =1y x =-D ．lg y x =与21lg 2y x =3．设0.60.6a =， 1.20.6b =，0.61.2c =中，则a ，b ，c 的大小关系是（） A ． a b c <<B ．a c b <<C ．b a c <<D ．b c a <<4．若函数()()23log 5f x x ax a =+++，()f x 在区间(),1-∞上是递减函数，则实数a的取值范围为（） A ．[]3,2--B ．[)3,2--C ．(],2-∞-D ．(),2-∞-5．函数()212()log 4f x x =-的单调递增区间为（）. A ．(0,+∞)B ．(-,0)C ．(2,+∞)D ．(-,-2)6．已知定义在R 上的函数()f x 满足(3)()f x f x +=，且当(1x ∈，3]时，4()log f x x =，则(2021)f =（）A ．12B ．0C ．4log 3D ．17．设函数()ln |31|ln |31|f x x x =+--，则()f x （） A ．是偶函数，且在11(,)33-单调递增 B ．是偶函数，且在1(,)3-∞-单调递增 C ．是奇函数，且在11(,)33-单调递减 D ．是奇函数，且在1(,)3-∞-单调递减8．已知2log 0.8a =，0.7log 0.6b =，0.60.7c =，则a ，b ，c 的大小关系是（） A ．a b c <<B ．b a c <<C ．a c b <<D ．b c a <<9．已知函数()f x 满足()()11f x f x -=+，当(],1-∞时，函数()f x 单调递减，设()41331=log ,log 3,92a f b f c f log ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，则,,a b c 的大小关系是（）A ．a b c <<B ．c a b <<C ．a c b <<D ．c b a <<10．已知235log log log 0x y z ==<，则2x 、3y 、5z的大小排序为 A ．235x y z <<B ．325y x z <<C ．523z x y <<D ．532z y x<<11．已知()lg(10)lg(10)f x x x =++-，则()f x 是（） A ．偶函数，且在(0,10)是增函数 B ．奇函数，且在(0,10)是增函数 C ．偶函数，且在(0,10)是减函数D ．奇函数，且在(0,10)是减函数12．若函数()()212log 45f x x x =-++在区间()32,2m m -+内单调递增，则实数m 的取值范围为（） A ．4,33⎡⎤⎢⎥⎣⎦B ．4,23⎡⎤⎢⎥⎣⎦C ．4,23⎡⎫⎪⎢⎣⎭D ．4,3⎡⎫+∞⎪⎢⎣⎭二、填空题13．已知函数()1122,121,1x x x f x x x --⎧-≤⎪=⎨-->⎪⎩，则关于x 的不等式()()10f x f x -+≤的解集为___________________．14．测量地震级别的里氏震级M 的计算公式为:0lg lg M A A =-，其中A 是测震仪记录的地震曲线的最大振幅，常数A 0是相应的标准地震的振幅.假设在一次地震中，测震仪记录的最大振幅是1000，而此次地震的里氏震级恰好为6级，那么里氏9级地震的最大的振幅是里氏5级地震最大振幅的______倍.15．已知函数()2log f x x =，正实数m ，n 满足m n <，且()()f m f n =，若()f x 在区间2,m n ⎡⎤⎣⎦上的最大值为2，则m n +=________.16．已知函数f (x )＝3x ＋x ，g(x )＝log 3x ＋2，h (x )＝log 3x ＋x 的零点依次为a ，b ，c ，则a ，b ，c 的大小关系是________. 17．已知1122x x-+=22165x x x x --+-=+-______.18．方程()()122log 44log 23xx x ++=+-的解为____；19．函数()22log 617y x x =-+的值域是__． 20．关于下列命题：①若函数2x y =的定义域是{}|0x x ≤，则它的值域是{}|1y y ≤ ②若函数1y x =的定义域是{}|2x x >，则它的值域是12y y ⎧⎫<⎨⎬⎩⎭ ③若函数2yx 的值域是{}|04y y ≤≤，则它的定义域可能是{}|22x x -≤≤④若函数2log y x =的值域是{}|3y y ≤，则它的定义域是{}|8x x ≤其中不正确的命题的序号是________.（注：把你认为不正确的命题的序号都填上）三、解答题21．已知函数()log (1)log (1)a a f x x x =+--，（0a >且1a ≠）（1）求()f x 的定义域；（2）判断()f x 的奇偶性，并予以证明；（3）求使()0f x >的x 取值范围.22．已知函数()x x f x a k a -=-⋅（0a >且1a ≠）是定义域为R 的奇．函数，且3(1)2f =. （1）求k 的值，并判断()f x 的单调性（不要求证明）；（2）是否存在实数()2,3mm m >≠，使函数()()22(2)log 1x xm g x a a mf x --⎡⎤=+-+⎣⎦在[]1,2上的最大值为0？如果存在，求出实数m 所有的值；如果不存在，请说明理由. 23．化简下列各式：（1）22.531050.064π-⎡⎤⎛⎫⎢⎥ ⎪⎢⎥⎝⎭⎣⎦；（2）2lg 2lg3111lg 0.36lg1624++⋅+ 24．已知函数()log (0,1)a f x x a a =>≠，且(4)(2)1f f -=. （1）求函数()f x 的表达式；（2）判断函数()(2)(2)g x f x f x =++-的奇偶性，并说明理由. 25．计算：（1）()210.2513110.02781369-︒--⎛⎫⎛⎫-++- ⎪ ⎪⎝⎭⎝⎭；. （2）()2lg32lg25lg8lg5lg20lg2103+++- 26．已知命题:p 关于x 的不等式()10,1xa a a >>≠的解集是{}0x x <，命题:q函数()2lg 1y ax =+的定义域为R ，如果“p q ∨”为真命题，“p q ∧”为假命题.求实数a的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B【分析】首先根据指对互化求出,,a b c ，再根据换底公式表示111,,a b c，最后根据对数运算法则化简. 【详解】设3a =4b =6c =k ，则a =log 3k ， b =log 4k ， c =log 6k ，∴311log 3log k a k ==，同理1log 4k b =，1log 6k c=，而11log 2,log 3log 22k k k b c ==+， ∴1112c a b =+，即221c a b =+．故选：B 【点睛】本题考查指对数运算，换底公式，以及对数运算的性质，关键是灵活应用对数运算公式，公式1log log a b b a=是关键. 2．B解析：B 【分析】分析各个选项中每组函数的定义域和对应关系，若定义域和对应关系均相同则为同一个函数，由此判断出正确选项. 【详解】A ．211x y x -=-的定义域为{}1x x ≠，1y x =+的定义域为R ，所以不是同一个函数；B ．y x =与log xa y a =的定义域均为R ，且log xa y a =即为y x =，所以是同一个函数； C．y =(][),11,-∞-+∞，1y x =-的定义域为R ，所以不是同一个函数；D ．lg y x =的定义域为()0,∞+，21lg 2y x =的定义域为{}0x x ≠，所以不是同一个函数，故选：B. 【点睛】思路点睛：同一函数的判断步骤：（1）先判断函数定义域，若定义域不相同，则不是同一函数；若定义域相同，再判断对应关系；（2）若对应关系不相同，则不是同一函数；若对应关系相同，则是同一函数.3．C解析：C 【分析】根据指数函数，幂函数的单调性即可判断．【详解】因为指数函数0.6xy =是单调减函数，0.6 1.2<，所以0.6 1.20.60.6>，即a b >；因为幂函数0.6y x=在()0,∞+上是增函数，0.6 1.2<，所以0.60.61.20.6>，即c a >．综上，b a c <<．故选：C ．【点睛】熟练掌握指数函数，幂函数的单调性是解题关键．4．A解析：A 【分析】判断复合函数的单调性，首先要分清楚内外层函数，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求即可. 【详解】由题意知，()f x 在区间(),1-∞上是递减函数，由()()23log 5f x x ax a =+++可知，此复合函数外层函数为：()3log f x x =，在定义域上为增函数，内层函数为()25h x x ax a =+++，要使()f x 在区间(),1-∞上是递减函数，根据复合函数“同增异减”原则，内层函数为()h x 在区间(),1-∞上必须是递减函数，同时须保证最大值()10h ≥，所以()1210a h ⎧-≥⎪⎨⎪≥⎩，解得32a --≤≤. 故选：A. 【点睛】易错点睛：判断复合函数的单调性，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求.5．D解析：D 【分析】求出函数的定义域，根据对数型复合函数的单调性可得结果. 【详解】函数()212()log 4f x x =-的定义域为()(),22,-∞-+∞，因为函数()f x 是由12log y u =和24u x =-复合而成，而12log y u =在定义域内单调递减，24u x =-在(),2-∞-内单调递减，所以函数()212()log 4f x x =-的单调递增区间为(),2-∞-，故选：D. 【点睛】易错点点睛：对于对数型复合函数务必注意函数的定义域.6．A解析：A 【分析】根据题意，由(3)()f x f x +=可得()f x 是周期为3的周期函数，则有(2021)f f =（2），结合函数的解析式计算可得答案. 【详解】根据题意，定义在R 上的函数()f x 满足(3)()f x f x +=，则()f x 是周期为3的周期函数，则(2021)(23673)(2)f f f =+⨯=，又由当(1x ∈，3]时，4()log f x x =，则f （2）41log 22==，故1(2021)2f =，故选：A. 【点睛】关键点点睛：根据函数的周期性将(2021)f 化为(2)f ，再利用函数解析式求值是解题关键.7．D解析：D 【分析】根据奇偶性定义判断奇偶性，然后判断单调性，排除错误选项得正确结论．【详解】函数定义域是1{|}3x x ≠±，()ln 31ln 31ln 31ln 31()f x x x x x f x -=-+---=--+=-，()f x 是奇函数，排除AB ，312()lnln 13131x f x x x +==+--，11,33x ⎛⎫∈- ⎪⎝⎭时，2310x -<-<，2231x <--，即21031x +<-，而131u x =-是减函数，∴2131v x =+-是增函数，∴()f x 在11,33⎛⎫- ⎪⎝⎭上是增函数，排除C ．只有D 可选．故选：D ．【点睛】结论点睛：本题考查函数的单调性与奇偶性，判断函数的奇偶性与单调性后用排除法确定正确选项，掌握复合函数的单调性是解题关键．()y f x =与()y f x =-的单调性相反，在()f x 恒为正或恒为负时，()y f x =与1()y f x =的单调性相反，若()0f x <，则()y f x =与()y f x =的单调性相反．0a >时，()y af x =与()y f x =的单调性相同．8．C解析：C 【解析】因为22log 0.8log 10a =<=，0.70.7log 0.6log 0.71b =>=，0.6000.70.71c <=<=，所以a c b <<，故选C.9．B解析：B 【分析】由()()11f x f x -=+可得函数()f x 关于直线1x =对称，根据对数的运算法则，结合函数的对称性，变形41log 2、13log 3、39log 到区间[)1,+∞内，由函数()f x 在[)1,+∞上单调递增，即可得结果. 【详解】根据题意，函数()f x 满足()()11f x f x -=+，则函数()f x 关于直线1x =对称，又由当(],1-∞时，函数()f x 单调递减，则函数在[)1,+∞上单调递增，又由()44115log log 2222a f f f f ⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ()()13log 313b f f f ⎛⎫==-= ⎪⎝⎭，()()3log 92c f f ==，则有c a b <<，故选B.【点睛】在比较()1f x ，()2f x ，，()n f x 的大小时，首先应该根据函数()f x 的奇偶性（对称性）与周期性将()1f x ，()2f x ，，()n f x 通过等值变形将自变量置于同一个单调区间，然后根据单调性比较大小．10．A解析：A 【解析】x y z ，，为正实数，且235log log log 0x y z ==<，111235235k k k x y z ---∴===，，，可得：1112352131,51k k k x y z---=>=>=>，．即10k -> 因为函数1kf x x -=（）单调递增，∴235x y z<<. 故选A.11．C解析：C 【分析】先判断函数的定义域关于原点对称，再由奇偶性的定义判断奇偶性，根据复合函数的单调判断其单调性，从而可得结论. 【详解】由100100x x +>⎧⎨->⎩，得(10,10)x ∈-，故函数()f x 的定义域为()10,10-，关于原点对称，又()()lg 10lg(10)()f x x x f x -=-++=，故函数()f x 为偶函数，而()()2lg(10)lg(10)lg 100f x x x x=++-=-，因为函数2100y x =-在()0,10上单调递减，lg y x =在()0,∞+上单调递增，故函数()f x 在()0,10上单调递减，故选C. 【点睛】本题主要考查函数的奇偶性与单调性，属于中档题. 判断函数的奇偶性首先要看函数的定义域是否关于原点对称，如果不对称，既不是奇函数又不是偶函数，如果对称常见方法有：（1）直接法， ()()f x f x -=±(正为偶函数，负为减函数)；（2）和差法，()()0f x f x -±=（和为零奇函数，差为零偶函数）；（3）作商法，()()1f x f x -=±（1 为偶函数，1- 为奇函数） .12．C解析：C 【分析】求得函数()y f x =的定义域，利用复合函数法求得函数()y f x =的单调递增区间，根据题意可得出区间的包含关系，由此可求得实数m 的取值范围.【详解】解不等式2450x x -++>，即2450x x --<，解得15x -<<，内层函数245u x x =-++在区间()1,2-上单调递增，在区间()2,5上单调递减，而外层函数12log y u =在定义域上为减函数，由复合函数法可知，函数()()212log 45f x x x =-++的单调递增区间为()2,5，由于函数()()212log 45f x x x =-++在区间()32,2m m -+上单调递增，所以，32232225m m m m -≥⎧⎪-<+⎨⎪+≤⎩，解得423m ≤<. 因此，实数m 的取值范围是4,23⎡⎫⎪⎢⎣⎭. 故选：C. 【点睛】本题考查利用对数型复合函数在区间上的单调性求参数，考查计算能力，属于中等题.二、填空题13．【分析】对自变量分情况讨论即然后对各种情况分别解不等式最后取并集；【详解】当时所以由此时不等式恒成立；当时则由则此时不等式恒成立；当时符合题意；当时解得∴综上可得不等式的解集为故答案为：【点睛】关键解析：7,2⎛⎤-∞ ⎥⎝⎦ 【分析】对自变量分情况讨论，即1x ≤，12x <≤，23x <<，3x ≥，然后对各种情况分别解不等式，最后取并集；【详解】当1x ≤时，10x -≤，121x -≤，121x -≥，所以()11220x x f x --=-≤由2122x -≤，222x -≥，()221220x xf x ---=-<，此时不等式()()10f x f x +-≤恒成立；当12x <≤时，()212110f x x x x =--=--=-<，011x <-≤，则()22122x xf x ---=-，由221x -≤，221x -≥，则()10f x -≤此时不等式()()10f x f x +-≤恒成立；当23x <<时，()()12131f x f x x x +-=--+--213110x x =--+--=-<，符合题意；当3x ≥时，()()12131270f x f x x x x +-=--+--=-≤，解得72x ≤， ∴732x ≤<．综上可得，不等式()()10f x f x +-<的解集为7,2⎛⎤-∞ ⎥⎝⎦．故答案为：7,2⎛⎤-∞ ⎥⎝⎦ 【点睛】关键点睛：本题考查分别函数解不等式的问题，涉及分类讨论思想的应用，解答本题的关键是对自变量x 的范围进行分类，即1x ≤，12x <≤，23x <<，3x ≥，从而得出()f x 和()1f x -的表达式，从而求解不等式，属于中档题.14．10000【分析】根据条件先计算出的值然后分别计算出里氏9级地震的最大的振幅和里氏5级地震最大振幅由此可求解出最终结果【详解】由条件可知：所以设里氏9级地震的最大的振幅为里氏5级地震最大振幅为所以所解析：10000 【分析】根据条件先计算出0A 的值，然后分别计算出里氏9级地震的最大的振幅和里氏5级地震最大振幅，由此可求解出最终结果. 【详解】由条件可知：06lg1000lg A =-，所以3010A -=，设里氏9级地震的最大的振幅为1A ，里氏5级地震最大振幅为2A ，所以31329lg lg105lg lg10A A --⎧=-⎨=-⎩，所以621210,10A A ==，所以1210000A A =，故答案为：10000. 【点睛】关键点点睛：解答本题的关键在于理解公式0lg lg M A A =-中各个量的含义并先求解出0A 的值，由此继续分析.15．【分析】先画出函数图像并判断再根据范围和函数单调性判断时取最大值最后计算得到答案【详解】如图所示：根据函数的图象得所以结合函数图象易知当时在上取得最大值所以又所以再结合可得所以故答案为：【点睛】本题解析：52【分析】先画出函数图像并判断01m n <<<，再根据范围和函数单调性判断2x=m 时取最大值，最后计算得到答案.【详解】如图所示：根据函数2()log x f x =的图象得01m n <<<，所以201m m <<<．结合函数图象，易知当2x=m 时()f x 在2,m n ⎡⎤⎣⎦上取得最大值，所以()222log 2f m m == 又01m <<，所以12m =，再结合()()f m f n =，可得2n =，所以21522m n +=+=. 故答案为：52【点睛】本题考查对数型函数的图像和性质、函数的单调性的应用和最值的求法，是中档题. 16．【解析】画出函数的图象如图所示：观察图象可知函数的零点依次是点的横坐标由图像可知故答案为点睛：函数的零点与方程根的分布问题解题时常用数形结合思想对于方程的根可分别画出与的图象则两个函数图象的交点的横解析：a b c <<【解析】画出函数3x y =，3log y x =，y x =-，2y =-的图象，如图所示：观察图象可知，函数()3x f x x =+，3()log 2g x x =+，3()log h x x x =+的零点依次是点A ，B ，C 的横坐标，由图像可知a b c <<.故答案为a b c <<点睛：函数的零点与方程根的分布问题，解题时常用数形结合思想，对于方程()()0f x g x -=的根，可分别画出()f x 与()g x 的图象，则两个函数图象的交点的横坐标即为方程()()0f x g x -=的根.17．【分析】对平方可得再平方可得即可求解【详解】两边同时平方得：所以对两边同时平方得：则故答案为：【点睛】此题考查指数式的化简求值进行整体变形处理利用平方关系得出等量关系解析：12- 【分析】对1122x x -+=13x x -+=，再平方可得227x x -+=，即可求解.【详解】1122x x -+=125x x -++=，所以13x x -+=对13x x -+=两边同时平方得：2229x x -++=，227x x -+= 则22167615352x x x x --+--==-+--. 故答案为：12-【点睛】此题考查指数式的化简求值，进行整体变形处理，利用平方关系得出等量关系. 18．【分析】直接利用对数的运算法则化简求解即可【详解】解：可得即：解得（舍去）可得经检验是方程的解故答案为：【点睛】本题考查方程的解的求法对数的运算法则的应用考查计算能力解析：2【分析】直接利用对数的运算法则化简求解即可．【详解】解：()()122log 44log 23x x x ++=+-()()1222log 44log log 232x x x +∴+=+-可得()()122log 44log 232x x x ++=-⎡⎤⎣⎦，即：()144232x x x ++=-， ()223240x x -⋅-=，解得21x =-（舍去）24x =，可得2x =．经检验2x =是方程的解．故答案为：2．【点睛】本题考查方程的解的求法，对数的运算法则的应用，考查计算能力．19．【分析】设转化为函数根据在上单调递增可求解【详解】设函数则函数∵在上单调递增∴当时最小值为故答案为：【点睛】本题考察了二次函数对数函数性质综合解决问题解析：[)3,+∞【分析】设()2261738t x x x =-+=-+，转化为函数2log y t =，[)8,t ∈+∞，根据2log y t =在[)8,t ∈+∞上单调递增，可求解．【详解】设()2261738t x x x =-+=-+函数()22log 617y x x =-+，则函数2log y t =，[)8,t ∈+∞，∵2log y t =，在[)8,t ∈+∞上单调递增，∴当8t =时，最小值为2log 83=，故答案为：[)3,+∞.【点睛】本题考察了二次函数，对数函数性质，综合解决问题． 20．①②④【分析】根据①②③④各个函数的定义域求出各个函数的值域判断正误即可【详解】①中函数的定义域值域;故①不正确;②中函数的定义域是值域;故②不正确;③中函数的值域是则它的定义域可能是故③是正确的; 解析：①②④【分析】根据①、②、③、④各个函数的定义域,求出各个函数的值域,判断正误即可.【详解】①中函数2x y =的定义域{}|0x x ≤,值域2(0,1]x y =∈;故①不正确;②中函数1y x =的定义域是{|2}x x >,值域110,2y x ⎛⎫=∈ ⎪⎝⎭;故②不正确; ③中函数2y x 的值域是{|04}y y ≤≤,则它的定义域可能是{}|22x x -≤≤,故③是正确的;④中函数2log y x =的值域是{|3}y y ≤,∵2log 3,08y x x =≤∴<≤,,故④不正确; 故答案为:①②④.【点睛】本题考查函数的定义域及其求法,函数的值域,指数函数的定义域和值域,对数函数的值域与最值,考查计算能力,属于基础题. 三、解答题21．（1）{|11}x x -<<；（2）函数()f x 是奇函数，证明见解析；（3）当1a >时，01x <<；当01a <<时，10x -<<【分析】（1）根据对数的真数为正数列式可解得结果；（2）函数()f x 是奇函数，根据奇函数的定义证明即可；（3）不等式化为log (1)log (1)a a x x +>-后，分类讨论底数a ，根据对数函数的单调性可解得结果.【详解】（1）要使函数数()f x 有意义，则必有1010x x +>⎧⎨->⎩，解得11x -<<，所以函数()f x 的定义域是{|11}x x -<< .（2）函数()f x 是奇函数，证明如下：∵(1,1)x ∈-，(1,1)x -∈-，()log (1)log (1)a a f x x x -=--+[]log (1)log (1)a a x x =-+--()f x =-，∴函数()f x 是奇函数（3）使()0f x >，即log (1)log (1)a a x x +>-当1a >时，有111010x x x x +>-⎧⎪->⎨⎪+>⎩，解得01x <<，当01a <<时，有111010x x x x +<-⎧⎪->⎨⎪+>⎩，解得10x -<<.综上所述：当1a >时，01x <<；当01a <<时，10x -<<.【点睛】方法点睛：已知函数解析式，求函数定义域的方法：有分式时：分母不为0；有根号时：开奇次方，根号下为任意实数，开偶次方，根号下大于或等于0；有指数时：当指数为0时，底数一定不能为0；有根号与分式结合时，根号开偶次方在分母上时：根号下大于0；有指数函数形式时：底数和指数都含有x ，指数底数大于0且不等于1；有对数函数形式时，自变量只出现在真数上时，只需满足真数上所有式子大于0，自变量同时出现在底数和真数上时，要同时满足真数大于0，底数要大0且不等于1.22．（1）1k =；()f x 为R 上的增函数；（2）存在，176m =. 【分析】（1）根据奇函数的性质和()312f =，代入求函数的解析式，并判断单调性；（2）由（1）可知()()2(2)2log 22221x x x x m g x m ---=+--+⎡⎤⎣⎦，并通过换元22x x t -=-，转化为()()()22log 3m g t t mt -=-+，讨论底数21m ->，和021m <-<两种情况，并讨论内层函数的对称轴和定义域的关系，结合外层函数的单调性，确定内层函数的最值，最后确定函数的最大值求m .【详解】（1）∵函数()x x f x a k a -=-⋅（0a >且1a ≠）是定义域为R 的奇函数，0R ∈，∴(0)0f =，10k -=，∴1k =. 因为3(1)2f =，∴132a a -=，22320a a --=，2a =或12a =-， ∵0a >，∴2a =，()22x x f x -=-，因为2x 为增函数，2x -为减函数，所以()f x 为R 上的增函数.（Ⅱ）()()22(2)log 1x x m g x a a mf x --⎡⎤=+-+⎣⎦()22(2)log 22221x x x x m m ---=+--+⎡⎤⎣⎦()()2(2)log 22223x x x x m m ---⎡⎤=---+⎢⎥⎣⎦，设22x x t -=-，则()()22222233x x x x m t mt -----+=-+， ∵[]1,2x ∈，∴315,24⎡⎤∈⎢⎥⎣⎦t ，记()23h t t mt =-+，（1）当021m <-<，即23m <<时，要使()g x 最大值为0，则要min ()1h t =， ∵22()()(3)24m m h t t =-+-，312m <<，315,24⎡⎤∈⎢⎥⎣⎦t ，∴()h t 在315,24⎡⎤⎢⎥⎣⎦上单调递增，∴min 3213()()242h t h m ==-，由min ()1h t =，得176m =，因17(2,3)6∈，所以176m =满足题意. （2）当21m ->，即3m >时，要使()g x 最大值为0，则要max ()1h t =，且min ()0h t >. ∵322m >， ①若321228m <≤ ，则max 1522515()()314164h t h m ==-+=，25760m =，又2min()()3024m m h t h ==->，∴3m <<25760>∴25760m =不合题意.②若2128m > ，即214m >，则max 32132132121()()02424248h t h m ==-<-⨯=-<，max ()1h t ≠，综上所述，只存在176m =满足题意. 【点睛】关键点点睛：本题考查对数型复合函数根据最值，求参数的取值范围，属于中档题型，本题的第一个关键点是换元化简函数，设22x x t -=-，则()()22222233x x x x m t mt -----+=-+，第二个关键点是需分析外层函数的单调性，并讨论内层函数的对称轴和定义域的关系.23．（1）0；（2）1.【分析】（1）根据指数幂的运算性质，准确运算，即可求解；（2）根据对数的运算性质，准确运算，即可求解.【详解】（1）根据指数幂的运算性质，可得原式22.5311536427110008-⎧⎫⎡⎤⎪⎪⎛⎫⎛⎫⎢⎥=--⎨⎬ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎪⎪⎣⎦⎩⎭ 1521335233431102⎛⎫⨯- ⎪⎝⎭⨯⎡⎤⎡⎤⎛⎫⎛⎫=--⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦531022=--=.（2）由对数的运算性质，可得原式242lg 2lg32lg 2lg311231lg 0.6lg 21lg lg 22410++==⨯++++ 2lg 2lg 32lg 2lg 311lg 2lg 3lg10lg 22lg 2lg 3++===++-++. 【点睛】本题主要考查了指数幂和对数的运算性质的化简、求值，其中解答中熟记指数幂与对数的运算性质，准确运算是解答的关键，着重考查运算与求解能力.24．（1）2()log f x x =（2）偶函数.见解析【分析】（1）根据(4)(2)1f f -=，代入到函数的解析式中可求得2a =，可求得函数()f x 的解析式; （2）由函数()f x 的解析式，求得函数()g x 的解析式，先求得函数()g x 的定义域，再由函数的奇偶性的判断方法证得函数的奇偶性.【详解】（1）因为()log (0,1)a f x x a a =>≠，且(4)(2)1f f -=，所以log 4log 21a a -=，即log 21a =.，解得2a =，所以2()log f x x =;（2）因为()log a f x x =，所以22()log (2)log (2)g x x x =++-,由2020x x +>⎧⎨->⎩,得22x -<<,所以()g x 的定义域为()22-，，又因为22()log (2)log (2)()g x x x g x -=-++=，所以22()log (2)log (2)g x x x =++-为偶函数.【点睛】本题考查对数函数的函数解析式的求解，函数的奇偶性的证明，属于基础题. 25．（1）29-；（2）0【分析】（1）由幂的运算法则计算；（2）根据对数运算法则计算．【详解】（1）原式1240.253271101()6(3)13631291000333-=-++-=-++-=- （2）原式2lg32lg52lg 2lg5(1lg 2)(lg 2)10=++++-2lg5lg 2(lg 2lg5)3330=+++-=-=【点睛】本题考查幂的运算和对数的运算，掌握幂的运算法则和对数运算法则是解题基础．26．[)10,1,2⎛⎤+∞ ⎥⎝⎦【分析】先根据命题p 、q 为真命题时求出对应的实数a 的取值范围，再由题中复合命题的真假判断出p 、q 中一真一假，然后分“p 真q 假”和“p 假q 真”两种情况讨论，进而可求得实数a 的取值范围.【详解】由题知:p 关于x 的不等式1x a >（0a >且1a ≠）的解集是{}0x x <，所以：01a <<. :q函数()2lg 1y ax =+的定义域为R ，等价于x R ∀∈，210ax +>. （i ）当0a =时，不等式10+>在R 上不恒成立；（ii ）当0a ≠时，0240a a >⎧⎨∆=-<⎩，解得12a >. 即1:2q a >. 如果p q ∨为真命题，p q ∧为假命题，则p 真q 假，或p 假q 真，若p 真q 假，则0112a a <<⎧⎪⎨≤⎪⎩，可得102a <≤；若p 假q 真，则0112a a a ≤≥⎧⎪⎨>⎪⎩或，可得1a ≥. 解得102a <≤或1a ≥. 所以，实数a 的取值范围是[)10,1,2⎛⎤⋃+∞ ⎥⎝⎦. 【点睛】本题考查根据复合命题的真假求参数，考查指数函数的单调性以及对数型复合函数的定义域问题，考查运算求解能力，属于中等题.。

北师大版高中数学必修一第三单元《指数函数和对数函数》检测卷(包含答案解析)(1)

一、选择题1．专家对某地区新冠肺炎爆发趋势进行研究发现，从确诊第一名患者开始累计时间t （单位：天）与病情爆发系数()f t 之间，满足函数模型：0.22(50)11()t f t e --=+，当()0.1f t =时，标志着疫情将要大面积爆发，则此时t 约为（）(参考数据： 1.13e ≈) A ．38 B ．40C ．45D ．472．函数()()221lg 21xxx f x -=+的部分图象大致为（）A ．B ．C ．D ．3．已知：23log 2a =，42log 3b =，232c -⎛⎫= ⎪⎝⎭，则a ，b ，c 的大小关系是（） A ．b c a <>B ．c a b >>C ．c b a >>D ．b c a >>6．若函数()()20.3log 54f x x x=+-在区间()1,1a a -+上单调递减，且lg 0.3=b ，0.32c =，则A ．b a c <0，a ≠1)的定义域和值域都是[0，1]，则log a 56＋log a 485＝( ) A ．1B ．2C ．3D ．48．已知2log 0.8a =，0.7log 0.6b =，0.60.7c =，则a ，b ，c 的大小关系是（） A ．a b c <>，则22a c +与2的大小关系是（） A ．222a c +> B ．222a c +≥ C ．222a c +≤D ．222a c +<10．已知函数()sin 2f x x x =-，且()0.3231ln ,log ,223a f b f c f ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，则以下结论正确的是 A ．c a b >> B ．a c b >>C ．a b c >>D ．b a c >>11．已知1()44x f x x -=+-e ，若正实数a 满足3(log )14a f <，则a 的取值范围为（）A ．34a >B ．304a <<或43a >C ．304a <<或1a > D ．1a >12．函数32ln ||()x x f x x-=的图象大致为（）A ．B ．C ．D ．二、填空题13．已知函数()1122,121,1x x x f x x x --⎧-≤⎪=⎨-->⎪⎩，则关于x 的不等式()()10f x f x -+≤的解集为___________________． 14．现有下列四个结论：①若25a b m ==且a b =时，则1m =； ②若236log log log a b c ==，则c ab =；③对函数()3xf x =定义域内任意的1x ，都存在唯一的2x ，使得()()121f x f x ⋅=成立；④存在实数a ，使得函数()()2ln g x x ax a =++的定义域和值域均为R .其中所有正确结论的序号是_________.15．测量地震级别的里氏震级M 的计算公式为:0lg lg M A A =-，其中A 是测震仪记录的地震曲线的最大振幅，常数A 0是相应的标准地震的振幅.假设在一次地震中，测震仪记录的最大振幅是1000，而此次地震的里氏震级恰好为6级，那么里氏9级地震的最大的振幅是里氏5级地震最大振幅的______倍.16．已知函数()()212log 23f x x ax =-+，若函数的增区间是(),1-∞，则实数a =______.17．函数()()cos1log sin f x x =的单调递增区间是____________. 18．给出下列命题：①函数2x y =与2log y x =互为反函数，其图象关于直线y x =对称； ②已知函数2(1)21f x x x -=-+，则(5)26f =；③当0a >且1a ≠时，函数()log (2)3a f x x =--的图像必过定点(3,3)-； ④用二分法求函数()ln 26f x x x =+-在区间(2,3)内的零点近似值，至少经过3次二分后精确度达到0.1；⑤函数2()2x f x x =-的零点有2个. 其中所有正确命题．．．．的序号是______ 19．下列结论正确的是____________①1()2(0,1)x f x a a a -=+>≠的图像经过定点(1,3)； ②已知28log 3,43yx ==，则2x y +的值为3； ③若3()6f x x ax =+-，且(2)6f -=，则(2)18f =；④11()()122x f x x =--为偶函数； ⑤已知集合{}{}1,1,|1A B x mx =-==；且B A ⊆，则m 的值为1或-1.20．设函数()f x 满足()22221x f x ax a =-+-，且()f x 在21222,2a aa --+⎡⎤⎣⎦上的值域为[]1,0-，则实数a 的取值范围为______.三、解答题21．已知函数1()log 1a mxf x x -=-（0a >且1a ≠）是奇函数．（1）求实数m 的值；（2）若关于x 的方程2()6(1)50f x kx x a -+--=对(1,)x ∈+∞恒有解，求k 的取值范围．22．已知函数122()log 2xf x x-=+．（1）求函数()f x 的定义域，并判断其奇偶性；（2）判断()f x 在其定义域上的单调性，并用单调性定义证明． 23．已知函数()f x 是定义在()(),00,-∞⋃+∞上的偶函数，当0x >时，()232f x ax ax =-+，（a R ∈）.（1）求()f x 的函数解析式：（2）当1a =时，求满足不等式()21log f x >的实数x 的取值范围.24．设函数101(),2axf x a -⎛⎫= ⎪⎝⎭是常数，且1(3)2f =. （1）求a 的值；（2）求使得()4f x ≥的x 值的取值范围.（3）设1(),2g x x m =-+对于区间[]34，上的每一个x 值，不等式()()f x g x >恒成立，求实数m 的取值范围.25．已知指数函数()x f x a =（0a >，且1a ≠）的图象过点12,4⎛⎫ ⎪⎝⎭．（1）求函数的解析式；（2）设函数()(1)1g x f x =--，(0)x ≥，求函数()g x 的值域． 26．设函数()log (0,1)a f x x a a =>≠. （1）解不等式(26)(5)f a f a +；（2）已知对任意的实数()23,14m f m m f ⎛⎫++ ⎪⎝⎭恒成立，是否存在实数k ，使得对任意的[1,0]x ∈-，不等式()()142240x x xf f k ++--⋅>恒成立，若存在，求出k 的范围；若不存在，请说明理由.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】根据()0.1f t =列式求解即可得答案.【详解】解：因为()0.1f t =，0.22(50)11()t f t e --=+，所以0.22(50)()0.111t f t e--==+，即0.22(50)011t e --=+，所以0.22(50)9t e --=，由于 1.13e ≈，故()21.12.29e e =≈，所以0.222().250t e e --=，所以()0.2250 2.2t --=，解得40t =. 故选：B. 【点睛】本题解题的关键在于根据题意得0.22(50)9t e --=，再结合已知 1.13e ≈得()21.12.29e e =≈，进而根据0.222().250t e e --=解方程即可得答案，是基础题.2．B解析：B 【分析】求出函数()f x 的定义域，分析函数()f x 的奇偶性及其在区间()0,1上的函数值符号，进而可得出合适的选项. 【详解】函数()()221lg 21xxx f x -=+的定义域为{}0x x ≠，()()()()()()()22221lg 221lg 12lg 2112221x x x xx xxxx x x f x f x ---------====-+++，函数()f x 为奇函数，当01x <<时，201x <<，则2lg 0x <，210x ->，210x +>，()0f x ∴<.因此，函数()f x 的图象如B 选项中的图象. 故选：B. 【点睛】函数图象的辨识可从以下方面入手：（1）从函数的定义域，判断图象的左右位置；（2）从函数的值域，判断图象的上下位置．（3）从函数的单调性，判断图象的变化趋势；（4）从函数的奇偶性，判断图象的对称性；（5）从函数的特征点，排除不合要求的图象.3．A解析：A 【分析】由换底公式和对数函数的性质可得112b a <<<，再由指数函数的性质可得102c <<，即可得解. 【详解】23ln3ln12log =02ln 2ln 2a ==>，4212ln ln 2ln1323log =03ln 4ln 2ln 2b ====<， a b ∴>22223231log log 410,239222a c -⎛⎫⎛⎫<===< ⎪ ⎪⎭=⎝>⎭=⎝，b c a ∴<<，故选：A 【点睛】方法点睛：本题考查了对数式、指数式的大小比较，比较大小的常用方法为同底的对数式和指数式利用其单调性进行比较，也可以借助于中间值0和1进行比较，考查了运算求解能力与逻辑推理能力，属于常考题.4．A解析：A 【分析】根据题意，由(3)()f x f x +=可得()f x 是周期为3的周期函数，则有(2021)f f =（2），结合函数的解析式计算可得答案. 【详解】根据题意，定义在R 上的函数()f x 满足(3)()f x f x +=，则()f x 是周期为3的周期函数，则(2021)(23673)(2)f f f =+⨯=，又由当(1x ∈，3]时，4()log f x x =，则f （2）41log 22==，故1(2021)2f =，故选：A. 【点睛】关键点点睛：根据函数的周期性将(2021)f 化为(2)f ，再利用函数解析式求值是解题关键.5．A解析：A 【分析】根据指数函数、对数函数的性质结合中间值0和1比较．【详解】由指数函数性质得0.34015⎛⎫<< ⎪⎝⎭，0.2514⎛⎫> ⎪⎝⎭，由对数函数性质得125log 04<， ∴b a c >>．故选：A ．【点睛】本题考查比较幂与对数的，掌握指数函数与对数函数的性质是解题关键．解题方法是借助中间值比较大小．6．A解析：A 【分析】求出原函数的定义域，再求出内函数二次函数的增区间，由题意列关于a 的不等式组，求得a 的范围，结合b=1g0.3＜0，c=20.3＞1得答案．【详解】由5+4x-x 2＞0，可得-1＜x ＜5，函数t=5+4x-x 2的增区间为（-1，2），要使f(x)＝log 0.3(5+4x−x 2)在区间（a-1，a+1）上单调递减，则1112a a -≥-⎧⎨+≤⎩，即0≤a≤1．而b=1g0.3＜0，c=20.3＞1， ∴b ＜a ＜c ．故选A ．【点睛】本题主要考查了复合函数的单调性以及单调区间的求法．对应复合函数的单调性，一要注意先确定函数的定义域，二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断，判断的依据是“同增异减”，是中档题．7．C解析：C 【分析】先分析得到a ＞1，再求出a =2,再利用对数的运算求值得解. 【详解】由题意可得a －a x ≥0，a x ≤a ，定义域为[0，1]，所以a >1，y ＝x a a -在定义域为[0，1]上单调递减，值域是[0，1]，所以f (0)＝1a -＝1，f (1)＝0，所以a ＝2，所log a 56＋log a 485＝log 256＋log 2485＝log 28＝3. 故选C 【点睛】本题主要考查指数和对数的运算，考查函数的单调性的应用，意在考查学生对这些知识的理解掌握水平，属于基础题.8．C解析：C 【解析】因为22log 0.8log 10a =<=，0.70.7log 0.6log 0.71b =>=，0.6000.70.71c <=<=，所以a c b <<，故选C.9．D解析：D 【分析】运用分段函数的形式写出()f x 的解析式，作出()21xf x =-的图象，由数形结合可得0c <且0a >，21c <且21a >，且()()0f c f a ->，去掉绝对值，化简即可得到结论．【详解】()21,02112,0x xxx f x x ⎧-≥=-=⎨-<⎩，作出()21xf x =-的图象如图所示，由图可知，要使c b a <<且()()()f c f a f b >>成立，则有0c <且0a >，故必有21c <且21a >，又()()0f c f a ->，即为()12210c a--->，∴222a c +<．故选：D ．【点睛】本题考查指数函数单调性的应用，考查用指数函数单调性确定参数的范围，本题借助函数图象来辅助研究，由图象辅助研究函数性质是函数图象的重要作用，以形助数的解题技巧必须掌握，是中档题．10．D解析：D 【解析】因为()cos 20f x x '=-<，所以函数()sin 2f x x x =-的单调递减函数，又因为0.3213log 0,ln ln 1,12232e <<=<<，即0.3213log ln 232<<，所以由函数的单调性可得：0.3213(log )(ln )(2)32f f f >>，应选答案D ．11．C解析：C 【分析】先判断1()44x f x x -=+-e 是R 上的增函数，原不等式等价于3log 14a <，分类讨论，利用对数函数的单调性求解即可. 【详解】因为1x y e -=与44y x =-都是R 上的增函数，所以1()44x f x x -=+-e 是R 上的增函数，又因为11(1)441f e -=+-=所以()3(log )114af f <=等价于3log 14a <，由1log a a =，知3log log 4aa a <, 当01a <<时，log a y x =在()0,∞+上单调递减，故34a <，从而304a <<；当1a >时，log ay x =在()0,∞+上单调递增，故34a >，从而1a >，综上所述， a 的取值范围是304a <<或1a >，故选C. 【点睛】解决抽象不等式()()f a f b <时，切勿将自变量代入函数解析式进行求解，首先应该注意考查函数()f x 的单调性．若函数()f x 为增函数，则a b <；若函数()f x 为减函数，则a b >．12．A解析：A 【分析】判断奇偶性可排除两个选项，再确定函数值的变化趋势排除一个，得出正确选项．【详解】解：函数的定义域为{0}xx ≠∣，因为3322()ln ||ln ||()()()x x x x f x f x x x-----===-，所以()f x 为偶函数，所以排除C ,D,又因为当0x >时，322ln ln ()x x xf x x x x-==-，当x →+∞时，()f x →+∞，所以排除B故选：A. 【点睛】本题考查由函数解析式选择函数图象，解题方法是排除法，即通过判断函数的性质，特殊的函数值或函数值的变化趋势等，排除错误选项，得出正确答案．二、填空题13．【分析】对自变量分情况讨论即然后对各种情况分别解不等式最后取并集；【详解】当时所以由此时不等式恒成立；当时则由则此时不等式恒成立；当时符合题意；当时解得∴综上可得不等式的解集为故答案为：【点睛】关键解析：7,2⎛⎤-∞ ⎥⎝⎦ 【分析】对自变量分情况讨论，即1x ≤，12x <≤，23x <<，3x ≥，然后对各种情况分别解不等式，最后取并集；【详解】当1x ≤时，10x -≤，121x -≤，121x -≥，所以()11220x x f x --=-≤由2122x -≤，222x -≥，()221220x xf x ---=-<，此时不等式()()10f x f x +-≤恒成立；当12x <≤时，()212110f x x x x =--=--=-<，011x <-≤，则()22122x xf x ---=-，由221x -≤，221x -≥，则()10f x -≤此时不等式()()10f x f x +-≤恒成立；当23x <<时，()()12131f x f x x x +-=--+--213110x x =--+--=-<，符合题意；当3x ≥时，()()12131270f x f x x x x +-=--+--=-≤，解得72x ≤， ∴732x ≤<．综上可得，不等式()()10f x f x +-<的解集为7,2⎛⎤-∞ ⎥⎝⎦．故答案为：7,2⎛⎤-∞ ⎥⎝⎦【点睛】关键点睛：本题考查分别函数解不等式的问题，涉及分类讨论思想的应用，解答本题的关键是对自变量x 的范围进行分类，即1x ≤，12x <≤，23x <<，3x ≥，从而得出()f x 和()1f x -的表达式，从而求解不等式，属于中档题.14．①②③【分析】利用换底公式结合求得的值可判断①的正误；设利用对数与指数的互化以及指数的运算性质可判断②的正误；由求得可判断③的正误；求出函数的定义域值域分别为时对应的实数的取值范围可判断④的正误【详解析：①②③ 【分析】利用换底公式结合a b =，求得m 的值，可判断①的正误；设236log log log a b c t ===，利用对数与指数的互化以及指数的运算性质可判断②的正误；由()()121f x f x ⋅=求得21x x =-，可判断③的正误；求出函数()g x 的定义域、值域分别为R 时，对应的实数a 的取值范围，可判断④的正误. 【详解】对于①，由于250abm ==>，可得2lg log lg 2m a m ==，5lg log lg 5mb m ==，由于a b =可得lg lg lg 2lg 5m m=，则lg 0m =，解得1m =，①正确；对于②，设236log log log a b c t ===，可得2t a =，3t b =，6t c =，则236t t t ab c =⋅==，②正确；对于③，对任意的1x R ∈，则()()1212123331xxx x f x f x +⋅=⋅==，120x x ∴+=，可得21x x =-，③正确；对于④，若函数()()2ln g x x ax a =++的定义域为R ，对于函数2y x ax a =++，240a a ∆=-<，解得01a <<；若函数()()2ln g x x ax a =++的值域为R ，则函数2y x ax a =++的值域包含()0,∞+，则240a a ∆=-≥，解得0a ≤或1a ≥.所以，不存在实数a ，使得函数()()2ln g x x ax a =++的定义域和值域均为R ，④错误.故答案为：①②③. 【点睛】关键点点睛：解本题第④问的关键点在于找到函数()()2ln g x x ax a =++的定义域为R的等价条件∆<0；函数()()2ln g x x ax a =++的值域为R 的等价条件0∆≥.15．10000【分析】根据条件先计算出的值然后分别计算出里氏9级地震的最大的振幅和里氏5级地震最大振幅由此可求解出最终结果【详解】由条件可知：所以设里氏9级地震的最大的振幅为里氏5级地震最大振幅为所以所解析：10000 【分析】根据条件先计算出0A 的值，然后分别计算出里氏9级地震的最大的振幅和里氏5级地震最大振幅，由此可求解出最终结果. 【详解】由条件可知：06lg1000lg A =-，所以3010A -=，设里氏9级地震的最大的振幅为1A ，里氏5级地震最大振幅为2A ，所以31329lg lg105lg lg10A A --⎧=-⎨=-⎩，所以621210,10A A ==，所以1210000A A =，故答案为：10000. 【点睛】关键点点睛：解答本题的关键在于理解公式0lg lg M A A =-中各个量的含义并先求解出0A 的值，由此继续分析.16．1或2【分析】因为函数在上单调递减要使的单调增区间为分两种情况讨论对称轴和对称轴分别计算可得；【详解】解：因为函数在上单调递减要使的单调增区间为①当函数对称轴为时因为所以恒成立满足条件②当函数对称轴解析：1或2 【分析】因为函数12log y x =在()0,∞+上单调递减，要使()()212log 23f x x ax =-+的单调增区间为(),1-∞，分两种情况讨论，对称轴1x =和对称轴1x a =>，分别计算可得；【详解】解：因为函数12log y x =在()0,∞+上单调递减，要使()()212log 23f x x ax =-+的单调增区间为(),1-∞，①当函数()223g x x x a =-+对称轴为1x a ==时，因为()22430∆=--⨯<，所以2230x ax -+>恒成立，满足条件，②当函数()223g x x x a =-+对称轴1x a =>时，需满足()10g =，即21230a -+=解得2a =；综上可得1a =或2 故答案为：1或2 【点睛】本题考查复合函数的单调性判断，已知函数的单调性求参数的取值范围，属于中档题.17．【分析】根据对数型复合函数单调性列不等式再根据正弦函数性质得结果【详解】单调递增区间为单调递减区间且所以故答案为：【点睛】本题考查对数型复合函数单调性以及正弦函数性质考查基本分析求解能力属基础题解析：[2,2),()2k k k Z ππππ++∈【分析】根据对数型复合函数单调性列不等式，再根据正弦函数性质得结果. 【详解】()()cos1cos1(0,1)log sin f x x ∈∴=单调递增区间为sin y x =单调递减区间且sin 0x >，所以22,()2k x k k Z ππππ+≤<+∈，故答案为：[2,2),()2k k k Z ππππ++∈【点睛】本题考查对数型复合函数单调性以及正弦函数性质，考查基本分析求解能力，属基础题.18．①③【分析】①求解出的反函数再根据反函数的特点进行判断；②采用换元法求解出的解析式由此计算出的值并进行判断；③分析当对数式的真数为时此时的值由此确定出函数所过定点并进行判断；④根据每经过一次操作区间解析：①③ 【分析】①求解出2x y =的反函数，再根据反函数的特点进行判断；②采用换元法求解出()f x 的解析式，由此计算出()5f 的值并进行判断；③分析当对数式的真数为1时，此时,x y 的值，由此确定出函数所过定点并进行判断； ④根据每经过一次操作区间长度变为原来的一半，由此列出关于次数的不等式，求解出次数的范围并进行判断；⑤根据()()2,4f f 的值以及零点的存在性定理进行判断. 【详解】①令2y x =，所以2log y x =，所以函数2x y =与2log y x =互为反函数，则图象关于y x =对称，故正确；②令1x t -=，则1x t =+，所以()()()221211f t t t t =+-++=，所以()2f x x =，所以()525f =，故错误；③令21x -=，所以3x =，所以()3log 133a f =-=-，所以()f x 过定点()3,3-，故正确；④因为区间()2,3的长度为1，经过n 次操作过后区间长度变为12n ，所以10.12n≤，所以4n ≥，故错误；⑤因为()()22422220,4240f f =-==-=，且()()()21011210,020102f f --=--=-<=-=>，所以()f x 在()1,0-上有零点，所以()f x 的零点至少有3个，故错误；故答案为：①③. 【点睛】结论点睛：（1）同底数的指数函数和对数函数互为反函数，图象关于y x =对称；（2）形如()()()log 0,1a f x g x b a a =+>≠的图象过定点问题，可考虑令()1g x =，由此求解出x 的值，从而对应的()f x 的值可求，则定点坐标可求；（3）利用二分法求解函数零点的近似值时，每进行一次操作，区间长度会变为原来的一半.19．①②④【分析】①根据指数函数的性质进行判断②根据对数的运算法则进行判断③根据函数的运算性质进行运算④根据偶函数的定义进行判断⑤根据集合关系利用排除法进行判断【详解】①当时（1）则函数的图象经过定点；解析：①②④ 【分析】①根据指数函数的性质进行判断，②根据对数的运算法则进行判断，③根据函数的运算性质进行运算，④根据偶函数的定义进行判断，⑤根据集合关系，利用排除法进行判断．【详解】①当1x =时，f （1）02123a =+=+=，则函数的图象经过定点(1,3)；故①正确， ②已知2log 3x =，843y=，则2823y=，282log 3y =，则2222882log 3log log (3)log 8333x y +=+=⨯==；故②正确， ③若3()6f x x ax =+-，且(2)6f -=，则32266a ---=，即10a =-，则f （2）32210618=-⨯-=-，故③错误；④函数的定义域为{|0}x x ≠，关于原点对称，1112()()?1222(12)xx x f x x x +=-=--，则122112()?··()2(12)2(21)2(12)x x xx x xf x x x x f x --+++-=-=-==---，即()f x 为偶函数，故④正确，⑤已知集合{1A =-，1}，{|1}B x mx ==，且B A ⊆，当0m =时，B =∅，也满足条件，故⑤错误，故正确的是①②④，故答案为：①②④ 【点睛】本题主要考查命题的真假判断，涉及指数函数的性质，函数奇偶性的判断，以及对数的运算法则，综合性较强，涉及的知识点较多．20．【分析】利用换元法可得然后采用等价转换的方法可得在的值域为最后根据二次函数的性质可得结果【详解】由令所以则令由在上的值域为等价为在的值域为的对称轴为且所以可得或所以故答案为：【点睛】本题主要考查函数解析：⎤⎡⋃⎥⎢⎣⎦⎣⎦【分析】利用换元法，可得()2221g x x ax a =-+-，然后采用等价转换的方法，可得()g x 在21,22a a a ⎡⎤--+⎣⎦的值域为[]1,0-，最后根据二次函数的性质，可得结果.【详解】由()22221xf xax a =-+-令22,log xt x t ==，所以()()2222log 2log 1f t t a t a =-+- 则令()2221g x x ax a =-+-由()f x 在21222,2a a a --+⎡⎤⎣⎦上的值域为[]1,0-等价为()g x 在21,22a a a ⎡⎤--+⎣⎦的值域为[]1,0-()g x 的对称轴为x a =，且()()1,10g a g a =--=所以()()22122222a a a a a a -+-+≤≤-+可得312a ≤≤或322a +≤≤所以332,22a ⎡⎤⎡∈⋃⎢⎥⎢⎣⎦⎣⎦故答案为：332,22⎡⎤⎡-⋃⎢⎥⎢⎣⎦⎣⎦【点睛】本题主要考查函数值域的应用，难点在于使用等价转换思想，使问题化繁为简，属中档题.三、解答题21．（1）1m =-；（2）(0,7)．【分析】（1）由函数()f x 为奇函数，则()()f x f x -=-，可得()2210m x -=，从而求出m 的值.(2)由（1）即将原问题化为2610kx x --=对(1,)x ∈+∞恒有解，即216k x x=+，令1t x =，则26k t t =+，(0,1)t ∈有解，从而得出答案. 【详解】解：（1）因为函数()f x 为奇函数，则()()f x f x -=-，即11log log 11a a mx mxx x +-=---- 化简得()2210m x-=，所以1m =±，当1m =时1101mx x +=-<--不成立，当1m =-时1111mx x x x +-=--+，经验证成立所以1m =-．（2）由（1）知函数1()log 1ax f x x +=-，则方程可化为： 216(1)501x kx x x +-+--=-，即2610kx x --=对(1,)x ∈+∞恒有解所以分离参数得216k x x=+，令1t x =，则26k t t =+，(0,1)t ∈有解而2067t t <+<，故k 的取值范围为(0,7)．【点睛】关键点睛：本题考查根据函数为奇函数求参数和不等式有解求参数的范围，解答本题的关键是将问题转化为2610kx x --=对(1,)x ∈+∞恒有解，分离参数即216k x x=+在(1,)x ∈+∞恒有解，属于中档题.22．（1）定义域为(2,2)-，奇函数（2）函数()f x 在(2,2)-上为增函数，证明见解析【分析】（1）根据真数大于0可得定义域，根据奇函数的定义可得函数为奇函数；（2）设1222x x -<<<，根据对数函数的单调性可得12()()f x f x <，再根据定义可证函数()f x 在(2,2)-上为增函数. 【详解】（1）由函数有意义得202xx->+，解得22x -<<，所以函数的定义域为(2,2)-，因为1112222()log log ()22x x f x f x x x -+-⎛⎫-===- ⎪-+⎝⎭，所以函数为奇函数. （2）因为124()log 12f x x ⎛⎫=-+ ⎪+⎝⎭，所以函数()f x 在(2,2)-上为增函数，证明：设1222x x -<<<，则120224x x <+<+<，则1244122x x >>++，则124411022x x -+>-+>++，因为1012<<，所以12()()f x f x <，所以函数()f x 在(2,2)-上为增函数，【点睛】思路点睛：判断函数的奇偶性的思路： ①求出定义域，并判断其是否关于原点对称；②若定义域不关于原点对称，则函数为非奇非偶函数，若定义域关于原点对称，再判断()f x -与()f x 的关系，若()()f x f x -=-，则函数为奇函数；若()()f x f x -=，则函数为偶函数.23．（1）()2232,032,0ax ax x f x ax ax x ⎧-+>=⎨++<⎩；（2）()()()()3,21,00,12,3---.【分析】（1）根据已知和函数的奇偶性可得0x <的解析式从而求得()f x ；（2）当1a =时，分别解每一段小于1的不等式，最后求两段的并集可得答案. 【详解】（1）设0x <，0x ->，()232f x ax ax -=++，又∵()f x 为偶函数，()()f x f x -=，∴()232f x ax ax =++.综上：()2232,032,0ax ax x f x ax ax x ⎧-+>=⎨++<⎩. （2）当1a =时，可知：0x >，()2232log 1x x -<+，原不等式等价于22320322x x x x ⎧-+>⎨-+<⎩，解得()()0,12,3x ∈，同理可知：0x <，()2232log 1x x +<+，原不等式等价于22320322x x x x ⎧++>⎨++<⎩，解得()()1,03,2x ∈---，综上：实数x 的取值范围为()()()()3,21,00,12,3---.【点睛】求分段函数的解析式，要根据函数的奇偶性、对称性、周期性等结合已知条件进行求解，要注意定义域.24．（1）3；（2）4x ≥；（3）2m < 【分析】（1）由1(3)2f =代值运算可求a ；（2）求得310()2x f x -=，结合指数函数增减性解不等式，即可求解x 值的取值范围；（3）分析函数()(),f x g x 增减性，结合端点值解不等式即可【详解】（1）因为10311(3)22af -⎛⎫==⎪⎝⎭，故3a =；（2）由（1）知1033101()22xx f x --⎛⎫== ⎪⎝⎭，故()4f x ≥等价于310222x -≥，解得4x ≥；（3）()f x 在[]34，单增，1()2g x x m =-+在[]34，单减，要使区间[]34，上的每一个x 值，不等式()()f x g x >恒成立，则需满足()()33f g >，即11322m >-⨯+，解得2m <【点睛】本题考查指数型函数解析式、指数不等式的求解，由函数在定区间恒成立问题求解参数取值范围，属于中档题25．（1）1()2xf x ⎛⎫= ⎪⎝⎭；（2）(]1,1-．【分析】（1）利用待定系数法求出参数a 的值，即可求出函数解析式；（2）由（1）可知11()12x g x -⎛⎫=- ⎪⎝⎭，再结合指数函数的性质计算可得；【详解】解：（1）设()x f x a =（0a >，且1a ≠），因为其图象过点12,4⎛⎫ ⎪⎝⎭，则214a =，计算得：12a =±，∵0a >，且1a ≠，∴12a =，所以1()2xf x ⎛⎫= ⎪⎝⎭．（2）依题意可知11()12x g x -⎛⎫=- ⎪⎝⎭，由函数1()2xf x ⎛⎫= ⎪⎝⎭为减函数可知：函数11()12x g x -⎛⎫=- ⎪⎝⎭(0)x ≥为减函数，当0x =时，max 1y =；又1102x -⎛⎫> ⎪⎝⎭，∴11112x -⎛⎫->- ⎪⎝⎭，所以()g x 的值域为(]1,1-．【点睛】本题考查待定系数法求函数解析式，以及指数函数的性质的应用，属于中档题. 26．（1）(0,1)[2,)a ∈⋃+∞（2）实数k 不存在，详见解析【分析】（1）分类讨论，利用对数函数的单调性，将不等式具体化，解不等式即可；（2）判断函数()f x 为增函数，将不等式具体化，再分离参数求最值，即可得出结论. 【详解】解：（1）当01a <<时，有2650a a +>，解得02a <≤，即(0,1)∈a ；当1a >时，有0265a a <+，解得2a ，即[2,)a ∈+∞. 综上可知，(0,1)[2,)a ∈⋃+∞.（2）由于221331244m m m ⎛⎫++=++⎪⎝⎭，且()2314f m m f ⎛⎫++ ⎪⎝⎭，可知()f x 为增函数. ()()142240x x x f f k ++--⋅>，即()()14224x x x f f k ++>-⋅，则有14224x x x k ++>-⋅在[1,0]-上恒成立，即1342x x k +<⋅+在[1,0]-上恒成立，令12,12xt ⎡⎤=∈⎢⎥⎣⎦，设2()32,()g t t t g t =+在1,12⎡⎤⎢⎥⎣⎦上单调递增，则min 17()24g t g ⎛⎫== ⎪⎝⎭，即74k <.又由于[1,0]x ∈-时，240x k -⋅>恒成立，解得2k >，故符合题意的实数k 不存在. 【点睛】本题考查对数函数的单调性、恒成立问题的转化分析、指数函数与二次函数的复合函数的最值问题.。

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试(含答案解析)

一、选择题1．函数()212()log 23f x x x =--+单调减区间为（） A ．(,1]-∞- B ．(3,1]--C ．[)1,1-D ．[)1-+∞， 2．已知函数()()2log 2xf x m =+，则满足函数()f x 的定义域和值域都是实数集R 的实数m 构成的集合为（） A ．{}|0m m =B ．{}0|m m ≤C ．{}|0m m ≥D ．{}|1m m =3．已知定义在R 上的函数()f x 满足(3)()f x f x +=，且当(1x ∈，3]时，4()log f x x =，则(2021)f =（）A ．12B ．0C ．4log 3D ．14．函数()213log 23y x x =-++的单调递增区间是（） A ．(]1,1- B ．(1)∞－，C ．[) 1,3D ．(1)∞，＋ 5．已知函数()f x 是定义在R 上的单调递增的函数，且满足对任意的实数x 都有[()3]4x f f x -=，则()()f x f x +-的最小值等于（）.A ．2B ．4C ．8D ．126．已知函数()y f x =与x y e =互为反函数，函数()y g x =的图象与()y f x =的图象关于x 轴对称，若()1g a =，则实数a 的值为 A ．e -B ．1e-C ．eD ．1e7．已知函数()2,01,0x x f x x x >⎧=⎨+≤⎩，若()()10f a f +=，则实数a 的值等于（）A ．-3B ．-1C ．1D ．3 8．若a ＞b ＞0，0＜c ＜1，则 A ．log a c ＜log b c B ．log c a ＜log c b C ．a c ＜b c D ．c a ＞c b9．函数213()log 4f x x =-的单调减区间是（）A ．(]()2,02,-+∞B ．(]2,0-和(2,)+∞ C ．(),20,2[)-∞-D ．(,2)-∞-和[0,2)10．已知对数函数()log a f x x =是增函数，则函数(||1)f x +的图象大致是A ．B ．C ．D ．11．实数,a b 满足2510a b ==，则下列关系正确的是（） A ．212a b+= B ．111a b+= C ．122a b+= D ．1212a b += 12．已知函数()22xa xf x -=+的图象关于直线1x =对称，若()log ,04,6,46a x x g x x x ⎧<≤=⎨-<≤⎩且123x x x <<，()()()123g x g x g x ==，则123x x x 的取值范围为（） A ．()0,2B ．()0,4C ．()4,6D ．(]4,6二、填空题13．已知函数f (x )＝3x ＋x ，g(x )＝log 3x ＋2，h (x )＝log 3x ＋x 的零点依次为a ，b ，c ，则a ，b ，c 的大小关系是________.14．函数()()cos1log sin f x x =的单调递增区间是____________.15．函数()()()212log 24f x ax x a R =-+∈，若()f x 的值域为(],1-∞，则a 的值为______.16．定义在(,0)(0,)-∞+∞上的函数1,0(),0x x e x f x e m x -⎧->=⎨+<⎩是奇函数，则实数m 的值为______．17．已知函数f （x ）＝[log a （x +2）]+3的图象恒过定点（m ，n ），且函数g （x ）＝mx 2﹣2bx +n 在[1，+∞）上单调递减，则实数b 的取值范围是________. 18．设函数()22x f x =+，则()()()()()()543456f f f f f f -+-+-++++=_____.19．已知27abm ==，1112a b +=，则m =_______. 20．设函数()f x 满足()22221xf x ax a =-+-，且()f x 在21222,2a a a --+⎡⎤⎣⎦上的值域为[]1,0-，则实数a 的取值范围为______.三、解答题21．计算下列各式的值：（1）3224031168()281π-⎛⎫⎛⎫-+- ⎪⎪⎝⎭⎝⎭；（2）()2log 1483log 3log 3log 22+⨯+.22．化简与求值：（1）2ln 43(0.125)e-++；（2）若1122x x -+=1x x --的值.23．（1）求满足不等式221139x x --⎛⎫> ⎪⎝⎭的x 的取值集合；（2）求函数235()log (45)f x x x =--的单调递减区间. 24．已知函数()lg(3)f x ax =-的图像经过定点(2,0)． (1)求a 的值；(2)设(3),(5)f m f n ==，求21log 63（用,m n 表示）； 25．已知函数1()log a f x a x ⎛⎫=-⎪⎝⎭，其中实数0a >且1a ≠. （1）当3a =时，求不等式()0f x >的解集；（2）若()f x 在区间[1,3]上单调递增，求a 的取值范围； 26．函数()2lg 34y x x=-+的定义域为M ，x M ∈，求()2234x x f x +=-⨯的最值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】根据复合函数的单调性可知，()()212log 23f x x x =--+的单调减区间为223t x x =--+在定义域上的单调增区间.再根据一元二次函数的单调性求单调增区间即可. 【详解】解：函数()()212log 23f x x x =--+的定义域为()3,1- 令223t x x =--+，则()12log g t t =为单调递减函数，由复合函数的单调性可知：()f x 的单调递减区间为223t x x =--+在()3,1-上的单调增区间.()222314t x x x =--+=-++，对称轴为1x =-，开口向下，所以223t x x =--+的单调增区间为(]3,1--. 故选：B. 【点睛】本题考查复合函数的单调性，属于中档题. 方法点睛：（1）先求出函数的定义域；（2）判断外层函数的单调性；（3）根据复合函数同增异减的原则，判断要求的内层函数的单调性；（4）求出单调区间.2．A解析：A 【分析】若定义域为实数集R ，则20x m +>对于x ∈R 恒成立，可得0m ≥，若值域为实数集R ，令2x t m =+，则2log y t = 此时需满足2x t m =+的值域包括()0,∞+，可得0m ≤，再求交集即可. 【详解】若()()2log 2xf x m =+定义域为实数集R ，则20x m +>对于x ∈R 恒成立，即2x m >-对于x ∈R 恒成立，因为20x >，所以20x -<，所以0m ≥，令2x t m =+，则2log y t =若()()2log 2xf x m =+值域为实数集R ，则2x t m =+的值域包括()0,∞+，因为t m >，所以0m ≤，所以0m =，故选：A 【点睛】关键点点睛：本题的关键点是要找到定义域为R 的等价条件即20x m +>对于x ∈R 恒成立，分离参数m 求其范围，值域为R 的等价条件即2x t m =+可以取遍所有大于0的数，由t m >，所以0m ≤，再求交集.3．A解析：A 【分析】根据题意，由(3)()f x f x +=可得()f x 是周期为3的周期函数，则有(2021)f f =（2），结合函数的解析式计算可得答案. 【详解】根据题意，定义在R 上的函数()f x 满足(3)()f x f x +=，则()f x 是周期为3的周期函数，则(2021)(23673)(2)f f f =+⨯=，又由当(1x ∈，3]时，4()log f x x =，则f （2）41log 22==，故1(2021)2f =，故选：A. 【点睛】关键点点睛：根据函数的周期性将(2021)f 化为(2)f ，再利用函数解析式求值是解题关键.4．C解析：C 【分析】由不等式2230x x -++>，求得函数的定义域()1,3-，令()223g x x x =-++，得到()g x 在区间(]1,1-上单调递增，在区间[1,3)上单调递减，结合复数函数的单调性的判定方法，即可求解. 【详解】由题意，函数213()log 23y x x =-++有意义，则满足2230x x -++>，即223(3)(1)0x x x x --=-+<，解得13x，即函数的定义域为()1,3-，令()223g x x x =-++，则函数()g x 表示开口向下，对称轴方程为1x =的抛物线，所以函数()g x 在区间(]1,1-上单调递增，在区间[1,3)上单调递减，又由函数13log y x =在定义上是递减函数，结合复数函数的单调性的判定方法，可得函数213()log 23y x x =-++的递增区间为[1,3).故选：C. 【点睛】函数单调性的判定方法与策略：定义法：一般步骤：设元→作差→变形→判断符号→得出结论；图象法：如果函数()f x 是以图象形式给出或函数()f x 的图象易作出，结合图象可求得函数的单调区间；导数法：先求出函数的导数，利用导数值的正负确定函数的单调区间；复合函数法：先将函数(())y f g x =分解为()y f t =和()t g x =，再讨论这两个函数的单调性，最后根据复合函数“同增异减”的规则进行判定.5．B解析：B 【分析】根据()3x f x -为定值，可假设()3x f x m =+，然后计算()()f x f x +-，并计算m 的值，然后使用基本不等式，可得结果. 【详解】由题可知：()3x f x -为定值故设()3xf x m -=，即()3x f x m =+ 又[()3]4xf f x -=，所以()341m f m m m =+=⇒= 则()31x f x =+()()3131x x f x f x -+-=+++则1()()32243x x f x f x +-=++≥= 当且仅当133xx=时，取等号所以()()f x f x +-的最小值为：4故选：B 【点睛】本题考查基本不等式的应用，还考查镶嵌函数的应用，难点在于()3xf x -为定值，审清题意，细心计算，属中档题.6．D解析：D 【分析】根据指数函数与对数函数的关系，以及函数()y g x =的图象与()y f x =的图象关于x 轴对称，求得()ln g x x =-，再由()1g a =，即可求解. 【详解】由题意，函数()y f x =与xy e =互为反函数，所以()ln f x x =，函数()y g x =的图象与()y f x =的图象关于x 轴对称，所以()ln g x x =-，又由()1g a =，即ln 1a -=，解得 1a e= 故选D. 【点睛】本题主要考查了指数函数与对数函数的关系，其中熟记指数函数与对数函数的关系，以及函数的对称性求得函数()g x 的解析式是解答的关键，着重考查了推理与运算能力，属于基础题.7．A解析：A 【分析】先求得()1f 的值，然后根据()f a 的值，求得a 的值. 【详解】由于()1212f =⨯=，所以()()20,2f a f a +==-，22a =-在()0,∞+上无解，由12a +=-解得3a =-，故选A.【点睛】本小题主要考查分段函数求函数值，考查已知分段函数值求自变量，属于基础题.8．B解析：B 【解析】试题分析：对于选项A ，a b 1gc 1gclog c ,log c lg a lg b==，01c <<，10gc ∴<，而0a b >>，所以lg lg a b >，但不能确定lg lg a b 、的正负，所以它们的大小不能确定;对于选项B ，c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >，两边同乘以一个负数1lg c改变不等号方向，所以选项B 正确;对于选项C ，利用cy x =在第一象限内是增函数即可得到c c a b >，所以C 错误;对于选项D ，利用xy c =在R 上为减函数易得a b c c <，所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较；若底数不同,可考虑利用中间量进行比较.9．B解析：B 【分析】先分析函数的定义域，然后根据定义域以及复合函数的单调性判断方法确定出()f x 的单调递减区间. 【详解】因为240x ->，所以定义域为()()(),22,22,-∞--+∞，令()24u x x =-，13log y u =在()0,∞+上单调递减，当(),2x ∈-∞-时，()u x 单调递减，所以()f x 单调递增；当(]2,0x ∈-时，()u x 单调递增，所以()f x 单调递减；当()0,2x ∈时，()u x 单调递减，所以()f x 单调递增；当()2,x ∈+∞时，()u x 单调递增，所以()f x 单调递减；综上可知：()f x 的单调递减区间为(]2,0-和()2,+∞. 故选：B.本题考查对数型复合函数的单调区间的求解，难度一般.分析复合函数的单调性，注意利用判断的口诀“同增异减”，当内外层函数单调性相同时，整个函数为增函数，当内外层函数单调性相反时，整个函数为减函数.10．B解析：B 【分析】利用对数函数的图象，以及函数的奇偶性和图象的变换，即可求解，得到答案. 【详解】由题意，由函数()log a f x x =是增函数知，1a >，当0x ≥时，函数(1)log (1)a y f x x =+=+，将函数1()log ,()a f x a x >=的图象向左平移1个单位，得到函数log (1)a y x =+的图象，又由函数(1)y f x =+满足(1)(1)f x f x -+=+，所以函数(1)y f x =+为偶函数，且图象关于y 轴对称，故选B. 【点睛】本题主要考查了对数函数的图象与性质，以及函数的图象变换的应用，其中解答中熟记对数函数的图象与性质和函数的图象变换是解答本题的关键，着重考查了分析问题和解答问题的能力，属于基础题.11．B解析：B 【分析】根据指数式与对数的互化公式，求得11lg2,lg5a b==，再结合对数的运算公式，即可求解. 【详解】因为2510a b ==，可得25log 10,log 10a b ==，所以11lg2,lg5a b==，则11lg 2lg5lg101a b +=+==. 故选：B. 【点睛】本题主要考查指数式与对数的互化，以及对数的运算公式的化简、求值，其中解答中熟记指数式与对数的互化公式，以及对数的运算公式，准确运算是解答的关键，着重考查运算与求解能力.12．C解析：C根据函数()22xa xf x -=+的图象关于直线1x =对称，求得a ，进而求得 ()g x ，利用数形结合法求解. 【详解】因为()()()2222a a x a xa x x f a x f x -----=+=+=，所以函数关于直线2ax =对称，因为函数()22xn xf x -=+的图象关于直线1x =对称，所以12a=，解得2a =，所以()2log ,04,6,46,x x g x x x ⎧<≤=⎨-<≤⎩，其图象如下图所示：因为123x x x <<，()()()123g x g x g x ==，所以2122log log x x =，2122log log x x -=， 22211log log x x =，所以121=x x ，所以()12334,6x x x x =∈．故选：C ．【点睛】本题主要考查函数的对称性和对数函数的图象和性质还考查了数形结合的思想和运算求解的能力，属于中档题.二、填空题13．【解析】画出函数的图象如图所示：观察图象可知函数的零点依次是点的横坐标由图像可知故答案为点睛：函数的零点与方程根的分布问题解题时常用数形结合思想对于方程的根可分别画出与的图象则两个函数图象的交点的横解析：a b c <<画出函数3xy =，3log y x =，y x =-，2y =-的图象，如图所示：观察图象可知，函数()3xf x x =+，3()log 2g x x =+，3()logh x x x =+的零点依次是点A ，B ，C 的横坐标，由图像可知a b c <<. 故答案为a b c <<点睛：函数的零点与方程根的分布问题，解题时常用数形结合思想，对于方程()()0f x g x -=的根，可分别画出()f x 与()g x 的图象，则两个函数图象的交点的横坐标即为方程()()0f x g x -=的根.14．【分析】根据对数型复合函数单调性列不等式再根据正弦函数性质得结果【详解】单调递增区间为单调递减区间且所以故答案为：【点睛】本题考查对数型复合函数单调性以及正弦函数性质考查基本分析求解能力属基础题解析：[2,2),()2k k k Z ππππ++∈【分析】根据对数型复合函数单调性列不等式，再根据正弦函数性质得结果. 【详解】()()cos1cos1(0,1)log sin f x x ∈∴=单调递增区间为sin y x =单调递减区间且sin 0x >，所以22,()2k x k k Z ππππ+≤<+∈，故答案为：[2,2),()2k k k Z ππππ++∈【点睛】本题考查对数型复合函数单调性以及正弦函数性质，考查基本分析求解能力，属基础题.15．【分析】根据对数的性质可知且最小值为即可求得的值【详解】因为的值域为所以函数的最小值为即解得故答案为：【点睛】本题考查对数函数的值域考查对数的性质合理转化是解题的关键考查了运算能力属于中档题解析：27【分析】根据对数的性质可知2240y ax x =-+>，且最小值为1，即可求得a 的值.【详解】因为()()()212log 24f x ax x a R =-+∈的值域为(],1-∞，所以2240ax x -+>，函数224y ax x =-+的最小值为12，即()20442142a a a >⎧⎪⎨⨯--=⎪⎩，解得27a =，故答案为：27【点睛】本题考查对数函数的值域，考查对数的性质，合理转化是解题的关键，考查了运算能力，属于中档题.16．【分析】由奇函数定义求解【详解】设则∴此时时为奇函数故答案为：【点睛】方法点睛：本题考查函数的奇偶性对于分段函数一般需要分类求解象这种由奇函数求参数可设求得参数值然后再验证这个参数值对也适用即可本题解析：1-．【分析】由奇函数定义求解．【详解】设0x >，则()1x f x e -=-，()x f x e m --=+，∴10x x e m e --++-=，1m =-．此时，0x <时，()1,x f x e =-()1()x f x e f x -=-=-，()f x 为奇函数．故答案为：1-．【点睛】方法点睛：本题考查函数的奇偶性，对于分段函数，一般需要分类求解．象这种由奇函数求参数，可设0x >，求得参数值，然后再验证这个参数值对0x <也适用即可．本题也可以由特殊值如(1)(1)f f -=-求出参数，然后检验即可．17．【分析】先求出m=-1n=3再利用二次函数的图像和性质分析得解【详解】因为函数f （x ）＝loga （x+2）+3的图象恒过定点所以m=-1n=3所以g （x ）＝-x2﹣2bx+3因为g （x ）＝-x2﹣2解析：[)1,-+∞【分析】先求出m =-1,n =3.再利用二次函数的图像和性质分析得解.【详解】因为函数f （x ）＝[log a （x +2）]+3的图象恒过定点(1,3)-，所以m =-1,n =3，所以g （x ）＝-x 2﹣2bx +3，因为g （x ）＝-x 2﹣2bx +3在[1，+∞）上单调递减，所以对称轴1x b =-≤，解得1b ≥-，故答案为：[)1,-+∞【点睛】关键点点睛：本题考查了对数型函数过定点，可求出,m n 的值，利用了二次函数的单调性与对称轴的关系求出b 的范围. 18．【分析】根据指数的运算律计算出的值由此可计算出所求代数式的值【详解】因此故答案为【点睛】本题考查指数幂的化简计算解题的关键在于观察代数式结构并计算出为定值考查计算能力属于中等题解析：【分析】根据指数的运算律计算出()()1f x f x +-=的值，由此可计算出所求代数式的值. 【详解】 ()f x =()1122xx f x ∴-====， ()()12x x x f x f x ∴+-=+===，因此，()()()()()()5434566f f f f f f -+-+-++++==.故答案为【点睛】本题考查指数幂的化简计算，解题的关键在于观察代数式结构并计算出()()1f x f x +-为定值，考查计算能力，属于中等题.19．196【分析】将指数式化成对数式再根据对数的运算及对数的性质计算可得；【详解】解：∵∴∵∴∴解得故答案为：【点睛】本题考查指数与对数的关系对数的运算及对数的性质的应用属于中档题解析：196【分析】将指数式化成对数式，再根据对数的运算及对数的性质计算可得；【详解】解：∵27a b m ==，∴2log a m =，7log b m =，1log 2m a ∴=，1log 7m b = ∵1112a b +=，∴1log 2log 7log 142m m m +==，∴14=，解得196m = 故答案为：196【点睛】本题考查指数与对数的关系，对数的运算及对数的性质的应用，属于中档题.20．【分析】利用换元法可得然后采用等价转换的方法可得在的值域为最后根据二次函数的性质可得结果【详解】由令所以则令由在上的值域为等价为在的值域为的对称轴为且所以可得或所以故答案为：【点睛】本题主要考查函数解析：332,22⎡⎤⎡-+⋃⎢⎥⎢⎣⎦⎣⎦【分析】利用换元法，可得()2221g x x ax a =-+-，然后采用等价转换的方法，可得()g x 在21,22a a a ⎡⎤--+⎣⎦的值域为[]1,0-，最后根据二次函数的性质，可得结果.【详解】由()22221x f x ax a =-+-令22,log x t x t ==，所以()()2222log 2log 1f t t a t a =-+-则令()2221g x x ax a =-+- 由()f x 在21222,2a a a --+⎡⎤⎣⎦上的值域为[]1,0- 等价为()g x 在21,22a a a ⎡⎤--+⎣⎦的值域为[]1,0- ()g x 的对称轴为x a =，且()()1,10g a g a =--=所以()()22122222a a a a a a -+-+≤≤-+1a ≤≤或2a ≤≤所以a ⎤⎡∈⋃⎥⎢⎣⎦⎣⎦故答案为：⎤⎡⋃⎥⎢⎣⎦⎣⎦【点睛】本题主要考查函数值域的应用，难点在于使用等价转换思想，使问题化繁为简，属中档题.三、解答题21．（1）1927-；（2）116. 【分析】（1）利用指数的运算法则化简求解；（2）利用对数的运算法则化简求解.【详解】（1）()3224031168281π-⎛⎫⎛⎫-+- ⎪⎪⎝⎭⎝⎭ ()324343224()13⎡⎤⎡⎤=-+-⎢⎥⎣⎦⎣⎦ 8194412727=-+-=-. （2）()2log 1483log 3log 3log 22++22311log 3log 3log 2123⎛⎫=++ ⎪⎝⎭ 235511log 3log 211666⎛⎫=+=+= ⎪⎝⎭. 【点睛】方法点睛：指数对数的运算化简，一般先观察指数对数的形式，再利用合适的运算法则化简求解.22．（1）14；（2）【分析】（1）利用幂的运算法则和对数的运算法则计算；（2）利用完全平方公式求得1x x -+，再求得22x x -+，然后可求得1x x --．【详解】(1)原式=236342464⎛⎫-⨯- ⎪⎝⎭++=++＝14;-(2)由1122x x -+= 1+25x x -+=，所以13x x -+=所以2222+29=7x x x x --+=+，则1222()2=5x x x x ---=-+所以1=x x --【点睛】幂的运算法则从整数范围推广到有理数范围，实数范围后，乘法公式也随之推广过来，即公式222()2a b a ab b +=++，222()2a b a ab b -=-+，22()()a b a b a b +-=-中,a b 是是分数指数幂时，公式也适用，解题时要注意体会．23．（1）32x x⎧⎨⎩或}1x <- （2）(5,)+∞ 【分析】（1）先使得()22222139x x ---⎛⎫= ⎪⎝⎭,再由3x y =的单调性求解即可；（2）先求定义域,再根据复合函数单调性的“同增异减”原则求解即可.【详解】解:（1）因为221139x x --⎛⎫> ⎪⎝⎭,且()22222139x x ---⎛⎫= ⎪⎝⎭,所以()222133x x --->,因为3x y =在R 上单调递增,所以()2221x x -->-,解得32x >或1x <-, 则满足不等式221139x x --⎛⎫> ⎪⎝⎭的x 的取值集合为32x x ⎧⎨⎩或}1x <- （2）由题,2450x x -->,解得5x >或1x <-,则定义域为()(),15,-∞-+∞, 设245u x x =--,35log y u =, 因为35log y u =单调递减,若求()f x 的递减区间,则求245u x x =--的递增区间, 因为245u x x =--的对称轴为2x =,所以在()5,+∞上单调递增,所以函数()f x 的单调减区间为()5,+∞【点睛】本题考查解指数不等式,考查复合函数的单调区间.24．（1）2a =；（2）2m n m n ++ 【分析】（1）根据对数运算求a 的值；（2）利用换底公式化简求值.【详解】(1)由已知得231a -=得：2a =(2)由(1)得()()lg 23f x x =-，则()()3lg3,5lg7f m f n ====， ∴21lg632lg3lg72log 63lg21lg3lg7m n m n ++===++ 【点睛】本题考查对数换底公式，考查基本分析求解能力，属基础题.25．(1) 10,4⎛⎫ ⎪⎝⎭;(2) 103a <<【分析】(1)代入3a =,根据对数函数的单调性求解即可.(2)先根据区间[1,3]结合定义域可求得a 的大致范围,从而确定log ay x =的单调性,再根据复合函数的单调性确定a 的取值范围即可.【详解】(1) 当3a =时, 31()log 3f x x ⎛⎫=- ⎪⎝⎭,故()0f x >即31log 30x ⎛⎫-> ⎪⎝⎭,即131x ->, 14x >,解得104x <<.故()0f x >解集为10,4⎛⎫ ⎪⎝⎭. (2)由定义域可知,10a x->,即1a x >在区间[1,3]上恒成立,故103a <<,所以log a y x =为减函数.又1y a x =-在区间[1,3]上为减函数,故1()log a f x a x ⎛⎫=- ⎪⎝⎭在区间[1,3]上为增函数.满足题意.故103a <<【点睛】本题主要考查了对数函数的不等式求解以及对数型复合函数的单调性求解参数的问题.属于中档题.26．最大值为43，无最小值. 【分析】首先根据对数真数大于0，解不等式2340x x -+>求出定义域M ，然后利用换元法，即可求出函数()f x 的最值．【详解】由2340x x -+>，解得1x <或3x >，所以(,1)(3,)M =-∞+∞，22()234423(2)x x x x f x +=-⨯=⨯-⨯，令2x t =，由x M ∈得02t <<或8t >，则原函数可化为2224()433()33g t t t t =-=--+，其对称轴为23t =，所以当02t <<时，4()(4,]3g t ∈-；当8t >时，()(,160)g t ∈-∞-．所以当23t =，即223log x =时，()g t 取得最大值43，即函数()f x 取得最大值43，函数()g t 无最小值，故函数()f x 无最小值．【点睛】本题主要考查函数定义域的求法及换元法求函数最值．。

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(含答案解析)

一、选择题1．下列等式成立的是（） A ．222log (35)log 3log 5+=+ B ．2221log 3log 32-= C ．222log 3log 5log (35)⋅=+D ．231log 3log 2=2．形如221n+(n 是非负整数)的数称为费马数，记为F n 数学家费马根据F 0，F 1，F 2，F 3，F 4都是质数提出了猜想：费马数都是质数.多年之后，数学家欧拉计算出F 5不是质数，请你估算F 5是（）位数(参考数据：lg2≈0.3010). A ．8B ．9C ．10D ．113．若函数()()23log 5f x x ax a =+++，()f x 在区间(),1-∞上是递减函数，则实数a的取值范围为（） A ．[]3,2--B ．[)3,2--C ．(],2-∞-D ．(),2-∞-4．已知0.20.33log 0.2,3,0.2a b c ===，则（）A ．a b c <<B ．a c b <<C ．c a b <<D ．b c a <<5．已知：23log 2a =，42log 3b =，232c -⎛⎫= ⎪⎝⎭，则a ，b ，c 的大小关系是（）A ．b c a <C．13a <<D．a >7．已知函数()f x 是定义在R 上的单调递增的函数，且满足对任意的实数x 都有[()3]4x f f x -=，则()()f x f x +-的最小值等于（）.A ．2B ．4C ．8D ．128．函数1()1x f x a +=-恒过定点（）A ．(1,1)B ．(1,1)-C ．(1,0)-D ．(1,1)--9．已知函数()f x 满足()()11f x f x -=+，当(],1-∞时，函数()f x 单调递减，设()41331=log ,log 3,92a f b f c f log ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，则,,a b c 的大小关系是（）A ．a b c <<B ．c a b <<C ．a c b <<D ．c b a <<10．已知235log log log 0x y z ==<，则2x 、3y 、5z的大小排序为A ．235x y z <<B ．325y x z <<C ．523z x y <<D ．532z y x<<11．已知函数()y f x =与x y e =互为反函数，函数()y g x =的图象与()y f x =的图象关于x 轴对称，若()1g a =，则实数a 的值为 A ．e - B ．1e-C ．eD ．1e12．设()lg (21)fx xa=-+是奇函数，则使f(x)<0的x 的取值范围是( )．A ．(－1,0)B ．(0, 1)C ．(－∞，0)D ．(－∞，0)∪(1，＋∞)二、填空题13．若3763,a b ==则21a b+的值为_______ 14．已知()f x 是定义在[0,)+∞的函数，满足(1)()f x f x +=-，当[0,1)x ∈时，()3x f x =，则3(log 30)f =________.15．若()2lg 2lg lg x y x y -=+，则2x y=______．16．函数1()a x f x x a -=+（0a >，且1a ≠）的图像恒过定点，其坐标为_____________.17．函数()213log 253y x x =--的单调递增区间为_______. 18．函数y ＝x 2与函数y ＝x ln x 在区间(0，＋∞)上增长较快的一个是________ .19．已知3(1)4,1()1,1a a x a x f x og x x -+<⎧=⎨≥⎩是R 上的减函数，那么a 的取值范围是__________. 20．如果()231log 2log 9log 64x x x f x =-+-，则使()0f x <的x 的取值范围是______.三、解答题21．已知函数()log (1)log (1)a a f x x x =+--，（0a >且1a ≠）（1）求()f x 的定义域；（2）判断()f x 的奇偶性，并予以证明；（3）求使()0f x >的x 取值范围. 22．已知函数122()log 2xf x x-=+．（1）求函数()f x 的定义域，并判断其奇偶性；（2）判断()f x 在其定义域上的单调性，并用单调性定义证明． 23．已知函数()x f x a =（0a >且1a ≠），满足(2)(1)6f f +=；（1）求()f x 的解析式；（2）若方程()(2),[0,1]m f x f x x =-∈有解，求m 的取值范围；（3）已知()g x 为奇函数，()h x 为偶函数，函数()()()f x g x h x =+；若存在[1,2]x ∈使得2()(2)0ag x h x +≤，求a 的取值范围．24．计算下列各式的值：（1）0113410.027167-⎛⎫-+ ⎪⎝⎭（2）3ln 2145log 2lg 4lg 82e +++ 25．（Ⅰ）)2321812-⎛⎫-+ ⎪⎝⎭；（Ⅱ）解关于x 的不等式：12aa x >--. 26．设函数()log (0,1)a f x x a a =>≠. （1）解不等式(26)(5)f a f a +；（2）已知对任意的实数()23,14m f m m f ⎛⎫++ ⎪⎝⎭恒成立，是否存在实数k ，使得对任意的[1,0]x ∈-，不等式()()142240x x xf f k ++--⋅>恒成立，若存在，求出k 的范围；若不存在，请说明理由.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】根据对数的运算法则和换底公式判断．【详解】22222log 3log 5log (35)log 15log (35)+=⨯=≠+，A 错误；22221log 32log 3log 32-=-≠，B 错误；222log 3log 5log (35)⋅≠+，C 错误； 3233log 31log 3log 2log 2==，D 正确．故选：D ．关键点点睛：本题考查对数的运算法则．log log log ()a a a M N MN +=，log log n a a b n b =，一般log ()log log a a a M N M N +≠+．log ()log log a a a MN M N ≠⋅， 1log log n a a b b n≠． 2．C解析：C 【分析】根据所给定义表示出9.632951010F =⨯，进而即可判断出其位数．【详解】根据题意，53223232lg232lg2320.30109.6320.6329521212101010101010F ⨯=+=+≈==≈==⨯，因为0.63211010<<，所以5F 的位数是10．故选：C 【点睛】关键点睛：解答本题的关键是转化成对数运算，即3232lg 2210=.3．A解析：A 【分析】判断复合函数的单调性，首先要分清楚内外层函数，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求即可. 【详解】由题意知，()f x 在区间(),1-∞上是递减函数，由()()23log 5f x x ax a =+++可知，此复合函数外层函数为：()3log f x x =，在定义域上为增函数，内层函数为()25h x x ax a =+++，要使()f x 在区间(),1-∞上是递减函数，根据复合函数“同增异减”原则，内层函数为()h x 在区间(),1-∞上必须是递减函数，同时须保证最大值()10h ≥，所以()1210a h ⎧-≥⎪⎨⎪≥⎩，解得32a --≤≤.【点睛】易错点睛：判断复合函数的单调性，根据复合函数“同增异减”原则，同时内层函数的值域要满足外层函数的定义域要求.4．B解析：B 【分析】根据指数函数的单调性以及对数函数的单调性分别判断出,,a b c 的取值范围，从而可得结果【详解】因为33log 0.2log 10<=，0.20331>=，...030002021<<=，a cb ∴<<．故选：B ．【点睛】比较大小问题，常见思路有两个：一是利用中间变量；二是利用函数的单调性直接解答5．A解析：A 【分析】由换底公式和对数函数的性质可得112b a <<<，再由指数函数的性质可得102c <<，即可得解. 【详解】23ln3ln12log =02ln 2ln 2a ==>，4212ln ln 2ln1323log =03ln 4ln 2ln 2b ====<， a b ∴>22223231log log 410,239222a c -⎛⎫⎛⎫<===< ⎪ ⎪⎭=⎝>⎭=⎝，b c a ∴<<，故选：A 【点睛】方法点睛：本题考查了对数式、指数式的大小比较，比较大小的常用方法为同底的对数式和指数式利用其单调性进行比较，也可以借助于中间值0和1进行比较，考查了运算求解能力与逻辑推理能力，属于常考题.6．C解析：C 【分析】令()()()22333log 6log 11log g x a a x a ⎡⎤=-++-⎣⎦，由题意得出()()0010g g ⎧>⎪⎨>⎪⎩，可得出关于实数a 的不等式组，由此可解得实数a 的取值范围. 【详解】令()()()22333log 6log 11log g x a a x a ⎡⎤=-++-⎣⎦，由题意可得()()()()23301log 0126log 0g a g a ⎧=->⎪⎨=->⎪⎩，可得311log 3a -<<，解得13a <<故选：C. 【点睛】思路点睛：求解一次函数不等式在区间上恒成立，一般限制一次函数在区间上的端点函数值符号即可，即可得出关于参数的不等式，求解即可.7．B解析：B 【分析】根据()3x f x -为定值，可假设()3xf x m =+，然后计算()()f x f x +-，并计算m 的值，然后使用基本不等式，可得结果. 【详解】由题可知：()3xf x -为定值故设()3xf x m -=，即()3xf x m =+又[()3]4xf f x -=，所以()341mf m m m =+=⇒= 则()31xf x =+()()3131x x f x f x -+-=+++则1()()32243x x f x f x +-=++≥= 当且仅当133xx=时，取等号所以()()f x f x +-的最小值为：4故选：B 【点睛】本题考查基本不等式的应用，还考查镶嵌函数的应用，难点在于()3xf x -为定值，审清题意，细心计算，属中档题.8．C解析：C 【分析】根据指数函数性质求定点. 【详解】因为01a =,所以()011f a -=-=0,因此过定点()1,0-,选C.【点睛】本题考查指数函数性质以及定点问题，考查基本分析求解能力，属于基础题.9．B解析：B 【分析】由()()11f x f x -=+可得函数()f x 关于直线1x =对称，根据对数的运算法则，结合函数的对称性，变形41log 2、13log 3、39log 到区间[)1,+∞内，由函数()f x 在[)1,+∞上单调递增，即可得结果. 【详解】根据题意，函数()f x 满足()()11f x f x -=+，则函数()f x 关于直线1x =对称，又由当(],1-∞时，函数()f x 单调递减，则函数在[)1,+∞上单调递增，又由()44115log log 2222a f f f f ⎛⎫⎛⎫⎛⎫==-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ()()13log 313b f f f ⎛⎫==-= ⎪⎝⎭，()()3log 92c f f ==，则有c a b <<，故选B.【点睛】在比较()1f x ，()2f x ，，()n f x 的大小时，首先应该根据函数()f x 的奇偶性（对称性）与周期性将()1f x ，()2f x ，，()n f x 通过等值变形将自变量置于同一个单调区间，然后根据单调性比较大小．10．A解析：A 【解析】x y z ，，为正实数，且235log log log 0x y z ==<，111235235k k k x y z ---∴===，，，可得：1112352131,51k k k x y z---=>=>=>，．即10k ->因为函数1kf x x -=（）单调递增，∴235x y z<<. 故选A.11．D解析：D 【分析】根据指数函数与对数函数的关系，以及函数()y g x =的图象与()y f x =的图象关于x 轴对称，求得()ln g x x =-，再由()1g a =，即可求解. 【详解】由题意，函数()y f x =与xy e =互为反函数，所以()ln f x x =，函数()y g x =的图象与()y f x =的图象关于x 轴对称，所以()ln g x x =-，又由()1g a =，即ln 1a -=，解得 1a e= 故选D. 【点睛】本题主要考查了指数函数与对数函数的关系，其中熟记指数函数与对数函数的关系，以及函数的对称性求得函数()g x 的解析式是解答的关键，着重考查了推理与运算能力，属于基础题.12．A解析：A 【解析】试题分析：由()lg (21)fxx a =-+为奇函数，则()()f xf x-=-，可得1a =-，即()lg 11f x x x =+-，又()0f x<，即lg110xx+-<，可变为0111x x <+-<，解得10x -<<．考点：函数的奇偶性，对数函数性质，分式不等式．二、填空题13．1【分析】将指数式化为对数式得代入可得根据换底公式可求值【详解】由题意可得∵故答案为：1【点睛】本题主要考查对数与指数的互化对数的换底公式的应用考查基本运算求解能力解析：1【分析】将指数式化为对数式得3log 63a =，7log 63b =，代入可得，372121log 63log 63a b +=+，根据换底公式可求值. 【详解】由题意可得，3log 63a =，7log 63b =， ∵6363363721212log 3log 7log 631log 63log 63a b +=+=+== 故答案为：1 【点睛】本题主要考查对数与指数的互化，对数的换底公式的应用，考查基本运算求解能力.14．【分析】利用对数的运算性质得出结合周期性即可得出的值【详解】且则则函数的周期为2故答案为：【点睛】本题主要考查了由抽象函数的周期求函数值涉及了对数的运算属于中档题解析：109-【分析】利用对数的运算性质得出3310log 303log 9=+，结合周期性，即可得出3(log 30)f 的值. 【详解】33333101010log 30log 27log 27log 3log 999⎛⎫=⨯=+=+ ⎪⎝⎭，且333100log log log 9131=<<= (1)()f x f x +=-，(11)(1)()f x f x f x ∴++=-+=，则(2)()f x f x +=，则函数()f x 的周期为2310log 3333310101010(log 30)21log 1log log 39999f f f f⎛⎫⎛⎫⎛⎫∴=++=+=-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故答案为：109- 【点睛】本题主要考查了由抽象函数的周期求函数值，涉及了对数的运算，属于中档题.15．16【分析】由通过对数运算得出由此再求的值要注意定义域【详解】∵∴解得∴故答案为：16【点睛】本题主要考查对数的运算还考查了运算求解能力属于基础题解析：16 【分析】由()2lg 2lg lg x y x y -=+，通过对数运算得出4x y =，由此再求2x y的值．要注意定义域. 【详解】∵()2lg 2lg lg x y x y -=+，∴2(2)2000x y xy x y x y ⎧-=⎪->⎪⎨>⎪⎪>⎩，解得4x y =，∴42216x y==．故答案为：16 【点睛】本题主要考查对数的运算，还考查了运算求解能力，属于基础题．16．（12）【分析】根据幂函数以及指数函数性质直接缺定点坐标【详解】因为所以当时即恒过定点（12）故答案为：（12）【点睛】本题考查根据幂函数以及指数函数性质求定点考查基本分析求解能力属基础题解析：（1，2）【分析】根据幂函数以及指数函数性质，直接缺定点坐标. 【详解】因为0=111=a a ，，所以当1x =时(1)2f =，即()f x 恒过定点（1，2）故答案为：（1，2）【点睛】本题考查根据幂函数以及指数函数性质求定点，考查基本分析求解能力，属基础题.17．【分析】先由求得函数的定义域然后令由复合函数的单调性求解【详解】由解得或所以函数的定义域为或因为在上递减在递减所以函数的单调递增区间为故答案为：【点睛】方法点睛：复合函数的单调性的求法：对于复合函数解析：1,2⎛⎫-∞- ⎪⎝⎭【分析】先由22530x x -->，求得函数的定义域，然后令2253t x x =--，由复合函数的单调性求解. 【详解】由22530x x -->，解得 12x <-或 3x >，所以函数()213log 253y x x =--的定义域为{1|2x x <-或 }3x >，因为2253t x x =--在1,2⎛⎫-∞- ⎪⎝⎭上递减，13log y t =在()0,∞+递减，所以函数()213log 253y x x =--的单调递增区间为1,2⎛⎫-∞- ⎪⎝⎭. 故答案为：1,2⎛⎫-∞-⎪⎝⎭【点睛】方法点睛：复合函数的单调性的求法：对于复合函数y ＝f [g (x )]，先求定义域，若t ＝g (x )与y ＝f (t )的单调性相同(同时为增或减)，则y ＝f [g (x )]为增函数；若t ＝g (x )与y ＝f (t )的单调性相反，则y ＝f [g (x )]为减函数．18．【解析】由于对数函数y=lnx 在区间(0＋∞)上的增长速度慢于一次函数y=x 所以函数y ＝x2比函数y ＝xlnx 在区间(0＋∞)上增长较快填解析：2y x【解析】由于对数函数y=lnx 在区间(0，＋∞)上的增长速度慢于一次函数y=x ，所以函数y ＝x 2比函数y ＝x ln x 在区间(0，＋∞)上增长较快，填2y x =. 19．【分析】由在R 上单调减确定a3a-1的范围再根据单调减确定在分界点x=1处两个值的大小从而解决问题【详解】因为是上的减函数所以解得故答案为：【点睛】本题考查分段函数单调性问题关键根据单调性确定在分段解析：3,17⎡⎫⎪⎢⎣⎭【分析】由()f x 在R 上单调减，确定a ， 3a -1的范围，再根据单调减确定在分界点x =1处两个值的大小，从而解决问题.【详解】因为3(1)4,1()1,1a a x a x f x og x x -+<⎧=⎨≥⎩是R 上的减函数，所以10013(1)4log 10a a a a a -<⎧⎪<<⎨⎪-+≥=⎩，解得317a ≤<，故答案为：3,17⎡⎫⎪⎢⎣⎭【点睛】本题考查分段函数单调性问题，关键根据单调性确定在分段点处两个值的大小，属于中档题. 20．【分析】可结合对数化简式将化简为再解对数不等式即可【详解】由由得即当时故；当时无解综上所述故答案为：【点睛】本题考查对数化简公式的应用分类讨论求解对数型不等式属于中档题解析：81,3⎛⎫ ⎪⎝⎭【分析】可结合对数化简式将()f x 化简为()1log 2log 3log 4x x x f x =-+-，再解对数不等式即可【详解】由()2323231log 2log 9log 641log 2log 3log 4x x x x x x f x =-+-=-+- 31log 2log 3log 41log 8x x x x =-+-=+，由()0f x <得81log 03x -<，即8log log 3x x x >，当1x >时，83x <，故81,3x ⎛⎫∈ ⎪⎝⎭；当()0,1x ∈时，83x >，无解综上所述，81,3x ⎛⎫∈ ⎪⎝⎭ 故答案为：81,3⎛⎫ ⎪⎝⎭【点睛】本题考查对数化简公式的应用，分类讨论求解对数型不等式，属于中档题三、解答题21．（1）{|11}x x -<<；（2）函数()f x 是奇函数，证明见解析；（3）当1a >时，01x <<；当01a <<时，10x -<<【分析】（1）根据对数的真数为正数列式可解得结果；（2）函数()f x 是奇函数，根据奇函数的定义证明即可；（3）不等式化为log (1)log (1)a a x x +>-后，分类讨论底数a ，根据对数函数的单调性可解得结果.【详解】（1）要使函数数()f x 有意义，则必有1010x x +>⎧⎨->⎩，解得11x -<<，所以函数()f x 的定义域是{|11}x x -<< .（2）函数()f x 是奇函数，证明如下：∵(1,1)x ∈-，(1,1)x -∈-，()log (1)log (1)a a f x x x -=--+[]log (1)log (1)a a x x =-+--()f x =-，∴函数()f x 是奇函数（3）使()0f x >，即log (1)log (1)a a x x +>-当1a >时，有111010x x x x +>-⎧⎪->⎨⎪+>⎩，解得01x <<，当01a <<时，有111010x x x x +<-⎧⎪->⎨⎪+>⎩，解得10x -<<.综上所述：当1a >时，01x <<；当01a <<时，10x -<<.【点睛】方法点睛：已知函数解析式，求函数定义域的方法：有分式时：分母不为0；有根号时：开奇次方，根号下为任意实数，开偶次方，根号下大于或等于0；有指数时：当指数为0时，底数一定不能为0；有根号与分式结合时，根号开偶次方在分母上时：根号下大于0；有指数函数形式时：底数和指数都含有x ，指数底数大于0且不等于1；有对数函数形式时，自变量只出现在真数上时，只需满足真数上所有式子大于0，自变量同时出现在底数和真数上时，要同时满足真数大于0，底数要大0且不等于1.22．（1）定义域为(2,2)-，奇函数（2）函数()f x 在(2,2)-上为增函数，证明见解析【分析】（1）根据真数大于0可得定义域，根据奇函数的定义可得函数为奇函数；（2）设1222x x -<<<，根据对数函数的单调性可得12()()f x f x <，再根据定义可证函数()f x 在(2,2)-上为增函数.【详解】（1）由函数有意义得202x x->+，解得22x -<<，所以函数的定义域为(2,2)-，因为1112222()log log ()22x x f x f x x x -+-⎛⎫-===- ⎪-+⎝⎭，所以函数为奇函数.（2）因为124()log 12f x x ⎛⎫=-+⎪+⎝⎭，所以函数()f x 在(2,2)-上为增函数，证明：设1222x x -<<<，则120224x x <+<+<，则1244122x x >>++，则124411022x x -+>-+>++，因为1012<<，所以12()()f x f x <，所以函数()f x 在(2,2)-上为增函数，【点睛】思路点睛：判断函数的奇偶性的思路：①求出定义域，并判断其是否关于原点对称；②若定义域不关于原点对称，则函数为非奇非偶函数，若定义域关于原点对称，再判断()f x -与()f x 的关系，若()()f x f x -=-，则函数为奇函数；若()()f x f x -=，则函数为偶函数.23．（1）()2x f x =；（2）[2,0]-；（3）17,12⎛⎤-∞-⎥⎝⎦．【分析】（1）根据(2)(1)6f f +=求解出a 的值，即可求解出()f x 的解析式；（2）采用换元法构造函数2(),[1,2]F t t t t =-∈，将m 的取值范围与()F t 的最值联系在一起，由此求解出结果；（3）先根据函数的奇偶性求解出()(),h x g x 的解析式，然后采用分离参数法得到1222222x x x x a --⎡⎤≤--+⎢⎥-⎣⎦，采用换元法求解出1222222x x x x --⎡⎤--+⎢⎥-⎣⎦的最大值，从而求解出a 的取值范围.【详解】（1）因为(2)(1)6f f +=，所以260,2a a a +-==或3a =-（舍去），所以()2x f x =；（2）由（1）知，()2x f x =，所以()222222x x x xm =-=-，令2,[1,2]x t t =∈，令2(),[1,2]F t t t t =-∈，所以()F t 的对称轴为12t =，且()F t 为开口向下的二次函数，所以()F t 在[]1,2上单调递减，所以()()ma min x (2)2,(1)0F t F F t F -====，所以m 的取值范围为[2,0]-；（3）因为()g x 为奇函数，()h x 为偶函数，所以()(),()()g x g x h x h x -=--=．由题()()()f x g x h x =+知，2()()2()()x x g x h x g x h x -⎧=+⎨=-+-⎩，即2()()2()()x x g x h x g x h x -⎧=+⎨=-+⎩ 解得2222(),()22x x x xh x g x --+-== 将上式代入2()(2)0ag x h x +≤，得()()221222202x x x x a ---++≤，易知()22222212211222222222222x x x x x x x x x x x x a -------++⎡⎤≤-⋅=-⋅=--+⎢⎥---⎣⎦．令12,[1,2]2x x t x =-∈，则315,24t ⎡⎤=⎢⎥⎣⎦，122a t t ⎛⎫≤-+ ⎪⎝⎭，因为存在[1,2]x ∈使得2()(2)0ag x h x +≤，所以max12132173222122a t t ⎛⎫ ⎪⎡⎤⎛⎫≤-+=-+=- ⎪ ⎪⎢⎥⎝⎭⎣⎦ ⎪⎝⎭ 所以a 的取值范围是17,12⎛⎤-∞-⎥⎝⎦．【点睛】方法点睛：不等式在指定区间上有解或恒成立求解参数范围问题的处理方法：（1）分类讨论法：根据参数的临界值作分类讨论；（2）分离参数法：将自变量和参数分离开来，自变量部分构造新函数，分析新函数的最值与参数的关系.24．（1）53-；（2）172. 【分析】（1）直接利用根式与分数指数幂的运算法则求解即可,化简过程注意避免出现符号错误；（2）直接利用对数的运算法则求解即可，解答过程注意避免出现计算错误.【详解】（1）原式()()1134340.321-⎡⎤=-+⎣⎦150.32143-=-+-=-. （2）原式32ln 2322log 2515lg 4lg lg 1621828log 4e ⎛⎫=+++=-+⨯+ ⎪⎝⎭ 172=. 【点晴】本题主要考查函数的定义域、指数幂的运算，属于中档题. 指数幂运算的四个原则：（1）有括号的先算括号里的，无括号的先做指数运算；（2）先乘除后加减，负指数幂化成正指数幂的倒数；（3）底数是负数，先确定符号，底数是小数，先化成分数，底数是带分数的，先化成假分数；（4）若是根式，应化为分数指数幂，尽可能用幂的形式表示，运用指数幂的运算性质来解答（化简过程中一定要注意等价性，特别注意开偶次方根时函数的定义域）25．（Ⅰ）2；（Ⅱ）答案见解析.【分析】（Ⅰ）利用指数幂的运算性质，即可得出结果.（Ⅱ）将分式不等式化简转化为()()()122020a x a x x ⎧⎡⎤-+-->⎪⎣⎦⎨-≠⎪⎩，分类讨论1a -，解一元二次不等式即可得出结果.【详解】解：（Ⅰ）原式)23201812-⎛⎫=-+ ⎪⎝⎭()()2332431ππ=-+--+443π1π2=-+--+=. （Ⅱ）12a a x >--，则()102a a x -->-，即()()1202a x a x -+->-，即()()()122020a x a x x ⎧⎡⎤-+-->⎪⎣⎦⎨-≠⎪⎩， ①当10a -=，即1a =时，不等式为20x ->，解集为()2,+∞；②当10a ->，即1a >时，原不等式与()2201a x x a ⎡-⎤⎛⎫--> ⎪⎢⎥-⎝⎭⎣⎦同解，当221a a -≥-，即01a ≤<时，与1a >矛盾，故此情况不存在；当221a a -<-，即0a <或1a >时，即1a >时，不等式的解集为()2,2,1a a -⎛⎫-∞⋃+∞ ⎪-⎝⎭； ③当10a -<，即1a <时，原不等式与()2201a x x a ⎡-⎤⎛⎫--> ⎪⎢⎥-⎝⎭⎣⎦同解，当221a a ->-，即01a <<时，不等式的解集为22,1a a -⎛⎫ ⎪-⎝⎭；当221a a -=-，即0a =时，不等式无解，即解集为∅；当221a a -<-，即0a <或1a >时，即0a <时，不等式的解集为2,21a a -⎛⎫ ⎪-⎝⎭；所以，综上所述：当1a >时，解集为()2,2,1a a -⎛⎫-∞⋃+∞ ⎪-⎝⎭，当1a =时，解集为()2,+∞，当01a <<时解集为22,1a a -⎛⎫ ⎪-⎝⎭，当0a =时，解集为∅，当0a <时，解集为2,21a a -⎛⎫⎪-⎝⎭. 【点睛】本题考查利用指数幂的运算性质进行化简求值，考查含参数的分式不等式的解法和一元二次不等式的解法，考查分类讨论思想和计算能力.26．（1）(0,1)[2,)a ∈⋃+∞（2）实数k 不存在，详见解析【分析】（1）分类讨论，利用对数函数的单调性，将不等式具体化，解不等式即可；（2）判断函数()f x 为增函数，将不等式具体化，再分离参数求最值，即可得出结论.【详解】解：（1）当01a <<时，有2650a a +>，解得02a <≤，即(0,1)∈a ；当1a >时，有0265a a <+，解得2a ，即[2,)a ∈+∞.综上可知，(0,1)[2,)a ∈⋃+∞. （2）由于221331244m m m ⎛⎫++=++ ⎪⎝⎭，且()2314f m m f ⎛⎫++ ⎪⎝⎭，可知()f x 为增函数. ()()142240x x x f f k ++--⋅>，即()()14224x x x f f k ++>-⋅，则有14224x x x k ++>-⋅在[1,0]-上恒成立，即1342x x k +<⋅+在[1,0]-上恒成立，令12,12x t ⎡⎤=∈⎢⎥⎣⎦，设2()32,()g t t t g t =+在1,12⎡⎤⎢⎥⎣⎦上单调递增，则min 17()24g t g ⎛⎫== ⎪⎝⎭，即74k <. 又由于[1,0]x ∈-时，240x k -⋅>恒成立，解得2k >，故符合题意的实数k 不存在.【点睛】本题考查对数函数的单调性、恒成立问题的转化分析、指数函数与二次函数的复合函数的最值问题.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中数学学习材料金戈铁骑整理制作第三章指数函数与对数函数测试题学号：________ 班级：________姓名：________得分：________（时间：120分钟满分：150分）一．选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知集合}1,)21(|{},1,log |{2>==>==x y y B x x y y A x，则A =B ( ) A ． ⎭⎬⎫⎩⎨⎧<<210|y y B. {}10|<<y y C. ⎭⎬⎫⎩⎨⎧<<121|y y D. Φ 2. 函数5log (23)x y x -=-的定义域为( ) A ．3(,5)2B ．3(,4)2C ．(4,5)D ．3(,4)2(4,5)3. 已知0.30.22log 0.3,2,0.3a b c ===，则,,a b c 三者的大小关系是( ) A ．b a c >>B. b c a >>C.a b c >>D.c b a >>4. 设函数221,1(),1x x f x x ax x ⎧+<⎪=⎨+≥⎪⎩，，若((0))4f f a =，则实数a 等于( )A.12B.45C.2D. 95. 化简()()4433log 3log 9log 2log 8++= ( ) A.6 B.6-C.12D.12-6. 下列各组函数中，表示同一个函数的是（）A ．()()f x g x x == B ．()()2log 2,x f x g x ==C ．()()2,x f x x g x x== D ．()()2ln ,2ln f x x g x x ==7. 与函数()a xf x =(01)a a >,≠且的图象关于直线y =x 对称的函数g (x )的图象过点（a,a ）,则1()2g 的值为 ( ) A.2B.1C.12D.-1 8.下列函数中，值域为(0,)+∞的是 ( )A．15xy = B ．11()3xy -= C ．1()12x y =- D ．22log (1)y x =+9. x=3log 131log 111121+的值属于区间（）A. (-3，-2)B. (-2，-1)C.(-1，0)D.(2，3) 10. 若函数24()(01)x f x a a a |-|=>,≠且满足1(1)9f =,则f (x )的单调递减区间是( )A.(2]-∞,B.[2,+)∞C. [-2,+)∞D.(2]-∞,-=log 2|x |，11. 函数f （x ）g （x ）=－x 2+2，则f （x ）g （x ）的图象只可能是( )12. 若函数f (x )＝log a (x ＋b )(其中a ，b 为常数)的图象如图所示，则函数g (x )＝a x＋b 的大致图象是( )二．填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上）13. 函数1()2,x 0xf x R =∈≠(x 且)的值域为14. 已知幂函数2()m y x m N -=∈的图象与x ，y 轴都无交点，且关于y 轴对称，则m =15. 已知函数()()331log 1a a x x f x x x ⎧--≤⎪=⎨>⎪⎩，，，在R 上单调递增，则实数a 的取值范围为 .16. 函数f (x )＝lg －x 2＋4x 的值域为________．三．解答题（本大题共6小题，共70分.解答题应写出文字说明、证明过程或演算步骤）17. (10分) 化简（1）()21151133662226300a b a b a b a b ⎛⎫⎛⎫⎛⎫-÷->> ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭且;（2）若log a m =0.32,求23log a m +的值. 18. (12分)已知函数522)2(2+⨯-=xx y . (1)求该函数的单调区间；（2）当]2,1[-∈x 时，求该函数的最大值和最小值． 19.已知函数()log (1)log (3),(01).a a f x x x a =-++<<（1）求函数f(x)的定义域；（2）若函数 f(x)的最小值为2-，求a 的值.20. (12分)设函数2()log ()x x f x a b =-，且(1)1f =，2(2)log 12f =．（1）求a b ，的值；（2）当[12]x ∈，时，求()f x 的最大值． 21. (12分)已知定义在R 上的函数()f x 满足(4)()f x f x +=，当26x ≤≤时，||1()(),(4)312x m f x n f -=+=.（1）求,m n 的值；（2）比较3(log )f m 与3(log )f n 的大小.22. (12分)已知定义域为R 的函数12()2x x bf x a+-+=+是奇函数．(１)求,a b 的值；(２)若对任意的t R ∈，不等式0)()2(22<--+-k t t f t t f 恒成立，求实数k 的取值范围.参考答案一．选择题1.A2.D3.B4.C5.A6.B7.B 8．B 9．B 10.B 11．C 12.D 提示：1.1{|0},{|0}2A y yB y y =>=<<，所以A =B ⎭⎬⎫⎩⎨⎧<<210|y y ． 2.由对数函数有意义的条件得5051230x x x ->⎧⎪-≠⎨⎪->⎩，，，即4x 523≠<<且x ，故选D ．3.0.30.22log 0.30,21,00.31a b c =<=><=<，所以b c a >>．4.0(0)212,f =+=2((0))(2)224,2f f f a a a ==+==所以． 5.()()2344334333log 27log 3log 9log 2log 8log 27log 16log 4236log 4++=⋅=⨯=⨯=．6.根据定义域与对应法则相同知B 正确． 7．依题意得g (x )=log 12x , 所以1()2g =log 12112=. 8. A 项中y ≠1，C,D 项中y 可以为09.10．由1(1)9f =,得219a =,所以13a =,因此f (x )241()3x |-|=.因为g (x )=|2x -4|在[2,+)∞上单调递增,所以f (x )的单调递减区间是[2,+)∞.11．因为函数)(),(x g x f 都为偶函数，所以F （x ）=)()(x g x f 也为偶函数，所以图象关于y 轴对称，排除A,D ；F （x ）=x x x g x f 22log )2()()(+-=，当10<<x 时，0)()(<x g x f ，排除B,选C. 12.由题意知01,0(0)log 1,a f ab <<⎧⎨<=<⎩所以01,1,a a b <<⎧⎨<<⎩则选D.二．填空题 13.(0,1)(1,)+∞ 14. 0或2 15.36a <≤ 16. (－∞，lg2]提示：13.因为0,x ≠所以()1f x ≠，又因为()0f x >，所以f （x ）的值域是(0,1)(1,)+∞．14.因为幂函数的图象与x,y 轴都无交点，所以m-2≤0,又m N ∈，所以0≤m ≤2，即m=0,1又图象关于y 轴对称，所以m-2为偶数，所以m 为偶数，所以m=0,2. 15.由题意知30a ->，且a>1，330a --≤，所以36a <≤．16.由题意知，－x 2＋4x ＝－(x －2)2＋4>0，所以－x 2＋4x ∈(0,4]，所以－x 2＋4x ∈(0,2]，所以函数f (x )的值域为(－∞，lg2]．三．解答题17.解：（1）211511336622(2)(6)(3)4a b a b a b a -÷-=； (2)由题意知01a a >,≠且，m>0,23log a m + =122132loglog a a m m -+=16log log 4a a m m -=6×0.32-10.324⨯=1.84.18. 解：设2x t =，则()2225=14y t t t =-+-+，其中t>0.（1）当t ≥1时，()214y t =-+在[)∞+，1上为增函数，由2x≥1得x ≥0，且t=2x在[)∞+，0上为增函数，所以原函数在[)∞+，0上为增函数.同理，原函数在（0-，∞］上为增函数.（2）因为]2,1[-∈x ，所以1[,4]2t ∈，则225y t t =-+，当1t =时，y 取最小值4，当4t =时，y 取最大值13.19.解：（1）要使函数有意义，则有1030x x ->⎧⎨+>⎩，解得-3<x<1，所以定义域为（-3,1） .（2）函数可化为2()log (1)(3)log (23)a a f x x x x x =-+=--+2log [(1)4]a x =-++ .因为-3<x<1，所以20(1)44x <-++≤ . 因为01a <<，4log ]4)1([log 2a a x ≥++-∴，即f(x)的最小值为log a 4.由log a 4=-2，得24a -=，12142a -∴==.20. 解：（1）由题意知22222log ()1246 2.log ()log 12a b a b a a b b a b -=⎧-==⎧⎧⎨⎨⎨+==-=⎩⎩⎩，，，即解得，，（2）由（1）知，2()log (42)x x f x =-，由4x-2x>0,得2x （2x-1）>0,因为2x>0,所以2x-1>0,所以x>0.所以f （x ）的定义域为x|x>0.因为]2,1[∈x 为），（∞+0的真子集，所以令2,[2,4]x t t =∈，222211()()log ()log (),24f x g t t t t ⎡⎤==-=--⎢⎥⎣⎦又g （t ）在]4,2[上为增函数，所以当t=4，即x=2时，g （t ）取最大值log 212，故f （x ）的最大值为f （2）=log 212.当4t =时，即2x =时，y 取最大值12，f （x ）的最大值为2log 12.21. 解:（1）因为()f x 在R 上满足(4)()f x f x +=，所以(2)(6)f f =，即|2||6|11()()22m m n n --+=+，所以|2||6|m m -=-，解得4m =，所以|4|1()().2x f x n -=+又(4)31f =，即|44|1312n -+=，所以n=30.（2）由（1）知|4|1()()30,[2,6]2x f x x -=+∈.因为1<log 34<2,所以5<log 34+4<6，所以3|log 444|3331(log )(log 4)(log 44)()302f m f f +-==+=+3log 41()30.2=+因为33log 304<<，所以3381log 4log 3030311(log 30)()30()3022f -=+=+. 因为3381log log 430<，所以3381log log 43011()()22<，所以3381log log 43011()30()3022+<+，所以33(log )(log )f m f n <.22.解：（１）因为()f x 是奇函数，所以(0)f =0，即111201()22xx b b f x a a +--===++，得，所以. 又由f （1）= -f （-1）知11122 2.41a a a --=-=++，得（２）由（１）知11211()22221x x x f x +-==-+++，易知()f x 在(,)-∞+∞上为减函数.又因为()f x 是奇函数，从而不等式0)()2(22<--+-k t t f t t f 恒成立等价于)()2(22k t t f t t f ---<-=)(2k t t f ++-恒成立，因为()f x 为R 上的减函数，所以222-++k t t t t ->，即k ＜3t 2－2t 恒成立,又3t 2－2t ＝32)31(-t －31≥－31，所以k ＜－31.实数k 的取值范围为k ＜－31.。

北师大版高中数学必修一第三章指数函数与对数函数测试题

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(有答案解析)(1)

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》测试(包含答案解析)(4)

北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(答案解析)(1)

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(含答案解析)(3)

北师大版高中数学必修一第三单元《指数函数和对数函数》测试(包含答案解析)

最新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(有答案解析)(1)

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(含答案解析)

最新北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(含答案解析)(2)

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测卷(包含答案解析)

北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(答案解析)

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(答案解析)(3)

最新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(有答案解析)

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(包含答案解析)(4)

新北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(包含答案解析)

北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(包含答案解析)

北师大版高中数学必修一第三单元《指数函数和对数函数》检测卷(包含答案解析)(1)

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试(含答案解析)

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(含答案解析)

北师大版高中数学必修一 第三章 指数函数与对数函数 测试题

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(有答案解析)(1)

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》测试(包含答案解析)(4)

北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(答案解析)(1)

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(含答案解析)(3)

北师大版高中数学必修一第三单元《指数函数和对数函数》测试(包含答案解析)

最新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(有答案解析)(1)

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(含答案解析)

最新北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(含答案解析)(2)

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测卷(包含答案解析)

北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(答案解析)

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(答案解析)(3)

最新北师大版高中数学必修一第三单元《指数函数和对数函数》测试题(有答案解析)

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(包含答案解析)(4)

新北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(包含答案解析)

北师大版高中数学必修一第三单元《指数函数和对数函数》测试卷(包含答案解析)

北师大版高中数学必修一第三单元《指数函数和对数函数》检测卷(包含答案解析)(1)

新北师大版高中数学必修一第三单元《指数函数和对数函数》测试(含答案解析)

(常考题)北师大版高中数学必修一第三单元《指数函数和对数函数》检测题(含答案解析)

北师大版高中数学必修一第三章指数函数与对数函数测试题