苏锡常镇四市高三教学情况调研二
2024届江苏省苏锡常镇四市高三教学情况调研(二)数学试卷

2024届江苏省苏锡常镇四市高三教学情况调研(二)数学试卷一、单选题(★★) 1. 已知集合,,则()A.B.C.D.(★★) 2. 已知双曲线C:经过点,则C的渐近线方程为()A.B.C.D.(★★) 3. 已知,是两个虚数,则“,均为纯虚数”是“为实数”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(★★★) 4. 已知随机变量,且,则的最小值为()A.B.C.D.(★★) 5. 羽毛球比赛水平相当的甲、乙、丙三人举行羽毛球比赛.规则为:每局两人比赛,另一人担任裁判.每局比赛结束时,负方在下一局比赛中担任裁判.如果第1局甲担任裁判,则第3局甲还担任裁判的概率为()A.B.C.D.(★★★) 6. 已知非零向量,,若,则()A.B.C.D.(★★★) 7. 已知椭圆E的中心在坐标原点O,焦点在x轴上,过E的右焦点且斜率为1的直线l交E于A,B两点,且原点O到直线l的距离等于E的短轴长,则E的离心率为()A.B.C.D.(★★★★) 8. 正三棱锥和正三棱锥Q-ABC共底面ABC,这两个正三棱锥的所有顶点都在同一个球面上,点P和点Q在平面ABC的异侧,这两个正三棱锥的侧面与底面ABC所成的角分别为,,则当最大时,()A.B.C.-1D.二、多选题(★★) 9. 设m,n是两条不同的直线,,是两个不同的平面,下列命题中正确的有()A.若,,,则B.,,,则C.若,,,则D.若,,,则(★★★) 10. 已知定义在R上的函数满足,且不是常函数,则下列说法中正确的有()A.若2为的周期,则为奇函数B.若为奇函数,则2为的周期C.若4为的周期,则为偶函数D.若为偶函数,则4为的周期(★★★★) 11. 在长方形ABCD中,,,点E,F分别为边BC和CD上两个动点(含端点),且,设,,则()A.,B.为定值C.的最小值50D.的最大值为三、填空题(★★★) 12. 已知圆O:,过点的直线l交圆O于A,B两点,且,则满足上述条件的一条直线l的方程为 ____________ . (★★★) 13. 设钝角三个内角A,B,C所对应的边分别为a,b,c,若,,,则 ________ .(★★★) 14. 如果函数在区间[ a,b]上为增函数,则记为,函数在区间[ a,b]上为减函数,则记为.如果,则实数m的最小值为 ________ ;如果函数,且,,则实数 ________ .四、解答题(★★) 15. 如图,直三棱柱的体积为1,,,.(1)求证:;(2)求二面角的余弦值.(★★)16. 某班统计了全班50名同学在某一周内到图书馆借阅次数的相关数据,结果如下表:若将该周内到图书馆借阅次数不少于3次的学生,称为“爱好阅读生”;少于3次的学生称为“一般阅读生”.(1)请完成以下列联表;问:能否有90%的把握认为爱好阅读与性别有关?阅读附:,.0.1k 2.706(2)班主任从该周内在图书馆借阅次数为0的同学中,一次性随机抽取3人了解有关情况,求抽到的男生人数的概率分布和数学期望.(★★★★) 17. 已知函数.(1)当时,证明:;(2)若在区间上有且只有一个极值点,求实数的取值范围.(★★★★★) 18. 已知F为抛物线C:的焦点,点A在C上,.点P(0,-2),M,N是抛物线上不同两点,直线PM和直线PN的斜率分别为,.(1)求C的方程;(2)存在点Q,当直线MN经过点Q时,恒成立,请求出满足条件的所有点Q的坐标;(3)对于(2)中的一个点Q,当直线MN经过点Q时,| MN|存在最小值,试求出这个最小值.(★★★★) 19. 如图所示数阵,第行共有个数,第m行的第1个数为,第2个数为,第个数为.规定:.(1)试判断每一行的最后两个数的大小关系,并证明你的结论;(2)求证:每一行的所有数之和等于下一行的最后一个数;(3)从第1行起,每一行最后一个数依次构成数列,设数列的前n项和为是否存在正整数k,使得对任意正整数n,恒成立?如存在,请求出k的最大值,如不存在,请说明理由.。
-苏锡常镇四市高三教学情况调研(二).docx

2015-2016学年度苏锡常镇四市高三教学情况调研(二)数学Ⅰ试题 2016.5参考公式:圆锥的体积公式:V 圆锥=13Sh ,其中S 是圆锥的底面积,h 是高.圆锥的侧面积公式:S 圆锥=rl p ,其中r 是圆柱底面的半径, l 为母线长.样本数据1x ,2x ,… ,n x 的方差2211()n i i s x x n ==-∑,其中x =11n i i x n =∑.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.已知全集{}12345U =,,,,,{}12A =,,{}234B =,,,那么()U A B =U ð ▲ . 2.已知2(i)2i a -=,其中i 是虚数单位,那么实数a = ▲ .3.从某班抽取5名学生测量身高(单位:cm ),得到的数据为160,162, 159,160,159,则该组数据的方差2s = ▲ .4.同时抛掷三枚质地均匀、大小相同的硬币一次,则至少有两枚硬币正面 向上的概率为 ▲ .5.若双曲线221x my +=过点()22-,,则该双曲线的虚轴长为 ▲ .6.函数()2ln 2()1x x f x x -=-的定义域为 ▲ .7.某算法流程图如右图所示,该程序运行后,若输出的15x =,则实数a 等 于 ▲ . 8.若1tan 2α=,1tan()3αβ-=-,则tan(2)βα-= ▲ . 注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,包含填空题(第1题——第14题)、解答题(第15题——第20题).本卷满分160分,考试时间为120分钟.考试结束后请将答题卡交回.2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整笔迹清楚.4.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.5.请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔. (第7题)结束开始 n ← 1 x ← a x ← 2x + 1输出x N n ≤3n ← n + 1Y9.若直线340x y m +-=与圆222440x y x y ++-+=始终有公共点,则实数m 的取值范围是▲ .10.设棱长为a 的正方体的体积和表面积分别为1V ,1S ,底面半径和高均为r 的圆锥的体积和侧面积分别为2V ,2S ,若123=V V p,则12S S 的值为 ▲ .11.已知函数3()2f x x x =+,若1(1)(log 3)0af f +>(0a >且1a ≠),则实数a 的取值范围是 ▲ . 12.设公差为d (d 为奇数,且1d >)的等差数列{}n a 的前n 项和为n S ,若19m S -=-,0m S =,其中3m >,且*m ∈N ,则n a = ▲ .13.已知函数2()f x x x a =-,若存在[]1,2x ∈,使得()2f x <,则实数a 的取值范围是 ▲ . 14.在平面直角坐标系xOy 中,设点(1 0)A ,,(0 1)B ,,( )C a b ,,( )D c d ,,若不等式2(2)()()CD m OC OD m OC OB OD OA -⋅+⋅⋅⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r≥对任意实数a b c d ,,,都成立,则实数m 的最大值是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在△ABC 中,角A B C ,,的对边分别是a b c ,,,已知向量(cos cos )B C =,m ,(4)a b c =-,n ,且∥m n .(1)求cos C 的值;(2)若3c =,△ABC 的面积15=4S ,求a b ,的值. 16.(本小题满分14分)在直三棱柱111ABC A B C -中,CA CB =,12AA AB =,D 是AB 的中点.(1)求证:1BC ∥平面1ACD ; (2)若点P 在线段1BB 上,且114BP BB =, 求证:AP ⊥平面1ACD . (第16题)C 1B 1A 1PDCBA某经销商计划销售一款新型的空气净化器,经市场调研发现以下规律:当每台净化器的利润为x (单位:元,0x >)时,销售量()q x (单位:百台)与x 的关系满足:若x 不超过20,则1260()1q x x =+;若x 大于或等于180,则销售量为零;当20180x ≤≤时,()q x a b x =-(a ,b 为实常数). (1)求函数()q x 的表达式;(2)当x 为多少时,总利润(单位:元)取得最大值,并求出该最大值. 18.(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C :22221(0)x y a b a b +=>>的左,右焦点分别是1F ,2F ,右顶点、上顶点分别为A ,B ,原点O 到直线AB 的距离等于ab ﹒ (1)若椭圆C 的离心率等于63,求椭圆C 的方程; (2)若过点(0,1)的直线l 与椭圆有且只有一个公共点P ,且P 在第二象限,直线2PF 交y 轴于点Q ﹒试判断以PQ 为直径的圆与点1F 的位置关系,并说明理由﹒已知数列{}n a 的前n 项和为n S ,13a =,且对任意的正整数n ,都有113n n n S S λ++=+,其中常数0λ>.设3nn n a b =()n *∈N ﹒ (1)若3λ=,求数列{}n b 的通项公式; (2)若1≠λ且3λ≠,设233n n n c a λ=+⨯-()n *∈N ,证明数列{}n c 是等比数列; (3)若对任意的正整数n ,都有3n b ≤,求实数λ的取值范围. 20.(本小题满分16分)已知函数2()e x f x a x bx =⋅+-(a b ∈R ,,e 2.71828=L 是自然对数的底数),其导函数为()y f x '=.(1)设1a =-,若函数()y f x =在R 上是单调减函数,求b 的取值范围; (2)设0b =,若函数()y f x =在R 上有且只有一个零点,求a 的取值范围;(3)设2b =,且0a ≠,点()m n ,(m ,n ∈R )是曲线()y f x =上的一个定点,是否存在实数0x (0x m ≠),使得000()()()2x mf x f x m n +'=-+成立?证明你的结论. 2015-2016学年度苏锡常镇四市高三教学情况调研(二)数学Ⅱ(附加题) 2016.521.【选做题】在A ,B ,C ,D 四小题中只能选做两题......,每小题10分,共计20分.请在答题卡指....定区域...内作答,解答时应写出文字说明、证明过程或演算步骤. 注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷只有解答题,供理工方向考生使用.本试卷第21题有A ,B ,C ,D 4个小题供选做,每位考生在4个选做题中选答2题.若考生选做了3题或4题,则按选做题中的前2题计分.第22,23题为必答题.每小题10分,共40分.考试时间30分钟.考试结束后,请将答题卡交回. 2. 答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3. 请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚.4. 如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.5. 请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔. D EO B C A(第21-A 题)A .选修4 —1:几何证明选讲已知△ABC 内接于O e ,BE 是O e 的直径,AD 是BC 边上的高. 求证:BA AC BE AD ⋅=⋅. B .选修4—2:矩阵与变换已知变换T 把平面上的点(34)-,,(5 0),分别变换成(21)-,,(1 2)-,,试求变换T 对应的矩阵M .C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,直线l 过点(12)M ,,倾斜角为3π﹒以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,圆:6cos C ρθ=﹒若直线l 与圆C 相交于A B ,两点,求MA MB ⋅的值. D .选修4—5:不等式选讲设x 为实数,求证:()()2242131x x x x ++++≤﹒【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)一个口袋中装有大小相同的3个白球和1个红球,从中有放回地摸球,每次摸出一个,若有3次摸到红球即停止.(1)求恰好摸4次停止的概率;(2)记4次之内(含4次)摸到红球的次数为X ,求随机变量X 的分布列. 23.(本小题满分10分)设实数12n a a a L ,,,满足120n a a a +++=L ,且12||||||1n a a a +++L ≤(*n ∈N 且2)n ≥,令(*)n n a b n n =∈N .求证:1211||22n b b b n+++-L ≤(*)n ∈N . 2015-2016学年度苏锡常镇四市高三教学情况调研(二)数学Ⅰ试题参考答案一、填空题:本大题共14小题,每小题5分,共70分. 1.{125},, 2.1- 3.65 4.12 5.4 6.()()0,11,2U 7.1 8.17- 9. [010], 10.32p11.()()0,13,+∞U 12.312n - 13.(1,5)- 14. 51- 二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤.15. 解:(1)∵∥m n ,∴cos (4)cos c B a b C =-, …………2分由正弦定理,得sin cos (4sin sin )cos C B A B C =-,化简,得sin()4sin cos B C A C +=﹒ …………4分 ∵A B C ++=p ,∴sin sin()A B C =+﹒ 又∵()0,A ∈p ,∵sin 0A >,∴1cos 4C =. …………6分(2)∵()0,C ∈p , 1cos 4C =,∴2115sin 1cos 1164C C =-=-=. ∵115sin 24S ab C ==,∴2ab =﹒① …………9分∵3c =,由余弦定理得22132a b ab =+-,∴224a b +=,② …………12分 由①②,得42440a a -+=,从而22a =,2a =±(舍负),所以2b =, ∴2a b ==. …………14分 16.证明:(1)连结1AC ,设交1A C 于点O ,连结OD .∵四边形11AA C C 是矩形,∴O 是1AC 的中点. …………2分 在△1ABC 中, O ,D 分别是1AC ,AB 的中点,∴1OD BC ∥. …………4分 又∵OD ⊂平面1ACD ,1BC ⊄平面1ACD , ∴1BC ∥平面1ACD . …………6分 (2)∵CA CB =,D 是AB 的中点,∴CD AB ⊥﹒又∵在直三棱柱111ABC A B C -中,底面ABC ⊥侧面11AA B B ,交线为AB ,CD ⊂平面ABC ,∴CD ⊥平面11AA B B ﹒ …………8分∵AP ⊂平面11A B BA ,∴CD AP ⊥. …………9分 ∵12BB BA =,11BB AA = ,114BP BB =, ∴12=4BP ADBA AA =, ∴Rt △ABP ∽Rt △1A AD , 从而∠1AA D =∠BAP ,所以∠1AA D +∠1A AP =∠BAP +∠1A AP =90︒,∴1AP A D ⊥. …………12分 又∵1CD A D D =I ,CD ⊂平面1ACD ,1A D ⊂平面1ACD ∴AP ⊥平面1ACD . …………14分17.解:(1)当20180x ≤≤时,由20601800a b a b ⎧-⋅=⎪⎨-⋅=⎪⎩,,得9035a b =⎧⎪⎨=⎪⎩,. …………2分故1260,020,1()9035,20180,0,180x x q x x x x ⎧<⎪+⎪⎪-<⎨⎪>⎪⎪⎩≤=≤ …………4分(2)设总利润()()f x x q x =⋅,由(1)得126000020,1()90003005201800180xx x f x x x x x x ⎧<<⎪+⎪⎪-⋅⎨⎪>⎪⎪⎩,=,≤≤,, …………6分 当020x <≤时,126000126000()12600011x f x x x ==-++,()f x 在[020],上单调递增, 所以当20x =时,()f x 有最大值120000. …………8分当20180x <≤时,()90003005f x x x x -⋅=,()90004505f x x '-⋅=,令()0f x '=,得80x =. …………10分当2080x <<时,()0f x '>,()f x 单调递增, 当8080x <≤1时,()0f x '<,()f x 单调递减,所以当80x =时,()f x 有最大值240000. …………12分 当180x <时,()0f x =﹒答:当x 等于80元时,总利润取得最大值240000元. …………14分 18.解:由题意,得点(,0)A a ,(0,)B b ,直线AB 的方程为1x ya b+=,即0ax by ab +-=﹒ 由题设,得22ab ab a b=+,化简,得221a b +=﹒① …………2分(1)∵63c e a ==,∴22223a b a -=,即223a b =﹒② 由①②,解得223414a b ⎧=⎪⎪⎨⎪=⎪⎩,﹒ …………5分所以,椭圆C 的方程为224413x y +=﹒ …………6分(2)点1F 在以PQ 为直径的圆上﹒由题设,直线l 与椭圆相切且l 的斜率存在,设直线l 的方程为:1y kx =+,由222211x y a b y kx ⎧+=⎪⎨⎪=+⎩,得22222222()20b a k x ka x a a b +++-=,(*) …………8分 则22222222=(2)4()()0ka b a k a a b ∆-+-=,化简,得22210b a k --=,所以,22211b k a-== ,∵点P 在第二象限,∴1k =﹒ …………10分 把1k =代入方程(*) ,得22420x a x a ++=,解得2x a =-,从而2y b =,所以22(,)P a b -﹒ …………11分从而直线2PF 的方程为:2222()b y b x a a c-=+--, 令0x =,得22b c y a c =+,所以点22(0,)+b cQ a c﹒ …………12分从而221=(,)F P a c b -+u u u r ,212=(,)+b c FQ c a cu u u r , …………13分 从而42112()+b c F P FQ c a c a c⋅=-++u u u r u u u r 22222424442222()()(+)()==0+++c b a b a c c a c b c a b c a c a c a c⎡⎤-++-+-++⎣⎦==, 又∵221a b +=,222=+a b c , ∴110F P F Q ⋅=u u u r u u u r﹒ …………15分 所以点1F 在以PQ 为直径的圆上﹒ …………16分 19.解:∵113n n n S S λ++=+,n *∈N , ∴当2n ≥时,-13n n n S S λ=+, 从而123n n n a a λ+=+⋅,2n ≥,n *∈N ﹒又在113n n n S S λ++=+中,令1n =,可得12123a a λ=+⋅,满足上式,所以123n n n a a λ+=+⋅, n *∈N ﹒ …………2分 (1)当3λ=时, 1323n n n a a +=+⋅,n *∈N ,从而112333n n n na a ++=+,即123n n b b +-=, 又11b =,所以数列{}n b 是首项为1,公差为23的等差数列, 所以213n n b +=. …………4分 (2)当0>λ且3λ≠且1≠λ时,1122323333n n n n n n c a a λλλ--=+⨯=+⨯+⨯-- 11111223(33)(3)33n n n n n a a c λλλλλλ-----=+⨯-+=+⨯=⋅--, …………7分 又163(1)3033c -=+=≠--λλλ, 所以{}n c 是首项为3(1)3λλ--,公比为λ的等比数列, 13(1)3n n c λλλ--=⋅-﹒…………8分 (3)在(2)中,若1λ=,则0n c =也适合,所以当3λ≠时,13(1)3n n c λλλ--=⋅-. 从而由(1)和(2)可知11(21)333(1)23333n n n n n a λλλλλλ--⎧+⨯=⎪=⎨-⋅-⨯≠⎪--⎩,,,.…………9分 当3λ=时,213n n b +=,显然不满足条件,故3λ≠. …………10分 当3λ≠时,112()333n n b λλλλ--=⨯---. 若3λ>时,103λλ->-,1n n b b +<,n *∈N ,[1,)n b ∈+∞,不符合,舍去. …………11分 若01λ<<时,103λλ->-,203λ->-,1n n b b +>,n *∈N ,且0n b >.所以只须11133a b ==≤即可,显然成立.故01λ<<符合条件; …………12分 若1λ=时,1n b =,满足条件.故1λ=符合条件; …………13分 若13λ<<时,103λλ-<-,203λ->-,从而1n n b b +<,n *∈N , 因为110b =>.故2[1)3n b λ∈--,, 要使3n b ≤成立,只须233λ--≤即可. 于是713λ<≤. …………15分综上所述,所求实数λ的范围是7(0]3,. …………16分20.解:(1)当1a =-时,2()e x f x x bx =-+-,∴()e 2x f x x b '=-+-,由题意()e 20x f x x b '=-+-≤对x ∈R 恒成立﹒ …………1分 由e 20x x b -+-≤,得e 2x b x +≥-,令()e 2x F x x =+-,则()e 2x F x '=+-,令()0F x '=,得ln2x =.当ln2x <时,()0F x '>,()F x 单调递增,当ln2x >时,()0F x '<,()F x 单调递减, 从而当ln2x =时,()F x 有最大值2ln22-,所以2ln22b -≥. …………3分 (2)当0b =时,2()e x f x a x =+,由题意2e 0x a x +=只有一解﹒由2e 0xa x +=,得2e x x a -=,令2()e x x G x =,则(2)()e xx x G x -'=,令()0G x '=,得0x =或2x =. …………5分 当0x ≤时,()0G x '≤,()G x 单调递减,()G x 的取值范围为[)0+∞,, 当02x <<时,()0G x '>,()G x 单调递增,()G x 的取值范围为240e ⎛⎫⎪⎝⎭,,当2x ≥时,()0G x '≤,()G x 单调递减,()G x 的取值范围为240e ⎛⎤⎥⎝⎦,,由题意,得0a -=或24e a ->,从而0a =或24ea <-, 所以当0a =或24e a <-时,函数()y f x =只有一个零点. …………8分 (3)2()e 2x f x a x x =+-,()e 22x f x a x '=+-,假设存在,则有00000()()()()()()22x m x mf x f x m n f x m f m ++''=-+=-+, 即000()()()2f x f m x m f x m -+'=-,∵0002()e 2222x mx m x m f a +++'=+⋅-,00220000000()()(e )()2()(e e )()2x m x m f x f m a e x m x m a x m x m x m x m--+----==++----,∴0020(e e )ex m x m a a x m+-=-﹒……(*)﹒ …………10分∵0a ≠,∴0020e e ex m x m x m +-=-,不妨设00t x m =->,则2e e e t t m m m t ++-=﹒ 两边同除以e m,得2e 1e t t t-=,即2e e 1tt t =-, …………12分令2()e e 1ttg t t =--,则2222()e (e e )e (e 1)22t t t t tt tg t '=-+=--,令2()e 12t t h t =--,则22111()e (e 1)0222t th t '=-=->,∴()h t 在(0)+∞,上单调递增,又∵(0)0h =,∴()0h t >对(0)t ∈+∞,恒成立, …………14分 即()0g t '>对(0)t ∈+∞,恒成立, ∴()g t 在(0)+∞,上单调递增,又(0)0g =,∴()0g t >对(0)t ∈+∞,恒成立,即(*)式不成立, …………15分 ∴不存在实数0x (0x m ≠),使得000()()()2x mf x f x m n +'=-+成立. …………16分苏锡常镇四市高三教学情况调研(一)数学Ⅱ(附加题)参考答案21、【选做题】在A、B、C、D 四小题中只能选做两题......,每小题10分,共计20分.A.选修4—1:几何证明选讲证明:连结AE.∵BE是Oe的直径,∴90BAE∠=︒.…………2分∴BAE ADC∠=∠.…………4分又∵BEA ACD∠=∠,∴△BEA∽△ACD.…………7分∴BE ACBA AD=,∴BA AC BE AD⋅=⋅.…………10分B.选修4—2:矩阵与变换解:设a bc d⎡⎤=⎢⎥⎣⎦M,由题意,得35214012a bc d-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦,…………3分∴342513415 2.a bac dc-=⎧⎪=-⎪⎨-=-⎪⎪=⎩,,,…………5分解得1,513,202,51120abcd⎧=-⎪⎪⎪=-⎪⎨⎪=⎪⎪⎪=⎩. …………9分即113520211520⎡⎤--⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦M.…………10分C.选修4—4:坐标系与参数方程解:直线l 的参数方程为112(322x tty t⎧=+⎪⎪⎨⎪=+⎪⎩,,为参数),…………2分圆C的普通方程为22(3)9x y-+=﹒…………4分直线l 的参数方程代入圆C 的普通方程,得22(31)10t t +--=, …………6分 设该方程两根为1t ,2t ,则121t t ⋅=-﹒ …………8分 ∴12==1MA MB t t ⋅⋅. …………10分 D .选修4—5:不等式选讲证明:因为 右—左=432222x x x --+ …………2分 =3222(1)(1)2(1)(1)x x x x x --=-++ …………4分=22132(1)024x x ⎡⎤⎛⎫-++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦≥, …………8分所以,原不等式成立. …………10分 【必做题】第22题、第23题,每题10分,共计20分. 22.解:(1)设事件“恰好摸4次停止”的概率为P ,则2231319()444256P C =⨯⨯⨯=. …………4分 (2)由题意,得=0123,,,X ,044381(=0)()4256P C =⨯=X , 1341327(=1)()()4464P C =⨯⨯=X , 22241327(=2)()()44128P C =⨯⨯=X , 81272713(=3)125664128256P =---=X , …………8分 ∴X 的分布列为…………10分23.证明:(1)当2n =时,12a a =-,∴1122||||||1a a a =+≤,即11||2a ≤,∴21121||111||||224222a ab b a +=+==-⨯≤,即当2n =时,结论成立. …………2分 (2)假设当n k =(*k ∈N 且2)k ≥时,结论成立,即当120k a a a +++=L ,且12||||||1k a a a +++L ≤时,有1211||22k b b b k +++-L ≤. …………3分则当1n k =+时,由1210k k a a a a +++++=L ,且121||||||1k a a a ++++L ≤,X 0 123 P8125627642712813256∵11211212|||||||||||1k k k k a a a a a a a a +++=+++++++L L ≤≤,∴11||2k a +≤, …………5分又∵1211()0k k k a a a a a -++++++=L ,且1211121||||||||||||||1k k k k a a a a a a a a -++++++++++L L ≤≤,由假设可得112111||22k k k a a b b b k k+-+++++-L ≤, …………7分 ∴1121121|||1k k k k k a ab b b b b b b k k ++-++++=++++++L L1111112111|()(||1221k k k k k k k a a a a a a b b b k k k k k k+++++-+=+++++-+++L -)|≤-111111111111()||()221221222(1)k a k k k k k k k +=-+-+⨯=-+++-≤-, 即当1n k =+时,结论成立.综上,由(1)和(2)可知,结论成立. …………10分。
江苏省苏锡常镇四市2024届高三下学期教学情况调研(二)生物
江苏省苏锡常镇四市2024届高三教学状况调研(二)生物试题一、单项选择题:本部分包括20题,每题2分,共计40分。
每题只有一个选项最符合题意。
1.细胞自噬作用是指细胞在应对短暂生存压力时,通过降解自身非必需的成分来供应养分和能量,从而维持生命。
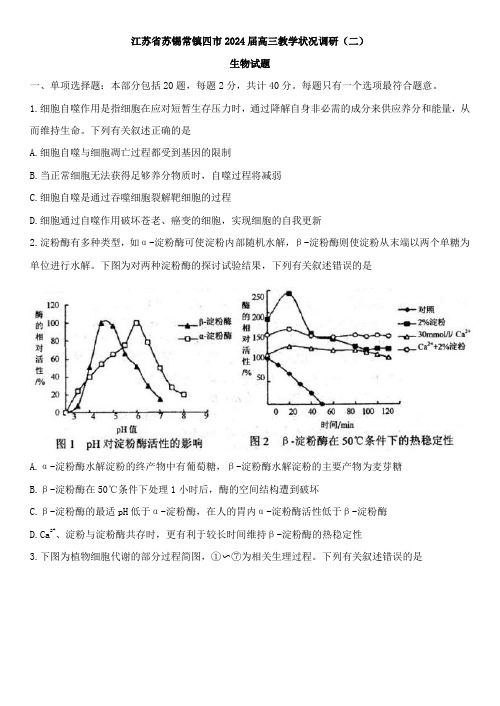
下列有关叙述正确的是A.细胞自噬与细胞凋亡过程都受到基因的限制B.当正常细胞无法获得足够养分物质时,自噬过程将减弱C.细胞自噬是通过吞噬细胞裂解靶细胞的过程D.细胞通过自噬作用破坏苍老、癌变的细胞,实现细胞的自我更新2.淀粉酶有多种类型,如α-淀粉酶可使淀粉内部随机水解,β-淀粉酶则使淀粉从末端以两个单糖为单位进行水解。
下图为对两种淀粉酶的探讨试验结果,下列有关叙述错误的是A.α-淀粉酶水解淀粉的终产物中有葡萄糖,β-淀粉酶水解淀粉的主要产物为麦芽糖B.β-淀粉酶在50℃条件下处理1小时后,酶的空间结构遭到破坏C.β-淀粉酶的最适pH低于α-淀粉酶,在人的胃内α-淀粉酶活性低于β-淀粉酶D.Ca2+、淀粉与淀粉酶共存时,更有利于较长时间维持β-淀粉酶的热稳定性3.下图为植物细胞代谢的部分过程简图,①〜⑦为相关生理过程。
下列有关叙述错误的是A.若植物缺Mg,则首先会受到显著影响的是③B.②的进行与⑤⑥亲密相关,与③⑦无干脆关系C.蓝藻细胞中③发生在类囊体膜上,④发生在叶绿体基质中D.叶肉细胞③中02的产生量小于⑥中02的汲取量,则该细胞内有机物的总量将削减4.下列有关生物学试验或调查的叙述中,正确的是A.调查人群中的遗传病时,多基因遗传病不能作为调査对象B.用溴麝香草酚蓝水溶液,可检测酵母菌培育液中C02的产生状况C.常用不同浓度的α—萘乙酸溶液处理带叶的柳枝,探究其促进生根的最适浓度D.在花生子叶组织切片上滴加苏丹Ⅲ染液,可视察到红色的脂肪颗粒5.下图表示细胞分裂过程中黏着素和分别酶的相关作用。
探讨还发觉S蛋白可以抑制分别酶的活性。
下列有关叙述错误的是A.黏着素存在时,基因重组仍可发生B.S蛋白可能导致子细胞中染色体数目发生异样C.S蛋白在细胞分裂间期合成,在姐妹染色单体分别后降解D.过程1表示同源染色体的分别,过程2表示姐妹染色单体的分别6.破骨细胞来自造血干细胞,负责骨组织的汲取。
江苏苏州等四市2024年高三下学期二模 生物试题

2023~2024学年度苏锡常镇四市高三教学情况调研(二)生物注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共8页,满分为100分,考试时间为75分钟。
考试结束后,请将答题卡交回。
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在答题卡的规定位置。
3.请认真核对答题卡上的姓名、准考证号与本人是否相符。
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案。
作答非选择题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5.如需作图,必须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗。
一、单项选择题:共14题,每题2分,共28分。
每题只有一个选项最符合题意。
1.下列关于细胞生命历程的叙述错误..的是()A.人体内可以同时存在无丝分裂、有丝分裂和减数分裂三种细胞分裂的方式B.衰老细胞中会出现细胞周期停滞、生物大分子受损、A TP合成效率下降等现象C.人体肿瘤细胞可大量摄取葡萄糖并产生酒精,改变机体局部微环境实现免疫逃逸D.细胞凋亡过程中,细胞表面产生许多含有染色质片段的泡状突起并形成凋亡小体2.下图为线粒体与溶酶体之间的三种相互作用示意图。
相关叙述正确的是()A.溶酶体中的水解酶在游离的核糖体中合成,线粒体可以为该过程提供能量B.溶酶体水解大分子得到的葡萄糖等产物可进入线粒体,为有氧呼吸提供原料C.溶酶体可为线粒体的分裂标记裂变位点,该过程是与细胞分裂同步进行的D.功能失调的线粒体产生氧自由基导致细胞衰老,并主要以自噬方式被清除3.“咸”“苦”“甜”等味觉感知依赖于味蕾中的不同味细胞,下图表示不同味觉的转导机制。
相关叙述错误..的是()A.味蕾中的味细胞属于感受器,味觉产生于大脑皮层B.Na+以协助扩散的方式进入细胞,使“咸”感知相关的细胞产生兴奋C.奎宁通过阻止K+外流,可使“苦”感知相关细胞的质膜外侧膜电位由正变负D.淀粉、纤维素等多糖没有甜味,是由于其无法进入味蕾中的神经上皮细胞4.下列关于实验操作或现象的叙述错误..的是()A.用菠菜叶进行观察叶绿体实验时,因上表皮与栅栏组织相连而更容易被撕取B.用成熟黑藻叶观察质壁分离时,因细胞质中含叶绿体而使原生质层易于分辨C.天竺葵叶片经光照和脱绿处理后,叶肉细胞中的叶绿体能够被碘液染成蓝色D.紫色月季叶中色素用有机溶剂层析,紫色花青素因溶解度低而离滤液细线最近5.分布于非洲等地的肺鱼是一类古老动物,在淡水中用鳃呼吸,短时间缺水时可利用鳔呼吸,具有很多适应陆地生活的特征。
2022届江苏省苏锡常镇四市高三教学情况调研(二)语文试卷 答案

2021~2022学年度苏锡常镇四市高三教学情况调研(二)语文试题参考答案一、现代文阅读(35分)(一)(19分)1.(3分)C2.(3分)B3.(3分)D4.(4分)材料一釆用总分结构:先从社会现代转型给中国传统文化带来的变化入手,提出如何借助科技的力量实现中国传统文化的现代转型的命题。
接着通过挙例的方式,分别从利用现代科技来修复保护传统文化、利用大众传媒传承与传播中国传统文化、以及创造新的文化体验方式等三个角度,具体阐释了解决的方法。
5.(6分)①以例代证,缺分析论证,未结合观点对例子进行具体分析;②举例不够全面,不具有代表性,且第二个例子是用观点代替具体事例;③观点先行,思维逻辑有漏洞。
(二)(16分)6.(3分)D7.(3分)B8.(4分)吃剩下来的茶叶蛋表现了主人公物质条件差,生活贫苦;“咧开了嘴的、畏缩地挤在一起的茶叶蛋”,写出了许灵均生活的寒酸和内心的窘迫;带茶叶蛋给父亲吃,表明他们生活、思想上的巨大差异;与前文父亲大大小小的箱子、花花绿绿的旅馆商标、飞机的标笺形成鲜明的对比,突出了父子二人在物质、思想上的巨大差异;为许灵均最后的选择做了铺垫。
9.(6分)有利于推动故事情节的发展,过去是对现在的一种补充、说明与解释,在过去与现在不断地交织穿插中,把整个故事完整地呈现在读者面前;在过去与现在交织穿插的叙述中,向我们展示了主人公如何从一个满心委屈、悲怆、意志消沉的人,变成一个对自然、生活充满热爱的自信的人,使人物形象更加立体丰满;过去与现在形成鲜明的对比,更増添艺术描写的真实感,同时凸显小说主旨,引发读者的思考。
二、古代诗文阅读(35分)(一)(20分)10.(3分)D 11.(3分)B 12.(3分)C13.(8分)(1)南宋的军队没有料到金兵会突然到来,于是都纷纷败逃,相互踩踏,士兵伤亡不能计算得尽。
(2)韩侂胄对金国打算惩治战争主谋的要求十分生气,和谈就中断了,再次态度坚决地进行战争。
江苏省苏锡常镇四市2024届高三下学期教学情况调研(二)(二模)化学试题

S2O3
2
3
而溶解。氯化碘
ICl
性质与卤素单质相似,常用作分析化学试剂。下列说法正确的是
A.基态 F 原子的核外电子排布式为 2s2 2p5
B. KHF2 中既含有离子键,又含有共价键
C.
ClO
2
、
ClO
3
和
ClO
4
中
O
Cl
O
键角依次逐渐减小
D. S2O32 (结构如上图)中两个 S 原子均可作配位原子
(须用 NBS 和 AlBN,无机试剂和有机溶剂任用,
16.实验室用磷矿脱镁废液制备 MgHPO4 3H2O 的实验过程可表示为
(1)磷矿脱镁废液中主要含
H
2
PO
4
及少量
Mg
2
、
Ca
2
、
Fe3
、
Al3
和
SO
2 4
。
①向废液中加入 NaOH 溶液调节 pH 为 4.5 ,可达到 Ca2、Fe3 和 Al3 的最佳沉淀效果。其中 Ca2 转化为
试卷第 1页,共 9页
的混合物,可制得 HCl 。氯还可形成 HClO2 、HClO3 、HClO4 等多种含氧酸。ClO2 是 Al 级高效安全灭菌消毒剂;
Cl2 与 CH4 反应可制备有机溶剂 CCl4 。在照相底片的定影过程中,底片上未曝光的 AgBr 浸入 Na 2S2O3 溶液转变
成
Ag
C C.制取粗硅: SiO2 Si
高温
CO D.冶炼生铁: Fe2O3 Fe
高温
9.非天然氨基酸 Y 是一种重要的药物中间体,其部分合成路线如下:
下列说法不.正.确.的是 A. X 分子存在顺反异构体 B. Y 分子中含有 2 个手性碳原子 C. X Y 的反应类型为还原反应 D. Y 能与 NaOH 反应,不能与 HCl 反应
江苏省苏锡常镇四市2022~2023学年度高三教学情况调研(二)数学试卷 附答案

2022~2023学年度苏锡常镇四市高三教学情况调研(二)数 学 2023.05注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答字写在答题卡上,写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中只有一项是符合题目要求的。
1.若复数z 满足(1-i)z =i ,则在复平面内z 表示的点所在的象限为A .第一象限B .第二象限C .第三象限D .第四象限 2.已知A ,B 为非空数集,A ={0,1},(C R A )∩B ={-1},则符合条件的B 的个数为A .1B .2C .3D .43.已经连续抛掷一枚质地均匀的硬币2次,都出现了正面向上的结果,第3次随机地抛掷这枚硬币,则其正面向上的概率为A .18B .14C .12 D .14.已知向量a ,b 的夹角为60°,且|a |=|a -b |=1,则A .|2a -b |=1B .|a -2b |=1C .<a ,a -b >=60°D .<b ,a -b >=60° 5.埃及胡夫金字塔是世界古代建筑奇迹之一,它的形状可视为一个正四棱锥,其侧面与底面所成角的余弦值为5-12,则侧面三角形的顶角的正切值为A .2B .3C .5-12 D .5+126.已知(2-1x )23=a 0+a 1x +a 2x 2+…+a 22x 22+a 23x 23,则a 0222+a 1221+…+a 212+a 22=A .-1B .0C .1D .2 7.设a =13,b =ln 32,c =tan 12,则A .a <b <cB .b <a <cC .c <a <bD .a <c <b 8.已知等比数列{a n }的前n 项和为S n ,S n +1+1=4a n (n ∈N *),则使得不等式a m +a m +1+…+a m +k -a m +1S k <2023(k ∈N *)成立的正整数m 的最大值为A .9B .10C .11D .12二、选择题:本题共4小题,每小题5分,共20分。
2020-2021学年度苏锡常镇四市高三教学情况调查(二)

2020-2021学年度苏锡常镇四市高三教学情况调查(二)英语注意:本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
两部分答案都做在答题卡上。
总分为150分。
考试时间120分钟。
第一部分:听力(共两节,满分20分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。
听完每段对话后, 你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. 【此处可播放相关音频,请去附件查看】How soon will the package arrive with EM?A. In about two weeks.B. In less than two days.C. In more than three days.【答案】B【解析】【原文】W: If I send this package third class, how long will it take to arrive?M: About two weeks. If you use EMS, it is $35 more expensive, but it can get there within two days.2. 【此处可播放相关音频,请去附件查看】What will the man do next week?A. Give a report.B. Make a presentation.C. Take a rest.【答案】A【解析】【原文】M: I’m sorry I have a bad cough, but I’ll manage to make my presentation.W: Thank you for your spirit. But let’s not take a risk. You’ll need to rest your voice for next week’s report.3. 【此处可播放相关音频,请去附件查看】What does the women advise the man to do?A. Find the article at the reference desk.B. Read the article on the computer.C. Turn to the librarians for help.【答案】C【解析】【原文】M: I don’t think I’m ever going to find the article that my professor told me about.W: Go to the reference desk. The librarians there can tell you how to track it down with the help of the computer.4. 【此处可播放相关音频,请去附件查看】What will the woman probably do?A. Cancel her membership.B. Rush to catch a busC. Call the man back later.【答案】C【解析】【原文】M: Jennifer, would you be interested in serving on the membership committee this year? W: Uh, I’m on a bus and can’t catch you very clearly. Can I get back to you on that?5. 【此处可播放相关音频,请去附件查看】What do we learn from the conversation?A. The woman didn't like classical music.B. The man didn’t think highly of the conductor.C. The conductor didn't like the choice of the music.【答案】B【解析】【原文】W: How did you like the concert? I found it really moving. The conductor almost burst into tears in the end.M: I love classical music, but the conductor seemed a bit inexperienced.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 11 页苏锡常镇四市高三教学情况调研(二)化 学注意事项:1.本卷满分120分,考试时间 100分钟。
2.请将答案填写到答题卡上,凡填写在试卷上一律无效;交卷只需交答题卡 可能用到的相对原子质量: H-1 C-12 N-14 O-16 Ca-40第I 卷 选择题(共40分)单项选择题(本题包括10小题,每小题2分,共计20分。
每小题只有一个....选项符合题意)。
1.化学与材料、生活和环境密切相关。
下列有关说法中错误的是 A .新型材料聚酯纤维、光导纤维都属于有机高分子B .医药中常用酒精来消毒,是因为酒精能够使细菌蛋白发生变性C .大力实施矿物燃料脱硫脱硝技术以减少硫、氮氧化物排放D .煤炭经气化、液化和干馏等过程,可获得清洁能源和重要的化工原料 2.下列表述正确的是A .中子数为10的氧原子:1810O B .Na 2S 的电子式:C .聚氯乙烯的结构简式:CH 2CHClD .Mg 5(Si 4O 10)2(OH)2·4H 2O 的氧化物形式:5MgO ·8SiO 2·5H 2O 3.常温下,下列各组离子在指定溶液中一定能大量共存的是 A .1.0 mol ·L -1 KNO 3溶液:H +、Fe 2+、SCN -、SO 42-B .c (H +)/ c (OH —)=10-10的溶液:K +、Ba 2+、NO 3-、Cl -C .pH =0的溶液:Al 3+、Ag(NH 3)2+、Cl -、SO 42-D .c (ClO -)=1.0 mol ·L-Na +、SO 32-、S 2-、SO 42-4.实验室可用NaNO 2+NH 42↑+2H 2O 制备N 2,下列说法正确的是 A .NaNO 2发生氧化反应 B .NH 4Cl 中的氮元素被还原 C .N 2既是氧化产物,又是还原产物D .每生成1mol N 2转移电子的物质的量为6mol 5.下列有关物质的性质与应用不相对应的是 A .氢氟酸具有弱酸性,可用于雕刻玻璃 B .MgO 、Al 2O 3熔点高,可用于制作耐火材料第 2 页 共 11 页Cl 2粗溴NaBrNaBrO 3热空气提取NaClH 2SO 4(aq)Br 2FeSO 4(aq)NaOH(aq) Fe(OH)2空气中灼烧Fe 2O 3煅烧H 2O 煅烧电解 O 2 Al 2O 3 NaOH(aq) NaAlO 2(aq) Al(OH)3CO 2 Na 2CO 3(aq) C .ClO 2具有强氧化性,可用于自来水的杀菌消毒D .油脂在碱性条件下易水解,可用于制作肥皂6A .用图1所示装置可制取氨气B .用图2所示装置可分离CH 3CH 2OH 和CH 3COOC 2H 5混合液 C .用图3所示装置可制取乙烯并验证其易被氧化D .用图4所示装置可说明浓H 2SO 4具有脱水性、强氧化性,SO 2具有漂白性、还原性7.下列物质转化在给定条件下能实现的是①FeS 2 SO 3 H 2SO 4② ③NaCl(aq ) Na Na 2O 2④Fe⑤海水A .①③⑤B .②③④C .②④⑤D .①④⑤ 8.设N A 为阿伏加德罗常数的值。
下列说法一定正确的是A .25℃,pH =13的NaOH 溶液中含有OH -为0.1 N AB .1 L 0.1 mol ·L -1 CuSO 4溶液中含有Cu 2+为0.1 N AC .2.24LN 2和NH 3混合气体中原子间含有的共用电子对数目为0.3N AD .2molSO 2和1molO 2在一定条件下充分反应后,所得混合气体的分子数大于2N A 9.下列表示对应化学反应的离子方程式正确的是A .漂白粉露置在空气中:ClO -+CO 2+H 2O =HClO +HCO 3-B .用过量氨水吸收二氧化硫:SO 2+NH 3·H 2O =HSO 3-+NH 4+C .用足量的氢氧化钠溶液吸收二氧化氮:3NO 2+2OH -=2NO 3-+NO +H 2O D .在强碱溶液中次氯酸钠与Fe(OH)3反应生成Na 2FeO 4:3ClO -+2Fe(OH)3+4OH -=2FeO 42-+3Cl -+5H 2O10.下列有关说法正确的是A .实验室制氢气,为了加快反应速率,可向稀H 2SO 4中滴加少量Cu(NO 3)2溶液蒸发母液稀H 2SO 4图1 图2 图3 图444第 3 页 共 11 页B .为处理锅炉水垢中的CaSO 4,可先用饱和Na 2CO 3溶液浸泡,再加入盐酸溶解C .N 2(g)+3H 2(g)2NH 3(g) ΔH <0,其他条件不变时升高温度,平衡时氢气转化率增大D .吸热反应“TiO 2(s)+2Cl 2(g)=TiCl 4(g)+O 2(g)”在一定条件下可自发进行,则该反应的ΔS <0不定项选择题(本题包括5小题,每小题4分,共计20分。
每小题有一个或两个选项符合题意。
若正确答案只包括一个选项,多选时,该题得0分;若正确答案包括两个选项,只选一个且正确得2分,选两个且都正确得4分,但只要选错一个,该小题就得0分。
) 11.阿司匹林是日常生活中应用广泛的医药之一。
它可由下列方法合成:下列说法正确的是A .邻羟基苯甲醛分子中所有的原子不可能在同一平面B .用酸性KMnO 4溶液直接氧化邻羟基苯甲醛可实现反应①C .反应②中加入适量的NaHCO 3可提高阿司匹林的产率D .与邻羟基苯甲酸互为同分异构体,苯环上一氯代物仅有2种且能发生银镜反应的酚类化合物共有3种12.短周期元素X 、Y 、Z 、W 在元素周期表中的相对位置如图5所示,其中W 原子的最外层电子数是最内层电子数的3倍。
下列判断正确的是A .原子半径:r W >r Z >r Y >r XB .含Y 元素的盐溶液有的显酸性,有的显碱性C .最简单气态氢化物的热稳定性:Z >WD .X 与氢元素组成的化合物XH 5与水反应可产生两种气体 13NaOH 图5 邻羟基苯甲醛 邻羟基苯甲酸 阿司匹林CHOOH COOHOO CH 3C 3O14.下列有关物质浓度关系的描述中,正确的是A.25℃时,NaB溶液的pH=8,c(Na+)-c(B-)=9.9×10-7mol·L-1B.25℃时,向0.1mol·L-1NH4HSO4溶液中滴加NaOH溶液至中性:c(Na+)>c(NH4+)>c(SO42—)>c(OH—)=c(H+)C.0.1mol·L-1的NaHCO3溶液中:c(OH-)+2c(CO32-)=c(H+)+c(H2CO3)D.同温下,pH相同时,溶液物质的量浓度:c(CH3COONa)>c(NaHCO3)>c(C6H5ONa)>c(Na2CO3)15.900℃时,向2.0L恒容密闭容器中充入0.40mol乙苯,发生反应:—C2H5(g) —CH=CH2(g)+H2(g) ΔH=a kJ·mol—1。
经一段时间后达到平衡。
反应过程中测定的部分数据见下表:A.反应在前20 min的平均速率为v(H2)=0.008mol·L-1·min-1B.保持其他条件不变,升高温度,平衡时,c(乙苯)=0.08mol·L-1,则a<0C.保持其他条件不变,向容器中充入不参与反应的水蒸气作为稀释剂,则乙苯的转化率为50.0%D.相同温度下,起始时向容器中充入0.10mol乙苯、0.10mol苯乙烯和0.30molH2,达到平衡前v正>v逆第Ⅱ卷非选择题(共80分)16.(12分)硫酸亚铁铵(NH4)2Fe(SO4)2·6H2O是一种浅绿色晶体,在水中的溶解度较小,不溶于乙醇。
某实验小组利用镀锌铁片来制备硫酸亚铁铵的过程如下:(1)加入盐酸是为了除去锌镀层,判断锌镀层已被除去的现象是▲。
(2)A物质可以是▲(选填序号)。
a.CuCl2b.CuO c.Cu(N O3)2d.CuSO4加入少量A物质的目的是▲。
(3)操作Ⅱ的名称为▲。
(4)采用晾干而不用加热烘干晶体的原因是▲。
第 4 页共11 页第 5 页 共 11 页(5)工业上常用K 2Cr 2O 7溶液测定硫酸亚铁铵的纯度,反应中Cr 2O 72—被还原成Cr 3+。
写出硫酸亚铁铵溶液与酸性K 2Cr 2O 7溶液反应的离子方程式 ▲ 。
17.(15分)喹硫平可用于精神疾病的治疗,它的合成路线如下:(1)写出C 13H 9NO 4S 中所有含氧官能团的名称 ▲ 。
(2)A 属于烃,且相对分子质量是54,写出A 的结构简式 ▲ 。
(3)反应①~⑤中属于取代反应的有 ▲ (选填序号)。
写出反应⑦的化学方程式 ▲ 。
(4)流程中设计反应⑤和⑦的目的是 ▲ 。
(5)物质C 的同分异构体有多种,其中既含有羟基,又含有醛基的同分异构体有 ▲ 种。
(6)已知:苯环上的羧基为间位定位基,如。
写出以 为原料 制备 的合成路线流程图(无机试剂任选,可利用本题中的相关信 息)。
合成路线流程图示例如下:。
▲18.(12分)过氧化钙晶体[CaO 2·8H 2O ]较稳定,呈白色,微溶于水,能溶于酸性溶液。
广泛应用于环境杀菌、消毒等领域。
★过氧化钙晶体的制备工业上生产CaO 2·8H 2O 的主要流程如下:(1)用上述方法制取CaO 2·8H 2O 的化学方程式是 ▲ 。
(2)沉淀时常用冰水控制温度在10℃以下和通入过量的NH 3,其可能原因分别是① ▲ ;② ▲ 。
★过氧化钙晶体含量的测定COOHBrCH 3NHC OnHBrNaOH(aq)△ CH 2=CH 2 CH 3CH2Br CH 3CH 2OH 3产品 ……准确称取0.3000g产品于锥形瓶中,加入30 mL蒸馏水和10 mL 2.000 mol·L-1 H2SO4,用0.0200 mol·L—1KMnO4标准溶液滴定至终点。
重复上述操作两次。
H2O2和KMnO4反应的离子方程式为2MnO4-+5 H2O2+6H+ =2Mn2++5O2↑+8H2O(3)滴定终点观察到的现象为▲。
(4)根据表1数据,计算产品中CaO ·8H/mL表1. KMnO4标准溶液滴定数据▲19.(15分)氧化铜矿石含有CuO和Cu2(OH) 2CO3,还含有Fe2O3、FeO和SiO2等。
铜、铁是畜禽所必需的微量元素。
某饲料厂联合生产硫酸铜和硫酸亚铁工艺流程如下:(1)氧化铜矿石粉碎的目的是▲。
(2)写出“酸浸”中Cu2(OH) 2CO3发生反应的离子方程式▲。
(3)“中和/过滤”中加入CaCO3的目的是▲。
(4)上述工艺流程中多处涉及“过滤”,实验室中过滤操作需要使用的玻璃仪器有▲ 。
