概率论第二章随机变量及其分布
合集下载
概率论课件第二章
第二章 随机变量及其分布 §2.1 随机变量
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S，若 X : S R为单值实范数，则称X为随机变量 （random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. （=1） 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
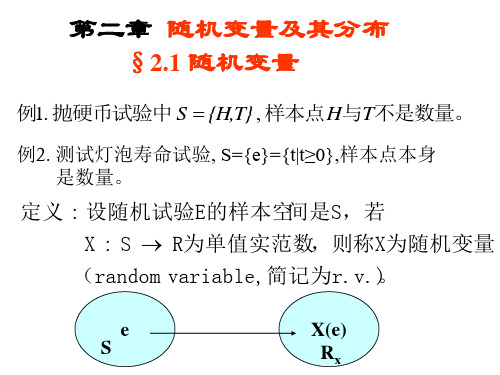
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S，若 X : S R为单值实范数，则称X为随机变量 （random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. （=1） 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
概率论与数理统计第二章 随机变量及其分布
15
例4: 甲、乙两名棋手约定进行10盘比赛，以赢的盘数 较多者为胜. 假设每盘棋甲赢的概率都为0.6，乙赢的概 率为0.4，且各盘比赛相互独立，问甲、乙获胜的概率 各为多少？ 解 每一盘棋可看作0-1试验. 设X为10盘棋赛中甲赢的 盘数，则 X ～ b(10, 0.6) . 按约定，甲只要赢6盘或6盘 以上即可获胜. 所以
定义：若随机变量X所有可能的取值为x1，x2，…，xi，…，且 X 取这些值的概率为 P(X=xi)= pi , i=1, 2, ... (*)
则称(*)式为离散型随机变量X 的分布律。 分布律的基本性质： (1) 表格形式表示: pi 0, i=1，2，... (2)
i
pi 1
X pk
x1 p1
这里n=500值较大，直接计算比较麻烦. 利用泊松定理作近似计算: n =500, np = 500/365=1.3699>0 ，用 =1.3699 的泊松分布作近似 计算：
(1.3669) 5 1.3669 P{ X 5} e 0.01 5!
23
例2: 某人进行射击，其命中率为0.02，独立射击400次，试求击 中的次数大于等于2的概率。 解 将每次射击看成是一次贝努里试验，X表示在400次射击中 击的次数，则X~B(400, 0.02)其分布律为
k 0,1
14
(2) 二项分布 设在一次伯努利试验中有两个可能的结果，且有 P(A)=p 。则在 n 重伯努利试验中事件 A发生的次数 X是一个 离散型随机变量，其分布为
P ( X k ) C nk p k q n k
k =0, 1, 2 ,, n
称X 服从参数为n，p的二项分布，记为 X~b(n, p) 对于n次重复一个0-1试验. 随机变量X表示: n次试验中, A发生的次数. 如： 掷一枚硬币100次, 正面出现的次数X服从二项分布. b(100, 1/2) 事件 X～
第二章随机变量及其概率分布(概率论)
当 x ≥ 1 时,F ( x) = P( X ≤ x) =P( X = 0) + P( X = 1) =1 ⎧0 x < 0
所以 F ( x) = ⎪⎨0.3 0 ≤ x < 1. ⎪⎩1 1 ≤ x
⎧0 x < 0 分布函数为 F ( x) = ⎪⎨0.3 0 ≤ x < 1
⎪⎩1 1 ≤ x
分布函数图形如下
F(x) 1 0.3
x 01
3
例 设X的概率分布律如下,求X的分布函数. X012 P 0.4 0.35 0.25
解
⎧0
x<0
F
(
x)
=
⎪⎪ ⎨
⎪
0.4 0.75
0≤ x<1 1≤ x<2
⎪⎩ 1
x≥2
由此可见
(1)离散型随机变量的分布函数是分段函数,分 段区间是由X的取值点划分成的左闭右开区间; (2)函数值从0到1逐段递增,图形上表现为阶梯 形跳跃递增; (3)函数值跳跃高度是X取值区间中新增加点的 对应概率值.
z 泊松在数学方面贡献很多。最突出的是1837 年在提出泊松分布。
z 除泊松分布外，还有许多数学名词是以他的 名字命名的，如泊松积分、泊松求和公式、 泊松方程、泊松定理。
当一个随机事件,以固定的平均瞬时速率 λ随机独立地出现时,那么这个事件在单 位时间(面积或体积)内出现的次数或个数 就近似地服从泊松分布。
解: 依题意, X可取值 0, 1, 2, 3.
设 Ai ={第i个路口遇红灯}, i=1,2,3
路口3
路口2
P(X=0)= P(A1)=1/2,
路口1
X=该汽车首次停下时通过的路口的个数. 设 Ai={第i个路口遇红灯}, i=1,2,3
概率论第二章随机变量及其分布小结
概率论第二章随机变量及其分布小结随机变量及其分布小结随机变量X=X(e)是定义在样本空间S={e}上的实值单值函数。
也就是说，它是随机试验结果的函数。
它的取值随试验的结果而定，是不能预先确定的，因此它的取值有一定的概率。
随机变量的引入，使概率论的研究由个别随机事件扩大为随机变量所表征的随即现象的研究。
一个随机变量，如果它所有可能取值是有限个或可列无穷多个，则称其为离散型随机变量，不是这种情况的则称为非离散型。
不论是离散型还是非离散型的随机变量X,都可以借助分布函数F ( x) P{X x}, x来描述。
若已知随机变量X的分布函数，就能知道X落在任意区间( x1 , x2 ]上的概率：P{x1 X x2 } F ( x1 ) F ( x2 ).这样，分布函数就完整的描述了随机变量取值的统计规律性。
对于离散型随机变量，我们需要掌握的是它可能取哪些值，以及它以怎样的概率取这些值，这就是离散型随机变量取值的统计规律性。
因而，对于离散型随机变量，用分布律P{X xk } pk ,k 1,2,或写成Xpkx1 x2 xk p1 p 2 p k来描述它的取值的统计规律性更为直观和简洁。
分布律与分布函数有以下关系：F ( x) P{X x} xk xP{X x }k它们是一一对应的。
分布律具有以下性质：1 pk 0;2pk 1k1.分布函数的基本性质：1 2F ( x)单调不减。
0 F ( x) 1, 且F ( ) lim F ( x) 0,x xF ( ) lim F ( x) 1.3F ( x) F ( x 0),即F ( x)是右连续的。
设随机变量X的分布函数为F(x),如果存在非负函数f(x),使得对于任意x,有F ( x)f ( x)dx,x则称X是连续型随机变量，其中f ( x) 0称为X的概率密度。
连续型随机变量的分布函数是连续的，连续型随机变量取任一指定实数值a的概率为0,这两点性质是离散型随+机变量不具备的。
《概率论与数理统计》第二章 随机变量及其分布
两点分布或（0-1）分布
对于一个随机试验，如果它的样本空间只包含两个
元素，即Ω={ω1,ω2}，我们总能在Ω上定义一个服从 (0-1)分布的随机变量
来描述这个随机X试验X的(结)果 。10,,当当
1, 2.
例如，对新生婴儿的性别进行登记，检查产品的质量 是否合格，某车间的电力消耗是否超过负荷以及前面多 次讨论过的“抛硬币”试验等都可以用(0-1)分布的随 机变量来描述。(0-1)分布是经常遇到的一种分布。
设随机变量X只可能取0与1两个值，它的分布律是 P{X＝k}＝pk(1-p)1-k，k＝0，1 (0<p<1)， 则称X服从(0-1)分布或两点分布。
(0-1)分布的分布律也可写成
X
0
1
pk
1-p
p
二项分布与伯努利试验
考虑n重伯努里试验中，事件A恰出现k次的概率。 以X表示n重伯努利试验中事件A发生的次数，X是一个 随机变量，我们来求它的分布律。X所有可能取的值为o， 1，2，…，n．由于各次试验是相互独立的，故在n次试 验中，事件A发生k次的概率为
X
x1
x2
…
xn
…
pk
p1
p2
…
pn
…
在离散型随机变量的概率分布中，事件 “X=x1”， “X=x2”....“X=xk”,...构成一个完备事件 组。因此，上述概率分布具有以下两个性质：
(1) pk 0, k 1, 2,L
(2) pk 1
k
满足上两式的任意一组数 pk , k 1, 2,L 都可以成为 离散型随机变量的概率分布。对于集合xk , k 1, 2,L
P{ X
k}
20 k
(0.2)k
概率论与数理统计第二章随机变量及其分布
设随机变量X服从参数为 分布,即 例2.3.1.设随机变量 服从参数为 的0-1分布 即: 设随机变量 服从参数为0.3的 分布 X P 0 1 ,求X的分布函数 求 的分布函数 的分布函数.
i
0.3 0.7
解:(1) 当x<0时,F(x)=P{X≤x}= 时
∑P{X = x }=0 (2)当0≤x<1时,F(x)=P{X≤x}= ∑P{X = x } =P{x=0}=0.3 当 时 (3)当1≤x时,F(x)=P{X≤x}= ∑P{X = x } 当 时
xi ≤x xi ≤x i xi ≤x i
=P{X=0}+P{X=1}=1 F(x) 分布函数图形如下 1 0.3 0 1 x
3.离散型随机变量 的分布函数的性质 离散型随机变量X的分布函数的性质 离散型随机变量 (1)分布函数是分段函数 分段区间是由 的取值点划分成的 分布函数是分段函数,分段区间是由 分布函数是分段函数 分段区间是由X的取值点划分成的 左闭右开区间; 左闭右开区间 (2)函数值从 到1逐段递增 图形上表现为阶梯形跳跃递增 函数值从0到 逐段递增 图形上表现为阶梯形跳跃递增; 逐段递增,图形上表现为阶梯形跳跃递增 函数值从 (3)函数值跳跃高度是 取值区间中新增加点的对应概率值 函数值跳跃高度是x取值区间中新增加点的对应概率值 函数值跳跃高度是 取值区间中新增加点的对应概率值; F(x) (4)分布函数是右连续的 分布函数是右连续的; 分布函数是右连续的 1 (5) P{X=xi}=F(xi)-F(xi-0) 0.3
记为 X~B(n,p)
m P X = m) = Cn pm(1− p)n−m (
m=0,1,2,...,n
随机变量X所服从的分布称为二项分布,n为实验次数 注:(1)随机变量 所服从的分布称为二项分布 为实验次数 随机变量 所服从的分布称为二项分布 为实验次数; (2)该实验模型称为 次独立重复实验模型或 重Bernoulli实验模型 该实验模型称为n次独立重复实验模型或 实验模型; 该实验模型称为 次独立重复实验模型或n重 实验模型 (3)若A和Ac是n重Bernoulli实验的两个对立结果 成功”可以指二 若 和 实验的两个对立结果,“成功 重 实验的两个对立结果 成功” 者中任意一个,p是 成功”的概率 者中任意一个 是“成功”的概率. 例如:一批产品的合格率为 有放回地抽取 有放回地抽取4次 每次一件 每次一件, 例如 一批产品的合格率为0.8,有放回地抽取 次,每次一件 取得合格 一批产品的合格率为 品件数X,以及取得不合格品件数 服从分布为二项分布 品件数 以及取得不合格品件数Y服从分布为二项分布 以及取得不合格品件数 服从分布为二项分布, X对应的实验次数为 对应的实验次数为n=4, “成功”即取得合格品的概率为 成功” 对应的实验次数为 成功 即取得合格品的概率为p=0.8,
概率论第二章
2.分布函数单调不减 分布函数单调不减 3.分布函数为右连续函数 分布函数为右连续函数
分布函数与密度函数的关系
x
F ( x) = ∫
−∞
f (t )dt
密度函数性质
1. f ( x) ≥ 0 2. f ( x)dx = 1 ∫
−∞ +∞
3. P ( x ∈ (a, b)) = ∫ f ( x)dx
,−∞ < x < +∞
• 其中 µ , σ (σ > 0 ) 为常数 则称 服从参数为 为常数,则称 则称X服从参数为 2 的正态 µ ,σ 分布(或高斯分布 记为X~ N ( µ , σ 2 ) 或高斯分布),记为 分布 或高斯分布 记为 • 正态分布密度函数的图形关于直线 x = 对称,即对 对称 即对 任意常数 a, f ( µ − a ) = f ( µ + a ) • x = µ 时, f (x ) 取到最大值 取到最大值.
(1) P (Y ≥ 2 ) = 1 − 0 .9876 5 − 5 × 0 .9876 4 × 0 .0124 = 0 .0015
(2) P (Y ≥ 2 Y ≥ 1) = P ((Y ≥ 2) ∩ (Y ≥ 1)) P(Y ≥ 2) 0.0015 = = = 0.0248 5 P (Y ≥ 1) P(Y ≥ 1) 1 − 0.9876
， = 0， ， k 1 L5 ，
例2 射击进行到目标被击中或4发子 弹被用完为止.如果每次射击的命中 率都是0.4,求总射击次数X的分布律.
解 X=k所对应的事件为前k-1次射击均 未击中,第k次射击击中,故X的分布律 为:
X
P
1
2
2
3
3
4
4
分布函数与密度函数的关系
x
F ( x) = ∫
−∞
f (t )dt
密度函数性质
1. f ( x) ≥ 0 2. f ( x)dx = 1 ∫
−∞ +∞
3. P ( x ∈ (a, b)) = ∫ f ( x)dx
,−∞ < x < +∞
• 其中 µ , σ (σ > 0 ) 为常数 则称 服从参数为 为常数,则称 则称X服从参数为 2 的正态 µ ,σ 分布(或高斯分布 记为X~ N ( µ , σ 2 ) 或高斯分布),记为 分布 或高斯分布 记为 • 正态分布密度函数的图形关于直线 x = 对称,即对 对称 即对 任意常数 a, f ( µ − a ) = f ( µ + a ) • x = µ 时, f (x ) 取到最大值 取到最大值.
(1) P (Y ≥ 2 ) = 1 − 0 .9876 5 − 5 × 0 .9876 4 × 0 .0124 = 0 .0015
(2) P (Y ≥ 2 Y ≥ 1) = P ((Y ≥ 2) ∩ (Y ≥ 1)) P(Y ≥ 2) 0.0015 = = = 0.0248 5 P (Y ≥ 1) P(Y ≥ 1) 1 − 0.9876
， = 0， ， k 1 L5 ，
例2 射击进行到目标被击中或4发子 弹被用完为止.如果每次射击的命中 率都是0.4,求总射击次数X的分布律.
解 X=k所对应的事件为前k-1次射击均 未击中,第k次射击击中,故X的分布律 为:
X
P
1
2
2
3
3
4
4
概率论与数理统计第2章随机变量及其分布
1 4
)0
(
3 4
)10
C110
(
1 4
)(
3 4
)9
0.756.
(2)因为
P{X
6}
C160
(
1)6 4
(
3 4
)4
0.016
,
即单靠猜测答对 6 道题的可能性是 0.016,概率很小,所
以由实际推断原理可推测,此学生是有答题能力的.
二项分布 b(n, p) 和 (0 1) 分布 b(1, p ) 还有一层密切关
P{X 4} P(A1 A2 ) P(A1)P(A2 ) 0.48 ,
P{X 6} P(A1A2 ) P(A1)P(A2 ) 0.08 , P{X 10} P(A1A2 ) P(A1)P(A2 ) 0.32 , 即 X 的分布律为
X 0 4 6 10
P 0.12 0.48 0.08 0.32
点 e, X 都有一个数与之对应. X 是定义在样本空间 S 上的
一个实值单值函数,它的定义域是样本空间 S ,值域是实数
集合 {0,1,2},使用函数记号将 X写成
0, e TT , X＝X (e) 1, e HT 或TH ,
2, e HH.
▪
例2.2 测试灯泡的寿命.
▪
样本空间是 S {t | t 0}.每一个灯泡的实际使用寿命可
(2)若一人答对 6 道题,则推测他是猜对的还是有答 题能力.
解 设 X 表示该学生靠猜测答对的题数,则
X
~
b(10,
1) 4
.
(1) X 的分布律为
P{X
k}
C1k0
(
1)k 4
(
3 4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第9页
分布列的基本性质
(1) pi 0， (非负性)
(2) pi 1. (正则性)
i
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
注 意 点 (1)
第10页
求离散随机变量的分布列应注意： (1) 确定随机变量的所有可能取值; (2) 计算每个取值点的概率.
0,
F
(x)
0.4, 0.8,
1,
x0 0 x1 1 x2 2 x
解：
X0 1 2 P 0.4 0.4 0.2
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第14页
2.1.4 连续随机变量的密度函数
➢ 连续随机变量X的可能取值充满某个区间 (a, b).
➢ 因为对连续随机变量X，有P(X=x)=0， 所以无法仿离散随机变量用 P(X=x) 来描述连续 随机变量X的分布.
第3页
2.1.1 随机变量的定义
定义2.1.1 设 ={}为某随机现象的样本空间， 称定义在上的实值函数X=X()为随机变量.
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第4页
注 意 点 (1)
(1) 随机变量X()是样本点的函数， 其定义域为 ，其值域为R=(，) 若 X 表示掷一颗骰子出现的点数， 则 {X=1.5} 是不可能事件.
第二章 随机变量及其分布
第1页
第二章 随机变量及其分布
§2.1 随机变量及其分布 §2.2 随机变量的数学期望 §2.3 随机变量的方差与标准差 §2.4 常用离散分布 §2.5 常用连续分布 §2.6 随机变量函数的分布 §2.7 分布的其他特征数
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
(4) 同一样本空间可以定义不同的随机变量.
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第6页
两类随机变量
➢ 若随机变量 X 可能取值的个数为有限个或 可列个，则称 X 为离散随机变量.
➢ 若随机变量 X 的可能取值充满某个区间 [a, b]，则称 X 为连续随机变量.
➢ 前例中的 X, Y, Z 为离散随机变量； 而 T 为连续随机变量.
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第8页
2.1.3 离散随机变量的分布列
➢ 设离散随机变量 X 的可能取值为： x1，x2，……，xn，……
称 pi=P(X=xi)， i =1, 2, …… 为 X 的分布列.
➢ 分布列也可用表格形式表示：
X x1 P p1
x2 …… xn …… p2 …… pn ……
第二章 随机变量及其分布
例2.1.1 已知 X 的分布列如下：
第12页
X0 1 2 P 1/3 1/6 1/2
求 X 的分布函数.
解：
0,
F(x)
1/ 1/
3, 2,
1,
x0 0 x1 1 x2 2 x
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第13页
例2.1.2
已知 X 的分布函数如下,求 X 的分布列.
(2) 若 X 为随机变量，则 {X = k} 、 {a < X b} 、……
均为随机事件.
即 {a < X b} ={；a < X() b }
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第5页
注 意 点 (2)
(3) 注意以下一些表达式：
{X = k}= {X k}{X < k}； {a < X b} = {X b}{X a}； { X > b} = {X b}.
➢ 注意离散随机变量与连续随机变量的差别.
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第15页
定义2.1.4
设随机变量X 的分布函数为F(x),
若存在非负可积函数 p(x) ，满足：
F
(
x)
x
p(t
)dt
则称 X 为连续随机变量，
称 p(x)为概率密度函数，简称密度函数.
2020年7月17日星期五
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
注 意 点 (2)
第11页
对离散随机变量的分布函数应注意： (1) F(x)是递增的阶梯函数; (2) 其间断点均为右连续的; (3) 其间断点即为X的可能取值点; (4) 其间断点的跳跃高度是对应的概率值.
2020年7月17日星期五
华东师范大学
第2页
§2.1 随机变量及其分布
(1) 掷一颗骰子， 出现的点数 X 1，2，……，6.
(2) n个产品中的不合格品个数 Y 0，1，2，……，n
(3) 某商场一天内来的顾客数 Z 0，1，2，……
(4) 某种型号电视机的寿命 T : [0, +)
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
第7页
2.1.2 随机变量的分布函数
定义2.1.2 设X为一个随机变量，对任意实数 x，
称 F(x)=P( X x) 为 X 的分布函数.
基本性质：
(1) F(x) 单调不降； (2) 有界：0F(x)1，F()=0，F(+)=1； (3) 右连续.
华东师范大学
第二章 随机变量及其分布
第16页
密度函数的基本性质
(1) p(x) 0; (非负性)
(2)
p(
x)dx
1.
(正则性)
满足(1) (2)的函数都可以看成某个 连续随机变量的概率密度函数.
2020年7月17日星期五
华ห้องสมุดไป่ตู้师范大学
第二章 随机变量及其分布
注意点(1)
第17页
(1) P(a X b) b p(x)dx. a
(2) F(x) 是 (∞, +∞) 上的连续函数;
(3) P(X=x) = F(x)F(x0) = 0;
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
注意点(2)
第18页
(4) P{a<X≤b} = P{a<X<b} = P{a≤X<b} = P{a≤X≤b} = F(b)F(a).
(5) 当F(x) 在x点可导时, p(x) = F(x)
当F(x) 在x点不可导时, 可令p(x) =0.
2020年7月17日星期五
华东师范大学
第二章 随机变量及其分布
离散型
第19页
连续型
1. 分布列: pn = P(X=xn) ( 唯一 )
1. 密度函数 X ~ p(x) ( 不唯一 )